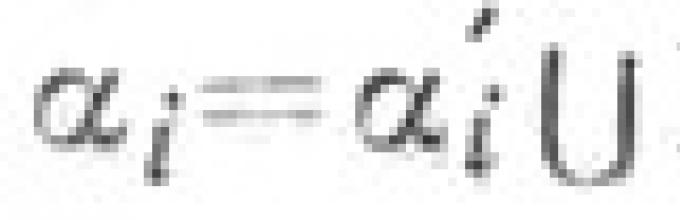Bir nuqtadan chiqadigan ikki xil nurlardan iborat. Nurlar deb ataladi. W. va ularning umumiy boshlanishining yon tomonlari - Vernex w Vetrex V.),[ Quyosh) -
Burchakning yon tomoni Ichida - Uning vertexi - V harfi - V. raqamlari tomonidan aniqlangan samolyot samolyotni ikki raqamga ajratadi ![]() i \u003d\u003d l, 2, ham chaqirilgan. U. yoki chaqirilgan tekis burchak. Kvartiraning ichki maydoni.
i \u003d\u003d l, 2, ham chaqirilgan. U. yoki chaqirilgan tekis burchak. Kvartiraning ichki maydoni.
Ikki burchak chaqirdi. Agar ular birlashtirilishi mumkin bo'lsa, teng (yoki mos keladi), agar ular o'zlarining partiyalari va vertikallari to'g'ri bo'lsa. Ushbu yo'nalishda samolyotda har qanday nurdan, Undan qoldirilishi mumkin, bu W. ni ushbu W. taqqoslash bilan teng ravishda amalga oshiriladi. Agar W. umumiy boshlanishning bir juftligi bilan bir juft nur sifatida qaralasa, ba'zi Ikkisini aniqlashtirish uchun V vertexining bir tekisligida bir nechta samolyotni bir tekislash uchun bir juftning bir tekisligida birlashtirilishi kerak (1-rasm). ). Agar W. ning ikkinchi tomoni W. boshqasida joylashgan bo'lsa, ular birinchi W. ikkinchisidan kamroq deb aytishadi. Uni taqqoslashning ikkinchi usuli har bir Nomni taqqoslashiga asoslanadi. Teng darajaga teng bo'ladi. - kattaroq y. - Ko'proq, kichikroq.

Ikki U. Naz. Agar ular umumiy vertex va bir tomoni bo'lsa, boshqa tomoni to'g'ri chiziq shaklida bo'lsa (2-rasmga qarang). Umuman olganda, V. Umumiy vertex va bitta umumiy tomoni bo'lgan. Ragisicial. W. Naz. Vertikal, agar uning yon tomonlari boshqa tomonlarning yon tomonlarining tepasida davom etsa, bir-biriga tengdir. W., yuqoriga qarab, xuddi to'g'ri shaklda, deyiladi. Kengaytirilgan. Yarim kengaytirilgan U. Naz. To'g'ridan-to'g'ri W. To'g'ridan-to'g'ri U. boshqa usul bilan teng bo'lishi mumkin: W., unga qo'shni, deyiladi. To'g'riga. Ichki kvartira U., Depvededdan oshmasligi, samolyotdagi konveks maydoni. W. to'g'ridan-to'g'ri UNC ning 90-ulushi uchun V. ni o'lchash birligi uchun. Daraja.

Foydalanilgan va hokazo U. USning rad etilishining sonining soniyal qiymati tomonlar tomonidan o'yilgan ARCning uzunligiga teng. Bitta radiolik V., Tegishli ARCga tegishli, bu uning radiusi bilan teng. Jo'min 'W. Radianlarga teng.
Ikkita tekis yolg'onni bir xil tekislikda yotqizishda uchinchi to'g'ri chiziq U. tomonidan shakllanadi (3-rasmga qarang): 1 va 5, 2 va 6, 4 va 7 va 7-chi. mos ravishda; 2 va 5, 3 va 8 - ichki bir tomonlama; 1 va 6, 4 va 7 - tashqi bir tomonlama; 3 va 5, 2 va 8 - Ichki ko'tarilishlar; 1 va 7, 4 va 6 - tashqi oyatlar yolg'on gapiradi.

Amalda. Vazifalar V. deb hisoblash tavsiya etiladi. V. ni qanday qilib o'lchashni o'z ichiga oladi. W. navbat yo'nalishi yo'nalishi bo'yicha ushbu holatda ham ijobiy va salbiy hisobga olinadi. Shunday qilib, u. Ushbu ma'noda har qanday qiymatga ega bo'lishi mumkin. V. Trigonetik nazariyada rayning boshlanishi qanday ko'rib chiqiladi. Vazifalar: argumentning har qanday qadriyatlari uchun siz trigonometrik qiymatlarni aniqlashingiz mumkin. funktsiyalar. Geometrichda V. tushunchasi. Tizim, K-Royning asoslari - bu nuqta va vektorning asosidir, radarlar W. raqamlari kabi - V. ma'lum bir metrikani tushunishadi. Scalar ko'paytirish operatsiyalaridan foydalangan holda ikki vektor bilan bog'liq kattalik. Aynan ai yalang'ochining har bir yo'nalishi ma'lum bir burchak - Vektor formulasi bilan bog'liq bo'lgan raqam
![]()
qayerda ( a, B.) -
Skarar vektor mahsulotlari.
V.-ning tekis rasm sifatida va boshqa raqamli geometrichda ba'zi raqamli o'lchamda qo'llaniladi. Vazifalar, der-ry u. Maxsus usulda aniqlanadi. Shunday qilib, "W" ostida, bu tangententlar tomonidan shakllantirilgan chorrahada ba'zi tangitantlar mavjud.
To'g'ri va tekislik orasidagi burchak U. tomonidan qabul qilinadi, uni tekis va tekislikdagi to'rtburchaklar proektsiyasi bilan shakllanadi; U 0 dan boshlab o'lchanadi
Matematik entsiklopediya. - m .: Sovet Entsiklopediyasi. I. M. Vinogradov. 1977-1985 yil.
Sinonimlar:Boshqa lug'atlarda "burchak" nima ekanligini tomosha qiling:
burchak - ANGLE / EK / ... Morfmlo-sehr lug'ati
Er. Yoriq, parchalanish, tizzasi, tirsagi, protrohish yoki zal (vydina) bir yuz haqida. Burchak chiziqli, har qanday ikkita yaqinlik belgilari va ular oralig'i; samolyot yoki samolyotlarning burchagi, ikkita samolyot yoki devor bilan tanishish; Burchakli qalin, tanasi, birida uchrashuv ... Dalyning izoh lug'ati
Burchak, burchak, burchak va (v) burchakda va (v) burchakda, m. 1. Bir nuqtadan (mat.) Bo'lgan ikki tekis chiziqlar orasidagi qism. Burchakning yuqori qismi. Burchakning yon tomoni. Daraja burchagini o'lchash. To'g'ri burchak. (90 °). O'tkir burchak. (90 ° dan kam). O'chirish burchagi ... ... Tushuntirish lug'ati Ushakov
Burchak (1) samolyot qanotida va qanot uchastkalarining akkordining yo'nalishi o'rtasidagi burchakka hujum qiling. Ushbu burchakdan ko'tarish kuchining qiymatiga bog'liq. Yuk ko'tarish kuchi maksimal darajadagi burchakka hujumning tanqidiy burchagi deyiladi. Da ... ... Yirik politexnika entsiklopediyasi
- (tekis) ikkita nur (burchak tomonlari) bir qismdan (burchakning cho'qqisidagi) hosil bo'lgan geometrik shakl. Ba'zi atrofdagi verteksda joylashgan har qanday burchak (markaziy burchak) AV, cheklangan ballar ... ... Katta entsiklopedik lug'at
Burchak boshlig'i, ayiq burchagi, yomon burchakda, barcha burchaklarda. ostida. Ed. N. Abravanova, m .: ruscha lug'atlar, 1999 yil. Vernex burchagi, burchak nuqtai nazar. Dereleng, Rulby, Ninerina, mo'rt, ... ... Sinonim lug'at
burchak - burchak, nasl. burchak; Yugurish. burchakda, burchakda va burchakdagi matematiklarning nutqida; Mn. Burchaklar, nasoslar. Burchaklar. Taklif etilayotgan va barqaror kombinatsiyalarda: burchakka burchakka (borish, o'rash va boshqalar), burchakka burchakka (ko'chirish, joy va boshqalar), burchakka ... ... Zamonaviy rus tillarida talaffuz va stress qiyinchiliklari lug'ati
Burchak, burchak, burchak haqida, (c) burchak, er. 1. (burchakda.). Geometriyada: bir nuqtadan chiqadigan ikkita nur (3 ta ma'noda) bo'lgan tekis rasm. Burchakning yuqori qismi. To'g'ri y. (90 °). O'tkir. (90 ° dan kam). Ahmoq y. (90 ° dan yuqori). Tashqi va ichki ... ... Ozegovning tushuntirish lug'ati
burchak - burchak, burchak, m. Xaritaning chetidan chetiga egilganda. ◘ Ace va Lece cho'qqisi, burchak bilan // o'ldirilgan. A.I. polzaxaev. Moskvada, 1832 yil. U tushlikdan keyin tarqalgan. Ponteps Crack Deklar, ... Karta terminologiyasi va XIX asr
Ta'rif
Bir nuqtadan tashqarida tuzilgan samolyotning barcha nuqtalaridan iborat geometrik shakli deyiladi tekis burchak.
Ta'rif
Ikki orasidagi burchakkesib o'tish To'g'riga To'g'ridan-to'g'ri ma'lumotlarni kesib o'tishda eng kichik tekislik burchagi kattaligi deyiladi. Agar ikkita to'g'ri parallel bo'lsa, ular orasidagi burchak nolga teng qabul qilinadi.
Ikki kesishqoqli burchakning kattaligi (samolyot radiolar burchaklari burchaklari) ni noldan $ \\ dfrac (\\ pi) gacha olishi mumkin.
Ta'rif
Ikki xoch mamlakat bo'ylab burchak Ikki kesishadigan ikki kesishadigan burchakka teng bo'lgan qiymat deb ataladi. To'g'ridan $ $ va $ B $ orasidagi burchak $ \\ burchak (A, B).
Ta'rif ta'rifining to'g'riligi quyidagi nazariy ko'rsatkichdan kelib chiqadi.
Parallel tomonlar bilan tekis burchaklarda teorema
Ikki konveks tekis burchaklarining qiymatlari mos ravishda parallel va bir xil yo'naltirilgan tomonlar tengdir.
Dalil
Agar burchaklar joylashtirilsa, ular ikkalasi $ \\ pi $ga teng. Agar ular vujudga kelmasa, biz $ \\ Ange ABB $ va $ \\ Ange teng segmentsning tegishli tomonlarini, $ O_1ON_1 $ va $ O_1M_1 $ ni keyinroq qoldiramiz.
To'rt tebratli $ O_1N_1NO $ bu parallelogram, chunki $ va $ O_1N_1 $ bir xil va parallel. Shunga o'xshab, to'rtta tetiklash uchun $ O_1M_MOO $ bu parallelogramm. Demak, $ NN_1 \u003d mm_1 $ va $ NN_1 \\ parallel mm_1 $ va $ NN_1 \\ $ villelly trankitriatda. To'rt barmoqning $ N_1M_1MN $ - parallelogrammalar, chunki uning qarama-qarshi tomonlari teng va parallel. Shunday qilib, $ NM $ va $ N_1M_1-sonli segmentlar teng. Uchburchaklar $ va $ O_1N_MM_1 $ uchburchaklar tengligini uchinchi belgisiga teng, demak, $ \\ burchakli NOME & N_1O_1M_1 $ teng.
Ikki nolga teng bo'lmagan vektorlarga samolyotda yoki uch o'lchovli makonda beriladi. O'zboshimchalik bilan kechiktirish O. o. Vektorlar va. Keyin quyidagi ta'rif to'g'ri.
Ta'rif.
Vektorlar orasidagi burchak va nurlar orasidagi burchakni chaqirdi Oa. va Ob..
Vektorlar orasidagi burchak va biz belgilang.
Vektorlar orasidagi burchak qiymatlarni olishi mumkin 0 ilgari yoki oldin nima bo'lgani haqida.
Vektorlar va vektorlararo yo'naltirilgan vektorlar va qoplangan bo'lsa.
Ta'rif.
Vektorlar va deyiladi perpendikulyarAgar ularning orasidagi burchak teng bo'lsa.
Agar kamida vektorlar va noldan bittasi bo'lsa, unda burchak aniqlanmagan.
Vektorlar, misollar va echimlar orasidagi burchakni topish.
Vektorlar orasidagi burchakning kosinasi, bu o'lchovni anglatadi, na ish joyida yoki vektorlarga qurilgan uchburchak uchun kosine teoremadan foydalanish mumkin.
Biz bu holatlarni tahlil qilamiz.
Ta'rif bo'yicha vektorlarning skalalar mahsuloti. Agar vektorlar va nolga teng bo'lmagan bo'lsa, siz oxirgi tenglikning ikkala qismini vektorlarning mahsulotiga, va biz olamiz nolilik vektorlar orasidagi kosin burchakni topish formulasi:. Vektorlarning uzunligi va ularning o'lchamlari ma'lum bo'lsa, ushbu formuladan foydalanish mumkin.
Misol.
Vektorlarning uzunligi teng bo'lsa, vektorlar orasidagi burchakning kosinasini hisoblang 3 va 6 Shunga ko'ra, ularning sklabar mahsuloti tengdir -9 .
Qaror.
Muammoning muammosi formulani qo'llash uchun zarur bo'lgan barcha qiymatlarga beriladi. Vektorlar orasidagi burchakning kosinasini hisoblang va:.
Endi biz vektorlar orasidagi burchakni topamiz :.
Javob:
Vektorlar koordinatalar tomonidan samolyotda yoki kosmosda koordinatalar tomonidan o'rnatiladigan vazifalar mavjud. Bunday hollarda, vektorlar orasidagi kosin burchagini topish uchun siz barcha bir xil formuladan foydalanishingiz mumkin, ammo muvofiqlashtiruvchi shaklda. Biz olamiz.
Vektor uzunligi ildiz uzunligi koordinatalar kvadratlari yig'indisidan, skalalar mahsuloti tegishli koordinatalarning mahsulotlari miqdoriga tengdir. Shunday qilib, vektorlar orasidagi kosin burchakni hisoblash formulasi Samolyot uch o'lchovli makonda vektorlar uchun ko'riladi.
Misol.
To'rtburchaklar koordinatalar tizimida ko'rsatilgan vektorlar orasidagi burchakni toping.
Qaror.
Siz darhol formulani qo'llashingiz mumkin:
Va formuladan foydalanish uchun vektorlar orasidagi kosin burchagini topish mumkin , vektorlarning uzunligini va skalar mahsulotni koordinatalar orqali oldindan hisoblang:
Javob:
Oldingi ish uch ball koordinatalari berilganida belgilangan ish uchun kamayadi (masalan Lekin, Ichida va Dan) To'rtburchaklar koordinata tizimida va siz biron bir burchakni topishingiz kerak (masalan,).
Darhaqiqat, burchak vektorlar orasidagi burchakka teng va. Ushbu vektorlarning koordinatalari hisoblanadi oxirgi ballar va vektorning boshi o'rtasidagi farq.
Misol.
Samolyotda karteziya koordinatalari tizimida uch ochko koordinatalari o'rnatiladi. Vektorlar orasidagi burchakning kosinasini toping va.
Qaror.
Biz vektorlarning koordinatalarini va belgilangan nuqtalarning koordinatalari tomonidan belgilaymiz:
Endi biz formuladan koordinatlarda samolyotdagi vektorlar orasidagi vektorlar orasidagi burchagini topish uchun foydalanamiz:
Javob:
Vektorlar orasidagi burchak va shuningdek hisoblab chiqilishi mumkin kosinoov teoremasi. Agar siz kechiktirsangiz O. o. vektorlar va keyin uchburchakdagi kosine teoremasi tomonidan OAK. Biz bu teng huquqni vektorlar orasidagi kosin burchagi topadigan narsani yozib olishimiz mumkin. Olingan formulanni qo'llash uchun bizga faqat vitorlarning uzunligi kerak va vektorlarning koordinatalari va koordinatalar bo'yicha osonlikcha joylashgan. Biroq, bu usul deyarli ishlatilmaydi, chunki vektorlar orasidagi burchakning kosinasi formulani topishda osonroq bo'ladi.
Ortogonal proektsiyani (proektsiya) hisoblash:
AXdagi Vektorli l doktorining vektor va o'qi orasidagi burchakning kosinisidagi vektor moduliga tengdir. I.E. PR kosh.
Dok: agar ph \u003d< , то пр l =+ = *cos φ.
Agar ph\u003e (ph≤), keyin p pr l \u003d \u003d * cos (-pox) \u003d cos (-CRIS10)
Agar ph \u003d, keyin PR l \u003d 0 \u003d kompyuterlar ph.
Fohisha: Axisdagi vektorni proektsiyasi ijobiy (salbiy), agar vektorning eksa o'tkir (ahmoq) burchak bilan shakllanadi va agar bu burchak to'g'ri bo'lsa.
Fohisha: Xuddi shu o'qda teng vektorlarning prognozlari bir-biriga tengdir.
Vektorlar yig'indisi (proepsiya) summasining orfogonal proektsiyasini hisoblash:
Xuddi shu o'qda bir nechta vektorlarning yig'indisini proektsion qilish ularning o'qi bo'yicha proektsiyalar yig'indisiga tengdir.
DOC: masalan, \u003d + +. Bizda PR l \u003d + \u003d + + + + - PR l (+ +) \u003d PR L + PR L + PR L (cris11)
Anjir. o'n bir
Vektor mahsulotini hisoblash:
Vektorning aqliyoti bilan comp, Ekisdagi proektsiyasini proektsiyalash ushbu raqamga ko'paytiriladi, i.e. PR l (l *) \u003d l * p pr l l.
Dock: X\u003e 0 Bizda PR l (l *) \u003d * cos ph \u003d l *
XL (lL) \u003d * cos (-ph) \u003d * (-coss) \u003d * cosh \u003d l * p l l.
Mulk adolatli va
Shunday qilib, vektorlar ustidan haddan tashqari operatsiyalar ushbu vektorlar prognozlarida tegishli chiziqli operatsiyalarga olib keladi.
Ushbu material bunday kesishma orasidagi burchak kabi burchakka bag'ishlangan. Birinchi nuqtada biz uning nimaligini tushuntirib, rasmlarga ko'rsatamiz. Keyin biz sinus qanday topishimiz mumkinligini, bu burchak va burchakning o'zi (samolyot va uch o'lchovli makon bilan alohida e'tiborni qaratamiz), biz kerakli formulalarni beramiz va ularda aynan ular qanday aniq formulalar beramiz amalda qo'llaniladi.
Ikkita to'g'ridan-to'g'ri yo'lning kesishishi natijasida qanday burchakning kesishishi natijasida hosil bo'lganligini tushunish uchun biz burchakni aniqlash, perpendikulyarlik va kesishish joylarini o'zgartirishimiz kerak.
1-ta'rif.
Agar bitta umumiy nuqta bo'lsa, biz ikkita tekis kesishishni chaqiramiz. Bu nuqta ikki tekis chiziqning kesishishi deb ataladi.
Har bir to'g'ridan-to'g'ri chiziqlar nurlardagi kesishish nuqtasi bilan ajralib turadi. Ikkala yo'nalishni bir vaqtning o'zida 4 burchakli shaklda, shundan ikkitasi vertikal va ikkitasi qo'shni. Agar biz ulardan birining o'lchovini bilsak, qolgan boshqa vaqtni aniqlashimiz mumkin.
Aytaylik, burchaklardan biri a ga teng ekanligini bilamiz. Bunday holda, unga nisbatan vertikal bo'lgan burchak shuningdek a ga teng bo'ladi. Qolgan burchaklarni topish uchun biz 180 ° - A o'rtasidagi farqni hisoblashimiz kerak. Agar a 90 darajaga teng bo'lsa, unda barcha burchaklar to'g'ri bo'ladi. Chiziqning o'ng burchagida kesish perpendikulyar deb ataladi (individual individuallik tushunchaga bag'ishlangan).
Chizmani ko'rib chiqing:
Keling, asosiy ta'rifni shakllantirishga murojaat qilaylik.
2-ta'rif.
Ikki kesishqoqli bir burchak - bu to'rtta burchakning kichikroq, bu ikkalasi bir tekis hosil bo'ladi.
Ta'rifdan, muhim xulosa qilish kerak: bu holatda burchak o'lchami har qanday haqiqiy raqam bilan ifodalanadi (0, 90). Agar to'g'ridan-to'g'ri perpendikulyar bo'lsa, unda burchak 90 ga teng bo'ladi daraja.

Ikki kesishqoq to'g'ridan-to'g'ri burchakni topish qobiliyati ko'plab amaliy vazifalarni hal qilish uchun foydalidir. Eritma usuli bir nechta variantlardan tanlanishi mumkin.
Boshlash uchun geometrik usullarni olishimiz mumkin. Agar biz qo'shimcha burchaklar haqida biron bir narsani bilsak, siz ularni teng yoki o'xshash shakllarning xususiyatlaridan foydalanish uchun kerakli burchak bilan bog'lab qo'yishingiz mumkin. Masalan, agar biz uchburchak tomonini bilsak va siz ushbu tomonlar joylashgan, keyinchalik echimlar uchun to'g'ridan-to'g'ri burchakni hisoblashingiz kerak. Agar bizda to'rtburchaklar uchburchak bo'lsa, biz hisob-kitoblar uchun biz ham Sinus bilimlaridan, kosin va tangent burchagidan ham foydalanamiz.
Koordinata usuli ushbu turdagi muammolarni hal qilish uchun juda qulaydir. Buni qanday qilib to'g'ri ishlatishni tushuntirib beramiz.
Bizda to'rtburchaklar (deganda) koordinariya tizimi o x y, unda ikkita tekis chiziqlar beriladi. Ularni a va b harflari bilan belgilang. Buning yordamida to'g'ridan-to'g'ri har qanday tenglamalar yordamida tasvirlanishi mumkin. Manba to'g'ri chiziqlar - kesish nuqtasi M. Kerakli burchakni qanday aniqlash mumkin (a) bu to'g'ri?
Belgilangan shartlarda burchakni topishning asosiy printsipidan boshlaylik.
Biz bilamizki, to'g'ri chiziq tushunchasi bilan qo'llanma va normal vektor sifatida bunday tushunchalar chambarchas bog'liq. Agar bizda bir oz tenglama bo'lsa, siz ushbu vektorlarning koordinatalarini olishingiz mumkin. Buni darhol ikki kesishadigan to'g'ri chiziqlar uchun buni amalga oshirishimiz mumkin.
Ikkita kesma chiziq bilan shakllangan burchakni quyidagilardan foydalanish mumkin:
- qo'llanma vektorlari orasidagi burchak;
- normal vektorlar orasidagi burchak;
- oddiy vektor o'rtasidagi burchak - bu to'g'ri va elektron qo'llanma vektor.
Endi har bir yo'lni alohida ko'rib chiqing.
1. Aytaylik, bizda qo'llanma vektorli a → \u003d (x, a) va qo'llanma vektori BICA BILAN BIBADI Endi ikki vektorni → va b → chorrahalaridan kechiktiring. Shundan so'ng, biz ular har biri o'zlarida joylashgan bo'lishlarini ko'ramiz. Keyin ularning o'zaro joylashuvi uchun to'rtta variant mavjud. Rasmga qarang:

Agar ikkita vektorning burchagi ahmoq emas bo'lsa, unda biz kesishadigan burchak bo'ladi, biz kesishadigan burchak bo'ladi Agar bu ahmoq bo'lsa, unda kerakli burchak → b burchakka tutashgan burchakka teng bo'ladi. Shunday qilib, a \u003d a → b → ^ Agar a → b ^ ≤ 90 ° - A \u003d B, b → ^\u003e 90 ° bo'lsa.
Teng burchaklarning kosinlari tengligi sababli, biz olib keladigan tenglikni qayta yozamiz: Cos a \u003d bas a → ^ ^ ^ ^ ^ ^ ^ 9 °; Cos a \u003d COS 180 ° - A → B → ^ \u003d - → b → ^ Agar → ^\u003e 90 ° bo'lsa.
Ikkinchi holatda formulalar ishlatilgan. Shunday qilib,
cos aos a → ^ ^, b → ^ b → ^ b ≥ 0) - Cos A → ^ b → ^ ^ ^< 0 ⇔ cos α = cos a → , b → ^
Biz oxirgi formulani so'zlar bilan yozamiz:
3-ta'rif.
Ikki kesishadigan bir burchakning kosinasi uning yo'nalishi vektorlari orasidagi burchakning kosinasi moduliga teng bo'ladi.
Ikki vektorning bir burchak formasini AC → \u003d (x, a y) va b → \u003d (b x, b y) orasidagi kosin formulasi paydo bo'lishi quyidagicha ko'rinadi:
cos A → ^ \u003d a → bda → · → · a ^ a x + b y € 2 + b y a
Undan biz Belgilangan ikkita yo'nalishda burchakning kosin formulasini olamiz:
cos a \u003d a x · b + b a x 2 + b 2 + b y y y y y y y y y y y y y y y y y y y y a x + b 2 + b 2 + b y
Keyin burchakning o'zi quyidagi formulada topilishi mumkin:
a \u003d a r c cos a x · b + a y + b y a x 2 + b 2 + b 2
Mana → \u003d (a x, a y) va b → \u003d (b x, b y) belgilangan yo'nalishda qo'llanma hisoblanadi.
Muammoni hal qilishga misol keltiraylik.
1-misol.
Samolyotdagi to'rtburchaklar koordinatalar tizimida A va B ning ikkita kesishadigan to'g'ri chiziqlari beriladi. Ularni parametrik tenglamalar bilan tasvirlash mumkin x \u003d 1 + 4 · l a \u003d 2 + l ∈ R va x 5 \u003d y 5 - 3. Bu to'g'ri burchakni hisoblang.
Qaror
Bizning ahvolimizda parametrlar mavjud, bu shuni anglatadiki, biz darhol uni vektorning koordinatalariga yozishimiz mumkin. Buning uchun biz parametrdagi koeffitsientlarning qadriyatlarini olishimiz kerak, i.e. To'g'ridan-to'g'ri x \u003d 1 + 4 · · li y \u003d 2 + l ∈ R qo'llanmada vektor vektorli a → (4, 1) bo'ladi.
Ikkinchi to'g'ridan-to'g'ri x 5 \u003d y to 6 - 3 yordamida to'g'ridan-to'g'ri tasvirlangan. Bu erda biz denominatorlarning koordinatalarini qabul qilishimiz mumkin. Shunday qilib, ushbu to'g'ridan-to'g'ri yo'naltirilgan Vektor vektori B → \u003d (5, - 3).
Keyinchalik burchakni topish uchun to'g'ridan-to'g'ri boring. Buning uchun biz shunchaki yuqorida ko'rsatilgan Forc A \u003d a r c cos x + a y + b y + b y y 2 + b 2 + b 2. Biz quyidagilarni olamiz:
a \u003d a r c cos 4 · 5 + 1 · (3) 4 2 + 1 2 · (- 3) 2 \u003d a r c co 17 17 17 17 · 2 \u003d 45 °
Javob: Ma'lumotlar 45 daraja burchakni yo'naltiradi.
Oddiy vektorlar orasidagi burchakni topish orqali biz bunday vazifani hal qilishimiz mumkin. Agar bizda normal NA → \u003d (nakh, naks) bilan to'g'ri NB → (NBX, NBB) bilan to'g'ri bo'lsa, NB → va NB → orasidagi burchakka teng bo'lsa Na →, NB → ^ ^ ga qo'shadigan burchak. Ushbu usul rasmda keltirilgan:

Oddiy vektorlarning koordinatalari yordamida kesishadigan burchakning kosinasini hisoblash uchun formulalar.
cos a \u003d cos na →, nb → ^ \u003d n i x · ney 2 + ney 2 + nay 2 + ney 2 + ney 2 · nay 2 + nay 2 + nay 2
Bu erda n a → n b → Ikkita oddiy vektorlarni belgilaydi.
2-misol.
To'rtburchaklar koordinatalar tizimida ikkita to'g'ri chiziqlar 3 x + 5 y - 0 va x + 4 y - 17 \u003d 0 yordamida ikkita to'g'ri chiziqlar beriladi. Sinusni toping, ular orasidagi va bu burchakning qiyofasi orasidagi kosin burchagi.
Qaror
Manba to'g'ri chiziqlar to'g'ridan-to'g'ri shakldagi normal tenglamalar yordamida beriladi x + b y + c \u003d 0. Normal vektor n ° \u003d (A, B) tomonidan diktokli. Biz birinchi oddiy vektorning koordinatalarini topamiz va ularni yozing: n a → \u003d (3, 5). Ikkinchi to'g'ridan-to'g'ri x + 4 y - 17 \u003d 0 uchun oddiy vektor n b → \u003d (1, 4) koordinata qiladi. Endi olingan qiymatlarni formulaga qo'shing va natijani hisoblang:
cos a \u003d cos n a → n b → · 1 + 5 · 1 + 5 2 2 2 2 2 2 2 \u003d 23 34 2 34
Agar biz kosin burchakka aylangan bo'lsa, unda biz uni asosiy trigonometrik identifikator yordamida Si sinusini hisoblashimiz mumkin. To'g'ri shakllangan a burchakli a \u003d 1 - Cos 2 a \u003d 1 - 23 2 34 2 \u003d 7 2 34.
Bunday holda, a \u003d a r c co 23 2 34 \u003d A r soti 7 2 34.
Javob: Cos a \u003d 23 2 34, Sin a \u003d 7 2 34, a \u003d a r c cos 23 2 34 \u003d A r c Sin 7 2 34
Biz oxirgi holatni tahlil qilamiz - agar biz to'g'ri orasidagi burchakni topish, agar biz bir tekis va normal vektorning qo'llanmasining koordinatalarini bilsak.
Aytaylik, to'g'ridan-to'g'ri yo'naltiriladi. Biz ushbu vektorlarni kesish nuqtasidan kechiktirishimiz va ularning o'zaro joylashuvi uchun barcha imkoniyatlarni ko'rib chiqishimiz kerak. Rasmda ko'ring:

Agar belgilangan vektorlar orasidagi burchakning qiymati 90 darajadan oshmasa, u A va B o'rtasidagi burchakni to'g'ridan-to'g'ri burchakka to'ldiradi.
a →, n b ^ ^ ^ \u003d 90 ° - A, agar a → n b → ^ ^ ≤ 9 °.
Agar u 90 darajadan kam bo'lsa, biz quyidagilarni olamiz:
a →, n b → ^\u003e 9 → n b → ^ \u003d 9 9)
Teng kosine teng burchaklar hukmronligidan foydalanib yozing:
cos A → n b → ^ ^ ^ ^ ^ ^ ° A) \u003d A SON → n b → ^ ≤ 9 °.
cos A →, n b → ^ ^ ^ \u003d COS 9 \u003d a → n b (→ ^\u003e 90 °).
Shunday qilib,
sin a \u003d cos a → ^ ^, a & nb → ^ ^ ^ ^ 9 ^ ^ ^, ^\u003e Sin ^ ^ ^ Sin A \u003d Cos A \u003d NB → ^, A →, nb → ^\u003e 0 - Cos A →, NB → ^, a → nb → ^ ^< 0 ⇔ ⇔ sin α = cos a → , n b → ^
Mahsulotni shakllantiramiz.
4-ta'rif.
Samolyotda kesilgan ikkita to'g'ri chiziq orasidagi sinin burchagini topish, ikkinchisining birinchi tekis va normal vektorining qo'llanmasi o'rtasidagi kosin modulini hisoblashingiz kerak.
Biz kerakli formulalarni yozamiz. Sinin burchagini topish:
sin a \u003d cos A \u003d n b → ^ ^ ^ \u003d a x a n b y y y a li + n b h 2 + n b 2 + n b 2
Burchakni topish:
a \u003d a r c gf \u003d a x i n B w b y a x 2 + b 2 + n B 2
Bu erda A → birinchi liniy qo'llanma vektor, n B → normal ikkinchi vektordir.
3-misol.
Ikkita kesma to'g'ri chiziqlar X - 5 \u003d Y - 3 va X + 4 Y - 0 tenglamalari bilan o'rnatiladi. O'tish burchagini toping.
Qaror
Belgilangan tenglamalar bo'yicha qo'llanma va normal vektorni olamiz. Bu → \u003d (- 5, 3) va n → b \u003d (1, 4) bo'ladi. Biz formulani olamiz A \u003d a r c gf \u003d a x a n b + n b a x 2 + b 2 + n B 2 +
a \u003d a r c Sin \u003d - 5 · 1 + 3 · 4 (- 5) 2 + 3 2 · 1 2 2 \u003d A r C Sin 7 2 34
E'tibor bering, biz oldingi vazifadan tenglashtirdik va xuddi shu natijaga erishdik, ammo boshqa yo'l bilan bir xil natijaga erishdik.
Javob: a \u003d a r c g sinov 7 2 34
Belgilangan yo'naltirilgan burchak koeffitsientlaridan foydalanib, kerakli burchakni topish uchun yana bir usulni beramiz.
Y \u003d K 1 · x + b + b 2 sifatida berilgan y \u003d k 1 tam + b 1 tenglamalaridan foydalangan holda to'rtburchaklar koordinata tizimida joylashgan to'g'ridan-to'g'ri a. Bu tenglamalar burchak koeffitsienti bilan to'g'ridan-to'g'ri. Chorruning burchagini topish uchun biz formulani ishlatamiz:
a \u003d a r c cos K 1 @ k 1 2 2 2 2 2 + 1 k 1 2 + 1 va 2 2 + 1, u erda belgilangan to'g'ridan-to'g'ri koeffitsientlar. Ushbu yozuvni olish uchun burchakni normal vektorlarning koordinatalari orqali aniqlash uchun formulalar ishlatilgan.
4 misol.
Y \u003d - 3 5 x + 6 va y \u003d - 1 4 x + 17 4 tenglamalarida ikkita tekis kesib o'tmoqda. Kesishish burchagi kattaligini hisoblang.
Qaror
Bizning chiziqlarimizning burchak koeffitsientlari K 1 \u003d 3 5 va K 2 \u003d 1 4 ga teng. Biz ularni formulaga qo'shamiz a \u003d a r c cos K 1 @ 1 2 2 + 1 K 1 + 1 K 1 + 1 1 + 1-ni qo'shamiz:
a \u003d a r c cos - 1 4 + 1 - 1 2 + 1 + 1 \u003d A r c Co COS 23 20 34 \u003d a r c co COS 23 2 34
Javob: a \u003d a r c co 23 2 34
Ushbu mahsulotning xulosalarida ta'kidlash kerakki, bu erda keltirilgan formulalar yurak tomonidan o'rganilishi shart emas. Buning uchun belgilangan qo'llanmaning qo'llanma va / yoki normal vektorlarining koordinatalari koordinatalarini bilish kifoya qiladi va ularni turli xil tenglamalarda aniqlay oladi. Ammo burchakning kosinasini hisoblash formulasi esda qoladi yoki yozib olinadi.
Qanday qilib kosmosda kesishish orasidagi burchakni qanday hisoblash kerak
Bunday burchakni hisoblash qo'llanma vektorlarining koordinatalarini hisoblash va ushbu vektorlar tomonidan shakllangan burchakni aniqlash uchun kamaytirish mumkin. Bunday misollar uchun biz unga olib boradigan bir xil dalillar qo'llaniladi.
Aytaylik, bizda uch o'lchovli makonda joylashgan to'rtburchaklar koordinatali tizim mavjud. A va B chorrahasi bilan A va B ikkita to'g'ri chiziqlarini o'z ichiga oladi. Qo'llanma vektorlarining koordinatalarini hisoblash uchun biz ushbu to'g'ridan-to'g'ri tenglamalarni bilishimiz kerak. AWR Vektorlarini A → \u003d (x, a z) va b → \u003d (b x, b, b z) bildiradi. Ularning orasidagi burchakning kosinasini hisoblash uchun biz formulani ishlatamiz:
cos a \u003d cos → ^ ^ a → ^ a → a → a → a x 2 + b 2 + b y № 2
Burchakning o'rnini topish uchun biz ushbu formulaga muhtojmiz:
a \u003d a r c cos x · b + a z a x 2 + a x 2 + a x 2 + a x 2 + a z 2 b · 2 + b z 2
5-misol.
X 1 \u003d Y - Y-3 - 2 tenglama yordamida uch o'lchovli maydonda bizda to'g'ri chiziq bor. Ma'lumki, u O ma'lumotlari bilan kesishadi. Ushbu burchakning kesishish burchagini va kosinani hisoblang.
Qaror
Hisoblab chiqilishi kerak bo'lgan burchakni, a harfi. Birinchi to'g'ridan-to'g'ri - a → \u003d (1, - 3, 2) uchun biz koordinatalarni yozamiz. Agile o'qi uchun biz Koordinata vektor k → \u003d (0, 0, 1) qo'llanma sifatida olib borishimiz mumkin. Biz kerakli ma'lumotlarni oldik va ularni kerakli formulaga qo'shish mumkin:
cos α \u003d cos a →, k → ^ \u003d a →, k → a → · k → \u003d 1 · 0 - 3 · 0 - 2 · 1 1 2 + (- 3) 2 + (- 2) 2 · 0 2 + 0 2 + 1 2 \u003d 2 8 \u003d 1 2
Natijada, biz kerakli burchakka teng bo'lgan burchakka teng bo'ladi, bu a r c co 1 2 \u003d 45 ° ga teng bo'ladi.
Javob: Cos a \u003d 1 2, a \u003d 45 °.
Agar siz matnda xatoga duch kelsangiz, uni tanlang va Ctrl + Enter ni bosing