"Üçbucaq növləri" - Üçbucaq növləri. Tərəflərin müqayisəli uzunluğuna əsasən aşağıdakı üçbucaq növləri fərqləndirilir. Bucaqların ölçüsünə əsasən aşağıdakı növlər fərqlənir. Nöqtələrə təpələr, seqmentlərə isə tərəflər deyilir.

"Üçbucağın bucaqları" - Kəskin üçbucaq. Üçbucağın iki düz bucağı ola bilərmi? Bərabər üçbucaq. İkitərəfli üçbucaq. Sağ üçbucaq. Kəpənək üçbucaq. Üçbucağın iki küt bucağı ola bilərmi? Bərabər üçbucaqda bucaqlar 600-ə bərabərdir. Düzgün ikitərəfli üçbucaqda iti bucaqlar 450-yə bərabərdir.

“7-ci sinifdə həndəsə dərsləri” - Məsələlərin həlli.” Ayaqlar BC və SA. Hazır çertyojlara uyğun işləyin. “Üçbucağın bucaqlarının cəmi. Yeni material. Sağ üçbucaq. Tapşırıq №1. Hazır çertyojlardan istifadə etməklə məsələlərin həlli. No 232 (şifahi), No 231. Sübut edin: ABC bucağı ADC bucağından kiçikdir. Şifahi test. Həndəsə dərsi 7 sinif. Hipotenuz AB.

"Sağ üçbucaq" - Evklid haqqında məlumat olduqca azdır. Üçbucaq üç tərəfi (və ya üç bucağı) olan çoxbucaqlıdır. Evklid astronomiya, optika, musiqi və s. üzrə əsərlərin müəllifidir. Üçbucağın xarici bucağı ona bitişik olmayan daxili bucaqların cəminə bərabərdir. Evklid İsgəndəriyyə məktəbinin ilk riyaziyyatçısıdır. Təriflər. Nəzarət testi.

“İkitərəfli üçbucaq və onun xassələri” - Bu üçbucaqların əsasını və tərəflərini adlandırın. 2 bucağın qiyməti 40 dərəcə olarsa, 1 bucağın qiymətini tapın? A, C – ikitərəfli üçbucağın təməlindəki bucaqlar. Üçbucaqlar bərabərdirmi? Həyatda ikitərəfli üçbucaqlar harada tapılır? AM – median. Bütün tərəfləri bərabər olan üçbucağa BƏRABƏRLƏR deyilir.

"Həndəsə Düz Üçbucaq" - Misir Rəqəmləri: Misirli bir kəndlinin üçbucaqlı formalı sahəsinin sahəsini hesablayın. Tədqiqatçılar. Misirlilər düzbucaqlı üçbucağı nə adlandırırdılar? Misirli inşaatçılar: Misirdə ayaq və hipotenuz Pifaqor: Həndəsədə ayaq və hipotenuz. Torpaq tədqiqatçılarının sualları: - Ayaq hipotenuzadan daha böyükdür. 60 dərəcə bucağa qarşı olan ayaq hipotenuzanın yarısına bərabərdir.

Məktəbdən bilirik ki, üçbucağın daxili bucaqlarının üç bissektrisaları bir nöqtədə - bu üçbucaqda yazılmış dairənin mərkəzində kəsişir.

Teorem 1. Bucaq bisektoru Aüçbucaq ABC bissektrisaların kəsişmə nöqtəsi nisbətdə bölünür , olduğu tərəfdən saymaqla a, b, c- yan uzunluqlar BC, AC, AB müvafiq olaraq.

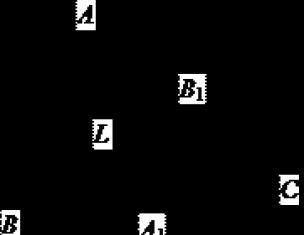
Sübut. Qoy AA 1 və BB 1 – bucaq bissektrisaları A Və IN müvafiq olaraq üçbucaqda ABC, L- onların kəsişmə nöqtəsi, a, b, c- yan uzunluqlar BC, AC, AB müvafiq olaraq (şək. 62). Sonra üçbucağa tətbiq olunan bissektrisa teoremi ilə ABC olacaq

Və ya b VA 1 = ac – VA ilə 1 və ya VA 1 (b + c)= ac, Vasitələri, VA 1 = ilə. Eyni teoremlə üçbucağa tətbiq edilir AVA 1 alırıq A 1 L : LA = : ilə, və ya = .

Teorem 2.Əgər L ABC sonra dairə

Ð ALB= 90° + R S.

Sübut. Nəzərə alsaq ki, üçbucağın bucaqlarının cəmi 180° və mərkəzidir L yazılan dairə üçbucağın bissektrisalarının kəsişmə nöqtəsidir, bizdə olacaq (şək. 62):

Ð ALB= 180° – ( Ð ABL + Ð VAL) = 180° – ( Ð ABC + Ð VAS) =

180° – (180° - Ð S) = 180° – 90° + R S= 90° + R S.

Teorem 3.Əgər L– bucağın bissektrisasında nöqtə İLƏüçbucaq ABC belə Ð ALB= 90° + R S, Bu L– yazılan üçbucağın mərkəzi ABC dairə.

Sübut. Gəlin sübut edək ki, bəndlərin heç biri L 1 arasında C Və L yazılmış dairənin mərkəzi ola bilməz (şək. 62a).

bizdə var Ð AL 1 İLƏ 1 < Ð ALC 1, üçbucağın xarici bucağından bəri AL 1 L ona bitişik olmayan istənilən daxili bucaqdan böyükdür. Həmçinin Ð VL 1 İLƏ < Р ВЛС 1 .

Buna görə də Ð AL 1 IN < Ð ALB= 90° + R S. O deməkdir ki, L 1 həkk olunmuş çevrənin mərkəzi deyil, çünki içə çəkilmiş dairənin mərkəzinin işarəsi üçün şərt təmin olunmur (bax. Teorem 2).

Əgər nöqtə L bissektrisa üzrə 2 SS 1 seqmentə aid deyil CL, Bu Ð AL 2 IN > Ð ALB= 90° + R S və yenə də həkk olunmuş dairənin mərkəzinin işarəsi şərti yerinə yetirilmir. Bu o deməkdir ki, yazılan dairənin mərkəzi nöqtədir L.

Teorem 4.Üçbucağın təpəsindən bu təpədən keçən tərəfi ilə yazılan çevrənin toxunma nöqtəsinə qədər olan məsafə bu üçbucağın əks tərəfin kiçildilmiş yarım perimetrinə bərabərdir.

Sübut. Qoy A 1 , IN 1 , İLƏ 1 – üçbucağın tərəfləri ilə yazılmış dairənin toxunma nöqtələri ABC(Şəkil 63), a, b, c- yan uzunluqlar BC, AC, AB müvafiq olaraq.

Qoy AC 1 = X, Sonra AB 1 = x, günəş 1 = c – x = VA 1 , IN 1 İLƏ = b – x = CA 1 ,

a = BC = VA 1 + SA 1 = (c – x) + (b – x) = c + b – 2 X.

Sonra a + a = a + b + c – 2 X, və ya 2 A = 2 R – 2 X, və ya x = p – a.

Teorem 5.İstənilən üçbucaqda ABC nöqtəsi vasitəsilə L onun iki xarici bucağının bissektorlarının kəsişməsi üçüncü bucağın bissektrisasından keçir, nöqtə isə Lüçbucağın tərəflərini ehtiva edən xətlərdən bərabər məsafədədir.

Sübut. Qoy L– iki xarici bucağın kəsişmə nöqtəsi IN Və İLƏüçbucaq ABC(Şəkil 64). Bisektorun hər bir nöqtəsi bucağın tərəflərindən eyni məsafədə olduğundan, nöqtə L AB Və Günəş, bissektrisa aid olduğu üçün VL. Düz xətlərdən eyni məsafədə yerləşir Günəş Və AC, bissektrisa aid olduğu üçün CL. Buna görə də nöqtə L düz xətlər arasında eyni məsafədədir VƏ SƏN Və Günəş. Məsələdən bəri L xətlərdən eyni məsafədədir AB Və AC, Bu ASC- bucaq bisektoru SƏN.

Üçbucağın bir tərəfinə və digər iki tərəfinin uzantılarına toxunan çevrə bu üçbucağın xarici dairəsi adlanır.

Nəticə 1.Üçbucağa ekssentrik dairələrin mərkəzləri onun xarici bucaqlarının bisektor cütlərinin kəsişmə nöqtələrində yerləşir.

Teorem 6.Üçbucağın içərisinə daxil edilmiş dairənin radiusu bu üçbucağın tərəfi ilə əks bucağın yarısının kosinusunun digər iki bucağın yarısının sinuslarına vurulan nisbətinə bərabərdir.

  • öyrənilmiş teoremləri təkrarlayır və ümumiləşdirir;
  • bir sıra problemlərin həllində onlardan istifadəni nəzərdən keçirin;
  • tələbələrin ali məktəblərə qəbul imtahanlarına hazırlanması;
  • tapşırıqlar üçün rəsmlərin estetik icrasını tərbiyə etmək.

Avadanlıq: multimedia proyektoru. Əlavə 1.

Dərslər zamanı:

1. Təşkilati məqam.

2. Ev tapşırığının yoxlanılması:

  • teoremlərin sübutu – 2 tələbə + 2 tələbə – məsləhətçi (dama);
  • ev tapşırıqlarının həlli – 3 tələbə;
  • siniflə işləmək - şifahi problemin həlli:

C 1 nöqtəsi ABC üçbucağının AB tərəfini 2: 1 nisbətində bölür. B 1 nöqtəsi AC tərəfinin C nöqtəsindən kənarda davamı üzərində yerləşir və AC = CB 1. B 1 C 1 düz xətti BC tərəfini hansı nisbətdə ayırır? (2-ci slaydda).

Həlli: Şərtə görə Menelaus teoremindən istifadə edərək tapırıq: .

ABC üçbucağında AD median, O nöqtəsi medianın ortasıdır. BO düz xətti AC tərəfini K nöqtəsində kəsir.

K nöqtəsi A nöqtəsindən saymaqla AC-ni hansı nisbətdə bölür? (slayd 3-də).

Həll: VD = DC = a, АО = ОД = m olsun. BK düz xətti ADC üçbucağının iki tərəfini və üçüncü tərəfinin davamını kəsir. Menelaus teoreminə görə .

ABC üçbucağında BC tərəfində N nöqtəsi götürülür ki, NC = 3ВN; AC tərəfinin davamında M nöqtəsi A nöqtəsi kimi götürülür ki, MA = AC olsun. MN xətti AB tərəfini F nöqtəsində kəsir. Nisbəti tapın. (4-cü slaydda).

Həlli: Məsələnin şərtlərinə görə MA = AC, NC = 3 ВN. MA = AC = b, BN = k, NC = 3k olsun. MN düz xətti ABC üçbucağının iki tərəfini və üçüncü tərəfin davamını kəsir. Menelaus teoreminə görə

PQR üçbucağının PQ tərəfində N nöqtəsi, PR tərəfində isə L nöqtəsi NQ = LR olmaqla götürülür. QL və NR seqmentlərinin kəsişmə nöqtəsi QR-ni m: n nisbətində bölür, Q nöqtəsindən hesablanır. PN: PR-i tapın. (5-ci slaydda).

Həlli: Şərtlə NQ = LR, . NA = LR = a, QF =km, LF = kn olsun. NR xətti PQL üçbucağının iki tərəfini və üçüncü tərəfin davamını kəsir. Menelaus teoreminə görə

3. Praktik bacarıqların tətbiqi.

1. Problemin həlli:

Teoremi sübut edin: Üçbucağın medianları bir nöqtədə kəsişir; kəsişmə nöqtəsi təpədən hesablanaraq onların hər birini 2:1 nisbətində bölür. (Şəkil 1 slayd 6).

Sübut: ABC üçbucağının medianları AM 1, VM 2, CM 3 olsun. Bu seqmentlərin bir nöqtədə kəsişdiyini sübut etmək üçün bunu göstərmək kifayətdir Sonra Çevanın (əks) teoreminə görə, AM 1, VM 2 və CM 3 seqmentləri bir nöqtədə kəsişir. Bizdə:

Beləliklə, üçbucağın medianlarının bir nöqtədə kəsişdiyi sübut edilmişdir.

Medianların kəsişmə nöqtəsi O olsun. M 3 C düz xətti ABM 2 üçbucağının iki tərəfini və bu üçbucağın üçüncü tərəfinin davamını kəsir. Menelaus teoreminə görə

və ya .

AM 1 C və AM 2 C üçbucaqları üçün Menelaus teoremini nəzərə alaraq, əldə edirik ki,

. Teorem sübut edilmişdir.

Teoremi sübut edin: Üçbucağın bissektrisaları bir nöqtədə kəsişir.(Şəkil 2 slayd 6).

Sübut: Bunu göstərmək kifayətdir . Sonra Ceva (əks) teoremi ilə AL 1, BL 2, CL 3 bir nöqtədə kəsişir. Üçbucağın bissektrisalarının xüsusiyyətinə görə:

. Yaranan bərabərlikləri terminə vuraraq, əldə edirik: . Beləliklə, üçbucağın bissektrisaları üçün Cheva bərabərliyi təmin edilir, buna görə də onlar bir nöqtədə kəsişirlər. Teorem sübut edilmişdir.

Problem 7

Teoremi sübut edin: Kəskin üçbucağın hündürlükləri bir nöqtədə kəsişir.(Şəkil 3 slayd 6).

Sübut: Tərəfləri a, b, c olan ABC üçbucağının hündürlükləri AH 1, AH 2, AH 3 olsun. Pifaqor teoremindən istifadə edərək, düzbucaqlı ABN 2 və BSN 2 üçbucaqlarından müvafiq olaraq, AH 2 = x, CH 2 = b – x ifadə edən BN 2 ümumi ayağının kvadratını ifadə edirik.

(VN 2) 2 = c 2 – x 2 və (VN 2) 2 = a 2 – (b – x) 2. yaranan bərabərliklərin sağ tərəflərini bərabərləşdirərək, c 2 – x 2 = a 2 – (b – x) 2 alırıq ki, ondan x =.

Onda b –x = b - =.

Beləliklə, AN 2 =, CH 2 =.

ASN 2 və VSN 3, VAN 1 və SAN 1 düzbucaqlı üçbucaqları üçün eyni şəkildə düşünərək, AN 3 =, VN 3 = və VN 1 = alırıq,

Teoremi sübut etmək üçün bunu göstərmək kifayətdir . Sonra, Çevanın (əks) teoreminə görə, AN 1, VN 2 və CH 3 seqmentləri bir nöqtədə kəsişir. Bərabərliyin sol tərəfində AN 3, VN 3, VN 1, CH 1, CH 2 və AN 2 seqmentlərinin a, b, c arasında uzunluqları üçün ifadələri əvəz etməklə əmin oluruq ki, Çevanın hündürlükləri üçün bərabərliyi. üçbucaq razıdır. Teorem sübut edilmişdir.

5-7-ci məsələlərin 3 şagird tərəfindən müstəqil həlli. (ekrandakı rəsmlər).

2. başqaları:

Teoremi sübut edin: Əgər üçbucağın içinə çevrə çəkilibsə, onda üçbucağın təpələrini əks tərəflərin təmas nöqtələri ilə birləşdirən seqmentlər bir nöqtədə kəsişir. (Şəkil 4 slayd 6).

Sübut: A 1, B 1 və C 1 ABC üçbucağının daxilə çəkilmiş çevrəsinin toxunan nöqtələri olsun. AA 1, BB 1 və CC 1 seqmentlərinin bir nöqtədə kəsişdiyini sübut etmək üçün Cheva bərabərliyinin əməl etdiyini göstərmək kifayətdir:

. Bir nöqtədən çəkilmiş tangenslərin xassəsindən istifadə edərək qeydi təqdim edirik: BC 1 = BA 1 = x, CA 1 = CB 1 = y, AB 1 = AC 1 = z.

. Cheva bərabərliyi təmin edilir, yəni göstərilən seqmentlər (üçbucağın bisektorları) bir nöqtədə kəsişir. Bu nöqtə Gerqon nöqtəsi adlanır. Teorem sübut edilmişdir.

3. 5, 6, 7-ci məsələlərin təhlili.

Problem 9

AD ABC üçbucağının medianı olsun. AD tərəfində K nöqtəsi götürülür ki, AK: KD = 3: 1. BK düz xətti ABC üçbucağını ikiyə ayırır. Bu üçbucaqların sahələrinin nisbətini tapın. (7-ci slaydda Şəkil 1)

Həlli: AD = DC = a, KD = m, onda AK = 3m olsun. BK düz xəttinin AC tərəfi ilə kəsişmə nöqtəsi P olsun. Bir əlaqə tapmaq lazımdır. ABP və RVS üçbucaqlarının B təpəsindən çəkilmiş hündürlükləri bərabər olduğundan, onda = . ADC üçbucağı və sekant PB üçün Menelaus teoreminə görə bizdə: . Beləliklə, =.

Problem 10

Dairə ətrafında əhatə olunmuş ABC üçbucağında AB = 8, BC = 5, AC = 4. A 1 və C 1 müvafiq olaraq BC və BA tərəflərinə aid toxunma nöqtələridir. P – AA 1 və CC 1 seqmentlərinin kəsişmə nöqtəsi. P nöqtəsi BB 1 bissektrisasında yerləşir. AR-ı tapın: RA 1.

(slayd 7-də şəkil 2)

Həlli: ABC üçbucağı skalen olduğundan dairənin AC tərəfi ilə təmas nöqtəsi B1 ilə üst-üstə düşmür. C 1 B = x olsun, onda bir nöqtədən çevrəyə çəkilmiş tangenslərin xassəsindən istifadə edərək (şəklə bax) 8 – x + 5 – x = 4, x = qeydini təqdim edirik.

Bu, C 1 B = VA 1 =, A 1 C = 5 - =, AC 1 = 8 - = deməkdir.

ABA 1 üçbucağında C 1 C xətti onun iki tərəfini və üçüncü tərəfin davamını kəsir. Menelaus teoreminə görə .

Cavab: 70:9.

Üçbucağın tərəfləri 5, 6 və 7-dir. Bu üçbucağın daha böyük bucağının bissektrisasının üçbucağa daxil edilmiş çevrənin mərkəzinə bölündüyü seqmentlərin nisbətini tapın. (7-ci slaydda).

Həlli: ABC üçbucağında AB = 5, BC = 7, AC = 6 olsun. Üçbucağın dairəsinin mərkəzi bissektrisaların kəsişməsində yerləşir. Bissektrisaların kəsişmə nöqtəsi O olsun. AO tapmaq lazımdır: OD. AD ABC üçbucağının bisektoru olduğundan, yəni BD = 5k, DC = 6k. çünki BF ABC üçbucağının bissektrisasıdır, yəni AF = 5m, FC = 7m. BF xətti ADC üçbucağının iki tərəfini və üçüncü tərəfinin uzantısını kəsir. Menelaus teoreminə görə .

4. 9, 10, 11-ci məsələlərin müstəqil həlli.- 3 tələbə.

Problem 12 (sinifdə qalan bütün tələbələr üçün):

ABC üçbucağının BE və AD bissektrisaları Q nöqtəsində kəsişir. BQD üçbucağının sahəsi = 1, 2AC = 3 AB, 3BC = 4 AB olarsa, ABC üçbucağının sahəsini tapın. (7-ci slaydda Şəkil 4).

Həlli: AB = a olsun, onda AC =, BC = olsun. AD ABC üçbucağının bissektrisasıdır, onda , yəni BD = 2p, DC = 3p. BE ABC üçbucağının bissektrisasıdır , AE = 3 k, EC = 4k. BEC üçbucağında AD xətti onun iki tərəfini və üçüncü tərəfinin uzantısını kəsir. Menelaus teoreminə görə , yəni EQ = 9m, QB = 14m. QBD və EBC üçbucaqlarının ümumi bucağı var, yəni , S EBC = .

ABC və BEC üçbucaqlarının B təpəsindən çəkilmiş bərabər hündürlükləri var, yəni S ABC = deməkdir.

5. 9, 10, 11-ci məsələlərin təhlili.

Problemin həlli - seminar:

A. Əsası AB olan ABC ikitərəfli üçbucağının BC, CA, AB tərəflərində A 1, B 1, C 1 nöqtələri götürülür, ona görə də AA 1, BB 1, CC 1 xətləri rəqabətlidir.

Bunu sübut et

Sübut:

Ceva teoreminə görə biz var: (1).

Sinus qanununa görə: , haradan CA 1 = CA.,

, buradan A 1 B = AB. , ,

buradan AB 1 = AB. , , buradan B 1 C = BC. , şərtlə CA = BC olduğundan. Nəticə bərabərlikləri bərabərliyə əvəz edərək (1) əldə edirik:

Q.E.D.

B. ABC üçbucağının AC tərəfində elə M nöqtəsi götürülür ki, AM = ?AC, BC tərəfinin davamında isə BN = CB olsun. AB və MN seqmentlərinin kəsişmə nöqtəsi olan P nöqtəsi bu seqmentlərin hər birini hansı əlaqədə bölür?

Menelaus teoreminə görə, ABC üçbucağı və sekant MN üçün:

. Şərtlə deməli,

0,5-dən bəri. (-2) . x = 1, - 2x = - 2, x = 1.

MNC üçbucağı və AB sekantı üçün Menelaus teoreminə görə bizdə: şərtlə

, - , haradan, deməkdir.

8. Problemin müstəqil həlli: Variant 1:

1. ABC üçbucağının AB, BC, AC tərəflərinin davamlarında müvafiq olaraq C 1, A 1, B 1 nöqtələri götürülür ki, AB = BC 1, BC = CA 1, CA = AB 1 olsun. AB 1 xəttinin A 1 B 1 C 1 üçbucağının A 1 C 1 tərəfini ayıran nisbəti tapın. (3 xal).

2. ABC üçbucağının orta CC 1-də M nöqtəsi götürülür, AM və BM düz xətləri müvafiq olaraq A 1 və B 1 nöqtələrində üçbucağın tərəflərini kəsir. AB və A 1 B 1 xətlərinin paralel olduğunu sübut edin. (3 xal).

3. ABC üçbucağının AB, BC və AC tərəflərinin davamında müvafiq olaraq C 1, A 1 və B 1 nöqtələri götürülsün, A 1, B 1, C 1 nöqtələrinin eyni düz xətt üzərində olduğunu və yalnız və yalnız o halda olduğunu sübut edin bərabərlik qorunur . (4 xal).

6. ABC üçbucağının müvafiq olaraq AB, BC və AC tərəflərində C 1, A 1 və B 1 nöqtələri götürülsün ki, AA 1, BB 1, CC 1 xətləri O nöqtəsində kəsilsin. Bərabərliyin yerinə yetirildiyini sübut edin. . (5 xal).

7 . ABCD tetraedrinin müvafiq olaraq AB, BC, CD və AD kənarlarında A 1, B 1, C 1, D 1 nöqtələri götürülsün, A 1, B 1, C 1, D 1 nöqtələrinin eyni yerdə olduğunu sübut edin müstəvi yalnız və yalnız o halda, bərabərlik təmin edildikdə (5 xal).

Seçim 2:

1. A 1 və B 1 nöqtələri ABC üçbucağının BC və AC tərəflərini 2: 1 və 1: 2 nisbətində ayırır. AA 1 və BB 1 xətləri O nöqtəsində kəsişir. ABC üçbucağının sahəsi 1-ə bərabərdir. Tapın OBC üçbucağının sahəsi. (3 xal).

2. ABCD dördbucağının AD və BC tərəflərinin orta nöqtələrini birləşdirən MN seqmenti diaqonallarla üç bərabər hissəyə bölünür. Sübut edin ki, ABCD trapesiyadır, AB və ya CD əsaslarından biri digərindən iki dəfə böyükdür. (3 xal).

3. ABC üçbucağının AB tərəfində və müvafiq olaraq BC və AC tərəflərinin davamında C 1, A 1 və B 1 nöqtələri götürülsün. Sübut edin ki, AA 1, BB 1, СС 1 xətləri bir nöqtədə kəsişir və ya bərabərlik təmin edildikdə paraleldir. . (4 xal).

4. Ceva teoremindən istifadə edərək üçbucağın hündürlüklərinin və ya onların uzantılarının bir nöqtədə kəsişdiyini sübut edin. (4 xal).

5. Üçbucağın təpələrindən keçən xətlərin və dairələrin toxunan nöqtələrinin bir nöqtədə (Nagel nöqtəsi) kəsişdiyini sübut edin. (Bu üçbucağın bir tərəfinə və digər iki tərəfinin uzantılarına toxunan çevrə üçbucaqda dairəvi adlanır). (5 xal).

6. ABC üçbucağının müvafiq olaraq AB, BC və AC tərəflərində C 1, A 1, B 1 nöqtələri götürülsün ki, AA 1, BB 1 və CC 1 xətləri O nöqtəsində kəsilsin. Bərabərliyin yerinə yetirildiyini sübut edin. . (5 xal).

7. ABCD tetraedrinin müvafiq olaraq AB, BC, CD və AD kənarlarında A 1, B 1, C 1, D 1 nöqtələri alınsın, A 1, B 1, C 1, D 1 nöqtələrinin yerləşdiyini sübut edin eyni müstəvi sonra və yalnız bərabərlik təmin edildikdə (5 bal).

9. Ev tapşırığı: dərslik § 3, No 855, No 861, No 859.