Принцип на най-малкото действие. Принцип на най-малкото действие Принцип на най-малкото действие във физиката

Когато бях в училище, нашият учител по физика, на име Бадер, веднъж ме извика след час и каза: „Изглеждаш така, сякаш си ужасно уморен от всичко; чуйте едно интересно нещо. И той ми каза нещо, което според мен беше наистина очарователно. Дори и сега, въпреки че е минало много време оттогава, тя продължава да ме очарова. И всеки път, когато си спомня какво съм казал, се връщам на работа. И този път, докато се подготвях за лекцията, се хванах, че отново анализирам същите неща. И вместо да се подготвя за лекцията, се заех с нов проблем. Темата, за която говоря е принцип на най-малко действие.

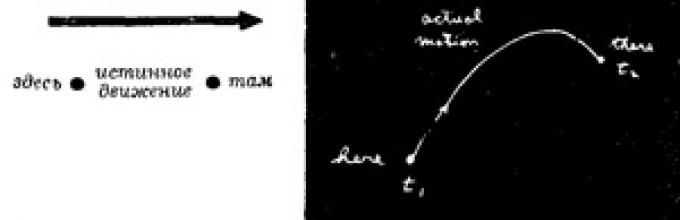
„Това ми каза моят учител Бадер тогава: „Нека например имате частица в гравитационното поле; тази частица, като излезе отнякъде, свободно се движи някъде другаде в друга точка. Вие го хвърлихте, да речем, нагоре и то излетя нагоре и после падна.

Отне й известно време да пътува от началното място до крайното място. Сега опитайте с друго движение. Нека тя се движи „от тук до тук“ вече не както преди, а така:

Но все пак се озовах на правилното място в същия момент във времето, както преди.”

„И така“, продължи учителят, „ако изчислите кинетичната енергия във всеки момент от времето по пътя на частицата, извадите от нея потенциалната енергия и интегрирате разликата за цялото време, когато се е случило движението, ще видите че числото, което ще получите, ще бъде Повече ▼,отколкото за истинското движение на частиците.

С други думи, законите на Нютон могат да бъдат формулирани не като F=ma, а по следния начин: средната кинетична енергия минус средната потенциална енергия достига най-ниската си стойност по траекторията, по която обектът действително се движи от едно място на друго.

Ще се опитам да ви обясня това малко по-ясно.
Ако вземем гравитационното поле и обозначим траекторията на частицата х(T), Където х- височина над земята (нека се справим с едно измерение засега; нека траекторията се движи само нагоре и надолу, а не настрани), тогава кинетичната енергия ще бъде г 2 м(dx/ дт) 2 , апотенциалната енергия в произволен момент от време ще бъде равна на mgx.

Сега, за някакъв момент на движение по траекторията, вземам разликата между кинетичната и потенциалната енергия и интегрирам през цялото време от началото до края. Нека в началния момент от време t x движението започна на някаква височина и свърши в момента T 2 на друга определена височина.

Тогава интегралът е равен на ∫ t2 t1 dt

Истинското движение възниква по определена крива (като функция на времето е парабола) и води до определена интегрална стойност. Но ти можеш предислагампредставете си някакво друго движение: първо рязко покачване, а след това някакви странни колебания.

Можете да изчислите разликата между потенциалната и кинетичната енергия по този път... или по който и да е друг. И най-удивителното е, че истинският път е този, по който този интеграл е най-малък.
Нека да го проверим. Първо, нека да разгледаме този случай: свободната частица изобщо няма потенциална енергия. Тогава правилото гласи, че при движение от една точка в друга за дадено време интегралът на кинетичната енергия трябва да бъде най-малък. Това означава, че частицата трябва да се движи равномерно. (И това е правилно, вие и аз знаем, че скоростта при такова движение е постоянна.) Защо равномерно? Нека да го разберем. Ако беше другояче, тогава на моменти скоростта на частицата щеше да надвишава средната, а на моменти щеше да е под нея и средната скорост щеше да е същата, защото частицата би трябвало да стигне „от тук до тук“ в уговореното време. Например, ако трябва да стигнете от вкъщи до училище с колата си за определено време, тогава можете да направите това по различни начини: можете да карате като луди в началото и да намалите скоростта накрая или да карате със същата скорост, или дори можете да отидете на противоположната страна и едва след това да завиете към училището и т.н. Във всички случаи средната скорост, разбира се, трябва да е една и съща - частното на разстоянието от дома до училището, разделено на времето. Но дори и при тази средна скорост, понякога сте се движили твърде бързо, а понякога твърде бавно. И средно квадратнещо, което се отклонява от средното, както знаем, винаги е по-голямо от квадрата на средното; Това означава, че интегралът на кинетичната енергия по време на колебания в скоростта на движение винаги ще бъде по-голям, отколкото при движение с постоянна скорост. Виждате, че интегралът ще достигне минимум, когато скоростта е постоянна (при липса на сили). Правилният начин е този.

Обект, хвърлен нагоре в поле на гравитация, се издига първо бързо, а след това все по-бавно. Това се случва, защото той също има потенциална енергия и нейната минимална стойност трябва да достигне веднъжностмежду кинетичната и потенциалната енергия. Тъй като потенциалната енергия се увеличава, докато се издигате, тогава по-малко разликаЩе работи, ако достигнете височини, където потенциалната енергия е висока възможно най-бързо. След това, като извадим този висок потенциал от кинетичната енергия, постигаме намаляване на средната стойност. Така че пътят, който върви нагоре и доставя добро отрицателно парче за сметка на потенциалната енергия, е по-печеливш.

Това е всичко, което учителят ми каза, защото той беше много добър учител и знаеше кога е време да спре. Аз самият, уви, не съм такъв. Трудно ми е да спра навреме. И така, вместо просто да предизвикам интереса ви с моята история, искам да ви сплаша, искам да ви досадя от сложността на живота - ще се опитам да докажа това, за което ви казах. Математическата задача, която ще решим е много трудна и уникална. Има определено количество С, Наречен действие.Тя е равна на кинетичната енергия минус потенциалната енергия, интегрирана във времето:

Но от друга страна, не можете да се движите твърде бързо или да отидете твърде високо, защото това ще изисква твърде много кинетична енергия. Трябва да се движите достатъчно бързо, за да се качвате и слизате в рамките на даденото време, което ви е налично. Така че не трябва да се опитвате да летите твърде високо, а просто да достигнете някакво разумно ниво. В резултат на това се оказва, че решението е един вид баланс между желанието да се получи възможно най-много потенциална енергия и желанието да се намали колкото е възможно повече количеството кинетична енергия - това е желанието да се постигне максимално намаляване в разликата между кинетичната и потенциалната енергия.

Не забравяйте, че p.e. и к.е.—и двете функции на времето. За всеки нов възможен път това действие придобива своето специфично значение. Математическият проблем е да се определи коя крива има това число по-малко от останалите.

Вие казвате: „О, това е просто прост пример за максимум и минимум. Трябва да изчислим действието, да го диференцираме и да намерим минимума.”

Но почакай. Обикновено имаме функция на някаква променлива и трябва да намерим стойността променлива,при което функцията става най-малка или най-голяма. Да кажем, че в средата има нагрята пръчка. Топлината се разпространява върху него и собствената му температура се установява във всяка точка на пръта. Трябва да намерите точката, където е най-високо. Но ние говорим за нещо съвсем различно - всеки път в космосаотговаря на неговия номер и трябва да намери този път,за които този брой е минимален. Това е напълно различна област на математиката. Това не е обикновено смятане, а вариационен(така му викат).

Тази област на математиката има много свои собствени проблеми. Да речем, окръжността обикновено се определя като геометрично място на точки, чиито разстояния от дадена точка са еднакви, но окръжността може да се дефинира по различен начин: тя е една от кривите дадена дължина,която обхваща най-голямата площ. Всяка друга крива със същия периметър обхваща площ, по-малка от кръга. Така че, ако поставим задачата: да намерим кривата на даден периметър, която ограничава най-голямата площ, тогава ще имаме проблем от вариационното смятане, а не от смятането, с което сте свикнали.

И така, искаме да вземем интеграла върху пътя, изминат от тялото. Нека го направим по този начин. Целият смисъл е да си представим, че има истински път и че всяка друга крива, която начертаем, не е реалният път, така че ако изчислим действието за него, ще получим число, по-високо от това, което получаваме за съответното действие към истинския начин.

И така, задачата е да се намери истинският път. Къде се крие? Един от начините, разбира се, би бил да преброим действието за милиони и милиони пътища и след това да видим кой път има най-малкото действие. Това е пътя, в който действието е минимално и ще бъде реално.

Този метод е напълно възможен. Въпреки това, може да се направи по-просто. Ако има количество, което има минимум (от обикновени функции, да речем температура), тогава едно от свойствата на минимума е, че когато се отдалечава от него на разстояние първиот порядъка на малкост функцията се отклонява от минималната си стойност само със сумата второпоръчка. И във всяко друго място на кривата, едно изместване с малко разстояние променя стойността на функцията също със стойност от първи порядък на малкост. Но като минимум леките отклонения встрани не водят до промяна във функцията като първо приближение.

Именно това свойство ще използваме, за да изчислим реалния път.

Ако пътят е правилен, тогава крива, малко по-различна от него, няма да доведе, като първо приближение, до промяна в големината на действието. Всички промени, ако това наистина е минимумът, ще се появят само във второто приближение.

Това е лесно доказуемо. Ако с известно отклонение от кривата настъпят промени в първия ред, тогава тези промени са в сила пропорционаленотклонение. Те вероятно ще увеличат ефекта; иначе нямаше да е минимум. Но след като промените пропорционаленотклонение, тогава промяната на знака на отклонението ще намали действието. Оказва се, че при отклонение в една посока ефектът се засилва, а при отклонение в обратната посока намалява. Единствената възможност това наистина да е минимум е, че като първо приближение не настъпват промени и промените са пропорционални на квадрата на отклонението от действителния път.

И така, ще вървим по следния път: обозначаваме с х(T) (с ред отдолу) истинският път е този, който искаме да намерим. Нека направим малко пробно пускане х(T), различаващ се от желаното с малко количество, което обозначаваме η (T).

Идеята е, че ако броим действието С на път х(T), тогава разликата между това С и от действието, което изчислихме за пътя х(T) (за простота ще бъде обозначено С), или разликата между С_ И С, трябва да е първо приближение η нула. Те могат да се различават във втория ред, но в първия разликата трябва да е нула.

И това трябва да се спазва за всички η . Въпреки това, не съвсем за всеки. Методът изисква да се вземат предвид само тези пътища, които всички започват и завършват в една и съща двойка точки, т.е. всеки път трябва да започва в определена точка в момента T 1 и завършват в друга конкретна точка в момента T 2 . Тези точки и моменти се записват. Така че нашата функция d) (отклонение) трябва да бъде нула в двата края: η (T 1 )= 0 И η (t 2)=0. При това условие нашият математически проблем става напълно дефиниран.

Ако не познавахте смятането, бихте могли да направите същото, за да намерите минимума на обикновена функция f(х). Бихте ли се замислили какво ще стане, ако вземете f(х) и добавете към хмалко количество ч, и ще твърди, че изменението на f(х) в първи ред ч трябва да бъде най-малко равно на нула. Бихте ли ме настроили x+ч вместо хи ще разшири j(x+h) до първа степен ч. . ., с една дума, ще повтори всичко, с което възнамеряваме да направим η .

Ако сега разгледаме това внимателно, ще видим, че първите два термина, написани тук, съответстват на това действие С, което бих написал за търсения верен път Х.Искам да насоча вниманието ви към промяната. С, т.е. върху разликата между С и така С_, което би довело до истинския път. Ще запишем тази разлика като bS и нека го наречем вариация С. Изхвърляйки „втория и по-висок ред“, получаваме за σS

Сега задачата изглежда така. Тук пред мен има някакъв интеграл. Все още не знам какво е, но знам със сигурност какво η Без значение какво, този интеграл трябва да е равен на нула. „Е,“ може да си помислите, „единственият начин това да се случи е множителят да го направи η беше равно на нула." Но какво да кажем за първия срок, където има д η / дт? Казвате: „Ако η се превръща в нищо, тогава неговата производна е същото нищо; това означава коефициентът при дв\/ дт също трябва да бъде нула." Е, това не е съвсем вярно. Това не е съвсем вярно, защото между отклонението η и неговата производна има връзка; те не са напълно независими, защото η (T) трябва да е нула и т 1 и при T 2 .

При решаването на всички проблеми на вариационното смятане винаги се използва един и същ общ принцип. Измествате леко това, което искате да варирате (подобно на това, което направихме, като добавихме η ), погледнете условията от първия ред, тогаваподредете всичко така, че да получите интеграл в следния вид: „отместване (η ), умножено по това, което се получава”, но така че да не съдържа никакви производни на η (не д η / дт). Абсолютно необходимо е да се трансформира всичко, така че да остане „нещо“, умножено по η . Сега ще разберете защо това е толкова важно. (Има формули, които ще ви кажат как в някои случаи можете да направите това без никакви изчисления; но те не са толкова общи, че да си струва да ги запомните; най-добре е да направите изчисленията по начина, по който го правим.)

Как мога да преправя пенис д η / дт, така че да се появи η ? Мога да постигна това, като интегрирам част по част. Оказва се, че в вариационното смятане целият трик е да се опише вариацията С и след това интегрирайте по части, така че производните на η изчезна. Във всички задачи, в които се появяват производни, се изпълнява същият трик.

Припомнете си общия принцип на интегриране по части. Ако имате произволна функция f, умножена по д η / дт и интегриран с T, след това пишете производната на η /T

Границите на интеграция трябва да бъдат заменени в първия член т 1 И T 2 . Тогава под интеграла ще получа члена от интегрирането по части и последния член, който остава непроменен при преобразуването.
И сега се случва това, което винаги се случва - интегрираната част изчезва. (И ако не изчезне, тогава принципът трябва да се преформулира, като се добавят условия, които осигуряват това изчезване!) Вече казахме, че η в краищата на пътя трябва да е равно на нула. Все пак какъв е нашият принцип? Факт е, че действието е минимално, при условие че вариращата крива започва и завършва в избрани точки. Означава, че η (t 1)=0 и η (t 2)=0. Следователно интегрираният член се оказва нула. Събираме останалите членове и пишем

Вариация С сега придоби формата, която искахме да му дадем: нещо е в скоби (нека го обозначим Е), и всичко това се умножава по η (T) и интегриран от t t преди T 2 .
Оказа се, че интегралът на някакъв израз, умножен по η (T), винаги равно на нула:

Има ли някаква функция от T; Умножавам го по η (T) и го интегрирайте от началото до края. И каквото и да е η, получавам нула. Това означава, че функцията Е(T) равно на нула. Като цяло това е очевидно, но за всеки случай ще ви покажа един начин да го докажете.

Нека като η (T) Ще избера нещо, което е равно на нула навсякъде, за всички T, с изключение на една предварително избрана стойност T. Остава нула, докато стигна там T, сСлед това подскача за момент и веднага пада назад. Ако вземете интеграла на това m), умножено по някаква функция Е, единственото място, където ще получите нещо различно от нула, е къде η (T) скочи нагоре; и ще получите стойността Е в тази точка върху интеграла върху скока. Интегралът върху самия скок не е равен на нула, а след умножение по Е трябва да дава нула. Това означава, че функцията на мястото, където е имало скок, трябва да се окаже нула. Но скокът можеше да бъде направен навсякъде; означава, Е трябва да е нула навсякъде.

Виждаме, че ако нашият интеграл е равен на нула за всяко η , тогава коефициентът при η трябва да отиде до нула. Интегралът на действието достига минимум по пътя, който ще удовлетвори такова сложно диференциално уравнение:

Всъщност не е толкова сложно; вие сте го срещали преди. Това е просто F=ma. Първият член е масата по ускорението; втората е производната на потенциалната енергия, т.е. силата.

Така ние показахме (поне за една консервативна система), че принципът на най-малкото действие води до правилния отговор; той заявява, че пътят, който има минимално действие, е пътят, който удовлетворява закона на Нютон.

Трябва да се направи още една забележка. Не съм доказал това минимум.Може би това е максимумът. Всъщност това не трябва да е минимумът. Тук всичко е същото като в „принципа на най-краткото време“, който обсъждахме, докато изучавахме оптиката. Там също за първи път говорихме за „най-краткото“ време. Оказа се обаче, че има ситуации, в които това време не е непременно „най-краткото“. Основополагащият принцип е, че за всеки отклонения от първи редот оптичния път променивъв времето ще бъде равно на нула; Тук е същата история. Под „минимум“ всъщност имаме предвид това до първия порядък на малка промяна на количеството Скогато отклоненията от пътя трябва да са равни на нула. И това не е непременно „минимумът“.

Сега искам да премина към някои обобщения. Първо, цялата тази история може да бъде направена в три измерения. Вместо просто хТогава бих имал x, yИ zкато функции T,и действието ще изглежда по-сложно. Когато се движите в 3D, трябва да използвате пълна кинетична енергия): (t/2),умножено по квадрата на общата скорост. С други думи

Освен това потенциалната енергия вече е функция x, yИ z.Какво можете да кажете за пътя? Пътят е определена обща крива в пространството; не е толкова лесно да се рисува, но идеята остава същата. Какво ще кажете за η? Е, η също има три компонента. Пътят може да се измести както в x, така и в y,и от z,или в трите посоки едновременно. Така η сега вектор. Това не създава големи усложнения. Само вариациите трябва да са равни на нула първа поръчкатогава изчислението може да се извърши последователно с три смени. Първо можете да се движите цсамо в посоката хи кажете, че коефициентът трябва да стигне до нула. Получавате едно уравнение. Тогава ще се преместим цв посоката прии получаваме второто. След това се движете в посока zи получаваме третото. Можете да направите всичко, ако желаете, в различен ред. Както и да е, възниква трио от уравнения. Но законът на Нютон също е три уравнения в три измерения, по едно за всеки компонент. Остава ви сами да видите, че всичко това работи в три измерения (тук няма много работа). Между другото, можете да вземете всяка координатна система, която желаете, полярна, всяка и веднага да получите законите на Нютон във връзка с тази система, като вземете предвид какво се случва, когато настъпи изместване η по радиус или по ъгъл и т.н.

Методът може да се обобщи за произволен брой частици. Ако, да речем, имате две частици и между тях действат някакви сили и има взаимна потенциална енергия, тогава просто добавяте техните кинетични енергии и изваждате потенциалната енергия на взаимодействието от сумата. Какво варирате? пътеки и дветечастици. Тогава за две частици, движещи се в три измерения, възникват шест уравнения. Можете да променяте позицията на частица 1 в посоката Х,в посоката прии към z,и направете същото с частица 2, така че има шест уравнения. И така трябва да бъде. Три уравнения определят ускорението на частица 1 поради силата, действаща върху нея, а другите три определят ускорението на частица 2 поради силата, действаща върху нея. Винаги следвайте едни и същи правила на играта и ще получите закона на Нютон за произволен брой частици.

Казах, че ще получим закона на Нютон. Това не е съвсем вярно, защото законът на Нютон включва и неконсервативни сили, като например триене. Нютон твърди това чее равно на всяко F. Принципът на най-малко действие е валиден само за консервативенсистеми, при които всички сили могат да бъдат получени от потенциална функция. Но вие знаете, че на микроскопично ниво, тоест на най-дълбокото физическо ниво, неконсервативни сили не съществуват. Неконсервативните сили (като триене) възникват само защото пренебрегваме микроскопичните сложни ефекти: просто има твърде много частици за анализ. Фундаменталенсъщите закони могада се изрази като принципа на най-малкото действие.

Нека да премина към по-нататъшни обобщения. Да предположим, че ни интересува какво ще се случи, когато частицата се движи релативистично. Досега не сме получили правилното релативистично уравнение на движението; F=ma е вярно само при нерелативистични движения. Възниква въпросът: има ли съответен принцип на най-малкото действие в релативистичния случай? Да, съществува. Формулата в релативистичния случай е:

Първата част от интеграла на действието е произведението на масата на покой t 0На от 2и към интеграла на скоростната функция √ (1- v 2 /c 2 ). Тогава, вместо да извадим потенциалната енергия, имаме интеграли на скаларния потенциал φ и векторния потенциал A, умножен по v. Разбира се, тук се вземат предвид само електромагнитните сили. Всички електрически и магнитни полета се изразяват чрез φ и A. Тази функция на действие дава пълна теория за релативистичното движение на отделна частица в електромагнитно поле.

Разбира се, трябва да разберете, че където и да съм написал v, преди да правите изчисления, трябва да замените dx/ дт вместо v x и т.н. Освен това, където просто написах x, y, z,трябва да си представите точките в момента T: х(T), г(T), z(T). Всъщност само след такива замествания и замествания на v ще получите формула за действието на релативистка частица. Нека най-квалифицираните сред вас се опитат да докажат, че тази формула за действие всъщност дава правилните уравнения на движение за теорията на относителността. Позволете ми само да ви посъветвам да започнете, като изхвърлите А, тоест засега се оправете без магнитни полета. След това ще трябва да получите компонентите на уравнението на движението dp/dt=—qVφ,където, както вероятно си спомняте, p=mv√(1-v 2 /c 2).

Много по-трудно е да се вземе предвид векторният потенциал A. Тогава вариациите стават несравнимо по-сложни. Но в крайна сметка силата се оказва равна на това, което трябва да бъде: g(E+v × B). Но се забавлявайте с него сами.

Бих искал да подчертая, че в общия случай (например в релативистката формула) интегралът в действие вече не включва разликата между кинетичната и потенциалната енергия. Това беше подходящо само в нерелативистично приближение. Например член m o c 2√(1-v 2 /c 2)-Това не е това, което се нарича кинетична енергия. Въпросът какво трябва да бъде действието за всеки отделен случай може да бъде решен след известен опит и грешка. Това е същия тип проблем като определянето какви трябва да бъдат уравненията на движението. Просто трябва да си поиграете с уравненията, които знаете, и да видите дали могат да бъдат записани като принципа на най-малкото действие.

Още една забележка относно терминологията. Тази функция, която се интегрира във времето, за да се получи действие С,Наречен ЛагранжΛ. Това е функция, която зависи само от скоростите и позициите на частиците. Така че принципът на най-малкото действие също е записан във формуляра

където под х азИ v i всички компоненти на координатите и скоростите се подразбират. Ако някога чуете някой да говори за "лагранжиан", той говори за функцията, използвана за получаване С. За релативистично движение в електромагнитно поле

Освен това трябва да отбележа, че най-педантичните и педантични хора не се обаждат Сдействие. Нарича се "първата главна функция на Хамилтън". Но изнасянето на лекция на тема „Принципът на Хамилтън за най-малката първа главна функция“ беше извън силите ми. Нарекох го "екшън". И освен това все повече и повече хора го наричат „екшън“. Виждате ли, в исторически план действието е било наричано нещо друго, което не е толкова полезно за науката, но мисля, че има по-голям смисъл да се промени определението. Сега вие също ще започнете да наричате новата функция действие и скоро всички ще започнат да я наричат с това просто име.

Сега искам да ви кажа нещо за нашата тема, което е подобно на разсъжденията, които имах относно принципа на най-краткото време. Има разлика в самата същност на закона, който казва, че някакъв интеграл, взет от една точка до друга, има минимум - законът, който ни казва нещо за целия път наведнъж, и законът, който казва, че когато се движите, тогава Това означава, че има сила, водеща до ускорение. Вторият подход ви докладва за всяка ваша стъпка, той проследява пътя ви инч по инч, а първият веднага дава някакво общо изявление за целия изминат път. Докато говорихме за светлината, говорихме за връзката между тези два подхода. Сега искам да ви обясня защо трябва да съществуват диференциални закони, ако има такъв принцип – принципът на най-малкото действие. Причината е следната: нека разгледаме действително изминатия път в пространството и времето. Както и преди, ще се задоволим с едно измерване, за да можем да начертаем графика на зависимостта хот T. По истинския път С достига минимум. Нека приемем, че имаме този път и че той минава през някаква точка Апространство и време и през друга съседна точка b.

Сега, ако целият интеграл на т 1 преди T 2 е достигнала минимум, необходимо е интегралът по малък участък от a до b също беше минимален. Не може да е тази част от Апреди bпоне малко повече от минимума. В противен случай можете да местите кривата напред-назад в този раздел и леко да намалите стойността на целия интеграл.

Това означава, че всяка част от пътя също трябва да осигурява минимум. И това е вярно за всякакви малки части от пътя. Следователно принципът, че целият път трябва да дава минимум, може да се формулира, като се каже, че безкрайно малък сегмент от пътя също е крива, върху която действието е минимално. И ако вземем достатъчно кратък отрязък от пътя – между много близки една до друга точки АИ б,- тогава няма значение как потенциалът се променя от точка на точка далеч от това място, защото, преминавайки през целия си кратък сегмент, вие почти никога не се местите от това място. Единственото нещо, което трябва да вземете предвид, е промяната на първия ред в малкия потенциал. Отговорът може да зависи само от производната на потенциала, а не от потенциала другаде. По този начин изявление за свойството на целия път като цяло се превръща в изявление за това, което се случва на кратък участък от пътя, т.е. диференциално изявление. И тази диференциална формулировка включва производни на потенциала, тоест силата в дадена точка. Това е качествено обяснение на връзката между закона като цяло и диференциалния закон.

Когато говорихме за светлината, обсъдихме и въпроса: как една частица намира правилния път? От диференциална гледна точка това е лесно за разбиране. Във всеки момент частицата изпитва ускорение и знае само какво трябва да направи в този момент. Но всичките ви инстинкти за причина и следствие се засилват, когато чуете, че една частица „решава“ кой път да поеме, като се стреми към минимално действие. Не „подушва“ ли съседните пътища, разбирайки до какво ще доведат - повече или по-малко действие? Когато поставихме екран на пътя на светлината, така че фотоните да не могат да пробват всички пътища, открихме, че те не могат да решат кой път да поемат, и получихме явлението дифракция.

Но това вярно ли е и за механиката? Вярно ли е, че една частица не само „върви по правилния път“, но преразглежда всички други възможни траектории? И какво, ако, поставяйки препятствия по пътя му, не му позволим да гледа напред, тогава ще получим някакъв аналог на явлението дифракция? Най-прекрасното във всичко това е, че всичко наистина е така. Точно това казват законите на квантовата механика. Така че нашият принцип на най-малко действие не е напълно формулиран. Той не се състои в това, че частицата избира пътя на най-малко действие, а в това, че тя „усеща” всички съседни пътища и избира този, по който действието е минимално, като методът на този избор е подобен на начин, по който светлината избира най-краткото време. Спомняте си, че начинът, по който светлината избира най-краткото време, е следният: ако светлината върви по път, който изисква различно време, тя ще пристигне с различна фаза. И общата амплитуда в даден момент е сумата от приносите на амплитудата за всички пътища, по които светлината може да достигне до нея. Всички тези пътища, чиито фази се различават рязко, не дават нищо след добавяне. Но ако успеете да намерите цялата последователност от пътища, чиито фази са почти еднакви, тогава малките вноски ще се сумират и в точката на пристигане общата амплитуда ще получи забележима стойност. Най-важният път е този, в близост до който има много близки пътища, които дават една и съща фаза.

Абсолютно същото се случва в квантовата механика. Пълната квантова механика (нерелативистка и пренебрегваща спина на електрона) работи по следния начин: вероятността частица да напусне точка 1 в момента т 1, ще стигне до точката 2 в момента T 2 , равна на квадрата на амплитудата на вероятността. Общата амплитуда може да бъде записана като сбор от амплитудите за всички възможни пътища - за всеки път на пристигане. За всеки х(T), което може да възникне за всяка възможна въображаема траектория, амплитудата трябва да се изчисли. След това всички те трябва да бъдат сгънати. Какво приемаме като амплитуда на вероятността на определен път? Нашият интеграл на действие ни казва каква трябва да бъде амплитудата на индивидуалния път. Амплитудата е пропорционална e tS/h, Където С - действие по този път. Това означава, че ако представим фазата на амплитудата като комплексно число, тогава фазовият ъгъл ще бъде равен на С/ ч. Действие С има измерението на енергията във времето и константата на Планк има същото измерение. Това е константата, която определя кога е необходима квантовата механика.

И така работи всичко. Нека действие за всички пътища С ще бъде много голям в сравнение с броя ч. Нека някакъв път води до определена стойност на амплитудата. Фазата на съседната пътека ще бъде напълно различна, защото с огромна С дори незначителни промени С рязко сменете фазата (в края на краищата чизключително малко). Това означава, че съседните пътища обикновено заличават своите приноси, когато се добавят. И само в една област това не е вярно - в тази, където и пътят, и неговият съсед - и двете, в първо приближение, имат една и съща фаза (или по-точно почти едно и също действие, вариращо в рамките на з).Само такива пътища се вземат предвид. И в граничния случай, когато константата на Планк чклони към нула, правилните закони на квантовата механика могат да бъдат обобщени, като се каже: „Забравете за всички тези вероятностни амплитуди. Частицата всъщност се движи по специален път - точно този, по който С в първо приближение не се променя.” Това е връзката между принципа на най-малкото действие и квантовата механика. Фактът, че квантовата механика може да бъде формулирана по този начин, беше открит през 1942 г. от ученик на същия учител, г-н Бадер, за когото ви разказах. [Квантовата механика първоначално е формулирана с помощта на диференциално уравнение за амплитудата (Шрьодингер), както и някои матрични математики (Хайзенберг).]

Сега искам да говоря за други принципи на минимума във физиката. Има много интересни принципи от този вид. Няма да ги изброявам всички, но ще назова само още един. По-късно, когато стигнем до един физически феномен, за който има отличен минимален принцип, ще ви разкажа за него. Сега искам да покажа, че не е необходимо да описвам електростатиката с помощта на диференциално уравнение за полето; вместо това може да се изисква някой интеграл да има максимум или минимум. Като начало, нека вземем случая, когато плътността на заряда е известна навсякъде, но трябва да намерим потенциала φ във всяка точка на пространството. Вече знаете, че отговорът трябва да бъде:

Друг начин да кажем същото е да оценим интеграла U*

това е обемен интеграл. Заема се в цялото пространство. При правилно разпределение на потенциала φ (х, y,z) този израз достига своя минимум.

Можем да покажем, че и двете твърдения относно електростатиката са еквивалентни. Да приемем, че сме избрали произволна функция φ. Искаме да покажем, че когато вземем като φ правилната стойност на потенциала _φ плюс малко отклонение f, тогава до първи ред на малка промяната в U* ще бъде равно на нула. Така че ние пишем

тук φ е това, което търсим; но ние ще променяме φ, за да видим какво трябва да бъде, за да има промяната U* се оказа от първи порядък на дребност. В първия срок U* трябва да пишем

Това трябва да бъде интегрирано от x, yи от z. И тук се предлага същият трик: за да се отървем от df/ dx, ще се интегрираме над хна части. Това ще доведе до допълнителна диференциацияφ по отношение на Х.Това е същата основна идея, с която се отървахме от производните по отношение на T. Ние използваме равенство

Интегрираният член е нула, защото приемаме f за нула в безкрайност. (Това съответства на η, изчезващо като T 1 И T 2 . Така че нашият принцип е по-точно формулиран, както следва: U* за правото φ по-малко от всеки друг φ(x, y,z), имащи същите стойности в безкрайност.) Тогава ще направим същото с прии с z. Нашият интеграл ΔU* ще се превърне в

За да бъде тази вариация равна на нула за всяко произволно f, коефициентът на f трябва да е равен на нула. означава,

Върнахме се към старото ни уравнение. Това означава, че нашето предложение за „минимум“ е правилно. Може да се обобщи, ако изчисленията са леко модифицирани. Нека се върнем назад и да интегрираме част по част, без да описваме всичко компонент по компонент. Нека започнем, като напишем следното равенство:

Като диференцирам лявата страна, мога да покажа, че тя е точно равна на дясната. Това уравнение е подходящо за извършване на интегриране по части. В нашия интеграл ΔU* заместваме Vφ*Vf nи fV 2 φ+V*(fVφ) и след това интегрирайте това върху обема. Членът на дивергенция след интегриране по обема се заменя с интеграл по повърхността:

И тъй като ние интегрираме цялото пространство, повърхността в този интеграл лежи в безкрайност. Това означава f=0 и получаваме същия резултат.

Едва сега започваме да разбираме как да решаваме проблемите, в които сме ние не знаемкъдето се намират всички заряди. Нека имаме проводници, върху които по някакъв начин се разпределят зарядите. Ако потенциалите на всички проводници са фиксирани, тогава нашият минимален принцип все още може да се прилага. Интегриране в U* ще начертаем само по площта, разположена извън всички проводници. Но тъй като не можем да променим (φ) на проводниците, тогава на тяхната повърхност f = 0 и повърхностният интеграл

трябва да се направи само в пространствата между проводниците. И ние, разбира се, отново получаваме уравнението на Поасон

Следователно показахме, че нашият първоначален интеграл U* достига минимум дори когато се изчислява в пространството между проводниците, всеки от които е с фиксиран потенциал [това означава, че всяка тестова функция φ(g, y,z) трябва да бъде равен на определения потенциал на проводника, когато (x, y,z) - точки от повърхността на проводника]. Има интересен специален случай, когато зарядите са разположени само върху проводници. Тогава

и нашият минимален принцип ни казва, че в случай, когато всеки проводник има свой предварително определен потенциал, потенциалите в пространствата между тях се регулират така, че интегралът U* се оказва възможно най-малък. Какъв вид интеграл е това? Терминът Vφ е електрическото поле. Това означава, че интегралът е електростатична енергия. Правилното поле е единственото, което от всички полета, получени като потенциален градиент, има най-ниската обща енергия.

Бих искал да използвам този резултат, за да разреша някакъв конкретен проблем и да ви покажа, че всички тези неща имат истинско практическо значение. Да предположим, че взех два проводника под формата на цилиндричен кондензатор.

Вътрешният проводник има потенциал, равен на, да речем, V, а за външната - нула. Нека радиусът на вътрешния проводник е равен на а,и външни - b.Сега можем да приемем, че разпределението на потенциалите между тях е всякакви.Но ако вземем правилностойност на φ и изчислете
(ε 0 /2) ∫ (Vφ) 2 dVтогава енергията на системата трябва да бъде 1/2CV 2.

Така че, като използвате нашия принцип, можете да изчислите капацитета СЪС.Ако вземем неправилно разпределение на потенциала и се опитаме да оценим капацитета на кондензатора, използвайки този метод, ще стигнем до твърде голяма стойност на капацитета за фиксиран V. Всеки изчислен потенциал φ, който не съвпада точно с истинската му стойност, също ще доведе до неправилна стойност на C, по-голяма от необходимата. Но ако неправилно избраният потенциал cp все още е грубо приближение, тогава капацитетът СЪСще се получи с добра точност, тъй като грешката в C е стойност от втори ред в сравнение с грешката в φ.

Да приемем, че не знам капацитета на цилиндричния кондензатор. Тогава, за да я разпозная, мога да използвам този принцип. Просто ще тествам различни функции на φ като потенциал, докато постигна най-ниската стойност СЪС.Да кажем, например, че съм избрал потенциал, който съответства на постоянно поле. (Знаете, разбира се, че полето тук всъщност не е постоянно; то варира като 1/r) Ако полето е постоянно, това означава, че потенциалът зависи линейно от разстоянието. За да бъде напрежението върху проводниците необходимо, функцията φ трябва да има формата

Тази функция е равна на V при r=a,нула при r =b,и между тях има постоянен наклон, равен на - V/(b—А).И така, за да определим интеграла U*, просто трябва да умножите квадрата на този градиент по ε o /2 и да интегрирате върху целия обем. Нека извършим това изчисление за цилиндър с единица дължина. Обемен елемент на радиус rе равно на 2πrdr. Извършвайки интеграцията, откривам, че първият ми тест дава следния капацитет:

Така че получавам формула за капацитет, която, макар и неправилна, е някакво приближение:

Разбира се, той е различен от правилния отговор C=2πε 0 /ln (b/a),но като цяло не е толкова зле. Нека се опитаме да го сравним с правилния отговор за няколко стойности b/a.Числата, които изчислих, са показани в следващата таблица.

Дори когато b/a=2(и това вече води до доста големи разлики между постоянните и линейните полета), все още получавам доста приемливо приближение. Отговорът, разбира се, както се очакваше, е малко прекалено висок. Но ако тънък проводник се постави вътре в голям цилиндър, тогава всичко изглежда много по-зле. Тогава полето се променя много силно и замяната му с постоянно поле не води до нищо добро. Когато b/a = 100, надценяваме отговора почти два пъти. За малки b/aситуацията изглежда много по-добре. В обратната граница, когато празнината между проводниците не е много широка (да речем, за b/a = 1,1), постоянното поле се оказва много добро приближение, то дава стойността СЪСс точност до десети от процента.

Сега ще ви кажа как да подобрите това изчисление. (Отговорът за цилиндъра е, разбира се, известен,но същият метод работи за някои други необичайни форми на кондензатор, за които може да не знаете правилния отговор.) Следващата стъпка е да намерите по-добро приближение за неизвестния истински потенциал φ. Да кажем, че можете да тествате константата плюс показателя φ и т.н. Но как да разберете, че имате най-доброто приближение, ако не знаете истинското φ? Отговор:Пребройте го СЪС;колкото по-ниска е, толкова по-близо до истината. Нека тестваме тази идея. Нека потенциалът не е линеен, а, да речем, квадратичен по r, а електрическото поле не е постоянно, а линейно. Повечето общквадратна форма, която се превръща в φ=O, когато r=би в φ=F при r=a,това ли е:

където α е постоянно число. Тази формула е малко по-сложна от предишната. Той включва както квадратичен, така и линеен член. Много лесно се получава поле от него. Това е равно на просто

Сега това трябва да бъде повдигнато на квадрат и интегрирано върху обема. Но чакай малко. Какво трябва да взема за α? Мога да приема f за парабола, но коя? Ето какво ще направя: изчисля капацитета при произволно α.ще взема

Това изглежда малко объркващо, но така се оказва след интегрирането на квадрата на полето. Сега мога да избирам сам. Знам, че истината е по-ниска от всичко, което смятам да изчисля. Без значение какво поставям вместо a, отговорът пак ще бъде твърде голям. Но ако продължа играта си с α и се опитам да постигна възможно най-ниската стойност С,тогава тази най-ниска стойност ще бъде по-близо до истината от всяка друга стойност. Следователно сега трябва да избера α, така че стойността СЪСдостигна своя минимум. Обръщайки се към обикновеното диференциално смятане, аз съм убеден, че минимумът СЪСще бъде, когато α =— 2 b/(b+а). Замествайки тази стойност във формулата, получавам най-малкия капацитет

Разбрах какво дава тази формула СЪСпри различни стойности b/a.Назовах тези числа СЪС(квадратичен). Ето таблица, която прави сравнение СЪС(квадратичен) с СЪС(вярно).

Например, когато съотношението на радиуса е 2:1, получавам 1,444. Това е много добро приближение до верния отговор, 1,4423. Дори и с големи У априближението остава доста добро - много по-добро от първото приближение. Той остава поносим (надценен само с 10%) дори при b/a = 10: 1. Голямо несъответствие възниква само при съотношение 100: 1. Получавам СЪСравно на 0,346 вместо на 0,267. От друга страна, за съотношение на радиуса 1,5 съгласието е отлично, а за b/a=1,1отговорът е 10.492065 вместо очакваните 10.492070. Където бихте очаквали добър отговор, той се оказва много, много добър.

Дадох всички тези примери, първо, за да демонстрирам теоретичната стойност на принципа на минималното действие и като цяло на всички принципи на минимума, и второ, за да ви покажа тяхната практическа полезност, а не изобщо, за да изчисля капацитета които вече имаме, знаем много добре. За всяка друга форма можете да опитате приблизително поле с няколко неизвестни параметъра (като α) и да ги напаснете до минимум. Ще получите превъзходни числени резултати за проблеми, които не могат да бъдат решени по друг начин.

Те му се подчиняват и затова този принцип е едно от ключовите положения на съвременната физика. Уравненията на движението, получени с негова помощ, се наричат уравнения на Ойлер-Лагранж.

Първата формулировка на принципа е дадена от P. Maupertuis през годината, като веднага изтъква универсалния му характер, считайки го за приложим в оптиката и механиката. От този принцип той извежда законите за отражение и пречупване на светлината.

История

Мопертюи стига до този принцип от чувството, че съвършенството на Вселената изисква известна икономия в природата и противоречи на всеки безполезен разход на енергия. Естественото движение трябва да е такова, че определено количество да бъде минимално. Всичко, което трябваше да направи, беше да намери тази стойност, което той продължи да прави. Това беше продуктът на продължителността (времето) на движение в системата с удвоената стойност, която сега наричаме кинетична енергия на системата.

Ойлер (в „Размисли върху quelques loix générales de la nature“, 1748) приема принципа на най-малкото действие, наричайки действието „усилие“. Неговият израз в статиката съответства на това, което сега бихме нарекли потенциална енергия, така че нейното твърдение за най-малко действие в статиката е еквивалентно на условието за минимална потенциална енергия за равновесна конфигурация.

В класическата механика

Принципът на най-малкото действие служи като фундаментална и стандартна основа на формулировките на Лагранж и Хамилтон на механиката.

Първо нека разгледаме конструкцията така: Лагранжева механика. Използвайки примера на физическа система с една степен на свобода, нека припомним, че действието е функционал по (обобщени) координати (в случай на една степен на свобода - една координата), т.е. изразява се чрез така че всяка възможна версия на функцията е свързана с определено число - действие (в този смисъл можем да кажем, че действието като функционал е правило, което позволява на всяка дадена функция да изчисли добре дефинирано число - също наречено действие). Действието изглежда така:

където е лагранжианът на системата, в зависимост от обобщената координата, нейната първа производна по време, а също, евентуално, изрично по време. Ако системата има по-голям брой степени на свобода, тогава лагранжианът зависи от по-голям брой обобщени координати и техните първи производни по време. По този начин действието е скаларен функционал в зависимост от траекторията на тялото.

Фактът, че действието е скаларно, улеснява записването му във всякакви обобщени координати, основното е позицията (конфигурацията) на системата да се характеризира недвусмислено от тях (например вместо декартови координати те могат да бъдат полярни координати, разстояния между точки на системата, ъгли или техните функции и др. .d.).

Действието може да бъде изчислено за напълно произволна траектория, колкото и „дива“ и „неестествена“ да е тя. В класическата механика обаче сред целия набор от възможни траектории има само една, по която тялото действително ще се движи. Принципът на стационарното действие точно дава отговор на въпроса как всъщност ще се движи тялото:

Това означава, че ако е даден лагранжианът на системата, тогава с помощта на вариационното смятане можем да установим как точно ще се движи тялото, като първо получим уравненията на движението - уравненията на Ойлер-Лагранж и след това ги решим. Това позволява не само сериозно да се обобщи формулировката на механиката, но и да се изберат най-удобните координати за всеки конкретен проблем, не само декартови, което може да бъде много полезно за получаване на най-простите и лесно решени уравнения.

където е функцията на Хамилтън на тази система; - (обобщени) координати, - спрегнати (обобщени) импулси, които заедно характеризират във всеки даден момент от времето динамичното състояние на системата и, като всеки е функция на времето, като по този начин характеризира еволюцията (движението) на системата. В този случай, за да се получат уравненията на движението на системата под формата на каноничните уравнения на Хамилтън, е необходимо да се променя действието, записано по този начин, независимо за всички и .

Трябва да се отбележи, че ако от условията на проблема по принцип е възможно да се намери законът на движението, тогава това автоматично Неозначава, че е възможно да се конструира функционал, който приема стационарна стойност по време на истинско движение. Пример е съвместното движение на електрически заряди и монополи - магнитни заряди - в електромагнитно поле. Техните уравнения на движение не могат да бъдат изведени от принципа на стационарното действие. По същия начин някои хамилтонови системи имат уравнения на движение, които не могат да бъдат извлечени от този принцип.

Примери

Тривиалните примери помагат да се оцени използването на принципа на работа чрез уравненията на Ойлер-Лагранж. Свободна частица (маса ми скорост v) в евклидовото пространство се движи по права линия. Използвайки уравненията на Ойлер-Лагранж, това може да се покаже в полярни координати, както следва. При липса на потенциал функцията на Лагранж е просто равна на кинетичната енергия

в ортогонална координатна система.

В полярни координати кинетичната енергия, а оттам и функцията на Лагранж става

Радиалните и ъгловите компоненти на уравненията стават съответно:

Решаване на тези две уравнения

Ето условна нотация за безкрайно множествена функционална интеграция по всички траектории x(t) и е константата на Планк. Подчертаваме, че по принцип действието в експонентата се появява (или може да се появи) само по себе си при изучаване на еволюционния оператор в квантовата механика, но за системи, които имат точен класически (неквантов) аналог, то е точно равно на обичайното класическо действие.

Математическият анализ на този израз в класическата граница - за достатъчно големи , т.е. за много бързи колебания на въображаемата експоненциална - показва, че огромното мнозинство от всички възможни траектории в този интеграл се компенсират взаимно в границата (формално за ). За почти всеки път има път, по който фазовото изместване ще бъде точно обратното и те ще дадат нулев принос. Само тези траектории, за които действието е близо до екстремната стойност (за повечето системи - до минимума), не се редуцират. Това е чисто математически факт от теорията на функциите на комплексна променлива; Например методът на стационарната фаза се основава на него.

В резултат на това частицата, в пълно съответствие със законите на квантовата механика, се движи едновременно по всички траектории, но при нормални условия само траектории, близки до стационарни (т.е. класически), допринасят за наблюдаваните стойности. Тъй като квантовата механика се трансформира в класическа механика в границите на високите енергии, можем да приемем, че това е квантово-механично извеждане на класическия принцип на стационарност на действието.

В квантовата теория на полето

В квантовата теория на полето принципът на стационарното действие също се прилага успешно. Лагранжианската плътност тук включва операторите на съответните квантови полета. Въпреки че тук е по-правилно по същество (с изключение на класическия предел и отчасти квазикласиката) да се говори не за принципа на стационарност на действието, а за интегрирането на Файнман по траектории в конфигурацията или фазовото пространство на тези полета - използвайки току-що споменатата лагранжева плътност.

Допълнителни обобщения

В по-широк смисъл едно действие се разбира като функционал, който дефинира преобразуване от конфигурационно пространство към набор от реални числа и като цяло не е необходимо да бъде интеграл, тъй като нелокалните действия са възможни по принцип, поне теоретично. Освен това конфигурационното пространство не е непременно функционално пространство, защото може да има некомутативна геометрия.

История

В класическата механика

Примери

в ортогонална координатна система.

В полярни координати кинетичната енергия, а оттам и функцията на Лагранж става

Радиалните и ъгловите компоненти на уравненията стават съответно:

Решаване на тези две уравнения

В квантовата теория на полето

Допълнителни обобщения

Принципът на най-малкото действие, формулиран за първи път точно от Якоби, е подобен на принципа на Хамилтън, но по-малко общ и по-труден за доказване. Този принцип е приложим само в случаите, когато връзките и силовата функция не зависят от времето и когато следователно има интеграл на живата сила.

Този интеграл има формата:

Посоченият по-горе принцип на Хамилтън гласи, че изменението на интеграла

е равно на нула при прехода на действителното движение към всяко друго безкрайно близко движение, което премества системата от същата начална позиция в същата крайна позиция за същия период от време.

Принципът на Якоби, напротив, изразява свойство на движението, което не зависи от времето. Якоби разглежда интеграла

определящо действие. Принципът, който той установи, гласи, че вариацията на този интеграл е нула, когато сравним действителното движение на системата с всяко друго безкрайно близко движение, което отвежда системата от същата начална позиция до същата крайна позиция. В този случай не обръщаме внимание на изразходвания период от време, а наблюдаваме уравнение (1), т.е. уравнението на работната сила със същата стойност на константата h, както при реалното движение.

Това необходимо условие за екстремум води, най-общо казано, до минимум на интеграла (2), откъдето идва и името принцип на най-малко действие. Минималното условие изглежда най-естествено, тъй като стойността на T е по същество положителна и следователно интеграл (2) трябва задължително да има минимум. Съществуването на минимум може да бъде строго доказано, ако само периодът от време е достатъчно малък. Доказателството за тази позиция може да се намери в известния курс на Darboux по теория на повърхността. Ние обаче няма да го представяме тук и ще се ограничим до извеждане на условието

432. Доказателство на принципа на най-малкото действие.

При действителното изчисление срещаме една трудност, която не присъства в доказателството на теоремата на Хамилтън. Променливата t вече не остава независима от вариацията; следователно вариации на q i и q. са свързани с изменението на t чрез сложна връзка, която следва от уравнение (1). Най-лесният начин да се преодолее тази трудност е да се промени независимата променлива, като се избере такава, чиито стойности попадат между постоянни граници, които не зависят от времето. Нека k е нова независима променлива, чиито граници се приемат за независими от t. При преместване на системата параметрите и t ще бъдат функции на тази променлива

Нека буквите с прости числа q означават производни на параметрите q по време.

Тъй като връзките, по предположение, не зависят от времето, декартовите координати x, y, z са функции на q, които не съдържат време. Следователно техните производни ще бъдат линейни хомогенни функции на q и 7 ще бъде хомогенна квадратна форма на q, коефициентите на която са функции на q. Ние имаме

За да разграничим производните на q по отношение на времето, ние означаваме, като използваме скоби, (q), производните на q, взети по отношение на и приведени в съответствие с това

тогава ще имаме

и интеграл (2), изразен чрез новата независима променлива A, ще приеме формата;

Производната може да бъде елиминирана с помощта на теоремата за живата сила. Наистина, интегралът на работната сила ще бъде

Замествайки този израз във формулата за, намаляваме интеграла (2) до формата

По този начин интегралът, определящ действието, придоби окончателната си форма (3). Функцията интегранд е квадратен корен от квадратната форма на количествата

Нека покажем, че диференциалните уравнения на екстремалите на интеграла (3) са точно уравненията на Лагранж. Уравненията на екстремалите, базирани на общите формули на вариационното смятане, ще бъдат:

Нека умножим уравненията по 2 и извършим частично диференциране, като вземем предвид, че не съдържа, тогава получаваме, ако не напишем индекс,

Това са уравнения на екстремалите, изразени чрез независимата променлива. Задачата сега е да се върнем към независимата променлива

Тъй като Γ е хомогенна функция от втора степен на и е хомогенна функция от първа степен, имаме

От друга страна, теоремата за живата сила може да се приложи към факторите на производните в уравненията на екстремалите, което води, както видяхме по-горе, до заместването

В резултат на всички замествания уравненията на екстремалите се свеждат до вида

Така стигнахме до уравненията на Лагранж.

433. Случаят, когато няма движещи сили.

В случая, когато няма движещи сили, има уравнение за жива сила и имаме

Условието интегралът да бъде минимален в този случай е, че съответната стойност от -10 трябва да бъде най-малката. По този начин, когато няма движещи сили, тогава сред всички движения, при които живата сила поддържа една и съща зададена стойност, действителното движение е това, което премества системата от нейното първоначално положение в нейното крайно положение за най-кратко време.

Ако системата се сведе до една точка, движеща се върху неподвижна повърхност, тогава действителното движение, сред всички движения на повърхността, извършени с една и съща скорост, е движението, при което точката се движи от първоначалната си позиция до крайната позиция в най-кратък

времеви интервал. С други думи, точката описва на повърхността най-късата линия между нейните две позиции, т.е. геодезическа линия.

434. Забележка.

Принципът на най-малкото действие предполага, че системата има няколко степени на свобода, тъй като ако имаше само една степен на свобода, тогава едно уравнение би било достатъчно, за да се определи движението. Тъй като в този случай движението може да бъде напълно определено от уравнението на живата сила, тогава действителното движение ще бъде единственото, което удовлетворява това уравнение и следователно не може да бъде сравнено с друго движение.

НАЙ-МАЛКО ЕФЕКТИВЕН ПРИНЦИП

Един от вариационните принципи на механиката, според Кром, за даден клас механични движения, сравнени едно с друго. система, валидна е тази, за която физ. размер, наречен действие, има най-малка (по-точно стационарна) стойност. Обикновено N. d. p. се използва в една от двете форми.

а) Н. д. п. под формата на Хамилтън - Остроградски установява, че сред всички кинематично възможни движения на система от една конфигурация в друга (близка до първата), извършени за един и същи период от време, валидно е това, за което хамилтоновото действие S ще бъде най-малкото. математика изразът на N. d.p. в този случай има формата: dS = 0, където d е символът на непълна (изохронна) вариация (т.е., за разлика от пълната вариация, времето не се променя в него).

б) N. d. p. във формата на Мопертюи - Лагранж установява, че сред всички кинематично възможни движения на система от една конфигурация към друга близка до нея, извършени при запазване на същата стойност на общата енергия на системата, валидното е, че за - Следователно действието на Лагранж W ще бъде най-малкото. математика изразът на N. d.p. в този случай има формата DW = 0, където D е символът на пълната вариация (за разлика от принципа на Хамилтън-Остроградски, тук се променят не само координатите и скоростите, но и времето на движение на система от една конфигурация в друга). Н.д.п.в. В този случай той е валиден само за консервативни и освен това за холономни системи, докато в първия случай неконсервативният принцип е по-общ и по-специално може да бъде разширен до неконсервативни системи. N.D.P. се използват за съставяне на уравнения на механичното движение. системи и да изучава общите свойства на тези движения. С подходящо обобщение на понятията NDP намира приложения в механиката на непрекъснатата среда, в електродинамиката и кванта. механика и др.

- същото като...
Физическа енциклопедия
- m-оператор, оператор за минимизиране, - метод за конструиране на нови функции от други функции, състоящ се от следното...
Математическа енциклопедия
- един от вариационните принципи на механиката, според който за даден клас механични движения се сравняват едно с друго. система се извършва това, за което действието е минимално...
Естествени науки. енциклопедичен речник
- един от най-важните закони на механиката, установен от руския учен М.В. Остроградски...
Руска енциклопедия
Речник на юридическите термини
- в конституционното право на редица държави принципът, според който общопризнатите принципи и норми на международното право са неразделна част от правната система на съответната държава ...
Енциклопедия на юриста
- в конституционното право на редица държави принципът, според който общопризнатите норми на международното право са неразделна част от националната правна система...
Голям юридически речник
- най-късото разстояние от центъра на експлозивния заряд до свободната повърхност - линия на най-малкото съпротивление - křivka nejmenšího odporu - Line der geringsten Festigkeit - robbantás minimális ellenállási tengelyvonala - hamgiin baga...
Строителен речник
- ако е възможно да се движат точки от деформируемо тяло в различни посоки, всяка точка от това тяло се движи в посока на най-малко съпротивление...
Енциклопедичен речник по металургия
- правило, по което съществуващите материални запаси обикновено се оценяват или на най-ниската цена, или на най-ниската продажна цена...
Речник на бизнес термините
- в конституционното право на редица държави - принципът, според който общопризнатите принципи и норми на международното право са неразделна част от правната система на съответната държава и действат...
Енциклопедичен речник по икономика и право
- един от вариационните принципи на механиката, според който за даден клас движения на механична система, съпоставени едно с друго, валидно е това, за което физичната величина,...
- същото като принципа на Гаус...
Велика съветска енциклопедия
- един от вариационните принципи на механиката; същото като принципа на най-малкото действие...
Велика съветска енциклопедия
- един от вариационните принципи на механиката, според който за даден клас движения на механична система, сравнени едно с друго, това, за което действието е минимално...
Голям енциклопедичен речник
- Книга Изберете най-лесния метод на действие, избягване на препятствия, избягване на трудности...
Фразеологичен речник на руския литературен език

„ПРИНЦИПЪТ НА НАЙ-МАЛКАТА СТОЙНОСТ“ в книгите

2.5.1. Принцип на работа на устройството

От книгата Развлекателна електроника [Нетрадиционна енциклопедия на полезни схеми] автор Кашкаров Андрей Петрович

2.5.1. Принципът на работа на устройството Принципът на работа на устройството е прост. Когато светлинният поток, излъчван от светодиода HL1, се отразява от обекта и удари фотодетектора, електронният блок, реализиран на 2 микросхеми - компаратора KR1401SA1 и таймера KR1006VI1, произвежда

Принципът на действие на терафимите

От книгата Тайните знания. Теория и практика на Агни Йога автор Рьорих Елена Ивановна

Принципът на действие на терафим 02.24.39 Вие знаете, че всяко осъзнаване и представяне на всеки обект по този начин ни доближава до него. Както знаете, психическите слоеве на един обект могат да бъдат пренесени върху неговите терафими. Астралните терафими на далечни светове и

Три условия за прилагане на закона за най-малкото усилие

От книгата Мъдростта на Дийпак Чопра [Получете това, което искате, като следвате 7-те закона на Вселената] от Тим Гудман

Три условия за действие на Закона за най-малкото усилие. Нека да видим какви условия са необходими, за да привлечете този творчески поток от енергия от Вселената в живота си – енергията на любовта, и следователно Законът за най-малкото усилие да започне да работи в живота ви .

Глава 19 ПРИНЦИП НА НАЙ-МАЛКИЯ ЕФЕКТ

От книга 6. Електродинамика автор Файнман Ричард Филипс

Глава 19 ПРИНЦИПЪТ НА НАЙ-МАЛШИЯ ЕФЕКТ Добавка, направена след лекция Когато бях в училище, нашият учител по физика, на име Бадер, веднъж ме извика след часа и каза: „Изглеждаш така, сякаш си ужасно уморен от всичко; чуйте едно интересно нещо

5. Принцип на най-малкото действие

От книгата Революция във физиката от дьо Бройл Луис

5. Принцип на най-малкото действие Уравненията за динамиката на материална точка в поле от сили с потенциал могат да бъдат получени въз основа на принципа, който най-общо се нарича принцип на Хамилтън или принцип на стационарно действие. Според този принцип от всички

Принцип на работа

От книгата Ръководство на ключаря за брави от Филипс Бил

Принцип на работа Възможността за въртене на цилиндъра зависи от позицията на щифтовете, която от своя страна се определя от гравитацията, действието на пружините и силата на ключа (или главния ключ; за информация относно главните ключове вижте Глава 9) . При липса на ключ гравитацията и пружините се натискат

Принцип на стационарно действие

От книгата Велика съветска енциклопедия (ST) на автора TSB

Принцип на най-малкото действие

TSB

Принцип на най-малката принуда

От книгата Велика съветска енциклопедия (НА) на автора TSB

2.5.1. Принцип на работа

От книгата Релейна защита в електрически разпределителни мрежи B90 автор Буличев Александър Виталиевич

2.5.1. Принцип на действие В електрически мрежи с двупосочно захранване и в пръстеновидни мрежи конвенционалната токова защита не може да работи избирателно. Например в електрическа мрежа с два източника на захранване (фиг. 2.15), където ключове и защити са монтирани от двете страни

Принцип на работа

От книгата Turbo Suslik. Как да спреш да се прецакваш и да започнеш да живееш автор Леушкин Дмитрий

Принципът на действие „Обработи това” всъщност е един вид „макро”, който с една фраза стартира цял куп процеси в подсъзнанието, чиято цел е да обработят избрания мисловен материал. Самият манипулатор включва 7 различни модула, някои от които

Как да започнете да следвате закона за най-малкото усилие: Три необходими действия

От книгата A Guide to Growing Capital от Джоузеф Мърфи, Дейл Карнеги, Екхарт Толе, Дийпак Чопра, Барбара Шер, Нийл Уолш автор Стърн Валентин

Как да започнете да следвате Закона за най-малкото усилие: три необходими действия За да започне да работи Законът за най-малкото усилие, трябва не само да спазвате трите условия, споменати по-горе, но и да извършите три действия Първо действие: започнете да приемате света такъв, какъвто е е Приемам

11. Физика и айкидо на най-малкото действие

автор Миндел Арнолд

11. Физика и айкидо с най-малък ефект Когато духа, има само вятър. Когато вали, има само дъжд. Когато облаците минават, слънцето грее през тях. Ако се отворите за прозрението, тогава вие сте едно с прозрението. И можете да го използвате напълно. Ако отворите

Принципът на Лайбниц за най-малко действие "Vis Viva"

От книгата Геопсихология в шаманизма, физиката и даоизма автор Миндел Арнолд

Принципът на Лайбниц за най-малкото действие „Vis Viva“ Ние всички трябва да благодарим на Вилхелм Готфрид Лайбниц (1646–1716) за принципа на най-малкото действие. Един от първите „модерни“ физици и математици, Лайбниц е живял по времето на Нютон – епоха, когато учените са били по-открити

Айкидо - въплъщение на принципа на най-малкото действие

От книгата Геопсихология в шаманизма, физиката и даоизма автор Миндел Арнолд

Айкидо - въплъщение на принципа на най-малкото действие Нашата психология и технология до голяма степен се ръководят от концепция, много близка до идеята за най-малко действие. Постоянно се опитваме да улесним живота си. Днешните компютри не са достатъчно бързи; Те трябва да