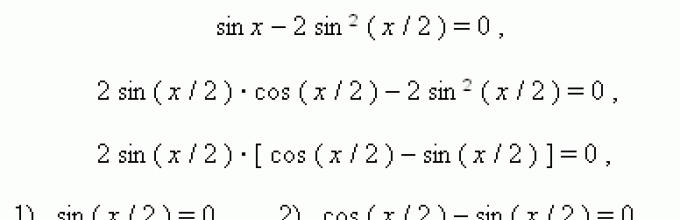Η επίλυση μιας τριγωνομετρικής εξίσωσης αποτελείται από δύο στάδια: μετασχηματισμός εξίσωσηςγια να το πάρεις πιο απλότύπου (βλ. παραπάνω) και λύσητο πιο απλό που προκύπτει τριγωνομετρική εξίσωση.Υπάρχουν επτά βασικές μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων.
1. Αλγεβρική μέθοδος.
(μέθοδος αντικατάστασης και αντικατάστασης μεταβλητής).
2. Παραγοντοποίηση.
Παράδειγμα 1. Λύστε την εξίσωση:αμαρτία Χ+κος Χ = 1 .
Λύση Ας μετακινήσουμε όλους τους όρους της εξίσωσης προς τα αριστερά:
Αμαρτία Χ+κος Χ – 1 = 0 ,
Ας μετασχηματίσουμε και παραγοντοποιήσουμε την έκφραση
Η αριστερή πλευρά της εξίσωσης:

Παράδειγμα 2. Λύστε την εξίσωση: cos 2 Χ+ αμαρτία Χ cos Χ = 1.
Λύση: cos 2 Χ+ αμαρτία Χ cos Χ– αμαρτία 2 Χ– cos 2 Χ = 0 ,
Αμαρτία Χ cos Χ– αμαρτία 2 Χ = 0 ,
Αμαρτία Χ· (συν Χ– αμαρτία Χ ) = 0 ,

Παράδειγμα 3. Λύστε την εξίσωση: cos 2 Χ– συν 8 Χ+ cos 6 Χ = 1.
Λύση: cos 2 Χ+ cos 6 Χ= 1 + συν 8 Χ,
2 ως 4 Χ cos 2 Χ= 2κοσ² 4 Χ ,
Cos 4 Χ · (συν 2 Χ– cos 4 Χ) = 0 ,
Cos 4 Χ · 2 αμαρτία 3 Χαμαρτία Χ = 0 ,
1). cos 4 Χ= 0, 2). αμαρτία 3 Χ= 0, 3). αμαρτία Χ = 0 ,

3. Μείωση σε ομοιογενής εξίσωση.Η εξίσωση που ονομάζεται ομοιογενής από Σχετικά με αμαρτίαΚαι cos , Αν όλα αυτά όρους του ίδιου βαθμού σε σχέση με αμαρτίαΚαι cosίδια γωνία. Για να λύσετε μια ομοιογενή εξίσωση, χρειάζεστε: ΕΝΑ) μετακινήστε όλα τα μέλη του στην αριστερή πλευρά. σι) βάλτε όλους τους κοινούς παράγοντες εκτός παρενθέσεων. V) εξισώνουν όλους τους παράγοντες και τις αγκύλες με μηδέν. σολ) παρενθέσεις ίσες με μηδέν δίνουν ομοιογενής εξίσωση μικρότερου βαθμού, η οποία πρέπει να χωριστεί σε cos(ή αμαρτία) στο ανώτερο πτυχίο? ρε) λύστε την αλγεβρική εξίσωση που προκύπτει ως προςβυρσοδέψω . αμαρτία 2 Χ+ 4 αμαρτία Χ cos Χ+ 5 κοσ 2 Χ = 2. Λύση: 3 sin 2 Χ+ 4 αμαρτία Χ cos Χ+ 5 co 2 Χ= 2 αμαρτία 2 Χ+ 2 συν 2 Χ , Αμαρτία 2 Χ+ 4 αμαρτία Χ cos Χ+ 3 co 2 Χ = 0 , Μαύρισμα 2 Χ+ 4 μαύρισμα Χ + 3 = 0 , από εδώ y 2 + 4y +3 = 0 , Οι ρίζες αυτής της εξίσωσης είναι:y 1 = - 1, y 2 = - 3, επομένως 1) μαύρισμα Χ= –1, 2) μαύρισμα Χ = –3, |
4. Μετάβαση στη μισή γωνία.
Ας δούμε αυτή τη μέθοδο χρησιμοποιώντας ένα παράδειγμα:
ΠΑΡΑΔΕΙΓΜΑ Λύστε την εξίσωση: 3αμαρτία Χ– 5 κοσ Χ = 7.
Λύση: 6 αμαρτία ( Χ/ 2) cos ( Χ/ 2) – 5 cos² ( Χ/ 2) + 5 αμαρτία² ( Χ/ 2) =
7 αμαρτία² ( Χ/ 2) + 7 cos² ( Χ/ 2) ,
2 αμαρτία² ( Χ/ 2) – 6 αμαρτία ( Χ/ 2) cos ( Χ/ 2) + 12 cos² ( Χ/ 2) = 0 ,
μαύρισμα²( Χ/ 2) – 3 μαύρισμα ( Χ/ 2) + 6 = 0 ,
. . . . . . . . . .
5. Εισαγωγή βοηθητικής γωνίας.
Θεωρήστε μια εξίσωση της μορφής:
ένααμαρτία Χ + σι cos Χ = ντο ,
Οπου ένα, σι, ντο– συντελεστές·Χ– άγνωστο.

Τώρα οι συντελεστές της εξίσωσης έχουν τις ιδιότητες του ημιτόνου και του συνημιτόνου, και συγκεκριμένα: συντελεστής (απόλυτη τιμή) του καθενός εκ των οποίων όχι περισσότερα από 1, και το άθροισμα των τετραγώνων τους είναι 1. Τότε μπορούμε να υποδηλώσουμε τους αναλόγως Πως cos and sin (εδώ - τα λεγόμενα βοηθητική γωνία), Καιπάρτε την εξίσωσή μας
Οι κύριες μέθοδοι για την επίλυση τριγωνομετρικών εξισώσεων είναι: η αναγωγή των εξισώσεων στην απλούστερη (χρησιμοποιώντας τριγωνομετρικούς τύπους), η εισαγωγή νέων μεταβλητών και η παραγοντοποίηση. Ας δούμε τη χρήση τους με παραδείγματα. Προσοχή στη μορφή γραφής λύσεων τριγωνομετρικών εξισώσεων.
Απαραίτητη προϋπόθεση για την επιτυχή επίλυση τριγωνομετρικών εξισώσεων είναι η γνώση τριγωνομετρικών τύπων (θέμα 13 της εργασίας 6).
Παραδείγματα.
1. Εξισώσεις ανάγονται στην απλούστερη.
1) Λύστε την εξίσωση
Λύση:
Απάντηση:
2) Να βρείτε τις ρίζες της εξίσωσης
(sinx + cosx) 2 = 1 – sinxcosx, που ανήκουν στο τμήμα.
Λύση:
Απάντηση:
2. Εξισώσεις που ανάγονται σε τετραγωνικό.
1) Λύστε την εξίσωση 2 sin 2 x – cosx –1 = 0.
Λύση:Χρησιμοποιώντας αμαρτία τύπος 2 x = 1 – cos 2 x, παίρνουμε
Απάντηση:
2) Λύστε την εξίσωση cos 2x = 1 + 4 cosx.
Λύση:Χρησιμοποιώντας τον τύπο cos 2x = 2 cos 2 x – 1, παίρνουμε
Απάντηση:
3) Λύστε την εξίσωση tgx – 2ctgx + 1 = 0
Λύση:
Απάντηση:
3. Ομογενείς εξισώσεις
1) Λύστε την εξίσωση 2sinx – 3cosx = 0
Λύση: Έστω cosx = 0, μετά 2sinx = 0 και sinx = 0 – αντίφαση με το γεγονός ότι sin 2 x + cos 2 x = 1. Αυτό σημαίνει cosx ≠ 0 και μπορούμε να διαιρέσουμε την εξίσωση με cosx. Παίρνουμε
Απάντηση:
2) Λύστε την εξίσωση 1 + 7 cos 2 x = 3 sin 2x
Λύση:
Χρησιμοποιούμε τους τύπους 1 = sin 2 x + cos 2 x και sin 2x = 2 sinxcosx, παίρνουμε
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Έστω cosx = 0, τότε sin 2 x = 0 και sinx = 0 – αντίφαση με το γεγονός ότι sin 2 x + cos 2 x = 1.
Αυτό σημαίνει cosx ≠ 0 και μπορούμε να διαιρέσουμε την εξίσωση με cos 2 x .
Παίρνουμε
tg 2 x – 6 tgx + 8 = 0
Ας συμβολίσουμε tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y2 = 2
α) tgx = 4, x= arctan4 + 2 κ, κ
β) tgx = 2, x= arctan2 + 2 κ, κ .
Απάντηση: arctg4 + 2 κ, arctan2 + 2 κ, κ
4. Εξισώσεις της φόρμας ένα sinx + σι cosx = s, s≠ 0.
1) Λύστε την εξίσωση.
Λύση:
Απάντηση:
5. Εξισώσεις που λύνονται με παραγοντοποίηση.
1) Λύστε την εξίσωση sin2x – sinx = 0.
Ρίζα της εξίσωσης φά (Χ) = φ ( Χ) μπορεί να χρησιμεύσει μόνο ως αριθμός 0. Ας ελέγξουμε αυτό:
cos 0 = 0 + 1 – η ισότητα είναι αληθής.
Ο αριθμός 0 είναι η μόνη ρίζα αυτής της εξίσωσης.
Απάντηση: 0.
Μπορείτε να παραγγείλετε αναλυτική λύσητο καθήκον σου!!!
Ισότητα που περιέχει το άγνωστο κάτω από το πρόσημο τριγωνομετρική συνάρτηση(«sin x, cos x, tan x» ή «ctg x») ονομάζεται τριγωνομετρική εξίσωση και είναι οι τύποι τους που θα εξετάσουμε περαιτέρω.
Οι απλούστερες εξισώσεις είναι «sin x=a, cos x=a, tg x=a, ctg x=a», όπου «x» είναι η γωνία που πρέπει να βρεθεί, «a» είναι οποιοσδήποτε αριθμός. Ας γράψουμε τους τύπους ρίζας για καθένα από αυτά.
1. Εξίσωση `sin x=a`.
Για το `|a|>1` δεν έχει λύσεις.
Όταν `|α| Το \leq 1` έχει άπειρο αριθμό λύσεων.
Τύπος ρίζας: `x=(-1)^n arcsin a + \pi n, n \in Z`
2. Εξίσωση `cos x=a`
Για `|a|>1` - όπως στην περίπτωση του ημιτονοειδούς, λύσεις μεταξύ πραγματικούς αριθμούςδεν έχει.
Όταν `|α| Το \leq 1` έχει άπειρο αριθμό λύσεων.
Τύπος ρίζας: `x=\pm arccos a + 2\pi n, n \in Z`

Ειδικές περιπτώσεις για ημίτονο και συνημίτονο σε γραφήματα. 
3. Εξίσωση `tg x=a`
Έχει άπειρο αριθμό λύσεων για οποιεσδήποτε τιμές του 'a'.
Τύπος ρίζας: `x=arctg a + \pi n, n \in Z`

4. Εξίσωση `ctg x=a`
Έχει επίσης έναν άπειρο αριθμό λύσεων για οποιεσδήποτε τιμές του 'a'.
Τύπος ρίζας: `x=arcctg a + \pi n, n \in Z`

Τύποι για τις ρίζες των τριγωνομετρικών εξισώσεων στον πίνακα
Για ημιτονοειδή:  Για το συνημίτονο:
Για το συνημίτονο:  Για εφαπτομένη και συνεφαπτομένη:
Για εφαπτομένη και συνεφαπτομένη:  Τύποι επίλυσης εξισώσεων που περιέχουν αντίστροφες τριγωνομετρικές συναρτήσεις:
Τύποι επίλυσης εξισώσεων που περιέχουν αντίστροφες τριγωνομετρικές συναρτήσεις:

Μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων
Η επίλυση οποιασδήποτε τριγωνομετρικής εξίσωσης αποτελείται από δύο στάδια:
- με τη βοήθεια της μετατροπής του στο απλούστερο.
- λύστε την απλούστερη εξίσωση που προκύπτει χρησιμοποιώντας τους τύπους ρίζας και τους πίνακες που γράφτηκαν παραπάνω.
Ας δούμε τις κύριες μεθόδους λύσης χρησιμοποιώντας παραδείγματα.
Αλγεβρική μέθοδος.
Αυτή η μέθοδος περιλαμβάνει την αντικατάσταση μιας μεταβλητής και την αντικατάστασή της σε μια ισότητα.
Παράδειγμα. Λύστε την εξίσωση: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
κάντε μια αντικατάσταση: `cos(x+\frac \pi 6)=y`, μετά `2y^2-3y+1=0`,
βρίσκουμε τις ρίζες: `y_1=1, y_2=1/2`, από τις οποίες ακολουθούν δύο περιπτώσεις:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.
Απάντηση: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Παραγοντοποίηση.
Παράδειγμα. Λύστε την εξίσωση: `sin x+cos x=1`.
Λύση. Ας μετακινήσουμε όλους τους όρους της ισότητας προς τα αριστερά: `sin x+cos x-1=0`. Χρησιμοποιώντας , μετασχηματίζουμε και παραγοντοποιούμε την αριστερή πλευρά:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.
Απάντηση: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Αναγωγή σε ομοιογενή εξίσωση
Αρχικά, πρέπει να μειώσετε αυτήν την τριγωνομετρική εξίσωση σε μία από τις δύο μορφές:
`a sin x+b cos x=0` (ομογενής εξίσωση πρώτου βαθμού) ή `a sin^2 x + b sin x cos x +c cos^2 x=0` (ομογενής εξίσωση δεύτερου βαθμού).
Στη συνέχεια, διαιρέστε και τα δύο μέρη με «cos x \ne 0» - για την πρώτη περίπτωση, και με «cos^2 x \ne 0» - για τη δεύτερη. Λαμβάνουμε εξισώσεις για «tg x»: «a tg x+b=0» και «a tg^2 x + b tg x +c =0», οι οποίες πρέπει να λυθούν χρησιμοποιώντας γνωστές μεθόδους.
Παράδειγμα. Λύστε την εξίσωση: `2 sin^2 x+sin x cos x - cos^2 x=1`.
Λύση. Ας γράψουμε τη δεξιά πλευρά ως `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Αυτή είναι μια ομοιογενής τριγωνομετρική εξίσωση του δεύτερου βαθμού, διαιρούμε την αριστερή και τη δεξιά πλευρά της με το 'cos^2 x \ne 0', παίρνουμε:
`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0`
`tg^2 x+tg x — 2=0`. Ας εισάγουμε την αντικατάσταση `tg x=t`, με αποτέλεσμα `t^2 + t - 2=0`. Οι ρίζες αυτής της εξίσωσης είναι «t_1=-2» και «t_2=1». Επειτα:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, `n \in Z`.
Απάντηση. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Μετακίνηση στη μισή γωνία
Παράδειγμα. Λύστε την εξίσωση: `11 sin x - 2 cos x = 10`.
Λύση. Ας εφαρμόσουμε τους τύπους διπλής γωνίας, με αποτέλεσμα: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 συν^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Εφαρμόζοντας τα παραπάνω αλγεβρική μέθοδος, παίρνουμε:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Απάντηση. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Εισαγωγή βοηθητικής γωνίας
Στην τριγωνομετρική εξίσωση «a sin x + b cos x =c», όπου a,b,c είναι συντελεστές και x είναι μια μεταβλητή, διαιρέστε και τις δύο πλευρές με το «sqrt (a^2+b^2)»:
`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2 ) +b^2))».
Οι συντελεστές στην αριστερή πλευρά έχουν τις ιδιότητες του ημιτόνου και του συνημιτόνου, δηλαδή το άθροισμα των τετραγώνων τους είναι ίσο με 1 και οι μονάδες τους δεν είναι μεγαλύτερες από 1. Ας τους συμβολίσουμε ως εξής: `\frac a(sqrt (a^2 +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, τότε:
`cos \varphi sin x + sin \varphi cos x =C`.
Ας ρίξουμε μια πιο προσεκτική ματιά στο ακόλουθο παράδειγμα:
Παράδειγμα. Λύστε την εξίσωση: `3 sin x+4 cos x=2`.
Λύση. Διαιρέστε και τις δύο πλευρές της ισότητας με το `sqrt (3^2+4^2)`, παίρνουμε:
`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))».
`3/5 αμαρτία x+4/5 cos x=2/5`.
Ας συμβολίσουμε `3/5 = cos \varphi` , `4/5=sin \varphi`. Εφόσον `sin \varphi>0`, `cos \varphi>0`, τότε λαμβάνουμε το `\varphi=arcsin 4/5` ως βοηθητική γωνία. Στη συνέχεια γράφουμε την ισότητά μας με τη μορφή:
`cos \varphi sin x+sin \varphi cos x=2/5`
Εφαρμόζοντας τον τύπο για το άθροισμα των γωνιών για το ημίτονο, γράφουμε την ισότητα μας με την ακόλουθη μορφή:
`sin (x+\varphi)=2/5`,
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Απάντηση. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Κλασματικές ορθολογικές τριγωνομετρικές εξισώσεις
Πρόκειται για ισότητες με κλάσματα των οποίων οι αριθμητές και οι παρονομαστές περιέχουν τριγωνομετρικές συναρτήσεις.
Παράδειγμα. Λύστε την εξίσωση. `\frac (sin x)(1+cos x)=1-cos x`.
Λύση. Πολλαπλασιάστε και διαιρέστε τη δεξιά πλευρά της ισότητας με το «(1+cos x)». Ως αποτέλεσμα παίρνουμε:
`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`
`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`
`\frac (sin x-sin^2 x)(1+cos x)=0`
Λαμβάνοντας υπόψη ότι ο παρονομαστής δεν μπορεί να είναι ίσος με μηδέν, παίρνουμε «1+cos x \ne 0», «cos x \ne -1», «x \ne \pi+2\pi n, n \in Z».
Ας εξισώσουμε τον αριθμητή του κλάσματος με μηδέν: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Στη συνέχεια `sin x=0` ή `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Δεδομένου ότι ` x \ne \pi+2\pi n, n \in Z`, οι λύσεις είναι `x=2\pi n, n \in Z` και `x=\pi /2+2\pi n` , `n \σε Z`.
Απάντηση. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Η τριγωνομετρία, και ειδικότερα οι τριγωνομετρικές εξισώσεις, χρησιμοποιούνται σχεδόν σε όλους τους τομείς της γεωμετρίας, της φυσικής και της μηχανικής. Η φοίτηση ξεκινά στη 10η τάξη, υπάρχουν πάντα εργασίες για την Ενιαία Κρατική Εξέταση, οπότε προσπαθήστε να θυμάστε όλους τους τύπους των τριγωνομετρικών εξισώσεων - σίγουρα θα σας φανούν χρήσιμες!
Ωστόσο, δεν χρειάζεται καν να τα απομνημονεύσετε, το κύριο πράγμα είναι να κατανοήσετε την ουσία και να μπορέσετε να την αντλήσετε. Δεν είναι τόσο δύσκολο όσο φαίνεται. Δείτε μόνοι σας βλέποντας το βίντεο.
Θέμα:"Μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων."
Στόχοι μαθήματος:
εκπαιδευτικός:
Να αναπτύξουν δεξιότητες για τη διάκριση μεταξύ τύπων τριγωνομετρικών εξισώσεων.
Εμβάθυνση της κατανόησης των μεθόδων για την επίλυση τριγωνομετρικών εξισώσεων.
εκπαιδευτικός:
Καλλιέργεια γνωστικού ενδιαφέροντος για την εκπαιδευτική διαδικασία.
Διαμόρφωση της ικανότητας ανάλυσης μιας δεδομένης εργασίας.
ανάπτυξη:
Να αναπτύξει τη δεξιότητα της ανάλυσης μιας κατάστασης και στη συνέχεια της επιλογής της πιο ορθολογικής διέξοδος από αυτήν.
Εξοπλισμός:αφίσα με βασικούς τριγωνομετρικούς τύπους, υπολογιστής, προβολέας, οθόνη.
Ας ξεκινήσουμε το μάθημα επαναλαμβάνοντας τη βασική τεχνική για την επίλυση οποιασδήποτε εξίσωσης: αναγωγή της σε τυπική μορφή. Μέσα από μεταμορφώσεις γραμμικές εξισώσειςμείωση στη μορφή akh = b, τετράγωνο - στη μορφή τσεκούρι 2 +bx +c =0.Στην περίπτωση των τριγωνομετρικών εξισώσεων, είναι απαραίτητο να αναχθούν στην απλούστερη, της μορφής: sinx = a, cosx = a, tgx = a, η οποία μπορεί να λυθεί εύκολα.
Πρώτα απ 'όλα, φυσικά, για αυτό είναι απαραίτητο να χρησιμοποιήσετε το βασικό τριγωνομετρικούς τύπουςπου παρουσιάζονται στην αφίσα: τύποι πρόσθεσης, τύποι διπλής γωνίας, μείωση της πολλαπλότητας της εξίσωσης. Γνωρίζουμε ήδη πώς να λύνουμε τέτοιες εξισώσεις. Ας επαναλάβουμε μερικά από αυτά:
Παράλληλα, υπάρχουν εξισώσεις των οποίων η λύση απαιτεί γνώση κάποιων ειδικών τεχνικών.
Το θέμα του μαθήματός μας είναι να εξετάσουμε αυτές τις τεχνικές και να συστηματοποιήσουμε μεθόδους για την επίλυση τριγωνομετρικών εξισώσεων.
Μέθοδοι επίλυσης τριγωνομετρικών εξισώσεων.
1. Μετατροπή σε τετραγωνική εξίσωσησε σχέση με κάποια τριγωνομετρική συνάρτηση ακολουθούμενη από αλλαγή μεταβλητής.
Ας δούμε καθεμία από τις μεθόδους που παρατίθενται με παραδείγματα, αλλά ας σταθούμε πιο αναλυτικά στις δύο τελευταίες, αφού έχουμε ήδη χρησιμοποιήσει τις δύο πρώτες κατά την επίλυση εξισώσεων.
1. Μετατροπή σε τετραγωνική εξίσωση ως προς κάποια τριγωνομετρική συνάρτηση.
2. Επίλυση εξισώσεων με τη μέθοδο της παραγοντοποίησης.
3. Επίλυση ομογενών εξισώσεων.
Οι ομοιογενείς εξισώσεις του πρώτου και του δεύτερου βαθμού είναι εξισώσεις της μορφής:
αντίστοιχα (a ≠ 0, b ≠ 0, c ≠ 0).
Όταν λύνετε ομοιογενείς εξισώσεις, διαιρέστε και τις δύο πλευρές του όρου της εξίσωσης με cosx για την (1) εξίσωση και με cos 2 x για (2). Αυτή η διαίρεση είναι δυνατή επειδή το sinx και το cosx δεν είναι ίσα με το μηδέν ταυτόχρονα - γίνονται μηδέν σε διαφορετικά σημεία. Ας εξετάσουμε παραδείγματα επίλυσης ομοιογενών εξισώσεων του πρώτου και του δεύτερου βαθμού.
Ας θυμηθούμε αυτή την εξίσωση: όταν εξετάζουμε την επόμενη μέθοδο - εισάγοντας ένα βοηθητικό όρισμα, ας τη λύσουμε με διαφορετικό τρόπο.
4. Εισαγωγή βοηθητικού ορίσματος.
Ας εξετάσουμε την εξίσωση που έχει ήδη λυθεί με την προηγούμενη μέθοδο:
Όπως μπορείτε να δείτε, προκύπτει το ίδιο αποτέλεσμα.
Ας δούμε ένα άλλο παράδειγμα:
Στα παραδείγματα που εξετάστηκαν, ήταν γενικά σαφές τι έπρεπε να χωριστεί στην αρχική εξίσωση προκειμένου να εισαχθεί ένα βοηθητικό όρισμα. Αλλά μπορεί να συμβεί να μην είναι προφανές ποιος διαιρέτης να επιλέξει. Υπάρχει μια ειδική τεχνική για αυτό, την οποία θα εξετάσουμε τώρα γενικά. Ας δοθεί μια εξίσωση.