Εάν το πρόβλημα απαιτεί πλήρη μελέτη της συνάρτησης f (x) = x 2 4 x 2 - 1 με την κατασκευή της γραφικής της παράστασης, τότε θα εξετάσουμε λεπτομερώς αυτήν την αρχή.
Για να λύσετε ένα πρόβλημα αυτού του τύπου, θα πρέπει να χρησιμοποιήσετε τις ιδιότητες και τα γραφήματα βασικών στοιχειωδών συναρτήσεων. Ο αλγόριθμος έρευνας περιλαμβάνει τα ακόλουθα βήματα:
Εύρεση του πεδίου ορισμού
Εφόσον διεξάγεται έρευνα στον τομέα ορισμού της συνάρτησης, είναι απαραίτητο να ξεκινήσουμε με αυτό το βήμα.
Παράδειγμα 1
Πίσω αυτό το παράδειγμαπεριλαμβάνει την εύρεση των μηδενικών του παρονομαστή προκειμένου να εξαιρεθούν από το ODZ.
4 x 2 - 1 = 0 x = ± 1 2 ⇒ x ∈ - ∞ ; - 1 2 ∪ - 1 2 ; 1 2 ∪ 1 2 ; +∞
Ως αποτέλεσμα, μπορείτε να λάβετε ρίζες, λογάριθμους και ούτω καθεξής. Στη συνέχεια, το ODZ μπορεί να αναζητηθεί για μια ρίζα ζυγού βαθμού του τύπου g (x) 4 από την ανισότητα g (x) ≥ 0, για λογάριθμο ημερολόγιο a g (x) από την ανισότητα g (x) > 0.
Μελέτη των ορίων του ΟΔΖ και εύρεση κάθετων ασυμπτωμάτων
Υπάρχουν κατακόρυφες ασύμπτωτες στα όρια της συνάρτησης, όταν τα μονόπλευρα όρια σε τέτοια σημεία είναι άπειρα.
Παράδειγμα 2
Για παράδειγμα, θεωρήστε τα σημεία συνόρων ίσα με x = ± 1 2.
Τότε είναι απαραίτητο να μελετηθεί η συνάρτηση για να βρεθεί το μονόπλευρο όριο. Τότε παίρνουμε ότι: lim x → - 1 2 - 0 f (x) = lim x → - 1 2 - 0 x 2 4 x 2 - 1 = = lim x → - 1 2 - 0 x 2 (2 x - 1 ) (2 x + 1) = 1 4 (- 2) · - 0 = + ∞ lim x → - 1 2 + 0 f (x) = lim x → - 1 2 + 0 x 2 4 x - 1 = = lim x → - 1 2 + 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 2) (+ 0) = - ∞ lim x → 1 2 - 0 f (x) = lim x → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 (- 0) 2 = - ∞ lim x → 1 2 - 0 f (x) = lim x → 1 2 - 0 x 2 4 x 2 - 1 = = lim x → 1 2 - 0 x 2 (2 x - 1) (2 x + 1) = 1 4 ( + 0 ) 2 = + ∞
Αυτό δείχνει ότι τα μονόπλευρα όρια είναι άπειρα, πράγμα που σημαίνει ότι οι ευθείες x = ± 1 2 είναι οι κατακόρυφες ασύμπτωτες του γραφήματος.
Μελέτη μιας συνάρτησης και αν είναι άρτια ή περιττή
Όταν η συνθήκη y (- x) = y (x) ικανοποιείται, η συνάρτηση θεωρείται άρτια. Αυτό υποδηλώνει ότι το γράφημα βρίσκεται συμμετρικά σε σχέση με το Oy. Όταν η συνθήκη y (- x) = - y (x) ικανοποιείται, η συνάρτηση θεωρείται περιττή. Αυτό σημαίνει ότι η συμμετρία είναι σχετική με την αρχή των συντεταγμένων. Εάν τουλάχιστον μία ανισότητα δεν ικανοποιείται, λαμβάνουμε μια συνάρτηση γενικής μορφής.
Η ισότητα y (- x) = y (x) δείχνει ότι η συνάρτηση είναι άρτια. Κατά την κατασκευή, είναι απαραίτητο να ληφθεί υπόψη ότι θα υπάρχει συμμετρία ως προς το Oy.
Για την επίλυση της ανισότητας, χρησιμοποιούνται διαστήματα αύξησης και μείωσης με τις συνθήκες f " (x) ≥ 0 και f " (x) ≤ 0, αντίστοιχα.
Ορισμός 1
Σταθερά σημεία- αυτά είναι τα σημεία που μηδενίζουν την παράγωγο.
Κρίσιμα σημεία - αυτά είναι εσωτερικά σημεία από το πεδίο ορισμού όπου η παράγωγος της συνάρτησης είναι ίση με μηδέν ή δεν υπάρχει.
Κατά τη λήψη μιας απόφασης, πρέπει να ληφθούν υπόψη οι ακόλουθες σημειώσεις:
- για υπάρχοντα διαστήματα αυξανόμενων και φθίνουσες ανισώσεις της μορφής f " (x) > 0, τα κρίσιμα σημεία δεν περιλαμβάνονται στη λύση.
- Τα σημεία στα οποία η συνάρτηση ορίζεται χωρίς πεπερασμένη παράγωγο πρέπει να περιλαμβάνονται στα διαστήματα αύξησης και μείωσης (για παράδειγμα, y = x 3, όπου το σημείο x = 0 καθορίζει τη συνάρτηση, η παράγωγος έχει την τιμή του άπειρου σε αυτό σημείο, y " = 1 3 x 2 3, y "(0) = 1 0 = ∞, x = 0 περιλαμβάνεται στο αυξανόμενο διάστημα).
- Για την αποφυγή διαφωνιών, συνιστάται η χρήση μαθηματικής βιβλιογραφίας που προτείνει το Υπουργείο Παιδείας.
Συμπερίληψη κρίσιμων σημείων σε διαστήματα αύξησης και μείωσης εάν ικανοποιούν το πεδίο ορισμού της συνάρτησης.
Ορισμός 2
Για προσδιορίζοντας τα διαστήματα αύξησης και μείωσης μιας συνάρτησης, είναι απαραίτητο να βρεθεί:
- παράγωγο;
- κρίσιμα σημεία?
- Διαιρέστε τον τομέα ορισμού σε διαστήματα χρησιμοποιώντας κρίσιμα σημεία.
- προσδιορίστε το πρόσημο της παραγώγου σε κάθε ένα από τα διαστήματα, όπου + είναι μια αύξηση και - είναι μια μείωση.
Παράδειγμα 3
Βρείτε την παράγωγο στον τομέα του ορισμού f " (x) = x 2 " (4 x 2 - 1) - x 2 4 x 2 - 1 " (4 x 2 - 1) 2 = - 2 x (4 x 2 - 1) 2 .
Λύση
Για να λύσετε χρειάζεστε:
- βρείτε σταθερά σημεία, αυτό το παράδειγμα έχει x = 0.
- βρείτε τα μηδενικά του παρονομαστή, το παράδειγμα παίρνει την τιμή μηδέν στο x = ± 1 2.
Τοποθετούμε σημεία στον αριθμητικό άξονα για να προσδιορίσουμε την παράγωγο σε κάθε διάστημα. Για να γίνει αυτό, αρκεί να πάρετε οποιοδήποτε σημείο από το διάστημα και να εκτελέσετε έναν υπολογισμό. Εάν το αποτέλεσμα είναι θετικό, απεικονίζουμε το + στο γράφημα, που σημαίνει ότι η συνάρτηση αυξάνεται και - σημαίνει ότι μειώνεται.
Για παράδειγμα, f " (- 1) = - 2 · (- 1) 4 - 1 2 - 1 2 = 2 9 > 0, που σημαίνει ότι το πρώτο διάστημα στα αριστερά έχει σύμβολο +. Εξετάστε την αριθμητική γραμμή.
Απάντηση:
- η συνάρτηση αυξάνεται στο διάστημα - ∞; - 1 2 και (- 1 2 ; 0 ] ;
- υπάρχει μείωση στο διάστημα [ 0 ; 1 2) και 1 2 ; + ∞ .
Στο διάγραμμα, χρησιμοποιώντας τα + και -, απεικονίζονται η θετικότητα και η αρνητικότητα της συνάρτησης και τα βέλη δείχνουν μείωση και αύξηση.
Τα ακραία σημεία μιας συνάρτησης είναι τα σημεία όπου ορίζεται η συνάρτηση και μέσω των οποίων η παράγωγος αλλάζει πρόσημο.
Παράδειγμα 4
Αν εξετάσουμε ένα παράδειγμα όπου x = 0, τότε η τιμή της συνάρτησης σε αυτό είναι ίση με f (0) = 0 2 4 · 0 2 - 1 = 0. Όταν το πρόσημο της παραγώγου αλλάζει από + σε - και διέρχεται από το σημείο x = 0, τότε το σημείο με συντεταγμένες (0; 0) θεωρείται το μέγιστο σημείο. Όταν το πρόσημο αλλάζει από - σε +, λαμβάνουμε ένα ελάχιστο σημείο.
Η κυρτότητα και η κοιλότητα προσδιορίζονται με την επίλυση ανισώσεων της μορφής f "" (x) ≥ 0 και f "" (x) ≤ 0. Λιγότερο συχνά χρησιμοποιείται το όνομα κυρτότητα προς τα κάτω αντί για κυρτότητα και κυρτότητα προς τα πάνω αντί για κυρτότητα.
Ορισμός 3
Για προσδιορισμός των διαστημάτων κοιλότητας και κυρτότηταςαπαραίτητη:
- βρείτε τη δεύτερη παράγωγο?
- Να βρείτε τα μηδενικά της δεύτερης παραγώγου συνάρτησης.
- διαιρέστε την περιοχή ορισμού σε διαστήματα με τα σημεία που εμφανίζονται.
- καθορίστε το πρόσημο του διαστήματος.
Παράδειγμα 5
Βρείτε τη δεύτερη παράγωγο από το πεδίο ορισμού.
Λύση
f "" (x) = - 2 x (4 x 2 - 1) 2 " = = (- 2 x) " (4 x 2 - 1) 2 - - 2 x 4 x 2 - 1 2 " (4 x 2 - 1) 4 = 24 x 2 + 2 (4 x 2 - 1) 3
Βρίσκουμε τα μηδενικά του αριθμητή και του παρονομαστή, όπου στο παράδειγμά μας έχουμε ότι τα μηδενικά του παρονομαστή x = ± 1 2
Τώρα πρέπει να σχεδιάσετε τα σημεία στην αριθμητική γραμμή και να προσδιορίσετε το πρόσημο της δεύτερης παραγώγου από κάθε διάστημα. Το καταλαβαίνουμε

Απάντηση:
- η συνάρτηση είναι κυρτή από το διάστημα - 1 2 ; 12 ;
- η συνάρτηση είναι κοίλη από τα διαστήματα - ∞ ; - 1 2 και 1 2; + ∞ .
Ορισμός 4
Σημείο καμπής– αυτό είναι ένα σημείο της μορφής x 0 ; f (x 0) . Όταν έχει εφαπτομένη στη γραφική παράσταση της συνάρτησης, τότε όταν διέρχεται από x 0 η συνάρτηση αλλάζει πρόσημο στο αντίθετο.
Με άλλα λόγια, αυτό είναι ένα σημείο από το οποίο περνά η δεύτερη παράγωγος και αλλάζει πρόσημο και στα ίδια τα σημεία είναι ίση με το μηδέν ή δεν υπάρχει. Όλα τα σημεία θεωρούνται το πεδίο της συνάρτησης.
Στο παράδειγμα, ήταν ξεκάθαρο ότι δεν υπάρχουν σημεία καμπής, αφού η δεύτερη παράγωγος αλλάζει πρόσημο ενώ διέρχεται από τα σημεία x = ± 1 2. Με τη σειρά τους, δεν περιλαμβάνονται στο πεδίο ορισμού.
Εύρεση οριζόντιων και πλάγιων ασυμπτωμάτων
Όταν ορίζετε μια συνάρτηση στο άπειρο, πρέπει να αναζητήσετε οριζόντιες και πλάγιες ασύμπτωτες.
Ορισμός 5
Πλάγιες ασύμπτωτεςαπεικονίζονται με ευθείες γραμμές, δίνεται από την εξίσωση y = k x + b, όπου k = lim x → ∞ f (x) x και b = lim x → ∞ f (x) - k x.
Για k = 0 και b που δεν ισούται με το άπειρο, βρίσκουμε ότι η πλάγια ασύμπτωτη γίνεται οριζόντιος.
Με άλλα λόγια, οι ασύμπτωτες θεωρούνται ευθείες στις οποίες η γραφική παράσταση μιας συνάρτησης πλησιάζει στο άπειρο. Αυτό διευκολύνει τη γρήγορη κατασκευή ενός γραφήματος συνάρτησης.
Εάν δεν υπάρχουν ασύμπτωτες, αλλά η συνάρτηση ορίζεται και στα δύο άπειρα, είναι απαραίτητο να υπολογιστεί το όριο της συνάρτησης σε αυτά τα άπειρα για να κατανοήσουμε πώς θα συμπεριφέρεται το γράφημα της συνάρτησης.
Παράδειγμα 6
Ας θεωρήσουμε ως παράδειγμα ότι
k = lim x → ∞ f (x) x = lim x → ∞ x 2 4 x 2 - 1 x = 0 b = lim x → ∞ (f (x) - k x) = lim x → ∞ x 2 4 x 2 - 1 = 1 4 ⇒ y = 1 4
είναι μια οριζόντια ασύμπτωτη. Αφού εξετάσετε τη συνάρτηση, μπορείτε να αρχίσετε να την κατασκευάζετε.
Υπολογισμός της τιμής μιας συνάρτησης σε ενδιάμεσα σημεία
Για να γίνει το γράφημα πιο ακριβές, συνιστάται να βρείτε πολλές τιμές συναρτήσεων σε ενδιάμεσα σημεία.
Παράδειγμα 7
Από το παράδειγμα που εξετάσαμε, είναι απαραίτητο να βρούμε τις τιμές της συνάρτησης στα σημεία x = - 2, x = - 1, x = - 3 4, x = - 1 4. Εφόσον η συνάρτηση είναι άρτια, παίρνουμε ότι οι τιμές συμπίπτουν με τις τιμές σε αυτά τα σημεία, δηλαδή παίρνουμε x = 2, x = 1, x = 3 4, x = 1 4.
Ας γράψουμε και ας λύσουμε:
F (- 2) = f (2) = 2 2 4 2 2 - 1 = 4 15 ≈ 0, 27 f (- 1) - f (1) = 1 2 4 1 2 - 1 = 1 3 ≈ 0 , 33 f - 3 4 = f 3 4 = 3 4 2 4 3 4 2 - 1 = 9 20 = 0 , 45 f - 1 4 = f 1 4 = 1 4 2 4 1 4 2 - 1 = - 1 12 ≈ - 0,08
Για να προσδιοριστούν τα μέγιστα και ελάχιστα της συνάρτησης, τα σημεία καμπής και τα ενδιάμεσα σημεία, είναι απαραίτητο να κατασκευαστούν ασύμπτωτες. Για βολικός προσδιορισμόςκαταγράφονται διαστήματα αύξησης, μείωσης, κυρτότητας, κοιλότητας. Ας δούμε την παρακάτω εικόνα.

Είναι απαραίτητο να σχεδιάσετε γραμμές γραφήματος μέσα από τα σημειωμένα σημεία, τα οποία θα σας επιτρέψουν να προσεγγίσετε τις ασύμπτωτες ακολουθώντας τα βέλη.

Αυτό ολοκληρώνει την πλήρη εξερεύνηση της συνάρτησης. Υπάρχουν περιπτώσεις κατασκευής κάποιων στοιχειωδών συναρτήσεων για τις οποίες χρησιμοποιούνται γεωμετρικοί μετασχηματισμοί.
Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter
Όταν σχεδιάζετε γραφήματα συναρτήσεων, είναι χρήσιμο να τηρείτε το ακόλουθο σχέδιο:
1. Βρείτε το πεδίο ορισμού της συνάρτησης και προσδιορίστε τα σημεία ασυνέχειας, εάν υπάρχουν.
2. Προσδιορίστε εάν η συνάρτηση είναι άρτια ή περιττή ή καμία. Εάν η συνάρτηση είναι άρτια ή περιττή, τότε αρκεί να εξετάσουμε τις τιμές της στο x>0, και μετά συμμετρικά ως προς τον άξονα OY ή την αρχή των συντεταγμένων, επαναφέρετέ το για τις τιμές Χ<0 .
3. Εξετάστε τη συνάρτηση για περιοδικότητα. Εάν η συνάρτηση είναι περιοδική, τότε αρκεί να την εξετάσουμε σε μία περίοδο.
4. Βρείτε τα σημεία τομής της γραφικής παράστασης συνάρτησης με τους άξονες συντεταγμένων (αν είναι δυνατόν)
5. Κάντε μια μελέτη της συνάρτησης στο άκρο και βρείτε τα διαστήματα αύξησης και μείωσης της συνάρτησης.
6. Να βρείτε τα σημεία καμπής της καμπύλης και τα διαστήματα κυρτότητας και κοιλότητας της συνάρτησης.
7. Να βρείτε τις ασύμπτωτες της γραφικής παράστασης της συνάρτησης.
8. Χρησιμοποιώντας τα αποτελέσματα των βημάτων 1-7, κατασκευάστε ένα γράφημα της συνάρτησης. Μερικές φορές υπάρχουν πολλά πρόσθετα σημεία για μεγαλύτερη ακρίβεια. Οι συντεταγμένες τους υπολογίζονται χρησιμοποιώντας την εξίσωση της καμπύλης.
Παράδειγμα. Λειτουργία εξερεύνησης y=x 3 -3xκαι φτιάξτε ένα γράφημα.
1) Η συνάρτηση ορίζεται στο διάστημα (-∞; +∞). Δεν υπάρχουν σημεία θραύσης.
2) Η συνάρτηση είναι περιττή, γιατί f(-x) = -x 3 -3(-x) = -x 3 +3x = -f(x), επομένως, είναι συμμετρικό ως προς την προέλευση.
3) Η συνάρτηση δεν είναι περιοδική.
4) Σημεία τομής της γραφικής παράστασης με τους άξονες συντεταγμένων: x 3 -3x=0, x = , x = -, x = 0,εκείνοι. η γραφική παράσταση της συνάρτησης τέμνει τους άξονες συντεταγμένων στα σημεία: ( ; 0 ), (0; 0 ), (-; 0 ).
5) Βρείτε πιθανά ακραία σημεία: y′ = 3x 2 -3; 3x 2 -3=0; x =-1; x = 1. Το πεδίο ορισμού της συνάρτησης θα χωριστεί σε διαστήματα: (-∞; -1), (-1; 1), (1; +∞). Ας βρούμε τα σημάδια της παραγώγου σε κάθε διάστημα που προκύπτει:
Στο διάστημα (-∞; -1) y′>0 –η λειτουργία αυξάνεται
Στο διάστημα (-1; 1) εσυ<0 – η συνάρτηση μειώνεται
Στο διάστημα (1; +∞) y′>0 –η λειτουργία αυξάνεται. Τελεία x =-1 – μέγιστος βαθμός. x = 1 – ελάχιστος βαθμός.
6) Βρείτε τα σημεία καμπής: y′′ = 6x; 6x = 0; x = 0. Τελεία x = 0διαιρεί το πεδίο ορισμού σε διαστήματα (-∞; 0), (0; +∞). Ας βρούμε τα πρόσημα της δεύτερης παραγώγου σε κάθε διάστημα που προκύπτει:
Στο διάστημα (-∞;0) εσυ"<0 – η συνάρτηση είναι κυρτή
Στο διάστημα (0; +∞) y′′>0 –η συνάρτηση είναι κοίλη. x = 0– σημείο καμπής.
7) Το γράφημα δεν έχει ασύμπτωτες
8) Ας σχεδιάσουμε τη συνάρτηση:
Παράδειγμα.Εξερευνήστε τη συνάρτηση και δημιουργήστε το γράφημά της.
1) Το πεδίο ορισμού της συνάρτησης είναι τα διαστήματα (-¥; -1) È (-1; 1) È (1; ¥). Εύρος τιμών αυτής της συνάρτησης είναι το διάστημα (-¥; ¥).
Τα σημεία διακοπής της συνάρτησης είναι τα σημεία x = 1, x = -1.
2) Η συνάρτηση είναι περιττή, γιατί .
3) Η συνάρτηση δεν είναι περιοδική.
4) Το γράφημα τέμνει τους άξονες συντεταγμένων στο σημείο (0; 0).
5) Βρείτε κρίσιμα σημεία.
Κρίσιμα σημεία: Χ = 0; Χ = -; Χ = ; Χ = -1; Χ = 1.
Να βρείτε τα διαστήματα της αύξουσας και φθίνουσας συνάρτησης. Για να γίνει αυτό, προσδιορίζουμε τα σημάδια της παραγώγου της συνάρτησης σε διαστήματα.
-¥ < Χ< -, y¢> 0, η συνάρτηση αυξάνεται
-< Χ < -1, y¢ < 0, функция убывает
1 < Χ < 0, y¢ < 0, функция убывает
0 < x < 1, y¢ < 0, функция убывает
1 < Χ < , y¢ < 0, функция убывает
< x < ¥, y¢ > 0, η συνάρτηση αυξάνεται
Είναι σαφές ότι το σημείο Χ= -είναι το μέγιστο σημείο, και το σημείο Χ= είναι το ελάχιστο σημείο. Οι τιμές συνάρτησης σε αυτά τα σημεία είναι ίσες με 3/2 και -3/2, αντίστοιχα.
6) Να βρείτε τη δεύτερη παράγωγο της συνάρτησης
Πλάγια ασύμπτωτη εξίσωση: y = x.
8) Ας φτιάξουμε ένα γράφημα της συνάρτησης.
Αυτό το μάθημα καλύπτει το θέμα «Διερεύνηση μιας συνάρτησης και συναφή προβλήματα». Αυτό το μάθημα καλύπτει γραφικές συναρτήσεις με χρήση παραγώγων. Η συνάρτηση μελετάται, κατασκευάζεται η γραφική της παράσταση και λύνονται μια σειρά από σχετικά προβλήματα.
Θέμα: Παράγωγο
Μάθημα: Εξερεύνηση μιας συνάρτησηςκαι σχετικές εργασίες
Είναι απαραίτητο να μελετήσουμε αυτή τη συνάρτηση, να κατασκευάσουμε ένα γράφημα, να βρούμε διαστήματα μονοτονίας, μέγιστα, ελάχιστα και ποια προβλήματα συνοδεύουν τη γνώση σχετικά με αυτή τη συνάρτηση.
Αρχικά, ας εκμεταλλευτούμε πλήρως τις πληροφορίες που παρέχει η συνάρτηση χωρίς παράγωγο.
1. Βρείτε τα διαστήματα σταθερού πρόσημου της συνάρτησης και κατασκευάστε ένα σκίτσο της γραφικής παράστασης της συνάρτησης:
1) Ας βρούμε.
2) Ρίζες συναρτήσεων: , από εδώ
3) Διαστήματα σταθερού πρόσημου της συνάρτησης (βλ. Εικ. 1):

Ρύζι. 1. Διαστήματα σταθερού πρόσημου μιας συνάρτησης.
Τώρα γνωρίζουμε ότι στο διάστημα και το γράφημα είναι πάνω από τον άξονα Χ, στο διάστημα - κάτω από τον άξονα Χ.
2. Ας φτιάξουμε ένα γράφημα κοντά σε κάθε ρίζα (βλ. Εικ. 2).

Ρύζι. 2. Γράφημα συνάρτησης κοντά στη ρίζα.
3. Κατασκευάστε ένα γράφημα της συνάρτησης κοντά σε κάθε σημείο ασυνέχειας στο πεδίο ορισμού. Το πεδίο ορισμού σπάει στο σημείο . Εάν η τιμή είναι κοντά στο σημείο, τότε η τιμή της συνάρτησης τείνει προς (βλ. Εικ. 3).

Ρύζι. 3. Γράφημα της συνάρτησης στην περιοχή του σημείου ασυνέχειας.
4. Ας προσδιορίσουμε πώς συμπεριφέρεται το γράφημα κοντά σε σημεία στο άπειρο:
Ας το γράψουμε χρησιμοποιώντας όρια
![]() . Είναι σημαντικό ότι για πολύ μεγάλες τιμές, η συνάρτηση δεν διαφέρει σχεδόν από τη μονάδα.
. Είναι σημαντικό ότι για πολύ μεγάλες τιμές, η συνάρτηση δεν διαφέρει σχεδόν από τη μονάδα.
Ας βρούμε την παράγωγο, τα διαστήματα του σταθερού πρόσημου της και θα είναι διαστήματα μονοτονίας για τη συνάρτηση, να βρούμε εκείνα τα σημεία στα οποία η παράγωγος είναι ίση με το μηδέν και να βρούμε πού είναι το μέγιστο σημείο και πού το ελάχιστο σημείο.
Από εδώ, . Αυτά τα σημεία είναι εσωτερικά σημεία του τομέα ορισμού. Ας μάθουμε ποιο πρόσημο της παραγώγου βρίσκεται στα διαστήματα, και ποιο από αυτά τα σημεία είναι το μέγιστο σημείο και ποιο το ελάχιστο σημείο (βλ. Εικ. 4).

Ρύζι. 4. Διαστήματα σταθερού πρόσημου της παραγώγου.
Από το Σχ. 4 μπορεί να φανεί ότι το σημείο είναι ένα ελάχιστο σημείο, το σημείο είναι ένα μέγιστο σημείο. Η τιμή της συνάρτησης στο σημείο είναι . Η τιμή της συνάρτησης στο σημείο είναι 4. Τώρα ας φτιάξουμε ένα γράφημα της συνάρτησης (βλ. Εικ. 5).

Ρύζι. 5. Γράφημα συνάρτησης.
Έτσι χτίσαμε γράφημα μιας συνάρτησης. Ας το περιγράψουμε. Ας γράψουμε τα διαστήματα στα οποία η συνάρτηση μειώνεται μονότονα: , είναι εκείνα τα διαστήματα όπου η παράγωγος είναι αρνητική. Η συνάρτηση αυξάνεται μονότονα στα διαστήματα και . - ελάχιστος βαθμός, - μέγιστος βαθμός.
Βρείτε τον αριθμό των ριζών της εξίσωσης ανάλογα με τις τιμές των παραμέτρων.
1. Κατασκευάστε ένα γράφημα της συνάρτησης. Το γράφημα αυτής της συνάρτησης απεικονίζεται παραπάνω (βλ. Εικ. 5).
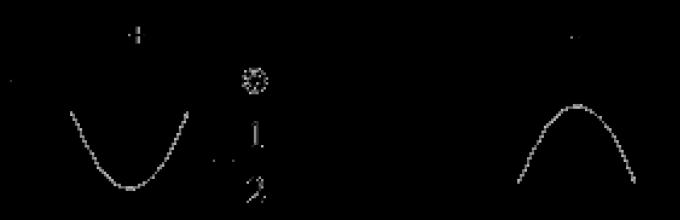
2. Κόψτε το γράφημα με μια οικογένεια ευθειών και γράψτε την απάντηση (βλ. Εικ. 6).

Ρύζι. 6. Τομή της γραφικής παράστασης μιας συνάρτησης με ευθείες γραμμές.
1) Πότε - μία λύση.
2) Πότε - δύο λύσεις.
3) Πότε - τρεις λύσεις.
4) Πότε - δύο λύσεις.
5) Πότε - τρεις λύσεις.
6) Πότε - δύο λύσεις.
7) Πότε - μία λύση.
Έτσι, λύσαμε ένα από τα σημαντικά προβλήματα, δηλαδή την εύρεση του αριθμού των λύσεων στην εξίσωση ανάλογα με την παράμετρο. Μπορεί να υπάρχουν διαφορετικές ειδικές περιπτώσεις, για παράδειγμα, στις οποίες θα υπάρχει μία λύση ή δύο λύσεις ή τρεις λύσεις. Σημειώστε ότι αυτές οι ειδικές περιπτώσεις, όλες οι απαντήσεις σε αυτές τις ειδικές περιπτώσεις περιλαμβάνονται στη γενική απάντηση.
1. Άλγεβρα και αρχή ανάλυσης, βαθμός 10 (σε δύο μέρη). Φροντιστήριο για Εκπαιδευτικά ιδρύματα (επίπεδο προφίλ) εκδ. A. G. Mordkovich. -Μ.: Μνημοσύνη, 2009.
2. Άλγεβρα και αρχή ανάλυσης, βαθμός 10 (σε δύο μέρη). Βιβλίο προβλημάτων για εκπαιδευτικά ιδρύματα (επίπεδο προφίλ), εκδ. A. G. Mordkovich. -Μ.: Μνημοσύνη, 2007.
3. Vilenkin N.Ya., Ivashev-Musatov O.S., Shvartsburd S.I. Άλγεβρα και λογισμός για την τάξη 10 ( φροντιστήριογια μαθητές σχολείων και τάξεων με σε βάθος μελέτημαθηματικά).-Μ.: Εκπαίδευση, 1996.
4. Galitsky M.L., Moshkovich M.M., Shvartsburd S.I. Σε βάθος μελέτη άλγεβρας και μαθηματική ανάλυση.-Μ.: Εκπαίδευση, 1997.
5. Συλλογή προβλημάτων στα μαθηματικά για αιτούντες σε ανώτατα εκπαιδευτικά ιδρύματα (επιμέλεια Μ.Ι. Σκαναβή) - Μ.: Ανώτατο Σχολείο, 1992.
6. Merzlyak A.G., Polonsky V.B., Yakir M.S. Αλγεβρικός προσομοιωτής.-Κ.: Α.Σ.Κ., 1997.
7. Zvavich L.I., Shlyapochnik L.Ya., Chinkina Algebra και οι απαρχές της ανάλυσης. 8-11 τάξεις: Εγχειρίδιο για σχολεία και τάξεις με εις βάθος μελέτη των μαθηματικών (διδακτικό υλικό) - M.: Bustard, 2002.
8. Sahakyan S.M., Goldman A.M., Denisov D.V. Προβλήματα στην άλγεβρα και αρχές ανάλυσης (εγχειρίδιο για μαθητές των τάξεων 10-11 των ιδρυμάτων γενικής εκπαίδευσης). - M.: Prosveshchenie, 2003.
9. Karp A.P. Συλλογή προβλημάτων άλγεβρας και αρχές ανάλυσης: σχολικό βιβλίο. επίδομα 10-11 τάξεων. με βάθος μελετημένος Μαθηματικά.-Μ.: Εκπαίδευση, 2006.
10. Glazer G.I. Η ιστορία των μαθηματικών στο σχολείο. Τάξεις 9-10 (εγχειρίδιο για εκπαιδευτικούς).-Μ.: Εκπαίδευση, 1983
Πρόσθετοι πόροι ιστού
2. Πύλη Φυσικές επιστήμες ().
Φτιάξτε το στο σπίτι
Νο. 45.7, 45.10 (Άλγεβρα και οι απαρχές της ανάλυσης, τάξη 10 (σε δύο μέρη). Βιβλίο προβλημάτων για ιδρύματα γενικής εκπαίδευσης (επίπεδο προφίλ) επιμέλεια A. G. Mordkovich. - M.: Mnemosyne, 2007.)