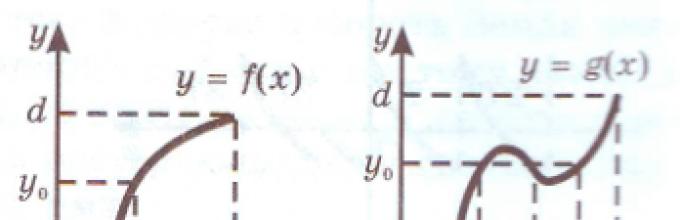Πώς να βρείτε το αντίστροφο ενός μαθήματος συνάρτησης. Αντίστροφη συνάρτηση. Θεωρία και εφαρμογή. Επεξήγηση νέου υλικού

Στόχοι μαθήματος:

Εκπαιδευτικός:

• οικοδομήσουμε τη γνώση νέο θέμασύμφωνα με το υλικό του προγράμματος·
• Μελετήστε την ιδιότητα της αντιστρεψιμότητας μιας συνάρτησης και διδάξτε πώς να βρείτε την αντίστροφη συνάρτηση μιας δεδομένης.

Αναπτυξιακή:

• ανάπτυξη δεξιοτήτων αυτοελέγχου, ουσιαστικής ομιλίας.
• κατακτήστε την έννοια της αντίστροφης συνάρτησης και μάθετε μεθόδους εύρεσης της αντίστροφης συνάρτησης.

Εκπαιδευτική: ανάπτυξη επικοινωνιακής ικανότητας.

Εξοπλισμός:υπολογιστής, προβολέας, οθόνη, διαδραστικός πίνακας SMART Board, φυλλάδια ( ανεξάρτητη εργασία) για ομαδική εργασία.

Κατά τη διάρκεια των μαθημάτων.

1. Οργανωτική στιγμή.

Στόχος – προετοιμασία των μαθητών για εργασία στην τάξη:

Ορισμός απουσιών,

Να αποκτήσουν οι μαθητές τη διάθεση για δουλειά, να οργανώσουν την προσοχή.

Δηλώστε το θέμα και το σκοπό του μαθήματος.

2. Ενημέρωση γνώσεις υποβάθρουΦοιτητές.Μετωπική έρευνα.

στόχος - διαπιστώνει την ορθότητα και επίγνωση του μελετημένου θεωρητικού υλικού, επανάληψη του καλυπτόμενου υλικού.<Приложение 1 >

Ένα γράφημα μιας συνάρτησης εμφανίζεται στον διαδραστικό πίνακα για τους μαθητές. Ο δάσκαλος διατυπώνει μια εργασία - εξετάστε τη γραφική παράσταση μιας συνάρτησης και απαριθμήστε τις ιδιότητες της συνάρτησης που μελετήθηκαν. Οι μαθητές απαριθμούν τις ιδιότητες μιας συνάρτησης σύμφωνα με τον ερευνητικό σχεδιασμό. Ο δάσκαλος, στα δεξιά της γραφικής παράστασης της συνάρτησης, σημειώνει τις ονομασμένες ιδιότητες με έναν δείκτη στον διαδραστικό πίνακα.

Ιδιότητες λειτουργίας:

Στο τέλος της μελέτης, ο δάσκαλος αναφέρει ότι σήμερα στο μάθημα θα εξοικειωθούν με μια άλλη ιδιότητα μιας συνάρτησης - την αντιστρεψιμότητα. Για να μελετήσει ουσιαστικά το νέο υλικό, ο δάσκαλος καλεί τα παιδιά να εξοικειωθούν με τις κύριες ερωτήσεις που πρέπει να απαντήσουν οι μαθητές στο τέλος του μαθήματος. Οι ερωτήσεις είναι γραμμένες σε έναν κανονικό πίνακα και κάθε μαθητής τις έχει ως φυλλάδια (διανέμονται πριν από το μάθημα)

1. Ποια συνάρτηση ονομάζεται αντιστρεπτή;
2. Είναι κάποια συνάρτηση αντιστρέψιμη;
3. Ποια συνάρτηση ονομάζεται αντίστροφο ενός δεδομένου;
4. Πώς σχετίζονται το πεδίο ορισμού και το σύνολο τιμών μιας συνάρτησης και το αντίστροφό της;
5. Εάν μια συνάρτηση δίνεται αναλυτικά, πώς μπορεί κανείς να ορίσει την αντίστροφη συνάρτηση με έναν τύπο;
6. Αν μια συνάρτηση δίνεται γραφικά, πώς να γραφτεί η αντίστροφη συνάρτησή της;

3. Επεξήγηση νέου υλικού.

Στόχος - δημιουργία γνώσεων για ένα νέο θέμα σύμφωνα με το υλικό του προγράμματος. Μελετήστε την ιδιότητα της αντιστρεψιμότητας μιας συνάρτησης και διδάξτε πώς να βρείτε την αντίστροφη συνάρτηση μιας δεδομένης. αναπτύξουν ουσιαστικό λόγο.

Ο εκπαιδευτικός παρουσιάζει το υλικό σύμφωνα με το υλικό της παραγράφου. Στον διαδραστικό πίνακα, ο δάσκαλος συγκρίνει τα γραφήματα δύο συναρτήσεων των οποίων τα πεδία ορισμού και τα σύνολα τιμών είναι τα ίδια, αλλά η μία από τις συναρτήσεις είναι μονότονη και η άλλη όχι, εισάγοντας έτσι τους μαθητές στην έννοια της αντιστρεπτής συνάρτησης .

Στη συνέχεια, ο δάσκαλος διατυπώνει τον ορισμό μιας αντιστρεπτής συνάρτησης και πραγματοποιεί μια απόδειξη του θεωρήματος της αντιστρεπτής συνάρτησης χρησιμοποιώντας τη γραφική παράσταση μιας μονότονης συνάρτησης στον διαδραστικό πίνακα.

Ορισμός 1: Καλείται η συνάρτηση y=f(x), x X αναστρεπτός, εάν λάβει κάποια από τις τιμές του μόνο σε ένα σημείο του συνόλου X.

Θεώρημα: Αν μια συνάρτηση y=f(x) είναι μονότονη σε ένα σύνολο Χ, τότε είναι αντιστρέψιμη.

Απόδειξη:

1. Αφήστε τη λειτουργία y=f(x)αυξάνεται κατά Χάστο να πάει x 1 ≠ x 2- δύο σημεία του σετ Χ.
2. Για να γίνουμε συγκεκριμένοι, ας x 1< x 2.
   Στη συνέχεια από το γεγονός ότι x 1< x 2ακολουθεί ότι f(x 1) < f(x 2).
3. Έτσι, διαφορετικές τιμές του ορίσματος αντιστοιχούν σε διαφορετικές τιμές της συνάρτησης, δηλ. η συνάρτηση είναι αντιστρέψιμη.

(Καθώς προχωρά η απόδειξη του θεωρήματος, ο δάσκαλος χρησιμοποιεί ένα μαρκαδόρο για να κάνει όλες τις απαραίτητες εξηγήσεις στο σχέδιο)

Πριν διατυπώσει τον ορισμό μιας αντίστροφης συνάρτησης, ο δάσκαλος ζητά από τους μαθητές να προσδιορίσουν ποια από τις προτεινόμενες συναρτήσεις είναι αντιστρέψιμη; Ο διαδραστικός πίνακας εμφανίζει γραφήματα συναρτήσεων και γράφει πολλές αναλυτικά καθορισμένες συναρτήσεις:

ΣΙ)

ΣΟΛ) y = 2x + 5

ΡΕ) y = -x 2 + 7

Ο δάσκαλος εισάγει τον ορισμό της αντίστροφης συνάρτησης.

Ορισμός 2: Έστω η αντιστρεπτή λειτουργία y=f(x)ορίζεται στο σετ ΧΚαι E(f)=Y. Ας ταιριάξουμε το καθένα yαπό Υαυτό είναι το μόνο νόημα Χ, στο οποίο f(x)=y.Τότε παίρνουμε μια συνάρτηση που ορίζεται στο Υ, ΕΝΑ Χ– εύρος λειτουργιών

Αυτή η λειτουργία έχει καθοριστεί x=f -1 (y)και ονομάζεται αντίστροφος της συνάρτησης y=f(x).

Ζητείται από τους μαθητές να βγάλουν ένα συμπέρασμα σχετικά με τη σύνδεση μεταξύ του πεδίου ορισμού και του συνόλου των τιμών των αντίστροφων συναρτήσεων.

Για να εξετάσει το ερώτημα πώς να βρείτε το αντίστροφο μιας δεδομένης συνάρτησης, ο δάσκαλος προσέλκυσε δύο μαθητές. Την προηγούμενη μέρα, τα παιδιά έλαβαν μια εργασία από τον δάσκαλο να αναλύσουν ανεξάρτητα τις αναλυτικές και γραφικές μεθόδους εύρεσης της αντίστροφης συνάρτησης μιας δεδομένης συνάρτησης. Ο δάσκαλος ενήργησε ως σύμβουλος στην προετοιμασία των μαθητών για το μάθημα.

Μήνυμα από τον πρώτο μαθητή.

Σημείωση: η μονοτονία της συνάρτησης είναι επαρκήςπροϋπόθεση για την ύπαρξη της αντίστροφης συνάρτησης. Αλλά δεν είναιαπαραίτητη προϋπόθεση.

Ο μαθητής έδωσε παραδείγματα διαφόρων καταστάσεων όταν μια συνάρτηση δεν είναι μονότονη αλλά αντιστρέψιμη, όταν μια συνάρτηση δεν είναι μονότονη και όχι αντιστρέψιμη, όταν είναι μονότονη και αντιστρέψιμη

Στη συνέχεια ο μαθητής εισάγει τους μαθητές σε μια μέθοδο εύρεσης της αντίστροφης συνάρτησης που δίνεται αναλυτικά.

Αλγόριθμος εύρεσης

1. Βεβαιωθείτε ότι η λειτουργία είναι μονότονη.
2. Να εκφράσετε τη μεταβλητή x ως y.
3. Μετονομασία μεταβλητών. Αντί για x=f -1 (y) γράψτε y=f -1 (x)

Στη συνέχεια λύνει δύο παραδείγματα για να βρει την αντίστροφη συνάρτηση μιας δεδομένης.

Παράδειγμα 1:Δείξτε ότι για τη συνάρτηση y=5x-3 υπάρχει αντίστροφη συνάρτηση και βρείτε την αναλυτική της έκφραση.

Λύση. Η γραμμική συνάρτηση y=5x-3 ορίζεται στο R, αυξάνεται στο R και το εύρος τιμών της είναι R. Αυτό σημαίνει ότι η αντίστροφη συνάρτηση υπάρχει στο R. Για να βρείτε την αναλυτική της έκφραση, λύστε την εξίσωση y=5x- 3 για x; παίρνουμε Αυτή είναι η απαιτούμενη αντίστροφη συνάρτηση. Ορίζεται και αυξάνεται στο R.

Παράδειγμα 2:Δείξτε ότι για τη συνάρτηση y=x 2, x≤0 υπάρχει αντίστροφη συνάρτηση και βρείτε την αναλυτική της έκφραση.

Η συνάρτηση είναι συνεχής, μονότονη στο πεδίο ορισμού της, επομένως είναι αντιστρεπτή. Έχοντας αναλύσει τα πεδία ορισμού και τα σύνολα τιμών της συνάρτησης, προκύπτει ένα αντίστοιχο συμπέρασμα σχετικά με την αναλυτική έκφραση για την αντίστροφη συνάρτηση.

Ο δεύτερος μαθητής κάνει μια παρουσίαση για γραφικόςμέθοδος εύρεσης της αντίστροφης συνάρτησης. Κατά την εξήγησή του ο μαθητής χρησιμοποιεί τις δυνατότητες του διαδραστικού πίνακα.

Για να ληφθεί μια γραφική παράσταση της συνάρτησης y=f -1 (x), αντίστροφη της συνάρτησης y=f(x), είναι απαραίτητο να μετασχηματιστεί η γραφική παράσταση της συνάρτησης y=f(x) συμμετρικά ως προς την ευθεία γραμμή. y=x.

Κατά την επεξήγηση στον διαδραστικό πίνακα, εκτελείται η ακόλουθη εργασία:

Κατασκευάστε μια γραφική παράσταση μιας συνάρτησης και μια γραφική παράσταση της αντίστροφης συνάρτησής της στο ίδιο σύστημα συντεταγμένων. Γράψτε την αναλυτική έκφραση για την αντίστροφη συνάρτηση.

4. Πρωτογενής ενοποίηση νέου υλικού.

στόχος - να προσδιορίσει την ορθότητα και την επίγνωση της κατανόησης του υλικού που μελετήθηκε, να εντοπίσει κενά στην πρωταρχική κατανόηση του υλικού και να τα διορθώσει.

Οι μαθητές χωρίζονται σε ζευγάρια. Τους δίνονται φύλλα εργασιών, στα οποία κάνουν την εργασία ανά δύο. Ο χρόνος ολοκλήρωσης της εργασίας είναι περιορισμένος (5-7 λεπτά). Ένα ζευγάρι μαθητών δουλεύει στον υπολογιστή, ο προβολέας σβήνει κατά τη διάρκεια αυτής της περιόδου και τα υπόλοιπα παιδιά δεν μπορούν να δουν πώς δουλεύουν οι μαθητές στον υπολογιστή.

Στο τέλος του χρόνου (υποτίθεται ότι η πλειοψηφία των μαθητών έχει ολοκληρώσει την εργασία), η εργασία των μαθητών εμφανίζεται στον διαδραστικό πίνακα (ο προβολέας ενεργοποιείται ξανά), όπου καθορίζεται κατά τον έλεγχο εάν η εργασία συμπληρώθηκε σωστά ανά ζευγάρια. Αν χρειαστεί, ο δάσκαλος εκτελεί διορθωτικές και επεξηγηματικές εργασίες.

Ανεξάρτητη εργασία σε ζευγάρια<Παράρτημα 2 >

5. Περίληψη μαθήματος.Σχετικά με τις ερωτήσεις που τέθηκαν πριν από τη διάλεξη. Ανακοίνωση βαθμών για το μάθημα.

Εργασία για το σπίτι §10. Αρ. 10.6(α,γ) 10.8-10.9(β) 10.12 (β)

Άλγεβρα και οι απαρχές της ανάλυσης. Βαθμός 10 Σε 2 μέρη για ιδρύματα γενικής εκπαίδευσης (επίπεδο προφίλ) / A.G. Mordkovich, L.O. Denishcheva, T.A. Koreshkova, κ.λπ. επεξεργάστηκε από A.G. Mordkovich, M: Mnemosyne, 2007

Αντίστοιχες εκφράσεις που αντιστρέφουν η μία την άλλη. Για να καταλάβετε τι σημαίνει αυτό, αξίζει να δείτε ένα συγκεκριμένο παράδειγμα. Ας πούμε ότι έχουμε y = cos(x). Εάν πάρετε το συνημίτονο από το όρισμα, μπορείτε να βρείτε την τιμή του y. Προφανώς, για αυτό πρέπει να έχετε Χ. Τι θα γινόταν όμως αν το παιχνίδι είχε δοθεί αρχικά; Εδώ είναι που έρχεται στην ουσία του θέματος. Για να λύσετε το πρόβλημα, πρέπει να χρησιμοποιήσετε την αντίστροφη συνάρτηση. Στην περίπτωσή μας είναι η αρκοσίνη.

Μετά από όλους τους μετασχηματισμούς παίρνουμε: x = arccos(y).

Δηλαδή, για να βρεθεί μια συνάρτηση αντίστροφη σε μια δεδομένη, αρκεί απλώς να εκφράσουμε ένα όρισμα από αυτήν. Αλλά αυτό λειτουργεί μόνο εάν το αποτέλεσμα που προκύπτει έχει ένα μόνο νόημα (περισσότερα για αυτό αργότερα).

Σε γενικές γραμμές, αυτό το γεγονός μπορεί να γραφτεί ως εξής: f(x) = y, g(y) = x.

Ορισμός

Έστω f μια συνάρτηση της οποίας το πεδίο ορισμού είναι το σύνολο X και της οποίας το πεδίο ορισμού είναι το σύνολο Y. Τότε, εάν υπάρχει μια g της οποίας τα πεδία εκτελούν αντίθετες εργασίες, τότε η f είναι αντιστρέψιμη.

Επιπλέον, σε αυτήν την περίπτωση το g είναι μοναδικό, πράγμα που σημαίνει ότι υπάρχει ακριβώς μία συνάρτηση που ικανοποιεί αυτήν την ιδιότητα (ούτε περισσότερο, ούτε λιγότερο). Τότε ονομάζεται αντίστροφη συνάρτηση, και στη γραφή συμβολίζεται ως εξής: g(x) = f -1 (x).

Με άλλα λόγια, μπορούν να θεωρηθούν ως μια δυαδική σχέση. Η αντιστρεψιμότητα εμφανίζεται μόνο όταν ένα στοιχείο του συνόλου αντιστοιχεί σε μια τιμή από ένα άλλο.

Η αντίστροφη συνάρτηση δεν υπάρχει πάντα. Για να γίνει αυτό, κάθε στοιχείο y є Y πρέπει να αντιστοιχεί το πολύ σε ένα x є X. Τότε η f ονομάζεται ένα προς ένα ή ένεση. Αν η f -1 ανήκει στο Y, τότε κάθε στοιχείο αυτού του συνόλου πρέπει να αντιστοιχεί σε κάποιο x ∈ X. Οι συναρτήσεις με αυτήν την ιδιότητα ονομάζονται υπερκείμενα. Ισχύει εξ ορισμού εάν το Y είναι εικόνα της f, αλλά αυτό δεν συμβαίνει πάντα. Για να είναι αντίστροφη, μια συνάρτηση πρέπει να είναι και έγχυση και έγχυση. Τέτοιες εκφράσεις ονομάζονται bijections.

Παράδειγμα: συναρτήσεις τετραγώνου και ρίζας

Η συνάρτηση ορίζεται στο $

Εφόσον αυτή η συνάρτηση είναι φθίνουσα και συνεχής στο διάστημα $X$, τότε στο διάστημα $Y=$, που είναι επίσης φθίνουσα και συνεχής σε αυτό το διάστημα (Θεώρημα 1).

Ας υπολογίσουμε $x$:

\ \

Επιλέξτε το κατάλληλο $x$:

Απάντηση:αντίστροφη συνάρτηση $y=-\sqrt(x)$.

Προβλήματα εύρεσης αντίστροφων συναρτήσεων

Σε αυτό το μέρος θα εξετάσουμε αντίστροφες συναρτήσεις για κάποιες στοιχειώδεις συναρτήσεις. Θα λύσουμε προβλήματα σύμφωνα με το σχήμα που δίνεται παραπάνω.

Παράδειγμα 2

Βρείτε την αντίστροφη συνάρτηση για τη συνάρτηση $y=x+4$

Ας βρούμε $x$ από την εξίσωση $y=x+4$:

Παράδειγμα 3

Βρείτε την αντίστροφη συνάρτηση για τη συνάρτηση $y=x^3$

Λύση.

Εφόσον η συνάρτηση είναι αύξουσα και συνεχής σε όλο το πεδίο ορισμού, τότε, σύμφωνα με το Θεώρημα 1, έχει μια αντίστροφη συνεχή και αύξουσα συνάρτηση σε αυτήν.

Ας βρούμε $x$ από την εξίσωση $y=x^3$:

Εύρεση κατάλληλων τιμών $x$

Η τιμή είναι κατάλληλη στην περίπτωσή μας (καθώς ο τομέας ορισμού είναι όλοι οι αριθμοί)

Ας επαναπροσδιορίσουμε τις μεταβλητές, παίρνουμε ότι η αντίστροφη συνάρτηση έχει τη μορφή

Παράδειγμα 4

Βρείτε την αντίστροφη συνάρτηση για τη συνάρτηση $y=cosx$ στο διάστημα $$

Λύση.

Θεωρήστε τη συνάρτηση $y=cosx$ στο σύνολο $X=\left$. Είναι συνεχές και φθίνουσα στο σύνολο $X$ και αντιστοιχίζει το σύνολο $X=\left$ στο σύνολο $Y=[-1,1]$, επομένως, με το θεώρημα για την ύπαρξη μιας αντίστροφης συνεχούς μονότονης συνάρτησης, η συνάρτηση $y=cosx$ στο σύνολο $ Y$ υπάρχει μια αντίστροφη συνάρτηση, η οποία είναι επίσης συνεχής και αυξανόμενη στο σύνολο $Y=[-1,1]$ και αντιστοιχίζει το σύνολο $[-1,1]$ στο σύνολο $\αριστερά$.

Ας βρούμε $x$ από την εξίσωση $y=cosx$:

Εύρεση κατάλληλων τιμών $x$

Ας επαναπροσδιορίσουμε τις μεταβλητές, παίρνουμε ότι η αντίστροφη συνάρτηση έχει τη μορφή

Παράδειγμα 5

Βρείτε την αντίστροφη συνάρτηση για τη συνάρτηση $y=tgx$ στο διάστημα $\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$.

Λύση.

Θεωρήστε τη συνάρτηση $y=tgx$ στο σύνολο $X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$. Είναι συνεχές και αυξάνεται στο σύνολο $X$ και αντιστοιχίζει το σύνολο $X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ στο σύνολο $Y =R$, επομένως, από το θεώρημα για την ύπαρξη μιας αντίστροφης συνεχούς μονότονης συνάρτησης, η συνάρτηση $y=tgx$ στο σύνολο $Y$ έχει μια αντίστροφη συνάρτηση, η οποία είναι επίσης συνεχής και αυξανόμενη στο σύνολο $Y=R $ και αντιστοιχίζει το σύνολο $R$ στο σύνολο $\left(- \frac(\pi )(2),\frac(\pi )(2)\right)$

Ας βρούμε $x$ από την εξίσωση $y=tgx$:

Εύρεση κατάλληλων τιμών $x$

Ας επαναπροσδιορίσουμε τις μεταβλητές, παίρνουμε ότι η αντίστροφη συνάρτηση έχει τη μορφή

Έστω μια συνάρτηση y=f(x), X είναι το πεδίο ορισμού της, Y είναι το εύρος τιμών της. Γνωρίζουμε ότι κάθε x 0  αντιστοιχεί σε μία μόνο τιμή y 0 =f(x 0), y 0 Y.

Μπορεί να αποδειχθεί ότι κάθε y (ή το μέρος του  1) αντιστοιχεί επίσης σε ένα μόνο x από το X.

Τότε λένε ότι στην περιοχή  (ή στο μέρος της  ) η συνάρτηση x=y ορίζεται ως η αντίστροφη συνάρτηση για τη συνάρτηση y=f(x).

Για παράδειγμα:




Χ =(f); Υ=)