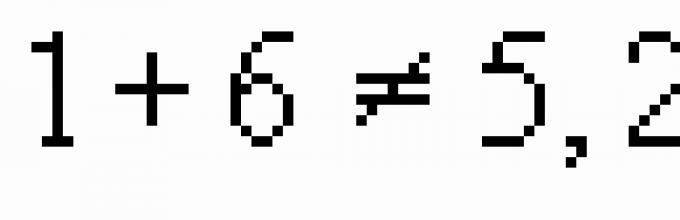Προφορική λύση τετραγωνικών εξισώσεων και θεώρημα Vieta. Πώς να λύσετε εξισώσεις χρησιμοποιώντας το θεώρημα του Vieta στα μαθηματικά Ο τύπος του θεωρήματος του Vieta για παραδείγματα τετραγωνικών εξισώσεων

Στην όγδοη τάξη, οι μαθητές εισάγονται στις δευτεροβάθμιες εξισώσεις και πώς να τις λύσουν. Ταυτόχρονα, όπως δείχνει η εμπειρία, οι περισσότεροι μαθητές, όταν λύνουν πλήρεις τετραγωνικές εξισώσεις, χρησιμοποιούν μόνο μία μέθοδο - τον τύπο ρίζας τετραγωνική εξίσωση. Για τους μαθητές που έχουν καλές νοητικές αριθμητικές δεξιότητες, αυτή η μέθοδος είναι σαφώς παράλογη. Οι μαθητές συχνά πρέπει να λύσουν δευτεροβάθμιες εξισώσεις ακόμη και στο γυμνάσιο, και εκεί είναι απλά κρίμα να ξοδεύουν χρόνο για να υπολογίσουν τη διάκριση. Κατά τη γνώμη μου, κατά τη μελέτη των δευτεροβάθμιων εξισώσεων, θα πρέπει να δοθεί περισσότερος χρόνος και προσοχή στην εφαρμογή του θεωρήματος του Vieta (σύμφωνα με το πρόγραμμα A.G. Mordkovich Algebra-8, προγραμματίζονται μόνο δύο ώρες για τη μελέτη του θέματος «Θεώρημα Vieta. Αποσύνθεση τετραγωνικού τριωνύμου σε γραμμικούς παράγοντες»).

Στα περισσότερα εγχειρίδια άλγεβρας, αυτό το θεώρημα διατυπώνεται για τη μειωμένη τετραγωνική εξίσωση και δηλώνει ότι αν η εξίσωση έχει ρίζες και , τότε οι ισότητες , , ικανοποιούνται για αυτές.Στη συνέχεια, διατυπώνεται μια δήλωση αντίθετη με το θεώρημα του Vieta, και προσφέρονται ορισμένα παραδείγματα για την εξάσκηση αυτού του θέματος.

Ας πάρουμε συγκεκριμένα παραδείγματα και ας ανιχνεύσουμε τη λογική της λύσης χρησιμοποιώντας το θεώρημα του Vieta.

Παράδειγμα 1. Λύστε την εξίσωση.

Ας πούμε ότι αυτή η εξίσωση έχει ρίζες, δηλαδή, και . Τότε, σύμφωνα με το θεώρημα του Vieta, οι ισότητες πρέπει να ισχύουν ταυτόχρονα:

Σημειώστε ότι το γινόμενο των ριζών είναι θετικός αριθμός. Αυτό σημαίνει ότι οι ρίζες της εξίσωσης έχουν το ίδιο πρόσημο. Και επειδή το άθροισμα των ριζών είναι επίσης θετικός αριθμός, συμπεραίνουμε ότι και οι δύο ρίζες της εξίσωσης είναι θετικές. Ας επιστρέψουμε ξανά στο προϊόν των ριζών. Ας υποθέσουμε ότι οι ρίζες της εξίσωσης είναι θετικοί ακέραιοι αριθμοί. Τότε η σωστή πρώτη ισότητα μπορεί να επιτευχθεί μόνο με δύο τρόπους (μέχρι τη σειρά των παραγόντων): ή . Ας ελέγξουμε για τα προτεινόμενα ζεύγη αριθμών τη σκοπιμότητα της δεύτερης δήλωσης του θεωρήματος του Vieta: . Έτσι, οι αριθμοί 2 και 3 ικανοποιούν και τις δύο ισότητες, και επομένως είναι οι ρίζες της δεδομένης εξίσωσης.

Απάντηση: 2; 3.

Ας επισημάνουμε τα κύρια στάδια του συλλογισμού κατά την επίλυση της παραπάνω τετραγωνικής εξίσωσης χρησιμοποιώντας το θεώρημα του Vieta:

γράψτε τη δήλωση του θεωρήματος του Βιέτα

(*)

• προσδιορίστε τα πρόσημα των ριζών της εξίσωσης (Εάν το γινόμενο και το άθροισμα των ριζών είναι θετικά, τότε και οι δύο ρίζες είναι θετικοί αριθμοί. Εάν το γινόμενο των ριζών είναι θετικός αριθμός και το άθροισμα των ριζών είναι αρνητικό, τότε Και οι δύο ρίζες είναι αρνητικοί αριθμοί. Εάν το γινόμενο των ριζών είναι αρνητικός αριθμός, τότε οι ρίζες έχουν διαφορετικά πρόσημα. Επιπλέον, εάν το άθροισμα των ριζών είναι θετικό, τότε η μεγαλύτερη ρίζα στο συντελεστή είναι θετικός αριθμός, και αν το άθροισμα των ριζών είναι μικρότερη από το μηδέν, τότε η μεγαλύτερη ρίζα σε συντελεστή είναι αρνητικός αριθμός).
• επιλέξτε ζεύγη ακεραίων αριθμών των οποίων το γινόμενο δίνει τη σωστή πρώτη ισότητα στον συμβολισμό (*).
• Από τα ζεύγη αριθμών που βρέθηκαν, επιλέξτε το ζεύγος που, όταν αντικατασταθεί στη δεύτερη ισότητα στον συμβολισμό (*), θα δώσει τη σωστή ισότητα.
• δώστε στην απάντησή σας τις ρίζες της εξίσωσης που βρέθηκαν.

Ας δώσουμε περισσότερα παραδείγματα.

Παράδειγμα 2: Λύστε την εξίσωση .

Λύση.

Έστω και είναι οι ρίζες της δεδομένης εξίσωσης. Στη συνέχεια, με το θεώρημα του Vieta, σημειώνουμε ότι το γινόμενο είναι θετικό και το άθροισμα είναι αρνητικός αριθμός. Αυτό σημαίνει ότι και οι δύο ρίζες είναι αρνητικοί αριθμοί. Επιλέγουμε ζεύγη παραγόντων που δίνουν γινόμενο 10 (-1 και -10; -2 και -5). Το δεύτερο ζεύγος αριθμών αθροίζεται σε -7. Αυτό σημαίνει ότι οι αριθμοί -2 και -5 είναι οι ρίζες αυτής της εξίσωσης.

Απάντηση: -2; -5.

Παράδειγμα 3: Λύστε την εξίσωση .

Λύση.

Έστω και είναι οι ρίζες της δεδομένης εξίσωσης. Στη συνέχεια, με το θεώρημα του Vieta, σημειώνουμε ότι το γινόμενο είναι αρνητικό. Αυτό σημαίνει ότι οι ρίζες είναι διαφορετικών ζωδίων. Αρνητικός αριθμός είναι και το άθροισμα των ριζών. Αυτό σημαίνει ότι η ρίζα με το μεγαλύτερο συντελεστή είναι αρνητική. Επιλέγουμε ζεύγη παραγόντων που δίνουν στο γινόμενο -10 (1 και -10, 2 και -5). Το δεύτερο ζεύγος αριθμών αθροίζεται σε -3. Αυτό σημαίνει ότι οι αριθμοί 2 και -5 είναι οι ρίζες αυτής της εξίσωσης.

Απάντηση: 2; -5.

Σημειώστε ότι το θεώρημα του Vieta μπορεί, καταρχήν, να διατυπωθεί για μια πλήρη τετραγωνική εξίσωση: αν τετραγωνική εξίσωση έχει ρίζες και , τότε οι ισότητες , , ικανοποιούνται για αυτές.Ωστόσο, η εφαρμογή αυτού του θεωρήματος είναι αρκετά προβληματική, αφού σε μια πλήρη τετραγωνική εξίσωση τουλάχιστον μία από τις ρίζες (αν υπάρχει, φυσικά) είναι κλασματικός αριθμός. Και η εργασία με την επιλογή κλασμάτων είναι μακρά και δύσκολη. Αλλά και πάλι υπάρχει διέξοδος.

Θεωρήστε την πλήρη τετραγωνική εξίσωση . Πολλαπλασιάστε και τις δύο πλευρές της εξίσωσης με τον πρώτο συντελεστή ΕΝΑκαι γράψτε την εξίσωση στη μορφή . Ας εισαγάγουμε μια νέα μεταβλητή και ας λάβουμε τη μειωμένη τετραγωνική εξίσωση, οι ρίζες της οποίας και (εάν υπάρχουν) μπορούν να βρεθούν χρησιμοποιώντας το θεώρημα του Vieta. Τότε οι ρίζες της αρχικής εξίσωσης θα είναι . Σημειώστε ότι είναι πολύ απλό να δημιουργήσετε τη βοηθητική μειωμένη εξίσωση: ο δεύτερος συντελεστής διατηρείται και ο τρίτος συντελεστής είναι ίσος με το γινόμενο μετα Χριστον. Με μια συγκεκριμένη ικανότητα, οι μαθητές δημιουργούν αμέσως μια βοηθητική εξίσωση, βρίσκουν τις ρίζες της χρησιμοποιώντας το θεώρημα του Vieta και υποδεικνύουν τις ρίζες της δεδομένης πλήρους εξίσωσης. Ας δώσουμε παραδείγματα.

Παράδειγμα 4: Λύστε την εξίσωση .

Ας δημιουργήσουμε μια βοηθητική εξίσωση και χρησιμοποιώντας το θεώρημα του Βιέτα θα βρούμε τις ρίζες του. Αυτό σημαίνει ότι οι ρίζες της αρχικής εξίσωσης .

Απάντηση: .

Παράδειγμα 5: Λύστε την εξίσωση .

Η βοηθητική εξίσωση έχει τη μορφή . Σύμφωνα με το θεώρημα του Vieta, οι ρίζες του είναι . Εύρεση των ριζών της αρχικής εξίσωσης .

Απάντηση: .

Και μια ακόμη περίπτωση όταν η εφαρμογή του θεωρήματος του Vieta σας επιτρέπει να βρείτε προφορικά τις ρίζες μιας πλήρους τετραγωνικής εξίσωσης. Δεν είναι δύσκολο να το αποδείξεις ο αριθμός 1 είναι η ρίζα της εξίσωσης , αν και μόνο αν. Η δεύτερη ρίζα της εξίσωσης βρίσκεται από το θεώρημα του Vieta και ισούται με . Μια ακόμη δήλωση: ώστε ο αριθμός –1 να είναι η ρίζα της εξίσωσης απαραίτητο και επαρκές για να. Τότε η δεύτερη ρίζα της εξίσωσης σύμφωνα με το θεώρημα του Vieta είναι ίση με . Παρόμοιες προτάσεις μπορούν να διατυπωθούν για την ανηγμένη τετραγωνική εξίσωση.

Παράδειγμα 6: Λύστε την εξίσωση.

Σημειώστε ότι το άθροισμα των συντελεστών της εξίσωσης είναι μηδέν. Άρα, οι ρίζες της εξίσωσης .

Απάντηση: .

Παράδειγμα 7. Λύστε την εξίσωση.

Οι συντελεστές αυτής της εξίσωσης ικανοποιούν την ιδιότητα (πράγματι, 1-(-999)+(-1000)=0). Άρα, οι ρίζες της εξίσωσης .

Απάντηση: ..

Παραδείγματα εφαρμογής του θεωρήματος του Vieta

Εργασία 1. Λύστε τη δεδομένη τετραγωνική εξίσωση χρησιμοποιώντας το θεώρημα του Vieta.

1.	6.	11.	16.
2.	7.	12.	17.
3.	8.	13.	18.
4.	9.	14.	19.
5.	10.	15.	20.

Εργασία 2. Λύστε την πλήρη τετραγωνική εξίσωση περνώντας στη βοηθητική ανηγμένη τετραγωνική εξίσωση.

1.	6.	11.	16.
2.	7.	12.	17.
3.	8.	13.	18.
4.	9.	14.	19.
5.	10.	15.	20.

Εργασία 3. Λύστε μια τετραγωνική εξίσωση χρησιμοποιώντας την ιδιότητα.

Σχεδόν κάθε τετραγωνική εξίσωση \μπορεί να μετατραπεί στη μορφή \ Ωστόσο, αυτό είναι δυνατό εάν αρχικά διαιρέσετε κάθε όρο με έναν συντελεστή \πριν \ Επιπλέον, μπορείτε να εισάγετε μια νέα σημείωση:

\[(\frac (b)(a))= p\] και \[(\frac (c)(a)) = q\]

Λόγω αυτού, θα έχουμε μια εξίσωση \ που ονομάζεται στα μαθηματικά μειωμένη τετραγωνική εξίσωση. Οι ρίζες αυτής της εξίσωσης και οι συντελεστές είναι αλληλένδετες, κάτι που επιβεβαιώνεται από το θεώρημα του Vieta.

Θεώρημα Vieta: Το άθροισμα των ριζών της ανηγμένης τετραγωνικής εξίσωσης \ ισούται με τον δεύτερο συντελεστή \ που λαμβάνεται με το αντίθετο πρόσημο, και το γινόμενο των ριζών είναι ο ελεύθερος όρος \

Για λόγους σαφήνειας, ας λύσουμε την ακόλουθη εξίσωση:

Ας λύσουμε αυτήν την τετραγωνική εξίσωση χρησιμοποιώντας τους γραπτούς κανόνες. Έχοντας αναλύσει τα αρχικά δεδομένα, μπορούμε να συμπεράνουμε ότι η εξίσωση θα έχει δύο διαφορετικές ρίζες, γιατί:

Τώρα, από όλους τους παράγοντες του αριθμού 15 (1 και 15, 3 και 5), επιλέγουμε αυτούς που η διαφορά τους είναι ίση με 2. Οι αριθμοί 3 και 5 υπάγονται σε αυτήν την συνθήκη. Βάζουμε ένα σύμβολο μείον μπροστά από το μικρότερο αριθμός. Έτσι, παίρνουμε τις ρίζες της εξίσωσης \

Απάντηση: \[ x_1= -3 και x_2 = 5\]

Πού μπορώ να λύσω μια εξίσωση χρησιμοποιώντας το θεώρημα του Vieta online;

Μπορείτε να λύσετε την εξίσωση στην ιστοσελίδα μας https://site. Ο δωρεάν διαδικτυακός λύτης θα σας επιτρέψει να λύσετε διαδικτυακές εξισώσεις οποιασδήποτε πολυπλοκότητας μέσα σε λίγα δευτερόλεπτα. Το μόνο που χρειάζεται να κάνετε είναι απλώς να εισαγάγετε τα δεδομένα σας στο πρόγραμμα επίλυσης. Μπορείτε επίσης να παρακολουθήσετε οδηγίες βίντεο και να μάθετε πώς να λύσετε την εξίσωση στον ιστότοπό μας. Και αν εξακολουθείτε να έχετε ερωτήσεις, μπορείτε να τις ρωτήσετε στην ομάδα VKontakte http://vk.com/pocketteacher. Γίνετε μέλος της ομάδας μας, είμαστε πάντα στην ευχάριστη θέση να σας βοηθήσουμε.

Μεταξύ των ριζών και των συντελεστών μιας τετραγωνικής εξίσωσης, εκτός από τους τύπους ρίζας, υπάρχουν και άλλες χρήσιμες σχέσεις που δίνονται Το θεώρημα του Βιέτα. Σε αυτό το άρθρο θα δώσουμε μια διατύπωση και απόδειξη του θεωρήματος του Vieta για μια τετραγωνική εξίσωση. Στη συνέχεια θεωρούμε το θεώρημα αντίστροφο με το θεώρημα του Vieta. Μετά από αυτό, θα αναλύσουμε τις λύσεις στα πιο χαρακτηριστικά παραδείγματα. Τέλος, καταγράφουμε τους τύπους Vieta που ορίζουν τη σχέση μεταξύ των πραγματικών ριζών αλγεβρική εξίσωση ο βαθμός n και οι συντελεστές του.

Πλοήγηση στη σελίδα.

Θεώρημα Vieta, διατύπωση, απόδειξη

Από τους τύπους των ριζών της δευτεροβάθμιας εξίσωσης a·x 2 +b·x+c=0 της μορφής, όπου D=b 2 −4·a·c, ακολουθούν οι εξής σχέσεις: x 1 +x 2 =− b/a, x 1 ·x 2 = c/a . Αυτά τα αποτελέσματα επιβεβαιώνονται Το θεώρημα του Βιέτα:

Θεώρημα.

Αν x 1 και x 2 είναι οι ρίζες της δευτεροβάθμιας εξίσωσης a x 2 +b x+c=0, τότε το άθροισμα των ριζών είναι ίσο με τον λόγο των συντελεστών b και a, που λαμβάνονται με το αντίθετο πρόσημο, και το γινόμενο του οι ρίζες είναι ίσες με τον λόγο των συντελεστών c και a, δηλαδή .

Απόδειξη.

Θα εκτελέσουμε την απόδειξη του θεωρήματος του Vieta σύμφωνα με το ακόλουθο σχήμα: συνθέτουμε το άθροισμα και το γινόμενο των ριζών της τετραγωνικής εξίσωσης χρησιμοποιώντας γνωστούς τύπους ρίζας, μετά μετασχηματίζουμε τις παραστάσεις που προκύπτουν και βεβαιωνόμαστε ότι είναι ίσες με −b/ α και γ/α, αντίστοιχα.

Ας ξεκινήσουμε με το άθροισμα των ριζών και ας το φτιάξουμε. Τώρα φέρνουμε τα κλάσματα σε έναν κοινό παρονομαστή, έχουμε . Στον αριθμητή του κλάσματος που προκύπτει, μετά από το οποίο:. Τελικά, μετά τις 2, παίρνουμε . Αυτό αποδεικνύει την πρώτη σχέση του θεωρήματος του Vieta για το άθροισμα των ριζών μιας τετραγωνικής εξίσωσης. Ας περάσουμε στο δεύτερο.

Συνθέτουμε το γινόμενο των ριζών της δευτεροβάθμιας εξίσωσης: . Σύμφωνα με τον κανόνα για τον πολλαπλασιασμό των κλασμάτων, τελευταίο κομμάτιμπορεί να γραφτεί ως . Τώρα πολλαπλασιάζουμε μια αγκύλη με μια αγκύλη στον αριθμητή, αλλά είναι πιο γρήγορο να συμπτύξουμε αυτό το γινόμενο με τύπος τετραγωνικής διαφοράς, Ετσι . Στη συνέχεια, θυμόμαστε, κάνουμε την επόμενη μετάβαση. Και εφόσον η διάκριση της δευτεροβάθμιας εξίσωσης αντιστοιχεί στον τύπο D=b 2 −4·a·c, τότε αντί για D στο τελευταίο κλάσμα μπορούμε να αντικαταστήσουμε το b 2 −4·a·c, παίρνουμε. Μετά το άνοιγμα των παρενθέσεων και το cast παρόμοιους όρουςφτάνουμε στο κλάσμα , και η αναγωγή του κατά 4·a δίνει . Αυτό αποδεικνύει τη δεύτερη σχέση του θεωρήματος του Vieta για το γινόμενο των ριζών.

Αν παραλείψουμε τις εξηγήσεις, η απόδειξη του θεωρήματος του Βιέτα θα πάρει λακωνική μορφή:
,
.

Μένει μόνο να σημειωθεί ότι εάν η διάκριση είναι ίση με μηδέν, η τετραγωνική εξίσωση έχει μία ρίζα. Ωστόσο, αν υποθέσουμε ότι η εξίσωση σε αυτή την περίπτωση έχει δύο ίδιες ρίζες, τότε ισχύουν και οι ισότητες από το θεώρημα του Vieta. Πράγματι, όταν D=0 η ρίζα της δευτεροβάθμιας εξίσωσης είναι ίση με , τότε και , και εφόσον D=0, δηλαδή, b 2 −4·a·c=0, από όπου b 2 =4·a·c, τότε .

Στην πράξη, το θεώρημα του Vieta χρησιμοποιείται συχνότερα σε σχέση με τη μειωμένη τετραγωνική εξίσωση (με τον κύριο συντελεστή a ίσο με 1) της μορφής x 2 +p·x+q=0. Μερικές φορές διατυπώνεται για τετραγωνικές εξισώσεις ακριβώς αυτού του τύπου, κάτι που δεν περιορίζει τη γενικότητα, αφού οποιαδήποτε τετραγωνική εξίσωση μπορεί να αντικατασταθεί από μια ισοδύναμη εξίσωση διαιρώντας και τις δύο πλευρές με έναν μη μηδενικό αριθμό α. Ας δώσουμε την αντίστοιχη διατύπωση του θεωρήματος του Vieta:

Θεώρημα.

Το άθροισμα των ριζών της ανηγμένης τετραγωνικής εξίσωσης x 2 +p x+q=0 είναι ίσο με τον συντελεστή x που λαμβάνεται με το αντίθετο πρόσημο και το γινόμενο των ριζών είναι ίσο με τον ελεύθερο όρο, δηλαδή x 1 +x 2 =−p, x 1 x 2 = q.

Το θεώρημα αντιστρέφεται με το θεώρημα του Βιέτα

Η δεύτερη διατύπωση του θεωρήματος του Vieta, που δόθηκε στην προηγούμενη παράγραφο, δείχνει ότι αν x 1 και x 2 είναι οι ρίζες της ανηγμένης τετραγωνικής εξίσωσης x 2 +p x+q=0, τότε οι σχέσεις x 1 +x 2 =−p , x 1 x 2 =q. Από την άλλη πλευρά, από τις γραπτές σχέσεις x 1 +x 2 =−p, x 1 x 2 =q προκύπτει ότι x 1 και x 2 είναι οι ρίζες της δευτεροβάθμιας εξίσωσης x 2 +p x+q=0. Με άλλα λόγια, το αντίστροφο του θεωρήματος του Vieta είναι αληθές. Ας το διατυπώσουμε με τη μορφή θεωρήματος και ας το αποδείξουμε.

Θεώρημα.

Αν οι αριθμοί x 1 και x 2 είναι τέτοιοι ώστε x 1 +x 2 =−p και x 1 · x 2 =q, τότε x 1 και x 2 είναι οι ρίζες της ανηγμένης τετραγωνικής εξίσωσης x 2 +p · x+q =0.

Απόδειξη.

Αφού αντικατασταθούν οι συντελεστές p και q στην εξίσωση x 2 +p x+q=0 από τις εκφράσεις τους μέσω x 1 και x 2 , μετατρέπεται σε ισοδύναμη εξίσωση.

Ας αντικαταστήσουμε τον αριθμό x 1 αντί για x στην εξίσωση που προκύπτει και έχουμε την ισότητα x 1 2 −(x 1 +x 2) x 1 +x 1 x 2 =0, που για οποιαδήποτε x 1 και x 2 αντιπροσωπεύει τη σωστή αριθμητική ισότητα 0=0, αφού x 1 2 −(x 1 +x 2) x 1 +x 1 x 2 = x 1 2 −x 1 2 −x 2 ·x 1 +x 1 ·x 2 =0. Επομένως, x 1 είναι η ρίζα της εξίσωσης x 2 −(x 1 +x 2) x+x 1 x 2 =0, που σημαίνει ότι το x 1 είναι η ρίζα της ισοδύναμης εξίσωσης x 2 +p·x+q=0.

Αν στην εξίσωση x 2 −(x 1 +x 2) x+x 1 x 2 =0Αντικαταστήστε τον αριθμό x 2 αντί για x, παίρνουμε την ισότητα x 2 2 −(x 1 +x 2) x 2 +x 1 x 2 =0. Αυτή είναι μια πραγματική ισότητα, αφού x 2 2 −(x 1 +x 2) x 2 +x 1 x 2 = x 2 2 −x 1 ·x 2 −x 2 2 +x 1 ·x 2 =0. Επομένως, το x 2 είναι επίσης ρίζα της εξίσωσης x 2 −(x 1 +x 2) x+x 1 x 2 =0, και επομένως οι εξισώσεις x 2 +p·x+q=0.

Αυτό συμπληρώνει την απόδειξη του θεωρήματος, αντίστροφο του θεωρήματος Vieta.

Παραδείγματα χρήσης του θεωρήματος του Vieta

Ήρθε η ώρα να μιλήσουμε για την πρακτική εφαρμογή του θεωρήματος του Βιέτα και του αντίστροφου θεωρήματος του. Σε αυτή την ενότητα θα αναλύσουμε λύσεις σε πολλά από τα πιο χαρακτηριστικά παραδείγματα.

Ας ξεκινήσουμε εφαρμόζοντας το θεώρημα αντίστροφα με το θεώρημα του Vieta. Είναι βολικό να το χρησιμοποιήσετε για να ελέγξετε εάν δύο δεδομένοι αριθμοί είναι ρίζες μιας δεδομένης τετραγωνικής εξίσωσης. Στην περίπτωση αυτή υπολογίζεται το άθροισμα και η διαφορά τους και μετά ελέγχεται η εγκυρότητα των σχέσεων. Εάν και οι δύο αυτές σχέσεις ικανοποιούνται, τότε δυνάμει του θεωρήματος που αντιστρέφεται με το θεώρημα του Vieta, συμπεραίνεται ότι αυτοί οι αριθμοί είναι οι ρίζες της εξίσωσης. Εάν τουλάχιστον μία από τις σχέσεις δεν ικανοποιείται, τότε αυτοί οι αριθμοί δεν είναι οι ρίζες της δευτεροβάθμιας εξίσωσης. Αυτή η προσέγγιση μπορεί να χρησιμοποιηθεί κατά την επίλυση δευτεροβάθμιων εξισώσεων για τον έλεγχο των ριζών που βρέθηκαν.

Παράδειγμα.

Ποιο από τα ζεύγη αριθμών 1) x 1 =−5, x 2 =3, ή 2) ή 3) είναι ζεύγος ριζών της δευτεροβάθμιας εξίσωσης 4 x 2 −16 x+9=0;

Λύση.

Οι συντελεστές της δεδομένης δευτεροβάθμιας εξίσωσης 4 x 2 −16 x+9=0 είναι a=4, b=−16, c=9. Σύμφωνα με το θεώρημα του Vieta, το άθροισμα των ριζών μιας δευτεροβάθμιας εξίσωσης πρέπει να είναι ίσο με −b/a, δηλαδή 16/4=4, και το γινόμενο των ριζών πρέπει να είναι ίσο με c/a, δηλαδή 9 /4.

Τώρα ας υπολογίσουμε το άθροισμα και το γινόμενο των αριθμών σε καθένα από τα τρία δεδομένα ζεύγη και ας τα συγκρίνουμε με τις τιμές που μόλις λάβαμε.

Στην πρώτη περίπτωση έχουμε x 1 +x 2 =−5+3=−2. Η τιμή που προκύπτει είναι διαφορετική από το 4, επομένως δεν μπορεί να πραγματοποιηθεί περαιτέρω έλεγχος, αλλά χρησιμοποιώντας το θεώρημα αντίστροφο προς το θεώρημα του Vieta, μπορεί κανείς να συμπεράνει αμέσως ότι το πρώτο ζεύγος αριθμών δεν είναι ζεύγος ριζών της δεδομένης τετραγωνικής εξίσωσης.

Ας περάσουμε στη δεύτερη περίπτωση. Εδώ, δηλαδή, πληρούται η πρώτη προϋπόθεση. Ελέγχουμε τη δεύτερη συνθήκη: η τιμή που προκύπτει είναι διαφορετική από το 9/4. Κατά συνέπεια, το δεύτερο ζεύγος αριθμών δεν είναι ζεύγος ριζών της τετραγωνικής εξίσωσης.

Απομένει μια τελευταία περίπτωση. Εδώ και . Και οι δύο προϋποθέσεις πληρούνται, επομένως αυτοί οι αριθμοί x 1 και x 2 είναι οι ρίζες της δεδομένης τετραγωνικής εξίσωσης.

Απάντηση:

Το αντίστροφο του θεωρήματος του Vieta μπορεί να χρησιμοποιηθεί στην πράξη για να βρούμε τις ρίζες μιας τετραγωνικής εξίσωσης. Συνήθως, επιλέγονται ακέραιες ρίζες των δεδομένων τετραγωνικών εξισώσεων με ακέραιους συντελεστές, αφού σε άλλες περιπτώσεις αυτό είναι αρκετά δύσκολο να γίνει. Σε αυτή την περίπτωση, χρησιμοποιούν το γεγονός ότι αν το άθροισμα δύο αριθμών είναι ίσο με τον δεύτερο συντελεστή μιας δευτεροβάθμιας εξίσωσης, που λαμβάνεται με αρνητικό πρόσημο, και το γινόμενο αυτών των αριθμών είναι ίσο με τον ελεύθερο όρο, τότε αυτοί οι αριθμοί είναι ο ρίζες αυτής της τετραγωνικής εξίσωσης. Ας το καταλάβουμε αυτό με ένα παράδειγμα.

Ας πάρουμε την τετραγωνική εξίσωση x 2 −5 x+6=0. Για να είναι οι αριθμοί x 1 και x 2 οι ρίζες αυτής της εξίσωσης, πρέπει να ικανοποιούνται δύο ισότητες: x 1 + x 2 =5 και x 1 · x 2 =6. Το μόνο που μένει είναι να επιλέξουμε τέτοιους αριθμούς. Σε αυτήν την περίπτωση, αυτό είναι πολύ απλό: τέτοιοι αριθμοί είναι το 2 και το 3, αφού 2+3=5 και 2·3=6. Έτσι, το 2 και το 3 είναι οι ρίζες αυτής της τετραγωνικής εξίσωσης.

Το θεώρημα αντίστροφο προς το θεώρημα του Vieta είναι ιδιαίτερα βολικό να χρησιμοποιηθεί για να βρεθεί η δεύτερη ρίζα μιας δεδομένης τετραγωνικής εξίσωσης όταν μία από τις ρίζες είναι ήδη γνωστή ή προφανής. Σε αυτήν την περίπτωση, η δεύτερη ρίζα μπορεί να βρεθεί από οποιαδήποτε από τις σχέσεις.

Για παράδειγμα, ας πάρουμε την τετραγωνική εξίσωση 512 x 2 −509 x −3=0. Εδώ είναι εύκολο να δούμε ότι η μονάδα είναι η ρίζα της εξίσωσης, αφού το άθροισμα των συντελεστών αυτής της τετραγωνικής εξίσωσης είναι ίσο με μηδέν. Άρα x 1 = 1. Η δεύτερη ρίζα x 2 μπορεί να βρεθεί, για παράδειγμα, από τη σχέση x 1 ·x 2 =c/a. Έχουμε 1 x 2 =−3/512, από το οποίο x 2 =−3/512. Έτσι προσδιορίσαμε και τις δύο ρίζες της δευτεροβάθμιας εξίσωσης: 1 και −3/512.

Είναι σαφές ότι η επιλογή των ριζών συνιστάται μόνο στις απλούστερες περιπτώσεις. Σε άλλες περιπτώσεις, για να βρείτε ρίζες, μπορείτε να χρησιμοποιήσετε τύπους για τις ρίζες μιας τετραγωνικής εξίσωσης μέσω ενός διαχωριστή.

Αλλο πρακτική χρήσητο θεώρημα, σε αντίθεση με το θεώρημα του Vieta, συνίσταται στη σύνθεση τετραγωνικών εξισώσεων σύμφωνα με δεδομένες ρίζες x 1 και x 2 . Για να γίνει αυτό, αρκεί να υπολογίσουμε το άθροισμα των ριζών, που δίνει τον συντελεστή για x με το αντίθετο πρόσημο της δεδομένης τετραγωνικής εξίσωσης, και το γινόμενο των ριζών, που δίνει ελεύθερο μέλος.

Παράδειγμα.

Να γράψετε μια τετραγωνική εξίσωση της οποίας οι ρίζες είναι −11 και 23.

Λύση.

Ας συμβολίσουμε x 1 =−11 και x 2 =23. Υπολογίζουμε το άθροισμα και το γινόμενο αυτών των αριθμών: x 1 +x 2 =12 και x 1 ·x 2 =−253. Επομένως, οι αριθμοί που υποδεικνύονται είναι οι ρίζες της ανηγμένης τετραγωνικής εξίσωσης με δεύτερο συντελεστή −12 και ελεύθερο όρο −253. Δηλαδή, x 2 −12·x−253=0 είναι η απαιτούμενη εξίσωση.

Απάντηση:

x 2 −12·x−253=0 .

Το θεώρημα του Vieta χρησιμοποιείται πολύ συχνά κατά την επίλυση προβλημάτων που σχετίζονται με τα σημάδια των ριζών των τετραγωνικών εξισώσεων. Πώς σχετίζεται το θεώρημα του Vieta με τα πρόσημα των ριζών της ανηγμένης τετραγωνικής εξίσωσης x 2 +p·x+q=0; Ακολουθούν δύο σχετικές δηλώσεις:

• Αν η τομή q είναι θετικός αριθμός και αν η τετραγωνική εξίσωση έχει πραγματικές ρίζες, τότε είτε είναι και οι δύο θετικές είτε και οι δύο αρνητικές.
• Αν ο ελεύθερος όρος q είναι αρνητικός αριθμός και αν η τετραγωνική εξίσωση έχει πραγματικές ρίζες, τότε τα πρόσημά τους είναι διαφορετικά, με άλλα λόγια, η μία ρίζα είναι θετική και η άλλη αρνητική.

Αυτές οι δηλώσεις προκύπτουν από τον τύπο x 1 · x 2 =q, καθώς και από τους κανόνες του θετικού πολλαπλασιασμού, αρνητικούς αριθμούςκαι αριθμοί με διαφορετικά πρόσημα. Ας δούμε παραδείγματα εφαρμογής τους.

Παράδειγμα.

R είναι θετικό. Χρησιμοποιώντας τον τύπο διάκρισης βρίσκουμε D=(r+2) 2 −4 1 (r−1)= r 2 +4 r+4−4 r+4=r 2 +8, την τιμή της παράστασης r 2 +8 είναι θετικό για κάθε πραγματικό r, επομένως D>0 για κάθε πραγματικό r. Κατά συνέπεια, η αρχική τετραγωνική εξίσωση έχει δύο ρίζες για οποιεσδήποτε πραγματικές τιμές της παραμέτρου r.

Τώρα ας μάθουμε πότε οι ρίζες έχουν διαφορετικά σημάδια. Εάν τα πρόσημα των ριζών είναι διαφορετικά, τότε το γινόμενο τους είναι αρνητικό και σύμφωνα με το θεώρημα του Vieta, το γινόμενο των ριζών της ανηγμένης τετραγωνικής εξίσωσης είναι ίσο με τον ελεύθερο όρο. Επομένως, μας ενδιαφέρουν εκείνες οι τιμές του r για τις οποίες ο ελεύθερος όρος r−1 είναι αρνητικός. Έτσι, για να βρούμε τις τιμές του r που μας ενδιαφέρουν, χρειαζόμαστε αποφασίζω γραμμική ανισότητα r−1<0 , откуда находим r<1 .

Απάντηση:

στο r<1 .

Φόρμουλες Vieta

Παραπάνω μιλήσαμε για το θεώρημα του Vieta για μια τετραγωνική εξίσωση και αναλύσαμε τις σχέσεις που υποστηρίζει. Αλλά υπάρχουν τύποι που συνδέουν τις πραγματικές ρίζες και τους συντελεστές όχι μόνο των τετραγωνικών εξισώσεων, αλλά και των κυβικών εξισώσεων, των εξισώσεων τέταρτου βαθμού και γενικά, αλγεβρικές εξισώσειςβαθμός n. Καλούνται Οι τύποι του Βιέτα.

Ας γράψουμε τον τύπο Vieta για μια αλγεβρική εξίσωση βαθμού n της μορφής και θα υποθέσουμε ότι έχει n πραγματικές ρίζες x 1, x 2, ..., x n (μεταξύ αυτών μπορεί να συμπίπτουν):

Οι τύποι του Vieta μπορούν να ληφθούν Θεώρημα για την αποσύνθεση ενός πολυωνύμου σε γραμμικούς παράγοντες, καθώς και τον ορισμό ίσων πολυωνύμων μέσω της ισότητας όλων των αντίστοιχων συντελεστών τους. Άρα το πολυώνυμο και η επέκτασή του σε γραμμικούς συντελεστές της μορφής είναι ίσα. Ανοίγοντας τις αγκύλες στο τελευταίο γινόμενο και εξισώνοντας τους αντίστοιχους συντελεστές, παίρνουμε τους τύπους του Vieta.

Συγκεκριμένα, για n=2 έχουμε τους ήδη γνωστούς τύπους Vieta για μια τετραγωνική εξίσωση.

Για μια κυβική εξίσωση, οι τύποι του Vieta έχουν τη μορφή

Μένει μόνο να σημειωθεί ότι στην αριστερή πλευρά των τύπων του Vieta υπάρχουν τα λεγόμενα στοιχειώδη συμμετρικά πολυώνυμα.

Βιβλιογραφία.

• Αλγεβρα:εγχειρίδιο για την 8η τάξη. γενική εκπαίδευση ιδρύματα / [Γιού. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; επεξεργάστηκε από S. A. Telyakovsky. - 16η έκδ. - Μ.: Εκπαίδευση, 2008. - 271 σελ. : Εγώ θα. - ISBN 978-5-09-019243-9.
• Mordkovich A. G.Αλγεβρα. 8η τάξη. Σε 2 ώρες Μέρος 1. Εγχειρίδιο για μαθητές γενικής εκπαίδευσης / A. G. Mordkovich. - 11η έκδ., σβησμένο. - Μ.: Μνημοσύνη, 2009. - 215 σελ.: εικ. ISBN 978-5-346-01155-2.
• Αλγεβρακαι η αρχή της μαθηματικής ανάλυσης. 10η τάξη: σχολικό βιβλίο. για γενική εκπαίδευση ιδρύματα: βασικά και προφίλ. επίπεδα / [Γιού. Μ. Kolyagin, Μ. V. Tkacheva, Ν. Ε. Fedorova, Μ. Ι. Shabunin]; επεξεργάστηκε από A. B. Zhizhchenko. - 3η έκδ. - Μ.: Εκπαίδευση, 2010.- 368 σελ. : Εγώ θα. - ISBN 978-5-09-022771-1.

Στα μαθηματικά, υπάρχουν ειδικές τεχνικές με τις οποίες πολλές δευτεροβάθμιες εξισώσεις μπορούν να λυθούν πολύ γρήγορα και χωρίς διακρίσεις. Επιπλέον, με την κατάλληλη εκπαίδευση, πολλοί αρχίζουν να λύνουν δευτεροβάθμιες εξισώσεις προφορικά, κυριολεκτικά «με την πρώτη ματιά».

Δυστυχώς, στο σύγχρονο μάθημα των σχολικών μαθηματικών, τέτοιες τεχνολογίες σχεδόν δεν μελετώνται. Αλλά πρέπει να ξέρετε! Και σήμερα θα εξετάσουμε μία από αυτές τις τεχνικές - το θεώρημα του Vieta. Αρχικά, ας εισαγάγουμε έναν νέο ορισμό.

Μια τετραγωνική εξίσωση της μορφής x 2 + bx + c = 0 ονομάζεται ανηγμένη. Σημειώστε ότι ο συντελεστής για το x 2 είναι 1. Δεν υπάρχουν άλλοι περιορισμοί στους συντελεστές.

1. x 2 + 7x + 12 = 0 είναι μια ανηγμένη τετραγωνική εξίσωση.
2. x 2 − 5x + 6 = 0 - επίσης μειωμένη.
3. 2x 2 − 6x + 8 = 0 - αλλά αυτό δεν δίνεται καθόλου, αφού ο συντελεστής x 2 είναι ίσος με 2.

Φυσικά, οποιαδήποτε τετραγωνική εξίσωση της μορφής ax 2 + bx + c = 0 μπορεί να μειωθεί - απλώς διαιρέστε όλους τους συντελεστές με τον αριθμό a. Μπορούμε πάντα να το κάνουμε αυτό, αφού ο ορισμός μιας τετραγωνικής εξίσωσης υπονοεί ότι ένα ≠ 0.

Είναι αλήθεια ότι αυτοί οι μετασχηματισμοί δεν θα είναι πάντα χρήσιμοι για την εύρεση ριζών. Παρακάτω θα φροντίσουμε να γίνει αυτό μόνο όταν στην τελική εξίσωση που δίνεται από το τετράγωνο όλοι οι συντελεστές είναι ακέραιοι. Προς το παρόν, ας δούμε τα πιο απλά παραδείγματα:

Εργο. Μετατρέψτε την τετραγωνική εξίσωση στη μειωμένη εξίσωση:

1. 3x 2 − 12x + 18 = 0;
2. −4x 2 + 32x + 16 = 0;
3. 1,5x 2 + 7,5x + 3 = 0;
4. 2x 2 + 7x − 11 = 0.

Ας διαιρέσουμε κάθε εξίσωση με τον συντελεστή της μεταβλητής x 2. Παίρνουμε:

1. 3x 2 − 12x + 18 = 0 ⇒ x 2 − 4x + 6 = 0 - διαιρούμε τα πάντα με το 3.
2. −4x 2 + 32x + 16 = 0 ⇒ x 2 − 8x − 4 = 0 - διαιρούμενο με −4;
3. 1,5x 2 + 7,5x + 3 = 0 ⇒ x 2 + 5x + 2 = 0 - διαιρούμενο με 1,5, όλοι οι συντελεστές έγιναν ακέραιοι.
4. 2x 2 + 7x − 11 = 0 ⇒ x 2 + 3,5x − 5,5 = 0 - διαιρούμενο με 2. Στην περίπτωση αυτή εμφανίστηκαν κλασματικοί συντελεστές.

Όπως μπορείτε να δείτε, οι παραπάνω τετραγωνικές εξισώσεις μπορεί να έχουν ακέραιους συντελεστές ακόμα κι αν η αρχική εξίσωση περιείχε κλάσματα.

Τώρα ας διατυπώσουμε το κύριο θεώρημα, για το οποίο, στην πραγματικότητα, εισήχθη η έννοια της ανηγμένης τετραγωνικής εξίσωσης:

Το θεώρημα του Βιέτα. Θεωρήστε τη μειωμένη τετραγωνική εξίσωση της μορφής x 2 + bx + c = 0. Υποθέστε ότι αυτή η εξίσωση έχει πραγματικές ρίζες x 1 και x 2. Σε αυτή την περίπτωση, οι ακόλουθες δηλώσεις είναι αληθείς:

1. x 1 + x 2 = −b. Με άλλα λόγια, το άθροισμα των ριζών της δεδομένης τετραγωνικής εξίσωσης είναι ίσο με τον συντελεστή της μεταβλητής x, που λαμβάνεται με το αντίθετο πρόσημο.
2. x 1 x 2 = γ. Το γινόμενο των ριζών μιας τετραγωνικής εξίσωσης είναι ίσο με τον ελεύθερο συντελεστή.

Παραδείγματα. Για απλότητα, θα εξετάσουμε μόνο τις παραπάνω τετραγωνικές εξισώσεις που δεν απαιτούν πρόσθετους μετασχηματισμούς:

1. x 2 − 9x + 20 = 0 ⇒ x 1 + x 2 = − (−9) = 9; x 1 x 2 = 20; ρίζες: x 1 = 4; x 2 = 5;
2. x 2 + 2x − 15 = 0 ⇒ x 1 + x 2 = −2; x 1 x 2 = −15; ρίζες: x 1 = 3; x 2 = −5;
3. x 2 + 5x + 4 = 0 ⇒ x 1 + x 2 = −5; x 1 x 2 = 4; ρίζες: x 1 = −1; x 2 = −4.

Το θεώρημα του Vieta μας δίνει πρόσθετες πληροφορίες για τις ρίζες μιας τετραγωνικής εξίσωσης. Με την πρώτη ματιά, αυτό μπορεί να φαίνεται δύσκολο, αλλά ακόμα και με ελάχιστη εκπαίδευση θα μάθετε να «βλέπετε» τις ρίζες και να τις μαντεύετε κυριολεκτικά μέσα σε λίγα δευτερόλεπτα.

Εργο. Λύστε την τετραγωνική εξίσωση:

1. x 2 − 9x + 14 = 0;
2. x 2 − 12x + 27 = 0;
3. 3x 2 + 33x + 30 = 0;
4. −7x 2 + 77x − 210 = 0.

Ας προσπαθήσουμε να γράψουμε τους συντελεστές χρησιμοποιώντας το θεώρημα του Vieta και να «μαντέψουμε» τις ρίζες:

1. x 2 − 9x + 14 = 0 είναι ανηγμένη τετραγωνική εξίσωση.
   Με το θεώρημα του Vieta έχουμε: x 1 + x 2 = −(−9) = 9; x 1 · x 2 = 14. Είναι εύκολο να δει κανείς ότι οι ρίζες είναι οι αριθμοί 2 και 7.
2. x 2 − 12x + 27 = 0 - επίσης μειωμένη.
   Με το θεώρημα του Vieta: x 1 + x 2 = −(−12) = 12; x 1 x 2 = 27. Εξ ου και οι ρίζες: 3 και 9;
3. 3x 2 + 33x + 30 = 0 - αυτή η εξίσωση δεν μειώνεται. Αλλά αυτό θα το διορθώσουμε τώρα διαιρώντας και τις δύο πλευρές της εξίσωσης με τον συντελεστή a = 3. Παίρνουμε: x 2 + 11x + 10 = 0.
   Λύνουμε χρησιμοποιώντας το θεώρημα του Vieta: x 1 + x 2 = −11; x 1 x 2 = 10 ⇒ ρίζες: −10 και −1;
4. −7x 2 + 77x − 210 = 0 - και πάλι ο συντελεστής για το x 2 δεν είναι ίσος με 1, δηλ. η εξίσωση δεν δίνεται. Διαιρούμε τα πάντα με τον αριθμό a = −7. Παίρνουμε: x 2 − 11x + 30 = 0.
   Με το θεώρημα του Vieta: x 1 + x 2 = −(−11) = 11; x 1 x 2 = 30; Από αυτές τις εξισώσεις είναι εύκολο να μαντέψει κανείς τις ρίζες: 5 και 6.

Από τον παραπάνω συλλογισμό είναι σαφές πώς το θεώρημα του Vieta απλοποιεί τη λύση των τετραγωνικών εξισώσεων. Χωρίς περίπλοκους υπολογισμούς, χωρίς αριθμητικές ρίζες και κλάσματα. Και δεν χρειαζόμασταν καν διάκριση (βλ. μάθημα «Επίλυση τετραγωνικών εξισώσεων»).

Φυσικά, σε όλους τους προβληματισμούς μας, προχωρήσαμε από δύο σημαντικές υποθέσεις, οι οποίες, γενικά, δεν συναντώνται πάντα σε πραγματικά προβλήματα:

1. Η τετραγωνική εξίσωση ανάγεται, δηλ. ο συντελεστής για το x 2 είναι 1.
2. Η εξίσωση έχει δύο διαφορετικές ρίζες. Από αλγεβρική άποψη, σε αυτή την περίπτωση η διάκριση είναι D > 0 - στην πραγματικότητα, αρχικά υποθέτουμε ότι αυτή η ανισότητα είναι αληθής.

Ωστόσο, σε τυπικά μαθηματικά προβλήματα πληρούνται αυτές οι προϋποθέσεις. Εάν ο υπολογισμός έχει ως αποτέλεσμα μια "κακή" τετραγωνική εξίσωση (ο συντελεστής x 2 είναι διαφορετικός από 1), αυτό μπορεί εύκολα να διορθωθεί - δείτε τα παραδείγματα στην αρχή του μαθήματος. Γενικά σιωπώ για τις ρίζες: τι είδους πρόβλημα είναι αυτό που δεν έχει απάντηση; Φυσικά θα υπάρχουν ρίζες.

Έτσι, το γενικό σχήμα για την επίλυση τετραγωνικών εξισώσεων χρησιμοποιώντας το θεώρημα του Vieta είναι το εξής:

1. Μειώστε τη δευτεροβάθμια εξίσωση στη δεδομένη, εάν αυτό δεν έχει ήδη γίνει στη δήλωση προβλήματος.
2. Αν οι συντελεστές στην παραπάνω τετραγωνική εξίσωση είναι κλασματικοί, λύνουμε χρησιμοποιώντας τη διάκριση. Μπορείτε ακόμη και να επιστρέψετε στην αρχική εξίσωση για να εργαστείτε με πιο "εύχρηστους" αριθμούς.
3. Στην περίπτωση των ακέραιων συντελεστών, λύνουμε την εξίσωση χρησιμοποιώντας το θεώρημα του Vieta.
4. Εάν δεν μπορείτε να μαντέψετε τις ρίζες μέσα σε λίγα δευτερόλεπτα, ξεχάστε το θεώρημα του Vieta και λύστε χρησιμοποιώντας το διαχωριστικό.

Εργο. Λύστε την εξίσωση: 5x 2 − 35x + 50 = 0.

Άρα, έχουμε μπροστά μας μια εξίσωση που δεν ανάγεται, γιατί συντελεστής a = 5. Διαιρούμε τα πάντα με το 5, παίρνουμε: x 2 − 7x + 10 = 0.

Όλοι οι συντελεστές μιας τετραγωνικής εξίσωσης είναι ακέραιοι - ας προσπαθήσουμε να τον λύσουμε χρησιμοποιώντας το θεώρημα του Vieta. Έχουμε: x 1 + x 2 = −(−7) = 7; x 1 · x 2 = 10. Σε αυτήν την περίπτωση, οι ρίζες είναι εύκολο να μαντέψει κανείς - είναι 2 και 5. Δεν χρειάζεται να μετρήσετε χρησιμοποιώντας το διαχωριστικό.

Εργο. Λύστε την εξίσωση: −5x 2 + 8x − 2,4 = 0.

Ας δούμε: −5x 2 + 8x − 2,4 = 0 - αυτή η εξίσωση δεν είναι μειωμένη, ας διαιρέσουμε και τις δύο πλευρές με τον συντελεστή a = −5. Παίρνουμε: x 2 − 1,6x + 0,48 = 0 - μια εξίσωση με κλασματικούς συντελεστές.

Είναι καλύτερα να επιστρέψετε στην αρχική εξίσωση και να μετρήσετε μέσω της διάκρισης: −5x 2 + 8x − 2,4 = 0 ⇒ D = 8 2 − 4 · (−5) · (−2,4) = 16 ⇒ ... ⇒ x 1 = 1,2; x 2 = 0,4.

Εργο. Λύστε την εξίσωση: 2x 2 + 10x − 600 = 0.

Αρχικά, ας διαιρέσουμε τα πάντα με τον συντελεστή a = 2. Παίρνουμε την εξίσωση x 2 + 5x − 300 = 0.

Αυτή είναι η ανηγμένη εξίσωση, σύμφωνα με το θεώρημα του Vieta έχουμε: x 1 + x 2 = −5; x 1 x 2 = −300. Είναι δύσκολο να μαντέψει κανείς τις ρίζες της τετραγωνικής εξίσωσης σε αυτήν την περίπτωση - προσωπικά, είχα κολλήσει σοβαρά όταν έλυνα αυτό το πρόβλημα.

Θα πρέπει να αναζητήσετε ρίζες μέσω του διαχωριστή: D = 5 2 − 4 · 1 · (−300) = 1225 = 35 2 . Εάν δεν θυμάστε τη ρίζα του διαχωριστικού, θα σημειώσω απλώς ότι 1225: 25 = 49. Επομένως, 1225 = 25 49 = 5 2 7 2 = 35 2.

Τώρα που είναι γνωστή η ρίζα της διάκρισης, η επίλυση της εξίσωσης δεν είναι δύσκολη. Παίρνουμε: x 1 = 15; x 2 = −20.

Υπάρχει ένας αριθμός σχέσεων στις δευτεροβάθμιες εξισώσεις. Οι κυριότερες είναι οι σχέσεις μεταξύ ριζών και συντελεστών. Επίσης στις τετραγωνικές εξισώσεις υπάρχει ένας αριθμός σχέσεων που δίνονται από το θεώρημα του Vieta.

Σε αυτό το θέμα, θα παρουσιάσουμε το ίδιο το θεώρημα του Βιέτα και την απόδειξή του για μια τετραγωνική εξίσωση, το θεώρημα αντίστροφο προς το θεώρημα του Βιέτα, και θα αναλύσουμε μια σειρά από παραδείγματα επίλυσης προβλημάτων. Στο υλικό θα δώσουμε ιδιαίτερη προσοχή στην εξέταση των τύπων του Vieta, που ορίζουν τη σύνδεση μεταξύ των πραγματικών ριζών μιας αλγεβρικής εξίσωσης βαθμού nκαι τους συντελεστές του.

Διατύπωση και απόδειξη του θεωρήματος του Vieta

Τύπος για τις ρίζες μιας τετραγωνικής εξίσωσης a x 2 + b x + c = 0της μορφής x 1 = - b + D 2 · a, x 2 = - b - D 2 · a, όπου D = b 2 − 4 a γ, δημιουργεί σχέσεις x 1 + x 2 = - b α, x 1 x 2 = γ α. Αυτό επιβεβαιώνεται από το θεώρημα του Vieta.

Θεώρημα 1

Σε μια τετραγωνική εξίσωση a x 2 + b x + c = 0, Οπου x 1Και x 2– ρίζες, το άθροισμα των ριζών θα είναι ίσο με τον λόγο των συντελεστών σιΚαι ένα, που λήφθηκε με το αντίθετο πρόσημο, και το γινόμενο των ριζών θα είναι ίσο με την αναλογία των συντελεστών ντοΚαι ένα, δηλ. x 1 + x 2 = - b α, x 1 x 2 = γ α.

Αποδεικτικά στοιχεία 1

Σας προσφέρουμε το ακόλουθο σχήμα για την εκτέλεση της απόδειξης: πάρτε τον τύπο των ριζών, συνθέστε το άθροισμα και το γινόμενο των ριζών της τετραγωνικής εξίσωσης και στη συνέχεια μετασχηματίστε τις παραστάσεις που προκύπτουν για να βεβαιωθείτε ότι είναι ίσες - β αΚαι γ ααντίστοιχα.

Ας κάνουμε το άθροισμα των ριζών x 1 + x 2 = - b + D 2 · a + - b - D 2 · a. Ας φέρουμε τα κλάσματα σε κοινό παρονομαστή - b + D 2 · a + - b - D 2 · a = - b + D + - b - D 2 · a. Ας ανοίξουμε τις παρενθέσεις στον αριθμητή του κλάσματος που προκύπτει και ας παρουσιάσουμε παρόμοιους όρους: - b + D + - b - D 2 · a = - b + D - b - D 2 · a = - 2 · b 2 · a . Ας μειώσουμε το κλάσμα κατά: 2 - b a = - b a.

Έτσι αποδείξαμε την πρώτη σχέση του θεωρήματος του Βιέτα, που σχετίζεται με το άθροισμα των ριζών μιας τετραγωνικής εξίσωσης.

Τώρα ας περάσουμε στη δεύτερη σχέση.

Για να γίνει αυτό, πρέπει να συνθέσουμε το γινόμενο των ριζών της δευτεροβάθμιας εξίσωσης: x 1 · x 2 = - b + D 2 · a · - b - D 2 · a.

Ας θυμηθούμε τον κανόνα για τον πολλαπλασιασμό των κλασμάτων και ας γράψουμε το τελευταίο γινόμενο ως εξής: - b + D · - b - D 4 · a 2.

Ας πολλαπλασιάσουμε μια αγκύλη με μια αγκύλη στον αριθμητή του κλάσματος ή ας χρησιμοποιήσουμε τον τύπο διαφοράς τετραγώνων για να μετατρέψουμε αυτό το γινόμενο πιο γρήγορα: - b + D · - b - D 4 · a 2 = - b 2 - D 2 4 · a 2 .

Ας χρησιμοποιήσουμε τον ορισμό της τετραγωνικής ρίζας για να κάνουμε την ακόλουθη μετάβαση: - b 2 - D 2 4 · a 2 = b 2 - D 4 · a 2 . Τύπος D = b 2 − 4 a γαντιστοιχεί στη διάκριση μιας τετραγωνικής εξίσωσης, επομένως, σε κλάσμα αντί για ρεμπορεί να αντικατασταθεί b 2 − 4 a c:

b 2 - D 4 a 2 = b 2 - (b 2 - 4 a c) 4 a 2

Ας ανοίξουμε τις αγκύλες, προσθέσουμε παρόμοιους όρους και πάρουμε: 4 · a · c 4 · a 2 . Αν το συντομεύσουμε σε 4 α, τότε αυτό που μένει είναι το c a . Έτσι αποδείξαμε τη δεύτερη σχέση του θεωρήματος του Vieta για το γινόμενο των ριζών.

Η απόδειξη του θεωρήματος του Βιέτα μπορεί να γραφτεί με πολύ λακωνική μορφή αν παραλείψουμε τις εξηγήσεις:

x 1 + x 2 = - b + D 2 a + - b - D 2 a = - b + D + - b - D 2 a = - 2 b 2 a = - b a , x 1 x 2 = - b + D 2 · a · - b - D 2 · a = - b + D · - b - D 4 · a 2 = - b 2 - D 2 4 · a 2 = b 2 - D 4 · a 2 = = D = b 2 - 4 · a · c = b 2 - b 2 - 4 · a · c 4 · a 2 = 4 · a · c 4 · a 2 = c a .

Όταν η διάκριση μιας τετραγωνικής εξίσωσης είναι ίση με μηδέν, η εξίσωση θα έχει μόνο μία ρίζα. Για να μπορέσουμε να εφαρμόσουμε το θεώρημα του Vieta σε μια τέτοια εξίσωση, μπορούμε να υποθέσουμε ότι η εξίσωση, με διάκριση ίση με μηδέν, έχει δύο ίδιες ρίζες. Πράγματι, όταν D=0η ρίζα της δευτεροβάθμιας εξίσωσης είναι: - b 2 · a, τότε x 1 + x 2 = - b 2 · a + - b 2 · a = - b + (- b) 2 · a = - 2 · b 2 · a = - b a και x 1 · x 2 = - b 2 · a · - b 2 · a = - b · - b 4 · a 2 = b 2 4 · a 2 , και αφού D = 0, δηλαδή, b 2 - 4 · a · c = 0, από όπου b 2 = 4 · a · c, μετά b 2 4 · a 2 = 4 · a · c 4 · a 2 = c a.

Τις περισσότερες φορές στην πράξη, το θεώρημα του Vieta εφαρμόζεται στη μειωμένη τετραγωνική εξίσωση της μορφής x 2 + p x + q = 0, όπου ο κύριος συντελεστής a είναι ίσος με 1. Από αυτή την άποψη, το θεώρημα του Vieta διατυπώνεται ειδικά για εξισώσεις αυτού του τύπου. Αυτό δεν περιορίζει τη γενικότητα λόγω του γεγονότος ότι οποιαδήποτε τετραγωνική εξίσωση μπορεί να αντικατασταθεί από μια ισοδύναμη εξίσωση. Για να γίνει αυτό, πρέπει να διαιρέσετε και τα δύο μέρη του με έναν αριθμό διαφορετικό από το μηδέν.

Ας δώσουμε μια άλλη διατύπωση του θεωρήματος του Vieta.

Θεώρημα 2

Άθροισμα ριζών στη δεδομένη τετραγωνική εξίσωση x 2 + p x + q = 0θα είναι ίσος με τον συντελεστή x, που λαμβάνεται με το αντίθετο πρόσημο, το γινόμενο των ριζών θα είναι ίσο με τον ελεύθερο όρο, δηλ. x 1 + x 2 = − p, x 1 x 2 = q.

Το θεώρημα αντιστρέφεται με το θεώρημα του Βιέτα

Αν κοιτάξετε προσεκτικά τη δεύτερη διατύπωση του θεωρήματος του Vieta, μπορείτε να δείτε ότι για τις ρίζες x 1Και x 2μειωμένη τετραγωνική εξίσωση x 2 + p x + q = 0θα ισχύουν οι ακόλουθες σχέσεις: x 1 + x 2 = − p, x 1 · x 2 = q. Από αυτές τις σχέσεις x 1 + x 2 = − p, x 1 x 2 = q προκύπτει ότι x 1Και x 2είναι οι ρίζες της δευτεροβάθμιας εξίσωσης x 2 + p x + q = 0. Φτάνουμε λοιπόν σε μια δήλωση που είναι το αντίστροφο του θεωρήματος του Vieta.

Τώρα προτείνουμε να επισημοποιηθεί αυτή η δήλωση ως θεώρημα και να πραγματοποιηθεί η απόδειξή της.

Θεώρημα 3

Αν οι αριθμοί x 1Και x 2είναι τέτοια που x 1 + x 2 = − pΚαι x 1 x 2 = q, Οτι x 1Και x 2είναι οι ρίζες της ανηγμένης τετραγωνικής εξίσωσης x 2 + p x + q = 0.

Αποδεικτικά στοιχεία 2

Αντικατάσταση πιθανοτήτων ΠΚαι qστην έκφρασή τους μέσω x 1Και x 2σας επιτρέπει να μετατρέψετε την εξίσωση x 2 + p x + q = 0σε ισοδύναμο .

Αν αντικαταστήσουμε τον αριθμό στην εξίσωση που προκύπτει x 1αντί Χ, τότε παίρνουμε την ισότητα x 1 2 − (x 1 + x 2) x 1 + x 1 x 2 = 0. Αυτό είναι ισότητα για οποιονδήποτε x 1Και x 2μετατρέπεται σε αληθινή αριθμητική ισότητα 0 = 0 , επειδή x 1 2 − (x 1 + x 2) x 1 + x 1 x 2 = x 1 2 − x 1 2 − x 2 x 1 + x 1 x 2 = 0. Αυτό σημαίνει ότι x 1- ρίζα της εξίσωσης x 2 − (x 1 + x 2) x + x 1 x 2 = 0, Και λοιπόν x 1είναι επίσης η ρίζα της ισοδύναμης εξίσωσης x 2 + p x + q = 0.

Αντικατάσταση σε εξίσωση x 2 − (x 1 + x 2) x + x 1 x 2 = 0αριθμοί x 2αντί του x μας επιτρέπει να αποκτήσουμε ισότητα x 2 2 − (x 1 + x 2) x 2 + x 1 x 2 = 0. Αυτή η ισότητα μπορεί να θεωρηθεί αληθινή, αφού x 2 2 − (x 1 + x 2) x 2 + x 1 x 2 = x 2 2 − x 1 x 2 − x 2 2 + x 1 x 2 = 0. Τελικά φαίνεται πως x 2είναι η ρίζα της εξίσωσης x 2 − (x 1 + x 2) x + x 1 x 2 = 0, και ως εκ τούτου οι εξισώσεις x 2 + p x + q = 0.

Το αντίστροφο του θεωρήματος του Βιέτα έχει αποδειχθεί.

Παραδείγματα χρήσης του θεωρήματος του Vieta

Ας αρχίσουμε τώρα να αναλύουμε τα πιο χαρακτηριστικά παραδείγματα για το θέμα. Ας ξεκινήσουμε αναλύοντας προβλήματα που απαιτούν την εφαρμογή του αντίστροφου θεωρήματος στο θεώρημα του Vieta. Μπορεί να χρησιμοποιηθεί για τον έλεγχο αριθμών που παράγονται από υπολογισμούς για να δούμε αν είναι οι ρίζες μιας δεδομένης τετραγωνικής εξίσωσης. Για να το κάνετε αυτό, πρέπει να υπολογίσετε το άθροισμα και τη διαφορά τους και στη συνέχεια να ελέγξετε την εγκυρότητα των σχέσεων x 1 + x 2 = - b a, x 1 · x 2 = a c.

Η εκπλήρωση και των δύο σχέσεων δείχνει ότι οι αριθμοί που λαμβάνονται κατά τους υπολογισμούς είναι οι ρίζες της εξίσωσης. Αν δούμε ότι τουλάχιστον μία από τις προϋποθέσεις δεν πληρούται, τότε αυτοί οι αριθμοί δεν μπορούν να είναι οι ρίζες της δευτεροβάθμιας εξίσωσης που δίνεται στη δήλωση του προβλήματος.

Παράδειγμα 1

Ποιο από τα ζεύγη αριθμών 1) x 1 = − 5, x 2 = 3, ή 2) x 1 = 1 - 3, x 2 = 3 + 3, ή 3) x 1 = 2 + 7 2, x 2 = 2 - 7 2 είναι ένα ζεύγος ριζών μιας τετραγωνικής εξίσωσης 4 x 2 − 16 x + 9 = 0?

Λύση

Ας βρούμε τους συντελεστές της δευτεροβάθμιας εξίσωσης 4 x 2 − 16 x + 9 = 0.Αυτό είναι a = 4, b = − 16, c = 9. Σύμφωνα με το θεώρημα του Vieta, το άθροισμα των ριζών μιας τετραγωνικής εξίσωσης πρέπει να είναι ίσο με - β α, αυτό είναι, 16 4 = 4 , και το γινόμενο των ριζών πρέπει να είναι ίσο γ α, αυτό είναι, 9 4 .

Ας ελέγξουμε τους ληφθέντες αριθμούς υπολογίζοντας το άθροισμα και το γινόμενο των αριθμών από τρία δεδομένα ζεύγη και συγκρίνοντάς τα με τις τιμές που προέκυψαν.

Στην πρώτη περίπτωση x 1 + x 2 = − 5 + 3 = − 2. Αυτή η τιμή είναι διαφορετική από το 4, επομένως, ο έλεγχος δεν χρειάζεται να συνεχιστεί. Σύμφωνα με το θεώρημα αντίστροφο προς το θεώρημα του Vieta, μπορούμε αμέσως να συμπεράνουμε ότι το πρώτο ζεύγος αριθμών δεν είναι οι ρίζες αυτής της τετραγωνικής εξίσωσης.

Στη δεύτερη περίπτωση, x 1 + x 2 = 1 - 3 + 3 + 3 = 4. Βλέπουμε ότι πληρούται η πρώτη προϋπόθεση. Αλλά η δεύτερη συνθήκη δεν είναι: x 1 · x 2 = 1 - 3 · 3 + 3 = 3 + 3 - 3 · 3 - 3 = - 2 · 3. Η αξία που πήραμε είναι διαφορετική από αυτή 9 4 . Αυτό σημαίνει ότι το δεύτερο ζεύγος αριθμών δεν είναι οι ρίζες της τετραγωνικής εξίσωσης.

Ας προχωρήσουμε στην εξέταση του τρίτου ζεύγους. Εδώ x 1 + x 2 = 2 + 7 2 + 2 - 7 2 = 4 και x 1 x 2 = 2 + 7 2 2 - 7 2 = 2 2 - 7 2 2 = 4 - 7 4 = 16 4 - 7 4 = 9 4. Και οι δύο προϋποθέσεις πληρούνται, πράγμα που σημαίνει ότι x 1Και x 2είναι οι ρίζες μιας δεδομένης τετραγωνικής εξίσωσης.

Απάντηση: x 1 = 2 + 7 2, x 2 = 2 - 7 2

Μπορούμε επίσης να χρησιμοποιήσουμε το αντίστροφο του θεωρήματος του Vieta για να βρούμε τις ρίζες μιας τετραγωνικής εξίσωσης. Ο απλούστερος τρόπος είναι να επιλέξετε ακέραιες ρίζες των δεδομένων τετραγωνικών εξισώσεων με ακέραιους συντελεστές. Μπορούν να εξεταστούν και άλλες επιλογές. Αλλά αυτό μπορεί να περιπλέξει σημαντικά τους υπολογισμούς.

Για να επιλέξουμε ρίζες, χρησιμοποιούμε το γεγονός ότι αν το άθροισμα δύο αριθμών είναι ίσο με τον δεύτερο συντελεστή μιας τετραγωνικής εξίσωσης, που λαμβάνεται με το πρόσημο μείον, και το γινόμενο αυτών των αριθμών είναι ίσο με τον ελεύθερο όρο, τότε αυτοί οι αριθμοί είναι ρίζες αυτής της τετραγωνικής εξίσωσης.

Παράδειγμα 2

Ως παράδειγμα, χρησιμοποιούμε την τετραγωνική εξίσωση x 2 − 5 x + 6 = 0. Αριθμοί x 1Και x 2μπορεί να είναι οι ρίζες αυτής της εξίσωσης εάν ικανοποιούνται δύο ισότητες x 1 + x 2 = 5Και x 1 x 2 = 6. Ας επιλέξουμε αυτούς τους αριθμούς. Αυτοί είναι οι αριθμοί 2 και 3, αφού 2 + 3 = 5 Και 2 3 = 6. Αποδεικνύεται ότι το 2 και το 3 είναι οι ρίζες αυτής της τετραγωνικής εξίσωσης.

Το αντίστροφο του θεωρήματος του Vieta μπορεί να χρησιμοποιηθεί για να βρεθεί η δεύτερη ρίζα όταν η πρώτη είναι γνωστή ή προφανής. Για να γίνει αυτό, μπορούμε να χρησιμοποιήσουμε τις σχέσεις x 1 + x 2 = - b a, x 1 · x 2 = c a.

Παράδειγμα 3

Θεωρήστε την τετραγωνική εξίσωση 512 x 2 − 509 x − 3 = 0. Είναι απαραίτητο να βρούμε τις ρίζες αυτής της εξίσωσης.

Λύση

Η πρώτη ρίζα της εξίσωσης είναι 1, αφού το άθροισμα των συντελεστών αυτής της τετραγωνικής εξίσωσης είναι μηδέν. Τελικά φαίνεται πως x 1 = 1.

Τώρα ας βρούμε τη δεύτερη ρίζα. Για αυτό μπορείτε να χρησιμοποιήσετε τη σχέση x 1 x 2 = γ α. Τελικά φαίνεται πως 1 x 2 = − 3.512, που x 2 = - 3.512.

Απάντηση:ρίζες της δευτεροβάθμιας εξίσωσης που καθορίζεται στη δήλωση προβλήματος 1 Και - 3 512 .

Είναι δυνατό να επιλέξετε ρίζες χρησιμοποιώντας το θεώρημα αντίστροφο προς το θεώρημα του Vieta μόνο σε απλές περιπτώσεις. Σε άλλες περιπτώσεις, είναι καλύτερο να κάνετε αναζήτηση χρησιμοποιώντας τον τύπο για τις ρίζες μιας τετραγωνικής εξίσωσης μέσω ενός διαχωριστή.

Χάρη στο αντίστροφο του θεωρήματος του Vieta, μπορούμε επίσης να κατασκευάσουμε τετραγωνικές εξισώσεις χρησιμοποιώντας τις υπάρχουσες ρίζες x 1Και x 2. Για να γίνει αυτό, πρέπει να υπολογίσουμε το άθροισμα των ριζών, το οποίο δίνει τον συντελεστή για Χμε το αντίθετο πρόσημο της δεδομένης τετραγωνικής εξίσωσης, και το γινόμενο των ριζών, που δίνει τον ελεύθερο όρο.

Παράδειγμα 4

Να γράψετε μια τετραγωνική εξίσωση της οποίας οι ρίζες είναι αριθμοί − 11 Και 23 .

Λύση

Ας υποθέσουμε ότι x 1 = − 11Και x 2 = 23. Το άθροισμα και το γινόμενο αυτών των αριθμών θα είναι ίσα: x 1 + x 2 = 12Και x 1 x 2 = − 253. Αυτό σημαίνει ότι ο δεύτερος συντελεστής είναι 12, ο ελεύθερος όρος − 253.

Ας κάνουμε μια εξίσωση: x 2 − 12 x − 253 = 0.

Απάντηση: x 2 − 12 x − 253 = 0 .

Μπορούμε να χρησιμοποιήσουμε το θεώρημα του Vieta για να λύσουμε προβλήματα που περιλαμβάνουν τα πρόσημα των ριζών των τετραγωνικών εξισώσεων. Η σύνδεση μεταξύ του θεωρήματος του Vieta σχετίζεται με τα σημάδια των ριζών της ανηγμένης τετραγωνικής εξίσωσης x 2 + p x + q = 0με τον εξής τρόπο:

• αν η τετραγωνική εξίσωση έχει πραγματικές ρίζες και αν ο όρος τομής qείναι θετικός αριθμός, τότε αυτές οι ρίζες θα έχουν το ίδιο πρόσημο "+" ή "-".
• αν η τετραγωνική εξίσωση έχει ρίζες και αν ο όρος τομής qείναι αρνητικός αριθμός, τότε η μία ρίζα θα είναι "+" και η δεύτερη "-".

Και οι δύο αυτές δηλώσεις είναι συνέπεια του τύπου x 1 x 2 = qκαι κανόνες για τον πολλαπλασιασμό θετικών και αρνητικών αριθμών, καθώς και αριθμών με διαφορετικά πρόσημα.

Παράδειγμα 5

Είναι οι ρίζες μιας τετραγωνικής εξίσωσης x 2 − 64 x − 21 = 0θετικός?

Λύση

Σύμφωνα με το θεώρημα του Vieta, οι ρίζες αυτής της εξίσωσης δεν μπορούν να είναι και οι δύο θετικές, αφού πρέπει να ικανοποιούν την ισότητα x 1 x 2 = − 21. Αυτό είναι αδύνατο με το θετικό x 1Και x 2.

Απάντηση:Οχι

Παράδειγμα 6

Σε ποιες τιμές παραμέτρων rτετραγωνική εξίσωση x 2 + (r + 2) x + r − 1 = 0θα έχει δύο πραγματικές ρίζες με διαφορετικά ζώδια.

Λύση

Ας ξεκινήσουμε βρίσκοντας τις τιμές των οποίων r, για το οποίο η εξίσωση θα έχει δύο ρίζες. Ας βρούμε το διακριτικό και ας δούμε τι rθα πάρει θετικές τιμές. D = (r + 2) 2 − 4 1 (r − 1) = r 2 + 4 r + 4 − 4 r + 4 = r 2 + 8. Τιμή έκφρασης r 2 + 8θετικό για κάθε πραγματικό r, επομένως, η διάκριση θα είναι μεγαλύτερη από το μηδέν για οποιοδήποτε πραγματικό r. Αυτό σημαίνει ότι η αρχική τετραγωνική εξίσωση θα έχει δύο ρίζες για οποιεσδήποτε πραγματικές τιμές της παραμέτρου r.

Τώρα ας δούμε πότε οι ρίζες έχουν διαφορετικά σημάδια. Αυτό είναι δυνατό εάν το προϊόν τους είναι αρνητικό. Σύμφωνα με το θεώρημα του Vieta, το γινόμενο των ριζών της ανηγμένης τετραγωνικής εξίσωσης είναι ίσο με τον ελεύθερο όρο. Αυτό σημαίνει ότι η σωστή λύση θα είναι αυτές οι τιμές r, για τον οποίο ο ελεύθερος όρος r − 1 είναι αρνητικός. Ας λύσουμε τη γραμμική ανισότητα r − 1< 0 , получаем r < 1 .

Απάντηση:στο r< 1 .

Φόρμουλες Vieta

Υπάρχει ένας αριθμός τύπων που ισχύουν για την εκτέλεση πράξεων με τις ρίζες και τους συντελεστές όχι μόνο τετραγωνικών, αλλά και κυβικών και άλλων τύπων εξισώσεων. Ονομάζονται τύποι του Βιέτα.

Για μια αλγεβρική εξίσωση βαθμού nτης μορφής a 0 · x n + a 1 · x n - 1 + . . . + a n - 1 x + a n = 0 η εξίσωση θεωρείται ότι έχει nπραγματικές ρίζες x 1 , x 2 , … , x n, μεταξύ των οποίων μπορεί να είναι τα ίδια:
x 1 + x 2 + x 3 + . . . + x n = - a 1 a 0 , x 1 · x 2 + x 1 · x 3 + . . . + x n - 1 · x n = a 2 a 0 , x 1 · x 2 · x 3 + x 1 · x 2 · x 4 + . . . + x n - 2 · x n - 1 · x n = - a 3 a 0 , . . . x 1 · x 2 · x 3 · . . . · x n = (- 1) n · a n a 0

Ορισμός 1

Οι τύποι του Vieta μας βοηθούν να αποκτήσουμε:

• Θεώρημα για την αποσύνθεση ενός πολυωνύμου σε γραμμικούς παράγοντες.
• προσδιορισμός ίσων πολυωνύμων μέσω της ισότητας όλων των αντίστοιχων συντελεστών τους.

Έτσι, το πολυώνυμο a 0 · x n + a 1 · x n - 1 + . . . + a n - 1 · x + a n και η επέκτασή του σε γραμμικούς συντελεστές της μορφής a 0 · (x - x 1) · (x - x 2) · . . . · (x - x n) είναι ίσα.

Αν ανοίξουμε τις αγκύλες στο τελευταίο γινόμενο και εξισώσουμε τους αντίστοιχους συντελεστές, παίρνουμε τους τύπους Vieta. Λαμβάνοντας n = 2, μπορούμε να λάβουμε τον τύπο του Vieta για την τετραγωνική εξίσωση: x 1 + x 2 = - a 1 a 0, x 1 · x 2 = a 2 a 0.

Ορισμός 2

Ο τύπος του Vieta για την κυβική εξίσωση:
x 1 + x 2 + x 3 = - a 1 a 0 , x 1 x 2 + x 1 x 3 + x 2 x 3 = a 2 a 0 , x 1 x 2 x 3 = - a 3 a 0

Η αριστερή πλευρά του τύπου Vieta περιέχει τα λεγόμενα στοιχειώδη συμμετρικά πολυώνυμα.

Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter