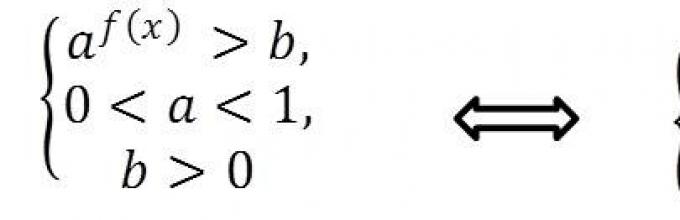Η ανισότητα είναι μια αριθμητική σχέση που απεικονίζει το μέγεθος των αριθμών σε σχέση μεταξύ τους. Οι ανισότητες χρησιμοποιούνται ευρέως στην αναζήτηση ποσοτήτων στις εφαρμοσμένες επιστήμες. Η αριθμομηχανή μας θα σας βοηθήσει να αντιμετωπίσετε ένα τόσο δύσκολο θέμα όπως η επίλυση γραμμικές ανισότητες.
Τι είναι η ανισότητα
Άνισοι λόγοι σε πραγματική ζωήσυσχετίζονται με συνεχής σύγκρισηδιάφορα αντικείμενα: ψηλότερα ή χαμηλότερα, πιο κοντά ή πιο κοντά, βαρύτερα ή ελαφρύτερα. Διαισθητικά ή οπτικά, μπορούμε να καταλάβουμε ότι ένα αντικείμενο είναι μεγαλύτερο, ψηλότερο ή βαρύτερο από ένα άλλο, αλλά στην πραγματικότητα μιλάμε πάντα για σύγκριση αριθμών που χαρακτηρίζουν τις αντίστοιχες ποσότητες. Τα αντικείμενα μπορούν να συγκριθούν σε οποιαδήποτε βάση και σε κάθε περίπτωση μπορούμε να δημιουργήσουμε μια αριθμητική ανισότητα.
Εάν τα άγνωστα μεγέθη είναι ίσα κάτω από συγκεκριμένες συνθήκες, τότε δημιουργούμε μια εξίσωση για να τα προσδιορίσουμε αριθμητικά. Αν όχι, τότε αντί για το πρόσημο «ίσο» μπορούμε να υποδείξουμε οποιαδήποτε άλλη σχέση μεταξύ αυτών των ποσοτήτων. Δύο αριθμοί ή μαθηματικά αντικείμενα μπορεί να είναι μεγαλύτεροι από ">", μικρότεροι από "<» или равны «=» относительно друг друга. В этом случае речь идет о строгих неравенствах. Если же в неравных соотношениях присутствует знак равно и числовые элементы больше или равны (a ≥ b) или меньше или равны (a ≤ b), то такие неравенства называются нестрогими.
Τα σημάδια ανισότητας στη σύγχρονη μορφή τους επινοήθηκαν από τον Βρετανό μαθηματικό Τόμας Χάριοτ, ο οποίος το 1631 δημοσίευσε ένα βιβλίο για τις άνισες αναλογίες. Σημάδια μεγαλύτερα από ">" και μικρότερα από "<» представляли собой положенные на бок буквы V, поэтому пришлись по вкусу не только математикам, но и типографам.
Επίλυση ανισοτήτων
Οι ανισότητες, όπως και οι εξισώσεις, υπάρχουν σε διαφορετικούς τύπους. Γραμμικές, τετραγωνικές, λογαριθμικές ή εκθετικές άνισες σχέσεις επιλύονται με διάφορες μεθόδους. Ωστόσο, ανεξάρτητα από τη μέθοδο, οποιαδήποτε ανισότητα πρέπει πρώτα να μειωθεί σε μια τυπική μορφή. Για αυτό, χρησιμοποιούνται μετασχηματισμοί ταυτότητας που είναι πανομοιότυποι με τροποποιήσεις ισοτήτων.
Πανομοιότυποι μετασχηματισμοί ανισοτήτων
Τέτοιοι μετασχηματισμοί εκφράσεων μοιάζουν πολύ με τις εξισώσεις φαντασμάτων, αλλά έχουν αποχρώσεις που είναι σημαντικό να ληφθούν υπόψη κατά την επίλυση ανισοτήτων.
Ο πρώτος μετασχηματισμός ταυτότητας είναι πανομοιότυπος με μια παρόμοια πράξη με ισότητες. Ο ίδιος αριθμός ή έκφραση με άγνωστο x μπορεί να προστεθεί ή να αφαιρεθεί και στις δύο πλευρές μιας άνισης σχέσης, ενώ το πρόσημο της ανισότητας παραμένει το ίδιο. Τις περισσότερες φορές, αυτή η μέθοδος χρησιμοποιείται σε απλοποιημένη μορφή ως μεταφορά όρων μιας έκφρασης μέσω ενός πρόσημου ανισότητας με αλλαγή του πρόσημου του αριθμού στο αντίθετο. Αυτό σημαίνει μια αλλαγή στο πρόσημο του ίδιου του όρου, δηλαδή, το +R όταν μεταφερθεί μέσω οποιουδήποτε πρόσημου ανισότητας θα αλλάξει σε – R και αντίστροφα.
Ο δεύτερος μετασχηματισμός έχει δύο σημεία:
- Και οι δύο πλευρές ενός άνισου λόγου επιτρέπεται να πολλαπλασιαστούν ή να διαιρεθούν με τον ίδιο θετικό αριθμό. Το σημάδι της ίδιας της ανισότητας δεν θα αλλάξει.
- Και οι δύο πλευρές μιας ανισότητας μπορούν να διαιρεθούν ή να πολλαπλασιαστούν με το ίδιο πράγμα ένας αρνητικός αριθμός. Το ίδιο το σημάδι της ανισότητας θα αλλάξει στο αντίθετο.
Ο δεύτερος ταυτόσημος μετασχηματισμός των ανισοτήτων έχει σοβαρές διαφορές με την τροποποίηση των εξισώσεων. Πρώτον, κατά τον πολλαπλασιασμό/διαίρεση με έναν αρνητικό αριθμό, το πρόσημο της άνισης παράστασης αντιστρέφεται πάντα. Δεύτερον, μπορείτε να διαιρέσετε ή να πολλαπλασιάσετε μέρη μιας αναλογίας μόνο με έναν αριθμό και όχι με οποιαδήποτε έκφραση που περιέχει έναν άγνωστο. Το γεγονός είναι ότι δεν μπορούμε να γνωρίζουμε με βεβαιότητα εάν ένας αριθμός είναι μεγαλύτερος ή μικρότερος από το μηδέν που κρύβεται πίσω από το άγνωστο, επομένως ο δεύτερος μετασχηματισμός ταυτότητας εφαρμόζεται στις ανισότητες αποκλειστικά με αριθμούς. Ας δούμε αυτούς τους κανόνες με παραδείγματα.
Παραδείγματα απελευθέρωσης ανισοτήτων
Στις αναθέσεις άλγεβρας, υπάρχει μια ποικιλία εργασιών σχετικά με το θέμα των ανισοτήτων. Ας μας δοθεί η έκφραση:
6x − 3(4x + 1) > 6.
Αρχικά, ας ανοίξουμε τις αγκύλες και ας μετακινήσουμε όλους τους άγνωστους προς τα αριστερά και όλους τους αριθμούς προς τα δεξιά.
6x − 12x > 6 + 3
Πρέπει να διαιρέσουμε και τις δύο πλευρές της παράστασης με το -6, οπότε όταν βρούμε τον άγνωστο x, το πρόσημο της ανισότητας θα αλλάξει στο αντίθετο.
Για την επίλυση αυτής της ανισότητας χρησιμοποιήσαμε και τα δύο μετασχηματισμοί ταυτότητας: Μετακινήστε όλους τους αριθμούς στα δεξιά του πρόσημου και διαιρέστε και τις δύο πλευρές του λόγου με τον αρνητικό αριθμό.
Το πρόγραμμά μας είναι μια αριθμομηχανή για την επίλυση αριθμητικών ανισώσεων που δεν περιέχουν αγνώστους. Το πρόγραμμα περιέχει τα ακόλουθα θεωρήματα για τις σχέσεις τριών αριθμών:
- αν ένα< B то A–C< B–C;
- αν A > B, τότε A–C > B–C.
Αντί να αφαιρέσετε τους όρους A-C, μπορείτε να καθορίσετε οποιαδήποτε αριθμητική πράξη: πρόσθεση, πολλαπλασιασμό ή διαίρεση. Με αυτόν τον τρόπο, η αριθμομηχανή θα εμφανίζει αυτόματα ανισότητες για αθροίσματα, διαφορές, γινόμενα ή κλάσματα.
συμπέρασμα
Στην πραγματική ζωή, οι ανισότητες είναι εξίσου κοινές με τις εξισώσεις. Φυσικά, η γνώση για την επίλυση των ανισοτήτων μπορεί να μην χρειάζεται στην καθημερινή ζωή. Ωστόσο, στις εφαρμοσμένες επιστήμες, οι ανισότητες και τα συστήματά τους χρησιμοποιούνται ευρέως. Για παράδειγμα, διάφορες μελέτες για τα προβλήματα της παγκόσμιας οικονομίας καταλήγουν στη συλλογή και αποσύνδεση συστημάτων γραμμικής ή τετραγωνικές ανισότητες, και ορισμένες άνισες σχέσεις χρησιμεύουν ως ένας σαφής τρόπος απόδειξης της ύπαρξης ορισμένων αντικειμένων. Χρησιμοποιήστε τα προγράμματά μας για να λύσετε γραμμικές ανισότητες ή να ελέγξετε τους δικούς σας υπολογισμούς.
Γειά σου! Αγαπητοί μου μαθητές, σε αυτό το άρθρο θα μάθουμε πώς να λύνουμε εκθετικές ανισότητες .
Ανεξάρτητα από το πόσο περίπλοκη μπορεί να σας φαίνεται η εκθετική ανισότητα, μετά από μερικούς μετασχηματισμούς (θα μιλήσουμε για αυτούς λίγο αργότερα) όλες οι ανισότητες καταλήγουμε να λύσουμε το πιο απλό εκθετικές ανισότητες :
α x > β, ένα x< b Και a x ≥ β, a x ≤ β.
Ας προσπαθήσουμε να καταλάβουμε πώς επιλύονται τέτοιες ανισότητες.
Θα αναζητήσουμε μια λύση αυστηρές ανισότητες. Η μόνη διαφορά κατά την επίλυση μη αυστηρών ανισοτήτων είναι ότι οι αντίστοιχες ρίζες που προκύπτουν περιλαμβάνονται στην απάντηση.
Ας υποθέσουμε ότι πρέπει να λύσουμε μια ανισότητα της μορφής και f (x) > β, Οπου α>1Και b>0.
Δείτε το διάγραμμα για την επίλυση τέτοιων ανισοτήτων (Εικόνα 1):
Ας δούμε τώρα ένα συγκεκριμένο παράδειγμα. Επίλυση ανισότητας: 5 x – 1 > 125.
Από 5 > 1 και 125 > 0, λοιπόν
x – 1 > log 5 125, δηλαδή
x – 1 > 3,
x > 4.
Απάντηση: (4; +∞) .
Ποια θα είναι η λύση σε αυτήν την ίδια ανισότητα; και f (x) >b, Αν 0
Έτσι, το διάγραμμα στο σχήμα 2

Παράδειγμα: Λύστε την ανισότητα (1/2) 2x - 2 ≥ 4
Εφαρμόζοντας τον κανόνα (Εικόνα 2), παίρνουμε
2х – 2 ≤ log 1/2 4,
2х – 2 ≤ –2,
2x ≤ 0,
x ≤ 0.
Απάντηση: (–∞; 0] .
Ας δούμε ξανά την ίδια ανισότητα και f (x) > β, Αν α>0Και σι<0 .
Έτσι, το διάγραμμα στο σχήμα 3:

Ένα παράδειγμα επίλυσης μιας ανισότητας (1/3) x + 2 > –9. Όπως παρατηρούμε, ανεξάρτητα από τον αριθμό που αντικαθιστούμε για το x, το (1/3) x + 2 είναι πάντα μεγαλύτερο από το μηδέν.
Απάντηση: (–∞; +∞) .
Πώς λύνονται οι ανισότητες της μορφής; και f(x)< b , Οπου α>1Και b>0?
Διάγραμμα στο Σχήμα 4:

Και το εξής παράδειγμα: 3 3 – x ≥ 8.
Από 3 > 1 και 8 > 0, λοιπόν
3 – x > log 3 8, δηλαδή
–x > log 3 8 – 3,
Χ< 3 – log
3 8.
Απάντηση: (0; 3–log 3 8) .
Πώς μπορεί να αλλάξει η λύση της ανισότητας; και f(x)< b
, στο 0
Διάγραμμα στο Σχήμα 5:

Και το ακόλουθο παράδειγμα: Λύστε την ανισότητα 0,6 2x – 3< 0,36 .
Ακολουθώντας το διάγραμμα στο σχήμα 5, παίρνουμε
2x – 3 > log 0,6 0,36,
2x – 3 > 2,
2x > 5,
x > 2,5
Απάντηση: (2,5; +∞) .
Ας εξετάσουμε το τελευταίο σχήμα για την επίλυση μιας ανισότητας της μορφής και f(x)< b , στο α>0Και σι<0 , που παρουσιάζεται στο Σχήμα 6:

Για παράδειγμα, ας λύσουμε την ανισότητα:

Σημειώνουμε ότι ανεξάρτητα από τον αριθμό που αντικαθιστούμε για το x, η αριστερή πλευρά της ανίσωσης είναι πάντα μεγαλύτερη από το μηδέν και η έκφρασή μας είναι μικρότερη από -8, δηλ. και μηδέν, που σημαίνει ότι δεν υπάρχουν λύσεις.
Απάντηση: χωρίς λύσεις.
Γνωρίζοντας πώς να λύσετε τις απλούστερες εκθετικές ανισώσεις, μπορείτε να προχωρήσετε επίλυση εκθετικών ανισώσεων.
Παράδειγμα 1.
Βρείτε τη μεγαλύτερη ακέραια τιμή του x που ικανοποιεί την ανίσωση

Δεδομένου ότι το 6 x είναι μεγαλύτερο από το μηδέν (στο κανένα x ο παρονομαστής πηγαίνει στο μηδέν), πολλαπλασιάζοντας και τις δύο πλευρές της ανισότητας επί 6 x, παίρνουμε:
440 – 2 6 2x > 8, λοιπόν
– 2 6 2x > 8 – 440,
– 2 6 2х > – 332,
6 2x< 216,
2x< 3,
Χ< 1,5. Наибольшее целое число из помежутка (–∞; 1,5) это число 1.
Απάντηση: 1.
Παράδειγμα 2.
Λύστε την ανισότητα 2 2 x – 3 2 x + 2 ≤ 0
Ας συμβολίσουμε το 2 x με y, λάβουμε την ανίσωση y 2 – 3y + 2 ≤ 0 και λύσουμε αυτήν την τετραγωνική ανισότητα.
y 2 – 3y +2 = 0,
y 1 = 1 και y 2 = 2.
Οι κλάδοι της παραβολής κατευθύνονται προς τα πάνω, ας σχεδιάσουμε ένα γράφημα:

Τότε η λύση της ανισότητας θα είναι η ανισότητα 1< у < 2, вернемся к нашей переменной х и получим неравенство 1< 2 х < 2, решая которое и найдем ответ 0 < x < 1.
Απάντηση: (0; 1) .
Παράδειγμα 3. Λύστε την ανισότητα 5 x +1 – 3 x +2< 2·5 x – 2·3 x –1
Ας συλλέξουμε εκφράσεις με τις ίδιες βάσεις σε ένα μέρος της ανισότητας
5 x +1 – 2 5 x< 3 x +2 – 2·3 x –1
Ας πάρουμε 5 x από αγκύλες στην αριστερή πλευρά της ανισότητας και 3 x στη δεξιά πλευρά της ανισότητας και παίρνουμε την ανισότητα
5 x (5 – 2)< 3 х (9 – 2/3),
3·5 x< (25/3)·3 х
Διαιρέστε και τις δύο πλευρές της ανισότητας με την παράσταση 3 3 x, το πρόσημο της ανισότητας δεν αλλάζει, αφού το 3 3 x είναι θετικός αριθμός, παίρνουμε την ανισότητα:


Χ< 2 (так как 5/3 > 1).
Απάντηση: (–∞; 2) .
Εάν έχετε ερωτήσεις σχετικά με την επίλυση εκθετικών ανισοτήτων ή θέλετε να εξασκηθείτε στην επίλυση παρόμοιων παραδειγμάτων, εγγραφείτε στα μαθήματά μου. Καθηγήτρια Valentina Galinevskaya.
ιστοσελίδα, όταν αντιγράφετε υλικό εν όλω ή εν μέρει, απαιτείται σύνδεσμος προς την πηγή.
Μέθοδος διαστήματος– ένας απλός τρόπος επίλυσης κλασματικών ορθολογικών ανισώσεων. Αυτό είναι το όνομα για ανισότητες που περιέχουν ορθολογικές (ή κλασματικές-ορθολογικές) εκφράσεις που εξαρτώνται από μια μεταβλητή.
1. Σκεφτείτε, για παράδειγμα, την ακόλουθη ανισότητα
Η μέθοδος διαστήματος σάς επιτρέπει να το λύσετε σε λίγα λεπτά.
Στην αριστερή πλευρά αυτής της ανισότητας - κλασματική ορθολογική συνάρτηση. Λογικό γιατί δεν περιέχει ρίζες, ημίτονο, λογάριθμους - μόνο ορθολογικές εκφράσεις. Στα δεξιά είναι το μηδέν.
Η μέθοδος διαστήματος βασίζεται στην ακόλουθη ιδιότητα μιας κλασματικής ορθολογικής συνάρτησης.
Μια κλασματική ορθολογική συνάρτηση μπορεί να αλλάξει πρόσημο μόνο σε εκείνα τα σημεία στα οποία είναι ίση με μηδέν ή δεν υπάρχει.
Ας σας υπενθυμίσουμε πώς να παραγοντοποιήσετε τετραγωνικό τριώνυμο, δηλαδή έκφραση της μορφής .
Πού και είναι οι ρίζες τετραγωνική εξίσωση.
Σχεδιάζουμε έναν άξονα και τοποθετούμε τα σημεία στα οποία ο αριθμητής και ο παρονομαστής μηδενίζονται.

Τα μηδενικά του παρονομαστή και είναι τρυπημένα σημεία, αφού σε αυτά τα σημεία δεν ορίζεται η συνάρτηση στην αριστερή πλευρά της ανίσωσης (δεν μπορείτε να διαιρέσετε με το μηδέν). Τα μηδενικά του αριθμητή και - είναι σκιασμένα, αφού η ανισότητα δεν είναι αυστηρή. Πότε και η ανισότητα μας ικανοποιείται, αφού και οι δύο πλευρές της είναι ίσες με μηδέν.
Αυτά τα σημεία σπάζουν τον άξονα σε διαστήματα.
Ας προσδιορίσουμε το πρόσημο της κλασματικής ορθολογικής συνάρτησης στην αριστερή πλευρά της ανισότητάς μας σε καθένα από αυτά τα διαστήματα. Θυμόμαστε ότι μια κλασματική ορθολογική συνάρτηση μπορεί να αλλάξει πρόσημο μόνο σε εκείνα τα σημεία στα οποία είναι ίση με μηδέν ή δεν υπάρχει. Αυτό σημαίνει ότι σε καθένα από τα διαστήματα μεταξύ των σημείων όπου ο αριθμητής ή ο παρονομαστής πηγαίνει στο μηδέν, το πρόσημο της έκφρασης στην αριστερή πλευρά της ανισότητας θα είναι σταθερό - είτε "συν" είτε "μείον".
Και επομένως, για να προσδιορίσουμε το πρόσημο της συνάρτησης σε κάθε τέτοιο διάστημα, παίρνουμε οποιοδήποτε σημείο που ανήκει σε αυτό το διάστημα. Αυτό που μας βολεύει.
. Πάρτε, για παράδειγμα, και ελέγξτε το πρόσημο της έκφρασης στην αριστερή πλευρά της ανισότητας. Κάθε μία από τις «αγκύλες» είναι αρνητική. Η αριστερή πλευρά έχει ένα σημάδι.

Επόμενο διάστημα: . Ας ελέγξουμε την πινακίδα στο . Διαπιστώνουμε ότι η αριστερή πλευρά έχει αλλάξει το πρόσημά της σε .

Ας το πάρουμε. Όταν η έκφραση είναι θετική - επομένως, είναι θετική σε ολόκληρο το διάστημα από έως.

Όταν η αριστερή πλευρά της ανισότητας είναι αρνητική.

Και τέλος, class="tex" alt="x>7"> . Подставим и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак .!}

Βρήκαμε σε ποια χρονικά διαστήματα η έκφραση είναι θετική. Το μόνο που μένει είναι να γράψουμε την απάντηση:
Απάντηση: .
Σημείωση: οι πινακίδες εναλλάσσονται μεταξύ των διαστημάτων. Αυτό συνέβη επειδή όταν περνούσε από κάθε σημείο, ακριβώς ένας από τους γραμμικούς παράγοντες άλλαζε πρόσημο, ενώ οι υπόλοιποι τον διατήρησαν αμετάβλητο.
Βλέπουμε ότι η μέθοδος του διαστήματος είναι πολύ απλή. Για να λύσουμε την κλασματική-ορθολογική ανισότητα χρησιμοποιώντας τη μέθοδο του διαστήματος, την ανάγουμε στη μορφή:
Ή class="tex" alt="\genfrac())()(0)(\displaystyle P\left(x \right))(\displaystyle Q\left(x \right)) > 0"> !}, ή ή .
(στην αριστερή πλευρά είναι μια κλασματική ορθολογική συνάρτηση, στη δεξιά πλευρά είναι μηδέν).
Στη συνέχεια σημειώνουμε στην αριθμητική γραμμή τα σημεία στα οποία ο αριθμητής ή ο παρονομαστής πηγαίνει στο μηδέν.
Αυτά τα σημεία διαιρούν ολόκληρη την αριθμητική γραμμή σε διαστήματα, σε καθένα από τα οποία η κλασματική-ορθολογική συνάρτηση διατηρεί το πρόσημό της.
Το μόνο που μένει είναι να ανακαλύπτουμε το πρόσημο του σε κάθε μεσοδιάστημα.
Αυτό το κάνουμε ελέγχοντας το πρόσημο της έκφρασης σε οποιοδήποτε σημείο που ανήκει σε ένα δεδομένο διάστημα. Μετά από αυτό, γράφουμε την απάντηση. Αυτό είναι όλο.
Όμως τίθεται το ερώτημα: τα ζώδια εναλλάσσονται πάντα; Όχι πάντα! Πρέπει να είστε προσεκτικοί και να μην τοποθετείτε πινακίδες μηχανικά και αλόγιστα.
2. Ας εξετάσουμε μια άλλη ανισότητα.
Class="tex" alt="\genfrac())()(0)(\displaystyle \left(x-2 \right)^2)(\displaystyle \left(x-1 \right) \ αριστερά(x-3 \δεξιά))>0"> !}
Τοποθετήστε ξανά τα σημεία στον άξονα. Οι τελείες και είναι τρυπημένες γιατί είναι μηδενικά του παρονομαστή. Το σημείο είναι επίσης κομμένο, αφού η ανισότητα είναι αυστηρή.

Όταν ο αριθμητής είναι θετικός, και οι δύο παράγοντες στον παρονομαστή είναι αρνητικοί. Αυτό μπορεί εύκολα να ελεγχθεί λαμβάνοντας οποιονδήποτε αριθμό από ένα δεδομένο διάστημα, για παράδειγμα, . Η αριστερή πλευρά έχει το σημάδι:

Όταν ο αριθμητής είναι θετικός. Ο πρώτος παράγοντας στον παρονομαστή είναι θετικός, ο δεύτερος παράγοντας είναι αρνητικός. Η αριστερή πλευρά έχει το σύμβολο:

Η κατάσταση είναι ίδια! Ο αριθμητής είναι θετικός, ο πρώτος παράγοντας στον παρονομαστή είναι θετικός, ο δεύτερος αρνητικός. Η αριστερή πλευρά έχει το σύμβολο:

Τέλος, με class="tex" alt="x>3">
все множители положительны, и левая часть имеет знак :!} 
Απάντηση: .
Γιατί διαταράχθηκε η εναλλαγή των πινακίδων; Διότι όταν διέρχεται από ένα σημείο ο πολλαπλασιαστής είναι «υπεύθυνος» για αυτό δεν άλλαξε πρόσημο. Κατά συνέπεια, ολόκληρη η αριστερή πλευρά της ανισότητάς μας δεν άλλαξε πρόσημο.
Συμπέρασμα: αν ο γραμμικός πολλαπλασιαστής είναι άρτια δύναμη (για παράδειγμα, στο τετράγωνο), τότε όταν διέρχεται από ένα σημείο το πρόσημο της παράστασης στην αριστερή πλευρά δεν αλλάζει. Σε περίπτωση περιττού βαθμού, το πρόσημο, φυσικά, αλλάζει.
3. Ας εξετάσουμε περισσότερα δύσκολη υπόθεση. Διαφέρει από την προηγούμενη στο ότι η ανισότητα δεν είναι αυστηρή:
Η αριστερή πλευρά είναι η ίδια όπως στο προηγούμενο πρόβλημα. Η εικόνα των πινακίδων θα είναι η ίδια:

Ίσως η απάντηση να είναι η ίδια; Οχι! Προστίθεται μια λύση Αυτό συμβαίνει επειδή και η αριστερή και η δεξιά πλευρά της ανισότητας είναι ίσες με μηδέν - επομένως, αυτό το σημείο είναι λύση.
Απάντηση: .
Αυτή η κατάσταση εμφανίζεται συχνά σε προβλήματα στην Ενιαία Κρατική Εξέταση στα μαθηματικά. Εδώ οι υποψήφιοι πέφτουν σε παγίδα και χάνουν βαθμούς. Πρόσεχε!
4. Τι πρέπει να κάνετε εάν ο αριθμητής ή ο παρονομαστής δεν μπορούν να αποσυντεθούν σε γραμμικούς παράγοντες? Σκεφτείτε αυτήν την ανισότητα:
Ένα τετράγωνο τριώνυμο δεν μπορεί να παραγοντοποιηθεί: η διάκριση είναι αρνητική, δεν υπάρχουν ρίζες. Αλλά αυτό είναι καλό! Αυτό σημαίνει ότι το πρόσημο της έκφρασης για όλους είναι το ίδιο, και συγκεκριμένα, θετικό. Μπορείτε να διαβάσετε περισσότερα σχετικά με αυτό στο άρθρο σχετικά με τις ιδιότητες των τετραγωνικών συναρτήσεων.
Και τώρα μπορούμε να διαιρέσουμε και τις δύο πλευρές της ανισότητάς μας με μια τιμή που είναι θετική για όλους. Ας καταλήξουμε σε μια ισοδύναμη ανισότητα:
Το οποίο λύνεται εύκολα με τη μέθοδο του διαστήματος.
Λάβετε υπόψη ότι διαιρέσαμε και τις δύο πλευρές της ανισότητας με μια τιμή που γνωρίζαμε με βεβαιότητα ότι ήταν θετική. Φυσικά, γενικά, δεν πρέπει να πολλαπλασιάσετε ή να διαιρέσετε μια ανισότητα με μια μεταβλητή της οποίας το πρόσημο είναι άγνωστο.
5 . Ας εξετάσουμε μια άλλη ανισότητα, φαινομενικά πολύ απλή:
Θέλω απλώς να το πολλαπλασιάσω με . Αλλά είμαστε ήδη έξυπνοι και δεν θα το κάνουμε αυτό. Άλλωστε, μπορεί να είναι και θετικό και αρνητικό. Και γνωρίζουμε ότι αν και οι δύο πλευρές της ανισότητας πολλαπλασιαστούν με μια αρνητική τιμή, το πρόσημο της ανισότητας αλλάζει.
Θα το κάνουμε διαφορετικά - θα συγκεντρώσουμε τα πάντα σε ένα μέρος και θα τα φέρουμε σε έναν κοινό παρονομαστή. Η δεξιά πλευρά θα παραμείνει μηδέν:
Class="tex" alt="\genfrac())()()(0)(\displaystyle x-2)(\displaystyle x)>0"> !}
Και μετά από αυτό - εφαρμόστε μέθοδος διαστήματος.
Για παράδειγμα, η ανισότητα είναι η έκφραση \(x>5\).
Τύποι ανισοτήτων:
Αν τα \(a\) και \(b\) είναι αριθμοί ή , τότε καλείται η ανισότητα αριθμητικός. Στην πραγματικότητα απλώς συγκρίνει δύο αριθμούς. Τέτοιες ανισότητες χωρίζονται σε πιστόςΚαι άπιστος.
Για παράδειγμα:
\(-5<2\) - верное числовое неравенство, ведь \(-5\) действительно меньше \(2\);
Το \(17+3\geq 115\) είναι μια λανθασμένη αριθμητική ανισότητα, αφού το \(17+3=20\), και το \(20\) είναι μικρότερο από \(115\) (και όχι μεγαλύτερο ή ίσο με) .
Εάν τα \(a\) και \(b\) είναι εκφράσεις που περιέχουν μια μεταβλητή, τότε έχουμε ανισότητα με μεταβλητή. Τέτοιες ανισότητες χωρίζονται σε τύπους ανάλογα με το περιεχόμενο:
|
\(2x+1\geq4(5-x)\) |
Μεταβλητή μόνο στην πρώτη δύναμη |
|||
|
\(3x^2-x+5>0\) |
Υπάρχει μια μεταβλητή στη δεύτερη δύναμη (τετράγωνο), αλλά δεν υπάρχουν ανώτερες δυνάμεις (τρίτη, τέταρτη, κ.λπ.) |
|||
|
\(\log_(4)((x+1))<3\) |
||||
|
\(2^(x)\leq8^(5x-2)\) |
Ποια είναι η λύση σε μια ανισότητα;
Αν αντικαταστήσετε έναν αριθμό αντί για μια μεταβλητή με μια ανισότητα, θα μετατραπεί σε αριθμητική.
Εάν μια δεδομένη τιμή για το x μετατρέψει την αρχική ανισότητα σε αληθινή αριθμητική, τότε καλείται λύση στην ανισότητα. Εάν όχι, τότε αυτή η τιμή δεν είναι λύση. Και στο λύσει την ανισότητα– πρέπει να βρείτε όλες τις λύσεις του (ή να δείξετε ότι δεν υπάρχουν).
Για παράδειγμα,Αν αντικαταστήσουμε τον αριθμό \(7\) στη γραμμική ανισότητα \(x+6>10\), παίρνουμε τη σωστή αριθμητική ανισότητα: \(13>10\). Και αν αντικαταστήσουμε το \(2\), θα υπάρξει μια λανθασμένη αριθμητική ανισότητα \(8>10\). Δηλαδή, το \(7\) είναι μια λύση στην αρχική ανισότητα, αλλά το \(2\) δεν είναι.
Ωστόσο, η ανισότητα \(x+6>10\) έχει άλλες λύσεις. Πράγματι, θα πάρουμε τις σωστές αριθμητικές ανισώσεις όταν αντικαταστήσουμε τα \(5\), και \(12\), και \(138\)... Και πώς μπορούμε να βρούμε όλες τις πιθανές λύσεις; Για αυτό χρησιμοποιούν Για την περίπτωσή μας έχουμε:
\(x+6>10\) \(|-6\)
\(x>4\)
Δηλαδή, οποιοσδήποτε αριθμός μεγαλύτερος από τέσσερα είναι κατάλληλος για εμάς. Τώρα πρέπει να γράψετε την απάντηση. Οι λύσεις των ανισώσεων συνήθως γράφονται αριθμητικά, σημειώνοντάς τες επιπλέον στον αριθμητικό άξονα με σκίαση. Για την περίπτωσή μας έχουμε:
Απάντηση:
\(x\in(4;+\infty)\)
Πότε αλλάζει το πρόσημο μιας ανισότητας;
Υπάρχει μια μεγάλη παγίδα στις ανισότητες που πραγματικά «λατρεύουν» να πέφτουν οι μαθητές:
Κατά τον πολλαπλασιασμό (ή τη διαίρεση) μιας ανίσωσης με έναν αρνητικό αριθμό, αντιστρέφεται ("περισσότερο" με "λιγότερο", "περισσότερο ή ίσο" με "λιγότερο από ή ίσο" και ούτω καθεξής)
Γιατί συμβαίνει αυτό; Για να το καταλάβουμε αυτό, ας δούμε τους μετασχηματισμούς αριθμητική ανισότητα\(3>1\). Είναι σωστό, το τρία είναι όντως μεγαλύτερο από ένα. Αρχικά, ας προσπαθήσουμε να το πολλαπλασιάσουμε με οποιονδήποτε θετικό αριθμό, για παράδειγμα, δύο:
\(3>1\) \(|\cdot2\)
\(6>2\)
Όπως μπορούμε να δούμε, μετά τον πολλαπλασιασμό η ανισότητα παραμένει αληθινή. Και ανεξάρτητα από το θετικό αριθμό που πολλαπλασιάζουμε, πάντα θα έχουμε τη σωστή ανισότητα. Τώρα ας προσπαθήσουμε να πολλαπλασιάσουμε με έναν αρνητικό αριθμό, για παράδειγμα, μείον τρία:
\(3>1\) \(|\cdot(-3)\)
\(-9>-3\)
Το αποτέλεσμα είναι μια λανθασμένη ανισότητα, γιατί το μείον εννέα είναι μικρότερο από το μείον τρία! Δηλαδή, για να γίνει αληθινή η ανισότητα (και επομένως, ο μετασχηματισμός του πολλαπλασιασμού με αρνητικό ήταν "νόμιμος"), πρέπει να αντιστρέψετε το πρόσημο σύγκρισης, ως εξής: \(−9<− 3\).
Με τη διαίρεση θα λειτουργήσει με τον ίδιο τρόπο, μπορείτε να το ελέγξετε μόνοι σας.
Ο κανόνας που γράφτηκε παραπάνω ισχύει για όλους τους τύπους ανισώσεων, όχι μόνο για αριθμητικές.
Παράδειγμα: Λύστε την ανίσωση \(2(x+1)-1<7+8x\)Λύση:
|
\(2x+2-1<7+8x\) |
Ας μετακινηθούμε \(8x\) προς τα αριστερά και \(2\) και \(-1\) προς τα δεξιά, χωρίς να ξεχνάμε να αλλάξουμε τα σημάδια |
|
\(2x-8x<7-2+1\) |
|
|
\(-6x<6\) \(|:(-6)\) |
Ας διαιρέσουμε και τις δύο πλευρές της ανισότητας με το \(-6\), χωρίς να ξεχνάμε να αλλάξουμε από "λιγότερο" σε "περισσότερο" |
|
Ας σημειώσουμε ένα αριθμητικό διάστημα στον άξονα. Ανισότητα, επομένως «τρυπάμε» την ίδια την τιμή \(-1\) και δεν την παίρνουμε ως απάντηση |
|
|
Ας γράψουμε την απάντηση ως ένα διάστημα |
Απάντηση: \(x\in(-1;\infty)\)
Ανισότητες και αναπηρία
Οι ανισότητες, όπως και οι εξισώσεις, μπορεί να έχουν περιορισμούς στο , δηλαδή στις τιμές του x. Συνεπώς, αυτές οι τιμές που είναι απαράδεκτες σύμφωνα με το DZ θα πρέπει να εξαιρεθούν από το φάσμα των λύσεων.
Παράδειγμα: Λύστε την ανισότητα \(\sqrt(x+1)<3\)
Λύση: Είναι σαφές ότι για να είναι η αριστερή πλευρά μικρότερη από \(3\), η ριζική έκφραση πρέπει να είναι μικρότερη από \(9\) (εξάλλου από \(9\) μόλις \(3\)). Παίρνουμε:
\(x+1<9\) \(|-1\)
\(Χ<8\)
Ολα; Οποιαδήποτε τιμή x μικρότερη από \(8\) θα μας ταιριάζει; Οχι! Διότι αν πάρουμε, για παράδειγμα, την τιμή \(-5\) που φαίνεται να ταιριάζει στην απαίτηση, δεν θα είναι λύση στην αρχική ανισότητα, αφού θα μας οδηγήσει στον υπολογισμό της ρίζας ενός αρνητικού αριθμού.
\(\sqrt(-5+1)<3\)
\(\sqrt(-4)<3\)
Επομένως, πρέπει επίσης να λάβουμε υπόψη τους περιορισμούς στην τιμή του X - δεν μπορεί να είναι τέτοιος ώστε να υπάρχει αρνητικός αριθμός κάτω από τη ρίζα. Έτσι, έχουμε τη δεύτερη απαίτηση για το x:
\(x+1\geq0\)
\(x\geq-1\)
Και για να είναι το x η τελική λύση, πρέπει να ικανοποιεί και τις δύο απαιτήσεις ταυτόχρονα: πρέπει να είναι μικρότερο από \(8\) (για να είναι λύση) και μεγαλύτερο από \(-1\) (για να είναι αποδεκτό κατ' αρχήν). Σχεδιάζοντας το στην αριθμητική γραμμή, έχουμε την τελική απάντηση:

Απάντηση: \(\αριστερά[-1;8\δεξιά)\)
Προσοχή!
Υπάρχουν επιπλέον
υλικά στο Ειδικό Τμήμα 555.
Για όσους είναι πολύ "όχι πολύ..."
Και για όσους «πολύ…»)
Τι συνέβη «τετραγωνική ανισότητα»;Καμία ερώτηση!) Αν πάρεις όποιοςτετραγωνική εξίσωση και αντικαταστήστε το πρόσημο σε αυτήν "=" (ίσο) με οποιοδήποτε πρόσημο ανισότητας ( > ≥ < ≤ ≠ ), παίρνουμε μια τετραγωνική ανισότητα. Για παράδειγμα:
1. x 2 -8x+12 ≥ 0
2. -x 2 +3x > 0
3. x 2 ≤ 4
Λοιπόν, καταλαβαίνεις...)
Δεν είναι για τίποτα που συνέδεσα εξισώσεις και ανισότητες εδώ. Το θέμα είναι ότι το πρώτο βήμα για την επίλυση όποιοςτετραγωνική ανισότητα - να λύσετε την εξίσωση από την οποία προκύπτει αυτή η ανισότητα.Για το λόγο αυτό, η αδυναμία επίλυσης δευτεροβάθμιων εξισώσεων οδηγεί αυτόματα σε πλήρη αποτυχία στις ανισώσεις. Είναι σαφής η υπόδειξη;) Αν μη τι άλλο, κοιτάξτε πώς να λύσετε οποιεσδήποτε δευτεροβάθμιες εξισώσεις. Εκεί περιγράφονται όλα αναλυτικά. Και σε αυτό το μάθημα θα ασχοληθούμε με τις ανισότητες.
Η έτοιμη για λύση ανισότητα έχει τη μορφή: στα αριστερά είναι ένα τετραγωνικό τριώνυμο τσεκούρι 2 +bx+c, στα δεξιά - μηδέν.Το σύμβολο της ανισότητας μπορεί να είναι απολύτως οτιδήποτε. Τα δύο πρώτα παραδείγματα είναι εδώ είναι ήδη έτοιμοι να πάρουν μια απόφαση.Το τρίτο παράδειγμα χρειάζεται ακόμη προετοιμασία.
Αν σας αρέσει αυτό το site...
Παρεμπιπτόντως, έχω μερικές ακόμη ενδιαφέρουσες τοποθεσίες για εσάς.)
Μπορείτε να εξασκηθείτε στην επίλυση παραδειγμάτων και να μάθετε το επίπεδό σας. Δοκιμή με άμεση επαλήθευση. Ας μάθουμε - με ενδιαφέρον!)
Μπορείτε να εξοικειωθείτε με συναρτήσεις και παραγώγους.