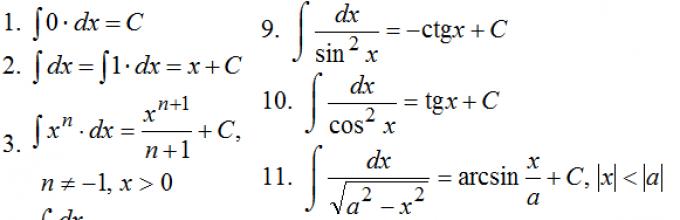Οι τέσσερις κύριες μέθοδοι ολοκλήρωσης παρατίθενται παρακάτω.
1)
Ο κανόνας για την ενσωμάτωση ενός αθροίσματος ή μιας διαφοράς.
.
Εδώ και παρακάτω u, v, w είναι συναρτήσεις της μεταβλητής ολοκλήρωσης x.
2)
Μετακίνηση της σταθεράς εκτός του ολοκληρώματος.
Έστω c σταθερά ανεξάρτητη του x. Στη συνέχεια, μπορεί να αφαιρεθεί από το ολοκλήρωμα.
3)
Μεταβλητή μέθοδος αντικατάστασης.
Ας θεωρήσουμε το αόριστο ολοκλήρωμα.
Αν μπορούμε να βρούμε μια τέτοια συνάρτηση φ (Χ)από το x, έτσι
,
τότε, αντικαθιστώντας τη μεταβλητή t = φ(x) , έχουμε
.
4)
Φόρμουλα για ενσωμάτωση ανά εξαρτήματα.
,
όπου u και v είναι συναρτήσεις της μεταβλητής ολοκλήρωσης.
Ο τελικός στόχος του υπολογισμού αόριστα ολοκληρώματα- αυτό είναι, μέσω μετασχηματισμών, να ανάγεται ένα δεδομένο ολοκλήρωμα στα απλούστερα ολοκληρώματα, τα οποία ονομάζονται ολοκληρώματα πίνακα. Τα ολοκληρώματα του πίνακα εκφράζονται μέσω στοιχειωδών συναρτήσεων χρησιμοποιώντας γνωστούς τύπους.
Δείτε Πίνακα Ολοκληρωμάτων >>>
Παράδειγμα
Υπολογίστε αόριστο ολοκλήρωμα
Λύση
Σημειώνουμε ότι το ολοκλήρωμα είναι το άθροισμα και η διαφορά τριών όρων:
, Και .
Εφαρμογή της μεθόδου 1
.
Στη συνέχεια, σημειώνουμε ότι τα ολοκληρώματα των νέων ολοκληρωμάτων πολλαπλασιάζονται με σταθερές 5, 4,
Και 2
, αντίστοιχα. Εφαρμογή της μεθόδου 2
.
Στον πίνακα των ολοκληρωμάτων βρίσκουμε τον τύπο
.
Υποθέτοντας n = 2
, βρίσκουμε το πρώτο ολοκλήρωμα.
Ας ξαναγράψουμε το δεύτερο ολοκλήρωμα στη μορφή
.
Παρατηρούμε ότι . Επειτα
Ας χρησιμοποιήσουμε την τρίτη μέθοδο. Αλλάζουμε τη μεταβλητή t = φ (x) = ln x.
.
Στον πίνακα των ολοκληρωμάτων βρίσκουμε τον τύπο
Εφόσον η μεταβλητή της ολοκλήρωσης μπορεί να υποδηλωθεί με οποιοδήποτε γράμμα, τότε
Ας ξαναγράψουμε το τρίτο ολοκλήρωμα στη μορφή
.
Εφαρμόζουμε τον τύπο της ολοκλήρωσης ανά μέρη.
Ας το βάλουμε.
Επειτα
;
;
;
;
.
Επιτέλους έχουμε
.
Ας συλλέξουμε όρους με x 3
.
.
Απάντηση
Βιβλιογραφικές αναφορές:
Ν.Μ. Gunther, R.O. Kuzmin, Συλλογή προβλημάτων στα ανώτερα μαθηματικά, "Lan", 2003.
Η ολοκλήρωση είναι μια από τις κύριες λειτουργίες στη μαθηματική ανάλυση. Οι πίνακες γνωστών αντιπαραγώγων μπορεί να είναι χρήσιμοι, αλλά τώρα, μετά την εμφάνιση των συστημάτων υπολογιστικής άλγεβρας, χάνουν τη σημασία τους. Παρακάτω είναι μια λίστα με τα πιο κοινά πρωτόγονα.
Πίνακας βασικών ολοκληρωμάτων
Μια άλλη, συμπαγής επιλογή

Πίνακας ολοκληρωμάτων τριγωνομετρικών συναρτήσεων
Από ορθολογικές συναρτήσεις
Από παράλογες λειτουργίες
Ολοκληρώματα υπερβατικών συναρτήσεων

Το "C" είναι μια αυθαίρετη σταθερά ολοκλήρωσης, η οποία προσδιορίζεται εάν είναι γνωστή η τιμή του ολοκληρώματος σε οποιοδήποτε σημείο. Κάθε συνάρτηση έχει έναν άπειρο αριθμό αντιπαραγώγων.
Οι περισσότεροι μαθητές και μαθητές έχουν προβλήματα στον υπολογισμό των ολοκληρωμάτων. Αυτή η σελίδα περιέχει ενσωματωμένους πίνακεςαπό τριγωνομετρικές, ορθολογικές, παράλογες και υπερβατικές συναρτήσεις που θα βοηθήσουν στη λύση. Ένας πίνακας παραγώγων θα σας βοηθήσει επίσης.
Βίντεο - πώς να βρείτε ολοκληρώματα
Αν δεν καταλαβαίνεις καλά αυτό το θέμα, δείτε το βίντεο, που τα εξηγεί όλα αναλυτικά.Πίνακας αντιπαραγώγων
Χρησιμοποιώντας τις ιδιότητες των αόριστων ολοκληρωμάτων και τον πίνακα των θεμελιωδών ολοκληρωμάτων,
Μπορείτε να ενσωματώσετε ορισμένες λειτουργίες.
ΤΕΧΝΙΚΕΣ ΕΝΣΩΜΑΤΩΣΗΣ
Μέθοδος αντικατάστασης
Η πιο κοινή μέθοδος ολοκλήρωσης συναρτήσεων είναι η μέθοδος
αντικατάσταση, η οποία εφαρμόζεται όταν το αναζητούμενο ολοκλήρωμα
είναι πίνακας, αλλά μέσω μιας σειράς στοιχειωδών μετασχηματισμών μπορεί να είναι
μειώνεται σε τραπέζι.
η μεταβλητή t αντικαθίσταται από τη μεταβλητή / χρησιμοποιώντας τον τύπο x=φ(t) και,
Επομένως, το dx είναι το γινόμενο του φ"(t)dt.
Ενσωμάτωση κατά εξαρτήματα
Παράδειγμα: πρέπει να βρείτε το ολοκλήρωμα
Εδώ, οι διπλές κάθετες γραμμές περικλείουν όλους τους υπολογισμούς που
είναι προπαρασκευαστικές για την εφαρμογή του τύπου ολοκλήρωσης
εξαρτήματα. Οι προπαρασκευαστικές εγγραφές μπορούν να ληφθούν εκτός της εξίσωσης.
ΟΡΙΣΤΟΣ ΟΛΟΚΛΗΡΩΜΕΝΟΣ
Εργο. Να βρείτε την προσαύξηση της συνάρτησης που είναι αντιπαράγωγος της συνάρτησης f(x), όταν
μετάβαση του ορίσματος x από την τιμή a στην τιμή b.
Λύση. Ας υποθέσουμε ότι με την ολοκλήρωση βρήκαμε
Όπως βλέπουμε, στην έκφραση για την προσαύξηση αντιπαράγωγη λειτουργία F(x) + C 1
δεν υπάρχει σταθερή τιμή C1. Και αφού το C 1 σήμαινε οποιοδήποτε
δεδομένου αριθμού, τότε το αποτέλεσμα που προκύπτει οδηγεί στο εξής συμπέρασμα: όταν
μετάβαση του ορίσματος x από την τιμή x=a στην τιμή x=b, όλες οι συναρτήσεις F(x) + C,
τα αντιπαράγωγα για μια δεδομένη συνάρτηση f(x) έχουν την ίδια αύξηση ίση με
F(b)-F(a).
Αυτή η προσαύξηση συνήθως ονομάζεται οριστικό ολοκλήρωμα και συμβολίζεται
σύμβολο
Έτσι, το απαιτούμενο ολοκλήρωμα είναι ίσο με 6.
Γεωμετρική σημασία οριστικό ολοκλήρωμα
1. Βρείτε το εμβαδόν ενός ημιτονοειδούς τόξου.
Το σώμα της επανάστασης φαίνεται στο σχήμα.
Για το αεροπλάνο θα επιλέξω το επίπεδο xy.
Παράδειγμα Νο. 2. Εύρεση ορισμένου ολοκληρώματος χρησιμοποιώντας τη μέθοδο μεταβλητής αλλαγής
ενσωμάτωση
Παράδειγμα Νο. 3. Εύρεση ορισμένου ολοκληρώματος με ολοκλήρωση
εξαρτήματα.
Σχέσεις μεταξύ μάζας m και πυκνότητας p:
Σχέσεις μεταξύ ηλεκτρικό φορτίο q και ρεύμα I:
Η σχέση μεταξύ της θερμοχωρητικότητας c και της ποσότητας θερμότητας Q:
Περιγραφή της κίνησης του παχύρρευστου υγρού, αίματος μέσω των αγγείων, κατανομή
αρτηριακή πίεση στο καρδιαγγειακό σύστημα, θερμική, ηλεκτρική,
μαγνητικές, οπτικές διεργασίες που σχετίζονται με τη ζωή
οργανισμός, απαιτεί τη χρήση της ολοκλήρωσης.
ΕΚΠΑΙΔΕΥΣΗ: ΕΠΙΛΥΣΗ ΠΑΡΑΔΕΙΓΜΑΤΩΝ
τα σημεία αλλάζουν σύμφωνα με το νόμο v = (6t +7) m/s
Προσδιορίστε πώς η διανυθείσα απόσταση εξαρτάται από το χρόνο εάν η ταχύτητα του υλικού
τα σημεία αλλάζουν σύμφωνα με το νόμο v = (6t +7) m/s, αν είναι γνωστό ότι την αρχική στιγμή
χρόνος (t=0), υλικό σημείοβρισκόταν σε απόσταση s 0 = 4 m από την αρχή
Βρείτε το έργο που έκανε το ελατήριο όταν εκτείνεται από x 1 σε x 2.
Λύση.
Για να ενσωματώσετε αυτή τη λειτουργία, πρέπει να κάνετε μια αντικατάσταση
μεταβλητός
Εφόσον υπάρχουν 4 2 ≤2 στο τμήμα [-1;2], τότε υπολογίζεται το εμβαδόν S αυτού του σχήματος
με τον εξής τρόπο:
Λύση.
u=sinx
du = cosxdx
νέα όρια ολοκλήρωσης: u 1 = 0 (αφού x 1 = 0, ας αντικαταστήσουμε αυτήν την τιμή με τη νέα
συνάρτηση - u = sinx, u 1 = sinx 1 = 0)
η εμφάνιση ενός ρεύματος επαγωγής σε αυτό,
| |
| απάντηση: |
ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
Οι διαφορικές εξισώσεις είναι εξισώσεις που περιέχουν τα απαιτούμενα
συναρτήσεις, τα παράγωγά τους διαφόρων τάξεων και ανεξάρτητων μεταβλητών.
Η θεωρία των διαφορικών εξισώσεων προέκυψε στα τέλη του 17ου αιώνα υπό
την επιρροή των αναγκών της μηχανικής και άλλων φυσικών επιστημών,
ουσιαστικά ταυτόχρονα με ολοκληρωτικό λογισμό και
διαφορικός λογισμός.
Οι απλούστερες διαφορικές εξισώσεις συναντήθηκαν ήδη στα έργα του I.
Newton and G. Leibniz; όρος "διαφορικές εξισώσεις"
ανήκει στον Leibniz. Το πρόβλημα της εύρεσης του αόριστου ολοκληρώματος F (x)
συναρτήσεις f(x) Newton θεωρούνται απλώς ως ειδική περίπτωσητο δεύτερο του
καθήκοντα. Αυτή ήταν η προσέγγιση για τον Νεύτωνα, ως δημιουργό των θεμελίων
η μαθηματική φυσική επιστήμη είναι απολύτως δικαιολογημένη: σε μια πολύ μεγάλη
Σε πολλές περιπτώσεις, οι νόμοι της φύσης που διέπουν ορισμένες διαδικασίες,
εκφράζονται με τη μορφή διαφορικών εξισώσεων, και ο υπολογισμός της ροής αυτών
διεργασίες ανάγεται στην επίλυση διαφορικών εξισώσεων.
Τα επόμενα δύο απλά παραδείγματαμπορεί να χρησιμεύσει ως απεικόνιση του
τι ειπώθηκε.
1) Εάν ένα σώμα που θερμαίνεται στη θερμοκρασία Τ τοποθετηθεί σε ένα μέσο, η θερμοκρασία
που ισούται με μηδέν, τότε υπό ορισμένες προϋποθέσεις μπορούμε να υποθέσουμε ότι
αύξηση ΔT (αρνητικό στην περίπτωση Τ> 0) της θερμοκρασίας του σε ένα μικρό
το χρονικό διάστημα Δt εκφράζεται με επαρκή ακρίβεια από τον τύπο
όπου k είναι σταθερός συντελεστής. Κατά την επεξεργασία αυτού μαθηματικά
σωματικό πρόβλημαπιστέψτε ότι ακριβώς το αντίστοιχο
περιοριστικός λόγος μεταξύ των διαφορικών
δηλ. λαμβάνει χώρα διαφορική εξίσωση
όπου το Τ δηλώνει την παράγωγο αριθ. t.
τεντώνοντας το ελατήριο, φέρνει το φορτίο μέσα
κίνηση. Αν το x(t) δηλώνει
το ποσό της απόκλισης του σώματος από
θέση ισορροπίας αυτή τη στιγμή
χρόνος t, τότε η επιτάχυνση του σώματος
εκφράζεται με τη 2η παράγωγο x" (t).
Η δύναμη tx" (t) που ενεργεί στο σώμα είναι
με μικρές εκτάσεις της πηγής
σύμφωνα με τους νόμους της θεωρίας ελαστικότητας, είναι ανάλογο με την απόκλιση x (t). Οτι.,
παίρνουμε μια διαφορική εξίσωση
 |
| Η λύση του μοιάζει με: |