Στόχοι μαθήματος:
1. Εκπαιδευτικά:
Εισάγετε την έννοια του παραλληλεπίπεδου και τους τύπους του.
- να διατυπώσει (χρησιμοποιώντας την αναλογία με παραλληλόγραμμο και ορθογώνιο) και να αποδείξει τις ιδιότητες ενός παραλληλεπίπεδου και ενός κυβοειδούς.
- επαναλάβετε ερωτήσεις που σχετίζονται με την παραλληλία και την καθετότητα στο χώρο.
2. Αναπτυξιακή:
Συνεχίστε να αναπτύσσετε τέτοιες δεξιότητες στους μαθητές γνωστικές διαδικασίεςως αντίληψη, κατανόηση, σκέψη, προσοχή, μνήμη.
- προωθεί την ανάπτυξη στοιχείων στους μαθητές δημιουργική δραστηριότηταως ιδιότητες της σκέψης (διαίσθηση, χωρική σκέψη).
- να αναπτύξουν στους μαθητές την ικανότητα να εξάγουν συμπεράσματα, συμπεριλαμβανομένης της αναλογίας, η οποία βοηθά στην κατανόηση των ενδοθεματικών συνδέσεων στη γεωμετρία.
3. Εκπαιδευτικά:
Συμβολή στην ανάπτυξη της οργάνωσης και των συνηθειών συστηματικής εργασίας.
- συμβάλλουν στη διαμόρφωση αισθητικών δεξιοτήτων κατά τη δημιουργία σημειώσεων και τη δημιουργία σχεδίων.
Τύπος μαθήματος: νέο υλικό μαθήματος (2 ώρες).
Δομή μαθήματος:
1. Οργανωτική στιγμή.
2. Επικαιροποίηση γνώσεων.
3. Μελέτη νέου υλικού.
4. Σύνοψη και ρύθμιση της εργασίας.
Εξοπλισμός: αφίσες (διαφάνειες) με στοιχεία, μακέτες διαφόρων γεωμετρικών σωμάτων, συμπεριλαμβανομένων όλων των τύπων παραλληλεπίπεδων, γραφικός προβολέας.
Κατά τη διάρκεια των μαθημάτων.
1. Οργανωτική στιγμή.
2. Επικαιροποίηση γνώσεων.
Επικοινωνία του θέματος του μαθήματος, διατύπωση στόχων και στόχων μαζί με τους μαθητές, επίδειξη της πρακτικής σημασίας της μελέτης του θέματος, επανάληψη θεμάτων που έχουν μελετηθεί προηγουμένως σχετικά με αυτό το θέμα.
3. Μελέτη νέου υλικού.
3.1. Παραλληλεπίπεδο και οι τύποι του.
Επιδεικνύονται μοντέλα παραλληλεπίπεδων, προσδιορίζοντας τα χαρακτηριστικά τους, τα οποία βοηθούν στη διατύπωση του ορισμού ενός παραλληλεπίπεδου χρησιμοποιώντας την έννοια του πρίσματος.
Ορισμός:
παραλληλεπίπεδοονομάζεται πρίσμα του οποίου η βάση είναι ένα παραλληλόγραμμο.
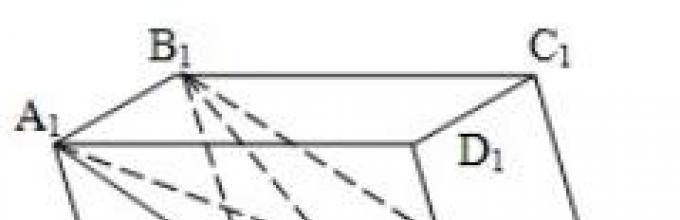
Γίνεται ένα σχέδιο παραλληλεπίπεδου (Εικόνα 1), παρατίθενται τα στοιχεία ενός παραλληλεπίπεδου ως ειδική περίπτωση πρίσματος. Εμφανίζεται η διαφάνεια 1.
Σχηματική σημειογραφία του ορισμού:
Τα συμπεράσματα από τον ορισμό διατυπώνονται:
1) Εάν το ABCDA 1 B 1 C 1 D 1 είναι ένα πρίσμα και το ABCD είναι ένα παραλληλόγραμμο, τότε ABCDA 1 B 1 C 1 D 1 - παραλληλεπίπεδο.
2) Εάν ABCDA 1 B 1 C 1 D 1 - παραλληλεπίπεδο, τότε το ABCDA 1 B 1 C 1 D 1 είναι ένα πρίσμα και το ABCD είναι ένα παραλληλόγραμμο.
3) Εάν το ABCDA 1 B 1 C 1 D 1 δεν είναι πρίσμα ή το ABCD δεν είναι παραλληλόγραμμο, τότε
ABCDA 1 B 1 C 1 D 1 – όχι παραλληλεπίπεδο.
4) . Εάν ABCDA 1 B 1 C 1 D 1 – όχι παραλληλεπίπεδο, τότε το ABCDA 1 B 1 C 1 D 1 δεν είναι πρίσμα ή το ABCD δεν είναι παραλληλόγραμμο.
Στη συνέχεια, εξετάζονται ειδικές περιπτώσεις παραλληλεπίπεδου με την κατασκευή ενός σχήματος ταξινόμησης (βλ. Εικ. 3), παρουσιάζονται μοντέλα, επισημαίνονται οι χαρακτηριστικές ιδιότητες ευθύγραμμων και ορθογώνιων παραλληλεπίπεδων και διατυπώνονται οι ορισμοί τους.
Ορισμός:
Ένα παραλληλεπίπεδο ονομάζεται ευθύγραμμο αν οι πλευρικές ακμές του είναι κάθετες στη βάση.
Ορισμός:
Το παραλληλεπίπεδο λέγεται ορθογώνιος, αν οι πλευρικές ακμές του είναι κάθετες στη βάση και η βάση είναι ορθογώνιο (βλ. Εικόνα 2).
Μετά την καταγραφή των ορισμών σε σχηματική μορφή, διατυπώνονται συμπεράσματα από αυτούς.
3.2. Ιδιότητες παραλληλεπίπεδων.
Αναζήτηση επιπεδομετρικών σχημάτων, των οποίων τα χωρικά ανάλογα είναι παραλληλεπίπεδα και κυβοειδή (παραλληλόγραμμο και ορθογώνιο). Στην περίπτωση αυτή, έχουμε να κάνουμε με την οπτική ομοιότητα των μορφών. Χρησιμοποιώντας τον κανόνα συμπερασμάτων κατ' αναλογία, συμπληρώνονται οι πίνακες.
Κανόνας συμπερασμάτων κατ' αναλογία:
1. Επιλέξτε από προηγουμένως μελετημένα φιγούρες σχήμα, παρόμοιο με αυτό.
2. Διατυπώστε την ιδιότητα του επιλεγμένου σχήματος.
3. Διατυπώστε μια παρόμοια ιδιότητα του αρχικού σχήματος.
4. Να αποδείξετε ή να απορρίψετε τη διατυπωμένη δήλωση.
Μετά τη διατύπωση των ιδιοτήτων, η απόδειξη καθεμιάς από αυτές πραγματοποιείται σύμφωνα με το ακόλουθο σχήμα:
- συζήτηση του σχεδίου απόδειξης·
- επίδειξη διαφάνειας με στοιχεία (διαφάνειες 2 – 6).
- Οι μαθητές συμπληρώνουν τεκμήρια στα τετράδιά τους.
3.3 Ο κύβος και οι ιδιότητές του.
Ορισμός: Ο κύβος είναι ένα ορθογώνιο παραλληλεπίπεδο στο οποίο και οι τρεις διαστάσεις είναι ίσες.
Κατ' αναλογία με ένα παραλληλεπίπεδο, οι μαθητές κάνουν ανεξάρτητα μια σχηματική σημειογραφία του ορισμού, αντλούν συνέπειες από αυτόν και διατυπώνουν τις ιδιότητες του κύβου.






4. Σύνοψη και ρύθμιση της εργασίας.
Εργασία για το σπίτι:
- Χρησιμοποιώντας τις σημειώσεις του μαθήματος από το εγχειρίδιο γεωμετρίας για τις τάξεις 10-11, L.S. Atanasyan και άλλοι, μελετήστε το Κεφάλαιο 1, §4, παράγραφος 13, Κεφάλαιο 2, §3, παράγραφος 24.
- Να αποδείξετε ή να καταρρίψετε την ιδιότητα του παραλληλεπίπεδου, στοιχείο 2 του πίνακα.
- Απάντησε σε ερωτήσεις ασφαλείας.
Ερωτήσεις ελέγχου.
1. Είναι γνωστό ότι μόνο δύο πλευρικές όψεις του παραλληλεπιπέδου είναι κάθετες στη βάση. Τι είδους παραλληλεπίπεδο;
2. Πόσες πλευρικές όψεις ορθογώνιου σχήματος μπορεί να έχει ένα παραλληλεπίπεδο;
3. Είναι δυνατόν να έχουμε παραλληλεπίπεδο με μία μόνο πλευρική όψη:
1) κάθετα στη βάση.
2) έχει σχήμα ορθογωνίου.
4. Σε ορθό παραλληλεπίπεδο όλες οι διαγώνιοι είναι ίσες. Είναι ορθογώνιο;
5. Είναι αλήθεια ότι σε ορθό παραλληλεπίπεδο τα διαγώνια τμήματα είναι κάθετα στα επίπεδα της βάσης;
6. Να διατυπώσετε το θεώρημα, αντίστροφο του θεωρήματοςπερίπου το τετράγωνο της διαγωνίου ενός ορθογώνιου παραλληλεπιπέδου.
7. Ποια πρόσθετα χαρακτηριστικά διακρίνουν έναν κύβο από ένα ορθογώνιο παραλληλεπίπεδο;
8. Θα είναι ένα παραλληλεπίπεδο ένας κύβος στον οποίο όλες οι ακμές σε μία από τις κορυφές είναι ίσες;
9. Να διατυπώσετε το θεώρημα στο τετράγωνο της διαγωνίου ενός κύβου για την περίπτωση ενός κύβου.
Ορθογώνιο παραλληλεπίπεδο
Ένα ορθογώνιο παραλληλεπίπεδο είναι ένα ορθογώνιο παραλληλεπίπεδο του οποίου όλες οι όψεις είναι ορθογώνια.
Αρκεί να κοιτάξουμε γύρω μας, και θα δούμε ότι τα αντικείμενα γύρω μας έχουν σχήμα παρόμοιο με παραλληλεπίπεδο. Μπορούν να διακριθούν από το χρώμα, έχουν πολλές πρόσθετες λεπτομέρειες, αλλά αν αυτές οι λεπτές απορρίψεις απορριφθούν, τότε μπορούμε να πούμε ότι, για παράδειγμα, ένα ντουλάπι, ένα κουτί κ.λπ., έχουν περίπου το ίδιο σχήμα.
Την έννοια του ορθογώνιου παραλληλεπιπέδου συναντάμε σχεδόν καθημερινά! Κοιτάξτε γύρω σας και πείτε μου πού βλέπετε ορθογώνια παραλληλεπίπεδα; Δείτε το βιβλίο, έχει ακριβώς το ίδιο σχήμα! Ένα τούβλο, ένα σπιρτόκουτο, ένα ξύλο έχουν το ίδιο σχήμα και ακόμη και αυτή τη στιγμή βρίσκεστε μέσα σε ένα ορθογώνιο παραλληλεπίπεδο, γιατί η τάξη είναι η πιο φωτεινή ερμηνεία αυτού του γεωμετρικού σχήματος.
Ασκηση:Ποια παραδείγματα παραλληλεπίπεδων μπορείτε να ονομάσετε;
Ας ρίξουμε μια πιο προσεκτική ματιά στο κυβοειδές. Και τι βλέπουμε;
Πρώτον, βλέπουμε ότι αυτό το σχήμα σχηματίζεται από έξι ορθογώνια, τα οποία είναι οι όψεις ενός κυβοειδούς.
Δεύτερον, ένα κυβοειδές έχει οκτώ κορυφές και δώδεκα άκρες. Οι άκρες ενός κυβοειδούς είναι οι πλευρές των όψεών του και οι κορυφές του κυβοειδούς είναι οι κορυφές των όψεων.
Ασκηση:
1. Πώς ονομάζεται καθεμία από τις όψεις ενός ορθογώνιου παραλληλεπίπεδου; 2. Χάρη σε ποιες παραμέτρους μπορεί να μετρηθεί ένα παραλληλόγραμμο; 3. Ορίστε αντίθετες όψεις.
Τύποι παραλληλεπίπεδων
Αλλά τα παραλληλεπίπεδα δεν είναι μόνο ορθογώνια, αλλά μπορούν επίσης να είναι ίσια και κεκλιμένα, και οι ευθείες γραμμές χωρίζονται σε ορθογώνιες, μη ορθογώνιες και κύβους.
Εργασία: Δείτε την εικόνα και πείτε ποια παραλληλεπίπεδα φαίνονται πάνω της. Σε τι διαφέρει ένα ορθογώνιο παραλληλεπίπεδο από έναν κύβο;

Ιδιότητες ορθογώνιου παραλληλεπίπεδου
Ένα ορθογώνιο παραλληλεπίπεδο έχει μια σειρά από σημαντικές ιδιότητες:
Πρώτον, το τετράγωνο της διαγωνίου αυτού του γεωμετρικού σχήματος είναι ίσο με το άθροισμα των τετραγώνων των τριών κύριων παραμέτρων του: ύψος, πλάτος και μήκος.
Δεύτερον, και οι τέσσερις διαγώνιοι του είναι απολύτως πανομοιότυπες.
Τρίτον, εάν και οι τρεις παράμετροι ενός παραλληλεπίπεδου είναι ίδιες, δηλαδή το μήκος, το πλάτος και το ύψος είναι ίσα, τότε ένα τέτοιο παραλληλεπίπεδο ονομάζεται κύβος και όλες οι όψεις του θα είναι ίσες με το ίδιο τετράγωνο.

Ασκηση
1. Ένα ορθογώνιο παραλληλεπίπεδο έχει ίσες πλευρές; Εάν υπάρχουν, τότε δείξτε τα στο σχήμα. 2. Ποιες; γεωμετρικά σχήματαΠοιες είναι οι πλευρές ενός ορθογώνιου παραλληλεπίπεδου; 3. Ποια είναι η διάταξη των ίσων άκρων μεταξύ τους; 4. Ονομάστε τον αριθμό των ζευγών ίσων όψεων αυτού του σχήματος. 5. Βρείτε τις ακμές σε ένα ορθογώνιο παραλληλεπίπεδο που να δείχνουν το μήκος, το πλάτος, το ύψος του. Πόσους μέτρησες;
Εργο
Για να διακοσμήσει όμορφα ένα δώρο γενεθλίων για τη μητέρα της, η Τάνια πήρε ένα κουτί σε σχήμα ορθογώνιου παραλληλεπίπεδου. Το μέγεθος αυτού του κουτιού είναι 25cm*35cm*45cm. Για να κάνει αυτή τη συσκευασία όμορφη, η Tanya αποφάσισε να την καλύψει με όμορφο χαρτί, το κόστος του οποίου είναι 3 hryvnia ανά 1 dm2. Πόσα χρήματα πρέπει να ξοδέψετε για χαρτί περιτυλίγματος;
Γνωρίζετε ότι ο διάσημος ψευδαισθητής Ντέιβιντ Μπλέιν πέρασε 44 ημέρες σε ένα γυάλινο παραλληλεπίπεδο κρεμασμένο πάνω από τον Τάμεση ως μέρος ενός πειράματος. Για αυτές τις 44 μέρες δεν έφαγε, αλλά ήπιε μόνο νερό. Στην εθελοντική του φυλακή, ο Ντέιβιντ πήρε μόνο υλικά γραφής, ένα μαξιλάρι και ένα στρώμα και μαντήλια.
ΚΕΙΜΕΝΟ ΜΕΤΑΓΡΑΦΗ ΤΟΥ ΜΑΘΗΜΑΤΟΣ:
Εξετάστε αυτά τα στοιχεία:
Οικοδομικά τούβλα, ζάρια, φούρνος μικροκυμάτων. Αυτά τα αντικείμενα ενώνονται με το σχήμα.
Μια επιφάνεια που αποτελείται από δύο ίσα παραλληλόγραμμα ABCD και A1B1C1D1
και τέσσερα παραλληλόγραμμα AA1B1B και BB1C1C, СС1D1D, AA1D1D ονομάζεται παραλληλεπίπεδο.
Τα παραλληλόγραμμα που αποτελούν ένα παραλληλεπίπεδο ονομάζονται όψεις. Πρόσωπο А1В1С1D1. Άκρη ВВ1С1С. Άκρη ABCD.
Σε αυτήν την περίπτωση, οι όψεις ABCD και A1B1C1D1 ονομάζονται συχνότερα βάσεις και οι υπόλοιπες όψεις είναι πλευρικές.
Οι πλευρές των παραλληλογραμμών ονομάζονται ακμές του παραλληλεπίπεδου. Νευρ Α1Β1. Rib CC1. Ρίβ μ.Χ.
Η άκρη CC1 δεν ανήκει στις βάσεις· ονομάζεται πλευρική ακμή.
Οι κορυφές των παραλληλογραμμών ονομάζονται κορυφές ενός παραλληλεπίπεδου.
Κορυφή D1. Vershina B. Vershina S.
Κορυφές Δ1 και Β
δεν ανήκουν στο ίδιο πρόσωπο και ονομάζονται αντίθετα.

Ένα παραλληλεπίπεδο μπορεί να απεικονιστεί με διαφορετικούς τρόπους
Ένα παραλληλεπίπεδο στη βάση του οποίου βρίσκεται ένας ρόμβος και οι εικόνες των προσώπων είναι παραλληλόγραμμα.
Ένα παραλληλεπίπεδο στη βάση του οποίου βρίσκεται ένα τετράγωνο. Οι αόρατες ακμές AA1, AB, AD απεικονίζονται με διακεκομμένες γραμμές.
Ένα παραλληλεπίπεδο στη βάση του οποίου βρίσκεται ένα τετράγωνο
Ένα παραλληλεπίπεδο στη βάση του οποίου βρίσκεται ένα ορθογώνιο ή παραλληλόγραμμο
Ένα παραλληλεπίπεδο με όλες τις όψεις τετράγωνο. Πιο συχνά ονομάζεται κύβος.
Όλα τα θεωρούμενα παραλληλεπίπεδα έχουν ιδιότητες. Ας τα διατυπώσουμε και ας τα αποδείξουμε.
Ιδιότητα 1. Οι απέναντι όψεις ενός παραλληλεπίπεδου είναι παράλληλες και ίσες.
Ας εξετάσουμε το παραλληλεπίπεδο ABCDA1B1C1D1 και ας αποδείξουμε, για παράδειγμα, τον παραλληλισμό και την ισότητα των όψεων BB1C1C και AA1D1D.
Σύμφωνα με τον ορισμό του παραλληλεπίπεδου, η όψη ABCD είναι ένα παραλληλόγραμμο, που σημαίνει, με την ιδιότητα ενός παραλληλογράμμου, η ακμή BC είναι παράλληλη στην ακμή AD.

Το πρόσωπο ABB1A1 είναι επίσης ένα παραλληλόγραμμο, που σημαίνει ότι οι ακμές BB1 και AA1 είναι παράλληλες.
Αυτό σημαίνει ότι δύο τεμνόμενες ευθείες BC και BB1 ενός επιπέδου, αντίστοιχα, είναι παράλληλες με δύο ευθείες AD και AA1, αντίστοιχα, ενός άλλου επιπέδου, πράγμα που σημαίνει ότι τα επίπεδα ABB1A1 και BCC1D1 είναι παράλληλα.
Όλες οι όψεις ενός παραλληλεπίπεδου είναι παραλληλόγραμμα, που σημαίνει BC = AD, BB1 = AA1.
Στην περίπτωση αυτή, οι πλευρές των γωνιών B1BC και A1AD είναι αντίστοιχα συν-κατευθυνόμενες, πράγμα που σημαίνει ότι είναι ίσες.
Έτσι, δύο γειτονικές πλευρές και η μεταξύ τους γωνία του παραλληλογράμμου ABB1A1 είναι αντίστοιχα ίσες με δύο γειτονικές πλευρές και η μεταξύ τους γωνία του παραλληλογράμμου BCC1D1, που σημαίνει ότι αυτά τα παραλληλόγραμμα είναι ίσα.
Το παραλληλεπίπεδο έχει επίσης μια ιδιότητα για διαγώνιους. Η διαγώνιος ενός παραλληλεπίπεδου είναι το τμήμα που συνδέεται γειτονικές κορυφές. Η διακεκομμένη γραμμή στο σχέδιο δείχνει τις διαγώνιους B1D, BD1, A1C.
Άρα, ιδιότητα 2. Οι διαγώνιοι ενός παραλληλεπίπεδου τέμνονται σε ένα σημείο και διαιρούνται στο μισό με το σημείο τομής.
Για να αποδείξετε την ιδιότητα, θεωρήστε το τετράπλευρο BB1D1D. Οι διαγώνιοι του B1D, BD1 είναι οι διαγώνιοι του παραλληλεπιπέδου ABCDA1B1C1D1.
Στην πρώτη ιδιότητα, έχουμε ήδη ανακαλύψει ότι η ακμή BB1 είναι παράλληλη και ίση με την ακμή AA1, αλλά η ακμή AA1 είναι παράλληλη και ίση με την ακμή DD1. Επομένως, οι ακμές BB1 και DD1 είναι παράλληλες και ίσες, γεγονός που αποδεικνύει ότι το τετράπλευρο BB1D1D είναι παραλληλόγραμμο. Και σε παραλληλόγραμμο, σύμφωνα με την ιδιότητα, οι διαγώνιοι Β1Δ, ΒΔ1 τέμνονται σε κάποιο σημείο Ο και διαιρούνται στο μισό με αυτό το σημείο.
Το τετράπλευρο BC1D1A είναι επίσης παραλληλόγραμμο και οι διαγώνιοι του C1A τέμνονται σε ένα σημείο και διχοτομούνται από αυτό το σημείο. Οι διαγώνιοι του παραλληλογράμμου C1A, ВD1 είναι οι διαγώνιοι του παραλληλεπίπεδου, που σημαίνει ότι η διατυπωμένη ιδιότητα έχει αποδειχθεί.

Για να εμπεδώσετε τις θεωρητικές γνώσεις σχετικά με το παραλληλεπίπεδο, εξετάστε το πρόβλημα απόδειξης.
Σημειώνεται στις άκρες του παραλληλεπιπέδου σημεία L,M,N,Pώστε BL=CM=A1N=D1P. Αποδείξτε ότι το ALMDNB1C1P είναι παραλληλεπίπεδο.
Η όψη BB1A1A είναι ένα παραλληλόγραμμο, που σημαίνει ότι η άκρη BB1 είναι ίση και παράλληλη με την ακμή AA1, αλλά σύμφωνα με την κατάσταση, τα τμήματα BL και A1N, που σημαίνει ότι τα τμήματα LB1 και NA είναι ίσα και παράλληλα.
3) Επομένως, το τετράπλευρο LB1NA είναι παραλληλόγραμμο.
4) Εφόσον το CC1D1D είναι παραλληλόγραμμο, σημαίνει ότι η ακμή CC1 είναι ίση και παράλληλη με την ακμή D1D και η CM είναι ίση με την D1P από συνθήκη, πράγμα που σημαίνει ότι τα τμήματα MC1 και DP είναι ίσα και παράλληλα
Επομένως, το τετράπλευρο MC1PD είναι επίσης παραλληλόγραμμο.
5) Οι γωνίες LB1N και MC1P είναι ίσες ως γωνίες με αντίστοιχα παράλληλες και πανομοιότυπα κατευθυνόμενες πλευρές.
6) Βρήκαμε ότι τα παραλληλόγραμμα και το MC1PD έχουν αντίστοιχες πλευρές ίσες και οι γωνίες μεταξύ τους είναι ίσες, που σημαίνει ότι τα παραλληλόγραμμα είναι ίσα.
7) Τα τμήματα είναι ίσα σύμφωνα με την συνθήκη, που σημαίνει ότι το BLMC είναι παραλληλόγραμμο και η πλευρά BC είναι παράλληλη προς την πλευρά LM είναι παράλληλη προς την πλευρά B1C1.
8) Ομοίως, από το παραλληλόγραμμο NA1D1P προκύπτει ότι η πλευρά A1D1 είναι παράλληλη προς την πλευρά NP και παράλληλη στην πλευρά AD.
9) Οι απέναντι όψεις ABB1A1 και DCC1D1 του παραλληλεπίπεδου είναι παράλληλες ως προς την ιδιότητα και τα τμήματα των παράλληλων ευθειών μεταξύ των παράλληλων επιπέδων είναι ίσα, πράγμα που σημαίνει ότι τα τμήματα B1C1, LM, AD, NP είναι ίσα.
Διαπιστώθηκε ότι στα τετράπλευρα ANPD, NB1C1P, LB1C1M, ALMD, δύο πλευρές είναι παράλληλες και ίσες, που σημαίνει ότι είναι παραλληλόγραμμα. Τότε η επιφάνειά μας ALMDNB1C1P αποτελείται από έξι παραλληλόγραμμα, δύο από τα οποία είναι ίσα, και εξ ορισμού είναι ένα παραλληλεπίπεδο.
Υπάρχουν διάφοροι τύποι παραλληλεπίπεδων:
· Ορθογώνιο παραλληλεπίπεδο- είναι ένα παραλληλεπίπεδο, του οποίου όλα τα πρόσωπα είναι - ορθογώνια;
· Ένα δεξιό παραλληλεπίπεδο είναι ένα παραλληλεπίπεδο που έχει 4 πλευρικές όψεις - παραλληλόγραμμα.
· Κεκλιμένο παραλληλεπίπεδο είναι το παραλληλεπίπεδο του οποίου οι πλευρικές όψεις δεν είναι κάθετες στις βάσεις.
Βασικά στοιχεία
Δύο όψεις ενός παραλληλεπίπεδου που δεν έχουν κοινή ακμή λέγονται απέναντι και αυτές που έχουν κοινή ακμή λέγονται γειτονικές. Δύο κορυφές ενός παραλληλεπίπεδου που δεν ανήκουν στην ίδια όψη ονομάζονται αντίθετες. Ευθύγραμμο τμήμα,λέγεται η σύνδεση απέναντι κορυφών διαγώνιαπαραλληλεπίπεδο. Τα μήκη των τριών άκρων ενός ορθογώνιου παραλληλεπιπέδου που έχει κοινή κορυφή ονομάζονται Μετρήσεις.
Ιδιότητες
· Το παραλληλεπίπεδο είναι συμμετρικό περίπου στο μέσο της διαγωνίου του.
· Οποιοδήποτε τμήμα με άκρα που ανήκουν στην επιφάνεια του παραλληλεπίπεδου και διέρχεται από το μέσο της διαγωνίου του διαιρείται στο μισό από αυτό. Συγκεκριμένα, όλες οι διαγώνιοι ενός παραλληλεπιπέδου τέμνονται σε ένα σημείο και διχοτομούνται από αυτό.
· Οι αντίθετες όψεις ενός παραλληλεπίπεδου είναι παράλληλες και ίσες.
· Το τετράγωνο του διαγώνιου μήκους ενός ορθογώνιου παραλληλεπίπεδου είναι ίσο με το άθροισμα των τετραγώνων των τριών του διαστάσεων
Βασικοί τύποι
Δεξί παραλληλεπίπεδο
· Πλάγια επιφάνεια S b =P o *h, όπου P o είναι η περίμετρος της βάσης, h είναι το ύψος
· τετράγωνο πλήρη επιφάνεια S p =S b +2S o, όπου S o είναι η περιοχή βάσης
· Ενταση ΗΧΟΥ V=S o *h
Ορθογώνιο παραλληλεπίπεδο
· Πλάγια επιφάνεια S b =2c(a+b), όπου a, b είναι οι πλευρές της βάσης, c είναι η πλευρική ακμή του ορθογώνιου παραλληλεπιπέδου
· Συνολική επιφάνεια S p =2(ab+bc+ac)
· Ενταση ΗΧΟΥ V=abc, όπου a, b, c είναι οι διαστάσεις ενός ορθογώνιου παραλληλεπιπέδου.
· Πλάγια επιφάνεια S=6*h 2, όπου h είναι το ύψος της ακμής του κύβου
34. Τετράεδρο- κανονικό πολύεδρο, έχει 4 άκρες που είναι κανονικά τρίγωνα. Κορυφές τετραέδρου 4 , συγκλίνει σε κάθε κορυφή 3 ribs, και total ribs 6 . Επίσης, ένα τετράεδρο είναι μια πυραμίδα.
Τα τρίγωνα που αποτελούν ένα τετράεδρο ονομάζονται πρόσωπα (AOS, OSV, ACB, AOB), τις πλευρές τους --- νευρώσεις (AO, OC, OB)και οι κορυφές --- κορυφές (A, B, C, O)τετράεδρο. Δύο ακμές ενός τετραέδρου που δεν έχουν κοινές κορυφές ονομάζονται απεναντι απο... Μερικές φορές ένα από τα πρόσωπα του τετραέδρου απομονώνεται και καλείται βάσηκαι τα άλλα τρία --- πλαϊνά πρόσωπα.
Το τετράεδρο ονομάζεται σωστός, αν όλα του τα πρόσωπα είναι ισόπλευρα τρίγωνα. Επιπλέον, ένα κανονικό τετράεδρο και μια κανονική τριγωνική πυραμίδα δεν είναι το ίδιο πράγμα.
U κανονικό τετράεδρο Όλες οι δίεδρες γωνίες στις άκρες και όλες οι τριεδρικές γωνίες στις κορυφές είναι ίσες.
35. Σωστό πρίσμα
Ένα πρίσμα είναι ένα πολύεδρο του οποίου οι δύο όψεις (βάσεις) βρίσκονται σε παράλληλα επίπεδα και όλες οι ακμές έξω από αυτές τις όψεις είναι παράλληλες μεταξύ τους. Οι επιφάνειες εκτός από τις βάσεις ονομάζονται πλευρικές όψεις και οι ακμές τους ονομάζονται πλευρικές ακμές. Όλες οι πλευρικές ακμές είναι ίσες μεταξύ τους ως παράλληλα τμήματα που οριοθετούνται από δύο παράλληλα επίπεδα. Όλες οι πλευρικές όψεις του πρίσματος είναι παραλληλόγραμμες. Οι αντίστοιχες πλευρές των βάσεων του πρίσματος είναι ίσες και παράλληλες. Ένα πρίσμα του οποίου η πλευρική ακμή είναι κάθετη στο επίπεδο της βάσης ονομάζεται ευθύ πρίσμα, ενώ τα άλλα πρίσματα ονομάζονται κεκλιμένα. Στη βάση σωστό πρίσμαβρίσκεται ένα κανονικό πολύγωνο. Όλες οι όψεις ενός τέτοιου πρίσματος είναι ίσα ορθογώνια.
Η επιφάνεια του πρίσματος αποτελείται από δύο βάσεις και μια πλευρική επιφάνεια. Το ύψος ενός πρίσματος είναι ένα τμήμα που είναι κοινή κάθετη στα επίπεδα στα οποία βρίσκονται οι βάσεις του πρίσματος. Το ύψος του πρίσματος είναι η απόσταση Hμεταξύ των επιπέδων των βάσεων.
Πλάγια επιφάνεια μικρό b ενός πρίσματος είναι το άθροισμα των εμβαδών των πλευρικών του όψεων. Συνολική επιφάνεια μικρό n ενός πρίσματος είναι το άθροισμα των εμβαδών όλων των όψεών του. μικρό n = μικρόβ + 2 μικρό,Οπου μικρό– περιοχή της βάσης του πρίσματος, μικρόβ – πλευρική επιφάνεια.
36. Ένα πολύεδρο που έχει μια όψη, που ονομάζεται βάση, – πολύγωνο,
και οι άλλες όψεις είναι τρίγωνα με κοινή κορυφή, που ονομάζεται πυραμίδα
.
Τα πρόσωπα εκτός της βάσης ονομάζονται πλευρικός.
Η κοινή κορυφή των πλευρικών όψεων ονομάζεται την κορυφή της πυραμίδας.
Οι άκρες που συνδέουν την κορυφή της πυραμίδας με τις κορυφές της βάσης ονομάζονται πλευρικός.
Ύψος πυραμίδας
ονομάζεται κάθετος που σύρεται από την κορυφή της πυραμίδας στη βάση της.
Η πυραμίδα ονομάζεται σωστός, αν η βάση του είναι κανονικό πολύγωνο και το ύψος του διέρχεται από το κέντρο της βάσης.
Απόθεμα η πλευρική όψη μιας κανονικής πυραμίδας είναι το ύψος αυτής της όψης που αντλείται από την κορυφή της πυραμίδας.
Ένα επίπεδο παράλληλο στη βάση της πυραμίδας την αποκόπτει σε παρόμοια πυραμίδα και κολοβωμένη πυραμίδα.
Ιδιότητες κανονικών πυραμίδων
- Οι πλευρικές ακμές μιας κανονικής πυραμίδας είναι ίσες.
- Οι πλευρικές όψεις μιας κανονικής πυραμίδας είναι ισοσκελή τρίγωνα ίσα μεταξύ τους.
Εάν όλες οι πλευρικές άκρες είναι ίσες, τότε
·Το ύψος προβάλλεται στο κέντρο του περιγεγραμμένου κύκλου.
Οι πλευρικές νευρώσεις σχηματίζουν ίσες γωνίες με το επίπεδο της βάσης.
Εάν οι πλευρικές όψεις έχουν κλίση προς το επίπεδο της βάσης με την ίδια γωνία, τότε
·το ύψος προβάλλεται στο κέντρο του εγγεγραμμένου κύκλου.
· τα ύψη των πλευρικών όψεων είναι ίσα.
·το εμβαδόν της πλευρικής επιφάνειας είναι ίσο με το μισό γινόμενο της περιμέτρου της βάσης και του ύψους της πλευρικής όψης
37. Συνάρτηση y=f(x), όπου το x ανήκει στο σύνολο φυσικούς αριθμούς, ονομάζεται συνάρτηση του φυσικού ορίσματος ή αριθμητική ακολουθία. Συμβολίζεται με y=f(n), ή (y n)
Οι ακολουθίες μπορούν να καθοριστούν με διάφορους τρόπους, προφορικά, έτσι καθορίζεται μια ακολουθία πρώτων αριθμών:
2, 3, 5, 7, 11, κ.λπ.
Μια ακολουθία θεωρείται ότι δίνεται αναλυτικά εάν δίνεται ο τύπος για τον nο όρο της:
1, 4, 9, 16, …, ν 2, …
2) y n = C. Μια τέτοια ακολουθία ονομάζεται σταθερή ή ακίνητη. Για παράδειγμα:
2, 2, 2, 2, …, 2, …
3) y n =2 n . Για παράδειγμα,
2, 2 2, 2 3, 2 4, …, 2 n, …
Μια ακολουθία λέγεται ότι είναι περιορισμένη παραπάνω αν όλοι οι όροι της δεν είναι μεγαλύτεροι από έναν ορισμένο αριθμό. Με άλλα λόγια, μια ακολουθία μπορεί να ονομαστεί δεσμευμένη εάν υπάρχει ένας αριθμός M τέτοιος ώστε η ανισότητα y n να είναι μικρότερη ή ίση με M. Ο αριθμός M ονομάζεται άνω φράγμα της ακολουθίας. Για παράδειγμα, η ακολουθία: -1, -4, -9, -16, ..., - n 2 ; περιορισμένη από πάνω.
Ομοίως, μια ακολουθία μπορεί να ονομαστεί περιορισμένη παρακάτω εάν όλοι οι όροι της είναι μεγαλύτεροι από έναν ορισμένο αριθμό. Αν μια ακολουθία είναι οριοθετημένη και πάνω και κάτω, ονομάζεται δεσμευμένη.
Μια ακολουθία ονομάζεται αύξουσα αν κάθε επόμενος όρος είναι μεγαλύτερος από τον προηγούμενο.
Μια ακολουθία ονομάζεται φθίνουσα εάν κάθε επόμενο μέλος είναι μικρότερο από το προηγούμενο. Οι αύξουσες και φθίνουσες ακολουθίες ορίζονται από έναν όρο - μονοτονικές ακολουθίες.
Εξετάστε δύο ακολουθίες:
1) y n: 1, 3, 5, 7, 9, …, 2n-1, …
2) x n: 1, ½, 1/3, 1/ 4, …, 1/n, …
Αν απεικονίσουμε τους όρους αυτής της ακολουθίας στην αριθμητική γραμμή, θα παρατηρήσουμε ότι, στη δεύτερη περίπτωση, οι όροι της ακολουθίας συμπυκνώνονται γύρω από ένα σημείο, αλλά στην πρώτη περίπτωση δεν συμβαίνει αυτό. Σε τέτοιες περιπτώσεις, η ακολουθία y n λέγεται ότι αποκλίνει και η ακολουθία x n συγκλίνει.
Ο αριθμός b ονομάζεται όριο της ακολουθίας y n εάν οποιαδήποτε προεπιλεγμένη γειτονιά του σημείου b περιέχει όλα τα μέλη της ακολουθίας, ξεκινώντας από έναν ορισμένο αριθμό.
Σε αυτή την περίπτωση μπορούμε να γράψουμε:
Εάν το πηλίκο μιας προόδου είναι μικρότερο από ένα σε συντελεστή, τότε το όριο αυτής της ακολουθίας, καθώς το x τείνει στο άπειρο, είναι ίσο με μηδέν.
Εάν η ακολουθία συγκλίνει, τότε μόνο σε ένα όριο
Εάν η ακολουθία συγκλίνει, τότε είναι οριοθετημένη.
Θεώρημα Weierstrass: Αν μια ακολουθία συγκλίνει μονοτονικά, τότε είναι οριοθετημένη.
Το όριο μιας ακίνητης ακολουθίας είναι ίσο με οποιονδήποτε όρο της ακολουθίας.
Ιδιότητες:
1) Το όριο ποσού είναι ίσο με το άθροισμα των ορίων
2) Το όριο ενός προϊόντος είναι ίσο με το γινόμενο των ορίων
3) Το όριο του πηλίκου είναι ίσο με το πηλίκο των ορίων
4) Ο σταθερός παράγοντας μπορεί να ληφθεί πέρα από το οριακό πρόσημο
Ερώτηση 38
άθροισμα άπειρης γεωμετρικής προόδου
Γεωμετρική πρόοδος- μια ακολουθία αριθμών b 1, b 2, b 3,.. (μέλη της προόδου), στην οποία κάθε επόμενος αριθμός, ξεκινώντας από τον δεύτερο, προκύπτει από τον προηγούμενο πολλαπλασιάζοντάς τον με έναν ορισμένο αριθμό q (παρονομαστής της προόδου), όπου b 1 ≠0, q ≠0.
Άθροισμα μιας άπειρης γεωμετρικής προόδουείναι ο οριακός αριθμός στον οποίο συγκλίνει η ακολουθία της προόδου.
Με άλλα λόγια, όσο καιρό κι αν είναι γεωμετρική πρόοδος, το άθροισμα των μελών του δεν είναι μεγαλύτερο από έναν ορισμένο αριθμό και είναι πρακτικά ίσο με αυτόν τον αριθμό. Αυτό ονομάζεται άθροισμα μιας γεωμετρικής προόδου.
Δεν έχει κάθε γεωμετρική πρόοδος τόσο περιοριστικό άθροισμα. Μπορεί να υπάρχει μόνο σε μια εξέλιξη της οποίας ο παρονομαστής είναι ένας κλασματικός αριθμόςλιγότερο από 1.
Το πρίσμα λέγεται παραλληλεπίπεδο, αν οι βάσεις του είναι παραλληλόγραμμες. Εκ. Εικ.1.
Ιδιότητες παραλληλεπίπεδου:
Οι απέναντι όψεις ενός παραλληλεπίπεδου είναι παράλληλες (δηλαδή βρίσκονται σε παράλληλα επίπεδα) και ίσες.
Οι διαγώνιοι ενός παραλληλεπίπεδου τέμνονται σε ένα σημείο και διχοτομούνται από αυτό το σημείο.
Παρακείμενες όψεις παραλληλεπίπεδου– δύο όψεις που έχουν κοινή άκρη.
Απέναντι όψεις παραλληλεπίπεδου– πρόσωπα που δεν έχουν κοινές άκρες.
Αντίθετες κορυφές παραλληλεπίπεδου– δύο κορυφές που δεν ανήκουν στην ίδια όψη.
Διαγώνιος παραλληλεπίπεδου– ένα τμήμα που συνδέει απέναντι κορυφές.
Αν οι πλευρικές ακμές είναι κάθετες στα επίπεδα των βάσεων, τότε το παραλληλεπίπεδο λέγεται απευθείας.
Το ορθογώνιο παραλληλεπίπεδο του οποίου οι βάσεις είναι ορθογώνια λέγεται ορθογώνιος. Ένα πρίσμα, του οποίου όλες οι όψεις είναι τετράγωνες, ονομάζεται κύβος.
Παραλληλεπίπεδο- ένα πρίσμα του οποίου οι βάσεις είναι παραλληλόγραμμα.
Δεξί παραλληλεπίπεδο- παραλληλεπίπεδο του οποίου οι πλευρικές ακμές είναι κάθετες στο επίπεδο της βάσης.
Ορθογώνιο παραλληλεπίπεδοείναι ορθογώνιο παραλληλεπίπεδο του οποίου οι βάσεις είναι ορθογώνια.
Κύβος– ορθογώνιο παραλληλεπίπεδο με ίσες ακμές.
παραλληλεπίπεδοονομάζεται ένα πρίσμα του οποίου η βάση είναι ένα παραλληλόγραμμο. Έτσι, ένα παραλληλεπίπεδο έχει έξι όψεις και όλες είναι παραλληλόγραμμα.
Οι αντίθετες όψεις είναι κατά ζεύγη ίσες και παράλληλες. Το παραλληλεπίπεδο έχει τέσσερις διαγώνιους. όλα τέμνονται σε ένα σημείο και χωρίζονται στο μισό σε αυτό. Οποιοδήποτε πρόσωπο μπορεί να ληφθεί ως βάση. ο όγκος είναι ίσος με το γινόμενο του εμβαδού της βάσης και του ύψους: V = Sh.
Ένα παραλληλεπίπεδο του οποίου οι τέσσερις πλευρικές όψεις είναι ορθογώνια ονομάζεται ευθύγραμμο παραλληλεπίπεδο.
Ένα ορθογώνιο παραλληλεπίπεδο του οποίου οι έξι όψεις είναι ορθογώνια ονομάζεται ορθογώνιο. Εκ. Εικ.2.
Ο όγκος (V) ενός δεξιού παραλληλεπίπεδου είναι ίσος με το γινόμενο του εμβαδού βάσης (S) και του ύψους (h): V = Sh .
Για ένα ορθογώνιο παραλληλεπίπεδο, επιπλέον, ισχύει ο τύπος V=abc, όπου τα a,b,c είναι ακμές.
Η διαγώνιος (δ) ενός ορθογώνιου παραλληλεπίπεδου σχετίζεται με τις ακμές του από τη σχέση d 2 = a 2 + b 2 + c 2 .
Ορθογώνιο παραλληλεπίπεδο- παραλληλεπίπεδο του οποίου οι πλευρικές ακμές είναι κάθετες στις βάσεις και οι βάσεις είναι ορθογώνιες.
Ιδιότητες ορθογώνιου παραλληλεπίπεδου:
Σε ένα ορθογώνιο παραλληλεπίπεδο, και οι έξι όψεις είναι ορθογώνια.
Όλες οι δίεδρες γωνίες ενός ορθογώνιου παραλληλεπιπέδου είναι ορθές.
Το τετράγωνο της διαγωνίου ενός ορθογώνιου παραλληλεπίπεδου είναι ίσο με το άθροισμα των τετραγώνων των τριών διαστάσεων του (τα μήκη τριών ακμών που έχουν κοινή κορυφή).
Οι διαγώνιοι ενός ορθογώνιου παραλληλεπιπέδου είναι ίσες.
Ένα ορθογώνιο παραλληλεπίπεδο, του οποίου όλες οι όψεις είναι τετράγωνες, ονομάζεται κύβος. Όλες οι άκρες του κύβου είναι ίσες. ο όγκος (V) ενός κύβου εκφράζεται με τον τύπο V=a 3, όπου a είναι η άκρη του κύβου.