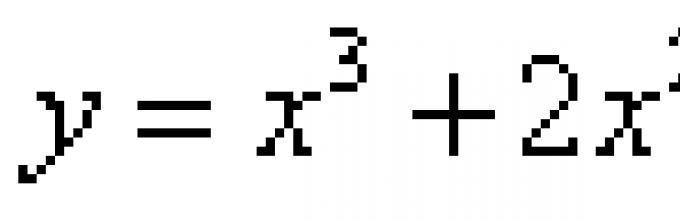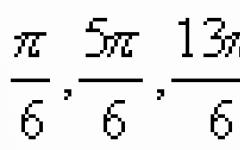A tangent is a straight line , which touches the graph of the function at one point and all points of which are at the shortest distance from the graph of the function. Therefore, the tangent passes tangent to the graph of the function at a certain angle, and several tangents at different angles cannot pass through the point of tangency. Tangent equations and normal equations to the graph of a function are constructed using the derivative.
The tangent equation is derived from the line equation .
Let us derive the equation of the tangent, and then the equation of the normal to the graph of the function.
y = kx + b .
In it k - slope.
From here we get the following entry:
y - y 0 = k(x - x 0 ) .
Derivative value f "(x 0 ) functions y = f(x) at the point x0 equal to the slope k= tg φ tangent to the graph of a function drawn through a point M0 (x 0 , y 0 ) , Where y0 = f(x 0 ) . This is geometric meaning derivative .
Thus, we can replace k on f "(x 0 ) and get the following equation of the tangent to the graph of a function :
y - y 0 = f "(x 0 )(x - x 0 ) .
In problems involving composing the equation of a tangent to the graph of a function (and we will move on to them soon), it is required to reduce the equation obtained from the above formula to equation of a straight line in general form. To do this, you need to move all the letters and numbers to the left side of the equation, and leave zero on the right side.
Now about the normal equation. Normal - this is a straight line passing through the point of tangency to the graph of the function perpendicular to the tangent. Normal equation :
(x - x 0 ) + f "(x 0 )(y - y 0 ) = 0
To warm up, you are asked to solve the first example yourself, and then look at the solution. There is every reason to hope that this task will not be a “cold shower” for our readers.
Example 0. Create a tangent equation and a normal equation for the graph of a function at a point M (1, 1) .
Example 1. Write a tangent equation and a normal equation for the graph of a function ![]() , if the abscissa is tangent .
, if the abscissa is tangent .
Let's find the derivative of the function:
Now we have everything that needs to be substituted into the entry given in the theoretical help to get the tangent equation. We get
![]()
In this example, we were lucky: the slope turned out to be zero, so there was no need to separately reduce the equation to its general form. Now we can create the normal equation:
![]()
In the figure below: graph of a function in burgundy color, tangent green, orange normal.

The next example is also not complicated: the function, as in the previous one, is also a polynomial, but the slope will not be equal to zero, so one more step will be added - bringing the equation to a general form.
Example 2.
Solution. Let's find the ordinate of the tangent point:
Let's find the derivative of the function:
![]() .
.
Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:
We substitute all the obtained data into the “blank formula” and get the tangent equation:
![]()
We bring the equation to its general form (we collect all letters and numbers other than zero on the left side, and leave zero on the right):
We compose the normal equation:

Example 3. Write a tangent equation and a normal equation to the graph of the function if the abscissa is the tangent point.
Solution. Let's find the ordinate of the tangent point:
Let's find the derivative of the function:
![]() .
.
Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:
![]() .
.
We find the tangent equation:
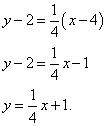
Before bringing the equation to its general form, you need to “comb it” a little: multiply term by term by 4. We do this and bring the equation to its general form:
We compose the normal equation:
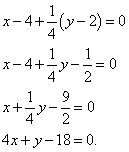
Example 4. Write a tangent equation and a normal equation to the graph of the function if the abscissa is the tangent point.
Solution. Let's find the ordinate of the tangent point:
![]() .
.
Let's find the derivative of the function:
Let's find the value of the derivative at the point of tangency, that is, the slope of the tangent:
![]() .
.
We get the tangent equation:
We bring the equation to its general form:
We compose the normal equation:
![]()
A common mistake when writing tangent and normal equations is not to notice that the function given in the example is complex and to calculate its derivative as the derivative of a simple function. The following examples are already from complex functions(the corresponding lesson will open in a new window).
Example 5. Write a tangent equation and a normal equation to the graph of the function if the abscissa is the tangent point.
Solution. Let's find the ordinate of the tangent point:
Attention! This function is complex, since the tangent argument (2 x) is itself a function. Therefore, we find the derivative of a function as the derivative of a complex function.
Definition: the normal to the curve y = ¦(x) at the point M 0 is a straight line passing through the point M 0 and perpendicular to the tangent at the point M 0 to this curve.
Let's write the equation of the tangent and normal, knowing the equation of the curve and the coordinates of the point M 0. The tangent has an angular coefficient k = t g = ¦, (x 0). From analytical geometry it is known that a straight line has the equation y-y 0 = k(x – x 0).
Therefore, the tangent equation is: y - y 0 = ¦, (x 0)(x – x 0); (1)
The angular coefficient of the normal is Kn = (since they are perpendicular), but then the equation of the normal is:
y-y 0 =(-1/ ¦, (x 0)(x – x 0); (2)
If a derivative does not exist at a point, then a tangent does not exist at this point.
For example, the function ¦(x)=|x| at the point x=0 has no derivative.
lim D x ®0 (D y/ D x)= lim D x ®0 (| D x|/ D x)=
One-sided limits exist, but lim D x ®0 (D y/ D x) does not exist
Tangent too.
This point is called the corner point of the graph.
§4. Relationship between continuity and differentiability of a function.
The following theorem about a differentiable function is valid.
Theorem: if a function y = ¦(x) has a finite derivative at the point x 0, then the function is continuous at this point.
Proof:
Because at the point x 0 there is a derivative ¦, (x 0), i.e. there is a limit
lim D x ®0 (D y/ D x)= ¦, (x 0), then D y/ D x= ¦, (x 0)+, where
B.m.v., depending on D x. When D x®0, ®0, because = (D y/ D x) - ¦, (x 0) ®0 at D x®0
Hence we have: D y= ¦, (x 0) D x + D x.
But then
An infinitesimal increment in the argument corresponds to an infinitesimal increment in the function, therefore ¦(x) is continuous at the point x0.
It is important to understand that converse theorem not true!
Not every continuous function is differentiable.
So, ¦(x) =|x| is continuous at the point x 0 =0, the graph is a solid line, but ¦, (0) does not exist.
§5. Derivatives of constant, sine, cosine and power functions.
1. y= ¦(x) =c; y, = (c) , = 0; (1)
Proof:
a) at any point x ¦(x) = c
b) give x the increment D x, x + D x, the value of the function ¦ (x + D x) = c;
c) ¦ (x + D x)- ¦ (x)= с- с= 0;
d) D y/ D x = 0/ D x = 0
e) lim D x ®0 (D y/ D x)= lim D x ®0 0 = 0
2. y= sin x; y, = (sin x), = cos x; (2)
Proof:
a) at any point x ¦(x) = sin x;
b) give x the increment of D x, x + D x, the value of the function
Topic : Concepts of tangent and normal.
Tangent and normal equations.
Goals:
Subject: introduce students to the concepts: tangent and normal to a curve; consolidate these concepts when solving problems on composing tangent and normal equations; find out what properties the angular coefficients of the tangent and normal have.
Communicative: argue your point of view, argue and defend your position in a non-hostile manner for opponents; be able to listen and hear each other.
Cognitive : establish cause-and-effect relationships; express the meaning of a situation using various means (drawings, symbols, diagrams, signs).
Regulatory: accept cognitive purpose, save it when executing educational activities, regulate the entire process of their implementation and clearly fulfill the requirements of the cognitive task.
Personal: formation of cognitive interest in learning new things, motivation for independent and collective research activities.
Lesson progress:
1. Update background knowledge students:
(Introduction of the concepts of tangent and normal to a curve)
We know analytical and physical meaning derivative: (student answers :
the analytical meaning is, the physical meaning is the speed of the process specified by the function).
Let us find out the geometric meaning of the derivative.
To do this, we introduce the concept of a tangent to a curve at a given point.
From school course geometry, you know the concept of a tangent to a circle. (student answers : a tangent to a circle is defined as a straight line lying in the same plane as the circle and having a single common point with it).
But such a definition of a tangent is not applicable for the case of an arbitrary curve. For example, for a parabola, the axes each have one common point with a parabola. However, the axis is tangent to the parabola, but the axis is not. Let's give general definition tangent to curve at a given point.
Let some points of an arbitrary curve be a secant of the curve. As a point approaches along a curve, the secant will rotate around the point
Definition. The limiting position of a secant when a point is approached indefinitely along a curve is calledtangent to the curve at the point
Definition . Normal to a curve at a point is a straight line passing through the point perpendicular to the tangent to the curve at that point.
If is a tangent to the curve at a point,
then the perpendicular will be the normal to the curve at the point
Explanation of new material:
(Let’s find out what the geometric meaning of the derivative is , what properties do the angular coefficients of the tangent and normal have?
Let the curve be the graph of a function. Points
lie on the graph of the function. A straight line is tangent to a curve.
Tangent angle
The derivative of a function at a point is equal to the tangent of the angle of inclination of the tangent drawn at the point or the slope of the tangent to the graph of the function at this point .
Tangent equation to the curve at a point has the form
Normal equation to the curve at a point has the form
(3)
Problematic issues : look at the tangent and normal equations, what are their differences and similarities?
What is the product equal to? Why is this happening?
(Students must give the following answers to the questions: -1, since the tangent and normal are mutually perpendicular)
Consolidation of theoretical material in practice:
( Solving problems in the classroom)
Example 1. Calculate the angular coefficients of the tangents to the parabola at the points.
Solution. From the geometric meaning of the derivative (formula 1) the slope of the tangent.
Let's find the derivative of the function: .
. Hence, .
Let's find the value of the derivative at the point
Hence, .
Example 2. The tangents of the parabola are drawn at the points. Find the angles of inclination of the tangents to the Ox axis.
Solution. According to formula (1)
Let's find it. .
Let's calculate the value of the derivative at the point: .
Therefore, and.
Likewise at the point.
Therefore, and
Example 3. At what point is the tangent to the curve inclined to the Ox axis?
at an angle
Solution. According to formula (1)
; . Therefore, and
Substituting into the function, we get. We got the point.
Example 4. Write an equation for the tangent and normal to the parabola at a point
Solution. The equation for a tangent to a curve is:
From the problem conditions. Let's find the derivative.
; .
Substituting all the values into the equation we get the tangent equation
or.
Let's create a normal equation using the formula:
or
Tasks for independent decision:
1. Find the angular coefficient of the tangent drawn to the curve at the point.
2. The curve is given by the equation Determine the angles of inclination of the tangents to the positive direction of the axis drawn to the curve at points at the points with abscissas.
3. Find the point on the curve at which the tangent is parallel to the line.
4. At what point is the tangent to the curve: a) parallel to the axis; b) forms an angle of 45 with the axis?
5. Find the abscissa of the point of the parabola at which the tangent is parallel to the abscissa axis.
6. Find the angular coefficient of the tangent drawn to the curve at the point.
7. At what point does the tangent to the curve form an angle of 30 with the axis?
8. At what point does the tangent to the graph of a function form an angle of 135
with an axle?
9. At what point is the tangent to the graph of a function parallel to the x-axis?
10. At what points is the angular coefficient of the tangent to a cubic parabola equal to 3?
11. Find the angle of inclination of the tangent to the curve at the point whose abscissa is equal to 2.
12.Make an equation for the tangent to the parabola at the point with the abscissa
13.Make an equation for the tangent to the hyperbola at a point
14.Make an equation for a tangent to a curve at a point.
15.Find the tangent to the curve at the point with the abscissa.
Answers : 1) .12 2). 45°,arctg 5 3) .(1;1) 4) .(0;-1) (0,5;-0,75) 5) .1/2 6) .1 7) .(/6;61/12) 8) .(0:-1) (4;3) 9) .(0;4) (1;-5) 10) .(1;1) (-1;-1) 11) . 45°12) .y = -2x-113) .y = -x+214) .y=4x+615) .y = 4x-2.
Evaluation criterion : "5"- 15 tasks
"4"- 11-14 tasks
"3"- 8 tasks
4. Lesson summary : grading; + and – lesson for the student (what did you understand and what still needs to be understood?)
5. Homework: prepare answers to the questions:
Define a tangent to a curve.
What is the normal to a curve?
What is the geometric meaning of a derivative? Write down the formula.
Write down the equation of the tangent to the curve at this point.
Write down the equation of the normal to the curve at this point.
Solve problems 1-15 on choosing an evaluation criterion;additionally upon request : make and solve a card on this topic.
Normal equation in general view written as:
If the function is specified in parametric form x(t) , y(t) , then the normal equation is found using the formula:
(x–x 0)x’+(y-y 0)y’=0
Purpose of the service. This service is designed to find equations of normal to curve. The solution is drawn up in Word format. To obtain the equation, it is necessary to select the type of the given function.
Algorithm for composing the equation of the normal to the graph of a function
- Calculation of the value of the function y 0 at the point x 0: y 0 = f(x 0). If the initial value y 0 is specified, then proceed to step 2.
- Finding the derivative y"(x).
- Calculation of the value of the derivative at x 0.
- Writing the equation of the normal to a curved line in the form: y k = y 0 - 1/y"(y 0)(x - x 0)
Example Task No. 1
Find the equation of the normal to the parabola y = 1/2*x 2 at the point (-2;2).
Solution find using a calculator.
Let us write the normal equations in general form: ![]()
According to the conditions of the problem x 0 = -2, then y 0 = 2
Now let's find the derivative:
y" = (1 / 2 x 2)" = x
hence:
f"(-2) = -2 = -2
As a result we have: ![]()
or
y k = 1 / 2 x+3
Task No. 2
Write the equations of the normal to the curve y 2 -1/2*x 3 -8 at the point M 0 (0;2).
Solution.
Since the function is specified implicitly, we look for the derivative using the formula: 
For our function: ![]()
Then: 
or
hence:
F x "(0;2) = 3 / 4 0 2 /2 = 0
As a result we have: ![]()
or
x = 0
Task No. 3
Write the equations of the normal to the ellipse given in parametric form: x = 5*sqrt(2)*cos(t);y = 3*sqrt(2)*sin(t) at point M 0 (-5;3).
Solution.
Let us write the equations of the normal in for a function specified in parametric form:
(x - x 0)x" + (y - y 0)y" = 0
This point M 0 (-5;3) corresponds to the value t = 3 / 4 π
For our function: ![]()
![]()
hence:
As a result we have:
(x +5)-5 + (y - 3)-3 = 0
or
y k = -5x-3y-16
How to find the equation of the normal to the graph of a function in given point?
In this lesson we will learn how to find the equation of the normal to function graph at a point and look at numerous examples that relate to this problem. To properly assimilate the material, you need to understand geometric meaning of derivative and be able to find them at least at the level of the following articles:
How to find the derivative? Derivative of a complex function And .
The listed lessons will allow “dummies” to quickly navigate the topic and improve their differentiation skills almost from scratch. complete zero. In essence, what follows now is a detailed continuation of the paragraph on tangent equation 3rd article from the above list. Why a sequel? The normal equation is closely related to the tangent equation. Among other things, I will consider problems on how to construct equations for these lines in situations where the function is specified implicitly or parametrically .
But first, let's refresh our memories: if the function differentiable at a point (i.e. if there is final derivative), then the equation of the tangent to the graph of a function at a point can be found using the following formula:
This is the most common case that we have already encountered in the lesson. The simplest problems with derivatives . However, the matter is not limited to this: if at a point there is an infinite derivative: , then the tangent will be parallel to the axis and its equation will take the form . Standard example: a function with a derivative that goes to infinity near critical point . The corresponding tangent will be expressed by the equation: (ordinate axis).
If the derivative does not exist (for example, derivative of at point), then, of course, does not exist and common tangent .
I’ll tell you how to distinguish between the last two cases a little later, but for now let’s return to the main course of today’s lesson:
What is normal? Normal to the graph of a function at a point is called straight , passing through a given point perpendicular to the tangent to the graph of the function at this point (it is clear that the tangent must exist). In short, a normal is a line perpendicular to the tangent and passing through the point of tangency.
How to find the normal equation? From analytical geometry course a very simple algorithm suggests itself: we find tangent equation and present it to general view . Next we “remove” normal vector and compose the equation of the normal at the point and the direction vector.
This method can be used, but in mathematical analysis it is customary to use a ready-made formula based on relationships between the angular coefficients of perpendicular lines
. If exists final And non-zero derivative, then the equation of the normal to the graph of the function at a point is expressed by the following equation: ![]()
We will definitely consider special cases when it is equal to zero or infinity, but first, “ordinary” examples:
Example 1
Write equations for the tangent and normal to the graph of a curve ![]() at the point whose abscissa is equal to .
at the point whose abscissa is equal to .
In practical tasks, you often need to find the tangent line too. However, this is only for the hand - it would be better to have “a full hand” =)
Solution: The first part of the task is well known; let’s compose the tangent equation using the formula:
In this case: 
Let's find derivative
:
 Here on the first step moved the constant beyond the sign of the derivative
, on the second – used rule for differentiating a complex function
.
Here on the first step moved the constant beyond the sign of the derivative
, on the second – used rule for differentiating a complex function
.
Now let's calculate derivative at a point :
Received final number and that makes me happy. Let's substitute it into the formula:
![]()
Let's move it to the top of the left side, open the brackets and present the tangent equation in general view
:
 The second part of the task is no more difficult. Let's compose the normal equation using the formula:
The second part of the task is no more difficult. Let's compose the normal equation using the formula:  Getting rid of three-story fraction
and bring the equation to mind:
Getting rid of three-story fraction
and bring the equation to mind: ![]() – the required equation.
– the required equation.
Answer:
Here you can perform a partial check. First, the coordinates of the point must satisfy each equation:
![]() - true equality.
- true equality.
![]() - true equality.
- true equality.
And secondly, normal vectors must be orthogonal. This can be easily verified using dot product : , which is what needed to be checked.
Alternatively, instead of normal vectors you can use direction vectors of straight lines .
! This check turns out to be useless if the derivative and/or the derivative at the point are found incorrectly. This is the “weak link” of the task - be extremely careful!
A drawing was not required, but for the sake of completeness:  It's funny, but in fact a complete check was obtained, since the drawing was made quite accurately =) By the way, the function
It's funny, but in fact a complete check was obtained, since the drawing was made quite accurately =) By the way, the function ![]() sets the top arc ellipse
.
sets the top arc ellipse
.
The following task is for you to solve on your own:
Example 2
Write down equations for the tangent and normal to the graph of the function at point .
An approximate sample of the final assignment at the end of the lesson.
Now let's look at two special cases:
1) If the derivative at a point is equal to zero: , then the tangent equation will be simplified:  That is, the tangent will be parallel to the axis.
That is, the tangent will be parallel to the axis.
Accordingly, the normal will pass through the point parallel to the axis, which means its equation will take the form .
2) If the derivative at a point exists, but is infinite: , then, as noted at the very beginning of the article, the tangent will become vertical: . And since the normal passes through the point parallel to the axis, its equation will be expressed in a “mirror” way:
It's simple:
Example 3
Write equations for the tangent and normal to a parabola ![]() at point . Make a drawing.
at point . Make a drawing.
I did not add the requirement to complete the drawing - this is how the task was formulated in the original. Although this is rare.
Solution: let's create an equation for the tangent. In this case
It would seem that the calculations are trivial, but it is more than possible to get confused in the signs: 
Thus: ![]()
Since the tangent is parallel to the axis (Case No. 1), then the normal passing through the same point will be parallel to the ordinate axis:
A drawing is, of course, additional trouble, but it is a good check of the analytical solution: 
Answer: ,
In school mathematics courses, a simplified definition of a tangent is common, which is formulated something like this: “A tangent to a graph of a function is a line that has a single common point with the given graph”. As you can see, in the general case this statement is incorrect. According to geometric meaning of the derivative , the tangent is the green line, not the blue line.
The following example is dedicated to the same Case No. 1, when:
Example 4
Write the equation of the tangent and normal to the curve at the point.
Brief solution and answer at the end of the lesson
Case No. 2, in which it rarely occurs in practice, so beginners should not worry too much and skip the fifth example with a light heart. Information in italics is intended for advanced readers who have a good understanding of definitions of derivative and tangent and also have experience finding the derivative by definition :
Example 5
Find the equations of the tangent and normal to the graph of a function at a point
Solution
: Vcritical point
derivative denominator ![]() vanishes, and therefore here you need to calculate one-sided derivatives using the definition of a derivative (see the end of the articleDerivative by definition
):
vanishes, and therefore here you need to calculate one-sided derivatives using the definition of a derivative (see the end of the articleDerivative by definition
):
 Both derivatives are infinite, therefore, at the point there is a common vertical tangent:
Well, it is obvious that the x-axis is the normal. Formally, according to the formula:
For a better understanding of the problem, here is a drawing:
Both derivatives are infinite, therefore, at the point there is a common vertical tangent:
Well, it is obvious that the x-axis is the normal. Formally, according to the formula:
For a better understanding of the problem, here is a drawing:
 Answer
:
Answer
:
I'm glad that you didn't go surfing the Internet, because all the fun is just beginning! To master the material in the next paragraph, you need to be able to find derivative of an implicit function :
How to find the tangent equation and the normal equation if the function is specified implicitly?
The tangent and normal formulas remain the same, but the solution technique changes:
Example 6
Find the equations of the tangent and normal to the curve at the point.
Solution: judging by the equation, this is some kind of 3rd order line , which one exactly does not interest us at all now.
There is malware in the equation, and so the prospect of expressing the function in explicitly looks quite foggy.
But this is not required! There is a much more ingenious solution. Let's compose the tangent equation using the same formula.
The values are known from the condition; by the way, it doesn’t hurt to make sure that they really satisfy the proposed equation:  The correct equality is obtained, which means that everything is in order with the point.
The correct equality is obtained, which means that everything is in order with the point.
All that remains is to calculate. First, using the standard scheme, we find derivative of a function specified implicitly
:

Let us rewrite the result with a notation more suitable for our task: ![]()
At the 2nd step, we substitute : into the found derivative expression:
That's it!
It remains to carefully understand the equation: 
Let's create a normal equation: 
Answer:
Ready! And at first everything seemed difficult. Although the derivative here, of course, is a vulnerable place. Thumbnail for self-solution:
Example 7
Find the equation of the normal to a line at a point
Enough with the tangent already =)
In this case it is easy to find out what it is circle
center at the radius point and even express the desired function ![]() . But why?! After all, find the derivative of implicit function
much easier! She is almost the most primitive here.
. But why?! After all, find the derivative of implicit function
much easier! She is almost the most primitive here.
A short solution and answer at the end of the lesson.
How to find the tangent equation and the normal equation if the function is specified parametrically?
Even easier. But for this you need to practice finding derivative of a parametrically defined function . And this is almost a freebie:
Example 8
Draw up equations for the tangent and normal to the cycloid drawn at the point for which .
A drawing of the cycloid can be found on the page S and V, if the line is specified parametrically (it just so happens that this article was created earlier). It even shows the point of contact.
Solution: The abscissa and ordinate of the tangent point are calculated directly from the parametric equations of the curve: 
Let's find 1st derivative of a parametrically defined function :
And let’s calculate its value at: 
Let’s compose the tangent equation using the usual formula, adjusted for slightly different notations: 
Normal equation: 
Answer:
In conclusion, I suggest you get acquainted with another interesting line:
Example 9
Write an equation for the normal to a semicubic parabola drawn at the point for which .
This is an example for you to solve on your own. Let me remind you that graphs of parametrically specified functions can be constructed, for example, using my design geometric layout .
Well, our lesson has come to an end, and I hope that the material presented was not tangential for you, but normal =)
Thank you for your attention and good luck!
Solutions and Answers:
Example 2:Solution
In this case:
 Thus:
Thus:
 Let's compose the normal equation using the formula
Let's compose the normal equation using the formula ![]() :
:
 Answer
:
Answer
:
Example 4:Solution
: let’s compose the tangent equation using the formula:
In this task:
 Thus:
Thus:
 At a point, the tangent is parallel to the axis, so the corresponding normal equation is:
Answer
:
At a point, the tangent is parallel to the axis, so the corresponding normal equation is:
Answer
:
Example 7:Solution
: in this problem: .
Let's find the derivative:
 Or:
Let's substitute the derivative into the expression:
Or:
Let's substitute the derivative into the expression:
![]() The required normal equation:
The required normal equation:
 Answer
:
Answer
:
Example 9:Solution
: in this case:
![]() Let's find the derivative and calculate its value at:
Let's find the derivative and calculate its value at:
 Normal equation:
Normal equation:
 Answer
:
Answer
:
Taken from the site http://www.mathprofi.ru