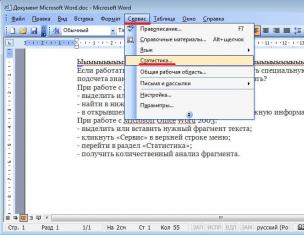
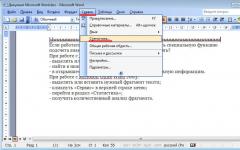
Often, when talking with high school students about research works in mathematics, I hear the following: "What can you discover new in mathematics?" But really: can all great discoveries be made, and theorems proven?
On August 8, 1900, at the International Mathematical Congress in Paris, mathematician David Hilbert laid out a list of problems that he believed would have to be solved in the twentieth century. There were 23 items on the list. Twenty one of them on this moment resolved. The last problem on Gilbert's list to be solved was Fermat's famous theorem, which scientists had been unable to solve for 358 years. In 1994, Briton Andrew Wiles proposed his solution. And it turned out to be true.Following the example of Gilbert at the end of the last century, many mathematicians tried to formulate such strategic tasks for the 21st century. One such list was made famous by Boston billionaire Landon T. Clay. In 1998, at his expense in Cambridge (Massachusetts, USA) was founded Mathematical Institute Clay (Clay Mathematics Institute) and established awards for solving some of the most important problems in modern mathematics. On May 24, 2000, the institute's experts selected seven problems - according to the number of millions of dollars allocated for awards. The list was named Millennium Prize Problems:
1. Cook's problem (formulated in 1971)
Let's say that you, being in a large company, want to make sure that your acquaintance is in the same place. If you are told that he is sitting in the corner, then a split second will be enough to, with a glance, be convinced of the truth of the information. In the absence of this information, you will be forced to go around the entire room, examining guests. This suggests that solving a problem often takes longer than checking the correctness of the solution.
Stephen Cook formulated the problem: can the verification of the correctness of the solution of the problem be more time-consuming than obtaining the solution itself, regardless of the verification algorithm. This problem is also one of the unsolved problems in the field of logic and computer science. Her solution could in a revolutionary way change the fundamentals of cryptography used in the transmission and storage of data.
2. Riemann hypothesis (formulated in 1859)
Some integers cannot be expressed as the product of two smaller integers, such as 2, 3, 5, 7, and so on. Such numbers are called prime and play an important role in pure mathematics and its applications. Distribution of primes among a number of all natural numbers does not obey any pattern. However, the German mathematician Riemann made an assumption regarding the properties of the sequence of prime numbers. If the Riemann hypothesis is proven, it will revolutionize our knowledge of encryption and lead to an unprecedented breakthrough in the field of Internet security.
3. Birch and Swinnerton-Dyer hypothesis (formulated in 1960)
It is related to the description of the set of solutions of some algebraic equations from several variables with integer coefficients. An example of such an equation is the expression x2 + y2 = z2. Euclid gave a complete description of the solutions of this equation, but for more complex equations finding solutions becomes extremely difficult.
4. Hodge hypothesis (formulated in 1941)
In the 20th century, mathematicians discovered a powerful method for studying the shape of complex objects. The main idea is to use simple "bricks" instead of the object itself, which are glued together and form its likeness. Hodge's hypothesis is associated with some assumptions about the properties of such "bricks" and objects.
5. Navier - Stokes equations (formulated in 1822)
If you sail in a boat on the lake, then waves will appear, and if you fly in an airplane, turbulent flows will appear in the air. It is assumed that these and other phenomena are described by equations known as the Navier-Stokes equations. The solutions to these equations are unknown, and it is not even known how to solve them. It is necessary to show that the solution exists and is a sufficiently smooth function. The solution to this problem will significantly change the methods of hydrodynamic and aerodynamic calculations.
6. Poincaré's problem (formulated in 1904)
If you pull the rubber band over the apple, you can, while slowly moving the band without taking it off the surface, squeeze it to a point. On the other hand, if the same rubber band is properly pulled around the donut, there is no way to squeeze the band to a point without ripping the band or breaking the donut. They say that the surface of an apple is simply connected, but the surface of a donut is not. It turned out to be so difficult to prove that only a sphere is simply connected that mathematicians are still looking for the correct answer.
7. Yang - Mills equations (formulated in 1954)
Equations quantum physics describe the world elementary particles... Physicists Young and Mills, having discovered the connection between geometry and particle physics, wrote their equations. Thus, they found a way to unify the theories of electromagnetic, weak and strong interactions. From the Yang - Mills equations, the existence of particles followed, which were actually observed in laboratories all over the world, therefore the Yang - Mills theory was accepted by most physicists, despite the fact that within the framework of this theory it is still not possible to predict the masses of elementary particles.
I think that this material published in the blog is interesting not only for students, but also for schoolchildren who are seriously involved in mathematics. There is something to think about when choosing topics and areas of research.
Unsolvable problems are 7 interesting mathematical problems. Each of them was proposed at one time by famous scientists, usually in the form of hypotheses. For many decades, mathematicians all over the world have been puzzling over their solution. Those who succeed will be rewarded with a million American dollars, offered by the Clay Institute.
Clay Institute
This is the name of a private non-profit organization headquartered in Cambridge, Massachusetts. It was founded in 1998 by Harvard mathematician A. Jeffy and businessman L. Clay. The aim of the Institute is to popularize and develop mathematical knowledge. To achieve this, the organization awards awards to scientists and sponsors promising research.
In the early 21st century, the Clay Institute of Mathematics offered an award to those who solve what are known as the most difficult unsolvable problems, calling their list the Millennium Prize Problems. From the "Hilbert's List" only the Riemann hypothesis was included in it.
Millennium Challenges
The Clay Institute's list originally included:
- the Hodge cycle hypothesis;
- equations of quantum theory Yang - Mills;
- Poincaré's conjecture;
- the problem of equality of the classes P and NP;
- the Riemann hypothesis;
- the existence and smoothness of its solutions;
- the Birch-Swinnerton-Dyer problem.
These open mathematical problems are of great interest, since they can have many practical implementations.

What Grigory Perelman proved
In 1900, the famous scientist-philosopher Henri Poincaré suggested that any simply connected compact 3-manifold without boundary is homeomorphic to a 3-sphere. In the general case, its proof has not been found for a century. Only in 2002-2003 the St. Petersburg mathematician G. Perelman published a number of articles on the solution of the Poincaré problem. They had the effect of a bomb exploding. In 2010, Poincaré's hypothesis was excluded from the list of "Unsolved Problems" of the Clay Institute, and Perelman himself was asked to receive a considerable reward due to him, which the latter refused, without explaining the reasons for his decision.
The most understandable explanation of what the Russian mathematician managed to prove can be given by imagining that a rubber disk is pulled over a donut (torus), and then they are trying to pull the edges of its circle into one point. This is obviously not possible. It is another matter if you perform this experiment with a ball. In this case, a seemingly three-dimensional sphere, resulting from a disk, the circumference of which has been pulled into a point by a hypothetical cord, will be three-dimensional in the understanding of an ordinary person, but two-dimensional in terms of mathematics.
Poincaré suggested that a three-dimensional sphere is the only three-dimensional "object", the surface of which can be contracted to one point, and Perelman was able to prove this. Thus, the list of "Unsolvable tasks" today consists of 6 problems.

Yang-Mills theory
This mathematical problem was proposed by its authors in 1954. The scientific formulation of the theory is as follows: for any simple compact gauge group, the quantum space theory created by Yang and Mills exists and has zero mass defect.
In a language that an ordinary person understands, the interactions between natural sites(particles, bodies, waves, etc.) are divided into 4 types: electromagnetic, gravitational, weak and strong. For many years, physicists have been trying to create general theory fields. It should become a tool for explaining all these interactions. The Yang-Mills theory is a mathematical language with the help of which it became possible to describe 3 of the 4 basic forces of nature. It does not apply to gravity. Therefore, it cannot be assumed that Young and Mills succeeded in creating a field theory.
In addition, the nonlinearity of the proposed equations makes them extremely difficult to solve. For small coupling constants, they can be approximately solved in the form of a perturbation theory series. However, it is not yet clear how these equations can be solved with strong coupling.

Navier-Stokes equations
These expressions describe processes such as air currents, fluid flow, and turbulence. For some special cases, analytical solutions of the Navier-Stokes equation have already been found, but no one has succeeded in doing this for the general one. At the same time, numerical simulations for specific values of speed, density, pressure, time, and so on, can achieve excellent results. It remains to be hoped that someone will be able to apply the Navier-Stokes equations in reverse direction, that is, to calculate the parameters with their help, or to prove that there is no solution method.
Birch - Swinnerton-Dyer problem
The category "Unsolved problems" also includes the hypothesis proposed by British scientists from the University of Cambridge. As early as 2300 years ago, the ancient Greek scientist Euclid gave a complete description of the solutions to the equation x2 + y2 = z2.
If for each of the primes we count the number of points on the curve modulo its modulus, we get an infinite set of integers. If you specifically "glue" it into 1 function of a complex variable, then you get the Hasse-Weil zeta function for a curve of the third order, denoted by the letter L. It contains information about the behavior modulo all primes at once.
Brian Birch and Peter Swinnerton-Dyer hypothesized about elliptic curves. According to her, the structure and number of the set of its rational decisions are related to the behavior of the L-function at unity. The currently unproven Birch - Swinnerton-Dyer conjecture depends on the description of algebraic equations of degree 3 and is the only relatively simple general method for calculating the rank of elliptic curves.
To understand the practical importance of this problem, suffice it to say that in modern cryptography on elliptic curves a whole class of asymmetric systems is based, and domestic standards for digital signatures are based on their application.

Equality of classes p and np
If the rest of the Millennium Problems are purely mathematical, then this one is related to the current theory of algorithms. The problem concerning the equality of the classes p and np, also known as the Cook-Levin problem, can be easily formulated as follows. Suppose that an affirmative answer to a certain question can be verified quickly enough, that is, in polynomial time (PV). Then is it correct to say that the answer to it can be found rather quickly? It sounds even simpler: is the solution to a problem really no more difficult to check than it is to find it? If the equality of the classes p and np is ever proved, then all the selection problems can be solved in a PV. At the moment, many experts doubt the truth of this statement, although they cannot prove the opposite.

Riemann hypothesis
Until 1859, no pattern was identified that would describe how prime numbers are distributed among naturals. Perhaps this was due to the fact that science was engaged in other issues. However, by the middle of the 19th century, the situation had changed, and they became one of the most relevant in which mathematicians began to study.
The Riemann hypothesis, which appeared during this period, is the assumption that there is a certain pattern in the distribution of primes.
Today, many modern scientists believe that if it is proven, then many of the fundamental principles of modern cryptography will have to be revised, which form the basis of much of the mechanisms of e-commerce.
According to the Riemann hypothesis, the nature of the distribution of primes may be significantly different from what is currently assumed. The fact is that until now no system has been discovered in the distribution of prime numbers. For example, there is the problem of "twins", the difference between which is 2. These numbers are 11 and 13, 29. Other primes form clusters. These are 101, 103, 107, etc. Scientists have long suspected that such clusters exist among very large prime numbers. If they are found, then the strength of modern crypto keys will be called into question.

Hodge cycles hypothesis
This still unsolved problem was formulated in 1941. The Hodge hypothesis assumes the possibility of approximating the shape of any object by "gluing" together simple bodies of higher dimension. This method was known and successfully applied for a long time. However, it is not known to what extent the simplification can be made.
Now you know what unsolvable problems exist at the moment. They are the subject of research by thousands of scientists around the world. It remains to be hoped that they will be resolved in the near future, and their practical use will help humanity to enter a new stage of technological development.
So, Fermat's Last Theorem (often called Fermat's Last Theorem), formulated in 1637 by the brilliant French mathematician Pierre Fermat, is very simple in essence and understandable to any person with a secondary education. It says that the formula a to the degree n + b to the degree n = c to the degree n has no natural (that is, non-fractional) solutions for n> 2. It seems that everything is simple and clear, but the best mathematicians and ordinary amateurs fought over seeking a solution for more than three and a half centuries.
Why is she so famous? We'll find out now ...
Are there few proven, unproven, and not yet proven theorems? The point is that Fermat's Last Theorem is the greatest contrast between simplicity of formulation and complexity of proof. Fermat's Last Theorem is an incredibly difficult task, and nevertheless, its formulation can be understood by everyone with the 5th grade of high school, but the proof is not even every professional mathematician. Neither in physics, nor in chemistry, nor in biology, nor in the same mathematics, there is not a single problem that would be formulated so simply, but remained unsolved for so long. 2. What does it consist of?
Let's start with the Pythagorean pants. The wording is really simple - at first glance. As we know from childhood, "Pythagorean pants are equal on all sides." The problem looks so simple because it was based on a mathematical statement that everyone knows - the Pythagorean theorem: in any right triangle the square built on the hypotenuse is equal to the sum of the squares built on the legs.
In the 5th century BC. Pythagoras founded the Pythagorean brotherhood. The Pythagoreans, among other things, studied triples of integers satisfying the equality x² + y² = z². They proved that there are infinitely many Pythagorean triplets, and received general formulas for finding them. They probably tried to look for triplets or more high degrees... Convinced that this did not work, the Pythagoreans gave up futile attempts. The members of the fraternity were more philosophers and aesthetes than mathematicians.
That is, it is easy to find a set of numbers that perfectly satisfy the equality x² + y² = z²
Starting from 3, 4, 5 - indeed, the elementary school student understands that 9 + 16 = 25.
Or 5, 12, 13: 25 + 144 = 169. Great.
And so on. And if we take a similar equation x³ + y³ = z³? Maybe there are such numbers too?
And so on (fig. 1).
So, it turns out that they are NOT. This is where the catch begins. Simplicity is apparent, because it is difficult to prove not the presence of something, but, on the contrary, the absence. When it is necessary to prove that there is a solution, you can and should just give this solution.
Proving the absence is more difficult: for example, someone says: such and such an equation has no solutions. Put him in a puddle? easy: bam - here it is, the solution! (please provide a solution). And that's it, the opponent is slain. How to prove absence?
Say, "I have not found such solutions"? Or maybe you were looking badly? What if they are, only very large, well, very, such that even a super-powerful computer does not have enough strength yet? This is what is difficult.
In a visual form, this can be shown as follows: if you take two squares of suitable sizes and disassemble into unit squares, then from this heap of unit squares you get the third square (Fig. 2):

And if we do the same with the third dimension (Fig. 3), it will not work. There are not enough cubes, or extra ones remain:

But the mathematician of the 17th century, the Frenchman Pierre de Fermat, enthusiastically studied general equation x n + y n = z n ... And finally, I came to the conclusion: there are no integer solutions for n> 2. Fermat's proof is irretrievably lost. The manuscripts are burning! All that remains is his remark in Diophantus' Arithmetic: "I have found a truly amazing proof of this proposition, but the margins here are too narrow to contain it."
Actually, a theorem without proof is called a hypothesis. But for Fermat the fame was fixed that he was never wrong. Even if he did not leave evidence of any statement, it was subsequently confirmed. In addition, Fermat proved his thesis for n = 4. So the hypothesis of the French mathematician went down in history as Fermat's Last Theorem.
After Fermat, such great minds as Leonard Euler worked on the search for proof (in 1770 he proposed a solution for n = 3),
Adrien Legendre and Johann Dirichlet (these scientists jointly found a proof for n = 5 in 1825), Gabriel Lame (who found a proof for n = 7) and many others. By the mid-80s of the last century, it became clear that the scientific world was on the way to a final solution. The great theorem Fermat, however, it was only in 1993 that mathematicians saw and believed that the three-century saga of finding a proof of Fermat's last theorem was practically over.
It is easy to show that it is enough to prove Fermat's theorem only for prime n: 3, 5, 7, 11, 13, 17, ... For composite n, the proof remains valid. But there are also infinitely many primes ...
In 1825, applying the method of Sophie Germain, women mathematicians, Dirichlet and Legendre independently proved the theorem for n = 5. In 1839, using the same method, the Frenchman Gabriel Lame showed the truth of the theorem for n = 7. Gradually, the theorem was proved for almost all n less than one hundred.
Finally, the German mathematician Ernst Kummer showed in a brilliant study that the theorem in general form cannot be proved by the methods of mathematics of the 19th century. Prize French Academy Science, founded in 1847 for the proof of Fermat's theorem, remained unchanged.
In 1907, the wealthy German industrialist Paul Wolfskel, out of unrequited love, decided to commit suicide. As a true German, he set the date and time for the suicide: exactly at midnight. On the last day, he drew up a will and wrote letters to friends and relatives. Business was over before midnight. I must say that Paul was interested in mathematics. Out of nothing to do, he went to the library and began to read the famous article by Kummer. Suddenly it seemed to him that Kummer made a mistake in the course of his reasoning. Wolfskel began to sort through this passage of the article, pencil in hand. Midnight has passed, morning has come. The gap in the evidence was filled. And the very reason for suicide now looked completely ridiculous. Paul tore up the farewell letters and rewrote the will.
He soon died a natural death. The heirs were quite surprised: 100,000 marks (more than 1,000,000 of the current pounds sterling) were transferred to the account of the Royal Scientific Society of Göttingen, which in the same year announced a competition for the Wolfskehl Prize. 100,000 marks were due to the prover of Fermat's theorem. Not a pfennig was supposed to refute the theorem ...
Most professional mathematicians considered the search for a proof of Fermat's Last Theorem a hopeless task and strongly refused to waste time on such a useless exercise. But the amateurs frolicked wonderfully. A few weeks after the announcement, an avalanche of "evidence" hit the University of Göttingen. Professor E.M. Landau, whose duty was to analyze the submitted evidence, handed out cards to his students:
Dear. ... ... ... ... ... ... ...
Thank you for the manuscript you sent me with the proof of Fermat's Last Theorem. The first error is on page ... in line .... Because of it, all evidence is null and void.
Professor E. M. Landau


In 1963, Paul Cohen, relying on Gödel's conclusions, proved the undecidability of one of Hilbert's twenty-three problems - the continuum hypothesis. What if Fermat's Last Theorem is also undecidable ?! But the true fanatics of the Great Theorem were not disappointed in the least. The advent of computers unexpectedly gave mathematicians new method proof. After World War II, groups of programmers and mathematicians proved Fermat's Last Theorem for all values of n up to 500, then up to 1,000, and later up to 10,000.
In the 80s, Samuel Wagstaff raised the limit to 25,000, and in the 90s, mathematicians declared that Fermat's Last Theorem is true for all values of n to 4 million. But if you subtract even a trillion trillion from infinity, it will not become smaller. Mathematicians are not convinced by statistics. To prove the Great Theorem meant to prove it for ALL n going to infinity.

In 1954, two young Japanese mathematician friends took up the study of modular forms. These forms generate rows of numbers, each with its own row. By chance Taniyama compared these series with the series generated by elliptic equations. They matched! But modular forms are geometric objects, and elliptic equations are algebraic. Connections have never been found between such different objects.
Nevertheless, friends, after careful testing, put forward a hypothesis: each elliptic equation has a double - a modular form, and vice versa. It was this hypothesis that became the foundation of a whole direction in mathematics, but until the Taniyama – Shimura hypothesis was proved, the entire building could collapse at any moment.
In 1984, Gerhard Frey showed that a solution to Fermat's equation, if it exists, can be included in some elliptic equation. Two years later, Professor Ken Ribet proved that this hypothetical equation cannot have a counterpart in the modular world. Henceforth, Fermat's Last Theorem was inextricably linked with the Taniyama – Shimura conjecture. Having proved that any elliptic curve is modular, we conclude that an elliptic equation with a solution to Fermat's equation does not exist, and Fermat's Last Theorem would be proved immediately. But for thirty years, the Taniyama-Shimura hypothesis could not be proved, and there were fewer and fewer hopes for success.
In 1963, when he was only ten years old, Andrew Wiles was already fascinated by mathematics. When he learned about the Great Theorem, he realized that he could not deviate from it. As a schoolboy, student, graduate student, he prepared himself for this task.
Learning about the conclusions of Ken Ribet, Wiles went headlong into proving the Taniyama – Shimura hypothesis. He decided to work in complete isolation and secrecy. "I understood that everything that has something to do with Fermat's Last Theorem is of too much interest ... Too many viewers deliberately interfere with the achievement of the goal." Seven years of hard work bore fruit, Wiles finally completed the proof of the Taniyama – Shimura conjecture.
In 1993, the English mathematician Andrew Wiles presented to the world his proof of Fermat's Last Theorem (Wiles read his sensational report at a conference at the Sir Isaac Newton Institute in Cambridge.), On which work lasted more than seven years.

While the hype in the press continued, serious work began to verify the evidence. Each piece of evidence must be scrutinized before the evidence can be considered rigorous and accurate. Wiles spent a hectic summer waiting for the reviewers' feedback, hoping he could get their approval. At the end of August, experts found an insufficiently substantiated judgment.
It turned out that this solution contains a gross error, although on the whole it is correct. Wiles did not give up, called for the help of a well-known expert in number theory Richard Taylor, and already in 1994 they published a corrected and supplemented proof of the theorem. The most amazing thing is that this work took as many as 130 (!) Pages in the mathematical journal "Annals of Mathematics". But the story did not end there either - the last point was only put in the next year, 1995, when the final and "ideal", from a mathematical point of view, version of the proof was published.
“… Half a minute after the start of the gala dinner on the occasion of her birthday, I presented Nadia with the manuscript of the complete proof” (Andrew Waltz). Have I said that mathematicians are strange people?

This time there was no doubt about the proof. Two articles were subjected to the most careful analysis and were published in May 1995 in the Annals of Mathematics.
A lot of time has passed since that moment, but there is still an opinion in society that Fermat's Last Theorem is undecidable. But even those who know about the found proof continue to work in this direction - very few people are satisfied that the Great Theorem requires a solution of 130 pages!
Therefore, now the forces of very many mathematicians (mostly amateurs, not professional scientists) are thrown into the search for a simple and laconic proof, but this path, most likely, will not lead anywhere ...
Lev Valentinovich Rudi, the author of the article "Pierre Fermat and his" unprovable "theorem", after reading a publication about one of the 100 geniuses of modern mathematics, who was called a genius due to his solution of Fermat's theorem, offered to publish his alternative opinion on this topic. To which we willingly responded and publish his article without abbreviations.
Pierre Fermat and his "unprovable" theorem
This year marks the 410th anniversary of the birth of the great French mathematician Pierre Fermat. Academician V.M. Tikhomirov writes about P. Fermat: “Only one mathematician was honored that his name became a household name. If they say "fermatist", then we are talking about a person who is madly obsessed with some unrealizable idea. But this word cannot be attributed to Pierre Fermat himself (1601-1665), one of the brightest minds in France.
P. Fermat is a man of amazing fate: one of the greatest mathematicians in the world, he was not a "professional" mathematician. Fermat was a lawyer by profession. He received an excellent education and was an outstanding connoisseur of art and literature. All his life he worked for public service, for the last 17 years has been an advisor to the parliament in Toulouse. He was attracted to mathematics by disinterested and sublime love, and it was this science that gave him everything that love can give a person: the rapture of beauty, pleasure and happiness.
In his papers and correspondence, Fermat formulated many beautiful statements, about which he wrote that he had their proof. And gradually such unproven statements became less and less and, finally, only one thing remained - his mysterious Great Theorem!
However, for those interested in mathematics, Fermat's name speaks volumes, regardless of his Great Theorem. He was one of the most astute minds of his time, he is considered the founder of number theory, he made a huge contribution to the development of analytical geometry, mathematical analysis. We are grateful to Fermat for opening a world full of beauty and mystery for us ”(nature.web.ru:8001›db/msg.html ...).
Strange, however, "gratitude" !? Math world and enlightened humanity ignored the 410th anniversary of the Farm. Everything was, as always, quiet, peaceful, everyday ... There was no fanfare, eulogies, toasts. Of all the mathematicians in the world, only Fermat "received" such a high honor that when the word "fermatist" is used, everyone understands that we are talking about a half-wit who is "madly obsessed with an unrealizable idea" to find the lost proof of Fermat's theorem!
In his remark in the margins of Diophantus, Fermat wrote: "I have found a truly amazing proof of my statement, but the margins of the book are narrow to accommodate it." So it was also "the moment of weakness of the mathematical genius of the 17th century." This dumbass did not understand that he was “mistaken”, and, most likely, he was simply “lying”, “cunning”.
If Fermat claimed, then he had proof !? The level of knowledge was no higher than that of a modern tenth grader, but if some engineer tries to find this proof, then he is ridiculed, declared insane. And it is quite another matter if the American 10-year-old boy E. Wiles "accepts as an initial hypothesis that Fermat could not know much more mathematics than he did," and begins to "prove" this "unprovable theorem." Of course, only a "genius" is capable of this.
By chance I got to the site (works.tarefer.ru ›50/100086 / index.html), where the student of the Chita State Technical University Kushenko V.V. writes about Fermat: “... The small town of Beaumont and all its five thousand inhabitants are unable to realize that the great Fermat was born here, the last mathematician-alchemist, who solved the idle problems of the coming centuries, the quietest judge's hook, the crafty sphinx who tortured mankind with his riddles , a cautious and well-behaved bureaucrat, a swindler, an intriguer, a couch potato, an envious person, a brilliant compiler, one of the four titans of mathematics ... Fermat almost never left Toulouse, where he settled after his marriage to Louise de Long, the daughter of a parliamentary councilor. Thanks to his father-in-law, he rose to the rank of adviser and acquired the coveted prefix "de". The son of the third estate, a practical offspring of wealthy tanners, stuffed with Latin and Franciscan piety, he did not set himself grandiose tasks in real life ...
In his turbulent age, he lived thoroughly and quietly. He did not write philosophical treatises, like Descartes, was not a confidante of French kings, like Viet, did not fight, did not travel, did not create mathematical circles, did not have students and did not publish during his lifetime ... Without discovering any conscious claims to a place in history, The farm dies on January 12, 1665. "
I was shocked, shocked ... And who was the first "mathematician-alchemist" !? What are these "idle tasks of the coming centuries" !? “A bureaucrat, a swindler, an intriguer, a homebody, an envious person” ... Where did these green youths and youths get so much disdain, contempt, cynicism for a person who lived 400 years before them !? What blasphemy, blatant injustice !? But, the youngsters themselves did not come up with all this !? They were advised by mathematicians, "kings of sciences", the very "humanity" that Fermat "sly sphinx" tortured with his riddles.
However, Fermat cannot bear any responsibility for the fact that the arrogant, but talentless descendants of more than three hundred years knocked their horns on his school theorem. By humiliating, spitting on Fermat, mathematicians are trying to save their uniform honor !? But there is no "honor" for a long time, not even a "uniform" !? Fermat's children's puzzle has become the greatest disgrace of the "selected, valiant" army of mathematicians in the world !?
The "kings of science" were disgraced by the fact that seven generations of mathematical "luminaries" could not prove the school theorem, which was proved by both P. Fermat and the Arab mathematician al-Khujandi 700 years before Fermat !? They disgraced themselves by the fact that instead of admitting their mistakes, they denounced P. Fermat as a deceiver and began to inflate the myth about the "unprovability" of his theorem !? Mathematicians were also disgraced by the fact that for a whole century they have been furiously poisoning amateur mathematicians, "hitting their smaller brothers on the head." This persecution became the most shameful act of mathematicians in history after the drowning of Hippasus by Pythagoras. scientific thought! They disgraced themselves by the fact that, under the guise of a "proof" of Fermat's theorem, they slipped to enlightened humanity the dubious "creation" of E. Wiles, which even the brightest luminaries of mathematics "do not understand" !?
The 410th anniversary of the birth of P. Fermat is undoubtedly a sufficiently strong argument for mathematicians to finally come to their senses and stop casting a shadow over the fence and restore the good, honest name of the great mathematician. P. Fermat "did not find any conscious claims to a place in history", but this wayward and capricious Lady herself brought it into her annals in her arms, but she spat out many zealous and zealous "applicants" like chewed gum. And nothing can be done about it, just one of his many beautiful theorems forever inscribed the name of P. Fermat in history.
But this unique creation of Fermat and itself for a whole century has been driven into the "underground", declared "outlawed", has become the most despicable and hated task in the entire history of mathematics. But the time has come for this "ugly duckling" of mathematics to turn into a beautiful swan! Fermat's amazing riddle has suffered its right to take its rightful place both in the treasury of mathematical knowledge and in every school of the world alongside its sister - the Pythagorean theorem.
Such a unique, graceful task simply cannot but have beautiful, graceful solutions. If the Pythagorean theorem has 400 proofs, then let Fermat's theorem have only 4 simple proofs at first. They are, gradually there will be more of them !? I believe that P. Fermat's 410th anniversary is the most suitable occasion or occasion for professional mathematicians to come to their senses and finally end this senseless, absurd, troublesome and absolutely useless "blockade" of amateurs !?