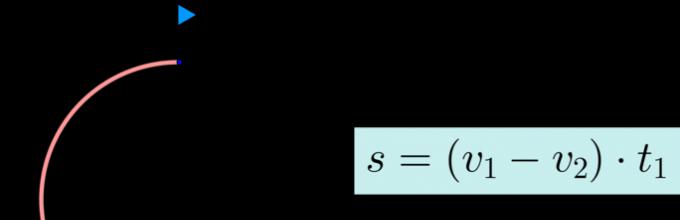“Lesson Tangent to a circle” - Prove that line AC is tangent to a given circle. Problem 1. Given: env.(O;OM), MR – tangent, angle KMR=45?. Calculate the length of BC if OD=3cm. General lesson. Draw a tangent to the given circle. Topic: “circle”. Solution: Problem solving. Practical work. Make notations and notes.
“Tangent to a circle” - Property of a tangent. Let d be the distance from the center O to the straight line KM. The segments AK and AM are called tangent segments drawn from A. Tangent to a circle. Then. A tangent to a circle is perpendicular to the radius drawn to the point of tangency. Proof. Let us prove that if AK and AM are tangent segments, then AK = AM, ?OAK = ? OAM.
“Circumference and Circle” - Calculate. Find the circumference. Find the radius of the circle. Find the area of the shaded figure. Circle. Circular sector. Draw a circle with center K and radius 2 cm. Complete the statement. Independent work. Circumference. Circle. Area of a circle. Calculate the length of the equator. Game.
“Equation of a circle” - Construct a circle in your notebook, given by equations: Center of the circle O(0;0), (x – 0)2 + (y – 0)2 = R 2, x2 + y2 = R 2? equation of a circle with center at the origin. . O (0;0) – center, R = 4, then x2 + y2 = 42; x2 + y2 = 16. Find the coordinates of the center and the radius if AB is the diameter of the given circle.
“Circle length 6th grade” - Lesson motto: History of numbers?. The diameter of the diesel locomotive wheel is 180 cm. Lambert found for? the first twenty-seven suitable fractions. Math lesson in 6th grade Math teacher: Nikonorova Lyubov Arkadyevna. Lesson plan. Competition "Mosaic of Presentations". But you can find an infinite sequence of suitable fractions.
This work A cyclist left point A of a circular route, and 30 minutes later a motorcyclist followed him. In 10 minutes (Test) on the subject (Macroeconomics and public administration), was made to order by specialists of our company and passed its successful defense. Work - A cyclist left point A of a circular track, and 30 minutes later a motorcyclist followed him. In 10 minutes, the subject Macroeconomics and Public Administration reflects its topic and the logical component of its disclosure, the essence of the issue under study is revealed, the main provisions and leading ideas of this topic are highlighted.
Work - A cyclist left point A of a circular track, and 30 minutes later a motorcyclist followed him. After 10 minutes, contains: tables, drawings, the latest literary sources, the year the work was submitted and defended - 2017. In the work A cyclist left point A of the circular route, and 30 minutes later a motorcyclist followed him. After 10 minutes (Macroeconomics and public administration), the relevance of the research topic is revealed, the degree of development of the problem is reflected, based on an in-depth assessment and analysis of scientific and methodological literature, in the work on the subject of Macroeconomics and public administration, the object of analysis and its issues are comprehensively considered, both from the theoretical and practical sides, the goal and specific objectives of the topic under consideration are formulated, there is a logic of presentation of the material and its sequence.
The same formulas are true: \[(\large(S=v\cdot t \quad \quad \quad v=\dfrac St \quad \quad \quad t=\dfrac Sv))\]
from one point in one direction with speeds \(v_1>v_2\) .
Then if \(l\) is the length of the circle, \(t_1\) is the time after which they will find themselves at one point for the first time, then:
That is, for \(t_1\) the first body will go the distance\(l\) greater than the second body.
If \(t_n\) is the time after which they will end up at the same point for the \(n\)th time, then the formula is valid: \[(\large(t_n=n\cdot t_1))\]
\(\blacktriangleright\) Let two bodies begin to move from different points in the same direction with speeds \(v_1>v_2\) .
Then the problem easily reduces to the previous case: you first need to find the time \(t_1\) after which they will end up at the same point for the first time.
If at the moment of starting the movement the distance between them \(\buildrel\smile\over(A_1A_2)=s\), That:

Task 1 #2677
Task level: Easier than the Unified State Exam
Two athletes start in the same direction from diametrically opposite points on the circular track. They run at different, inconsistent speeds. It is known that at the moment when the athletes first caught up, they stopped training. How many more laps did the athlete run at a higher average speed than the other athlete?
Let's call the athlete with the higher average speed first. First, the first athlete had to run half a circle to reach the starting point of the second athlete. After that, he had to run as much as the second athlete ran (roughly speaking, after the first athlete ran half a circle, before the meeting he had to run every meter of the track that the second athlete ran, and the same number of times as the second athlete ran this meter ).
Thus, the first athlete ran \(0.5\) more laps.
Answer: 0.5
Task 2 #2115
Task level: Easier than the Unified State Exam
The cat Murzik runs in a circle from the dog Sharik. The speeds of Murzik and Sharik are constant. It is known that Murzik runs \(1.5\) times faster than Sharik and in \(10\) minutes they run two laps in total. How many minutes will it take Sharik to run one lap?
Since Murzik runs \(1.5\) times faster than Sharik, then in \(10\) minutes Murzik and Sharik in total run the same distance that Sharik would run in \(10\cdot (1 + 1.5) ) = 25\) minutes. Consequently, Sharik runs two circles in \(25\) minutes, then Sharik runs one circle in \(12.5\) minutes
Answer: 12.5
Task 3 #823
Task level: Equal to the Unified State Exam
From point A of the circular orbit of a distant planet, two meteorites simultaneously flew out in the same direction. The speed of the first meteorite is 10,000 km/h greater than the speed of the second. It is known that for the first time after departure they met 8 hours later. Find the length of the orbit in kilometers.
At the moment when they first met, the difference in the distances they flew was equal to the length of the orbit.
In 8 hours the difference became \(8 \cdot 10000 = 80000\) km.
Answer: 80000
Task 4 #821
Task level: Equal to the Unified State Exam
A thief who stole a handbag runs away from the owner of the handbag along a circular road. The thief's speed is 0.5 km/h greater than the speed of the owner of the handbag, who is running after him. In how many hours will the thief catch up with the owner of the handbag for the second time, if the length of the road along which they are running is 300 meters (assume that he caught up with her the first time after the theft of the handbag)?
First way:
The thief will catch up with the owner of the handbag for the second time at the moment when the distance he will run becomes 600 meters greater than the distance that the owner of the handbag will run (from the moment of theft).
Since his speed is \(0.5\) km/h higher, then in an hour he runs 500 meters more, then in \(1: 5 = 0.2\) hours he runs \(500: 5 = 100\) meters more. He will run 600 meters more in \(1 + 0.2 = 1.2\) hours.
Second way:
Let \(v\) km/h be the speed of the owner of the handbag, then
\(v + 0.5\) km/h – the speed of the thief.
Let \(t\) h be the time after which the thief will catch up with the owner of the handbag for the second time, then
\(v\cdot t\) – the distance that the owner of the handbag will run in \(t\) hours,
\((v + 0.5)\cdot t\) – the distance that the thief will cover in \(t\) hours.
The thief will catch up with the owner of the handbag for the second time at the moment when he runs exactly 2 laps more than her (that is, \(600\) m = \(0.6\) km), then \[(v + 0.5)\cdot t - v\cdot t = 0.6\qquad\Leftrightarrow\qquad 0.5\cdot t = 0.6,\] whence \(t = 1.2\) h.
Answer: 1.2
Task 5 #822
Task level: Equal to the Unified State Exam
Two motorcyclists start simultaneously from one point on a circular track in different directions. The speed of the first motorcyclist is twice that of the second. An hour after the start, they met for the third time (consider that the first time they met after the start). Find the speed of the first motorcyclist if the length of the road is 40 km. Give your answer in km/h.
At the moment when the motorcyclists met for the third time, the total distance they traveled was \(3 \cdot 40 = 120\) km.
Since the speed of the first is 2 times greater than the speed of the second, then out of 120 km he traveled a part 2 times greater than the second, that is, 80 km.
Since they met for the third time an hour later, the first one drove 80 km in an hour. Its speed is 80 km/h.
Answer: 80
Task 6 #824
Task level: Equal to the Unified State Exam
Two runners start simultaneously in the same direction from two diametrically opposite points on a circular track 400 meters long. How many minutes will it take for the runners to meet each other for the first time if the first runner runs 1 kilometer more in an hour than the second?
In an hour, the first runner runs 1000 meters more than the second, which means he will run 100 meters more in \(60: 10 = 6\) minutes.
The initial distance between runners is 200 meters. They will be equal when the first runner runs 200 meters more than the second.
This will happen in \(2 \cdot 6 = 12\) minutes.
Answer: 12
Task 7 #825
Task level: Equal to the Unified State Exam
A tourist left city M along a circular road 220 kilometers long, and 55 minutes later a motorist followed him from city M. 5 minutes after departure he caught up with the tourist for the first time, and another 4 hours after that he caught up with him for the second time. Find the speed of the tourist. Give your answer in km/h.
First way:
After the first meeting, the motorist caught up with the tourist (for the second time) 4 hours later. By the time of the second meeting, the motorist had driven a circle more than the tourist had covered (that is, \(220\) km).
Since during these 4 hours the motorist overtook the tourist by \(220\) km, the speed of the motorist is \(220: 4 = 55\) km/h greater than the speed of the tourist.
Let now the speed of the tourist be \(v\) km/h, then he managed to walk before the first meeting \ the motorist managed to pass \[(v + 55)\dfrac(5)(60) = \dfrac(v + 55)(12)\ \text(km).\] Then \[\dfrac(v + 55)(12) = v,\] from where we find \(v = 5\) km/h.
Second way:
Let \(v\) km/h be the speed of the tourist. When using quantities in the exercise that are related to distance (speed, circle length), they can be solved by reducing them to movement in a straight line. The greatest difficulty for schoolchildren in Moscow and other cities, as practice shows, is caused by tasks on Roundabout Circulation in the Unified State Examination, the search for an answer in which is associated with the use of an angle. To solve the exercise, the circumference can be specified as a part of a circle. You can repeat these and other algebraic formulas in the “Theoretical Help” section. In order to learn how to apply them in practice, solve exercises on this topic in the “Catalogue”.
Let \(w\) km/h be the speed of the motorist. Since \(55\) minutes \(+ 5\) minutes \(= 1\) hour, then
\(v\cdot 1\) km is the distance that the tourist traveled before the first meeting. Since \(5\) minutes \(= \dfrac(1)(12)\) hours, then
\(w\cdot \dfrac(1)(12)\) km – the distance that the motorist traveled before the first meeting. The distances they traveled before their first meeting are: \
Over the next 4 hours, the motorist drove more than the tourist covered in a circle (by \(220\)
\
\
From point A of a circular track, the length of which is 75 km, two cars started simultaneously in the same direction. The speed of the first car is 89 km/h, the speed of the second car is 59 km/h. How many minutes after the start will the first car be ahead of the second by exactly one lap?
Problem solution
This lesson shows how, using physical formula to determine the time during uniform motion: draw up a proportion to determine the time when one car overtakes another in a circle. When solving the problem, a clear sequence of actions is indicated for solving such problems: we enter a specific designation for what we want to find, write down the time it takes one and the second car to cover a certain number of laps, taking into account that this time is same size– we equate the resulting equalities. The solution involves finding the unknown quantity in a linear equation. To get the results, you must remember to substitute the number of laps obtained into the formula for determining the time.
The solution to this problem is recommended for 7th grade students when studying the topic “ Mathematical language. Mathematical model" ( Linear equation with one variable"). When preparing for the OGE, the lesson is recommended when repeating the topic “Mathematical language. Mathematical model".
Sections: Mathematics
The article discusses tasks to help students: to develop skills in solving word problems in preparation for the Unified State Exam, when learning to solve problems on composing mathematical model real situations in all parallels of primary and high school. It presents tasks: movement in a circle; to find the length of a moving object; to find the average speed.
I. Problems involving movement in a circle.
Circular motion problems turned out to be difficult for many schoolchildren. They are solved in almost the same way as ordinary movement problems. They also use the formula. But there is a point to which we would like to pay attention.
Task 1. A cyclist left point A of the circular track, and 30 minutes later a motorcyclist followed him. 10 minutes after departure, he caught up with the cyclist for the first time, and another 30 minutes after that he caught up with him for the second time. Find the speed of the motorcyclist if the length of the route is 30 km. Give your answer in km/h.
Solution. The speeds of the participants will be taken as X km/h and y km/h. For the first time, a motorcyclist overtook a cyclist 10 minutes later, that is, an hour after the start. Up to this point, the cyclist had been on the road for 40 minutes, that is, hours. The participants in the movement traveled the same distances, that is, y = x. Let's enter the data into the table.
Table 1
The motorcyclist then passed the cyclist a second time. This happened 30 minutes later, that is, an hour after the first overtaking. How far did they travel? A motorcyclist overtook a cyclist. This means he completed one more lap. This is the moment
which you need to pay attention to. One lap is the length of the track, it is 30 km. Let's create another table.
Table 2
We get the second equation: y - x = 30. We have a system of equations: 
![]() In the answer we indicate the speed of the motorcyclist.
In the answer we indicate the speed of the motorcyclist.
Answer: 80 km/h.
Tasks (independently).
I.1.1. A cyclist left point “A” of the circular route, and 40 minutes later a motorcyclist followed him. 10 minutes after departure, he caught up with the cyclist for the first time, and another 36 minutes after that he caught up with him for the second time. Find the speed of the motorcyclist if the length of the route is 36 km. Give your answer in km/h.
I.1. 2. A cyclist left point “A” of the circular route, and 30 minutes later a motorcyclist followed him. 8 minutes after departure, he caught up with the cyclist for the first time, and another 12 minutes after that he caught up with him for the second time. Find the speed of the motorcyclist if the length of the route is 15 km. Give your answer in km/h.
I.1. 3. A cyclist left point “A” of the circular route, and 50 minutes later a motorcyclist followed him. 10 minutes after departure, he caught up with the cyclist for the first time, and another 18 minutes after that he caught up with him for the second time. Find the speed of the motorcyclist if the length of the route is 15 km. Give your answer in km/h.
Two motorcyclists start simultaneously in the same direction from two diametrically opposite points on a circular track, the length of which is 20 km. How many minutes will it take for the motorcyclists to meet each other for the first time if the speed of one of them is 15 km/h greater than the speed of the other?
Solution.

Figure 1
With a simultaneous start, the motorcyclist who started from “A” traveled half a lap more than the one who started from “B”. That is, 10 km. When two motorcyclists move in the same direction, the removal velocity v = -. According to the conditions of the problem, v = 15 km/h = km/min = km/min – removal speed. We find the time after which the motorcyclists reach each other for the first time.
10:= 40(min).
Answer: 40 min.
Tasks (independently).
I.2.1. Two motorcyclists start simultaneously in the same direction from two diametrically opposite points on a circular track, the length of which is 27 km. How many minutes will it take for the motorcyclists to meet each other for the first time if the speed of one of them is 27 km/h greater than the speed of the other?
I.2.2. Two motorcyclists start simultaneously in the same direction from two diametrically opposite points on a circular track, the length of which is 6 km. How many minutes will it take for the motorcyclists to meet each other for the first time if the speed of one of them is 9 km/h greater than the speed of the other?
From one point on a circular track, the length of which is 8 km, two cars started simultaneously in the same direction. The speed of the first car is 89 km/h, and 16 minutes after the start it was one lap ahead of the second car. Find the speed of the second car. Give your answer in km/h.
Solution.
x km/h is the speed of the second car.
(89 – x) km/h – removal speed.
8 km is the length of the circular route.
Equation.
(89 – x) = 8,
89 – x = 2 15,
Answer: 59 km/h.
Tasks (independently).
I.3.1. From one point on a circular track, the length of which is 12 km, two cars started simultaneously in the same direction. The speed of the first car is 103 km/h, and 48 minutes after the start it was one lap ahead of the second car. Find the speed of the second car. Give your answer in km/h.
I.3.2. From one point on a circular track, the length of which is 6 km, two cars started simultaneously in the same direction. The speed of the first car is 114 km/h, and 9 minutes after the start it was one lap ahead of the second car. Find the speed of the second car. Give your answer in km/h.
I.3.3. From one point on a circular track, the length of which is 20 km, two cars started simultaneously in the same direction. The speed of the first car is 105 km/h, and 48 minutes after the start it was one lap ahead of the second car. Find the speed of the second car. Give your answer in km/h.
I.3.4. From one point on a circular track, the length of which is 9 km, two cars started simultaneously in the same direction. The speed of the first car is 93 km/h, and 15 minutes after the start it was one lap ahead of the second car. Find the speed of the second car. Give your answer in km/h.
The clock with hands shows 8 hours 00 minutes. In how many minutes will the minute hand line up with the hour hand for the fourth time?
Solution. We assume that we are not solving the problem experimentally.
In one hour, the minute hand travels one circle, and the hour hand travels one circle. Let their speeds be 1 (laps per hour) and ![]() Start - at 8.00. Let's find the time it takes for the minute hand to catch up with the hour hand for the first time.
Start - at 8.00. Let's find the time it takes for the minute hand to catch up with the hour hand for the first time.
The minute hand will move further, so we get the equation

This means that for the first time the arrows will align through
Let the arrows align for the second time after time z. The minute hand will travel a distance of 1·z, and the hour hand will travel one circle more. Let's write the equation:
Having solved it, we get that .
So, through the arrows they will align for the second time, after another - for the third time, and after another - for the fourth time.
Therefore, if the start was at 8.00, then for the fourth time the hands will align through
![]()
4h = 60 * 4 min = 240 min.
Answer: 240 minutes.
Tasks (independently).
I.4.1.The clock with hands shows 4 hours 45 minutes. In how many minutes will the minute hand line up with the hour hand for the seventh time?
I.4.2. The clock with hands shows 2 o'clock exactly. In how many minutes will the minute hand line up with the hour hand for the tenth time?
I.4.3. The clock with hands shows 8 hours 20 minutes. In how many minutes will the minute hand line up with the hour hand for the fourth time? fourth
II. Problems to find the length of a moving object.
A train, moving uniformly at a speed of 80 km/h, passes a roadside pole in 36 s. Find the length of the train in meters.
Solution. Since the speed of the train is indicated in hours, we will convert the seconds to hours.
1) 36 sec = ![]()
2) find the length of the train in kilometers.
80· ![]()
Answer: 800m.
Tasks (independently).
II.2. A train, moving uniformly at a speed of 60 km/h, passes a roadside pole in 69 s. Find the length of the train in meters. Answer: 1150m.
II.3. A train, moving uniformly at a speed of 60 km/h, passes a forest belt 200 m long in 1 min 21 s. Find the length of the train in meters. Answer: 1150m.
III. Medium speed problems.
On a math exam, you may encounter a problem about finding the average speed. We must remember that the average speed is not equal to the arithmetic mean of the speeds. The average speed is found using a special formula:
If there were two sections of the path, then ![]() .
.
The distance between the two villages is 18 km. A cyclist traveled from one village to another for 2 hours, and returned along the same road for 3 hours. What is the average speed of the cyclist along the entire route?
Solution:
2 hours + 3 hours = 5 hours - spent on the entire movement,
.The tourist walked at a speed of 4 km/h, then for exactly the same time at a speed of 5 km/h. What is the average speed of the tourist along the entire route?
Let the tourist walk t h at a speed of 4 km/h and t h at a speed of 5 km/h. Then in 2t hours he covered 4t + 5t = 9t (km). The average speed of a tourist is = 4.5 (km/h).
Answer: 4.5 km/h.
We note that the average speed of the tourist turned out to be equal to the arithmetic mean of the two given speeds. You can verify that if the travel time on two sections of the route is the same, then the average speed of movement is equal to the arithmetic mean of the two given speeds. To do this, let us solve the same problem in general form.
The tourist walked at a speed of km/h, then for exactly the same time at a speed of km/h. What is the average speed of the tourist along the entire route?
Let the tourist walk t h at a speed of km/h and t h at a speed of km/h. Then in 2t hours he traveled t + t = t (km). The average speed of a tourist is
= (km/h).The car covered some distance uphill at a speed of 42 km/h, and downhill at a speed of 56 km/h.
![]() .
.
The average speed of movement is 2 s: (km/h).
Answer: 48 km/h.
The car covered some distance uphill at a speed of km/h, and down the mountain at a speed of km/h.
What is the average speed of the car along the entire route?
Let the length of the path section be s km. Then the car traveled 2 s km in both directions, spending the entire journey ![]() .
.
The average speed of movement is 2 s: ![]() (km/h).
(km/h).
Answer: km/h.
Consider a problem in which the average speed is given, and one of the speeds needs to be determined. Application of the equation will be required.
The cyclist rode uphill at a speed of 10 km/h, and down the mountain at a slightly different speed. constant speed. As he calculated, the average speed was 12 km/h.
.III.2. Half the time spent on the road, the car was traveling at a speed of 60 km/h, and the second half of the time at a speed of 46 km/h. Find the average speed of the car along the entire journey.
III.3. On the way from one village to another, the car walked for some time at a speed of 60 km/h, then for exactly the same time at a speed of 40 km/h, then for exactly the same time at a speed equal to the average speed on the first two sections of the journey . What is the average speed of travel along the entire route from one village to another?
III.4. A cyclist travels from home to work at an average speed of 10 km/h, and back at an average speed of 15 km/h, since the road goes slightly downhill. Find the average speed of the cyclist all the way from home to work and back.
III.5. A car traveled from point A to point B empty at a constant speed, and returned along the same road with a load at a speed of 60 km/h. At what speed was he driving empty if the average speed was 70 km/h?
III.6. The car drove for the first 100 km at a speed of 50 km/h, for the next 120 km at a speed of 90 km/h, and then for 120 km at a speed of 100 km/h. Find the average speed of the car along the entire journey.
III.7. The car drove for the first 100 km at a speed of 50 km/h, the next 140 km at a speed of 80 km/h, and then 150 km at a speed of 120 km/h. Find the average speed of the car along the entire journey.
III.8. The car drove for the first 150 km at a speed of 50 km/h, the next 130 km at a speed of 60 km/h, and then 120 km at a speed of 80 km/h. Find the average speed of the car along the entire journey.
III. 9. The car drove for the first 140 km at a speed of 70 km/h, the next 120 km at a speed of 80 km/h, and then 180 km at a speed of 120 km/h. Find the average speed of the car along the entire journey.