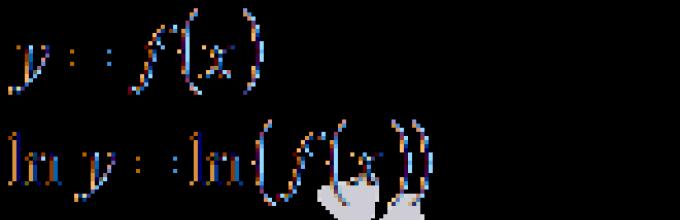Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.
Collection and use of personal information
Personal information refers to data that can be used to identify or contact a specific person.
You may be asked to provide your personal information at any time when you contact us.
Below are some examples of the types of personal information we may collect and how we may use such information.
What personal information do we collect:
- When you submit an application on the site, we may collect various information, including your name, telephone number, address email etc.
How we use your personal information:
- Collected by us personal information allows us to contact you and inform you about unique offers, promotions and other events and upcoming events.
- From time to time, we may use your personal information to send important notices and communications.
- We may also use personal information for internal purposes such as auditing, data analysis and various studies in order to improve the services we provide and provide you with recommendations regarding our services.
- If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.
Disclosure of information to third parties
We do not disclose the information received from you to third parties.
Exceptions:
- If necessary - in accordance with the law, judicial procedure, legal proceedings, and/or based on public requests or requests from government agencies on the territory of the Russian Federation - disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
- In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.
Protection of personal information
We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.
Respecting your privacy at the company level
To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.
Let
(1)
is a differentiable function of the variable x. First we'll look at it for the set of values of x for which y takes positive values: . In the following we will show that all the results obtained are also applicable for negative values of .
In some cases, in order to find the derivative of function (1), it is convenient to pre-logarithm it
,
and then calculate the derivative. Then, according to the rule of differentiation of a complex function,
.
From here
(2)
.
The derivative of the logarithm of a function is called the logarithmic derivative:
.
Logarithmic derivative of the function y = f(x) is a derivative natural logarithm this function: (ln f(x))′.
The case of negative y values
Now consider the case when a variable can take both positive and negative values. In this case, take the logarithm of the modulus and find its derivative:
.
From here
(3)
.
That is, in the general case, you need to find the derivative of the logarithm of the modulus of the function.
Comparing (2) and (3) we have:
.
That is, the formal result of calculating the logarithmic derivative does not depend on whether we took the modulo or not. Therefore, when calculating the logarithmic derivative, we do not have to worry about what sign the function has.
This situation can be clarified using complex numbers. Let, for some values of x, be negative: . If we only consider real numbers, then the function is not defined. However, if we introduce into consideration complex numbers, then we get the following:
.
That is, the functions and differ by a complex constant:
.
Since the derivative of a constant is zero, then
.
Property of the logarithmic derivative
From such a consideration it follows that the logarithmic derivative will not change if you multiply the function by an arbitrary constant :
.
Indeed, using properties of logarithm, formulas derivative sum And derivative of a constant, we have:
.
Application of logarithmic derivative
It is convenient to use the logarithmic derivative in cases where the original function consists of a product of power or exponential functions. In this case, the logarithm operation turns the product of functions into their sum. This simplifies the calculation of the derivative.
Example 1
Find the derivative of the function:
.
Solution
Let's logarithm the original function:
.
Let's differentiate with respect to the variable x.
In the table of derivatives we find:
.
We apply the rule of differentiation of complex functions.
;
;
;
;
(A1.1) .
Multiply by:
.
So, we found the logarithmic derivative:
.
From here we find the derivative of the original function:
.
Note
If we want to use only real numbers, then we should take the logarithm of the modulus of the original function:
.
Then
;
.
And we got formula (A1.1). Therefore the result has not changed.
Answer
Example 2
Using the logarithmic derivative, find the derivative of the function
.
Solution
Let's take logarithms:
(A2.1) .
Differentiate with respect to the variable x:
;
;
;
;
;
.
Multiply by:
.
From here we get the logarithmic derivative:
.
Derivative of the original function:
.
Note
Here the original function is non-negative: . It is defined at . If we do not assume that the logarithm can be defined for negative values of the argument, then formula (A2.1) should be written as follows:
.
Because
And
,
this will not affect the final result.
Answer
Example 3
Find the derivative
.
Solution
We perform differentiation using the logarithmic derivative. Let's take a logarithm, taking into account that:
(A3.1) .
By differentiating, we obtain the logarithmic derivative.
;
;
;
(A3.2) .
Since then
.
Note
Let us carry out the calculations without the assumption that the logarithm can be defined for negative values of the argument. To do this, take the logarithm of the modulus of the original function:
.
Then instead of (A3.1) we have:
;
.
Comparing with (A3.2) we see that the result has not changed.
When differentiating, it is indicative power function or cumbersome fractional expressions, it is convenient to use the logarithmic derivative. In this article we will look at examples of its application with detailed solutions.
Further presentation assumes the ability to use the table of derivatives, differentiation rules and knowledge of the formula for the derivative of a complex function.
Derivation of the formula for the logarithmic derivative.
First, we take logarithms to the base e, simplify the form of the function using the properties of the logarithm, and then find the derivative of the implicitly specified function: 
For example, let's find the derivative of an exponential power function x to the power x.
Taking logarithms gives . According to the properties of the logarithm. Differentiating both sides of the equality leads to the result: 
Answer: 
.
The same example can be solved without using the logarithmic derivative. You can carry out some transformations and move from differentiating an exponential power function to finding the derivative of a complex function: 
Example.
Find the derivative of a function 
.
Solution.
In this example the function 
is a fraction and its derivative can be found using the rules of differentiation. But due to the cumbersomeness of the expression, this will require many transformations. In such cases, it is more reasonable to use the logarithmic derivative formula 
. Why? You will understand now.
Let's find it first. In transformations we will use the properties of the logarithm (the logarithm of a fraction is equal to the difference of logarithms, and the logarithm of a product is equal to the sum of logarithms, and the degree of the expression under the logarithm sign can be taken out as a coefficient in front of the logarithm): 
These transformations have led us to quite simple expression, the derivative of which can easily be found: 
We substitute the result obtained into the formula for the logarithmic derivative and get the answer:
To consolidate the material, we will give a couple more examples without detailed explanations.
Example.
Find the derivative of an exponential power function 
Do you feel like there is still a lot of time before the exam? Is this a month? Two? Year? Practice shows that a student copes best with an exam if he begins to prepare for it in advance. There are a lot of difficult tasks, which stand in the way of schoolchildren and future applicants to the highest scores. You need to learn to overcome these obstacles, and besides, it’s not difficult to do. You need to understand the principle of working with various tasks from tickets. Then there will be no problems with the new ones.
Logarithms at first glance seem incredibly complex, but with a detailed analysis the situation becomes much simpler. If you want to take the Unified State Exam highest score, you should understand the concept in question, which is what we propose to do in this article.
First, let's separate these definitions. What is a logarithm (log)? This is an indicator of the power to which the base must be raised to obtain the specified number. If it’s not clear, let’s look at an elementary example.
In this case, the base at the bottom must be raised to the second power to get the number 4.
Now let's look at the second concept. The derivative of a function in any form is a concept that characterizes the change of a function at a given point. However, this school curriculum, and if you have problems with these concepts individually, it is worth repeating the topic.
Derivative of logarithm
IN Unified State Exam assignments On this topic, several problems can be given as examples. To begin with, the simplest logarithmic derivative. It is necessary to find the derivative of the following function.
We need to find the next derivative
There is a special formula.
In this case x=u, log3x=v. We substitute the values from our function into the formula.
The derivative of x will be equal to one. The logarithm is a little more difficult. But you will understand the principle if you simply substitute the values. Recall that the derivative of lg x is the derivative decimal logarithm, and the derivative ln x is the derivative of the natural logarithm (to base e).
Now just plug the resulting values into the formula. Try it yourself, then we’ll check the answer.
What could be the problem here for some? We introduced the concept of natural logarithm. Let's talk about it, and at the same time figure out how to solve problems with it. You won’t see anything complicated, especially when you understand the principle of its operation. You should get used to it, since it is often used in mathematics (in higher educational institutions especially).
Derivative of the natural logarithm
At its core, it is the derivative of the logarithm to base e (this is irrational number, which is approximately 2.7). In fact, ln is very simple, so it is often used in mathematics in general. Actually, solving the problem with it will not be a problem either. It is worth remembering that the derivative of the natural logarithm to the base e will be equal to one divided by x. The solution to the following example will be the most revealing.
Let's imagine it as complex function, consisting of two simple ones.
It is enough to convert
We are looking for the derivative of u with respect to x
