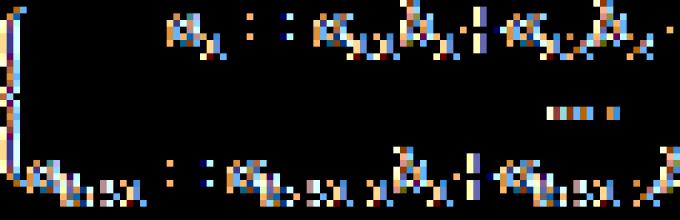Lemma 1 : If in a matrix of size n n at least one row (column) is zero, then the rows (columns) of the matrix are linearly dependent.

Proof: Let the first line be zero, then

Where a 1 0. That's what was required.

Definition: A matrix whose elements located below the main diagonal are equal to zero is called triangular:

and ij = 0, i>j.

Lemma 2: The determinant of a triangular matrix is ​​equal to the product of the elements of the main diagonal.

The proof is easy to carry out by induction on the dimension of the matrix.

Theorem O linear independence vectors.

A)Necessity: linearly dependent D=0 .

Proof: Let them be linearly dependent, j=,

that is, there are a j , not all equal to zero, j= , What a 1 A 1 + a 2 A 2 + ... a n A n = , A j – matrix columns A. Let, for example, a n¹0.

We have a j * = a j / a n , j£ n-1a 1 * A 1 + a 2 * A 2 + ... a n -1 * A n -1 + A n = .

Let's replace the last column of the matrix A on

A n * = a 1 * A 1 + a 2 * A 2 + ... a n -1 A n -1 + A n = .

According to the above-proven property of the determinant (it will not change if another column multiplied by a number is added to any column in the matrix), the determinant of the new matrix is ​​equal to the determinant of the original one. But in the new matrix one column is zero, which means that, expanding the determinant over this column, we get D=0, Q.E.D.

b)Adequacy: Size matrix n nwith linearly independent rows can always be reduced to a triangular form using transformations that do not change absolute value determinant. Moreover, from the independence of the rows of the original matrix, it follows that its determinant is equal to zero.

1. If in the size matrix n n with linearly independent rows element a 11 is equal to zero, then the column whose element a 1 j ¹ 0. According to Lemma 1, such an element exists. The determinant of the transformed matrix may differ from the determinant of the original matrix only in sign.

2. From lines with numbers i>1 subtract the first line multiplied by the fraction a i 1 /a 11. Moreover, in the first column of rows with numbers i>1 will result in zero elements.

3. Let's start calculating the determinant of the resulting matrix by decomposing over the first column. Since all elements in it except the first are equal to zero,

D new = a 11 new (-1) 1+1 D 11 new,

Where d 11 new is the determinant of a matrix of smaller size.

Next, to calculate the determinant D 11 repeat steps 1, 2, 3 until the last determinant turns out to be the determinant of the size matrix 1 1. Since step 1 only changes the sign of the determinant of the matrix being transformed, and step 2 does not change the value of the determinant at all, then, up to the sign, we will ultimately obtain the determinant of the original matrix. In this case, since due to the linear independence of the rows of the original matrix, step 1 is always satisfied, all elements of the main diagonal will turn out to be unequal to zero. Thus, the final determinant, according to the described algorithm, is equal to the product of non-zero elements located on the main diagonal. Therefore, the determinant of the original matrix is ​​not equal to zero. Q.E.D.

Appendix 2

The following give several criteria for linear dependence and, accordingly, linear independence of vector systems.

Theorem. (Necessary and sufficient condition for linear dependence of vectors.)

A system of vectors is dependent if and only if one of the vectors of the system is linearly expressed through the others of this system.

Proof. Necessity. Let the system be linearly dependent. Then, by definition, it represents the zero vector non-trivially, i.e. there is a non-trivial combination of this system of vectors equal to the zero vector:

where at least one of the coefficients of this linear combination is not equal to zero. Let , .

Let's divide both sides of the previous equality by this non-zero coefficient (i.e. multiply by:

Let's denote: , where .

those. one of the vectors of the system is linearly expressed through the others of this system, etc.

Adequacy. Let one of the vectors of the system be linearly expressed through other vectors of this system:

Let's move the vector to the right of this equality:

Since the coefficient of the vector is equal to , then we have a nontrivial representation of zero by a system of vectors, which means that this system of vectors is linearly dependent, etc.

The theorem has been proven.

Consequence.

1. Vector system vector space is linearly independent if and only if none of the vectors of the system is linearly expressed in terms of other vectors of this system.

2. A system of vectors containing a zero vector or two equal vectors is linearly dependent.

Proof.

1) Necessity. Let the system be linearly independent. Let us assume the opposite and there is a vector of the system that is linearly expressed through other vectors of this system. Then, according to the theorem, the system is linearly dependent and we arrive at a contradiction.

Adequacy. Let none of the vectors of the system be expressed in terms of the others. Let's assume the opposite. Let the system be linearly dependent, but then it follows from the theorem that there is a vector of the system that is linearly expressed through other vectors of this system, and we again come to a contradiction.

2a) Let the system contain a zero vector. Let us assume for definiteness that the vector :. Then the equality is obvious

those. one of the vectors of the system is linearly expressed through the other vectors of this system. It follows from the theorem that such a system of vectors is linearly dependent, etc.

Note that this fact can be proven directly from a linearly dependent system of vectors.

Since , the following equality is obvious

This is a non-trivial representation of the zero vector, which means the system is linearly dependent.

2b) Let the system have two equal vectors. Let for . Then the equality is obvious

Those. the first vector is linearly expressed through the remaining vectors of the same system. It follows from the theorem that this system linearly dependent, etc.

Similar to the previous one, this statement can be proven directly by the definition of a linearly dependent system. Then this system represents the zero vector non-trivially

whence follows the linear dependence of the system.

The theorem has been proven.

Consequence. A system consisting of one vector is linearly independent if and only if this vector is nonzero.

Def. The set w is called a linear space, and its element. -vectors if:

*law is specified (+) according to cat. any two elements x, y from w are associated with an element called. their sum [x + y]

*a law is given (* for the number a), according to the cat element x from w and a, an element from w is compared, called the product of x and a [ax];

* completed

the following requirements (or axioms):

Trace c1. zero vector (ctv 0 1 and 0 2. by a3: 0 2 + 0 1 = 0 2 and 0 1 + 0 2 = 0 1. by a1 0 1 + 0 2 = 0 2 + 0 1 => 0 1 = 0 2.)

c2.

.(ctv, a4)

c3. 0 vect.(a7)

c4. a(number)*0=0.(a6,c3)

c5.

x (*) -1 =0 vector, opposite to x, i.e. (-1)x = -x. (a5,a6) c6. In w, the subtraction action is defined: the vector x is called the difference of vectors b and a, if x + a = b, and is denoted x = b - a. Number n called dimension lin. pr-a dimension L c6. In w, the subtraction action is defined: the vector x is called the difference of vectors b and a, if x + a = b, and is denoted x = b - a., if in c6. In w, the subtraction action is defined: the vector x is called the difference of vectors b and a, if x + a = b, and is denoted x = b - a. there is a system of dimension= c6. In w, the subtraction action is defined: the vector x is called the difference of vectors b and a, if x + a = b, and is denoted x = b - a. lin. nezav. vectors, and any system of dimension +1 vector - lin. dependent dim

. Space called n-dimensional.

An ordered collection of n lines. nezav. vectors n dimensional independent. space –

Let (1) be the basis of an n-dimensional linear. pr-va V, i.e. a collection of linearly independent vectors. The set of vectors will be linear. dependent, because their n+ 1.

Those. there are numbers that are not all equal to zero at the same time, what does that have to do with it (otherwise (1) are linearly dependent).

Then where is the vector decomposition x by basis(1) .

This expression is unique, because if another expression exists (**)

subtracting equality (**) from (*),

we get

Because

are linearly independent, then . Chtd

Theorem. If - lin. independent vectors of the space V and each vector x from V can be represented through , then these vectors form a basis of V

Doc: (1)-lin.independent =>the document remains that is linear-independent. According to the convention Each vector a is expressed through (1): , consider , rang≤n => among the columns no more than n are linearly independent, but m > n=> m columns are linearly dependent => s=1, n

That is, the vectors are linear dependent

№4Thus, the space V is n-dimensional and (1) its basis Def.

Subset L lin. production V is called lin. cond. of this space if, with respect to the operations (+) and (*a) specified in V, the subspace L is a linear space

Theorem The set l of vectors of space V is linear. A subspace of this space performs

(advance) let (1) and (2) be satisfied, in order for L to be a subsimple.V it remains to prove that all the axioms of lin are satisfied. pr-va. (-x): -x+x=0 d

. a(x + y) = ax + ay;

(a-b) and (e-h) follows from the validity of V; let us prove (c)

Thus, the space V is n-dimensional and (1) its basis(necessity) Let L be lin. subspace of this space, then (1) and (2) are satisfied by virtue of the definition of lines. pr-va

Theorem A collection of all kinds of lines. combinations of some elements (x j) line. the product is called a linear shell an arbitrary set of all lines. combinations of vectors V with real. coefficient is lin. subpr V (linear shell )

given system of vectors lin. pr. is the linear subpr of this pr. ODA

.Non-empty subset of L line vectors. production V is called lin. subspace if:

a) the sum of any vectors from L belongs to L

b) the product of each vector from L by any number belongs to LdimensionSum of two subspacesdimension

is again a subspace<=>1) Let y 1 +y 2 (L 1 +L 2)

y 1 =x 1 +x 2, y 2 =x’ 1 +x’ 2, where (x 1,x’ 1) L 1, (x 2,x’ 2) L 2. y 1 +y 2 =(x 1 +x 2)+(x' 1 +x' 2)=(x 1 +x' 1)+(x 2 +x' 2), where (x 1 +x' 1 ) L 1 , (x 2 +x' 2) L 2 => the first condition of a linear subspace is satisfied.

ay 1 =ax 1 +ax 2, where (ax 1) L 1, (ax 2) L 2 => because (y 1 +y 2) (L 1 +L 2) , (ly 1) (L 1 +L 2) => conditions are met => L 1 +L 2 is a linear subspace.dimension 1 The intersection of two subdivisionsdimension 2 lin. pr-vadimension is also a subsp. this space.

Consider two arbitrary vectors x,y, belonging to the intersection of subspaces, and two arbitrary numbers a,b:.

According to def. intersections of sets:

=> by definition of a subspace of a linear space:,.

T.K. vector ax + by belongs to many dimension 1, and many dimension 2, then it belongs, by definition, to the intersection of these sets. Thus:

given system of vectors lin. pr. is the linear subpr of this pr..They say that V is the direct sum of its subdivisions. if and b) this decomposition is unique

b") Let us show that b) is equivalent to b’)

When b) is true b’)

All sorts of (M, N) from intersect only along the zero vector

Let ∃ z ∈

Fair returndimension=

contradiction

Theorem To (*) is necessary and sufficient for the union of bases ( formed the basis of space

(Required) let (*) and vectors be bases of subsets. and there is an expansion in ;

(x is expanded over the basis L, in order to assert that ( constitute a basis, it is necessary to prove their linear independence; they all contain 0 0=0+...+0. Due to the uniqueness of the expansion of 0 over : => due to the linear independence of the basis => ( – basis Ext.)

Let ( forms the basis of L unique decomposition (**) at least one decomposition exists. By uniqueness (*) => uniqueness (**)

Comment. The dimension of the direct sum is equal to the sum of the dimensions of the subspace

Any non-singular quadratic matrix can serve as a transition matrix from one basis to another Let in n dimensional linear space

V there are two bases and

(1) =A, where the elements * and ** are not numbers, but we will extend certain operations on a numeric matrix to such rows.

Because otherwise the vectors ** would be linear dependent Back.

If then the columns of A are linearly independent =>form a basis The intersection of two subdivisions Coordinates related by relation , Where

transition matrix elements

Let the decomposition of the elements of the “new” basis into the “old” one be known

Then the equalities are true

But if a linear combination of linearly independent elements is equal to 0 then =>

Basic Linear Dependence Theorem If (*) is linearly expressed throughc6. In w, the subtraction action is defined: the vector x is called the difference of vectors b and a, if x + a = b, and is denoted x = b - a.<= (**) That

m

Let us prove by induction on m

m=1: system (*) contains 0 and lin. manager - impossible

let it be true for m=k-1

let's prove for m=k It may turn out that 1) , i.e. v-ry (1) are lin.comb. lin. in-ditch (2)System (1) linear undependable, because is part of lin.nezav. systems (*). Because in system (2) there are only k-1 vectors, then by the induction hypothesis we obtain k+1

3.3. Linear independence of vectors. Basis. Linear combination

vector systems

called a vector where a 1, a 2, ..., a n

- arbitrary numbers. = 0, then the linear combination is called trivial . In this case, obviously

Definition 5.

If for a system of vectors there is a non-trivial linear combination (at least one ai¹ 0) equal to the zero vector: then the system of vectors is called linear dependent. If equality (1) is possible only in the case when all a i =0, then the system of vectors is called linear independent .

Theorem 2 (Conditions of linear dependence).

Definition 6.

From Theorem 3 it follows that if a basis is given in space, then by adding an arbitrary vector to it, we obtain a linearly dependent system of vectors. In accordance with Theorem 2 (1) , one of them (it can be shown that the vector) can be represented as a linear combination of the others:

.

Definition 7.

Numbers are called coordinates vectors in the basis (denoted

If the vectors are considered on the plane, then the basis will be an ordered pair of non-collinear vectors

and the coordinates of the vector in this basis are a pair of numbers:

Note 3. It can be shown that for a given basis, the coordinates of the vector are determined uniquely . From this, in particular, it follows that if the vectors are equal, then their corresponding coordinates are equal, and vice versa .

Thus, if a basis is given in a space, then each vector of the space corresponds to an ordered triple of numbers (coordinates of the vector in this basis) and vice versa: each triple of numbers corresponds to a vector.

On the plane, a similar correspondence is established between vectors and pairs of numbers.

Theorem 4 (Linear operations through vector coordinates).

If in some basis And a is an arbitrary number, then in this basis

In other words:

When a vector is multiplied by a number, its coordinates are multiplied by that number ;

when adding vectors, their corresponding coordinates are added .

Example 1 . In some basis the vectorshave coordinates

Show that the vectors form a basis and find the coordinates of the vector in this basis.

Vectors form a basis if they are non-coplanar, therefore (in accordance with by Theorem 3(2) ) are linearly independent.

By definition 5 this means that equality

only possible ifx = y = z = 0.

The functions are called linearly independent, If

(only a trivial linear combination of functions that is identically equal to zero is allowed). In contrast to the linear independence of vectors, here the linear combination is identical to zero, and not equality. This is understandable, since the equality of a linear combination to zero must be satisfied for any value of the argument.

The functions are called linearly dependent, if there is a non-zero set of constants (not all constants are equal to zero) such that (there is a non-trivial linear combination of functions identically equal to zero).

Theorem.In order for functions to be linearly dependent, it is necessary and sufficient that any of them is linearly expressed through the others (represented as their linear combination).

Prove this theorem yourself; it is proven in the same way as a similar theorem about the linear dependence of vectors.

Vronsky's determinant.

The Wronski determinant for functions is introduced as a determinant whose columns are the derivatives of these functions from zero (the functions themselves) to the n-1st order.

.

Theorem. If the functions are linearly dependent, then

Proof. Since the functions are linearly dependent, then any of them is linearly expressed through the others, for example,

The identity can be differentiated, so

Then the first column of the Wronski determinant is linearly expressed through the remaining columns, so the Wronski determinant is identically equal to zero.

Theorem.In order for the solutions of a linear homogeneous differential equation of the nth order to be linearly dependent, it is necessary and sufficient that.

Proof. Necessity follows from the previous theorem.

Adequacy. Let's fix some point. Since , the columns of the determinant calculated at this point are linearly dependent vectors.

, that the relations are satisfied

Since a linear combination of solutions to a linear homogeneous equation is its solution, we can introduce a solution of the form

A linear combination of solutions with the same coefficients.

Note that this solution satisfies zero initial conditions; this follows from the system of equations written above. But the trivial solution of a linear homogeneous equation also satisfies the same zero initial conditions. Therefore, from Cauchy’s theorem it follows that the introduced solution is identically equal to the trivial one, therefore,

therefore the solutions are linearly dependent.

Consequence.If the Wronski determinant, built on solutions of a linear homogeneous equation, vanishes at least at one point, then it is identically equal to zero.

Proof. If , then the solutions are linearly dependent, therefore, .

Theorem.1. For linear dependence of solutions it is necessary and sufficient(or ).

2. For linear independence of solutions it is necessary and sufficient.

Proof. The first statement follows from the theorem and corollary proved above. The second statement can be easily proven by contradiction.

Let the solutions be linearly independent. If , then the solutions are linearly dependent. Contradiction. Hence, .

Let . If the solutions are linearly dependent, then , hence, a contradiction. Therefore, the solutions are linearly independent.

Consequence.The vanishing of the Wronski determinant at least at one point is a criterion for the linear dependence of solutions to a linear homogeneous equation.

The difference between the Wronski determinant and zero is a criterion for the linear independence of solutions to a linear homogeneous equation.

Theorem.The dimension of the space of solutions to a linear homogeneous equation of the nth order is equal to n.

Proof.

a) Let us show that there exist n linearly independent solutions to a linear homogeneous differential equation of the nth order. Let's consider solutions , satisfying the following initial conditions:

...........................................................

Such solutions exist. Indeed, according to Cauchy’s theorem, through the point passes through a single integral curve—the solution. Through the point the solution passes through the point

- solution, through a point - solution .

These solutions are linearly independent, since .

b) Let us show that any solution to a linear homogeneous equation is linearly expressed through these solutions (is their linear combination).

Let's consider two solutions. One - an arbitrary solution with initial conditions . Fair ratio