Dok sam bio u školi, naš profesor fizike, po imenu Bader, jednom me pozvao poslije nastave i rekao: “Izgledaš kao da si užasno umoran od svega; poslušajte jednu zanimljivu stvar.” I rekao mi je nešto što sam smatrao doista fascinantnim. Čak i sada, iako je od tada prošlo dosta vremena, nastavlja me fascinirati. I svaki put kad se sjetim što sam rekao, vratim se na posao. I ovaj put, pripremajući se za predavanje, opet sam se zatekla kako analiziram iste stvari. I, umjesto pripreme za predavanje, prihvatio sam se novog problema. Tema o kojoj govorim je princip najmanjeg djelovanja.


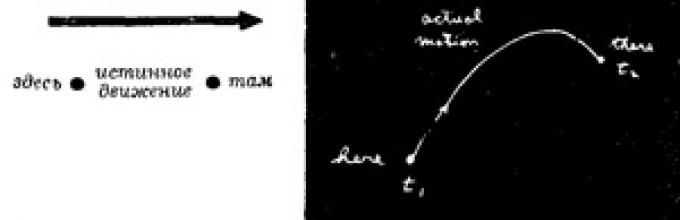
“Ovo mi je tada rekao moj učitelj Bader: “Neka, na primjer, imate česticu u gravitacijskom polju; ova se čestica, izašavši odnekud, slobodno kreće negdje drugdje u drugu točku. Bacio si ga, recimo, uvis, a on je odletio i pao.

Trebalo joj je neko vrijeme da putuje od startnog mjesta do konačnog mjesta. Sada pokušajte s nekim drugim pokretom. Neka se kreće "odavde odavde" ne više kao prije, nego ovako:

Ali ipak sam se našao na pravom mjestu u istom trenutku kao i prije.”

“I tako,” nastavio je učitelj, “ako izračunate kinetičku energiju u svakom trenutku duž putanje čestice, oduzmete potencijalnu energiju od nje i integrirate razliku kroz cijelo vrijeme kada se kretanje dogodilo, vidjet ćete da će broj koji dobijete biti više, nego za pravo gibanje čestica.

Drugim riječima, Newtonovi zakoni se ne mogu formulirati kao F=ma, već na sljedeći način: prosječna kinetička energija minus prosječna potencijalna energija doseže svoju najnižu vrijednost duž putanje kojom se tijelo zapravo kreće s jednog mjesta na drugo.

Pokušat ću vam ovo malo jasnije objasniti.
Ako uzmemo gravitacijsko polje i označimo putanju čestice x(t), Gdje x- visina iznad tla (za sada se snađimo s jednom dimenzijom; putanja neka ide samo gore-dolje, a ne u stranu), tada će kinetička energija biti g 2 m(dx/ dt) 2 , a potencijalna energija u proizvoljnom trenutku vremena bit će jednaka mgx.


Sada, za neki trenutak kretanja duž putanje, uzimam razliku između kinetičke i potencijalne energije i integriram kroz cijelo vrijeme od početka do kraja. Neka u početnom trenutku vremena t x kretanje je počelo na nekoj visini i završilo u trenutku t 2 na drugoj određenoj visini.

Tada je integral jednak ∫ t2 t1 dt

Istinsko gibanje događa se duž određene krivulje (u funkciji vremena to je parabola) i dovodi do određene integralne vrijednosti. Ali možeš prijestaviti zamislite neko drugo kretanje: prvo nagli porast, a zatim neke bizarne fluktuacije.

Možete izračunati razliku između potencijalne i kinetičke energije na ovoj stazi... ili na bilo kojoj drugoj. A najnevjerojatnije je da je pravi put onaj na kojem je taj integral najmanji.
Idemo to provjeriti. Prvo, pogledajmo ovaj slučaj: slobodna čestica uopće nema potencijalnu energiju. Tada pravilo kaže da pri prelasku iz jedne točke u drugu u određenom vremenu integral kinetičke energije treba biti najmanji. To znači da se čestica mora gibati jednoliko. (I to je točno, ti i ja znamo da je brzina u takvom kretanju konstantna.) Zašto ravnomjerno? Hajdemo shvatiti. Da je drugačije, ponekad bi brzina čestice bila veća od prosjeka, a ponekad bi bila ispod prosjeka, a prosječna brzina bi bila ista, jer bi čestica morala doći “odavde dovde” u dogovoreno vrijeme. Na primjer, ako trebate automobilom stići od kuće do škole u određeno vrijeme, onda to možete učiniti na različite načine: možete u početku voziti kao ludi, a na kraju usporiti, ili voziti istom brzinom, ili čak možete prijeći na suprotnu stranu, pa tek onda skrenuti prema školi itd. U svim slučajevima prosječna brzina bi, naravno, trebala biti ista - kvocijent udaljenosti od kuće do škole podijeljen s vremenom. Ali čak i pri ovoj prosječnoj brzini, ponekad ste se kretali prebrzo, a ponekad presporo. I prosječan kvadrat nešto što odstupa od prosjeka je, kao što znamo, uvijek veće od kvadrata prosjeka; To znači da će integral kinetičke energije pri fluktuacijama brzine gibanja uvijek biti veći nego pri kretanju konstantnom brzinom. Vidite da će integral doseći minimum kada je brzina konstantna (u nedostatku sila). Pravi način je ovaj.

Predmet bačen uvis u polje gravitacije diže se prvo brzo, a zatim sve sporije. To se događa jer ima i potencijalnu energiju, a njezina minimalna vrijednost trebala bi doseći jednomnost između kinetičke i potencijalne energije.. Budući da potencijalna energija raste kako se dižete, onda manje razlika Uspjet će ako što je brže moguće dosegnete one visine gdje je potencijalna energija visoka. Zatim, oduzimanjem ovog visokog potencijala od kinetičke energije, postižemo smanjenje prosjeka. Dakle, put koji ide gore i daje dobar negativni dio nauštrb potencijalne energije je isplativiji.

To je sve što mi je moj učitelj rekao, jer on je bio jako dobar učitelj i znao je kada je vrijeme da prestane. Ja sam, nažalost, nisam takav. Teško mi je stati na vrijeme. I tako, umjesto da samo potaknem vaše zanimanje svojom pričom, želim vas zastrašiti, želim vam se smučiti od složenosti života - pokušat ću dokazati ono o čemu sam vam govorio. Matematički problem koji ćemo riješiti vrlo je težak i jedinstven. Postoji određena količina S, nazvao akcijski. Jednaka je kinetičkoj energiji umanjenoj za potencijalnu energiju integriranu tijekom vremena:

Ali s druge strane, ne možete se kretati prebrzo ili ići previsoko, jer bi to zahtijevalo previše kinetičke energije. Morate se kretati dovoljno brzo da biste se popeli i spustili unutar vremena koje vam je na raspolaganju. Dakle, ne pokušavajte letjeti previsoko, već samo dosegnite neku razumnu razinu. Kao rezultat toga, ispada da je rješenje neka vrsta ravnoteže između želje da se dobije što više potencijalne energije i želje da se količina kinetičke energije smanji što je više moguće - to je želja da se postigne maksimalno smanjenje u razlici između kinetičke i potencijalne energije.”

Ne zaboravite da p.e. i k.e.-obje funkcije vremena. Za svaki novi zamislivi put, ova radnja poprima svoje specifično značenje. Matematički problem je odrediti koja krivulja ima taj broj manji od ostalih.

Kažete: “Oh, ovo je samo jednostavan primjer maksimuma i minimuma. Moramo izračunati akciju, razlikovati je i pronaći minimum.”

Ali čekaj. Obično imamo funkciju neke varijable i trebamo pronaći vrijednost varijabla, pri čemu funkcija postaje najmanja ili najveća. Recimo da je u sredini grijana šipka. Po njemu se širi toplina i na svakoj točki štapa se uspostavlja vlastita temperatura. Morate pronaći točku gdje je najviši. Ali mi govorimo o nečem sasvim drugom - svaki put u prostoru odgovara na njegov broj, i trebao bi pronaći taj staza, za koje je ovaj broj minimalan. Ovo je sasvim drugo područje matematike. Ovo nije obična računica, već varijacijski(tako ga zovu).

Ovo područje matematike ima mnogo svojih problema. Recimo, kružnica se obično definira kao geometrijsko mjesto točaka čije su udaljenosti od dane točke iste, ali se kružnica može definirati drugačije: ona je jedna od krivulja dana duljina, koja obuhvaća najveću površinu. Bilo koja druga krivulja istog opsega obuhvaća površinu manju od kruga. Dakle, ako postavimo zadatak: pronaći krivulju zadanog opsega koja omeđuje najveće područje, tada ćemo imati problem iz varijacijskog računa, a ne iz računa na koji ste navikli.

Dakle, želimo uzeti integral preko puta koji je prešlo tijelo. Učinimo to ovako. Cijela poanta je zamisliti da postoji pravi put i da bilo koja druga krivulja koju nacrtamo nije pravi put, tako da ako izračunamo akciju za nju, dobit ćemo broj veći od onoga što smo dobili za akciju koja odgovara na pravi način.

Dakle, zadatak je pronaći pravi put. Gdje leži? Jedan od načina bi, naravno, bio brojanje akcije za milijune i milijune staza i zatim vidjeti koja staza ima najmanju akciju. Ovo je put u kojem je akcija minimalna i bit će stvarna.

Ova metoda je sasvim moguća. Međutim, može se učiniti jednostavnije. Ako postoji veličina koja ima minimum (od običnih funkcija, recimo temperatura), tada je jedno od svojstava minimuma da kada se od njega udalji na udaljenost prvi reda malenosti, funkcija odstupa od minimalne vrijednosti samo za iznos drugi narudžba. I na bilo kojem drugom mjestu na krivulji, pomak za malu udaljenost mijenja vrijednost funkcije također za vrijednost prvog reda malenosti. Ali barem mala odstupanja u stranu ne dovode do promjene funkcije kao prve aproksimacije.

To je svojstvo koje ćemo koristiti za izračunavanje pravog puta.

Ako je putanja točna, tada krivulja malo drugačija od nje neće dovesti, kao prvu aproksimaciju, do promjene u veličini djelovanja. Sve promjene, ako je to doista minimum, pojavit će se tek u drugoj aproksimaciji.

To je lako dokazati. Ako uz neko odstupanje od krivulje dođe do promjena u prvom redu, tada su te promjene na snazi proporcionalan odstupanje. Oni će vjerojatno povećati učinak; inače ne bi bio minimum. Ali jednom promjene proporcionalan odstupanje, tada će promjena predznaka odstupanja smanjiti učinak. Ispada da kada se skrene u jednom smjeru, učinak se povećava, a kada se skrene u suprotnom smjeru, smanjuje se. Jedina mogućnost da to doista bude minimum je da se, u prvoj aproksimaciji, ne događaju nikakve promjene i da su promjene proporcionalne kvadratu odstupanja od realne putanje.

Dakle, ići ćemo sljedećim putem: označiti sa x(t) (s crtom ispod) pravi put je onaj koji želimo pronaći. Idemo probno x(t), razlikuje se od željenog za mali iznos, što označavamo η (t).

Ideja je da ako računamo akciju S na putu x(t), onda razlika između ovoga S i radnjom koju smo izračunali za put x(t) (radi jednostavnosti bit će označeno S), ili razlika između S_ I S, trebala bi biti prva aproksimacija η nula. Mogu se razlikovati u drugom redu, ali u prvom razlika mora biti nula.

I to se mora poštovati za sve η . Međutim, ne baš za svakoga. Metoda zahtijeva uzimanje u obzir samo onih staza koje počinju i završavaju u istom paru točaka, tj. svaka staza mora započeti u određenoj točki u trenutku t 1 i završiti na drugoj određenoj točki u ovom trenutku t 2 . Ove točke i trenuci se bilježe. Dakle, naša funkcija d) (odstupanje) mora biti nula na oba kraja: η (t 1 )= 0 I η (t 2)=0. Pod ovim uvjetom naš matematički problem postaje potpuno definiran.

Ako niste poznavali račun, mogli biste učiniti istu stvar da pronađete minimum obične funkcije f(x). Biste li razmislili što bi se dogodilo da uzmete f(x) i dodati u x mala količina h, i tvrdio bi da je amandman na f(x) u prvom redu h mora biti minimalno jednak nuli. Hoćeš li mi smjestiti x+h umjesto x i proširio bi j(x+h) do prve potencije h. . ., jednom riječju, ponovio bi sve ono s čime namjeravamo η .

Ako sada ovo pažljivo pogledamo, vidjet ćemo da prva dva pojma ovdje napisana odgovaraju toj radnji S, koju bih napisao za traženi pravi put X.Želim usmjeriti vašu pozornost na promjenu. S, tj. na razlici između S i tako S_, što bi rezultiralo za pravi put. Ovu razliku ćemo napisati kao bS i nazovimo to varijacijom S. Odbacujući “drugi i viši red”, dobivamo za σS

Sada zadatak izgleda ovako. Ovdje preda mnom je neki integral. Još ne znam kako je, ali znam sigurno da, što η Bez obzira na sve, ovaj integral mora biti jednak nuli. “Pa,” mogli biste pomisliti, “jedini način da se to dogodi je da množitelj to učini η bila jednaka nuli." Ali što je s prvim terminom, gdje ga ima d η / dt? Kažete: "Ako η pretvara u ništa, onda je njegova izvedenica isto ništa; to znači koeficijent at dv\/ dt također mora biti nula." Pa to nije sasvim točno. To nije posve točno jer između odstupanja η i njegova izvedenica postoji veza; nisu potpuno neovisni jer η (t) mora biti nula i t 1 i kod t 2 .


Pri rješavanju svih problema varijacijskog računa uvijek se koristi isti opći princip. Malo pomaknete ono što želite da varirate (slično onome što smo učinili dodavanjem η ), pogled na uvjete prvog reda, zatim posložite sve tako da dobijete integral u sljedećem obliku: “pomak (η ), pomnoženo s onim što ispadne”, ali tako da ne sadrži nikakve izvedenice od η (Ne d η / dt). Apsolutno je potrebno sve preobraziti tako da “nešto” ostane, pomnoženo sa η . Sada ćete shvatiti zašto je to toliko važno. (Postoje formule koje će vam reći kako u nekim slučajevima to možete učiniti bez ikakvih izračuna; ali one nisu toliko općenite da bi ih vrijedilo zapamtiti; najbolje je izračunati na način na koji mi to radimo.)

Kako mogu prepraviti penis d η / dt, tako da se pojavljuje η ? To mogu postići integracijom dio po dio. Ispada da je u varijacijskom računu cijeli trik u opisivanju varijacije S a zatim integrirati po dijelovima tako da izvodnice od η nestao. U svim zadacima u kojima se pojavljuju izvodnice izvodi se isti trik.

Prisjetite se općeg načela integracije po dijelovima. Ako imate proizvoljnu funkciju f pomnoženu s d η / dt i integriran sa t, onda napišeš izvedenicu od η /t

Granice integracije moraju se zamijeniti u prvi izraz t 1 I t 2 . Tada ću pod integral dobiti član iz integracije po dijelovima i zadnji član koji ostaje nepromijenjen tijekom transformacije.
I sada se događa ono što se uvijek događa - integrirani dio nestaje. (A ako ne nestane, onda je potrebno načelo preformulirati, dodajući uvjete koji osiguravaju takav nestanak!) Već smo rekli da η na krajevima staze mora biti jednak nuli. Uostalom, koji je naš princip? Poanta je da je djelovanje minimalno pod uvjetom da varirana krivulja počinje i završava na odabranim točkama. To znači da η (t 1)=0 i η (t 2)=0. Stoga se ispostavlja da je integrirani član jednak nuli. Okupljamo ostale članove i pišemo

Varijacija S je sada dobio oblik koji smo mu htjeli dati: nešto je u zagradama (označimo to F), a sve se to množi sa η (t) i integrirani iz t t prije t 2 .
Pokazalo se da je integral nekog izraza pomnožen s η (t), uvijek jednak nuli:

Postoji li neka funkcija od t; pomnožim s η (t) i integrirati ga od početka do kraja. I što god da je η, Dobivam nulu. To znači da funkcija F(t) jednaka nuli. Općenito, ovo je očito, ali za svaki slučaj, pokazat ću vam jedan način da to dokažete.

Neka kao η (t) Izabrat ću nešto što je svugdje, za sve, jednako nuli t, osim jedne unaprijed odabrane vrijednosti t. Ostaje nula dok ne stignem tamo t, s Zatim na trenutak poskoči i odmah se vrati. Ako uzmete integral ovog m) pomnožen nekom funkcijom F, jedino mjesto gdje ćete dobiti nešto što nije nula je gdje η (t) skočiti gore; i dobit ćete vrijednost F u ovom trenutku na integral preko skoka. Integral po samom skoku nije jednak nuli, već nakon množenja sa F trebao bi dati nulu. To znači da funkcija na mjestu gdje je došlo do skoka mora ispasti nula. Ali skok se mogao napraviti bilo gdje; Sredstva, F mora posvuda biti nula.

Vidimo da ako je naš integral jednak nuli za bilo koji η , tada koeficijent at η treba ići na nulu. Akcijski integral doseže minimum duž puta koji će zadovoljiti tako složenu diferencijalnu jednadžbu:

Zapravo i nije tako komplicirano; već ste ga sreli. To je samo F=ma. Prvi član je masa puta ubrzanje; druga je derivacija potencijalne energije, tj. sile.

Tako smo pokazali (barem za konzervativni sustav) da načelo najmanjeg djelovanja vodi do točnog odgovora; on tvrdi da je put koji ima minimalno djelovanje put koji zadovoljava Newtonov zakon.

Potrebno je dati još jednu napomenu. Nisam ovo dokazao minimum. Možda je ovo maksimum. Zapravo, to ne mora biti minimum. Ovdje je sve isto kao u “načelu najkraćeg vremena”, o kojem smo govorili dok smo proučavali optiku. I tu smo prvo govorili o “najkraćem” vremenu. No, pokazalo se da postoje situacije u kojima to vrijeme nije nužno “najkraće”. Temeljno načelo je da za bilo koji odstupanja prvog reda od optičkog puta promjene u vremenu bi bila jednaka nuli; Ovdje je ista priča. Pod "minimumom" zapravo mislimo na prvi red male promjene količine S kada odstupanja od putanje trebaju biti jednaka nuli. A to nije nužno "minimum".

Sada želim prijeći na neke generalizacije. Prije svega, cijela ova priča mogla bi se raditi trodimenzionalno. Umjesto jednostavnog x Ja bih tada imao x, y I z kao funkcije t, a radnja bi izgledala kompliciranije. Kada se krećete u 3D morate koristiti punu kinetičku energiju): (t/2), pomnoženo s kvadratom ukupne brzine. Drugim riječima

Dodatno, potencijalna energija je sada funkcija x, y I z.Što možete reći o putu? Put je određena opća krivulja u prostoru; nije tako lako nacrtati, ali ideja ostaje ista. Što je s η? Pa, η također ima tri komponente. Staza se može pomaknuti i po x i po in y, i po z, ili u sva tri smjera istovremeno. Tako η sada vektor. To ne stvara veće komplikacije. Samo varijacije moraju biti jednake nuli prva narudžba tada se proračun može provesti uzastopno u tri smjene. Prvo se možete kretati ts samo u pravcu x i reći da koeficijent treba ići na nulu. Dobili ste jednu jednadžbu. Onda ćemo se preseliti ts u pravcu na i dobijemo drugu. Zatim se pomaknite u smjeru z a mi dobijemo treći. Sve možete učiniti, ako želite, drugim redoslijedom. Bilo kako bilo, pojavljuje se trio jednadžbi. Ali Newtonov zakon su također tri jednadžbe u tri dimenzije, po jedna za svaku komponentu. Ostaje vam da se sami uvjerite da sve ovo radi u tri dimenzije (tu nema puno posla). Usput, možete uzeti bilo koji koordinatni sustav koji želite, polarni, bilo koji, i odmah dobiti Newtonove zakone u odnosu na ovaj sustav, s obzirom na to što se događa kada dođe do pomaka η po radijusu ili po kutu itd.

Metoda se može generalizirati na proizvoljan broj čestica. Ako, recimo, imate dvije čestice i između njih djeluju neke sile i postoji međusobna potencijalna energija, tada jednostavno zbrojite njihove kinetičke energije i od zbroja oduzmete potencijalnu energiju interakcije. Što varirate? Staze obačestice. Tada za dvije čestice koje se kreću u tri dimenzije nastaje šest jednadžbi. Možete mijenjati položaj čestice 1 u smjeru X, u pravcu na i prema z, i učinite isto s česticom 2, tako da postoji šest jednadžbi. I tako treba biti. Tri jednadžbe određuju ubrzanje čestice 1 zbog sile koja na nju djeluje, a ostale tri određuju ubrzanje čestice 2 zbog sile koja na nju djeluje. Uvijek slijedite ista pravila igre i dobit ćete Newtonov zakon za proizvoljan broj čestica.

Rekao sam da ćemo dobiti Newtonov zakon. To nije sasvim točno, jer Newtonov zakon uključuje i nekonzervativne sile, poput trenja. Newton je to tvrdio da jednako je bilo kojem F. Načelo najmanjeg djelovanja vrijedi samo za konzervativan sustavi, takvi gdje se sve sile mogu dobiti iz potencijalne funkcije. Ali znate da na mikroskopskoj razini, odnosno na najdubljoj fizičkoj razini, nekonzervativne sile ne postoje. Nekonzervativne sile (kao što je trenje) nastaju samo zato što zanemarujemo mikroskopske složene učinke: jednostavno postoji previše čestica za analizu. Temeljno isti zakoni limenka izraziti kao princip najmanjeg djelovanja.

Dopustite mi da prijeđem na daljnje generalizacije. Pretpostavimo da nas zanima što će se dogoditi kada se čestica kreće relativistički. Do sada nismo dobili ispravnu relativističku jednadžbu gibanja; F=ma vrijedi samo u nerelativističkim gibanjima. Postavlja se pitanje: postoji li odgovarajući princip najmanjeg djelovanja u relativističkom slučaju? Da, postoji. Formula u relativističkom slučaju je:

Prvi dio integrala djelovanja umnožak je mase mirovanja t 0 na od 2 a na integral funkcije brzine √ (1- v 2 /c 2 ). Zatim, umjesto oduzimanja potencijalne energije, imamo integrale skalarnog potencijala φ i vektorskog potencijala A puta v. Naravno, ovdje se uzimaju u obzir samo elektromagnetske sile. Sva električna i magnetska polja izražena su u terminima φ i A. Ova akcijska funkcija daje potpunu teoriju relativističkog gibanja pojedinačne čestice u elektromagnetskom polju.

Naravno, morate razumjeti da gdje god sam napisao v, prije izračunavanja, trebate zamijeniti dx/ dt umjesto v x itd. Štoviše, gdje sam jednostavno napisao x, y, z, morate trenutno zamisliti bodove t: x(t), g(t), z(t). Zapravo, tek nakon takvih zamjena i zamjena v dobit ćete formulu za djelovanje relativističke čestice. Neka najvještiji među vama pokušaju dokazati da ova formula za djelovanje zapravo daje točne jednadžbe gibanja za teoriju relativnosti. Dopustite mi samo da vam savjetujem da počnete odbacivanjem A, to jest, za sada bez magnetskih polja. Tada ćete morati dobiti komponente jednadžbe gibanja dp/dt=—qVφ, gdje je, kao što se vjerojatno sjećate, p=mv√(1-v 2 /c 2).

Puno je teže uključiti vektorski potencijal A u razmatranje. Varijacije tada postaju neusporedivo složenije. Ali na kraju se ispostavi da je sila jednaka onom što bi trebala biti: g(E+v × B). Ali zabavite se sami s tim.

Naglasio bih da u općem slučaju (npr. u relativističkoj formuli) integral u djelu više ne uključuje razliku između kinetičke i potencijalne energije. Ovo je bilo prikladno samo u nerelativističkoj aproksimaciji. Na primjer, član m o c 2√(1-v 2 /c 2)-Ovo nije ono što se zove kinetička energija. O pitanju koja bi radnja trebala biti za svaki pojedini slučaj može se odlučiti nakon nekoliko pokušaja i pogrešaka. Ovo je ista vrsta problema kao i određivanje jednadžbi gibanja. Samo se morate poigrati s jednadžbama koje poznajete i vidjeti mogu li se napisati kao načelo najmanjeg djelovanja.

Još jedna napomena o terminologiji. Funkcija koja se integrira tijekom vremena kako bi se dobila akcija S, nazvao LagrangeovΛ. To je funkcija koja ovisi samo o brzinama i položajima čestica. Dakle, princip najmanjeg djelovanja također je zapisan u obrascu

gdje pod x ja I v i podrazumijevaju se sve komponente koordinata i brzina. Ako ikada čujete nekoga da govori o "Lagrangianu", oni govore o funkciji koja se koristi za dobivanje S. Za relativističko gibanje u elektromagnetskom polju

Osim toga, moram napomenuti da najpedantniji i najpedantniji ljudi ne zovu S akcijski. Naziva se "Hamiltonova prva glavna funkcija". Ali držanje predavanja o “Hamiltonovom principu najmanje prve glavne funkcije” bilo je izvan moje snage. Ja sam to nazvao "akcija". Osim toga, sve više i više ljudi to naziva "akcijom". Vidite, povijesno se akcija nazivala nečim drugim što nije toliko korisno za znanost, ali mislim da ima više smisla promijeniti definiciju. Sada ćete i vi početi zvati novu funkciju radnjom, a uskoro će je svi početi zvati ovim jednostavnim imenom.

Sada vam želim reći nešto o našoj temi što je slično razmišljanju koje sam imao o načelu najkraćeg vremena. Postoji razlika u samoj biti zakona koji kaže da neki integral uzet od jedne točke do druge ima minimum - zakon koji nam govori nešto o cijelom putu odjednom, i zakon koji kaže da kada se krećete, onda To znači da postoji sila koja dovodi do ubrzanja. Drugi pristup izvještava vas o svakom vašem koraku, prati vaš put inč po inč, a prvi odmah daje neku opću izjavu o cijelom prijeđenom putu. Govoreći o svjetlu, govorili smo o povezanosti ova dva pristupa. Sada vam želim objasniti zašto bi diferencijalni zakoni trebali postojati ako postoji takav princip - princip najmanjeg djelovanja. Razlog je sljedeći: razmotrimo stvarno pređeni put u prostoru i vremenu. Kao i do sada, zadovoljit ćemo se jednim mjerenjem, kako bismo mogli nacrtati graf ovisnosti x iz t. Uz pravi put S doseže minimum. Pretpostavimo da imamo taj put i da on prolazi kroz neku točku A prostor i vrijeme i kroz drugu susjednu točku b.

Sada, ako cijeli integral od t 1 prije t 2 dosegla minimum, potrebno je da integral duž malog odsječka od a do b također bila minimalna. To ne može biti taj dio A prije b barem malo više od minimuma. Inače, možete pomicati krivulju naprijed-natrag u ovom dijelu i malo smanjiti vrijednost cijelog integrala.

To znači da bilo koji dio staze također treba osigurati minimum. I to vrijedi za sve male dijelove staze. Stoga se načelo da cijeli put treba dati minimum može formulirati tako da se kaže da je infinitezimalni segment puta također krivulja na kojoj je djelovanje minimalno. I ako uzmemo dovoljno kratak segment puta - između točaka vrlo blizu jedna drugoj A I b,- tada nije važno kako se potencijal mijenja od točke do točke daleko od ovog mjesta, jer, prolazeći kroz cijeli vaš kratki segment, gotovo se nikada ne pomaknete s tog mjesta. Jedina stvar koju trebate uzeti u obzir je promjena prvog reda u malenosti u potencijalu. Odgovor može ovisiti samo o derivatu potencijala, a ne o potencijalu negdje drugdje. Tako iskaz o svojstvu cijelog puta kao cjeline postaje iskaz o tome što se događa na kratkom dijelu puta, tj. diferencijalni iskaz. I ova diferencijalna formulacija uključuje izvodnice potencijala, odnosno sile u danoj točki. Ovo je kvalitativno objašnjenje veze između zakona u cjelini i diferencijalnog zakona.

Kad smo govorili o svjetlosti, raspravljali smo i o pitanju: kako čestica pronalazi pravi put? S različitog gledišta, ovo je lako razumjeti. U svakom trenutku čestica doživljava ubrzanje i zna samo što u tom trenutku treba učiniti. Ali svi vaši instinkti uzroka i posljedice se dižu kada čujete da čestica "odlučuje" kojim će putem krenuti, težeći minimumu djelovanja. Nije li ona "njuškala" susjedne staze, shvaćajući do čega će dovesti - više ili manje akcije? Kad smo postavili ekran na stazu svjetlosti tako da fotoni ne mogu isprobati sve staze, otkrili smo da se ne mogu odlučiti kojom će stazom krenuti i dobili smo fenomen difrakcije.

Ali vrijedi li to i za mehaniku? Je li istina da čestica ne samo da "ide pravim putem", već preispituje sve druge zamislive putanje? A što ako mu, postavljajući mu prepreke na putu, ne dopustimo da gleda naprijed, tada ćemo dobiti neku vrstu analogije fenomena difrakcije? Ono što je najdivnije u svemu ovome je da je sve zaista tako. Upravo to kažu zakoni kvantne mehanike. Dakle, naše načelo najmanjeg djelovanja nije u potpunosti formulirano. On se ne sastoji u tome da čestica izabere stazu najmanjeg djelovanja, već u tome da "osjeti" sve susjedne staze i izabere onu duž koje je djelovanje minimalno, a metoda tog izbora je slična način na koji svjetlost odabire najkraće vrijeme. Sjećate se da je način na koji svjetlost odabire najkraće vrijeme sljedeći: ako svjetlost ide putem koji zahtijeva različito vrijeme, stići će s drugačijom fazom. A ukupna amplituda u nekoj točki je zbroj doprinosa amplitude za sve staze duž kojih svjetlost može doći do nje. Svi ti putovi čije se faze jako razlikuju ne daju ništa nakon zbrajanja. Ali ako ste uspjeli pronaći cijeli niz staza, čije su faze gotovo iste, tada će se mali doprinosi zbrajati, a na točki dolaska ukupna amplituda će dobiti zamjetnu vrijednost. Najvažniji put je onaj u blizini kojeg postoji mnogo bliskih putova koji daju istu fazu.

Upravo se ista stvar događa u kvantnoj mehanici. Potpuna kvantna mehanika (nerelativistička i zanemarujući spin elektrona) funkcionira ovako: vjerojatnost da čestica napusti točku 1 u trenutku t 1, doći će do točke 2 u trenutku t 2 , jednaka kvadratu amplitude vjerojatnosti. Ukupna amplituda može se napisati kao zbroj amplituda za sve moguće staze—za bilo koju stazu dolaska. Za bilo koga x(t), koja bi se mogla dogoditi za bilo koju zamislivu imaginarnu putanju, mora se izračunati amplituda. Zatim ih sve treba presavijati. Što uzimamo kao amplitudu vjerojatnosti određenog puta? Naš akcijski integral nam govori kolika bi trebala biti amplituda pojedinog puta. Amplituda je proporcionalna e tS/h, Gdje S - djelovanje na ovom putu. To znači da ako fazu amplitude predstavimo kao kompleksan broj, tada će fazni kut biti jednak S/ h. Akcijski S ima dimenziju energije tijekom vremena, a Planckova konstanta ima istu dimenziju. Ovo je konstanta koja određuje kada je potrebna kvantna mehanika.

I tako to sve funkcionira. Neka akcija za sve staze S bit će vrlo velik u usporedbi s brojem h. Neka neki put vodi do određene vrijednosti amplitude. Faza susjedne staze bit će potpuno drugačija, jer s ogromnim S čak i manje promjene S naglo promijeniti fazu (uostalom h izuzetno malo). To znači da susjedne staze obično ugase svoje doprinose kada se dodaju. A samo u jednom području to nije točno - u onom gdje i put i njegov susjed - oboje, u prvoj aproksimaciji, imaju istu fazu (ili, točnije, gotovo isto djelovanje, varirajući unutar h). Samo takve staze se uzimaju u obzir. I u graničnom slučaju, kada je Planckova konstanta h teži nuli, ispravni zakoni kvantne mehanike mogu se sažeti riječima: “Zaboravite na sve te amplitude vjerojatnosti. Čestica se zapravo kreće posebnom putanjom – upravo onom po kojoj S u prvoj aproksimaciji se ne mijenja.” Ovo je veza između načela najmanjeg djelovanja i kvantne mehanike. Činjenicu da se kvantna mehanika može formulirati na ovaj način otkrio je 1942. godine učenik istog učitelja, g. Bader, o kojem sam vam govorio. [Kvantna mehanika je izvorno formulirana korištenjem diferencijalne jednadžbe za amplitudu (Schrödinger) kao i neke matrične matematike (Heisenberg).]

Sada želim govoriti o drugim principima minimuma u fizici. Postoji mnogo zanimljivih principa ove vrste. Neću ih sve nabrajati, već ću navesti samo još jednu. Kasnije, kada dođemo do jednog fizičkog fenomena za koji postoji izvrsno načelo minimuma, ispričat ću vam o njemu. Sada želim pokazati da nije potrebno opisati elektrostatiku pomoću diferencijalne jednadžbe za polje; umjesto toga može se zahtijevati da neki integral ima maksimum ili minimum. Za početak, uzmimo slučaj kada je gustoća naboja svugdje poznata, ali moramo pronaći potencijal φ u bilo kojoj točki prostora. Već znate da bi odgovor trebao biti:

Drugi način da se kaže ista stvar je procjena integrala U*

ovo je volumenski integral. Uzima se po cijelom prostoru. Uz pravilnu raspodjelu potencijala φ (x, y,z) ovaj izraz doseže svoj minimum.

Možemo pokazati da su obje ove tvrdnje o elektrostatici ekvivalentne. Pretpostavimo da smo odabrali proizvoljnu funkciju φ. Želimo pokazati da kada kao φ uzmemo ispravnu vrijednost potencijala _φ plus malo odstupanje f, tada do prvog reda malenosti promjena u U* bit će jednaka nuli. Pa pišemo

ovdje je φ ono što tražimo; ali ćemo mijenjati φ da vidimo kakav mora biti da bi došlo do varijacije U* pokazalo se da je prvog reda malenkosti. U prvom terminu U* moramo pisati

Ovo treba integrirati x, y i po z. I ovdje se nameće isti trik: kako bismo se riješili df/ dx, mi ćemo integrirati preko x u dijelovima. To će dovesti do dodatne diferencijacijeφ u odnosu na X. To je ista osnovna ideja s kojom smo se riješili izvedenica u odnosu na t. Koristimo jednakost

Integrirani član je nula jer uzimamo da je f nula u beskonačnosti. (Ovo odgovara nestajanju η kao t 1 I t 2 . Stoga je naše načelo preciznije formulirano na sljedeći način: U* za pravo φ manje nego za bilo koju drugu φ(x, y,z), koji imaju iste vrijednosti u beskonačnosti.) Onda ćemo učiniti isto sa na i sa z. Naš integral ΔU* će se pretvoriti u

Da bi ova varijacija bila jednaka nuli za bilo koji proizvoljni f, koeficijent f mora biti jednak nuli. Sredstva,

Vratili smo se našoj staroj jednadžbi. To znači da je naš prijedlog “minimuma” točan. Može se generalizirati ako se izračuni malo modificiraju. Vratimo se i integrirajmo dio po dio, bez opisivanja svega komponentu po komponentu. Počnimo pisanjem sljedeće jednakosti:

Diferenciranjem lijeve strane mogu pokazati da je potpuno jednaka desnoj. Ova jednadžba je prikladna za izvođenje integracije po dijelovima. U našem integralnom ΔU* zamjenjujemo Vφ*Vf n i fV 2 φ+V*(fVφ) i zatim to integrirati preko volumena. Član divergencije nakon integracije po volumenu zamjenjuje se integralom po površini:

A budući da integriramo po cijelom prostoru, površina u ovom integralu leži u beskonačnosti. To znači f=0, a dobivamo isti rezultat.

Tek sada počinjemo shvaćati kako riješiti probleme u kojima se nalazimo ne znamo gdje se nalaze svi naboji. Neka imamo vodiče na kojima se naboji nekako raspoređuju. Ako su potencijali na svim vodičima fiksni, tada je još uvijek dopuštena primjena našeg minimalnog principa. Integracija u U* povući ćemo samo duž područja koje leži izvan svih vodiča. Ali kako na vodičima ne možemo promijeniti (φ), onda je na njihovoj površini f = 0, a površinski integral

treba obaviti samo u međuprostorima vodiča. I, naravno, opet dobivamo Poissonovu jednadžbu

Stoga smo pokazali da je naš izvorni integral U* doseže minimum čak i kada se izračunava u prostoru između vodiča, od kojih je svaki na fiksnom potencijalu [to znači da svaka ispitna funkcija φ(g, y,z) mora biti jednak navedenom potencijalu vodiča kada (x, y,z) - točke površine vodiča]. Postoji zanimljiv poseban slučaj kada se naboji nalaze samo na vodičima. Zatim

a naše minimalno načelo govori nam da u slučaju kada svaki vodič ima svoj unaprijed određeni potencijal, potencijali u međuprostorima su prilagođeni tako da integralni U* ispadne što manji. Kakav je ovo integral? Izraz Vφ je električno polje. To znači da je integral elektrostatička energija. Ispravno polje je jedino koje od svih polja dobivenih kao potencijalni gradijent ima najmanju ukupnu energiju.

Želio bih upotrijebiti ovaj rezultat za rješavanje nekog određenog problema i pokazati vam da sve te stvari imaju stvarno praktično značenje. Pretpostavimo da uzmem dva vodiča u obliku cilindričnog kondenzatora.

Unutarnji vodič ima potencijal jednak, recimo, V, a za vanjski - nula. Neka polumjer unutarnjeg vodiča bude jednak A, i vanjski - b. Sada možemo pretpostaviti da je raspodjela potencijala između njih bilo koji. Ali ako uzmemo ispraviti vrijednost φ i izračunati
(ε 0 /2) ∫ (Vφ) 2 dV tada bi energija sustava trebala biti 1/2CV 2.

Dakle, pomoću našeg principa možete izračunati kapacitet S. Ako uzmemo netočnu raspodjelu potencijala i pokušamo procijeniti kapacitet kondenzatora pomoću ove metode, doći ćemo do prevelike vrijednosti kapaciteta za fiksni V. Svaki procijenjeni potencijal φ koji se točno ne poklapa sa svojom stvarnom vrijednošću također će dovesti do netočne vrijednosti C, veće od potrebne. Ali ako je krivo odabrani potencijal cp još uvijek gruba aproksimacija, tada kapacitet S pokazat će se s dobrom točnošću, jer je pogreška u C vrijednost drugog reda u usporedbi s pogreškom u φ.

Pretpostavimo da ne znam koliki je kapacitet cilindričnog kondenzatora. Zatim, da je prepoznam, mogu koristiti ovaj princip. Jednostavno ću testirati različite funkcije φ kao potencijala dok ne postignem najnižu vrijednost S. Recimo, na primjer, da sam izabrao potencijal koji odgovara konstantnom polju. (Znate, naravno, da polje ovdje zapravo nije konstantno; varira kao 1/r) Ako je polje konstantno, to znači da potencijal linearno ovisi o udaljenosti. Da bi napon na vodičima bio potreban, funkcija φ mora imati oblik

Ova funkcija je jednaka V na r=a, nula na r =b, a između njih je konstantan nagib jednak - V/(b—A). Dakle, za određivanje integrala U*, trebate samo pomnožiti kvadrat ovog gradijenta s ε o /2 i integrirati po cijelom volumenu. Provedimo ovaj izračun za cilindar jedinične duljine. Element volumena na radijusu r jednako 2πrdr. Provodeći integraciju, nalazim da moj prvi test daje sljedeći kapacitet:

Tako sam dobio formulu za kapacitet, koja je, iako netočna, neka vrsta aproksimacije:

Naravno da se razlikuje od točnog odgovora C=2πε 0 /ln (b/a), ali sve u svemu nije tako loše. Pokušajmo ga usporediti s točnim odgovorom za nekoliko vrijednosti b/a. Brojevi koje sam izračunao prikazani su u sljedećoj tablici.

Čak i kada b/a=2(a to već dovodi do prilično velikih razlika između konstantnih i linearnih polja), još uvijek dobivam prilično prihvatljivu aproksimaciju. Odgovor je, naravno, očekivano, malo previsok. Ali ako se tanka žica stavi unutar velikog cilindra, onda sve izgleda puno gore. Tada se polje jako mijenja i njegova zamjena s konstantnim poljem ne vodi ničemu dobrom. Kada je b/a = 100, precjenjujemo odgovor gotovo dvostruko. Za male b/a situacija izgleda puno bolje. U suprotnoj granici, kada razmak između vodiča nije jako širok (recimo, za b/a = 1,1), konstantno polje pokazuje se kao vrlo dobra aproksimacija, ono daje vrijednost S točan do desetinki postotka.

Sada ću vam reći kako poboljšati ovaj izračun. (Odgovor za cilindar je, naravno, poznat, ali ista metoda radi za neke druge neobične oblike kondenzatora za koje možda ne znate točan odgovor.) Sljedeći korak je pronaći bolju aproksimaciju za nepoznati pravi potencijal φ. Recimo da možete testirati konstantu plus eksponent φ, itd. Ali kako znate da ste dobili najbolju aproksimaciju ako ne znate pravi φ? Odgovor: Izbroji to S;što je niža, to je bliža istini. Testirajmo ovu ideju. Neka potencijal nije linearan, već, recimo, kvadratan po r, a električno polje nije konstantno, već linearno. Najviše Općenito kvadratni oblik, koji prelazi u φ=O kada r=b a u φ=F pri r=a, Je li ovo:

gdje je α konstantan broj. Ova formula je malo kompliciranija od prethodne. Uključuje i kvadratni i linearni član. Iz nje je vrlo lako dobiti polje. Jednako je jednostavnom

Sada ovo treba kvadrirati i integrirati preko volumena. Ali čekaj malo. Što trebam uzeti za α? Mogu uzeti da je f parabola, ali koja? Evo što ću učiniti: izračunati kapacitet na proizvoljni α. dobit ću

Ovo izgleda malo zbunjujuće, ali tako ispada nakon integriranja kvadrata polja. Sada mogu sama birati. Znam da je istina niža od svega što namjeravam izračunati. Bez obzira što stavim umjesto a, odgovor će i dalje biti prevelik. Ali ako nastavim svoju igru ​​s α i pokušam postići najmanju moguću vrijednost S, tada će ta najniža vrijednost biti bliža istini od bilo koje druge vrijednosti. Stoga, sada trebam odabrati α tako da vrijednost S je dosegla svoj minimum. Okrećući se običnom diferencijalnom računu, uvjeren sam da je minimum S bit će kada je α =— 2 b/(b+a). Zamjenom ove vrijednosti u formulu, dobivam najmanji kapacitet

Shvatio sam što ova formula daje S na različite vrijednosti b/a. Imenovao sam ove brojeve S(kvadratni). Evo tablice koja uspoređuje S(kvadratni) sa S(pravi).

Na primjer, kada je omjer radijusa 2:1, dobivam 1,444. Ovo je vrlo dobra aproksimacija točnom odgovoru, 1,4423. Čak i s velikim da aproksimacija ostaje prilično dobra - mnogo bolja od prve aproksimacije. Ostaje podnošljiv (precijenjen za samo 10%) čak i s b/a = 10:1. Velika razlika javlja se samo pri omjeru 100:1. Dobivam S jednako 0,346 umjesto 0,267. S druge strane, za omjer radijusa od 1,5 slaganje je izvrsno, a za b/a=1,1 odgovor je 10,492065 umjesto očekivanih 10,492070. Tamo gdje biste očekivali dobar odgovor, on se pokazao vrlo, vrlo dobrim.

Naveo sam sve ove primjere, prvo, da pokažem teorijsku vrijednost načela minimalnog djelovanja i općenito svih načela minimuma, i, drugo, da vam pokažem njihovu praktičnu korisnost, a ne uopće da bih izračunao kapacitet koje već imamo vrlo dobro znamo. Za bilo koji drugi oblik, možete isprobati približno polje s nekoliko nepoznatih parametara (poput α) i prilagoditi ih na minimum. Dobit ćete vrhunske numeričke rezultate na problemima koji se ne mogu drugačije riješiti.

Oni ga poštuju i stoga je ovo načelo jedna od ključnih odredbi moderne fizike. Jednadžbe gibanja dobivene uz njegovu pomoć nazivaju se Euler-Lagrangeove jednadžbe.

Prvu formulaciju principa dao je P. Maupertuis godine, odmah ističući njegovu univerzalnu prirodu, smatrajući ga primjenjivim na optiku i mehaniku. Iz tog je principa izveo zakone refleksije i loma svjetlosti.

Priča

Maupertuis je došao do ovog načela iz osjećaja da savršenstvo Svemira zahtijeva određenu ekonomičnost u prirodi i proturječi svakom beskorisnom trošenju energije. Prirodno kretanje mora biti takvo da određena količina bude minimalna. Sve što je trebao učiniti bilo je pronaći tu vrijednost, što je i nastavio činiti. Bio je to umnožak trajanja (vremena) kretanja unutar sustava s dvostrukom vrijednošću, koju danas nazivamo kinetičkom energijom sustava.

Euler (u "Réflexions sur quelques loix générales de la nature", 1748) prihvaća načelo najmanje količine djelovanja, nazivajući djelovanje "napor". Njegov izraz u statici odgovara onome što bismo sada nazvali potencijalnom energijom, tako da je njegova izjava o najmanjem djelovanju u statici ekvivalentna uvjetu minimalne potencijalne energije za ravnotežnu konfiguraciju.

U klasičnoj mehanici

Načelo najmanjeg djelovanja služi kao temeljna i standardna osnova Lagrangeovih i Hamiltonovih formulacija mehanike.

Prvo pogledajmo konstrukciju ovako: Lagrangeova mehanika. Na primjeru fizičkog sustava s jednim stupnjem slobode, podsjetimo da je djelovanje funkcional u odnosu na (generalizirane) koordinate (u slučaju jednog stupnja slobode - jedna koordinata), odnosno izražava se kroz tako da je svaka zamisliva verzija funkcije pridružena određenom broju - akciji (u tom smislu, možemo reći da je akcija kao funkcional pravilo koje dopušta bilo kojoj danoj funkciji da izračuna potpuno specifičan broj - također se naziva U Akciji). Akcija izgleda ovako:

gdje je Lagrangian sustava, ovisno o generaliziranoj koordinati, njegova prva derivacija u odnosu na vrijeme, a također, eventualno, eksplicitno u odnosu na vrijeme. Ako sustav ima veći broj stupnjeva slobode, tada Lagrangian ovisi o većem broju generaliziranih koordinata i njihovih prvih izvodnica po vremenu. Dakle, djelovanje je skalarni funkcional ovisno o putanji tijela.

Činjenica da je radnja skalarna olakšava zapisivanje u bilo koje generalizirane koordinate, glavna stvar je da je položaj (konfiguracija) sustava nedvosmisleno karakteriziran njima (na primjer, umjesto Kartezijevih koordinata, to mogu biti polarne koordinate, udaljenosti između točaka sustava, kutovi ili njihove funkcije itd. .d.).

Radnja se može proračunati za sasvim proizvoljnu putanju, koliko god ona bila “divlja” i “neprirodna”. Međutim, u klasičnoj mehanici, među cijelim skupom mogućih putanja, postoji samo jedna kojom će se tijelo stvarno kretati. Princip stacionarnosti upravo daje odgovor na pitanje kako će se tijelo zapravo kretati:

To znači da ako je zadan Lagrangian sustava, onda pomoću varijacijskog računa možemo točno utvrditi kako će se tijelo gibati tako da prvo dobijemo jednadžbe gibanja - Euler-Lagrangeove jednadžbe, a zatim ih riješimo. To omogućuje ne samo ozbiljnu generalizaciju formulacije mehanike, već i odabir najprikladnijih koordinata za svaki specifičan problem, ne ograničavajući se na kartezijanske, što može biti vrlo korisno za dobivanje najjednostavnijih i najlakše rješivih jednadžbi.

gdje je Hamiltonova funkcija ovog sustava; - (generalizirane) koordinate, - konjugirani (generalizirani) impulsi, koji zajedno karakteriziraju u svakom danom trenutku vremena dinamičko stanje sustava i, svaki je funkcija vremena, karakteriziraju tako evoluciju (kretanje) sustava. U ovom slučaju, da bi se dobile jednadžbe gibanja sustava u obliku Hamiltonovih kanonskih jednadžbi, potrebno je tako napisanu radnju neovisno varirati za sve i .

Treba napomenuti da ako je iz uvjeta problema načelno moguće pronaći zakon gibanja, onda je to automatski Ne znači da je moguće konstruirati funkcional koji uzima stacionarnu vrijednost tijekom pravog gibanja. Primjer je zajedničko kretanje električnih naboja i monopola - magnetskih naboja - u elektromagnetskom polju. Njihove jednadžbe gibanja ne mogu se izvesti iz principa stacionarnog djelovanja. Isto tako, neki Hamiltonovi sustavi imaju jednadžbe gibanja koje se ne mogu izvesti iz ovog principa.

Primjeri

Trivijalni primjeri pomažu u procjeni korištenja principa rada kroz Euler-Lagrangeove jednadžbe. Slobodna čestica (masa m i brzina v) u euklidskom prostoru kreće se pravocrtno. Koristeći Euler-Lagrangeove jednadžbe, to se može prikazati u polarnim koordinatama kako slijedi. U nedostatku potencijala, Lagrangeova funkcija je jednostavno jednaka kinetičkoj energiji

u ortogonalnom koordinatnom sustavu.

U polarnim koordinatama kinetička energija, a time i Lagrangeova funkcija, postaje

Radijalna i kutna komponenta jednadžbi postaju:

Rješavanje ove dvije jednadžbe

Ovdje je uvjetna oznaka za beskonačno višestruku funkcionalnu integraciju po svim putanjama x(t), a to je Planckova konstanta. Naglašavamo da se, u načelu, djelovanje u eksponencijalu pojavljuje (ili se može pojaviti) samo po sebi pri proučavanju evolucijskog operatora u kvantnoj mehanici, ali za sustave koji imaju egzaktni klasični (nekvantni) analog, ono je točno jednako uobičajenom klasično djelovanje.

Matematička analiza ovog izraza u klasičnom limitu - za dovoljno velike , odnosno za vrlo brze oscilacije imaginarnog eksponencijala - pokazuje da se velika većina svih mogućih trajektorija u ovom integralu poništava u limitu (formalno za ). Za gotovo svaki put postoji put na kojem će fazni pomak biti upravo suprotan, i oni će dati nulti doprinos. Ne reduciraju se samo one putanje za koje je djelovanje blizu ekstremne vrijednosti (za većinu sustava - na minimum). Ovo je čisto matematička činjenica iz teorije funkcija kompleksne varijable; Na primjer, na njoj se temelji metoda stacionarne faze.

Kao rezultat toga, čestica se, u potpunom skladu sa zakonima kvantne mehanike, kreće istovremeno duž svih putanja, ali u normalnim uvjetima samo putanje bliske stacionarnim (tj. klasičnim) doprinose promatranim vrijednostima. Budući da kvantna mehanika prelazi u klasičnu mehaniku u granici visokih energija, možemo pretpostaviti da je ovo kvantno mehaničko izvođenje klasičnog principa stacionarnosti djelovanja.

U kvantnoj teoriji polja

U kvantnoj teoriji polja također se uspješno primjenjuje princip stacionarnog djelovanja. Lagrangeova gustoća ovdje uključuje operatore odgovarajućih kvantnih polja. Iako je ovdje u biti ispravnije (s iznimkom klasične granice i djelomično kvaziklasike) govoriti ne o principu stacionarnosti djelovanja, već o Feynmanovoj integraciji po trajektorijama u konfiguracijskom ili faznom prostoru tih polja - koristeći upravo spomenuta Lagrangeova gustoća.

Daljnje generalizacije

Šire gledano, akcija se shvaća kao funkcional koji definira preslikavanje iz konfiguracijskog prostora u skup realnih brojeva i, općenito, ne mora biti integral, jer su nelokalne radnje moguće u načelu, barem teoretski. Štoviše, konfiguracijski prostor nije nužno funkcijski prostor jer može imati nekomutativnu geometriju.

Oni ga poštuju i stoga je ovo načelo jedna od ključnih odredbi moderne fizike. Jednadžbe gibanja dobivene uz njegovu pomoć nazivaju se Euler-Lagrangeove jednadžbe.

Prvu formulaciju principa dao je P. Maupertuis godine, odmah ističući njegovu univerzalnu prirodu, smatrajući ga primjenjivim na optiku i mehaniku. Iz tog je principa izveo zakone refleksije i loma svjetlosti.

Priča

Maupertuis je došao do ovog načela iz osjećaja da savršenstvo Svemira zahtijeva određenu ekonomičnost u prirodi i proturječi svakom beskorisnom trošenju energije. Prirodno kretanje mora biti takvo da određena količina bude minimalna. Sve što je trebao učiniti bilo je pronaći tu vrijednost, što je i nastavio činiti. Bio je to umnožak trajanja (vremena) kretanja unutar sustava s dvostrukom vrijednošću, koju danas nazivamo kinetičkom energijom sustava.

Euler (u "Réflexions sur quelques loix générales de la nature", 1748) prihvaća načelo najmanje količine djelovanja, nazivajući djelovanje "napor". Njegov izraz u statici odgovara onome što bismo sada nazvali potencijalnom energijom, tako da je njegova izjava o najmanjem djelovanju u statici ekvivalentna uvjetu minimalne potencijalne energije za ravnotežnu konfiguraciju.

U klasičnoj mehanici

Načelo najmanjeg djelovanja služi kao temeljna i standardna osnova Lagrangeovih i Hamiltonovih formulacija mehanike.

Prvo pogledajmo konstrukciju ovako: Lagrangeova mehanika. Na primjeru fizičkog sustava s jednim stupnjem slobode, podsjetimo da je djelovanje funkcional u odnosu na (generalizirane) koordinate (u slučaju jednog stupnja slobode - jedna koordinata), odnosno izražava se kroz tako da je svaka zamisliva verzija funkcije pridružena određenom broju - akciji (u tom smislu, možemo reći da je akcija kao funkcional pravilo koje dopušta bilo kojoj danoj funkciji da izračuna potpuno specifičan broj - također se naziva U Akciji). Akcija izgleda ovako:

gdje je Lagrangian sustava, ovisno o generaliziranoj koordinati, njegova prva derivacija u odnosu na vrijeme, a također, eventualno, eksplicitno u odnosu na vrijeme. Ako sustav ima veći broj stupnjeva slobode, tada Lagrangian ovisi o većem broju generaliziranih koordinata i njihovih prvih izvodnica po vremenu. Dakle, djelovanje je skalarni funkcional ovisno o putanji tijela.

Činjenica da je radnja skalarna olakšava zapisivanje u bilo koje generalizirane koordinate, glavna stvar je da je položaj (konfiguracija) sustava nedvosmisleno karakteriziran njima (na primjer, umjesto Kartezijevih koordinata, to mogu biti polarne koordinate, udaljenosti između točaka sustava, kutovi ili njihove funkcije itd. .d.).

Radnja se može proračunati za sasvim proizvoljnu putanju, koliko god ona bila “divlja” i “neprirodna”. Međutim, u klasičnoj mehanici, među cijelim skupom mogućih putanja, postoji samo jedna kojom će se tijelo stvarno kretati. Princip stacionarnosti upravo daje odgovor na pitanje kako će se tijelo zapravo kretati:

To znači da ako je zadan Lagrangian sustava, onda pomoću varijacijskog računa možemo točno utvrditi kako će se tijelo gibati tako da prvo dobijemo jednadžbe gibanja - Euler-Lagrangeove jednadžbe, a zatim ih riješimo. To omogućuje ne samo ozbiljnu generalizaciju formulacije mehanike, već i odabir najprikladnijih koordinata za svaki specifičan problem, ne ograničavajući se na kartezijanske, što može biti vrlo korisno za dobivanje najjednostavnijih i najlakše rješivih jednadžbi.

gdje je Hamiltonova funkcija ovog sustava; - (generalizirane) koordinate, - konjugirani (generalizirani) impulsi, koji zajedno karakteriziraju u svakom danom trenutku vremena dinamičko stanje sustava i, svaki je funkcija vremena, karakteriziraju tako evoluciju (kretanje) sustava. U ovom slučaju, da bi se dobile jednadžbe gibanja sustava u obliku Hamiltonovih kanonskih jednadžbi, potrebno je tako napisanu radnju neovisno varirati za sve i .

Treba napomenuti da ako je iz uvjeta problema načelno moguće pronaći zakon gibanja, onda je to automatski Ne znači da je moguće konstruirati funkcional koji uzima stacionarnu vrijednost tijekom pravog gibanja. Primjer je zajedničko kretanje električnih naboja i monopola - magnetskih naboja - u elektromagnetskom polju. Njihove jednadžbe gibanja ne mogu se izvesti iz principa stacionarnog djelovanja. Isto tako, neki Hamiltonovi sustavi imaju jednadžbe gibanja koje se ne mogu izvesti iz ovog principa.

Primjeri

Trivijalni primjeri pomažu u procjeni korištenja principa rada kroz Euler-Lagrangeove jednadžbe. Slobodna čestica (masa m i brzina v) u euklidskom prostoru kreće se pravocrtno. Koristeći Euler-Lagrangeove jednadžbe, to se može prikazati u polarnim koordinatama kako slijedi. U nedostatku potencijala, Lagrangeova funkcija je jednostavno jednaka kinetičkoj energiji

u ortogonalnom koordinatnom sustavu.

U polarnim koordinatama kinetička energija, a time i Lagrangeova funkcija, postaje

Radijalna i kutna komponenta jednadžbi postaju:

Rješavanje ove dvije jednadžbe

Ovdje je uvjetna oznaka za beskonačno višestruku funkcionalnu integraciju po svim putanjama x(t), a to je Planckova konstanta. Naglašavamo da se, u načelu, djelovanje u eksponencijalu pojavljuje (ili se može pojaviti) samo po sebi pri proučavanju evolucijskog operatora u kvantnoj mehanici, ali za sustave koji imaju egzaktni klasični (nekvantni) analog, ono je točno jednako uobičajenom klasično djelovanje.

Matematička analiza ovog izraza u klasičnom limitu - za dovoljno velike , odnosno za vrlo brze oscilacije imaginarnog eksponencijala - pokazuje da se velika većina svih mogućih trajektorija u ovom integralu poništava u limitu (formalno za ). Za gotovo svaki put postoji put na kojem će fazni pomak biti upravo suprotan, i oni će dati nulti doprinos. Ne reduciraju se samo one putanje za koje je djelovanje blizu ekstremne vrijednosti (za većinu sustava - na minimum). Ovo je čisto matematička činjenica iz teorije funkcija kompleksne varijable; Na primjer, na njoj se temelji metoda stacionarne faze.

Kao rezultat toga, čestica se, u potpunom skladu sa zakonima kvantne mehanike, kreće istovremeno duž svih putanja, ali u normalnim uvjetima samo putanje bliske stacionarnim (tj. klasičnim) doprinose promatranim vrijednostima. Budući da kvantna mehanika prelazi u klasičnu mehaniku u granici visokih energija, možemo pretpostaviti da je ovo kvantno mehaničko izvođenje klasičnog principa stacionarnosti djelovanja.

U kvantnoj teoriji polja

U kvantnoj teoriji polja također se uspješno primjenjuje princip stacionarnog djelovanja. Lagrangeova gustoća ovdje uključuje operatore odgovarajućih kvantnih polja. Iako je ovdje u biti ispravnije (s iznimkom klasične granice i djelomično kvaziklasike) govoriti ne o principu stacionarnosti djelovanja, već o Feynmanovoj integraciji po trajektorijama u konfiguracijskom ili faznom prostoru tih polja - koristeći upravo spomenuta Lagrangeova gustoća.

Daljnje generalizacije

Šire gledano, akcija se shvaća kao funkcional koji definira preslikavanje iz konfiguracijskog prostora u skup realnih brojeva i, općenito, ne mora biti integral, jer su nelokalne radnje moguće u načelu, barem teoretski. Štoviše, konfiguracijski prostor nije nužno funkcijski prostor jer može imati nekomutativnu geometriju.

Načelo najmanjeg djelovanja, koje je prvi formulirao upravo Jacobi, slično je Hamiltonovom načelu, ali je manje općenito i teže ga je dokazati. Ovaj princip je primjenjiv samo u slučaju kada veze i djelovanje sile ne ovise o vremenu i kada, dakle, postoji integral žive sile.

Ovaj integral ima oblik:

Gore navedeni Hamiltonov princip kaže da varijacija integrala

jednaka je nuli pri prijelazu stvarnog gibanja u bilo koje drugo beskonačno blisko gibanje, koje prenosi sustav iz istog početnog položaja u isti konačni položaj u istom vremenskom razdoblju.

Jacobijevo načelo, naprotiv, izražava svojstvo gibanja koje ne ovisi o vremenu. Jacobi smatra integral

određivanje radnje. Načelo koje je uspostavio kaže da je varijacija ovog integrala jednaka nuli kada usporedimo stvarno gibanje sustava s bilo kojim drugim beskonačno bliskim gibanjem koje dovodi sustav iz istog početnog položaja u isti konačni položaj. U ovom slučaju ne obraćamo pažnju na utrošeni vremenski period, već promatramo jednadžbu (1), odnosno jednadžbu radne snage s istom vrijednošću konstante h kao u stvarnom kretanju.

Ovaj nužni uvjet za ekstrem vodi, općenito govoreći, do minimuma integrala (2), otuda naziv princip najmanjeg djelovanja. Čini se da je minimalni uvjet najprirodniji, budući da je vrijednost T u biti pozitivna, pa stoga integral (2) nužno mora imati minimum. Postojanje minimuma može se strogo dokazati samo ako je vremensko razdoblje dovoljno malo. Dokaz ove pozicije može se pronaći u Darbouxovom poznatom tečaju teorije površina. Mi ga, međutim, ovdje nećemo iznositi i ograničit ćemo se na izvođenje uvjeta

432. Dokaz načela najmanjeg djelovanja.

U stvarnom proračunu nailazimo na jednu poteškoću koja nije prisutna u dokazu Hamiltonovog teorema. Varijabla t više ne ostaje neovisna o varijaciji; dakle varijacije q i i q. povezani su s varijacijom t složenim odnosom koji slijedi iz jednadžbe (1). Najjednostavniji način da se zaobiđe ova poteškoća je promijeniti nezavisnu varijablu, odabirom one čije vrijednosti padaju između konstantnih granica koje ne ovise o vremenu. Neka je k nova nezavisna varijabla za čije se granice pretpostavlja da su neovisne o t. Prilikom pomicanja sustava, parametri i t bit će funkcije ove varijable

Neka slova s ​​prostim brojevima q označavaju derivacije parametara q po vremenu.

Kako veze, prema pretpostavci, ne ovise o vremenu, Kartezijeve koordinate x, y, z su funkcije od q koje ne sadrže vrijeme. Stoga će njihove derivacije biti linearne homogene funkcije od q, a 7 će biti homogeni kvadratni oblik od q, čiji su koeficijenti funkcije od q. Imamo

Da bismo razlikovali derivacije od q u odnosu na vrijeme, označavamo, koristeći zagrade, (q), derivacije od q uzete u odnosu na i stavljene u skladu s ovim

onda ćemo imati

a integral (2), izražen kroz novu nezavisnu varijablu A, poprimit će oblik;

Derivacija se može eliminirati korištenjem teorema žive sile. Doista, sastavni dio radne snage bit će

Zamjenom ovog izraza u formulu za, svodimo integral (2) na oblik

Integral koji definira akciju tako je dobio svoj konačni oblik (3). Funkcija integranda je kvadratni korijen kvadratnog oblika veličina

Pokažimo da su diferencijalne jednadžbe ekstremala integrala (3) upravo Lagrangeove jednadžbe. Jednadžbe ekstrema, temeljene na općim formulama varijacijskog računa, bit će:

Pomnožimo jednadžbe s 2 i izvršimo parcijalna diferenciranja, uzimajući u obzir da ne sadrži, tada dobivamo, ako ne napišemo indeks,

Ovo su jednadžbe ekstremala izražene u terminima nezavisne varijable. Sada je zadatak vratiti se na nezavisnu varijablu

Budući da je Γ homogena funkcija drugog stupnja od i homogena funkcija prvog stupnja, imamo

S druge strane, teorem o životnoj sili može se primijeniti na faktore derivacija u jednadžbama ekstremala, što dovodi, kao što smo vidjeli gore, do supstitucije

Kao rezultat svih supstitucija, jednadžbe ekstremala se svode na oblik

Time smo došli do Lagrangeovih jednadžbi.

433. Slučaj kada nema pogonskih snaga.

U slučaju kada nema pogonskih sila, postoji jednadžba za živu snagu i imamo

Uvjet da bi integral bio minimalan je u ovom slučaju da odgovarajuća vrijednost -10 mora biti najmanja. Dakle, kad nema pokretačkih sila, onda je među svim gibanjima, u kojima živa sila održava istu zadanu vrijednost, stvarno gibanje ono, koje sustav u najkraćem vremenu prenosi iz početnog položaja u konačni položaj.

Ako se sustav svede na jednu točku koja se kreće po nepokretnoj plohi, tada je stvarno gibanje, između svih gibanja na površini koja se odvijaju istom brzinom, ono gibanje u kojem se točka pomiče iz svog početnog položaja u konačni položaj u najkraći

vremenski interval. Drugim riječima, točka na plohi opisuje najkraću liniju između svoja dva položaja, tj. geodetsku liniju.

434. Napomena.

Načelo najmanjeg djelovanja pretpostavlja da sustav ima nekoliko stupnjeva slobode, jer kada bi postojao samo jedan stupanj slobode, tada bi jedna jednadžba bila dovoljna za određivanje gibanja. Kako se kretanje u ovom slučaju može u potpunosti odrediti jednadžbom žive sile, tada će stvarno gibanje jedino zadovoljavati ovu jednadžbu, pa se stoga ne može usporediti ni s jednim drugim gibanjem.


NAČELO NAJMANJE UČINKOVITOSTI

Jedan od varijacijskih principa mehanike, prema Kromu, za danu klasu mehaničkih gibanja koja se međusobno uspoređuju. sustava, valjano je ono za koje tjelesne. veličina, tzv djelovanje, ima najmanju (točnije, stacionarnu) vrijednost. Obično se N. d. p. koristi u jednom od dva oblika.

a) N. d. p. u obliku Hamiltona - Ostrogradskog utvrđuje da među svim kinematički mogućim gibanjima sustava iz jedne konfiguracije u drugu (blisku prvoj), ostvarenim u istom vremenskom razdoblju, vrijedi ono za koje Hamiltonovo djelovanje S bit će najmanje. matematika izraz N. d.p. u ovom slučaju ima oblik: dS = 0, gdje je d simbol nepotpune (izokrone) varijacije (tj. za razliku od potpune varijacije vrijeme u njoj ne varira).

b) N. d. p. u obliku Maupertuis - Lagrange utvrđuje da među svim kinematički mogućim gibanjima sustava iz jedne konfiguracije u drugu njemu blisku, izvedenih uz zadržavanje iste vrijednosti ukupne energije sustava, vrijedi ono da za - Stoga će Lagrangeovo djelovanje W biti najmanje. matematika izraz N. d.p. u ovom slučaju ima oblik DW = 0, gdje je D simbol ukupne varijacije (za razliku od principa Hamilton-Ostrogradskog, ovdje ne variraju samo koordinate i brzine, već i vrijeme kretanja sustav iz jedne konfiguracije u drugu) . N.d.p.v. U ovom slučaju vrijedi samo za konzervativne i, štoviše, holonomne sustave, dok je u prvom slučaju nekonzervativno načelo općenitije i, posebno, može se proširiti na nekonzervativne sustave. N.D.P. se koriste za sastavljanje jednadžbi mehaničkog gibanja. sustava i proučavati opća načela tih pokreta. Uz odgovarajuću generalizaciju pojmova, NDP nalazi primjenu u mehanici kontinuiranog medija, u elektrodinamici i kvantumu. mehanika itd.

  • - isto kao...

    Fizička enciklopedija

  • - m-operator, operator minimizacije, - metoda konstruiranja novih funkcija iz drugih funkcija, koja se sastoji od sljedećeg...

    Matematička enciklopedija

  • - jedno od varijacijskih načela mehanike, prema kojem se za određenu klasu mehaničkih kretanja međusobno uspoređuju. sustav provodi ono za što je djelovanje minimalno...

    Prirodna znanost. enciklopedijski rječnik

  • - jedan od najvažnijih zakona mehanike, koji je uspostavio ruski znanstvenik M.V. Ostrogradski...

    Ruska enciklopedija

  • Rječnik pravnih pojmova

  • - u ustavnom pravu niza država načelo po kojem su općepriznata načela i norme međunarodnog prava sastavni dio pravnog sustava odgovarajuće zemlje...

    Enciklopedija pravnika

  • - u ustavnom pravu niza država načelo prema kojem su općepriznate norme međunarodnog prava sastavni dio nacionalnog pravnog sustava...

    Veliki pravni rječnik

  • - najkraća udaljenost od središta eksplozivnog punjenja do slobodne površine - linija na nai-malkoto otporu - křivka nejmenšího odporu - Line der geringsten Festigkeit - robbantás minimális ellenállási tengelyvonala - hamgiin baga...

    Građevinski rječnik

  • - ako je moguće pomicati točke deformabilnog tijela u različitim smjerovima, svaka se točka tog tijela pomiče u smjeru najmanjeg otpora...

    Enciklopedijski rječnik metalurgije

  • - pravilo prema kojem se postojeće zalihe obično vrednuju ili po najnižoj cijeni ili po najnižoj prodajnoj cijeni...

    Rječnik poslovnih pojmova

  • - u ustavnom pravu niza država - načelo prema kojemu su općepriznata načela i norme međunarodnog prava sastavni dio pravnog sustava dotične države i djeluju...

    Enciklopedijski rječnik ekonomije i prava

  • - jedno od varijacijskih načela mehanike, prema kojem za danu klasu gibanja mehaničkog sustava međusobno uspoređenih vrijedi ona za koju je fizikalna veličina,...
  • - isto kao Gaussov princip...

    Velika sovjetska enciklopedija

  • - jedan od varijacijskih principa mehanike; isto kao i princip najmanje akcije...

    Velika sovjetska enciklopedija

  • - jedno od varijacijskih načela mehanike, prema kojem se za danu klasu gibanja mehaničkog sustava međusobno uspoređuje ono za koje je djelovanje minimalno...

    Veliki enciklopedijski rječnik

  • - Knjiga Odaberite najlakši način djelovanja, izbjegavanje prepreka, izbjegavanje poteškoća...

    Frazeološki rječnik ruskog književnog jezika

"NAČELO NAJMANJE VRIJEDNOSTI" u knjigama

2.5.1. Princip rada uređaja

Iz knjige Zabavna elektronika [Nekonvencionalna enciklopedija korisnih sklopova] Autor Kaškarov Andrej Petrovič

2.5.1. Princip rada uređaja Princip rada uređaja je jednostavan. Kada se svjetlosni tok koji emitira LED HL1 reflektira od objekta i pogodi fotodetektor, elektronička jedinica, implementirana na 2 mikro kruga - komparator KR1401SA1 i mjerač vremena KR1006VI1, proizvodi

Princip rada terafima

Iz knjige Tajna znanja. Teorija i praksa Agni joge Autor Roerich Elena Ivanovna

Princip rada terafima 02.24.39 Znate da nas svaka svijest i predstava o bilo kojem objektu time približava njemu. Kao što znate, psihički slojevi objekta mogu se prenijeti na njegove terafme. Astralni terafi dalekih svjetova i

Tri uvjeta za primjenu zakona najmanjeg napora

Iz knjige Mudrost Deepaka Chopre [Ostvarite ono što želite slijedeći 7 zakona svemira] Tima Goodmana

Tri uvjeta za djelovanje Zakona najmanjeg napora Pogledajmo koji su uvjeti potrebni da u svoj život privučete ovaj kreativni tok energije iz Svemira - energiju ljubavi, a time i da Zakon najmanjeg napora počne djelovati u vašem životu .

Poglavlje 19 NAČELO NAJMANJEG UČINKA

Iz knjige 6. Elektrodinamika Autor Feynman Richard Phillips

Poglavlje 19 NAČELO NAJMANJEG UČINKA Dodatak nakon predavanja Kad sam bio u školi, naš profesor fizike, po imenu Bader, jednom me pozvao nakon nastave i rekao: “Izgledaš kao da si užasno umoran od svega; poslušajte jednu zanimljivu stvar

5. Načelo najmanjeg djelovanja

Iz knjige Revolucija u fizici od de Broglie Louisa

5. Načelo najmanjeg djelovanja Jednadžbe za dinamiku materijalne točke u polju sila s potencijalom mogu se dobiti na temelju načela koje se općenito naziva Hamiltonovo načelo ili načelo stacionarnog djelovanja. Prema ovom principu, od svih

Princip rada

Iz knjige Bravarski vodič kroz brave autora Phillipsa Billa

Princip rada Sposobnost okretanja cilindra ovisi o položaju klinova, koji je pak određen gravitacijom, djelovanjem opruga i silom ključa (ili glavnog ključa; za informacije o glavnim ključevima, vidi Poglavlje 9) . U nedostatku ključa, gravitacija i opruge pritišću

Princip stacionarnog djelovanja

Iz knjige Velika sovjetska enciklopedija (ST) autora TSB

Načelo najmanjeg djelovanja

TSB

Načelo najmanje prisile

Iz knjige Velika sovjetska enciklopedija (NA) autora TSB

2.5.1. Princip rada

Iz knjige Relejna zaštita u elektrodistribucijskim mrežama B90 Autor Bulychev Alexander Vitalievich

2.5.1. Princip rada U električnim mrežama s dvosmjernim napajanjem iu prstenastim mrežama, konvencionalna strujna zaštita ne može djelovati selektivno. Na primjer, u električnoj mreži s dva izvora napajanja (sl. 2.15), gdje su prekidači i zaštite ugrađeni s obje strane

Princip rada

Iz knjige Turbo Suslik. Kako se prestati zajebavati i početi živjeti Autor Leuškin Dmitrij

Princip djelovanja “Process this” zapravo je svojevrsni “makro” koji jednom rečenicom pokreće čitav niz procesa u podsvijesti čija je svrha obrada odabranog mentalnog materijala. Sam ovaj rukovatelj uključuje 7 različitih modula, od kojih neki

Kako početi slijediti zakon najmanjeg napora: tri potrebne radnje

Iz knjige A Guide to Growing Capital od Joseph Murphy, Dale Carnegie, Eckhart Tolle, Deepak Chopra, Barbara Sher, Neil Walsh autor Stern Valentin

Kako početi slijediti Zakon najmanjeg napora: tri potrebne radnje Da bi Zakon najmanjeg napora počeo djelovati, morate ne samo ispuniti tri gore navedena uvjeta, već i izvršiti tri radnje. Prva radnja: počnite prihvaćati svijet onakvim kakav je je Prihvatiti

11. Fizika i aikido najmanjeg djelovanja

Autor Mindell Arnold

11. Fizika i aikido najmanjeg učinka Kad puše, ima samo vjetar. Kad pada kiša, postoji samo kiša. Kad oblaci prođu, sunce sja kroz njih. Ako se otvorite uvidu, tada ste jedno s uvidom. I možete ga koristiti u potpunosti. Ako se otvoriš

Leibnizovo načelo najmanjeg djelovanja "Vis Viva"

Iz knjige Geopsihologija u šamanizmu, fizici i taoizmu Autor Mindell Arnold

Leibnizovo načelo najmanjeg djelovanja "Vis Viva" Svi imamo zahvalnost Wilhelmu Gottfriedu Leibnizu (1646.–1716.) za načelo najmanjeg djelovanja. Jedan od prvih "modernih" fizičara i matematičara, Leibniz je živio u Newtonovo doba - doba kada su znanstvenici bili otvorenije

Aikido - utjelovljenje načela najmanje akcije

Iz knjige Geopsihologija u šamanizmu, fizici i taoizmu Autor Mindell Arnold

Aikido - utjelovljenje načela najmanje akcije Naša psihologija i tehnologija u velikoj su mjeri vođeni konceptom vrlo bliskim ideji najmanje akcije. Stalno pokušavamo olakšati svoj život. Današnja računala nisu dovoljno brza; Moraju