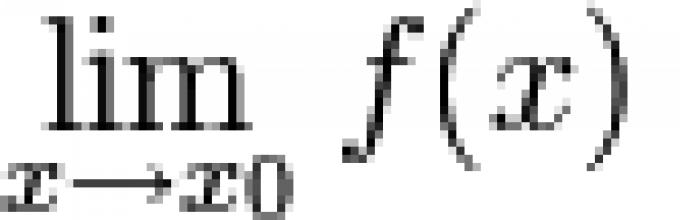Je li funkcija infinitezimalna pri. Definicija beskonačno velike funkcije. Definiranje ograničenog niza

Račun infinitezimalnih i velikih

Infinitezimalni račun- proračuni koji se izvode s infinitezimalnim veličinama, u kojima se izvedeni rezultat smatra beskonačnim zbrojem infinitezimalnih veličina. Račun infinitezimala opći je pojam za diferencijalni i integralni račun koji čini osnovu moderne više matematike. Pojam infinitezimalne količine usko je povezan s pojmom granice.

Infinitezimalno

Naknadna slijed a n nazvao infinitezimalnog, Ako . Na primjer, niz brojeva je infiniteziman.

Funkcija se zove infinitezimalna u blizini točke x 0 ako .

Funkcija se zove infinitesimal u beskonačnosti, Ako ili .

Također infinitezimalna je funkcija koja je razlika između funkcije i njezine granice, odnosno if , To f(x) − a = α( x) , .

Beskrajno velika količina

U svim formulama ispod, podrazumijeva se da beskonačnost desno od jednakosti ima određeni predznak (bilo "plus" ili "minus"). To je npr. funkcija x grijeh x, neograničen s obje strane, nije beskonačno velik na .

Naknadna slijed a n nazvao beskrajno velika, Ako .

Funkcija se zove beskonačno velika u blizini točke x 0 ako .

Funkcija se zove beskonačno velik u beskonačnosti, Ako ili .

Svojstva beskonačno malog i beskonačno velikog

Usporedba infinitezimalnih veličina

Kako usporediti infinitezimalne količine?
Omjer infinitezimalnih veličina čini tzv. nesigurnost.

Definicije

Pretpostavimo da imamo infinitezimalne vrijednosti α( x) i β( x) (ili, što za definiciju nije bitno, infinitezimalni nizovi).

Za izračun takvih granica prikladno je koristiti L'Hopitalovo pravilo.

Usporedni primjeri

Korištenje OKO-simbolika, dobiveni rezultati mogu se napisati u sljedećem obliku x 5 = o(x 3). U ovom slučaju, sljedeći unosi su istiniti: 2x 2 + 6x = O(x) I x = O(2x 2 + 6x).

Ekvivalentne vrijednosti

Definicija

Ako , tada se infinitezimalne veličine α i β nazivaju ekvivalent ().
Očito je da su ekvivalentne količine poseban slučaj infinitezimalnih veličina istog reda malenosti.

Kada vrijede sljedeći odnosi ekvivalencije (kao posljedice tzv. značajnih granica):

Teorema

Granica kvocijenta (omjera) dviju infinitezimalnih veličina neće se promijeniti ako se jedna od njih (ili obje) zamijeni ekvivalentnom količinom.

Ovaj teorem ima praktično značenje pri pronalaženju granica (vidi primjer).

Primjer upotrebe

Zamjena sjan 2x ekvivalentna vrijednost 2 x, dobivamo

Povijesna crtica

O konceptu "infinitezimalnog" raspravljalo se još u antičko doba u vezi s konceptom nedjeljivih atoma, ali nije bio uključen u klasičnu matematiku. Ponovno je oživljena dolaskom "metode nedjeljivih" u 16. stoljeću - dijeljenjem figure koja se proučava u infinitezimalne dijelove.

U 17. stoljeću došlo je do algebraizacije infinitezimalnog računa. Počele su se definirati kao numeričke veličine koje su manje od bilo koje konačne (različite od nule) količine, a opet nisu jednake nuli. Umijeće analize sastojalo se u sastavljanju relacije koja sadrži infinitezimalne vrijednosti (diferencijale) i zatim njenom integriranju.

Matematičari stare škole stavili su koncept na test infinitezimalnog oštra kritika. Michel Rolle je napisao da je novi račun " skup genijalnih grešaka"; Voltaire je zajedljivo primijetio da je račun umijeće računanja i točnog mjerenja stvari čije se postojanje ne može dokazati. Čak je i Huygens priznao da ne razumije značenje diferencijala višeg reda.

Kao ironija sudbine može se smatrati pojava sredinom stoljeća nestandardne analize, koja je dokazala da je izvorno gledište - stvarne infinitezimale - također dosljedno i da se može koristiti kao osnova za analizu.

vidi također

Zaklada Wikimedia. 2010.

Pogledajte što je "infinitezimalna količina" u drugim rječnicima:

BESKRAJNO MALA KOLIČINA- promjenljiva veličina u nekom procesu, ako se u tom procesu beskonačno približava (teži) nuli... Velika politehnička enciklopedija

Infinitezimalno- ■ Nešto nepoznato, a vezano za homeopatiju... Leksikon običnih istina

Funkcija y=f(x) nazvao infinitezimalnog na x→a ili kada x→∞, ako ili , tj. infinitezimalna funkcija je funkcija čiji je limit u danoj točki nula.

Primjeri.

1. Funkcija f(x)=(x-1) 2 je infinitezimalno na x→1, jer (vidi sliku).

2. Funkcija f(x)= tg x– infinitezimalno pri x→0.

3. f(x)= log(1+ x) – infinitezimalno pri x→0.

4. f(x) = 1/x– infinitezimalno pri x→∞.

Uspostavimo sljedeći važan odnos:

Teorema. Ako funkcija y=f(x) reprezentativan sa x→a kao zbroj konstantnog broja b i infinitezimalne veličine α(x): f (x)=b+ α(x) taj .

Obrnuto, ako je , tada f (x)=b+α(x), Gdje sjekira)– infinitezimalno pri x→a.

Dokaz.

1. Dokažimo prvi dio tvrdnje. Iz ravnopravnosti f(x)=b+α(x) trebao bi |f(x) – b|=| α|. Ali budući da sjekira) infinitezimalna, tada za proizvoljan ε postoji δ – okolina točke a, pred svima x iz kojih, vrijednosti sjekira) zadovoljiti odnos |α(x)|< ε. Zatim |f(x) – b|< ε. A ovo znači to.

2. Ako je , tada za bilo koji ε >0 za sve x iz neke δ – okoline točke a htjeti |f(x) – b|< ε. Ali ako označimo f(x) – b= α, To |α(x)|< ε, što znači da a– infinitezimalno.

Razmotrimo osnovna svojstva infinitezimalnih funkcija.

Teorem 1. Algebarski zbroj dva, tri i općenito bilo kojeg konačnog broja infinitezimala je infinitezimalna funkcija.

Dokaz. Dajmo dokaz za dva pojma. Neka f(x)=α(x)+β(x), gdje i . Moramo dokazati da za bilo koje proizvoljno malo ε > 0 pronađeno δ> 0, tako da za x, zadovoljavajući nejednakost |x – a|<δ , izvedena |f(x)|< ε.

Dakle, fiksirajmo proizvoljan broj ε > 0. Budući da prema uvjetima teorema α(x) je infinitezimalna funkcija, onda postoji takav δ 1 > 0, što je |x – a|< δ 1 imamo |α(x)|< ε / 2. Isto tako, budući da β(x) je infinitezimalno, onda postoji takav δ 2 > 0, što je |x – a|< δ 2 imamo | β(x)|< ε / 2.

Idemo uzeti δ=min(δ 1 , δ2 } .Onda u okolini točke a radius δ svaka od nejednakosti će biti zadovoljena |α(x)|< ε / 2 i | β(x)|< ε / 2. Stoga će u ovom susjedstvu biti

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

oni. |f(x)|< ε, što je i trebalo dokazati.

Teorem 2. Umnožak infinitezimalne funkcije sjekira) za ograničenu funkciju f(x) na x→a(ili kada x→∞) je infinitezimalna funkcija.

Dokaz. Budući da funkcija f(x) je ograničen, onda postoji broj M takav da za sve vrijednosti x iz neke okoline točke a|f(x)|≤M.Štoviše, budući da sjekira) je infinitezimalna funkcija na x→a, tada za proizvoljan ε > 0 postoji okolina točke a, u kojem će vrijediti nejednakost |α(x)|< ε /M. Zatim u manjim od ovih četvrti koje imamo | αf|< ε /M= ε. A ovo znači to af– infinitezimalno. Za tu priliku x→∞ dokaz se provodi na sličan način.

Iz dokazanog teoreme slijedi:

Korolar 1. Ako i, onda.

Korolar 2. Ako c= const, tada .

Teorem 3. Omjer infinitezimalne funkcije α(x) po funkciji f(x), čija je granica različita od nule, je infinitezimalna funkcija.

Dokaz. Neka . Zatim 1 /f(x) postoji ograničena funkcija. Dakle, razlomak je umnožak infinitezimalne funkcije i ograničene funkcije, tj. funkcija je infinitezimalna.

Def: Funkcija se zove infinitezimalnog u , ako .

U oznaci “ ” pretpostavit ćemo da x 0 može uzeti kao konačnu vrijednost: x 0= Sonst, i beskonačno: x 0= ∞.

Svojstva infinitezimalnih funkcija:

1) Algebarski zbroj konačnog broja infinitezimalnih funkcija je infinitezimalni zbroj funkcija.

2) Umnožak konačnog broja infinitezimalnih funkcija je infinitezimalna funkcija.

3) Umnožak ograničene funkcije i infinitezimalne funkcije je infinitezimalna funkcija.

4) Kvocijent dijeljenja infinitezimalne funkcije s funkcijom čija je granica različita od nule je infinitezimalna funkcija.

Primjer: Funkcija g = 2 + x je infinitezimalna na , jer .

Def: Funkcija se zove beskrajno velika u , ako .

Svojstva beskonačno velikih funkcija:

1) Zbroj beskonačno velikih funkcija je beskonačno velika funkcija.

2) Umnožak beskonačno velike funkcije i funkcije čija je granica različita od nule je beskonačno velika funkcija.

3) Zbroj beskonačno velike funkcije i ograničene funkcije je beskonačno velika funkcija.

4) Kvocijent dijeljenja beskonačno velike funkcije s funkcijom koja ima konačnu granicu je beskonačno velika funkcija.

Primjer: Funkcija g= je beskonačno velik na , jer .

Teorema.Odnos između beskonačno malih i beskonačno velikih veličina. Ako je funkcija infinitezimalna na , onda je funkcija beskonačno velika na . I obrnuto, ako je funkcija beskonačno velika na , tada je funkcija infinitezimalna na .

Omjer dviju infinitezimalnih veličina obično se označava simbolom , a omjer dviju infinitezimalnih veličina simbolom . Oba odnosa su neodređena u smislu da njihova granica može i ne mora postojati, biti jednaka određenom broju ili biti beskonačna, ovisno o vrsti specifičnih funkcija uključenih u neodređene izraze.

Uz nesigurnosti vrste i nesigurnosti, sljedeći izrazi su:

Razlika beskonačno velikih jednakih predznaka;

Umnožak infinitezimalnog i beskonačno velikog;

Eksponencijalna funkcija čija baza teži 1, a eksponent teži ;

Eksponencijalna funkcija čija je baza infinitezimalna, a eksponent beskonačno velik;

Eksponencijalna funkcija čija su baza i eksponent infinitezimalni;

Eksponencijalna funkcija čija je baza beskonačno velika, a eksponent infinitezimalan.

Kaže se da postoji nesigurnost odgovarajućeg tipa. U tim se slučajevima poziva granični izračun otkrivajući neizvjesnost. Da bi se otkrila nesigurnost, izraz ispod znaka granice pretvara se u oblik koji ne sadrži nesigurnost.

Pri računanju limita koriste se svojstva limita, kao i svojstva infinitezimalnih i beskonačno velikih funkcija.

Pogledajmo primjere izračuna raznih granica.

1) . 2) .

4) , jer umnožak infinitezimalne funkcije na i ograničene funkcije je infiniteziman.

5) . 6) .

7) = =

. U ovom slučaju, postojala je nesigurnost tipa, koja je riješena faktoriziranjem polinoma i njihovim svođenjem na zajednički faktor.

= .

U ovom slučaju, postojala je nesigurnost tipa , koja je riješena množenjem brojnika i nazivnika s izrazom, korištenjem formule, a zatim smanjenjem razlomka za (+1).

9)
. U ovom primjeru, nesigurnost tipa otkrivena je dijeljenjem brojnika i nazivnika razlomka s vodećom potencijom.

Divna ograničenja

Prva divna granica : .

Dokaz. Razmotrimo jedinični krug (slika 3).

sl.3. Jedinični krug

Neka x– radijanska mjera središnjeg kuta MOA(), Zatim OA = R= 1, MK= grijeh x, NA= tg x. Uspoređivanje površina trokuta OMA, OTA i sektorima OMA, dobivamo:

Posljednju nejednakost podijeli s grijehom x, dobivamo:

Budući da je na , onda po svojstvu 5) granice

Otuda inverzna vrijednost za , što je trebalo dokazati.

Komentar: Ako je funkcija infinitezimalna na , tj. , tada prva značajna granica ima oblik:

Pogledajmo primjere proračuna granica koristeći prvu značajnu granicu.

Pri izračunu ove granice koristili smo trigonometrijsku formulu: .

Pogledajmo primjere proračuna ograničenja koristeći drugu izvanrednu granicu.

2) .

3) . Postoji nesigurnost tipa. Napravimo onda zamjenu; u .

Račun infinitezimalnih i velikih

Infinitezimalno

Naknadna slijed a n nazvao infinitezimalnog, Ako . Na primjer, niz brojeva je infiniteziman.

Funkcija se zove infinitezimalna u blizini točke x 0 ako .

Funkcija se zove infinitesimal u beskonačnosti, Ako ili .

Također infinitezimalna je funkcija koja je razlika između funkcije i njezine granice, odnosno if , To f(x) − a = α( x) , .

Beskrajno velika količina

Naknadna slijed a n nazvao beskrajno velika, Ako .

Funkcija se zove beskonačno velika u blizini točke x 0 ako .

Funkcija se zove beskonačno velik u beskonačnosti, Ako ili .

U svim slučajevima podrazumijeva se da beskonačnost desno od jednakosti ima određeni predznak (bilo "plus" ili "minus"). To je npr. funkcija x grijeh x nije beskonačno velik na .

Svojstva beskonačno malog i beskonačno velikog

Usporedba infinitezimalnih veličina

Kako usporediti infinitezimalne količine?
Omjer infinitezimalnih veličina čini tzv. nesigurnost.

Definicije

Pretpostavimo da imamo infinitezimalne vrijednosti α( x) i β( x) (ili, što za definiciju nije bitno, infinitezimalni nizovi).

Za izračun takvih granica prikladno je koristiti L'Hopitalovo pravilo.

Usporedni primjeri

Korištenje OKO-simbolika, dobiveni rezultati mogu se napisati u sljedećem obliku x 5 = o(x 3). U ovom slučaju, sljedeći unosi su istiniti: 2x 2 + 6x = O(x) I x = O(2x 2 + 6x).

Ekvivalentne vrijednosti

Definicija

Ako , tada se infinitezimalne veličine α i β nazivaju ekvivalent ().
Očito je da su ekvivalentne količine poseban slučaj infinitezimalnih veličina istog reda malenosti.

Kada vrijede sljedeći odnosi ekvivalencije: , , .

Teorema

Granica kvocijenta (omjera) dviju infinitezimalnih veličina neće se promijeniti ako se jedna od njih (ili obje) zamijeni ekvivalentnom količinom.

Ovaj teorem ima praktično značenje pri pronalaženju granica (vidi primjer).

Primjer upotrebe

Zamjena sjan 2x ekvivalentna vrijednost 2 x, dobivamo

Povijesna crtica

vidi također

Zaklada Wikimedia. 2010.

Pogledajte što je "beskonačno velik" u drugim rječnicima:

Varijabilna veličina Y je inverzna infinitezimalnoj količini X, to jest, Y = 1/X... Veliki enciklopedijski rječnik

Varijabla y je inverzna od infinitezimalnog x, to jest, y = 1/x. * * * BESKONAČNO VELIKA BESKONAČNO VELIKA, varijabilna veličina Y, inverzna infinitezimalnoj količini X, odnosno Y = 1/X ... enciklopedijski rječnik

U matematici, varijabilna veličina koja, u određenom procesu promjene, postaje i ostaje veća u apsolutnoj vrijednosti od bilo kojeg unaprijed određenog broja. Studija B. b. količine se mogu svesti na proučavanje infinitezimala (vidi... ... Velika sovjetska enciklopedija

Funkcija se zove infinitezimalno at
ili kada
, Ako
ili
.

Na primjer: funkcija
infinitezimalno at
; funkcija
infinitezimalno at
.

Napomena 1. Bez naznake smjera promjene argumenta nijednu funkciju ne možemo nazvati infinitezimalnom. Da, funkcija
na
je infinitezimalna, a kada
više nije infinitezimalno (
).

Napomena 2. Iz definicije limita funkcije u točki, za infinitezimalne funkcije vrijedi sljedeća nejednakost:
Tu ćemo činjenicu koristiti više puta u budućnosti.

Ustanovimo neke važne svojstva infinitezimalnih funkcija.

Teorema (o vezi između funkcije, njezine granice i infinitezimala): Ako funkcija
može se prikazati kao zbroj konstantnog broja A i infinitezimalna funkcija
na
, zatim broj

Dokaz:

Iz uvjeta teorema slijedi da funkcija
.

Izrazimo odavde
:
. Budući da funkcija
infinitezimalno, za njega vrijedi nejednakost
, zatim za izraz (
) nejednakost također vrijedi

A ovo znači to
.

Teorema (naličje): ako
, zatim funkcija
može se predstaviti kao zbroj broja A a infinitezimalne at
funkcije
, tj.
.

Dokaz:

Jer
, zatim za
nejednakost vrijedi
(*) Razmotrimo funkciju
kao jednu i prepišite nejednakost (*) u obliku

Iz posljednje nejednakosti slijedi da je vrijednost (
) je infinitezimalna na
. Označimo to
.

Gdje
. Teorem je dokazan.

Teorem 1 . Algebarski zbroj konačnog broja infinitezimalnih funkcija je infinitezimalna funkcija.

Dokaz:

Provedimo dokaz za dva člana, budući da je za svaki konačan broj članova dan na sličan način.

Neka
I
infinitezimalno at
funkcije i
– zbroj ovih funkcija. Dokažimo to za
, postoji takva stvar
to je za sve x, zadovoljavajući nejednakost
, nejednakost vrijedi
.

Budući da funkcija
infinitezimalna funkcija
to je za sve
nejednakost vrijedi
.

Budući da funkcija
infinitezimalna funkcija
, i stoga postoji takav to je za sve
nejednakost vrijedi
.

Idemo uzeti jednak manjem broju I , zatim unutra – okolina točke A nejednakosti će biti zadovoljene
,
.

Kreirajmo funkcijski modul
i ocijeniti njegov značaj.

To je
, tada je funkcija infinitezimalna, što je i trebalo dokazati.

Teorem 2. Umnožak infinitezimalne funkcije
na
za ograničenu funkciju
je infinitezimalna funkcija.

Dokaz:

Budući da funkcija
ograničen, onda postoji pozitivan broj
to je za sve nejednakost vrijedi
.

Budući da funkcija
infinitezimalno at
, onda postoji takav – okolina točke to je za sve u ovom susjedstvu nejednakost
.

Razmotrite funkciju
i ocijeniti njegov modul

Tako
, i onda
– infinitezimalno.

Teorem je dokazan.

Granični teoremi.

Teorem 1. Limit algebarskog zbroja konačnog broja funkcija jednak je algebarskom zbroju limita tih funkcija

Dokaz:

Da bismo to dokazali, dovoljno je razmotriti dvije funkcije; to neće narušiti općenitost razmišljanja.

Neka
,
.

Prema teoremu o vezi između funkcije, njezine granice i infinitezimalne funkcije
I
može se prikazati u obliku
Gdje
I
– infinitezimalno pri
.

Nađimo zbroj funkcija
I

Veličina
postoji konstantna vrijednost
– količina je infinitezimalna. Dakle funkcija
predstavljena kao zbroj konstantne vrijednosti i infinitezimalne funkcije.

Zatim broj
je granica funkcije
, tj.

Teorem je dokazan.

Teorem 2 . Limes umnoška konačnog broja funkcija jednak je umnošku limesa tih funkcija

Dokaz:

Ne gubeći općenitost zaključivanja, provest ćemo dokaz za dvije funkcije
I
.

Neka bude onda
,

Nađimo produkt funkcija
I

Veličina
je konstantna veličina, infinitezimalna funkcija. Stoga se broj
je granica funkcije
, odnosno jednakost je istinita

Posljedica:
.

Teorem 3. Limit kvocijenta dviju funkcija jednak je kvocijentu limesa tih funkcija ako je limit nazivnika različit od nule.

Dokaz: Neka
,

Zatim
,
.

Nađimo kvocijent i izvršiti neke identične transformacije na njemu

Veličina konstanta, razlomak
beskrajno malen. Prema tome, funkcija predstavljen kao zbroj konstantnog broja i infinitezimalne funkcije.

Zatim
.

Komentar. Teoremi 1-3 su dokazani za slučaj
. Međutim, oni mogu biti primjenjivi kada
, budući da se dokaz teorema u ovom slučaju provodi na sličan način.

Na primjer. Pronađite ograničenja:

Prvo i drugo su divne granice.

Funkcija nije definirano na
. Međutim, njegove vrijednosti u blizini nulte točke postoje. Stoga možemo razmotriti limit ove funkcije na
. Ova granica se zove prvi prekrasno ograničiti .

Izgleda kao:
.

Na primjer . Pronađite granice: 1.
. Odrediti
, Ako
, To
.
; 2.
. Transformirajmo ovaj izraz tako da se granica svede na prvu značajnu granicu.
; 3..

Razmotrimo varijablu oblika
, pri čemu uzima vrijednosti prirodnih brojeva u rastućem redoslijedu. Dajmo različita značenja: ako

Davanje sljedeće vrijednosti iz skupa
, lako je vidjeti da izraz
na
htjeti
. Štoviše, dokazano je da
ima granicu. Ova granica je označena slovom :
.

Broj iracionalno:
.

Sada razmotrite granicu funkcije
na
. Ova granica se zove drugo značajno ograničenje

Izgleda kao
.

Na primjer.

A)
. Izraz
zamijenite proizvodom identične faktore
, primjenjujemo teorem o granici proizvoda i drugu izvanrednu granicu; b)
. Stavimo
, Zatim
,
.

Drugo značajno ograničenje koristi se u problem kontinuiranog slaganja

Pri izračunu novčanih prihoda na depozite često se koristi formula složenih kamata koja izgleda ovako:

Gdje - početni doprinos,

- godišnje bankovne kamate,

- broj obračunatih kamata godišnje,

- vrijeme, u godinama.

Međutim, u teorijskim studijama, prilikom opravdavanja investicijskih odluka, često se koristi formula eksponencijalnog (eksponencijalnog) zakona rasta

Formula za zakon eksponencijalnog rasta dobiva se kao rezultat primjene druge značajne granice na formulu složenih kamata

Kontinuitet funkcija.

Razmotrite funkciju
definiran u nekom trenutku i neko susjedstvo točke . Neka funkcija ima vrijednost u naznačenoj točki
.

Definicija 1. Funkcija
nazvao kontinuirano u točki , ako je definiran u susjedstvu točke, uključujući samu točku i
.

Definicija kontinuiteta može se drugačije formulirati.

Neka funkcija
definirana na neku vrijednost ,
. Ako argument dati prirast
, tada će funkcija dobiti inkrement

Neka funkcija u točki kontinuirano (prema prvoj definiciji neprekidnosti funkcije u točki),

To jest, ako je funkcija kontinuirana u točki , zatim infinitezimalno povećanje argumenta
u ovoj točki odgovara infinitezimalni inkrement funkcije.

Vrijedi i obrnuto: ako infinitezimalni prirast u argumentu odgovara infinitezimalnom prirastu u funkciji, tada je funkcija kontinuirana.

Definicija 2. Funkcija
naziva se kontinuirano pri
(u točki ), ako je definiran u ovoj točki i nekoj njegovoj okolini i ako
.

Uzimajući u obzir prvu i drugu definiciju kontinuiteta funkcije u točki, možemo dobiti sljedeću tvrdnju:

ili
, Ali
, Zatim
.

Stoga, da bi se našla granica kontinuirane funkcije na
dovoljno je umjesto argumenta koristiti izraz analitičke funkcije zamijeniti njegovu vrijednost .

Definicija 3. Funkcija koja je kontinuirana u svakoj točki određenog područja naziva se stalan u ovom području.

Na primjer:

Primjer 1. Dokažite da funkcija
kontinuirana je u svim točkama domene definicije.

Upotrijebimo drugu definiciju neprekidnosti funkcije u točki. Da biste to učinili, uzmite bilo koju vrijednost argumenta i dajte mu prirast
. Nađimo odgovarajući inkrement funkcije

Primjer 2. Dokaži da funkcija
kontinuirano u svim točkama iz
.

Dajmo argumentaciju prirast
, tada će se funkcija povećati

Nađimo budući da funkcija
, odnosno ograničeno.

Slično se može dokazati da su sve osnovne elementarne funkcije kontinuirane u svim točkama svoje domene definicije, odnosno da se domena definicije elementarne funkcije podudara s njezinom domenom kontinuiteta.

Definicija 4. Ako je funkcija
kontinuirano u svakoj točki nekog intervala
, tada kažemo da je funkcija kontinuirana na tom intervalu.