Решавањето равенки во математиката зазема посебно место. На овој процес му претходат многу часови учење теорија, при што студентот учи како да решава равенки, да го одредува нивниот тип и да ја доведе вештината до целосна автоматизација. Сепак, потрагата по корени не секогаш има смисла, бидејќи тие можеби едноставно не постојат. Постојат посебни техники за наоѓање корени. Во оваа статија ќе ги анализираме главните функции, нивните домени на дефиниција, како и случаите кога недостасуваат нивните корени.
Која равенка нема корени?
Равенката нема корени ако нема вистински аргументи x за кои равенката е идентично вистинита. За лаик оваа формулација, како и повеќето математички теоремии формули, изгледа многу матно и апстрактно, но ова е во теорија. Во пракса, сè станува исклучително едноставно. На пример: равенката 0 * x = -53 нема решение, бидејќи не постои број x чиј производ со нула би дал нешто друго освен нула.
Сега ќе погледнеме најмногу основни типовиравенки.
1. Линеарна равенка
Равенката се нарекува линеарна ако нејзината десна и лева страна се претставени во форма линеарни функции: ax + b = cx + d или во генерализирана форма kx + b = 0. Каде a, b, c, d се познати броеви, а x е непозната величина. Која равенка нема корени? Примери на линеарни равенки се претставени на илустрацијата подолу.
Во основа, линеарните равенки се решаваат со едноставно пренесување на бројниот дел на еден дел и содржината на x во друг. Резултатот е равенка од формата mx = n, каде што m и n се броеви, а x е непозната. За да најдете x, само поделете ги двете страни со m. Тогаш x = n/m. Повеќето линеарни равенки имаат само еден корен, но има случаи кога има или бесконечно многу корени или воопшто нема корени. Кога m = 0 и n = 0, равенката добива форма 0 * x = 0. Решението на таквата равенка ќе биде апсолутно секој број.
Меѓутоа, која равенка нема корени?
За m = 0 и n = 0, равенката нема корени од множеството реални броеви. 0 * x = -1; 0 * x = 200 - овие равенки немаат корени.
2. Квадратна равенка
Квадратна равенка е равенка од формата ax 2 + bx + c = 0 за a = 0. Најчестото решение е преку дискриминантата. Формула за пронаоѓање на дискриминаторот квадратна равенка: D = b 2 - 4 * a * c. Потоа има два корени x 1,2 = (-b ± √D) / 2 * a.
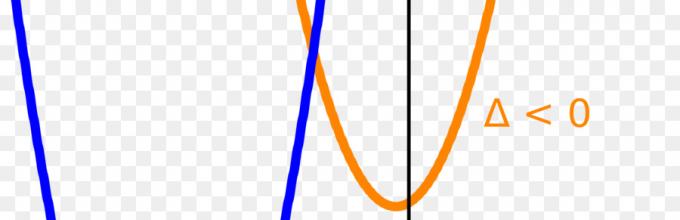
За D > 0 равенката има два корени, за D = 0 има еден корен. Но, која квадратна равенка нема корени? Најлесен начин да се набљудува бројот на корените на квадратната равенка е со графички приказ на функцијата, која е парабола. За a > 0 гранките се насочени нагоре, за a< 0 ветви опущены вниз. Если дискриминант отрицателен, такое квадратное уравнение не имеет корней на множестве действительных чисел.

Можете исто така визуелно да го одредите бројот на корените без да го пресметате дискриминаторот. За да го направите ова, треба да го пронајдете темето на параболата и да одредите во која насока се насочени гранките. Координатата x на темето може да се одреди со помош на формулата: x 0 = -b / 2a. Во овој случај, y координатата на темето се наоѓа со едноставно замена на вредноста x 0 во првобитната равенка.

Квадратната равенка x 2 - 8x + 72 = 0 нема корени, бидејќи има негативна дискриминантна D = (-8) 2 - 4 * 1 * 72 = -224. Ова значи дека параболата не ја допира оската x и функцијата никогаш не ја зема вредноста 0, затоа равенката нема вистински корени.
3. Тригонометриски равенки
Тригонометриските функции се разгледуваат на тригонометриски круг, но можат да бидат претставени и во Декартов координатен систем. Во оваа статија ќе разгледаме две главни тригонометриски функциии нивните равенки: sinx и cosx. Бидејќи овие функции се формираат тригонометриски кругсо радиус 1, |sinx| и |cosx| не може да биде поголема од 1. Значи, која равенка синкс нема корени? Да го погледнеме графикот sinx функции, прикажан на сликата подолу.

Гледаме дека функцијата е симетрична и има период на повторување од 2pi. Врз основа на ова, можеме да кажеме дека максималната вредност на оваа функција може да биде 1, а минималната -1. На пример, изразот cosx = 5 нема да има корени, бидејќи неговата апсолутна вредност е поголема од еден.
Ова е наједноставниот пример на тригонометриски равенки. Всушност, нивното решавање може да потрае многу страници, на крајот од кои сфаќате дека сте користеле погрешна формула и треба да започнете одново. Понекогаш, дури и ако правилно ги пронајдете корените, може да заборавите да ги земете предвид ограничувањата на ОД, поради што во одговорот се појавува дополнителен корен или интервал, а целиот одговор се претвора во грешка. Затоа, строго следете ги сите ограничувања, бидејќи не сите корени се вклопуваат во опсегот на задачата.
4. Системи на равенки
Систем од равенки е збир на равенки споени со кадрави или квадратни загради. Кадравите загради покажуваат дека сите равенки се поставени заедно. Односно, ако барем една од равенките нема корени или противречи на друга, целиот систем нема решение. Квадратни загради го означуваат зборот „или“. Ова значи дека ако барем една од равенките на системот има решение, тогаш целиот систем има решение.

Одговорот на системот c е множество од сите корени на поединечните равенки. И системите со кадрави загради имаат само заеднички корени. Системите на равенки можат да вклучуваат сосема различни функции, така што таквата сложеност не ни дозволува веднаш да кажеме која равенка нема корени.
Пронајден во проблематични книги и учебници различни видовиравенки: оние што имаат корени и оние што немаат. Како прво, ако не можете да ги најдете корените, немојте да мислите дека воопшто ги нема. Можеби сте згрешиле некаде, тогаш само треба внимателно да ја проверите вашата одлука.
Ги разгледавме најосновните равенки и нивните типови. Сега можете да кажете која равенка нема корени. Во повеќето случаи тоа не е тешко да се направи. Постигнувањето успех во решавањето на равенките бара само внимание и концентрација. Вежбајте повеќе, тоа ќе ви помогне многу подобро и побрзо да се движите низ материјалот.
Значи, равенката нема корени ако:
- во линеарната равенка mx = n вредноста е m = 0 и n = 0;
- во квадратна равенка, ако дискриминантата е помала од нула;
- В тригонометриска равенкаод формата cosx = m / sinx = n, ако |m| > 0, |n| > 0;
- во систем на равенки со кадрави загради, ако барем една равенка нема корени, и со квадратни загради, ако сите равенки немаат корени.
Видео туторијал 2: Решавање на квадратни равенки
Предавање: Квадратни равенки
Равенка
Равенка- ова е еден вид еднаквост во чии изрази има променлива.
Решете ја равенката- значи наоѓање број наместо променлива што ќе го доведе во правилна еднаквост.
Равенката може да има едно решение, неколку или воопшто да нема.
За да се реши која било равенка, треба да се поедностави колку што е можно во формата:
Линеарно: a*x = b;
Плоштад: a*x 2 + b*x + c = 0.
Односно, сите равенки мора да се претворат во стандардна форма пред да се решат.
Секоја равенка може да се реши на два начина: аналитички и графички.
На графиконот како решение на равенката се сметаат точките во кои графикот ја пресекува оската OX.
Квадратни равенки
Равенката може да се нарече квадратна ако, кога е поедноставена, ја има формата:
a*x 2 + b*x + c = 0.
Во исто време а, б, все коефициенти на равенката кои се разликуваат од нула. А "Х"- коренот на равенката. Се верува дека квадратната равенка има два корени или можеби нема воопшто решение. Добиените корени може да бидат исти.
"А"- коефициентот што стои пред квадратниот корен.
"б"- стои пред непознатото во прв степен.
"Со" - слободен членравенки
Ако, на пример, имаме равенка од формата:
2x 2 -5x+3=0
Во него, „2“ е коефициентот на водечкиот член на равенката, „-5“ е вториот коефициент, а „3“ е слободен член.
Решавање на квадратна равенка
Има огромна разновидност на начини за решавање на квадратна равенка. Меѓутоа, во училишен курсВо математиката, решението се изучува со помош на теоремата на Виета, како и со користење на дискриминантот.
Дискриминантно решение:
При решавање со овој методпотребно е да се пресмета дискриминаторот користејќи ја формулата:
![]()
Ако за време на вашите пресметки откриете дека дискриминаторот е помал од нула, тоа значи дека оваа равенка нема решенија.
Ако дискриминаторот е нула, тогаш равенката има две идентични решенија. Во овој случај, полиномот може да се склопи со помош на скратената формула за множење во квадрат од збирот или разликата. Потоа решете го како линеарна равенка. Или користете ја формулата:
Ако дискриминаторот е поголем од нула, тогаш мора да го користите следниов метод:

Теорема на Виета
Ако е дадена равенката, односно коефициентот на водечкиот член е еднаков на еден, тогаш можете да го користите Теорема на Виета.
Значи, да претпоставиме дека равенката е:
Корените на равенката се наоѓаат на следниов начин:

Нецелосна квадратна равенка
Постојат неколку опции за добивање на нецелосна квадратна равенка, чиј тип зависи од присуството на коефициенти.
1. Ако вториот и третиот коефициент се нула (b = 0, c = 0), тогаш квадратната равенка ќе изгледа вака:
Оваа равенка ќе има единственото решение. Равенството ќе биде точно само ако решението на равенката е нула.
Некои проблеми во математиката бараат способност да се пресмета вредноста на квадратниот корен. Таквите проблеми вклучуваат решавање равенки од втор ред. Во оваа статија ќе презентираме ефективен методпресметки квадратни корении користете го при работа со формули за корени на квадратна равенка.
Што е квадратен корен?
Во математиката, овој концепт одговара на симболот √. Историските податоци велат дека за прв пат бил употребен околу првата половина на 16 век во Германија (првото германско дело за алгебра од Кристоф Рудолф). Научниците веруваат дека наведениот симбол е трансформирана латинска буква r (радикс значи „корен“ на латински).
Коренот на кој било број е еднаков на вредноста чиј квадрат одговара на радикалниот израз. На јазикот на математиката, оваа дефиниција ќе изгледа вака: √x = y, ако y 2 = x.
Коренот на позитивен број (x > 0) е исто така позитивен број (y > 0), но ако го земете коренот на негативен број (x< 0), то его результатом уже будет комплексен број, вклучувајќи ја имагинарната единица i.
Еве два едноставни примери:
√9 = 3, бидејќи 3 2 = 9; √(-9) = 3i, бидејќи i 2 = -1.
Хероновата итеративна формула за пронаоѓање на вредностите на квадратните корени
Горенаведените примери се многу едноставни, а пресметувањето на корените во нив не е тешко. Почнуваат да се појавуваат тешкотии при наоѓање коренски вредности за која било вредност што не може да се претстави како квадрат природен број, на пример √10, √11, √12, √13, а да не зборуваме за фактот дека во пракса е неопходно да се најдат корени за нецелобројни броеви: на пример √(12,15), √(8,5) и така натаму.

Во сите горенаведени случаи, треба да се користи посебен метод за пресметување на квадратниот корен. Во моментов, познати се неколку такви методи: на пример, проширување на серијата Тејлор, поделба на колони и некои други. Од сите познати методи, можеби наједноставниот и најефикасен е употребата на Хероновата итеративна формула, која е позната и како вавилонски метод за одредување квадратни корени (постојат докази дека античките Вавилонци го користеле во своите практични пресметки).
Нека биде неопходно да се одреди вредноста на √x. Формулата за наоѓање на квадратен корен е како што следува:
a n+1 = 1/2(a n +x/a n), каде што lim n->∞ (a n) => x.
Ајде да ја дешифрираме оваа математичка нотација. За да пресметате √x, треба да земете одреден број a 0 (може да биде произволен, но за брзо да го добиете резултатот, треба да го изберете така што (a 0) 2 е што е можно поблиску до x. Потоа заменете го во означена формула за пресметување на квадратниот корен и да се добие нов број a 1, кој веќе ќе биде поблиску до саканата вредност По ова, потребно е да се замени 1 во изразот и да се добие 2. Оваа постапка треба да се повтори додека. се добива потребната точност.
Пример за користење на итеративната формула на Херон
Алгоритмот опишан погоре за добивање на квадратен корен на даден број може да звучи прилично комплициран и збунувачки за многумина, но во реалноста сè се покажува многу поедноставно, бидејќи оваа формула се конвергира многу брзо (особено ако се избере успешен број a 0) .
Да дадеме едноставен пример: треба да пресметате √11. Ајде да избереме 0 = 3, бидејќи 3 2 = 9, што е поблиску до 11 отколку 4 2 = 16. Заменувајќи во формулата, добиваме:
a 1 = 1/2 (3 + 11/3) = 3,333333;
a 2 = 1/2 (3,33333 + 11/3,33333) = 3,316668;
a 3 = 1/2 (3,316668 + 11/3,316668) = 3,31662.
Нема смисла да се продолжи со пресметките, бидејќи откривме дека 2 и 3 почнуваат да се разликуваат само на 5-то децимално место. Така, беше доволно да се примени формулата само 2 пати за да се пресмета √11 со точност од 0,0001.
Во денешно време, калкулаторите и компјутерите се широко користени за пресметување на корените, меѓутоа, корисно е да се запамети означената формула за да може рачно да се пресмета нивната точна вредност.
Равенки од втор ред
Разбирањето што е квадратен корен и способноста за негово пресметување се користи при решавање на квадратни равенки. Овие равенки се нарекуваат еднаквости со една непозната, чија општа форма е прикажана на сликата подолу.

Овде c, b и a претставуваат некои броеви, а a не смее да биде еднаква на нула, а вредностите на c и b можат да бидат целосно произволни, вклучително и еднакви на нула.
Сите вредности на x што ја задоволуваат еднаквоста наведена на сликата се нарекуваат негови корени (овој концепт не треба да се меша со квадратниот корен √). Бидејќи равенката што се разгледува е од втор ред (x 2), тогаш не може да има повеќе од два корени за неа. Ајде да погледнеме понатаму во статијата како да ги пронајдеме овие корени.
Наоѓање на корените на квадратна равенка (формула)
Овој метод на решавање на видот на еднаквостите што се разгледуваат уште се нарекува и универзален метод, или метод на дискриминација. Може да се користи за какви било квадратни равенки. Формулата за дискриминација и корените на квадратната равенка е следна:

Тоа покажува дека корените зависат од вредноста на секој од трите коефициенти на равенката. Покрај тоа, пресметката на x 1 се разликува од пресметката на x 2 само со знакот пред квадратниот корен. Радикалниот израз, кој е еднаков на b 2 - 4ac, не е ништо повеќе од дискриминатор на односната еднаквост. Дискриминантот во формулата за корените на квадратна равенка игра важна улога, бидејќи го одредува бројот и видот на решенијата. Значи, ако е еднакво на нула, тогаш ќе има само едно решение, ако е позитивно, тогаш равенката има два реални корени, и на крајот, негативната дискриминантна води до два сложени корени x 1 и x 2.
Теорема на Виета или некои својства на корените на равенките од втор ред
На крајот на 16 век, еден од основачите на модерната алгебра, Французин, кој ги проучувал равенките од втор ред, можел да ги добие својствата на нејзините корени. Математички тие можат да бидат напишани вака:
x 1 + x 2 = -b / a и x 1 * x 2 = c / a.
Двете еднаквости може лесно да ги добие секој за да го направи тоа, само треба да ги извршите соодветните математички операции со корените добиени преку формулата со дискриминаторот.

Комбинацијата на овие два изрази со право може да се нарече втората формула за корените на квадратната равенка, што овозможува да се погодат нејзините решенија без користење на дискриминатор. Овде треба да се забележи дека иако и двата израза се секогаш валидни, погодно е да се користат за решавање на равенката само ако може да се факторизира.
Задача за консолидирање на стекнатото знаење
Ајде да одлучиме математички проблем, во која ќе ги демонстрираме сите техники што се дискутирани во статијата. Условите на проблемот се следни: треба да најдете два броја за кои производот е -13, а збирот е 4.

Оваа состојба веднаш не потсетува на теоремата на Виета, користејќи ги формулите за збир на квадратни корени и нивниот производ, пишуваме:
x 1 + x 2 = -b / a = 4;
x 1 * x 2 = c / a = -13.
Ако претпоставиме дека a = 1, тогаш b = -4 и c = -13. Овие коефициенти ни овозможуваат да создадеме равенка од втор ред:
x 2 - 4x - 13 = 0.
Ајде да ја користиме формулата со дискриминаторот и да ги добиеме следните корени:
x 1,2 = (4 ± √D)/2, D = 16 - 4 * 1 * (-13) = 68.
Односно, проблемот се сведе на пронаоѓање на бројот √68. Забележете дека 68 = 4 * 17, а потоа, користејќи го својството на квадратен корен, добиваме: √68 = 2√17.
Сега да ја користиме формулата за разгледување квадратен корен: a 0 = 4, а потоа:
a 1 = 1/2 (4 + 17/4) = 4,125;
a 2 = 1/2 (4,125 + 17/4,125) = 4,1231.
Нема потреба да се пресметува 3, бидејќи пронајдените вредности се разликуваат само за 0,02. Така, √68 = 8,246. Заменувајќи го во формулата за x 1,2, добиваме:
x 1 = (4 + 8,246)/2 = 6,123 и x 2 = (4 - 8,246)/2 = -2,123.
Како што можеме да видиме, збирот на пронајдените броеви е навистина еднаков на 4, но ако го најдеме нивниот производ, тогаш тој ќе биде еднаков на -12,999, што ги задоволува условите на проблемот со точност од 0,001.
Ве потсетуваме дека целосната квадратна равенка е равенка од формата:
Решавањето на целосни квадратни равенки е малку потешко (само малку) од овие.
Запомнете Секоја квадратна равенка може да се реши со помош на дискриминатор!
Дури и нецелосни.
Останатите методи ќе ви помогнат да го направите тоа побрзо, но ако имате проблеми со квадратните равенки, прво совладајте го решението користејќи ја дискриминаторот.
1. Решавање на квадратни равенки со помош на дискриминант.
Решавањето на квадратните равенки со помош на овој метод е многу едноставно, главната работа е да се запамети низата дејства и неколку формули.
Ако, тогаш равенката има 2 корени. Треба да обрнете посебно внимание на чекор 2.
Дискриминантот D ни го кажува бројот на корените на равенката.
- Ако, тогаш формулата во чекорот ќе се сведе на. Така, равенката ќе има само корен.
- Ако, тогаш нема да можеме да го извлечеме коренот на дискриминаторот на чекорот. Ова покажува дека равенката нема корени.
Да се свртиме кон геометриска смислаквадратна равенка.
Графикот на функцијата е парабола:
Да се вратиме на нашите равенки и да погледнеме неколку примери.
Пример 9
Решете ја равенката
Чекор 1прескокнуваме.
Чекор 2.
Го наоѓаме дискриминаторот:
Ова значи дека равенката има два корени.
Чекор 3.
Одговор:
Пример 10
Решете ја равенката
Равенката е претставена во стандардна форма, па Чекор 1прескокнуваме.
Чекор 2.
Го наоѓаме дискриминаторот:
Ова значи дека равенката има еден корен.
Одговор:
Пример 11
Решете ја равенката
Равенката е претставена во стандардна форма, па Чекор 1прескокнуваме.
Чекор 2.
Го наоѓаме дискриминаторот:
Ова значи дека нема да можеме да го извлечеме коренот на дискриминаторот. Нема корени на равенката.
Сега знаеме како правилно да ги запишеме таквите одговори.
Одговор:без корени
2. Решавање на квадратни равенки со помош на теоремата на Виета
Ако се сеќавате, постои еден вид равенка што се нарекува намалена (кога коефициентот a е еднаков на):
Ваквите равенки се многу лесно да се решат користејќи ја теоремата на Виета:
Збир на корени даденаквадратната равенка е еднаква, а производот на корените е еднаков.
Треба само да изберете пар броеви чиј производ е еднаков на слободниот член на равенката, а збирот е еднаков на вториот коефициент, земен со спротивен знак.
Пример 12
Решете ја равенката
Оваа равенка може да се реши со помош на теоремата на Виета бидејќи .
Збирот на корените на равенката е еднаков, т.е. ја добиваме првата равенка:
И производот е еднаков на:
Ајде да го составиме и решиме системот:
- И. Износот е еднаков на;
- И. Износот е еднаков на;
- И. Износот е еднаков.
и се решение за системот:
Одговор: ; .
Пример 13
Решете ја равенката
Одговор:
Пример 14
Решете ја равенката
Равенката е дадена, што значи:
Одговор:
КВАДРАТНИ РАВЕНКИ. СРЕДНО НИВО
Што е квадратна равенка?
Со други зборови, квадратна равенка е равенка на формата, каде што - непознатото, - некои броеви и.
Бројот се нарекува највисок или првиот коефициентквадратна равенка, - втор коефициент, А - слободен член.
Затоа што ако равенката веднаш стане линеарна, затоа што ќе исчезне.
Во овој случај, и може да биде еднаква на нула. Во овој стол се вика равенката нецелосни.
Ако сите поими се на место, тоа е, равенката е комплетен.
Методи за решавање на нецелосни квадратни равенки
Прво, да ги погледнеме методите за решавање на нецелосни квадратни равенки - тие се поедноставни.
Можеме да ги разликуваме следниве видови равенки:
I., во оваа равенка коефициентот и слободниот член се еднакви.
II. , во оваа равенка коефициентот е еднаков.
III. , во оваа равенка слободниот член е еднаков на.
Сега да го погледнеме решението за секој од овие подтипови.
Очигледно, оваа равенка секогаш има само еден корен:
Квадратен број не може да биде негативен, бидејќи кога се множат два негативни или два позитивни броја, резултатот секогаш ќе биде позитивен број. Затоа:
ако, тогаш равенката нема решенија;
ако имаме два корени
Нема потреба да ги меморирате овие формули. Главната работа што треба да се запамети е дека не може да биде помала.
Примери за решавање на квадратни равенки
Пример 15
Одговор:
Никогаш не заборавајте за корените со негативен знак!
Пример 16
Квадратот на број не може да биде негативен, што значи дека равенката
без корени.
За накратко да запишеме дека проблемот нема решенија, ја користиме иконата за празно поставување.
Одговор:
Пример 17
Значи, оваа равенка има два корени: и.
Одговор:
Да го извадиме заедничкиот фактор од загради:
Производот е еднаков на нула ако барем еден од факторите е еднаков на нула. Ова значи дека равенката има решение кога:
Значи, оваа квадратна равенка има два корени: и.
Пример:
Решете ја равенката.
Решение:
Да ја пресметаме левата страна на равенката и да ги најдеме корените:
Одговор:
Методи за решавање на целосни квадратни равенки
1. Дискриминаторски
Решавањето на квадратните равенки на овој начин е лесно, главната работа е да се запамети низата на дејства и неколку формули. Запомнете, секоја квадратна равенка може да се реши со помош на дискриминатор! Дури и нецелосни.
Дали го забележавте коренот од дискриминантот во формулата за корени?
Но, дискриминаторот може да биде негативен.
Што да се прави?
Треба да обрнеме посебно внимание на чекор 2. Дискриминаторот ни го кажува бројот на корените на равенката.
- Ако, тогаш равенката има корени:
- Ако, тогаш равенката има исти корени, а всушност, еден корен:
Таквите корени се нарекуваат двојни корени.
- Ако, тогаш коренот на дискриминаторот не е извлечен. Ова покажува дека равенката нема корени.
Зошто е можно различни количиникорени?
Да се свртиме кон геометриското значење на квадратната равенка. Графикот на функцијата е парабола:

Во посебен случај, кој е квадратна равенка, .
Ова значи дека корените на квадратната равенка се точките на пресек со оската на апсцисата (оската).
Параболата може воопшто да не ја пресекува оската или може да ја пресече на една (кога темето на параболата лежи на оската) или две точки.
Покрај тоа, коефициентот е одговорен за насоката на гранките на параболата. Ако, тогаш гранките на параболата се насочени нагоре, а ако, тогаш надолу.
4 примери за решавање на квадратни равенки
Пример 18
Одговор:
Пример 19
Одговор:.
Пример 20
Одговор:
Пример 21
Ова значи дека нема решенија.
Одговор:.
2. Теорема на Виета
Користењето на теоремата на Виета е многу лесно.
Се што ви треба е подигнететаков пар на броеви, чиј производ е еднаков на слободниот член на равенката, а збирот е еднаков на вториот коефициент, земен со спротивен знак.
Важно е да се запамети дека теоремата на Виета може да се примени само во намалени квадратни равенки ().
Ајде да погледнеме неколку примери:
Пример 22
Решете ја равенката.
Решение:
Оваа равенка може да се реши со помош на теоремата на Виета бидејќи . Други коефициенти: ; .
Збирот на корените на равенката е:
И производот е еднаков на:
Ајде да избереме парови на броеви чиј производ е еднаков и да провериме дали нивниот збир е еднаков:
- И. Износот е еднаков на;
- И. Износот е еднаков на;
- И. Износот е еднаков.
и се решение за системот:
Така, и се корените на нашата равенка.
Одговор: ; .
Пример 23
Решение:
Ајде да избереме парови на броеви што даваат во производот, а потоа да провериме дали нивниот збир е еднаков:
и: вкупно даваат.
и: вкупно даваат. За да се добие, доволно е едноставно да се сменат знаците на наводните корени: и, на крајот на краиштата, производот.
Одговор:
Пример 24
Решение:
Слободниот член на равенката е негативен, и затоа производот на корените е негативен број. Ова е можно само ако еден од корените е негативен, а другиот е позитивен. Затоа збирот на корените е еднаков на разлики во нивните модули.
Дозволете ни да избереме парови на броеви кои даваат во производот, а чија разлика е еднаква на:
и: нивната разлика е еднаква - не одговара;
и: - не е соодветно;
и: - не е соодветно;
и: - погоден. Останува само да се запамети дека еден од корените е негативен. Бидејќи нивниот збир мора да биде еднаков, коренот со помал модул мора да биде негативен: . Проверуваме:
Одговор:
Пример 25
Решете ја равенката.
Решение:
Равенката е дадена, што значи:
Слободниот член е негативен, и затоа производот на корените е негативен. И ова е можно само кога едниот корен од равенката е негативен, а другиот позитивен.
Ајде да избереме парови чиј производ е еднаков, а потоа да одредиме кои корени треба да имаат негативен знак:
Очигледно, само корените се погодни за првиот услов:
Одговор:
Пример 26
Решете ја равенката.
Решение:
Равенката е дадена, што значи:
Збирот на корените е негативен, што значи дека барем еден од корените е негативен. Но, бидејќи нивниот производ е позитивен, тоа значи дека двата корени имаат знак минус.
Дозволете ни да избереме парови на броеви чиј производ е еднаков на:
Очигледно, корените се броевите и.
Одговор:
Се согласувам, многу е погодно да се дојде до корени усно, наместо да се брои овој гаден дискриминатор.
Обидете се да ја користите теоремата на Виета што е можно почесто!
Но, теоремата на Виета е потребна за да се олесни и забрза пронаоѓањето на корените.
За да имате корист од неговото користење, мора да ги доведете дејствата до автоматизам. И за ова, решете уште пет примери.
Но, не изневерувајте: не можете да користите дискриминатор! Само теорема на Виета!
5 примери на теоремата на Виета за самостојна работа
Пример 27
Задача 1. ((x)^(2))-8x+12=0
Според теоремата на Виета:
Како и обично, изборот го започнуваме со парчето:
Не е погоден бидејќи износот;
: износот е токму она што ви треба.
Одговор: ; .
Пример 28
Задача 2.
И повторно нашата омилена теорема Виета: збирот мора да биде еднаков, а производот мора да биде еднаков.
Но бидејќи не смее, туку, ги менуваме знаците на корените: и (вкупно).
Одговор: ; .
Пример 29
Задача 3.
Хм... Каде е тоа?
Треба да ги преместите сите термини во еден дел:
Збирот на корените е еднаков на производот.
Добро, застани! Равенката не е дадена.
Но, теоремата на Виета е применлива само во дадените равенки.
Значи, прво треба да дадете равенка.
Ако не можете да водите, откажете се од оваа идеја и решете ја на друг начин (на пример, преку дискриминатор).
Дозволете ми да ве потсетам дека да се даде квадратна равенка значи да се направи водечки коефициент еднаков:
Тогаш збирот на корените е еднаков на и производот.
Овде е лесно да се избере како лупење круши: на крајот на краиштата, тоа е прост број (извинете за тавтологијата).
Одговор: ; .
Пример 30
Задача 4.
Слободниот член е негативен.
Што е посебно за ова?
И факт е дека корените ќе имаат различни знаци.
И сега, при изборот, не го проверуваме збирот на корените, туку разликата во нивните модули: оваа разлика е еднаква, но производ.
Значи, корените се еднакви на и, но еден од нив е минус.
Теоремата на Виета ни кажува дека збирот на корените е еднаков на вториот коефициент со спротивен знак, т.е.
Ова значи дека помалиот корен ќе има минус: и, бидејќи.
Одговор: ; .
Пример 31
Задача 5.
Што треба прво да направите?
Така е, дајте ја равенката:
Повторно: ги избираме факторите на бројот и нивната разлика треба да биде еднаква на:
Корените се еднакви на и, но еден од нив е минус. Која? Нивниот збир треба да биде еднаков, што значи дека минусот ќе има поголем корен.
Одговор: ; .
Ајде да го сумираме
- Теоремата на Виета се користи само во дадените квадратни равенки.
- Користејќи ја теоремата на Виета, можете да ги најдете корените со избор, усно.
- Ако равенката не е дадена или не се најде соодветен пар фактори од слободниот член, тогаш нема цели корени и треба да го решите на друг начин (на пример, преку дискриминатор).
3. Метод за избор на целосен квадрат
Ако сите поими што ја содржат непознатата се претставени во форма на поими од скратените формули за множење - квадратот на збирот или разликата - тогаш по замена на променливите, равенката може да се претстави во форма на нецелосна квадратна равенка од типот.
На пример:
Пример 32
Решете ја равенката: .
Решение:
Одговор:
Пример 33
Решете ја равенката: .
Решение:
Одговор:
Во принцип, трансформацијата ќе изгледа вака:
Следува: .
Не те потсетува на ништо?
Ова е дискриминаторска работа! Токму така ја добивме формулата за дискриминација.
КВАДРАТНИ РАВЕНКИ. НАКРАТКО ЗА ГЛАВНИТЕ РАБОТИ
Квадратна равенка- ова е равенка на формата, каде што - непознатото, - коефициентите на квадратната равенка, - слободниот член.
Целосна квадратна равенка- равенка во која коефициентите не се еднакви на нула.
Намалена квадратна равенка- равенка во која коефициентот, односно: .
Нецелосна квадратна равенка- равенка во која коефициентот и или слободниот член c се еднакви на нула:
- ако коефициентот, равенката изгледа вака:
- ако има слободен член, равенката има форма: ,
- ако и, равенката изгледа вака: .
1. Алгоритам за решавање на нецелосни квадратни равенки
1.1. Нецелосна квадратна равенка на формата, каде што, :
1) Да го изразиме непознатото: ,
2) Проверете го знакот на изразот:
- ако, тогаш равенката нема решенија,
- ако, тогаш равенката има два корени.
1.2. Нецелосна квадратна равенка на формата, каде што, :
1) Да го извадиме заедничкиот фактор од загради: ,
2) Производот е еднаков на нула ако барем еден од факторите е еднаков на нула. Според тоа, равенката има два корени:
1.3. Нецелосна квадратна равенка на формата, каде што:
Оваа равенка секогаш има само еден корен: .
2. Алгоритам за решавање на целосни квадратни равенки од формата каде
2.1. Решение со помош на дискриминант
1) Да ја доведеме равенката во стандардна форма: ,
2) Да ја пресметаме дискриминаторот користејќи ја формулата: , која го означува бројот на корените на равенката:
3) Најдете ги корените на равенката:
- ако, тогаш равенката има корени, кои се наоѓаат со формулата:
- ако, тогаш равенката има корен, кој се наоѓа со формулата:
- ако, тогаш равенката нема корени.
2.2. Решение со помош на теоремата на Виета
Збирот на корените на намалената квадратна равенка (равенка на формата каде) е еднаков, а производот на корените е еднаков, т.е. , А.
2.3. Решение со методот на избор на целосен квадрат
Квадратна равенкаили равенка од втор степен со една непозната е равенка која, по трансформациите, може да се сведе на следната форма:
секира 2 + bx + в = 0 - квадратна равенка
Каде x- ова е непознатото, но а, бИ в- коефициенти на равенката. Во квадратни равенки анаречен првиот коефициент ( а ≠ 0), бсе нарекува втор коефициент, и внаречен познат или слободен член.
Равенка:
секира 2 + bx + в = 0
повикани комплетенквадратна равенка. Ако еден од коефициентите били ве еднакво на нула, или двата од овие коефициенти се еднакви на нула, тогаш равенката е претставена во форма на нецелосна квадратна равенка.
Намалена квадратна равенка
Целосната квадратна равенка може да се сведе на попогодна форма со делење на сите нејзини членови со а, односно за првиот коефициент:
Равенка x 2 + px + q= 0 се нарекува намалена квадратна равенка. Според тоа, секоја квадратна равенка во која првиот коефициент е еднаков на 1 може да се нарече намалена.
На пример, равенката:
x 2 + 10x - 5 = 0
се намалува, а равенката:
3x 2 + 9x - 12 = 0
може да се замени со горната равенка, поделувајќи ги сите нејзини членови со -3:
x 2 - 3x + 4 = 0
Решавање на квадратни равенки
За да решите квадратна равенка, треба да ја намалите на една од следниве форми:
секира 2 + bx + в = 0
секира 2 + 2kx + в = 0
x 2 + px + q = 0
За секој тип на равенка има своја формула за наоѓање корени:
Забележете ја равенката:
секира 2 + 2kx + в = 0
ова е трансформираната равенка секира 2 + bx + в= 0, во кој коефициентот б- дури, што ви овозможува да го замените со тип 2 к. Затоа, формулата за наоѓање на корените за оваа равенка може да се поедностави со замена на 2 во неа кнаместо да б:

Пример 1.Реши ја равенката:
3x 2 + 7x + 2 = 0
Бидејќи во равенката вториот коефициент не е парен број, а првиот коефициент не е еднаков на единството, тогаш ќе ги бараме корените користејќи ја првата формула, наречена општа формула за наоѓање корени на квадратна равенка. На почетокот
а = 3, б = 7, в = 2
Сега, за да ги најдеме корените на равенката, едноставно ги заменуваме вредностите на коефициентите во формулата:

| x 1 = | -2 | = - | 1 | , x 2 = | -12 | = -2 |
| 6 | 3 | 6 |
| Одговор: - | 1 | , -2. |
| 3 |
Пример 2:
x 2 - 4x - 60 = 0
Ајде да одредиме кои се коефициентите:
а = 1, б = -4, в = -60
Бидејќи вториот коефициент во равенката е парен број, ќе ја користиме формулата за квадратни равенки со парен втор коефициент:
x 1 = 2 + 8 = 10, x 2 = 2 - 8 = -6
Одговор: 10, -6.
Пример 3.
y 2 + 11y = y - 25
Да ја намалиме равенката на општ изглед:
y 2 + 11y = y - 25
y 2 + 11y - y + 25 = 0
y 2 + 10y + 25 = 0
Ајде да одредиме кои се коефициентите:
а = 1, стр = 10, q = 25
Бидејќи првиот коефициент е еднаков на 1, ќе бараме корени користејќи ја формулата за горенаведените равенки со парен втор коефициент:
Одговор: -5.
Пример 4.
x 2 - 7x + 6 = 0
Ајде да одредиме кои се коефициентите:
а = 1, стр = -7, q = 6
Бидејќи првиот коефициент е еднаков на 1, ќе бараме корени користејќи ја формулата за горенаведените равенки со непарен втор коефициент:
x 1 = (7 + 5) : 2 = 6, x 2 = (7 - 5) : 2 = 1