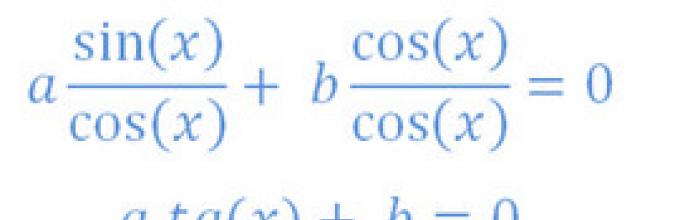Тригонометриски равенки преку дискриминант. Лекција „тригонометриски равенки сведени на квадратни равенки“. Проблеми кои треба да се решаваат самостојно

Час и презентација на тема: „Решавање едноставни тригонометриски равенки“

Дополнителни материјали
Почитувани корисници, не заборавајте да ги оставите вашите коментари, критики, желби! Сите материјали се проверени со антивирусна програма.

Прирачници и симулатори во онлајн продавницата Integral за одделение 10 од 1C
Решаваме проблеми во геометријата. Интерактивни задачи за градење во просторот
Софтверско опкружување „1C: Mathematical Constructor 6.1“

Што ќе проучуваме:
1. Што се тригонометриски равенки?

3. Два главни методи на решение тригонометриски равенки.
4. Хомогени тригонометриски равенки.
5. Примери.

Што се тригонометриски равенки?

Момци, ние веќе проучувавме арксин, аркозин, арктангенс и аркотангенс. Сега да ги погледнеме тригонометриските равенки воопшто.

Тригонометриските равенки се равенки во кои променливата е содржана под знакот на тригонометриска функција.

Да ја повториме формата за решавање на наједноставните тригонометриски равенки:

1)Ако |a|≤ 1, тогаш равенката cos(x) = a има решение:

X= ± arccos(a) + 2πk

2) Ако |a|≤ 1, тогаш равенката sin(x) = a има решение:

3) Ако |а| > 1, тогаш равенката sin(x) = a и cos(x) = a немаат решенија 4) Равенката tg(x)=a има решение: x=arctg(a)+ πk

5) Равенката ctg(x)=a има решение: x=arcctg(a)+ πk

За сите формули k е цел број

Наједноставните тригонометриски равенки имаат форма: T(kx+m)=a, T е некоја тригонометриска функција.

Пример.

Решете ги равенките: а) sin(3x)= √3/2

Решение:

А) Да означиме 3x=t, а потоа ќе ја преработиме нашата равенка во форма:

Решението на оваа равенка ќе биде: t=((-1)^n)arcsin(√3 /2)+ πn.

Од табелата со вредности добиваме: t=((-1)^n)×π/3+ πn.

Да се вратиме на нашата променлива: 3x =((-1)^n)×π/3+ πn,

Тогаш x= ((-1)^n)×π/9+ πn/3

Одговор: x= ((-1)^n)×π/9+ πn/3, каде што n е цел број. (-1)^n – минус еден до моќта на n.

Повеќе примери на тригонометриски равенки.

Реши ги равенките: а) cos(x/5)=1 b)tg(3x- π/3)= √3

Решение:

А) Овој пат да преминеме директно на пресметување на корените на равенката веднаш:

X/5= ± arccos(1) + 2πk. Тогаш x/5= πk => x=5πk

Одговор: x=5πk, каде k е цел број.

Б) Го пишуваме во форма: 3x- π/3=arctg(√3)+ πk. Знаеме дека: арктан(√3)= π/3

3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3

Одговор: x=2π/9 + πk/3, каде k е цел број.

Решете ги равенките: cos(4x)= √2/2. И пронајдете ги сите корени на сегментот.

Решение:

Да ја решиме нашата равенка во општа форма: 4x= ± arccos(√2/2) + 2πk

4x= ± π/4 + 2πk;

X= ± π/16+ πk/2;

Сега да видиме кои корени паѓаат на нашиот сегмент. На k Во k=0, x= π/16, ние сме во даден сегмент.
Со k=1, x= π/16+ π/2=9π/16 повторно удираме.
За k=2, x= π/16+ π=17π/16, но овде не погодивме, што значи дека за големо k ние исто така очигледно нема да погодиме.

Одговор: x= π/16, x= 9π/16

Два главни методи на решение.

Ги разгледавме наједноставните тригонометриски равенки, но има и посложени. За нивно решавање се користи методот на воведување на нова променлива и методот на факторизација. Ајде да погледнеме примери.

Да ја решиме равенката:

Решение:
За да ја решиме нашата равенка, ќе го користиме методот на воведување нова променлива, која означува: t=tg(x).

Како резултат на замена добиваме: t 2 + 2t -1 = 0

Да ги најдеме корените на квадратната равенка: t=-1 и t=1/3

Потоа tg(x)=-1 и tg(x)=1/3, ја добиваме наједноставната тригонометриска равенка, ајде да ги најдеме нејзините корени.

X=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.

Одговор: x= -π/4+πk; x=arctg(1/3) + πk.

Пример за решавање на равенка

Решете ги равенките: 2sin 2 (x) + 3 cos(x) = 0

Решение:

Да го искористиме идентитетот: sin 2 (x) + cos 2 (x)=1

Нашата равенка ќе ја има формата: 2-2cos 2 (x) + 3 cos (x) = 0

2 cos 2 (x) - 3 cos(x) -2 = 0

Да ја воведеме замената t=cos(x): 2t 2 -3t - 2 = 0

Решението на нашата квадратна равенка се корените: t=2 и t=-1/2

Потоа cos(x)=2 и cos(x)=-1/2.

Бидејќи косинус не може да земе вредности поголеми од една, тогаш cos(x)=2 нема корени.

За cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk

Одговор: x= ±2π/3 + 2πk

Хомогени тригонометриски равенки.

Дефиниција: Равенките од формата a sin(x)+b cos(x) се нарекуваат хомогени тригонометриски равенки од прв степен.

Равенки на формата

хомогени тригонометриски равенки од втор степен.

За да решите хомогена тригонометриска равенка од прв степен, поделете ја со cos(x): Не можете да поделите со косинус ако е еднаков на нула, ајде да се увериме дека тоа не е случај:
Нека cos(x)=0, тогаш asin(x)+0=0 => sin(x)=0, но синусот и косинусот не се еднакви на нула во исто време, добиваме контрадикција, па можеме безбедно да се подели со нула.

Реши ја равенката:
Пример: cos 2 (x) + sin (x) cos(x) = 0

Решение:

Да го извадиме заедничкиот фактор: cos(x)(c0s(x) + sin (x)) = 0

Потоа треба да решиме две равенки:

Cos(x)=0 и cos(x)+sin(x)=0

Cos(x)=0 при x= π/2 + πk;

Размислете за равенката cos(x)+sin(x)=0 Поделете ја нашата равенка со cos(x):

1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk

Одговор: x= π/2 + πk и x= -π/4+πk

Како да се решат хомогени тригонометриски равенки од втор степен?
Момци, секогаш следете ги овие правила!

1. Види на што е еднаков коефициентот a, ако a=0 тогаш нашата равенка ќе има форма cos(x)(bsin(x)+ccos(x)), чиешто решение е пример на претходниот слајд

2. Ако a≠0, тогаш треба да ги поделите двете страни на равенката со косинусот на квадрат, добиваме:

Ја менуваме променливата t=tg(x) и ја добиваме равенката:

Реши пример бр.:3

Реши ја равенката:
Решение:

Ајде да ги поделиме двете страни на равенката со косинусниот квадрат:

Ја менуваме променливата t=tg(x): t 2 + 2 t - 3 = 0

Да ги најдеме корените на квадратната равенка: t=-3 и t=1

Тогаш: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk

Tg(x)=1 => x= π/4+ πk

Одговор: x=-arctg(3) + πk и x= π/4+ πk

Реши пример бр.:4

Реши ја равенката:

Решение:
Ајде да го трансформираме нашиот израз:

Можеме да решиме такви равенки: x= - π/4 + 2πk и x=5π/4 + 2πk

Одговор: x= - π/4 + 2πk и x=5π/4 + 2πk

Реши пример бр.:5

Реши ја равенката:

Решение:
Ајде да го трансформираме нашиот израз:

Да ја воведеме замената tg(2x)=t:2 2 - 5t + 2 = 0

Решението на нашата квадратна равенка ќе бидат корените: t=-2 и t=1/2

Тогаш добиваме: tg(2x)=-2 и tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2

2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2

Одговор: x=-arctg(2)/2 + πk/2 и x=arctg(1/2)/2+ πk/2

Проблеми за самостојно решавање.

1) Реши ја равенката

А) sin(7x)= 1/2 б) cos(3x)= √3/2 в) cos(-x) = -1 г) tg(4x) = √3 г) ctg(0.5x) = -1.7

2) Реши ги равенките: sin(3x)= √3/2. И најдете ги сите корени на отсечката [π/2; π].

3) Решете ја равенката: креветче 2 (x) + 2 креветче (x) + 1 =0

4) Реши ја равенката: 3 sin 2 (x) + √3sin (x) cos(x) = 0

5) Реши ја равенката: 3sin 2 (3x) + 10 sin(3x)cos(3x) + 3 cos 2 (3x) =0

6) Решете ја равенката: cos 2 (2x) -1 - cos(x) =√3/2 -sin 2 (2x)

Главните методи за решавање на тригонометриски равенки се: намалување на равенките на наједноставни (со користење на тригонометриски формули), воведување нови променливи и факторинг. Ајде да ја разгледаме нивната употреба со примери. Обрнете внимание на форматот на пишување решенија за тригонометриски равенки.

Неопходен услов за успешно решавање на тригонометриските равенки е познавањето на тригонометриските формули (тема 13 од работа 6).

Примери.

1. Равенки сведени на наједноставните.

1) Реши ја равенката

Решение:

Одговор:

2) Најдете ги корените на равенката

(sinx + cosx) 2 = 1 - sinxcosx, кои припаѓаат на сегментот.

Решение:

Одговор:

2. Равенки кои се сведуваат на квадратни.

1) Решете ја равенката 2 sin 2 x – cosx –1 = 0.

Решение:Користење на формула за грев 2 x = 1 – cos 2 x, добиваме

Одговор:

2) Решете ја равенката cos 2x = 1 + 4 cosx.

Решение:Користејќи ја формулата cos 2x = 2 cos 2 x – 1, добиваме

Одговор:

3) Решете ја равенката tgx – 2ctgx + 1 = 0

Решение:

Одговор:

3. Хомогени равенки

1) Решете ја равенката 2sinx – 3cosx = 0

Решение: Нека cosx = 0, потоа 2sinx = 0 и sinx = 0 – контрадикција со фактот дека sin 2 x + cos 2 x = 1. Тоа значи cosx ≠ 0 и можеме да ја поделиме равенката со cosx. Добиваме

Одговор:

2) Решете ја равенката 1 + 7 cos 2 x = 3 sin 2x

Решение:

Ги користиме формулите 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, добиваме

sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0

Нека cosx = 0, потоа sin 2 x = 0 и sinx = 0 - контрадикција со фактот дека sin 2 x + cos 2 x = 1.
Ова значи cosx ≠ 0 и можеме да ја поделиме равенката со cos 2 x . Добиваме

tg 2 x – 6 tgx + 8 = 0
Да означиме tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y2 = 2
а) tgx = 4, x= арктан4 + 2 к, к
б) tgx = 2, x= арктан2 + 2 к, к .

Одговор: arctg4 + 2 к, арктан2 + 2 к, к

4. Равенки на формата а sinx + б cosx = с, с≠ 0.

1) Реши ја равенката.

Решение:

Одговор:

5. Равенки решени со факторизација.

1) Решете ја равенката sin2x – sinx = 0.

Корен на равенката ѓ (X) = φ ( X) може да послужи само како број 0. Ајде да го провериме ова:

cos 0 = 0 + 1 - еднаквоста е вистина.

Бројот 0 е единствениот корен од оваа равенка.

Одговор: 0.

Тема на лекцијата:Тригонометриски равенки сведени на квадратни, хомогени тригонометриски равенки.

Тип на лекција: Комбинирана лекција.

Цели на лекцијата:

Воведување на концептот на хомогени тригонометриски равенки сведени на квадратни;
Воведување на концептот на тригонометриски равенки од 1 и 2 степен;
Да се развие кај учениците способност за решавање на разгледуваните равенки на основно ниво.

Развивање на способност за анализа и извлекување заклучоци;
Развијте ги вештините за самоанализа и контрола.

Негувајте чувство на одговорност;
Развијте вештини за работа во тим.
Опрема за лекција: постери, картички, самооценки, збир на картички за самостојна работа, сигнални картички.

Структура на лекцијата:

1. Организациска фаза.

2. Фаза на проверка на домашната задача.

3. Фаза на подготовка на учениците за активно и свесно асимилирање на нов материјал. Вовед во темата на лекцијата. Поставување цели и задачи.

4. Фаза на асимилација на ново знаење.

5. Фаза на проверка на разбирањето на новиот материјал од страна на учениците.

6. Фаза на консолидација на нов материјал.

7. Фаза на информирање на учениците за домашните задачи.

8. Фаза на сеопфатно тестирање на знаењето.

9. Сумирајќи. Рефлексија.

1. Организациска фаза .

подгответе ги учениците за работа на час.

2. Фаза на проверка на домашната задача .

да се утврди присуството и исправноста на домашните задачи од страна на сите ученици.

3. Фаза на подготовка на учениците за активно и свесно асимилирање на нов материјал.

преку креирање проблемска ситуација да ги доведе учениците до нови видови тригонометриски равенки. Наставникот го привлекува вниманието на учениците на магнетната табла, каде што се наоѓаат картички со неколку тригонометриски равенки и бара од нив да наведат како да ги решат.

1) cos (4x-2)=2

3) cos 2 x-2cosx=0

5) 8 грев 2 x-6 грев x-5=0

6)8 cos 2 2x+6 sin 2x-3=0

7)2sin x- 3 cos x=0

9)3 sin 2 x- 4sin x cos x +cos 2 x=0

Учениците внимателно ја разгледуваат магнетната табла и објаснуваат како да ја решат оваа или онаа равенка. Доколку наставникот нема коментари, картичката со горната равенка се отстранува од магнетната табла.

Како резултат на сработеното, равенките останаа на магнетната табла, учениците не можеа да најдат начин да ги решат. (бр. 5, 7)

4. Фаза на асимилација на ново знаење.

Воведување на концептот „Тригонометриски равенки сведени на квадратни“;

воведување на концептот на „тригонометриски равенки сведени на квадратни“;
воведување на концептот на хомогени тригонометриски равенки;
анализира методи за решавање на хомогени тригонометриски равенки од 1 и 2 степен;
постигне способност за одредување на формата на хомогени тригонометриски равенки;
совладува општи техники за решавање тригонометриски равенки сведени на квадратни и хомогени тригонометриски равенки.

Наставникот ги именува видовите преостанати равенки и ги повикува учениците да ја запишат темата на часот „Тригонометриски равенки решени со намалување на квадратни. Хомогени тригонометриски равенки од 1 и 2 степен."

Наставникот прави белешки на таблата, а учениците во своите тетратки пишуваат:

Тригонометриски равенки решени со редукција на квадратни равенки.

1) Равенките од формата A×sin2 t +B×sin t + C = 0, каде што A ¹ 0, се решаваат со намалување на квадрат со замена на sin t = y (равенките со cos t, tg t, сtg t се решени слично).

2) Равенки од формата A×sin2 t +B×cos t + C = 0. При решавањето, основната тригонометриски идентитет sin2 t = 1 - cos2 t.

3) грев 2 t = a, a= . 4) cos 2 t = a, a = .

5) tg 2 t = a, a = . 6) креветче 2 t = a, a =

Детално се анализира решението на равенката бр. 5, 4. Решението на равенката бр. 6 се изведува со активно учество на часот. За да се реши равенката бр.8 се повикува ученик (по избор).

Хомогени тригонометриски равенки од 1 и 2 степен.

Равенката во која секој член има ист степен се нарекува хомогена.

1) Равенките од формата A×sin t +B×cos t = 0, каде што A ¹ 0, B ¹ 0, се нарекуваат хомогени тригонометриски равенки од степен 1. Тие се решаваат со делење на двете страни со cos t ¹ 0. Имаме A× tg t + B = 0.

2) Равенките од формата A×sin2 t +B sin t×cos t + С×cos2 t = 0 се нарекуваат хомогени тригонометриски равенки од степен 2. Тие се решаваат со делење на двете страни со cos2 t ¹ 0. Имаме A× tg2 t + B× tg t + C = 0.

Наставникот ја решава равенката бр.7, со детално објаснување. При решавањето на равенката бр.9, користејќи прашања, ги поврзува учениците со активна работа. Откако ќе ја намалите равенката на формата 3tg2 t - 4 tg t + 1 = 0, ги повикува учениците да одат на табла ако сакаат и да ја решат добиената равенка.

Фаза на проверка на разбирањето на новиот материјал од страна на учениците.

Задача: утврдете дали учениците научиле како да решаваат нов тип равенки.

СФЗ ( самостојна работаза формирање на знаење).

Определете го типот на равенката и наведете како да ја решите.

2)5 грев 3x+4cos3x=0 ;

3) sin 2 x+14sinx*cosx-15cos 2 x=0;

4) 1 + 7cos2 x + 3sin2 x = 0;

5)sin2x+sin 2 x=0 .

6. Фаза на консолидација на нов материјал.

Задача: да ги консолидираат кај учениците знаењата и вештините што ги добиле на часот.

Наставникот бара од учениците да ги решат следните равенки на табла:

7. Фаза на информирање на учениците за домашните задачи.

Цели: информирање на учениците домашна работа, дајте кратки упатства за неговата имплементација.

прегледајте ги белешките во вашата тетратка;
анализирајте го решението на примерите бр.1 - 6 од учебникот, стр.78 - 79.
комплетен бр. 167а), б); бр. 168 б); бр. 169а); бр. 170v).
Јаките ученици, наместо бр. 167, 168, можат да ја решат равенката:

15*(грев 2 x+грев x+ cos 2 2x) 2 +17+31sinx

8. Фаза на сеопфатно тестирање на знаењето.

Цели: сеопфатно да се тестира знаењето на учениците при решавање на равенки слични на оние што се дискутирани на часот, да се развијат вештините за самоанализа и контрола.

SFN (самостојна работа на развој на вештини).

Решете ги равенките.

Опција 1.

Опција 2

Опција 3

Опција 4

9. Сумирајќи. Рефлексија.

При решавање на многу математички проблеми , особено оние кои се случуваат пред одделение 10, јасно е дефиниран редоследот на извршените дејствија кои ќе доведат до целта. Таквите проблеми вклучуваат, на пример, линеарни и квадратни равенки, линеарни и квадратни неравенки, дробни равенки и равенки кои се сведуваат на квадратни. Принципот на успешно решавање на секој од наведените проблеми е како што следува: потребно е да се утврди каков тип на проблем се решава, запомнете ја потребната низа на дејства што ќе доведат до посакуваниот резултат, т.е. одговори и следете ги овие чекори.

Очигледно е дека успехот или неуспехот во решавањето на одреден проблем зависи главно од тоа колку правилно се одредува типот на равенката што се решава, колку правилно се репродуцира низата од сите фази на неговото решение. Се разбира, неопходно е да се поседуваат вештини за изведување идентитетски трансформациии пресметување.

Поинаква е ситуацијата со тригонометриски равенки.Воопшто не е тешко да се утврди фактот дека равенката е тригонометриска. Потешкотии се јавуваат при определување на редоследот на дејствијата што би довеле до точниот одговор.

Од страна на изгледравенка, понекогаш е тешко да се одреди неговиот тип. И без да се знае типот на равенката, речиси е невозможно да се избере вистинската од неколку десетици тригонометриски формули.

За да решите тригонометриска равенка, треба да се обидете:

1. доведете ги сите функции вклучени во равенката до „исти агли“;
2. доведете ја равенката до „идентични функции“;
3. фактор на левата страна на равенката итн.

Ајде да размислиме основни методи за решавање на тригонометриски равенки.

I. Намалување на наједноставните тригонометриски равенки

Дијаграм за решение

Чекор 1.Изрази тригонометриска функција во однос на познати компоненти.

Чекор 2.Најдете го аргументот на функцијата користејќи ги формулите:

cos x = a; x = ±arccos a + 2πn, n ЄZ.

sin x = a; x = (-1) n arcsin a + πn, n Є Z.

tan x = a; x = арктан a + πn, n Є Z.

ctg x = a; x = arcctg a + πn, n Є Z.

Чекор 3.Најдете ја непознатата променлива.

Пример.

2 cos(3x – π/4) = -√2.

Решение.

1) cos(3x – π/4) = -√2/2.

2) 3x – π/4 = ±(π – π/4) + 2πn, n Є Z;

3x – π/4 = ±3π/4 + 2πn, n Є Z.

3) 3x = ±3π/4 + π/4 + 2πn, n Є Z;

x = ±3π/12 + π/12 + 2πn/3, n Є Z;

x = ±π/4 + π/12 + 2πn/3, n Є Z.

Одговор: ±π/4 + π/12 + 2πn/3, n Є Z.

II. Замена на променлива

Дијаграм за решение

Чекор 1.Намалете ја равенката во алгебарска форма во однос на една од тригонометриските функции.

Чекор 2.Означете ја добиената функција со променливата t (ако е потребно, воведете ограничувања за t).

Чекор 3.Запишете и решете ја добиената алгебарска равенка.

Чекор 4.Направете обратна замена.

Чекор 5.Решете ја наједноставната тригонометриска равенка.

Пример.

2cos 2 (x/2) – 5sin (x/2) – 5 = 0.

Решение.

1) 2(1 – грев 2 (x/2)) – 5sin (x/2) – 5 = 0;

2sin 2 (x/2) + 5sin (x/2) + 3 = 0.

2) Нека sin (x/2) = t, каде што |t| ≤ 1.

3) 2t 2 + 5t + 3 = 0;

t = 1 или e = -3/2, не го задоволува условот |t| ≤ 1.

4) грев (x/2) = 1.

5) x/2 = π/2 + 2πn, n Є Z;

x = π + 4πn, n Є Z.

Одговор: x = π + 4πn, n Є Z.

III. Метод за намалување на редоследот на равенките

Дијаграм за решение

Чекор 1.Заменете ја оваа равенка со линеарна, користејќи ја формулата за намалување на степенот:

грев 2 x = 1/2 · (1 – cos 2x);

cos 2 x = 1/2 · (1 + cos 2x);

tg 2 x = (1 – cos 2x) / (1 + cos 2x).

Чекор 2.Решете ја добиената равенка користејќи ги методите I и II.

Пример.

cos 2x + cos 2 x = 5/4.

Решение.

1) cos 2x + 1/2 · (1 + cos 2x) = 5/4.

2) cos 2x + 1/2 + 1/2 · cos 2x = 5/4;

3/2 cos 2x = 3/4;

2x = ±π/3 + 2πn, n Є Z;

x = ±π/6 + πn, n Є Z.

Одговор: x = ±π/6 + πn, n Є Z.

IV. Хомогени равенки

Дијаграм за решение

Чекор 1.Намалете ја оваа равенка на формата

а) a sin x + b cos x = 0 (хомогена равенка од прв степен)

или кон погледот

б) a sin 2 x + b sin x · cos x + c cos 2 x = 0 (хомогена равенка од втор степен).

Чекор 2.Поделете ги двете страни на равенката со

а) cos x ≠ 0;

б) cos 2 x ≠ 0;

и добијте ја равенката за tan x:

а) a tan x + b = 0;

б) тен 2 x + b арктан x + c = 0.

Чекор 3.Решете ја равенката користејќи познати методи.

Пример.

5sin 2 x + 3sin x cos x – 4 = 0.

Решение.

1) 5sin 2 x + 3sin x · cos x – 4(sin 2 x + cos 2 x) = 0;

5sin 2 x + 3sin x · cos x – 4sin² x – 4cos 2 x = 0;

sin 2 x + 3sin x · cos x – 4cos 2 x = 0/cos 2 x ≠ 0.

2) tg 2 x + 3tg x – 4 = 0.

3) Нека tg x = t, тогаш

t 2 + 3t – 4 = 0;

t = 1 или t = -4, што значи

tg x = 1 или tg x = -4.

Од првата равенка x = π/4 + πn, n Є Z; од втората равенка x = -arctg 4 + πk, k Є Z.

Одговор: x = π/4 + πn, n Є Z; x = -arctg 4 + πk, k Є Z.

V. Метод на трансформација на равенка со помош на тригонометриски формули

Дијаграм за решение

Чекор 1.Користење на сите видови на тригонометриски формули, сведете ја оваа равенка на равенка решена со методите I, II, III, IV.

Чекор 2.Решете ја добиената равенка користејќи познати методи.

Пример.

грев x + грев 2x + грев 3x = 0.

Решение.

1) (грев х + грев 3х) + грев 2х = 0;

2sin 2x cos x + грев 2x = 0.

2) грев 2x (2cos x + 1) = 0;

грев 2x = 0 или 2cos x + 1 = 0;

Од првата равенка 2x = π/2 + πn, n Є Z; од втората равенка cos x = -1/2.

Имаме x = π/4 + πn/2, n Є Z; од втората равенка x = ±(π – π/3) + 2πk, k Є Z.

Како резултат на тоа, x = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.

Одговор: x = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.

Способноста и вештината за решавање на тригонометриски равенки е многу важно, нивниот развој бара значителен напор, како од страна на ученикот, така и од страна на наставникот.

Со решавањето на тригонометриските равенки се поврзани многу проблеми од стереометријата, физиката итн.. Процесот на решавање на ваквите проблеми отелотворува многу од знаењата и вештините кои се стекнуваат со проучување на елементите на тригонометријата.

Тригонометриските равенки заземаат важно место во процесот на учење математика и воопшто на личниот развој.

Сè уште имате прашања? Не знаете како да решавате тригонометриски равенки?
За да добиете помош од учител, регистрирајте се.
Првата лекција е бесплатна!

веб-страница, при копирање на материјал во целост или делумно, потребна е врска до изворот.

МОСКВА ОДДЕЛЕНИЕ ЗА ОБРАЗОВАНИЕ

ДРЖАВНИОТ БУЏЕТ СТРУЧЕН

ОБРАЗОВНА ИНСТИТУЦИЈА во Москва

„Политехнички колеџ бр.47 на име В.Г.Федоров“

Лекција

во дисциплината Математика

„Тригонометриски равенки сведени на квадратни“

Наставник

Протасевич Олга Николаевна

ПРОФЕСИЈА: Хардверски и софтверски инженер

ДИСЦИПЛИНА: Математика

ДОБРО : 1

СЕМЕСТАР : 2

ГРУПА :

Тема на лекцијата:

„Тригонометриските равенки сведени на квадратни равенки“.

Тип на лекција: комбинирана лекција

Формат на лекција: колективна обука по методологија на В.К. Дјаченко

(образование во мали групни системи)

Цели на лекцијата:

Образовни – разгледајте општи пристапи, сумирајте информации за видовите и методите на решавање тригонометриски равенки што може да се сведат на квадратни; да развива вештини и способности за примена на знаењата при решавање на основни равенки и примена на стекнатото знаење во професионалните активности.

Развојна - промовирање на развојот логично размислувањемеѓу учениците, развивање на вештини за анализа, расудување, споредување, донесување заклучоци, разбирање на материјалот;

Образовни – негување когнитивен интерес, елементи на култура на комуникација, поттикнување на учениците да ги надминат тешкотиите во процесот на ментална активност, развивање вештини за работа во работен и образовен тим.

Цел на лекцијата:

Да ги запознае учениците со главните видови и методи на решавање тригонометриски равенки кои можат да се сведат на квадратни.

Поддршка (ресурси):

Хардвер: компјутер, мултимедијален проектор.

Софтвер:МајкрософтExcel.

Основни концепти:

Квадратна равенка; едноставни тригонометриски равенки; инверзни тригонометриски функции; тригонометриски равенки сведени на квадратни.

Литература:

Башмаков М.И. Математика: учебник за основно и средно стручно образование.– М.; „Академија“, 2010. - 256 стр.

Дјаченко В.К. - М.; „Јавно образование“, 2001 г. - 496 с.

Методолошка литература:

Башмаков М.И. Математика: книга за наставници. Методолошки прирачник - М. « Академија“, 2013 - 224 стр.

Електронски ресурси:

Материјали на локацијатасоцијално и педагошко движење за создавање колективен начин на настава:www.kco-kras.ru.

Чекори од лекцијата

Време на организирање.

Проверка на домашната задача.

Ажурирање на основните знаења.

Учење нов материјал.

Консолидација и систематизација на стекнатото знаење.

Рефлексија. Сумирајќи. Домашна работа.

За време на часовите

Време на организирање.

Наставникот им поставува цели на часот за учениците:

1) Воведете ги главните типови на тригонометриски равенки кои можат да се сведат на квадратни;

2) Воведување на стандардни методи за решавање на тригонометриски равенки кои можат да се сведат на квадратни.

3) Научи како да ги применуваат стекнатите знаења и вештини за решавање на стандардни равенки;

4) Научете како да работите со информациите презентирани во различни форми, остваруваат меѓусебна контрола и самоконтрола, го применуваат стекнатото знаење во професионалните активности.

II . Проверка на домашната задача.

Наставникот вклучува презентација „Домашна работа“, според која учениците самостојно ја проверуваат домашната задача и, доколку е потребно, прават измени и корекции на работата.

Наставникот на барање на учениците ги коментира решенијата на равенките кои предизвикале потешкотии, по што ги објавува имињата на учениците кои на крајот од часот ги предаваат своите тетратки на проверка.

№ 1

Одговор:

№ 2

Одговор:

№ 3

Одговор:

№ 4

бидејќи тогаш равенката нема корени

Одговор: нема корени

№ 5

Одговор:

№ 6

Одговор:

III . Ажурирање на основните знаења.

Наставникот формира студиски групи/парови и предлага да се користат дадените форми за да се воспостави кореспонденција помеѓу равенките и одговорите: „Пред вас е слајд со едукативна задача. Поврзете ги равенките (левата страна на табелата) со одговорите (десната страна на табелата). Запишете ги броевите на точните парови на искази во вашата тетратка“.

Наведените задачи се дуплираат во вклучената презентација.

Натпревар

стр/стр

Равенката

стр/стр

Одговори

без корени

На крајот од работата, наставникот фронтално ги интервјуира претставниците на групата, по што ја вклучува страницата за презентација со точните решенија.

Вистински одговори

стр/стр

Равенката

стр/стр

Одговори

без корени

11.

13.

10.

12.

IV . Учење нов материјал.

Наставникот вклучува презентација на нов материјал „Тригонометриски равенки сведени на квадратни. Видови равенки и методи за нивни решенија“.

Ги повикува учениците да ги запишат потребните точки и почнува да коментира за секој слајд, по што ја вклучуваат презентацијата.

Ајде да го претставиме концептот:

Општ приказ на квадратна равенка:

1 тип на тригонометриски равенки кои можат да се сведуваат на квадратни равенки – равенки кои се алгебарски во однос на една од тригонометриските функции.

Наставникот ги објаснува решенијата.

1. Директна замена

Замена ,

без корени

Одговор:

Слично решение имаат и равенките на формата

Замена

2. Равенки кои бараат конверзија со помош на формулата за тригонометриска единица

Замена , тогаш равенката добива форма

без корени

Одговор:

Равенките на формата имаат слично решение:

ќе замениме , користејќи ја формулата за тригонометриска единица

Добиваме равенка која содржи само една тригонометриска функција :

Замена

3. Равенки кои бараат трансформација користејќи ја формулата за поврзување tgx И Со tgx

Ја применуваме формулата:

Помножете ја равенката со

Замена , тогаш равенката добива форма

Одговор:

Тип 2 тригонометриски равенки сведувајќи се на квадратни равенки– хомогени равенки во кои секој член има ист степен.

Поделете ја равенката со

Замена , тогаш равенката добива форма

Одговор:

Наставникот предлага да се сумира презентираниот материјал и поставува прашања: „На колку видови се поделени тригонометриските равенки што може да се сведуваат на квадратни равенки? Нивното име? Наведете начини за решавање на тригонометриски равенки што може да се сведат на квадратни“.

Наставникот ги води постапките на учениците при креирање на алгоритам за решавање на равенки од овој тип.

Тригонометриските равенки кои се сведуваат на квадратни равенки се поделени на два главни типа:

tgx И Со tgx :

Тип 2 - хомогени равенки во кои секој член има ист степен:

Наставникот прави приспособена Алгоритам за решение:

1. Определи го типот на равенката. Доколку е потребно, трансформирајте ја равенката така што ќе има само една тригонометриска функција. За да го направите ова, изберете ја саканата формула: илиили подели на

2. Воведена е замена (на пример, sinx = т , cosx = т , tgx = т ).

5. Запишете го одговорот.

За да се консолидираат стекнатите знаења, наставникот предлага да се воспостави кореспонденција помеѓу равенките и можните методи за нивно решавање: „Пред вас е слајд со задача за обука.

1. Класифицирајте ги равенките според методите за решавање според табелата подолу

(печатените верзии на табелата се на вашите клупи).

2. Внесете го бројот на методот на решение во соодветното поле.

Пополнете ја табелата“.

Работата се врши во парови.

стр/стр

Равенката

метод

Методи:

1) Внесете нова променлива.

2) Внесете нова променлива

3) Внесете нова променлива.

4) Трансформирајте ја равенката користејќи ја формулата и воведете нова променлива.

5) Трансформирајте ја равенката користејќи ја формулата, воведете нова променлива.

6) Поделете го секој член од равенката со, воведете нова променлива.

7) Трансформирајте ја равенката користејќи ја формулата, помножете ги условите на равенката со, внесете нова променлива.

Задачата се проверува во форма на фронтален разговор.

Наставник: „Пред вас е слајд со точни одговори на воспитно-образовната задача. . Проверете со проверка на точните одговори на задачата за учење. Работете на грешките во вашата тетратка“.

Листовите со задачи се собираат на крајот од часот.

стр/стр

Равенката

метод

VI . Консолидација и систематизација на стекнатото знаење.

Наставникот ги повикува учениците да продолжат да работат во групи.

Наставник: „Реши ги равенките. Проверете го резултатот во уредникот Мајкрософт Excel . На крајот од решението, претставник од групата оди на таблата и го презентира решението на равенката пополнета од групата. Наставникот го проверува решението, ја оценува работата на групата и, доколку е потребно, укажува на грешки“.

Наставник:

1 ) Разговарајте за решенијата како група.

2) Решението и добиениот одговор запишете ги во вашата тетратка.

3) Проверете го резултатот во уредникот Мајкрософт Excel .

4) Известете го вашиот наставник дека сте подготвени.

5) Објаснете ја вашата одлука со тоа што ќе ја запишете на таблата на членовите на другите групи.

6) Внимателно слушајте ги говорите на вашите другари, поставувајте прашања доколку е потребно.

Студиските групи кои целосно ги завршиле задачите се поканети да ги завршат задачите на другите групи. Успешните групи се наградуваат со зголемување на конечниот резултат за една единица.

Првата група:

Ја применуваме формулата:

без корени

бидејќи

Одговор:

Втора група:

Ја применуваме формулата:

Замена, тогаш равенката станува

Одговор: ;

Трета група:

Ја применуваме формулата:

Помножете ја равенката со

Замена, тогаш равенката станува

Одговор:

Четврта група:

Поделете ја равенката со

Замена, тогаш равенката станува

Одговор:

Петта група:

Замена, тогаш равенката станува

Одговор:; .

VII . Рефлексија. Сумирајќи. Домашна работа.

Наставник: Ајде да ја сумираме вашата работа, поврзувајќи ги резултатите од вашите активности со вашата цел.

Да повториме концепти:

„Тригонометриските равенки кои се сведуваат на квадратни равенки со трансформација и промена на променливата се нарекуваат тригонометриски равенки сведени на квадратни равенки“.

Тип 1 - равенки, алгебарски во однос на една од тригонометриските функции:

- директна замена - замена или;

- равенки кои бараат конверзија со помош на формулата за тригонометриска единица;

- равенки кои бараат трансформација според формулата за поврзување tgx и со tgx :

Тип 2 - хомогени равенки во кои секој член има ист степен: поделете ја равенката со, па заменете.

Алгоритам за решение:

1. Определи го типот на равенката. Доколку е потребно, преуредете ја равенката така што да содржи само една тригонометриска функција.

За да го направите ова, изберете ја саканата формула:

или или подели на

2. Воведена е замена (на пример, sinx = т , cosx = т , tgx = т ).

3. Реши ја квадратната равенка.

4. Направена е обратна замена, и се решава наједноставната тригонометриска равенка.

5. Запишете го одговорот.

Наставникот ја оценува работата на учениците, студиски групии ги објавува бодовите.

Наставник: „Запиши ја домашната задача: Башмаков М.И. Математика: учебник за основни и средни стручни лица. образование – М.; „Академија“, 2010. Стр. 114-115. Во бројот 10 решете ги равенките број 4,5,7,9. стр. 118. Проверете го резултатот во уредникот Мајкрософт Excel ».