Најчесто тоа е геометриски проблемипредизвикуваат потешкотии за апликантите, дипломираните студенти, учесниците математички олимпијади. Ако ја погледнете статистиката на обединетиот државен испит 2010 година, можете да видите дека околу 12% од учесниците го започнале геометрискиот проблем C4, а само 0,2% од учесниците добиле целосна оценка и воопшто проблемот се покажал најтешкиот од сите предложени.
Очигледно, колку побрзо им нудиме на учениците убави или неочекувани начини за решавање на проблемите, толку е поголема веројатноста сериозно и долго да ги заинтересираме и плениме. Но, колку е тешко да се најдат интересни и сложени проблеми на ниво на 7-мо одделение, кога систематското изучување на геометријата допрва започнува. Што може да му се понуди на ученик заинтересиран за математика кој ги знае само знаците на еднаквост на триаголниците и својствата на соседните и вертикалните агли? Сепак, може да се воведе концептот на тангента на круг, како права линија која има една заедничка точка со кругот; да претпоставиме дека радиусот нацртан до точката на допир е нормален на тангентата. Се разбира, вреди да се разгледаат сите можни случаи на распоред на два круга и заеднички тангенти на нив, кои можат да се извлечат од нула до четири. Со докажување на теоремите предложени подолу, можете значително да го проширите множеството проблеми за седмоодделенците. Во исто време, истовремено да се покаже важно или едноставно интересно и Забавни факти. Покрај тоа, бидејќи многу изјави не се вклучени во училишниот учебник, тие може да се дискутираат на часовите во круг и со матурантите кога се повторува планиметријата. Овие факти се покажаа како релевантни минатата академска година. Бидејќи многу дијагностичка работа сама по себе Работа на унифициран државен испитсодржеше проблем за чие решавање беше потребно да се искористи својството на тангентната отсечка докажано подолу.
Т 1
Сегменти на тангенти на круг извлечен од
еднаква на една точка (сл. 1)
Ова е теоремата што прво можете да ја запознаете со седмоодделенците.
Во процесот на докажување, го користевме знакот за еднаквост на правоаголните триаголници и заклучивме дека центарот на кругот лежи на симетралата на аголот BSA.
По патот, се сетивме дека симетралата на аголот е локус на точки во внатрешниот регион на аголот, подеднакво оддалечен од неговите страни. Решението на далеку од тривијален проблем се заснова на овие факти, достапни дури и за оние што штотуку почнуваат да ја проучуваат геометријата.

1. Симетрали на агли А, ВОИ СОконвексен четириаголник А БЕ ЦЕ ДЕсе вкрстуваат во една точка. Зраци АБИ DCсе сечат во точка Е, и зраците
СонцетоИ АДво точката Ф. Докажи дека неконвексен четириаголник AECFзбировите на должините на спротивните страни се еднакви.
Решение (сл. 2).Нека ЗА– точка на вкрстување на овие симетрали. Потоа ЗАеднакво оддалечено од сите страни на четириаголникот А БЕ ЦЕ ДЕ, тоа е
е центар на круг впишан во четириаголник. По теорема 1
следните еднаквости се вистинити: АР = А.К.,
ЕР = Е.П., Ф.Т. = ФК. Да ги собереме левата и десната страна член по член и да ја добиеме точната еднаквост:
(АР + ЕР) + Ф.Т. = (А.К. +ФК) + Е.П.; А.Е. + (Ф.Ц. + Ц.Т.) = А.Ф. + (ЕУ + компјутер). Бидејќи СВ = РС, Тоа AE + Ф.Ц. = А.Ф. + ЕУ, што требаше да се докаже.
Да разгледаме проблем со необична формулација, за чие решение е доволно да се знае теоремата 1 .
2. Дали има n-триаголник чии страни се последователно 1, 2, 3, ..., n, во која може да се впише круг?
Решение. Да го кажеме ова n-Гон постои. А 1 А 2 =1, …, А n-1 А n= n– 1,А n А 1 = n. Б 1 , …, Б n – соодветни точки на контакт. Потоа со теорема 1 А 1 Б 1 = А 1 Б n< 1, n – 1 < А n Б n< n.По својство на тангентни отсечки А n Б n= А n Б n-1 . Но, А n Б n-1< А n-1 А n= n - 1. Контрадикторност. Затоа бр n-Гон задоволување на условите на проблемот.

Т 2Збировите на спротивните страни на четириаголник опишани за
круговите се еднакви (сл. 3)
Учениците, по правило, лесно го докажуваат ова својство на опишаниот четириаголник. По докажувањето на теоремата 1 , тоа е вежба за вежбање. Можеме да го генерализираме овој факт - збировите на страните на ограничениот парен триаголник, земени преку едната страна, се еднакви. На пример, за шестоаголник АБЦДЕФдесно: AB + CD + EF = BC + DE + FA.

Решение (сл. 1). Бидејќи четириаголниците ABEF и ECDF се циклични, тогаш според теорема 2 P ABEF = 2 (AB + EF) и P ECDF = 2 (CD + EF), по услов
P ABEF – P ECDF = 2(AB + EF) – 2(CD + EF) = 2p. AB – CD = стр. AB = a + стр.

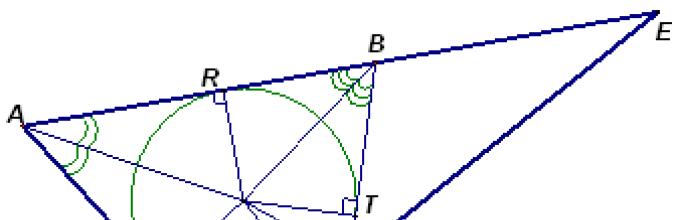
е нацртана тангента на кругот што ги пресекува отсечките АБИ ACна точките МИ Рсоодветно. Докажи дека периметарот на триаголник AMRи големината на аголот МПАне зависат од изборот на точката X.
Решение (сл. 5).Со теорема 1 MV = MX и RS = RH.Затоа, периметарот на триаголникот AMRеднаков на збирот на отсечките АБИ AC.Или двојна тангента нацртана на кружницата за триаголник AMR . Вредноста на аголот MOP се мери со половина од аголот VOS, што не зависи од изборот на точка X.

Решение (сл. 6). Првиот метод (алгебарски). Нека АК = АН = x,Потоа BK = BM = c – x, CM = CN = a – c + x. AC = AN + NC,тогаш можеме да создадеме равенка за x: b = x + (a – c + x).Каде
![]() .
.
Втор метод (геометриски). Ајде да го погледнеме дијаграмот. Сегменти од еднакви тангенти, земени еден по еден, се собираат до полупериметарот
тријаголник. Црвената и зелената боја сочинуваат една страна А.Потоа сегментот за кој сме заинтересирани x = p – a.Се разбира, добиените резултати се совпаѓаат.


4. Најдете го радиусот на кругот впишан во правоаголен триаголник со катети а, би хипотенуза Со. Решение (сл. 8). Тдобро како OMCN -квадрат, тогаш радиусот на впишаниот круг е еднаков на тангентата отсечка CN.
![]() .
.


5. Докажете дека точките на тангенција на впишаната и заокружувањето со страната на триаголникот се симетрични околу средината на оваа страна.
Решение (сл. 9).Забележете дека АК е тангентна отсечка од кружницата за триаголник ABC.Според формулата (2)
![]() . ВМ- линиски сегмент
тангента на кружницата за триаголник ABC.Според формулата (1)
. ВМ- линиски сегмент
тангента на кружницата за триаголник ABC.Според формулата (1)
![]() . АК = ВМ,а тоа значи дека точките К и Мподеднакво оддалечено од средината на страната АБ, Q.E.D.
. АК = ВМ,а тоа значи дека точките К и Мподеднакво оддалечено од средината на страната АБ, Q.E.D.

6. Две заеднички надворешни тангенти и една внатрешна тангента се нацртани на два круга. Внатрешната тангента ги пресекува надворешните тангенти во точките А, Би ги допира круговите во точките А 1И ВО 1.Докажете го тоа AA 1 = BB 1.
Решение (сл. 10). Стоп... Што има да се одлучи? Ова е само поинаква формулација на претходниот проблем. Очигледно, еден од круговите е впишан, а другиот е круг за одреден триаголник ABC.И сегментите AA 1 и BB 1одговараат на сегменти АКИ ВМзадачи 5. Вреди да се одбележи дека задачата предложена во Серуска Олимпијадаученици по математика, се решава на таков очигледен начин.

7. Страните на петаголникот по редослед на премин се 5, 6, 10, 7, 8. Докажете дека во овој петаголник не може да се впише круг.
Решение (сл. 11). Да претпоставиме дека во пентагон ABCDEможете да впишете круг. Згора на тоа, партиите АБ, п.н.е., ЦД, ДЕИ ЕАсе еднакви на 5, 6, 10, 7 и 8, соодветно.Да ги означиме тангентните точки во низа – Ф, Г, Х, МИ Н. Нека должината на сегментот А.Ф.еднаква на X.
Потоа Б.Ф. = ФД – А.Ф. = 5 – x = Б.Г.. Г.Ц. = п.н.е. – Б.Г. = = 6 – (5 – x) = 1 + x = CH. И така натаму: HD = ДМ = 9 – x; М.Е. = МК = x – 2, АН = 10 – X.
Но, А.Ф. = АН. Тоа е 10 - X = X; X= 5. Меѓутоа, тангентната отсечка А.Ф.не може да биде еднаква страна АБ. Добиената противречност докажува дека кругот не може да биде впишан во даден петаголник.
8. Круг е впишан во шестоаголник, неговите страни по редослед на обиколување се 1, 2, 3, 4, 5. Најдете ја должината на шестата страна.
Решение. Се разбира, можеме да означиме тангентна отсечка како X, како и во претходниот проблем, креирајте равенка и добијте го одговорот. Но, многу поефикасно и поефективно е да се користи забелешка на теоремата 2 : збировите на страните на ограничен шестаголник, земени еден низ друг, се еднакви.
Потоа 1 + 3 + 5 = 2 + 4 + X, Каде X– непозната шеста страна, X = 3.

Решение (сл. 12). Бидејќи должините на сите страни се цели броеви, фракционите делови на должините на отсечките се еднакви БТ, Б.П., ДМ, DN, А.К.И AT. Ние имаме AT + телевизија= 1, и фракциони делови од должини на сегменти ATИ ТБсе еднакви. Ова е можно само кога AT + телевизија= 0,5. По теорема 1
ВТ + VR.
Средства, VR= 0,5. Забележете дека состојбата ЦД= 3 се покажа како неподигнато. Очигледно, авторите на проблемот претпоставувале некое друго решение. Одговор: 0,5.

10. Во четириаголник ABCD AD = DC, AB = 3, BC = 5.Кругови впишани во триаголници ABDИ CBDдопрете сегмент БДна точките МИ Нсоодветно. Најдете ја должината на сегментот МН.
Решение (сл. 13). MN = DN – DM.Според формулата (1) за триаголници DBAИ ДБЦсоодветно, имаме:

11. Во четириаголник А БЕ ЦЕ ДЕможете да впишете круг. Кругови впишани во триаголници ABDИ CBDимаат радиуси РИ рсоодветно. Најдете го растојанието помеѓу центрите на овие кругови.
Решение (сл. 13). Бидејќи по услов четириаголникот А БЕ ЦЕ ДЕвпишана, по теорема 2 ние имаме: AB + DC = AD + BC.Ајде да ја искористиме идејата за решавање на претходниот проблем. . Тоа значи дека допирните точки на круговите со отсечката ДМпоклопуваат. Растојанието помеѓу центрите на круговите е еднакво на збирот на радиусите. Одговор: R+r.
Всушност, докажано е дека состојбата е во четириаголник А БЕ ЦЕ ДЕможете да впишете круг, што е еквивалентно на условот - во конвексен четириаголник А БЕ ЦЕ ДЕкругови впишани во триаголници ABCИ ADCдопирајте еден со друг. Спротивното е точно.
Се предлага да се докажат овие две меѓусебно инверзни тврдења во следниот проблем, што може да се смета за генерализација на овој.

12. Во конвексен четириаголник А БЕ ЦЕ ДЕ (оризот. 14) кругови впишани во триаголници ABCИ ADCдопирајте еден со друг. Докажете дека круговите се впишани во триаголници ABDИ BDCисто така се допираат едни со други.

13. Во триаголник ABCсо странките а, бИ вна страна Сонцетоозначена точка Дтака што круговите впишани во триаголници ABDИ ACDдопрете сегмент АДво еден момент. Најдете ја должината на сегментот БД.
Решение (сл. 15). Да ја примениме формулата (1) за триаголници ADCИ А.Д.Б., пресметување ДМдва 
Излегува, Д– точка на допир со страната Сонцетокруг впишан во триаголник ABC. Спротивното е точно: ако темето на триаголникот е поврзано со тангентната точка на впишан круг на спротивната страна, тогаш круговите впишани во добиените триаголници се допираат еден со друг.

14. Центри ЗА 1 , ЗА 2 и ЗА 3 три непресечни кругови со ист радиус се наоѓаат на темињата на триаголникот. Од поени ЗА 1 , ЗА 2 , ЗА 3, тангентите на овие кругови се нацртани како што е прикажано на сликата.
Познато е дека овие тангенти, вкрстувајќи се, формирале конвексен шестоаголник, чии страни се обоени со црвена и сина боја. Докажете дека збирот на должините на црвените отсечки е еднаков на збирот на должините на сините.
Решение (сл. 16). Важно е да се разбере како да се користи фактот дека дадените кругови имаат еднакви радиуси. Забележете дека сегментите БРИ ДМсе еднакви, што произлегува од еднаквоста на правоаголните триаголници ЗА 1 БРИ О 2 Б.М.. Исто така Д.Л. = Д.П., FN = ФК. Ги додаваме еднаквостите член по член, а потоа од добиените збирови одземаме идентични отсечки на тангенти извлечени од темињата А, СО, И Ешестоаголник АБЦДЕФ: АРИ А.К., Ц.Л.И ЦМ., МКИ Е.П.. Го добиваме она што ни треба.
Еве пример за проблем во стереометријата, предложен на XII меѓународен математички турнир за средношколци „Куп во сеќавање на А. Н. Колмогоров“.
16. Дадена е пентагонална пирамида SA 1 A 2 A 3 A 4 A 5 .Има сфера w,кој ги допира сите рабови на пирамидата и друга сфера w 1,кој ги допира сите страни на основата А 1 А 2 А 3 А 4 А 5и продолжетоци на страничните ребра SA 1, SA 2, SA 3, SA 4, SA 5надвор од врвовите на основата. Докажете дека врвот на пирамидата е подеднакво оддалечен од темињата на основата. (Берлов С. Л., Карпов Д. В.)

бидејќи тангентните отсечки се еднакви. Нека C i A i = a i. Потоа p SAiAi +1 = с+а и +а и+1, а од еднаквоста на периметрите следува дека а 1 = а 3 = а 5 = а 2 = а 4, од каде С.А. 1 = С.А. 2 = С.А. 3 = С.А. 4 = С.А. 5 .
17. Единствен државен испит. Дијагностичка работа 8.12.2009 година, С–4.Даден е трапезоид А БЕ ЦЕ ДЕ, чии темели п.н.е. = 44,АД = 100, AB = CD= 35. Заокружи тангента на правите АДИ А.Ц., ја допира страната ЦДво точката К. Најдете ја должината на сегментот CK.BDC и БДА, допрете ги страните ВДна точките ЕИ Ф. Најдете ја должината на сегментот Е.Ф..
Решение. Можни се два случаи (сл. 20 и сл. 21). Користејќи ја формулата (1) ги наоѓаме должините на отсечките ДЕИ ДФ.

Во првиот случај АД = 0,1AC, ЦД = 0,9А.Ц.. Во втората - АД = 0,125AC, ЦД = 1,125А.Ц.. Ги заменуваме податоците и добиваме одговор: 4.6 или 5.5.
Проблеми за самостојно решавање/

1. Периметарот на рамнокрак трапез ограничен околу круг е еднаков на 2 Бришење.Најдете ја проекцијата на дијагоналата на трапезот на поголемата основа. (1/2r)
2. Отворена банка Проблеми со унифициран државен испитматематика. НА 4. На круг впишан во триаголник ABC (Сл. 22),нацртани се три тангенти. Периметрите на исечените триаголници се 6, 8, 10. Најдете го периметарот на овој триаголник. (24)
3. Во триаголник ABCе впишан круг. MN -тангента на кругот, MÎ AC, NÎ BC, BC = 13, AC = 14, AB = 15.Најдете го периметарот на триаголникот МНЦ. (12)
4. На круг впишан во квадрат со страна a, е нацртана тангента која ги пресекува нејзините две страни. Најдете го периметарот на исечениот триаголник. (А)
5. Круг е впишан во петаголник со страни А, г, в, гИ д. Најдете ги отсечките на кои точката на тангенција ја дели страната еднаква на А.
6. Круг е впишан во триаголник со страни 6, 10 и 12. На кругот е нацртана тангента така што таа пресекува две долги страни. Најдете го периметарот на исечениот триаголник. (16)
7. ЦД– средина на триаголникот ABC. Кругови впишани во триаголници ACDИ BCD, допрете го сегментот ЦДна точките МИ Н. Најдете МН, Ако AC – Сонцето = 2. (1)
8. Во триаголник ABCсо странките а, бИ вна страна Сонцетоозначена точка Д. На кругови впишани во триаголници ABDИ ACD, заедничка тангента е нацртана вкрстувајќи се АДво точката М. Најдете ја должината на сегментот AM. (должина AMне зависи од положбата на точката ДИ
еднакво на ½ ( c + b – a))
9. Б правоаголен триаголниквпишан во круг со радиус А. Радиусот на кругот тангентен на хипотенузата и продолжетоците на нозете е еднаков на Р.Најдете ја должината на хипотенузата. ( R–a)
10. Во триаголник ABCДолжините на страните се познати: АБ = Со, AC = б, Сонцето = А. Круг впишан во триаголник допира страна АБво точката C 1. Ексциркулата го допира продолжетокот на страната АБпо поен Аво точката C 2. Одреди ја должината на сегментот C 1 C 2. (б)
11. Најдете ги должините на страните на триаголникот поделени со точката на тангенција на впишаниот круг со радиус 3 cm на отсечки од 4 cm и 3 cm (7, 24 и 25 cm во правоаголен триаголник)
12. Сорос олимпијада 1996 година, 2. коло, 11 одделение. Даден е триаголник ABC, на чии страни се означени точките A 1, B 1, C 1. Радиус на кругови впишани во триаголници AC 1 B 1, BC 1 A 1, SA 1 B 1еднакви во р. Радиус на круг впишан во триаголник A 1 B 1 C 1еднакви Р. Најдете го радиусот на кругот впишан во триаголник ABC. (Р +р).
Задачите 4–8 се преземени од проблематичната книга на Гордин Р.К. „Геометрија. Планиметрија“. Москва. Издавачка куќа MCNMO. 2004 година.
Доказ
Ако акордот е со дијаметар, тогаш теоремата е очигледна.
Слика 287 покажува круг со центар O, M е точката на пресек на дијаметарот CD и акордот AB, CD ⊥ AB. Треба да докажеме дека AM = MB.
Да ги нацртаме радиусите OA и OB. ВО рамнокрак триаголник AOB (OA = OB) отсечка OM е висината, а со тоа и медијаната, т.е. AM = MB.
Теорема 20.2
Дијаметарот на кругот што дели акорд различен од дијаметарот на половина е нормален на оваа акорд.
Докажете ја оваа теорема сами. Размислете дали оваа изјава би била точна ако акордот е со дијаметар.
Слика 288 ги прикажува сите можни случаи на релативна положба на права линија и круг. На слика 288, а немаат заеднички точки, на слика 288, б - имаат две заеднички точки, на слика 288, во - еден.
|
Ориз. 288 |
||
|
|
|
|
Дефиниција
Права која има само една заедничка точка со круг се нарекува тангента на кругот.
Тангента на круг има само една заедничка точка со кругот ограничен со таа кружница. На слика 288, правата a е тангента на кругот со центар во точката O, A е точката на тангенција.
Ако отсечка (зрак) припаѓа на тангента на кружница и има заедничка точка со оваа кружница, тогаш се вели дека отсечката (зракот) е тангента на кружницата. На пример, Слика 289 покажува отсечка AB, која го допира кругот во точката C.
Теорема 20.3
(тангентна сопственост)
Тангента на круг е нормална на радиусот нацртан до точката на тангенција.
Доказ
Слика 290 покажува круг со центар O, A е точката на тангенција помеѓу права линија a и кругот. Треба да докажеме дека ОП ⊥ a.
|
Ориз. 289 |
Ориз. 290 |
Ориз. 291 |
|
|
|
|
Да претпоставиме дека тоа не е така, односно отсечката ОА е наклонета кон правата а. Потоа од точката О ја спуштаме нормалната ОМ на права линија a (сл. 291). Бидејќи точката А е единствената заедничка точка на права a и круг со центар O, тогаш точката М не припаѓа на оваа кружница. Оттука OM = MB + OB, каде што точката B е пресечната точка на кругот и нормалната OM. Сегментите OA и OB се еднакви како радиусите на кругот. Така OM > OA. Добивме контрадикција: нормалната ОМ е поголема од косиот ОА. Затоа, ОП ⊥ a.
Теорема 20.4
(знак за тангента на круг)
Ако права линија што минува низ точка на круг е нормална на радиусот нацртан до оваа точка, тогаш оваа права линија е тангента на оваа кружница.
Доказ
|
Ориз. 292 |
|
|
Слика 290 покажува круг со центар во точката O, сегментот OA е неговиот радиус, точката A припаѓа на правата a, OA ⊥ a. Да докажеме дека правата a е тангента на кругот.
Нека правата а не е тангента, туку има друга заедничка точка B со кружницата (сл. 292). Тогаш ∆ AOB е рамнокрак (OA = OB како радиуси). Оттука ∠ OBA = ∠ OAB = 90°. Добиваме контрадикторност: триаголникот AOB има два прави агли. Според тоа, правата a е тангента на кругот.
Последица
Ако растојанието од центарот на кругот до одредена права линија е еднакво на радиусот на кругот, тогаш оваа права линија е тангента на овој круг.
|
Ориз. 293 |
|
|
Докажете ја оваа последица сами.
Задача. Докажете дека ако преку оваа точкадве тангенти се нацртани на круг, тогаш тангентните отсечки што поврзуваат дадена точка со точките на тангенција се еднакви.
Решение. Слика 293 покажува круг со центар O. Правилата AB и AC се тангенти, точките B и C се тангентни точки. Треба да докажеме дека AB = AC.
Да ги нацртаме радиусите OB и OC до точките на допир. Според тангентното својство, OB ⊥ AB и OC ⊥ AC. Во правоаголните триаголници AOB и AOC, катетите OB и OC се еднакви како радиусите на една кружница, AO е заедничка хипотенуза. Според тоа, триаголниците AOB и AOC се еднакви по хипотенуза и крак. Оттука AB = AC.

- Како дијаметарот нормално на него дели акорд?
- Кој е аголот помеѓу акордот освен дијаметарот и дијаметарот што ја дели оваа акорд на половина?
- Опишете ги сите можни случаи на релативна положба на права и круг.
- Која права се нарекува тангента на круг?
- Какво својство има радиусот нацртан до точката на тангенција на права и круг?
- Формулирајте го тестот за тангента на круг.
- Какво својство имаат тангентите нацртани на круг низ една точка?

Практични задачи

507. Нацртајте круг со центар О, нацртајте акорд AB. Користејќи квадрат, поделете го овој акорд на половина.
508. Нацртајте круг со центар О, нацртајте ЦД со акорд. Со помош на линијар со скала, нацртајте дијаметар нормално на ЦД-то на акордот.
509. Нацртајте круг, означете ги точките A и B. Со линијар и квадрат нацртајте прави линии што ја допираат кружницата во точките A и B.
510. Нацртајте права a и на неа означете ја точката M. Со квадрат, линијар и компас нацртајте круг со радиус 3 cm што ја допира правата a во точката M. Колку такви кругови може да се нацртаат?

Вежби
511. На Слика 294, точката O е центарот на кругот, дијаметарот CD е нормален на акорд AB. Докажете дека ∠AOD = ∠BOD.
512. Докажете дека еднаквите акорди на кругот се подеднакво оддалечени од неговиот центар.
513. Докажете дека ако акордите на кругот се еднакво оддалечени од неговиот центар, тогаш тие се еднакви.
514. Дали е вистина дека права линија нормална на радиусот на кругот го допира овој круг?
515. Директно CD допира круг со центар O во точката A, отсечката AB е акорд на кругот, ∠ BAD = 35° (сл. 295). Најдете ∠AOB.
516. Директно CD допира круг со центар O во точката A, отсечката AB е акорд на кругот, ∠ AOB = 80° (види Сл. 295). Најдете ∠BAC.
517. Дадена е кружница чиј дијаметар е 6 cm Правата a се отстранува од центарот за: 1) 2 cm; 2) 3 см; 3) 6 cm Во кој случај правата е тангента на кругот?
518. Во триаголникот ABC знаеме дека ∠ C = 90°. Докажете дека:
1) директно BC е тангента на кругот со центар A што минува низ точката C;
2) директно AB не е тангента на кружницата со центар C што минува низ точката А.

519. Докажете дека дијаметарот на кругот е поголем од која било акорда освен дијаметарот.
520. Во круг со центар О, акорд AB е повлечен низ средината на радиусот, нормално на него. Докажете дека ∠ AOB = 120°.
521. Најдете го аголот помеѓу радиусите OA и OB на кругот ако растојанието од центарот O на кругот до акордот AB е 2 пати помало од: 1) должината на акордот AB; 2) радиус на кругот.
522. Дијаметарот AB и акордите AC и CD се нацртани во кругот така што AC = 12 cm, ∠ BAC = 30 °, AB ⊥ CD. Најдете ја должината на ЦД-то на акордот.
523. Преку точка M на кружницата со центар O ги цртаме тангентите MA и MB, A и B се точки на тангенција, ∠ OAB = 20°. Најдете ∠AMB.
524. Низ краевите на акордот AB, еднаков на радиусот на кружницата, се исцртуваат две тангенти кои се сечат во точката C. Најдете ∠ ACB.
525. Преку точка Од круг со центар О цртаме тангента на оваа кружница, AB е дијаметарот на кругот. Од точката А нормална АД се спушта на тангента. Докажете дека зракот AC е симетрала на аголот BAD.
526. Директно AC допира круг со центар О во точката А (сл. 296). Докажете дека аголот BAC е 2 пати помал од аголот AOB.
|
Ориз. 294 |
Ориз. 295 |
Ориз. 296 |
|
|
|
|
527. Сегменти AB и BC се акорд и дијаметар на кругот, соодветно, ∠ ABC = 30°. Преку точката A, нацртајте тангента на кружната права што ја пресекува BC во точката D. Докажете дека ∆ ABD е рамнокрак.
528. Познато е дека дијаметарот AB го преполовува акордот CD, но не е нормален на него. Докажете дека ЦД е исто така дијаметар.

529. Најдете го локусот на центрите на круговите што ја допираат дадената права во дадена точка.
530. Најдете го локусот на центрите на круговите што ги допираат двете страни на даден агол.
531. Најдете го локусот на центрите на круговите што ја допираат дадената линија.
532. Прави тангентни на кружница со центар O во точките A и B се сечат во точката K, ∠ AKB = 120°. Докажете дека AK + BK = ОК.
533. Кругот ја допира страната AB на триаголникот ABC во точката M и го допира продолжетокот на другите две страни. Докажете дека збирот на должините на отсечките BC и BM е еднаков на половина од периметарот на триаголникот ABC.
|
Ориз. 297 |
|
|
534. Преку точка C се тангенти AC и BC на кружницата, A и B се точки на тангенција (сл. 297). На кругот зедовме произволна точка М која лежи во иста полурамнина со точка C во однос на правата AB и преку неа нацртавме тангента на кругот што ги пресекува правите AC и BC во точките D и E, соодветно. Докажете дека периметарот на триаголникот DEC не зависи од изборот на точката М.
Вежби за повторување
535. Докажете дека средната точка М на отсечка чии краеви припаѓаат на две паралелни прави е средната точка на која било отсечка што минува низ точката М и чии краеви припаѓаат на овие прави.
536. Сегменти AB и CD лежат на иста линија и имаат заедничка средна точка. Точката М е избрана така што триаголникот AMB е рамнокрак со основа AB. Докажете дека ∆ CMD е исто така рамнокрак со основното ЦД.
537. На страна MK на триаголникот MPK ги означи точките E и F така што точката E лежи помеѓу точките M и F, ME = EP, PF = FK. Најдете го аголот M ако ∠ EPF = 92°, ∠ K = 26°.
538. ВО акутен триаголник ABC, се црта симетрала BM, се црта нормална MK од точката M на страната BC, ∠ ABM = ∠ KMC. Докажете го тоа триаголник ABC- рамнокрак.
Набљудувајте, цртајте, дизајнирајте, фантазирајте
539. Воспоставете ја шемата на формите на фигурите прикажани на Слика 298. Која фигура треба да биде поставена следната?
|
Ориз. 298 |
Секанта, тангента - сето ова можеше да се слушне стотици пати на часовите по геометрија. Но, дипломирањето е зад нас, минуваат години, а сето ова знаење се заборава. Што треба да запомните?
Суштина
Терминот „тангента на круг“ е веројатно познат на сите. Но, малку е веројатно дека секој ќе може брзо да ја формулира неговата дефиниција. Во меѓувреме, тангента е права линија која лежи во иста рамнина како круг што ја сече само во една точка. Можеби ги има огромен број, но сите ги имаат идентични својства, за што ќе се дискутира подолу. Како што може да претпоставите, точката на тангенција е местото каде што се сечат кругот и правата линија. Во секој конкретен случај има само еден, но ако ги има повеќе, тогаш тоа ќе биде секант.
Историја на откривање и проучување
Концептот на тангента се појавил во античко време. Изградбата на овие прави линии, прво до круг, а потоа и до елипси, параболи и хиперболи со помош на линијар и компас, беше извршена уште во далечната почетни фазиразвој на геометријата. Се разбира, историјата не го зачувала името на откривачот, но очигледно е дека дури и во тоа време луѓето биле сосема запознаени со својствата на тангента на круг.
Во модерните времиња, интересот за овој феномен повторно се разгоре - започна нов круг на проучување на овој концепт, комбиниран со откривање на нови кривини. Така, Галилео го вовел концептот на циклоид, а Ферма и Декарт конструирале тангента на него. Што се однесува до круговите, се чини дека на овие простори не останале тајни за старите.
Својства
Радиусот нацртан до пресечната точка ќе биде Ова
главното, но не и единственото својство што го има тангента на круг. Друга важна карактеристика вклучува две прави линии. Значи, преку една точка што лежи надвор од кругот, може да се нацртаат две тангенти, а нивните отсечки ќе бидат еднакви. Постои уште една теорема на оваа тема, но таа ретко се испитува во рамките на стандардот училишен курс, иако е исклучително погодно за решавање на некои проблеми. Звучи вака. Од една точка лоцирана надвор од кругот, кон неа се нацртани тангента и секант. Се формираат отсечките AB, AC и AD. A е пресек на правите, B е точка на тангенција, C и D се пресеци. Во овој случај, ќе важи следната еднаквост: должината на тангентата на кругот, на квадрат, ќе биде еднаква на производот на отсечките AC и AD.
Има важна последица од горенаведеното. За секоја точка на кругот можете да конструирате тангента, но само една. Доказот за ова е прилично едноставен: теоретски испуштајќи ја нормалната од радиусот на неа, дознаваме дека формираниот триаголник не може да постои. А тоа значи дека тангентата е единствената.
Градба
Меѓу другите проблеми во геометријата постои посебна категорија, како по правило, не

сакан од учениците и студентите. За да ги решите проблемите од оваа категорија, потребен ви е само компас и линијар. Ова се градежни задачи. Има и такви за конструирање на тангента.
Значи, даден круг и точка што лежи надвор од нејзините граници. И потребно е да се нацрта тангента низ нив. Како да го направите ова? Пред сè, треба да нацртате отсечка помеѓу центарот на кругот О и дадената точка. Потоа користете компас за да го поделите на половина. За да го направите ова, треба да поставите радиус - малку повеќе од половина од растојанието помеѓу центарот на оригиналниот круг и оваа точка. По ова, треба да изградите два вкрстени лаци. Покрај тоа, радиусот на компасот не треба да се менува, а центарот на секој дел од кругот ќе биде оригиналната точка и О, соодветно. Треба да се поврзат раскрсниците на лаците, што ќе го подели сегментот на половина. Поставете радиус на компасот еднаков на ова растојание. Следно, конструирајте друг круг со центарот на пресечната точка. На неа ќе лежат и првобитната точка и О. Во овој случај, ќе има уште две пресеци со кружницата дадена во проблемот. Тие ќе бидат точки на контакт за првично наведената точка.
Тоа беше изградбата на тангенти на кругот што доведе до раѓање

диференцијална пресметка. Првото дело на оваа тема го објави познатиот германски математичар Лајбниц. Тој предвидуваше можност за наоѓање максими, миними и тангенти без разлика на фракционите и ирационалните величини. Па, сега се користи за многу други пресметки.
Покрај тоа, тангентата на круг е поврзана со геометриското значење на тангентата. Оттука доаѓа неговото име. Преведено од латински tangens значи „тангента“. Така, овој концепт е поврзан не само со геометријата и диференцијалното сметање, туку и со тригонометријата.
Два круга
Тангентата не секогаш влијае само на една фигура. Ако огромен број прави линии може да се нацртаат на еден круг, тогаш зошто да не и обратно? Може. Но, задачата во овој случај станува сериозно комплицирана, бидејќи тангентата на два круга може да не помине низ ниедна точка, а релативната положба на сите овие бројки може да биде многу

различни.
Видови и сорти
Кога зборуваме за два круга и една или повеќе прави линии, дури и ако се знае дека тоа се тангенти, не е веднаш јасно како сите овие фигури се наоѓаат во однос на едни со други. Врз основа на ова, се разликуваат неколку сорти. Така, круговите може да имаат една или две заеднички точки или воопшто да ги немаат. Во првиот случај тие ќе се вкрстат, а во вториот ќе се допрат. И тука се разликуваат две сорти. Ако еден круг е, како што беше, вграден во вториот, тогаш тангенцијата се нарекува внатрешна, ако не, тогаш надворешна. Можете да ја разберете релативната положба на фигурите не само врз основа на цртежот, туку и да имате информации за збирот на нивните радиуси и растојанието помеѓу нивните центри. Ако овие две количини се еднакви, тогаш круговите се допираат. Ако првиот е поголем, тие се вкрстуваат, а ако е помал, тогаш немаат заеднички точки.
Истото важи и за прави линии. За кои било два круга што немаат заеднички точки, можете

конструирај четири тангенти. Две од нив ќе се вкрстат меѓу фигурите, тие се нарекуваат внатрешни. Неколку други се надворешни.
Ако зборуваме за кругови кои имаат една заедничка точка, тогаш проблемот е многу поедноставен. Поентата е дека без разлика на се релативна положбаво овој случај тие ќе имаат само една тангента. И ќе помине низ точката на нивното вкрстување. Така, изградбата нема да биде тешка.
Ако фигурите имаат две точки на пресек, тогаш за нив може да се конструира права линија, тангентна на кругот и на едната и на другата, но само надворешна. Решението за овој проблем е слично на она што ќе се дискутира подолу.
Решавање на проблем
И внатрешната и надворешната тангента на два круга не се толку едноставни за конструирање, иако овој проблем може да се реши. Факт е дека за ова се користи помошна фигура, така што треба сами да го смислите овој метод

доста проблематично. Значи, дадени се два круга со различни радиуси и центри O1 и O2. За нив треба да конструирате два пара тангенти.
Пред сè, треба да изградите помошен во близина на центарот на поголемиот круг. Во овој случај, разликата помеѓу радиусите на двете почетни фигури треба да се утврди на компасот. Тангентите на помошниот круг се конструирани од центарот на помалиот круг. По ова, перпендикуларите се цртаат од О1 и О2 на овие прави додека не се вкрстат со оригиналните фигури. Како што следува од основното својство на тангентата, се наоѓаат бараните точки на двете кругови. Проблемот е решен, барем првиот дел.
За да конструирате внатрешни тангенти, ќе треба да решите практично

слична задача. Повторно ќе ви треба помошна фигура, но овој пат нејзиниот радиус ќе биде еднаков на збирот на оригиналните. Тангентите се конструирани кон него од центарот на еден од овие кругови. Понатамошниот тек на решението може да се разбере од претходниот пример.
Тангента на круг или дури два или повеќе не е така тешка задача. Се разбира, математичарите одамна престанаа да ги решаваат ваквите проблеми рачно и се потпираат на пресметки специјални програми. Но, не треба да мислите дека сега не треба да можете сами да го направите тоа, бидејќи за правилно формулирање на задача за компјутер треба да направите и да разберете многу. За жал, постои загриженост дека по конечната транзиција кон тест форма на контрола на знаењето, градежните задачи ќе им предизвикуваат на учениците сè повеќе потешкотии.
Што се однесува до изнаоѓање заеднички тангенти за поголем број кругови, тоа не е секогаш можно, дури и ако тие лежат во иста рамнина. Но, во некои случаи можете да најдете таква права линија.
Примери од животот
Во пракса често се јавува заедничка тангента на два круга, иако тоа не е секогаш забележливо. Транспортери, блок системи, ремени за пренос на макара, затегнување на конецот во машина за шиење, па дури и само синџир за велосипеди - сето тоа се вистински примери. Затоа, не треба да мислите дека геометриските проблеми остануваат само во теорија: во инженерството, физиката, градежништвото и многу други области тие наоѓаат практична примена.
Написот дава детално објаснување на дефинициите, геометриско значењеизвод со графичка нотација. Равенката на тангента права ќе се разгледа со примери, ќе се најдат равенките на тангента на криви од 2-ри ред.
Дефиниција 1Аголот на наклонетост на правата y = k x + b се нарекува агол α, кој се мери од позитивната насока на оската x кон правата y = k x + b во позитивна насока.
На сликата, насоката x е означена со зелена стрелка и зелен лак, а аголот на наклон со црвен лак. Сината линија се однесува на права линија.
Дефиниција 2
Наклонот на правата y = k x + b се нарекува нумерички коефициент k.
Аголниот коефициент е еднаков на тангентата на правата линија, со други зборови k = t g α.
- Аголот на наклонетост на права линија е еднаков на 0 само ако е паралелен околу x, а наклонот е еднаков на нула, бидејќи тангентата на нула е еднаква на 0. Тоа значи дека формата на равенката ќе биде y = b.
- Ако аголот на наклон на правата y = k x + b е остар, тогаш условите 0 се задоволени< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение наклон k се смета за позитивен број, бидејќи тангентата вредност го задоволува условот t g α > 0, а на графикот има зголемување.
- Ако α = π 2, тогаш локацијата на правата е нормална на x. Равенството се одредува со x = c со вредноста c е реален број.
- Ако аголот на наклонетост на правата y = k x + b е тап, тогаш одговара на условите π 2< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает негативно значење, а графикот се намалува.
Секанта е права која минува низ 2 точки од функцијата f (x). Со други зборови, секанта е права линија која се повлекува низ кои било две точки на графикот дадена функција.

Сликата покажува дека A B е секант, а f (x) е црна крива, α е црвен лак, што го покажува аголот на наклон на секантот.
Кога аголниот коефициент на права линија е еднаков на тангентата на аголот на наклонетост, јасно е дека тангентата на правоаголен триаголник A B C може да се најде со односот на спротивната страна со соседната.
Дефиниција 4
Добиваме формула за наоѓање секант на формата:
k = t g α = B C A C = f (x B) - f x A x B - x A, каде што апсцисите на точките A и B се вредностите x A, x B и f (x A), f (x Б) се вредностите функции на овие точки.
Очигледно, аголниот коефициент на секантата се одредува со помош на еднаквоста k = f (x B) - f (x A) x B - x A или k = f (x A) - f (x B) x A - x B , а равенката мора да се запише како y = f (x B) - f (x A) x B - x A x - x A + f (x A) или
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .
Секантата визуелно го дели графикот на 3 дела: лево од точката А, од А до Б, десно од Б. Сликата подолу покажува дека има три секанти кои се сметаат за случајни, односно се поставени со помош на слична равенка.

По дефиниција, јасно е дека правата линија и нејзиниот секант во овој случај се совпаѓаат.
Секанта може повеќе пати да го пресекува графикот на дадена функција. Ако постои равенка од формата y = 0 за секанта, тогаш бројот на точки на пресек со синусоидот е бесконечен.
Дефиниција 5
Тангента на графикот на функцијата f (x) во точката x 0 ; f (x 0) е права линија што минува низ дадена точка x 0; f (x 0), со присуство на сегмент кој има многу x вредности блиску до x 0.
Пример 1
Да го разгледаме подетално примерот подолу. Тогаш е јасно дека правата дефинирана со функцијата y = x + 1 се смета за тангента на y = 2 x во точката со координати (1; 2). За јасност, неопходно е да се земат предвид графиконите со вредности блиски до (1; 2). Функцијата y = 2 x е прикажана со црно, сината линија е тангента линија, а црвената точка е пресечната точка.

Очигледно, y = 2 x се спојува со правата y = x + 1.
За да ја одредиме тангентата, треба да го разгледаме однесувањето на тангентата A B бидејќи точката B бесконечно се приближува до точката A. За јасност, претставуваме цртеж.

Секантата A B, означена со сината линија, се стреми кон положбата на самата тангента, а аголот на наклонетост на секантата α ќе почне да се стреми кон аголот на наклонетост на самата тангента α x.
Дефиниција 6
Тангентата на графикот на функцијата y = f (x) во точката A се смета за гранична позиција на секантата A B бидејќи B се стреми кон A, односно B → A.
Сега да продолжиме да го разгледуваме геометриското значење на изводот на функцијата во точка.
Да продолжиме со разгледување на секантата A B за функцијата f (x), каде A и B со координати x 0, f (x 0) и x 0 + ∆ x, f (x 0 + ∆ x), а ∆ x е означено како зголемување на аргументот. Сега функцијата ќе има форма ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) . За јасност, да дадеме пример за цртеж.

Да го разгледаме добиениот правоаголен триаголник A B C. За решавање ја користиме дефиницијата за тангента, односно ја добиваме релацијата ∆ y ∆ x = t g α . Од дефиницијата за тангента произлегува дека lim ∆ x → 0 ∆ y ∆ x = t g α x. Според правилото на изводот во точка, имаме дека изводот f (x) во точката x 0 се нарекува граница на односот на зголемувањето на функцијата со зголемувањето на аргументот, каде што ∆ x → 0 , тогаш го означуваме како f (x 0) = lim ∆ x → 0 ∆ y ∆ x.
Следи дека f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x, каде што k x се означува како наклон на тангентата.
Односно, наоѓаме дека f ' (x) може да постои во точката x 0, и како тангентата на даден график на функцијата во точката на тангенција еднаква на x 0, f 0 (x 0), каде што вредноста на наклонот на тангентата во точката е еднаков на изводот во точката x 0 . Тогаш добиваме дека k x = f " (x 0) .
Геометриското значење на изводот на функцијата во точка е тоа што го дава концептот за постоење на тангента на графикот во истата точка.
За да се запише равенката на која било права линија на рамнина, потребно е да се има аголен коефициент со точката низ која минува. Неговата нотација е земена како x 0 на пресекот.
Тангентата равенка на графикот на функцијата y = f (x) во точката x 0, f 0 (x 0) добива форма y = f "(x 0) x - x 0 + f (x 0).
Ова значи дека конечната вредност на изводот f "(x 0) може да ја одреди положбата на тангентата, односно вертикално, под услов lim x → x 0 + 0 f "(x) = ∞ и lim x → x 0 - 0 f "(x) = ∞ или воопшто отсуство под условот lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) .
Локацијата на тангентата зависи од вредноста на нејзиниот аголен коефициент k x = f "(x 0). Кога е паралелна со оската o x, добиваме дека k k = 0, кога е паралелна со o y - k x = ∞ и формата на тангентната равенка x = x 0 се зголемува со k x > 0, се намалува како k x< 0 .
Пример 2
Состави равенка за тангентата на графикот на функцијата y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 во точката со координати (1; 3) и определи го аголот на наклонетост.
Решение
По услов имаме функцијата да е дефинирана за сите реални броеви. Откриваме дека точката со координатите наведени со условот (1; 3) е точка на тангенција, потоа x 0 = - 1, f (x 0) = - 3.
Неопходно е да се најде изводот во точката со вредност - 1. Го добиваме тоа
y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3
Вредноста на f' (x) на точката на тангенција е наклонот на тангентата, кој е еднаков на тангентата на наклонот.
Тогаш k x = t g α x = y " (x 0) = 3 3
Следи дека α x = a r c t g 3 3 = π 6
Одговор:тангентната равенка добива форма
y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3
За јасност, даваме пример во графичка илустрација.
Црната боја се користи за графикот на оригиналната функција, сината боја е сликата на тангентата, а црвената точка е точката на тангенција. Сликата од десната страна покажува зголемен приказ.

Пример 3
Определи постоење на тангента на графикот на дадена функција
y = 3 · x - 1 5 + 1 во точката со координати (1 ; 1) . Напиши равенка и определи го аголот на наклон.
Решение
По услов, имаме доменот на дефиниција на дадена функција да се смета за множество од сите реални броеви.
Ајде да продолжиме со наоѓање на дериватот
y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5
Ако x 0 = 1, тогаш f' (x) е недефиниран, но границите се напишани како lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞ , што значи постоење вертикална тангента во точката (1; 1).
Одговор:равенката ќе има форма x = 1, каде што аголот на наклон ќе биде еднаков на π 2.
За јасност, ајде да го прикажеме графички.

Пример 4
Најдете ги точките на графикот на функцијата y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2, каде
- Нема тангента;
- Тангентата е паралелна на x;
- Тангентата е паралелна со правата y = 8 5 x + 4.
Решение
Неопходно е да се обрне внимание на опсегот на дефиницијата. По услов, имаме функцијата да е дефинирана на множеството од сите реални броеви. Го прошируваме модулот и го решаваме системот со интервали x ∈ - ∞ ; 2 и [-2; + ∞). Го добиваме тоа
y = - 1 15 x 3 + 18 x 2 + 105 x + 176, x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12, x ∈ [-2; + ∞)
Неопходно е да се разликува функцијата. Ние го имаме тоа
y " = - 1 15 x 3 + 18 x 2 + 105 x + 176", x ∈ - ∞; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35), x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3, x ∈ [-2; + ∞)
Кога x = − 2, тогаш изводот не постои бидејќи едностраните граници не се еднакви во таа точка:
lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3
Вредноста на функцијата ја пресметуваме во точката x = - 2, каде што го добиваме тоа
- y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, односно тангентата во точката ( - 2; - 2) нема да постои.
- Тангентата е паралелна на x кога наклонот е нула. Тогаш k x = t g α x = f "(x 0). Тоа е, неопходно е да се најдат вредностите на таквиот x кога изводот на функцијата ќе го претвори на нула. Тоа е, вредностите на f ' (x) ќе бидат точките на тангенција, каде што тангентата е паралелна на x .
Кога x ∈ - ∞ ; - 2, потоа - 1 5 (x 2 + 12 x + 35) = 0, а за x ∈ (- 2; + ∞) добиваме 1 5 (x 2 - 4 x + 3) = 0.
1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2 ; +∞
Пресметајте ги соодветните функциски вредности
y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3
Оттука - 5; 8 5, - 4; 4 3, 1; 8 5, 3; 4 3 се сметаат за барани точки на графикот на функцијата.
Ајде да размислиме графичка сликарешенија.

Црната линија е графикот на функцијата, црвените точки се тангентните точки.
- Кога правите се паралелни, аголните коефициенти се еднакви. Потоа, потребно е да се бараат точки на графикот на функции каде што наклонот ќе биде еднаков на вредноста 8 5. За да го направите ова, треба да решите равенка од формата y "(x) = 8 5. Потоа, ако x ∈ - ∞; - 2, добиваме дека - 1 5 (x 2 + 12 x + 35) = 8 5, и ако x ∈ ( - 2 ; + ∞), тогаш 1 5 (x 2 - 4 x + 3) = 8 5.
Првата равенка нема корени бидејќи дискриминантата е помала од нула. Ајде да го запишеме тоа
1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0
Друга равенка има два реални корени, значи
1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2 ; +∞
Ајде да продолжиме со наоѓање на вредностите на функцијата. Го добиваме тоа
y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3
Поени со вредности - 1; 4 15, 5; 8 3 се точките во кои тангентите се паралелни на правата y = 8 5 x + 4.
Одговор:црна линија – графикон на функцијата, црвена линија – график на y = 8 5 x + 4, сина линија – тангенти на точките - 1; 4 15, 5; 8 3.

Можно постоење бесконечен бројтангенти за дадени функции.
Пример 5
Напишете ги равенките на сите достапни тангенти на функцијата y = 3 cos 3 2 x - π 4 - 1 3, кои се наоѓаат нормално на правата y = - 2 x + 1 2.
Решение
За да се состави тангентната равенка, потребно е да се најдат коефициентот и координатите на тангентата точка, врз основа на условот за перпендикуларност на правите. Дефиницијата е следна: производот на аголните коефициенти кои се нормални на правите е еднаков на - 1, односно запишан како k x · k ⊥ = - 1. Од условот имаме дека аголниот коефициент се наоѓа нормално на правата и е еднаков на k ⊥ = - 2, тогаш k x = - 1 k ⊥ = - 1 - 2 = 1 2.
Сега треба да ги пронајдете координатите на точките на допир. Треба да го пронајдете x и потоа неговата вредност за дадена функција. Забележете дека од геометриското значење на изводот во точката
x 0 добиваме дека k x = y "(x 0). Од оваа еднаквост ги наоѓаме вредностите на x за допирните точки.
Го добиваме тоа
y " (x 0) = 3 cos 3 2 x 0 - π 4 - 1 3 " = 3 - грев 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 грев 3 2 x 0 - π 4 3 2 = - 9 2 грев 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 грев 3 2 x 0 - π 4 = 1 2 ⇒ грев 3 2 x 0 - π 4 = - 1 9
Ова тригонометриска равенкаќе се користи за пресметување на ординатите на тангентните точки.
3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk или 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk
3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk или 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk
x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z
Z е множество од цели броеви.
x точки на контакт се пронајдени. Сега треба да продолжите кон пребарување на вредностите на y:
y 0 = 3 cos 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - грев 2 3 2 x 0 - π 4 - 1 3 или y 0 = 3 - 1 - грев 2 3 2 x 0 - π 4 - 1 3
y 0 = 3 1 - - 1 9 2 - 1 3 или y 0 = 3 - 1 - - 1 9 2 - 1 3
y 0 = 4 5 - 1 3 или y 0 = - 4 5 + 1 3
Од ова добиваме дека 2 3 π 4 - a r c sin 1 9 + 2 πk ; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 се точките на тангенција.
Одговор:потребните равенки ќе бидат напишани како
y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z
За визуелно претставување, разгледајте функција и тангента на координатна права.
Сликата покажува дека функцијата се наоѓа на интервалот [-10; 10 ], каде што црната линија е графикот на функцијата, сините линии се тангенти, кои се наоѓаат нормално на дадената права од формата y = - 2 x + 1 2. Црвените точки се точки на допир.

Канонските равенки на кривите од втор ред не се функции со една вредност. Тангентни равенки за нив се составени според познати шеми.
Тангента на круг
Да се дефинира круг со центар во точката x c e n t e r ; y c e n t e r и радиус R, примени ја формулата x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 .
Оваа еднаквост може да се запише како унија на две функции:
y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r
Првата функција се наоѓа на врвот, а втората на дното, како што е прикажано на сликата.

Да се состави равенката на круг во точката x 0; y 0 , која се наоѓа во горниот или долниот полукруг, треба да ја пронајдете равенката на графикот на функција од формата y = R 2 - x - x c e n t e r 2 + y c e n t e r или y = - R 2 - x - x c e n t e r 2 + y c e n t e r на посочената точка.
Кога во точките x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r - R тангентите може да се дадат со равенките y = y c e n t e r + R и y = y c e n t e r - R , и во точките x c e n t e r + R ; y c e n t e r и
x c e n t e r - R ; y c e n t e r ќе биде паралелна со o y, тогаш добиваме равенки од формата x = x c e n t e r + R и x = x c e n t e r - R .

Тангента на елипса
Кога елипсата има центар на x c e n t e r ; y c e n t e r со полуоски a и b, тогаш може да се специфицира со помош на равенката x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1.
Елипса и круг може да се означат со комбинирање на две функции, имено горната и долната полуелипса. Тогаш го добиваме тоа
y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Ако тангентите се наоѓаат на темињата на елипсата, тогаш тие се паралелни околу x или околу y. Подолу, за јасност, разгледајте ја фигурата.

Пример 6
Напишете ја равенката на тангентата на елипсата x - 3 2 4 + y - 5 2 25 = 1 во точки со вредности x еднакви на x = 2.
Решение
Потребно е да се најдат тангентните точки кои одговараат на вредноста x = 2. Ја заменуваме постоечката равенка на елипсата и го наоѓаме тоа
x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5
Потоа 2; 5 3 2 + 5 и 2; - 5 3 2 + 5 се тангентните точки кои припаѓаат на горната и долната полуелипса.
Да продолжиме со наоѓање и решавање на равенката на елипсата во однос на y. Го добиваме тоа
x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2
Очигледно, горната полуелипса е специфицирана со помош на функција од формата y = 5 + 5 2 4 - x - 3 2, а долната половина елипса y = 5 - 5 2 4 - x - 3 2.
Ајде да примениме стандарден алгоритам за да создадеме равенка за тангента на графикот на функција во точка. Да напишеме дека равенката за првата тангента во точка 2; 5 3 2 + 5 ќе изгледа
y " = 5 + 5 2 4 - x - 3 2" = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2" = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5
Откриваме дека равенката на втората тангента со вредност во точката
2 ; - 5 3 2 + 5 ја зема формата
y " = 5 - 5 2 4 - (x - 3) 2" = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2" = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5
Графички, тангентите се означени на следниов начин:

Тангента на хипербола
Кога хиперболата има центар на x c e n t e r ; y c e n t e r и темиња x c e n t e r + α ; y c e n t e r и x c e n t e r - α ; y c e n t e r, се одвива неравенката x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1, ако со темиња x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r - b , потоа се одредува со помош на неравенката x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 .

Хиперболата може да се претстави како две комбинирани функции на формата
y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r или y = b a · (x - x c e n t e r) 2 + a 2 b a r (x - x c e n t e r) 2 + a 2 + y c e n t e r

Во првиот случај имаме дека тангентите се паралелни на y, а во вториот се паралелни на x.
Следи дека за да се најде равенката на тангентата на хипербола, потребно е да се открие на која функција и припаѓа точката на тангенција. За да се утврди ова, неопходно е да се замени во равенките и да се провери идентитетот.
Пример 7
Напиши равенка за тангентата на хиперболата x - 3 2 4 - y + 3 2 9 = 1 во точката 7; - 3 3 - 3 .
Решение
Потребно е да се трансформира записот за решение за наоѓање хипербола со помош на 2 функции. Го добиваме тоа
x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 и y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3
Неопходно е да се идентификува на која функција припаѓа поставена точкасо координати 7; - 3 3 - 3 .
Очигледно, за да се провери првата функција потребно е y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3, тогаш точката не припаѓа на графикот, бидејќи еднаквоста не важи.
За втората функција имаме дека y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3, што значи дека точката припаѓа на дадениот график. Од тука треба да го најдете наклонот.
Го добиваме тоа
y " = - 3 2 (x - 3) 2 - 4 - 3" = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3
Одговор:тангентната равенка може да се претстави како
y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3
Тоа е јасно прикажано вака:

Тангента на парабола
За да креирате равенка за тангентата на параболата y = a x 2 + b x + c во точката x 0, y (x 0), мора да користите стандарден алгоритам, тогаш равенката ќе има форма y = y "(x 0) x - x 0 + y ( x 0). Таквата тангента на темето е паралелна на x.
Треба да ја дефинирате параболата x = a y 2 + b y + c како заедница на две функции. Затоа, треба да ја решиме равенката за y. Го добиваме тоа
x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a
Графички прикажан како:

За да дознаете дали точка x 0, y (x 0) припаѓа на функција, постапете нежно според стандардниот алгоритам. Таквата тангента ќе биде паралелна со o во однос на параболата.
Пример 8
Напишете ја равенката на тангентата на графикот x - 2 y 2 - 5 y + 3 кога имаме тангентен агол од 150 °.
Решение
Решението го започнуваме со претставување на параболата како две функции. Го добиваме тоа
2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4
Вредноста на наклонот е еднаква на вредноста на изводот во точката x 0 од оваа функција и е еднаква на тангентата на аголот на наклон.
Добиваме:
k x = y "(x 0) = t g α x = t g 150 ° = - 1 3
Од тука ја одредуваме вредноста на x за допирните точки.
Првата функција ќе биде напишана како
y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3
Очигледно, нема вистински корени, бидејќи добивме негативна вредност. Заклучуваме дека за таква функција нема тангента со агол од 150°.
Втората функција ќе биде напишана како
y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4
Имаме дека допирните точки се 23 4 ; - 5 + 3 4 .
Одговор:тангентната равенка добива форма
y = - 1 3 x - 23 4 + - 5 + 3 4
Ајде да го прикажеме графички вака:

Доколку забележите грешка во текстот, означете ја и притиснете Ctrl+Enter
Правата која има само една заедничка точка со круг се нарекува тангента на кружницата, а нивната заедничка точка се нарекува тангента на правата и кругот.
Теорема (својство на тангента на круг)
Тангента на круг е нормална на радиусот нацртан до точката на тангенција.
Со оглед на
А – точка на контакт
Доказ:p ОА
Доказ.
Да го докажеме тоа со контрадикторност.
Да претпоставиме дека p е OA, тогаш OA е наклонет кон правата линија p.
Ако од точката O нацртаме нормална OH на права линија p, тогаш неговата должина ќе биде помала од радиусот: OH< ОА=r

Откриваме дека растојанието од центарот на кругот до правата линија p (OH) е помало од радиусот (r), што значи дека правата линија p е секантна (односно, има две заеднички точки со кругот). што е во спротивност со условите на теоремата (p е тангента).
Ова значи дека претпоставката е неточна, затоа правата p е нормална на ОА.
Теорема (својство на тангентни отсечки извлечени од една точка)
Тангентните отсечки на кругот нацртан од една точка се еднакви и еднакви еднакви аглисо права линија што минува низ оваа точка и центарот на кругот. 
Со оглед на: прибл. (О;р)
AB и AC се тангенти на околината. (О;р)
Доказ: AB=AC
Доказ
1) OB AB, OS AC, како радиуси нацртани до точката на тангенција (тангентна својство)
2) Размислете за tr. AOB, итн. AOS – p/u
АД – генерал
OB=OS (како радиуси)
Ова значи ABO = AOC (по хипотенуза и нога). Оттука,
AB = AC,<3 = < 4 (как соответственные элементы в равных тр-ках). ч.т.д.
Теорема (тангенцијален тест)
Ако правата минува низ крајот на радиусот што лежи на круг и е нормална на овој радиус, тогаш таа е тангента. 
Со оглед на: ОА – радиус на кругот
Доказ: p- тангента на кругот
Доказ
ОА – радиус на кругот (според условот) (OA=r)
OA – нормално од O на права линија p (OA =d)
Тоа значи дека r=OA=d, што значи дека правата p и кругот имаат една заедничка точка.
Според тоа, правата p е тангента на кругот. итн.
3.Својства на акордите и секантите.
Својства на тангента и секанта
ДЕФИНИЦИЈА
Обеме локус на точки еднакво оддалечени од една точка, што се нарекува центар на кругот.

Се нарекува отсечка што поврзува две точки на круг акорд(на сликата ова е сегмент). Акорд што минува низ центарот на кругот се нарекува дијаметаркругови.
1. Тангентата е нормална на радиусот нацртан до точката на допир.
2. Тангентните отсечки извлечени од една точка се еднакви.
3. Ако тангента и секанта се нацртани од точка што лежи надвор од кругот, тогаш квадратот на должината на тангентата е еднаков на производот на секантата и нејзиниот надворешен дел.