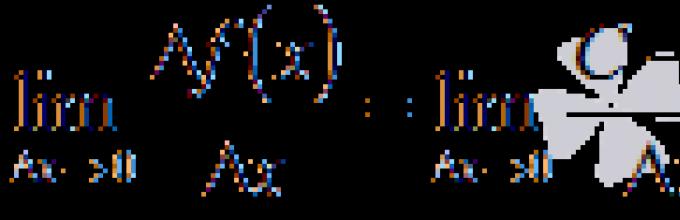При изведување на првата формула од табелата, ќе продолжиме од дефиницијата на дериватната функција во точка. Ајде да земеме каде x– било кој реален број, тоа е, x– кој било број од доменот на дефинирање на функцијата. Дозволете ни да ја запишеме границата на односот на зголемувањето на функцијата до зголемувањето на аргументот на: ![]()
Треба да се напомене дека под граничниот знак се добива изразот, кој не е неизвесност на нула поделена со нула, бидејќи броителот не содржи бесконечно мала вредност, туку точно нула. Со други зборови, зголемувањето на константна функција е секогаш нула.
Така, извод на константна функцијае еднаква на нула низ целиот домен на дефиниција.
Извод на функција на моќност.
Формулата за изводот на функцијата моќност има форма ![]() , каде што експонентот стр– кој било реален број.
, каде што експонентот стр– кој било реален број.
Прво да ја докажеме формулата за природниот експонент, односно за p = 1, 2, 3,…
Ќе ја користиме дефиницијата за извод. Дозволете ни да ја запишеме границата на односот на зголемување на функцијата на моќност до зголемувањето на аргументот: 
За да го поедноставиме изразот во броителот, се свртуваме кон биномната формула на Њутн: 
Оттука, 
Ова ја докажува формулата за извод на функција на моќност за природен експонент.
Извод на експоненцијална функција.
Ви ја претставуваме изведбата на формулата за извод врз основа на дефиницијата:
Дојдовме до неизвесност. За да го прошириме, воведуваме нова променлива, и на . Потоа. Во последната транзиција ја користевме формулата за премин кон нова логаритамска основа.
Ајде да го замениме оригиналното ограничување: 
Ако се потсетиме на втората извонредна граница, доаѓаме до формулата за изводот на експоненцијалната функција: 
Извод на логаритамска функција.
Да ја докажеме формулата за изводот на логаритамска функција за сите xод доменот на дефиниција и сите валидни вредности на основата алогаритам По дефиниција за дериват имаме: 
Како што забележавте, за време на докажувањето, трансформациите беа извршени користејќи ги својствата на логаритамот. Еднаквост  е точно поради втората извонредна граница.
е точно поради втората извонредна граница.
Изводи на тригонометриски функции.
За да изведеме формули за изводи на тригонометриски функции, ќе треба да потсетиме на некои тригонометриски формули, како и на првата забележителна граница.
По дефиниција на изводот за синусната функција имаме ![]() .
.
Да ја искористиме формулата за разлика во синусите: 
Останува да се свртиме кон првата извонредна граница: 
Така, изводот на функцијата грев хЕте го cos x.
Точно на ист начин се докажува формулата за дериватот на косинус. 
Според тоа, изводот на функцијата cos xЕте го – грев х.
Ќе изведеме формули за табелата со деривати за тангента и котангента користејќи докажани правила на диференцијација (дериват на дропка). 
Деривати на хиперболични функции.
Правилата за диференцијација и формулата за изводот на експоненцијалната функција од табелата со деривати ни овозможуваат да изведеме формули за дериватите на хиперболичен синус, косинус, тангента и котангента. 
Извод на инверзната функција.
За да не дојде до забуна при презентацијата, да го означиме под знакот аргументот на функцијата со која се врши диференцијација, односно тоа е извод на функцијата f(x)Од страна на x.
Сега да формулираме правило за наоѓање извод на инверзна функција.
Оставете ги функциите y = f(x)И x = g(y)меѓусебно инверзно, дефинирано на интервалите и соодветно. Ако во некоја точка постои конечен ненулти извод на функцијата f(x), тогаш во точката постои конечен извод на инверзната функција g(y), и ![]() . Во друг пост
. Во друг пост ![]() .
.
Ова правило може да се преформулира за било кој xод интервалот , тогаш добиваме  .
.
Ајде да ја провериме валидноста на овие формули.
Да ја најдеме инверзната функција за природниот логаритам ![]() (Тука yе функција, и x- аргумент). Откако ја решивме оваа равенка за x, добиваме (тука xе функција, и y– нејзиниот аргумент). Тоа е,
(Тука yе функција, и x- аргумент). Откако ја решивме оваа равенка за x, добиваме (тука xе функција, и y– нејзиниот аргумент). Тоа е, ![]() и меѓусебно инверзни функции.
и меѓусебно инверзни функции.
Од табелата на деривати гледаме дека ![]() И
И ![]() .
.
Да се увериме дека формулите за пронаоѓање на изводите на инверзната функција нè водат до истите резултати: 
Час и презентација на тема: „Број д. Функција. График. Својства“
Дополнителни материјали
Почитувани корисници, не заборавајте да ги оставите вашите коментари, критики, желби! Сите материјали се проверени со антивирусна програма.
Наставни средства и симулатори во онлајн продавницата Integral за 11 одделение
Интерактивен прирачник за 9-11 одделение „Тригонометрија“
Интерактивен прирачник за 10-11 одделение „Логаритми“
Момци, денес ќе проучуваме посебен број. Зазема посебно место во математиката за „возрасни“ и има многу извонредни својства, од кои некои ќе разгледаме.
Да се вратиме на експоненцијалните функции $y=a^x$, каде што $a>1$. Можеме да нацртаме многу различни графикони на функции за различни бази.
Но, треба да се забележи дека:
- сите функции минуваат низ точката (0;1),
- за $x→-∞$, графикот има хоризонтална асимптота $y=0$,
- сите функции се зголемуваат и конвексираат надолу,
- а исто така и континуирани, што пак значи дека се диференцијабилни.
Да ја разгледаме функцијата $y=2^x$ и да конструираме тангента на неа.
Откако внимателно ги нацртавме нашите графикони, можете да видите дека аголот на наклонетост на тангентата е 35°.
Сега да ја нацртаме функцијата $y=3^x$ и исто така да ја нацртаме тангентата линија: 
Овој пат аголот на тангента е приближно 48°. Во принцип, вреди да се напомене: колку е поголема основата експоненцијална функција, толку е поголем аголот на наклон.
Од особен интерес е тангентата со агол на наклон еднаков на 45°. На графикот од која експоненцијална функција може да се нацрта ваква тангента во точката (0;1)?
Основата на експоненцијалната функција мора да биде поголема од 2, но помала од 3, бидејќи бараниот тангентен агол е постигнат некаде помеѓу функциите $y=2^x$ и $y=3^x$. Таков број е пронајден и се покажа дека е доста уникатен.
Експоненцијална функција во која тангентата што минува низ точката (0;1) има агол на наклон еднаков на 45° обично се означува со: $y=e^x$ .
Основата на нашата функција е ирационален број. Математичарите ја извлекоа приближната вредност на овој број $e=2,7182818284590…$.
Во училишните курсеви по математика, вообичаено е да се заокружи до најблиската десетина, односно $e=2,7$.
Ајде да изградиме график на функцијата $y=e^x$ и тангента на овој график. 
Нашата функција обично се нарекува експоненцијална.
Својства на функцијата $y=e^x$.
1. $D(f)=(-∞;+∞)$.
2. Не е ниту парен ниту непарен.
3. Се зголемува низ целиот домен на дефиниција.
4. Не е ограничено одозгора, ограничено одоздола.
5. Најголема вредностНе, најниска вредностбр.
6. Континуирано.
7. $E(f)=(0; +∞)$.
8. Конвексен надолу.
Во вишата математика е докажано дека експоненцијалната функција е секаде диференцијабилна, а нејзиниот извод е еднаков на самата функција: $(e^x)"=e^x$.
Нашата функција е широко користена во многу области од математиката (во математичката анализа, во теоријата на веројатност, во програмирањето), а многу реални објекти се поврзани со овој број.
Пример.
Најдете ја тангентата на графикот на функцијата $y=e^x$ во точката $x=2$.
Решение.
Тангентната равенка е опишана со формулата: $y=f(a)+f"(a)(x-a)$.
Секвенцијално ги наоѓаме бараните вредности:
1. $f(a)=f(2)=e^2$.
2. $f"(a)=e^a$.
3. $f"(2)=e^2$.
4. $y=f(a)+f"(a)(x-a)=e^2+e^2(x-2)=e^2*x-e^2$.
Одговор: $y=e^2*x-e^2$
Пример.
Најдете ја вредноста на изводот на функцијата $y=e^(3x-15)$ во точката $x=5$.
Решение.
Да се потсетиме на правилото за диференцирање на функција од формата $y=f(kx+m)$.
$y"=k*f"(kx+m)$.
Во нашиот случај $f(kx+m)=e^(3x-15)$.
Ајде да го најдеме дериватот:
$y"=(e^(3x-15))"=3*e^(3x-15)$.
$y"(5)=3*e^(15-15)=3*e^0=3$.
Одговор: 3.
Пример.
Испитајте ја функцијата $y=x^3*e^x$ за екстреми.
Решение.
Да го најдеме изводот на нашата функција $y"=(x^3*e^x)"=(x^3)"*e^x+x^3(e^x)"=3x^2*e^x +x^ 3*e^x=x^2*e^x(x+3)$.
Функцијата нема критични точки, бидејќи изводот постои за кој било x.
Изедначувајќи го изводот со 0, добиваме два корени: $x_1=0$ и $x_2=-3$.
Да ги означиме нашите точки на бројната линија: 
Проблеми кои треба да се решаваат самостојно
1. Најдете ја тангентата на графикот на функцијата $y=e^(2x)$ во точката $x=2$.2. Најдете ја вредноста на изводот на функцијата $y=e^(4x-36)$ во точката $x=9$.
3. Испитајте ја функцијата $y=x^4*e^(2x)$ за екстреми.
За да користите прегледи на презентации, креирајте сметка на Google и најавете се на неа: https://accounts.google.com
Наслов на слајд:
ДЕРИВАТ НА ЕКСПОНЕНЦИЈАЛНА ФУНКЦИЈА Број e Одделение 11
ПОВТОРУВАЊЕТО е мајка на учењето!
Дефиниција на експоненцијална функција Функција, дадена со формулата y = a x (каде a > 0, a ≠ 1) се нарекува експоненцијална функција со основа a.
Својства на експоненцијалната функција y = a x a>1 0
Определување на изводот на функцијата во точка x 0. како Δ → 0. Изводот на функцијата f во точката x 0 е бројот кон кој односот на разликата се стреми како Δx → 0.
Геометриско значење на изводот x ₀ α A y = f(x) 0 x y к = tan α = f "(x ₀) Коефициентот на аголот на тангентата на графикот на функцијата f (x) во точката (x 0 ; f (x 0) е еднаква на изводните функции f "(x ₀). f(x 0)
Игра: „Најди ги паровите“ (u + v)“ cos x e (u v)“ n xⁿ ⁻“ p (u / v)“ - 1 /(sin² x) a (x ⁿ)“ - sin x n C „u“ v +u v" до (C u)" 1 / (cos ² x) t (sin x)" (u" v – u v") / v² c (cos x)" 0 o (tg x)" u " + v " e (ctg x) "C u " n
Проверете сами! (u + v)" u" + v" e (u v)" u" v + u v "до (u /v)" (u' v –u v") / v² s (x ⁿ)" n x ⁿ ⁻1 p C" 0 o (Cu)" C u "n (sin x)" Cos x e (cos x)" - sin x n (tg x)" 1 / (cos² x) t (ctg x)" - 1 / (sin² x ) А
Експонентот е функција за напојување. Експонент е функција каде што e е основа на природните логаритми.
1 y= e x 45° Функцијата y= e x се нарекува „експонент“ x ₀ =0; tg 45° = 1 Во точката (0;1) наклонот кон тангентата на графикот на функцијата k = tg 45° = 1 - геометриско значењеизвод на експонентот Експонент y = e x
Теорема 1. Функцијата y = e е диференцијабилна во секоја точка од доменот на дефиниција, и (e)" = e x x x Природниот логаритам (ln) е логаритам на основата e: ln x = log x e Експоненцијалната функција е диференцијабилна во секоја точка од доменот на дефиниција, и (а)" = a ∙ ln a x x Теорема 2.
Формули за диференцирање на експоненцијалната функција (e)" = e ; (e)" = k e ; (а)" = a ∙ ln a; (а)" = k a ∙ ln a. x kx + b x x x kx + b kx + b kx + b F(a x) = + C; F(e x) = e x +C.
„Вежбањето раѓа мајсторство“. Тацит Публиј Корнелиј - антички римски историчар
Примери: Најдете ги изводите на функциите: 1. = 3 e. 2. (e)" = (5x)" e = 5 e. 3. (4)" = 4 ln 4. 4. (2)" = (-7 x)" 2 ∙ ln 2 = -7 ∙ 2 ∙ ln 2. 5 x 5 x x (3 e)" 5 x - 7 x x x -7 x -7 x x
Интересни работи во близина
Леонхард Ојлер 1707 -1783 година Руски научник - математичар, физичар, механичар, астроном... Воведе ознака за бројот e Докажа дека бројот e ≈ 2, 718281... е ирационален. Џон Непиер 1550 - 1617 година Шкотски математичар, пронаоѓач на логаритми. Во негова чест, бројот e се нарекува „непер број“.
Растот и распаѓањето на функцијата со експоненцијална брзина се нарекуваат експоненцијални
Цели на лекцијата:формирајте идеја за број д; докаже диференцијабилност на функција во која било точка X;да го разгледа доказот на теоремата за диференцијабилноста на функцијата; проверка на зрелоста на вештините и способностите при решавање на примери за нивна примена.
Цели на часот.
Образовни: повторете ја дефиницијата за извод, правилата за диференцијација, изводот на елементарните функции, запомнете го графикот и својствата на експоненцијалната функција, развиете способност за наоѓање извод на експоненцијална функција, тестирајте го знаењето со помош на задача за верификација и тест.
Развојно: промовирање на развојот на вниманието, развој на логично размислување, математичка интуиција, способност за анализа и примена на знаењето во нестандардни ситуации.
Образовни: негувајте информациска култура, развивајте вештини за работа во група и индивидуално.
Наставни методи: вербални, визуелни, активни.
Форми на обука: колективна, индивидуална, групна.
Опрема : учебник „Алгебра и почетоците на анализата“ (уредил Колмогоров), сите задачи од групата Б „Затворен сегмент“ уредено од А.Л. Семенова, И.В. Јашченко, мултимедијален проектор.
Чекори на лекцијата:
- Изјава за темата, целта и целите на часот (2 мин.).
- Подготовка за учење нов материјал со повторување на претходно научениот материјал (15 мин.).
- Вовед во нов материјал (10 мин.)
- Почетно разбирање и консолидација на новите знаења (15 мин.).
- Домашна задача (1 мин.).
- Сумирање (2 мин.).
За време на часовите
1. Организациски момент.
Се објавува темата на часот: „Извод на експоненцијална функција. Број д.“, цели, цели. Слајд 1. Презентација
2. Активирање на потпорното знаење.
За да го направите ова, во првата фаза од лекцијата ќе одговориме на прашања и ќе решаваме проблеми со повторување. Слајд 2.
На таблата, двајца студенти работат на картички, завршувајќи задачи како што е унифициран државен испит Б8.
Задача за првиот ученик:
Задача за вториот ученик:

Останатите ученици работат самостојна работа според следниве опции:
| Опција 1 | Опција 2 | ||
| 1. |  |
1. |  |
| 2. |  |
2. |  |
| 3. |  |
3. |  |
| 4. |  |
4. |  |
| 5. |  |
5. |  |
Паровите разменуваат решенија и си ја проверуваат работата, проверувајќи ги одговорите на слајдот 3.
Се разгледуваат решенијата и одговорите на студентите кои работат на одборот.
Испитување домашна работабр.1904 година. Прикажан е слајдот 4.
3. Ажурирање на темата на часот, создавање проблемска ситуација.
Наставникот бара да се дефинира експоненцијална функција и да се наведат својствата на функцијата y = 2 x. Графиконите на експоненцијалните функции се прикажани како мазни линии, на кои може да се нацрта тангента во секоја точка. Но, постоењето на тангента на графикот на функцијата во точка со апсциса x 0 е еквивалентно на нејзината диференцијабилност на x 0.
За графиците на функцијата y = 2 x и y = 3 x, цртаме тангенти на нив во точката со апсциса 0. Аглите на наклонетост на овие тангенти на оската на апсцисата се приближно еднакви на 35° и 48°, соодветно . Слајд 5.
Заклучок: ако основата на експоненцијалната функција Асе зголемува од 2 на, на пример, 10, тогаш аголот помеѓу тангентата на графикот на функцијата во точката x = 0 и апсцисата постепено се зголемува од 35° на 66,5°. Логично е да се претпостави дека има причина А, за кој соодветниот агол е 45
Докажано е дека има број поголем од 2 и помал од 3. Обично се означува со буквата д. Во математиката е утврдено дека бројот д– ирационално, т.е. претставува бесконечна децимална непериодична дропка.
e = 2,7182818284590…
Забелешка (не многу сериозно). Слајд 6.
На следниот слајд 7 се појавуваат портрети на големи математичари - Џон Непиер, Леонхард Ојлер и кратки информацииза нив.
- Разгледајте ги својствата на функцијата y=e x
- Доказ за теорема 1. Слајд 8.
- Доказ за теорема 2. Слајд 9.
4. Динамична пауза или релаксација за очите.
(Почетна позиција - седење, секоја вежба се повторува 3-4 пати):
1. Наведнувајќи се наназад, земете длабок здив, а потоа, наведнувајќи се напред, издишете.
2. Наведнувајќи се на столот, затворете ги очните капаци, цврсто затворете ги очите без да ги отворите очните капаци.
3. Рацете по телото, кружни движења на рамената напред-назад.
5. Консолидација на изучениот материјал.
5.1 Решение на вежби бр.538, бр.540, бр.544в.
5.2 Самостојна примена на знаењата, вештините и способностите. Работа за верификацијаво форма на тест. Време на завршување на задачата – 5 минути.
Критериуми за оценување:
„5“ - 3 поени
„4“ – 2 поени
„3“ - 1 поен
6. Сумирање на резултатите од работата во лекцијата.
- Рефлексија.
- Оценување.
- Поднесување на тест задачи.
7. Домашна задача: став 41 (1, 2); бр.539 (а, б, г); 540 (в, г), 544 (а, б).
„Затворен сегмент“ бр.1950, 2142 г.
Графикот на експоненцијална функција е крива, мазна линија без кривини, на која може да се нацрта тангента во секоја точка низ која минува. Логично е да се претпостави дека ако може да се нацрта тангента, тогаш функцијата ќе биде диференцијабилна во секоја точка од нејзиниот домен на дефиниција.
Ќе прикажеме во некои координатни оскинеколку графикони на функцијата y = x a, За a = 2; a = 2,3; a = 3; a = 3,4.
Во точка со координати (0;1). Аглите на овие тангенти ќе бидат приближно 35, 40, 48 и 51 степени соодветно. Логично е да се претпостави дека во интервалот од 2 до 3 постои број на кој аголот на наклонетост на тангентата ќе биде еднаков на 45 степени.
Да дадеме прецизна формулација на оваа изјава: има број поголем од 2 и помал од 3, означен со буквата e, така што експоненцијалната функција y = e x во точката 0 има извод еднаков на 1. Тоа е: (e ∆x -1) / ∆x се стреми кон 1 како што ∆x се стреми кон нула.
Овој број де ирационална и се пишува како бесконечна непериодична децимална дропка:
e = 2,7182818284…
Бидејќи e е позитивно и не е нула, постои логаритам за основата e. Овој логаритам се нарекува природен логаритам . Се означува со ln(x) = log e (x).
Извод на експоненцијална функција
Теорема: Функцијата e x е диференцијабилна во секоја точка од нејзиниот домен на дефиниција, и (e x)’ = e x.
Експоненцијалната функција a x е диференцијабилна во секоја точка од нејзиниот домен на дефиниција, и (a x)’ = (a x)*ln(a).
Последица на оваа теорема е фактот дека експоненцијалната функција е континуирана во која било точка од нејзиниот домен на дефиниција.
Пример: најдете го изводот на функцијата y = 2 x.
Користејќи ја формулата за изводот на експоненцијалната функција, добиваме:
(2 x)’ = (2 x)*ln(2).
Одговор: (2 x)*ln(2).
Антидериват на експоненцијалната функција
За експоненцијална функција a x дефинирана на множеството реални броеви, антидериватот ќе биде функцијата (a x)/(ln(a)).
ln(a) е некоја константа, тогаш (a x / ln(a))’= (1 / ln(a)) * (a x) * ln(a) = a x за кој било x. Ја докажавме оваа теорема.
Да разгледаме пример за наоѓање на антидериватот на експоненцијалната функција.
Пример: најдете го антидериватот на функцијата f(x) = 5 x. Да ја искористиме формулата дадена погоре и правилата за наоѓање антидеривати. Добиваме: F(x) = (5 x) / (ln(5)) +C.