Нека е даден правоаголен координатен систем.
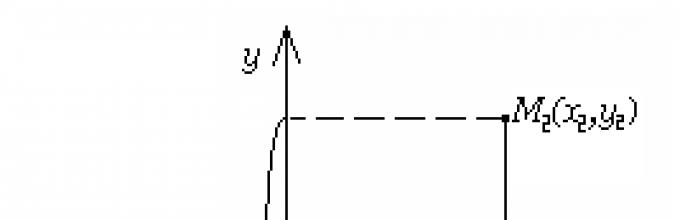
Теорема 1.1.За било кои две точки M 1 (x 1;y 1) и M 2 (x 2;y 2) од рамнината, растојанието d меѓу нив се изразува со формулата
Доказ.Дозволете ни да ги отфрлиме перпендикуларите M 1 B и M 2 A од точките M 1 и M 2, соодветно
 на оската Oy и Ox и означете ја со K точката на пресек на правите M 1 B и M 2 A (сл. 1.4). Можни се следниве случаи:
на оската Oy и Ox и означете ја со K точката на пресек на правите M 1 B и M 2 A (сл. 1.4). Можни се следниве случаи:
1) Точките M 1, M 2 и K се различни. Очигледно, точката К има координати (x 2; y 1). Лесно е да се види дека M 1 K = ôx 2 – x 1 ô, M 2 K = ôу 2 – y 1 ô. Бидејќи ∆M 1 KM 2 е правоаголен, тогаш според Питагоровата теорема d = M 1 M 2 =  = .
= .
2) Точката K се совпаѓа со точката M 2, но е различна од точката M 1 (сл. 1.5). Во овој случај y 2 = y 1
 и d = M 1 M 2 = M 1 K = ôx 2 – x 1 ô=
и d = M 1 M 2 = M 1 K = ôx 2 – x 1 ô=  =
=
3) Точката К се совпаѓа со точката М 1, но се разликува од точката М 2. Во овој случај x 2 = x 1 и d =
M 1 M 2 = KM 2 = ôу 2 - y 1 ô=  = .
= .
4) Точката М 2 се совпаѓа со точката М 1. Тогаш x 1 = x 2, y 1 = y 2 и
d = M 1 M 2 = O = .
Поделба на сегмент во овој поглед.
Нека е дадена произволна отсечка M 1 M 2 на рамнината и нека M ─ која било точка од ова
 сегмент различен од точката M 2 (сл. 1.6). Бројот l, дефиниран со еднаквоста l =
сегмент различен од точката M 2 (сл. 1.6). Бројот l, дефиниран со еднаквоста l =  , повикан став,во која точка M ја дели отсечката M 1 M 2.
, повикан став,во која точка M ја дели отсечката M 1 M 2.
Теорема 1.2.Ако точка M(x;y) ја дели отсечката M 1 M 2 во однос на l, тогаш координатите на оваа точка се одредуваат со формулите
x =  , y =
, y =  ,
(4)
,
(4)
каде што (x 1;y 1) ─ координати на точката M 1, (x 2;y 2) ─ координати на точката M 2.
Доказ.Да ја докажеме првата од формулите (4). Втората формула е докажана на сличен начин. Постојат два можни случаи.
x = x 1 =  =
=  =
=  .
.
2) Правата линија M 1 M 2 не е нормална на оската Ox (сл. 1.6). Дозволете ни да ги спуштиме перпендикуларите од точките M 1, M, M 2 на оската Ox и да ги означиме точките на нивното вкрстување со оската Ox како P 1, P, P 2, соодветно. По теоремата за пропорционални отсечки  = l.
= l.
Бидејќи P 1 P = ôx – x 1 ô, PP 2 = ôx 2 – xô и броевите (x – x 1) и (x 2 – x) имаат ист знак (на x 1< х 2 они положительны, а при х 1 >x 2 се негативни), тогаш
l = =  ,
,
x – x 1 = l(x 2 – x), x + lx = x 1 + lx 2,
x =  .
.
Заклучок 1.2.1.Ако M 1 (x 1;y 1) и M 2 (x 2;y 2) се две произволни точки и точката M(x;y) е средината на отсечката M 1 M 2, тогаш
x =  , y =
, y =  (5)
(5)
Доказ.Бидејќи M 1 M = M 2 M, тогаш l = 1 и користејќи формули (4) ги добиваме формулите (5).
Плоштина на триаголник.
Теорема 1.3.За сите точки A(x 1;y 1), B(x 2;y 2) и C(x 3;y 3) кои не лежат на истото
право, област С триаголник ABCизразено со формулата
S = ô(x 2 – x 1)(y 3 – y 1) – (x 3 – x 1)(y 2 – y 1)ô (6)
Доказ.Плоштина ∆ ABC прикажана на сл. 1.7, ние пресметуваме на следниов начин
 S ABC = S ADEC + S BCEF – S ABFD .
S ABC = S ADEC + S BCEF – S ABFD .
Ја пресметуваме областа на трапезоиди:
S ADEC =  ,
,
S BCEF = 
S ABFD = 
Сега имаме
S ABC = ((x 3 – x 1) (y 3 + y 1) + (x 3 – x 2) (y 3 + y 2) - (x 2 – -x 1) (y 1 + y 2)) = (x 3 y 3 – x 1 y 3 + x 3 y 1 – x 1 y 1 + + x 2 y 3 – -x 3 y 3 + x 2 y 2 – x 3 y 2 – x 2 y 1 + x 1 y 1 – x 2 y 2 + x 1 y 2) = (x 3 y 1 – x 3 y 2 + x 1 y 2 – x 2 y 1 + x 2 y 3 –
X 1 y 3) = (x 3 (y 1 – y 2) + x 1 y 2 – x 1 y 1 + x 1 y 1 – x 2 y 1 + y 3 (x 2 – x 1)) = (x 1 (y 2 – y 1) – x 3 (y 2 – y 1) + +y 1 (x 1 – x 2) – y 3 (x 1 – x 2)) = ((x 1 – x 3)( y 2 – y 1) + (x 1 – x 2) (y 1 – y 3)) = ((x 2 – x 1) (y 3 – y 1) –
- (x 3 – x 1) (y 2 – y 1)).
За друга локација ∆ ABC, формулата (6) се докажува на сличен начин, но може да испадне со знак „-“. Затоа во формулата (6) го ставаат знакот за модул.
Предавање 2.
Равенка на права линија на рамнина: равенка на права линија со главен коефициент, општа равенкаправа, равенка на права во отсечки, равенка на права што минува низ две точки. Аголот помеѓу прави, условите на паралелизам и нормалност на прави на рамнина.
2.1. Нека се дадени правоаголен координатен систем и некоја права L на рамнината.
Дефиниција 2.1.Равенката од формата F(x;y) = 0, која ги поврзува променливите x и y, се вика линиска равенка Л(во даден координатен систем), ако оваа равенка е задоволена со координатите на која било точка што лежи на правата L, а не со координатите на која било точка што не лежи на оваа права.
Примери на равенки на прави на рамнина.
1) Размислете за права линија паралелна со оската Oy на правоаголниот координатен систем (сл. 2.1). Да ја означиме со буквата А пресечната точка на оваа права со оската Ox, (a;o) ─ нејзината или-
 динати. Равенката x = a е равенката на дадената права. Навистина, оваа равенка е задоволена со координатите на која било точка M(a;y) од оваа права и не е задоволена со координатите на која било точка што не лежи на правата. Ако a = 0, тогаш правата линија се совпаѓа со оската Oy, која има равенка x = 0.
динати. Равенката x = a е равенката на дадената права. Навистина, оваа равенка е задоволена со координатите на која било точка M(a;y) од оваа права и не е задоволена со координатите на која било точка што не лежи на правата. Ако a = 0, тогаш правата линија се совпаѓа со оската Oy, која има равенка x = 0.
2) Равенката x - y = 0 го дефинира множеството точки на рамнината што ги сочинуваат симетралите на координатните агли I и III.
3) Равенката x 2 - y 2 = 0 ─ е равенка на две симетрали на координатни агли.
4) Равенката x 2 + y 2 = 0 дефинира една точка O(0;0) на рамнината.
5) Равенка x 2 + y 2 = 25 ─ равенка на круг со радиус 5 со центар на почетокот.
Со помош на координати, се одредува локацијата на објектот на земјината топка. Координатите се означени со географска ширина и должина. Широчините се мерат од линијата на екваторот од двете страни. На северната хемисфера географските широчини се позитивни, на јужната хемисфера се негативни. Географската должина се мери од главниот меридијан или исток или запад, соодветно, се добива или источна или западна географска должина.Според општо прифатената позиција, како главен меридијан се зема оној што минува низ старата опсерваторија Гринич во Гринич. Географските координати на локацијата може да се добијат со помош на GPS навигатор. Овој уред прима сигнали од системот за позиционирање на сателитот во координатниот систем WGS-84, униформни за целиот свет.
Моделите на навигатори се разликуваат по производителот, функционалноста и интерфејсот. Во моментов, вградените GPS навигатори се достапни и во некои модели на мобилни телефони. Но, секој модел може да ги сними и зачува координатите на точка.
Растојание помеѓу GPS координати
За да се решат практични и теоретски проблеми во некои индустрии, неопходно е да може да се одредат растојанијата помеѓу точките по нивните координати. Постојат неколку начини на кои можете да го направите ова. Канонска форма на претставување географски координати: степени, минути, секунди.На пример, можете да го одредите растојанието помеѓу следните координати: точка бр. 1 - географска ширина 55°45′07″ N, должина 37°36′56″ E; точка бр. 2 - географска ширина 58°00′02″ N, географска должина 102°39′42″ E.
Најлесен начин е да користите калкулатор за да ја пресметате должината помеѓу две точки. Во пребарувачот на прелистувачот, мора да ги поставите следните параметри за пребарување: онлајн - за да го пресметате растојанието помеѓу две координати. Во онлајн калкулаторот, вредностите на географската ширина и должина се внесуваат во полињата за пребарување за првата и втората координата. При пресметувањето, онлајн калкулаторот го даде резултатот - 3.800.619 m.
Следниот метод е повеќе трудоинтензивен, но и повеќе визуелен. Мора да користите која било достапна програма за мапирање или навигација. Програмите во кои можете да креирате точки користејќи координати и да ги измерите растојанијата меѓу нив ги вклучуваат следните апликации: BaseCamp (современ аналог на програмата MapSource), Google Earth, SAS.Planet.
Сите горенаведени програми се достапни за секој мрежен корисник. На пример, за да го пресметате растојанието помеѓу две координати во Google Earth, треба да креирате две етикети што ги означуваат координатите на првата точка и втората точка. Потоа, користејќи ја алатката „Владетел“, треба да ги поврзете првата и втората ознака со линија, програмата автоматски ќе го прикаже резултатот од мерењето и ќе ја покаже патеката на сателитска сликаЗемјата.
Во случајот на примерот даден погоре, програмата Google Earth го врати резултатот - должината на растојанието помеѓу точката бр. 1 и точката бр. 2 е 3.817.353 m.
Зошто има грешка при одредување на растојанието
Сите пресметки на обемот помеѓу координатите се засноваат на пресметката на должината на лакот. Радиусот на Земјата е вклучен во пресметувањето на должината на лакот. Но, бидејќи обликот на Земјата е блиску до образен елипсоид, радиусот на Земјата се разликува во одредени точки. За да се пресмета растојанието помеѓу координатите се зема просечната вредност на Земјиниот радиус што дава грешка во мерењето. Колку е поголемо растојанието што се мери, толку е поголема грешката.Нека , (Слика 2.3). Потребно е да се најде.
Слика 2.3. Растојанието помеѓу две точки.
Од правоаголникот според Питагоровата теорема имаме
Тоа е,
Оваа формула важи за која било локација на точки и .
II. Поделба на сегмент во овој поглед:
Нека,. Потребно е да се најде , лежејќи на сегментот и да се дели во даден сооднос (Слика 2.4.).
Слика 2.4. Поделба на сегмент во овој поглед.
Од сличноста ~, односно од каде. Исто така.
Така,
– формула за делење отсечка во однос на .
Ако, тогаш
– координати на средината на отсечката.
Коментар.Изведените формули може да се генерализираат во случај на просторен правоаголен Декартов координатен систем. Нека поени , . Потоа
- формула за наоѓање на растојанието помеѓу точките и .
Формула за делење отсечка во врска.
Покрај декартов во авион и во вселената, можете да конструирате голем бројдруги координатни системи, односно начини за карактеризирање на положбата на точка на рамнина или во просторот користејќи два или три нумерички параметри (координати). Да разгледаме некои од постојните координатни системи.
Во авион е можно да се одреди поларен координатен систем , кој се користи, особено, во проучувањето на ротационите движења.
Слика 2.5. Поларен координатен систем.
Дозволете ни да поправиме точка на рамнината и полуправа што излегува од неа, а исто така да избереме единица за скала (Слика 2.5). Точката се нарекува столб , полу-линија - поларна оска . Дозволете ни да доделиме два броја на произволна точка:
– поларен радиус , еднакво на растојаниеод точката М до полот О;
– поларен агол , еднаков на аголотпомеѓу поларната оска и полуправата.
Мерено во радијани, позитивната насока на вредностите се брои спротивно од стрелките на часовникот, обично се претпоставува.
Поларниот радиус одговара на полот, поларниот агол не е дефиниран за него.
Да ја најдеме врската помеѓу правоаголните и поларните координати (Слика 2.6).
Слика 2.6. Врска помеѓу правоаголни и поларни координатни системи.
Потеклото на правоаголниот координатен систем ќе го сметаме за пол, а зракот ќе биде поларната оска. Нека - во правоаголен Декартов координатен систем и - во поларен координатен систем. Да ја најдеме врската помеѓу правоаголните и поларните координати.
Од правоаголни, и од правоаголни. Така, формулите
искажуваат правоаголни координати на точка во однос на нејзините поларни координати.
Инверзната врска се изразува со формулите
Коментар.Поларниот агол може да се одреди и од формулата, откако претходно се определиле од правоаголни координати во кој квадрант се наоѓа точката.
Пример 1.Најдете ги поларните координати на точка.
Решение.Ние пресметуваме; Поларниот агол се наоѓа од условите:
Затоа, затоа.
Пример 2.Најдете ги правоаголните координати на точката.
Решение.Ние пресметуваме
Добиваме.
Во тридимензионалниот простор, покрај правоаголниот Декартов координатен систем, често се користат и цилиндрични и сферични координатни системи.
Цилиндричен координатен системе поларен координатен систем во рамнината, на кој му се додава просторна оска нормална на оваа рамнина (слика 2.7). Положбата на која било точка се карактеризира со три броја - неговите цилиндрични координати: , каде и се поларните координати (поларен радиус и поларен агол) на проекцијата на точката на рамнината во која е избран поларниот координатен систем - апликативната, што е еднакво на растојанието од точката до наведената рамнина.
Слика 2.7. Цилиндричен координатен систем
За да ја утврдиме врската помеѓу правоаголниот Декартов координатен систем и цилиндричниот, ги поставуваме релативно едни на други како на слика 2.8 (ја поставуваме рамнината во рамнината, а поларната оска се совпаѓа со позитивната насока на оската, оската е вообичаено во двата координатни системи).
Нека се правоаголните координати на точката, цилиндричните координати на оваа точка и проекцијата на точката на рамнината. Потоа
формули за поврзување на правоаголни и цилиндрични координати на точка.
Слика 2.8. Односот помеѓу правоаголниот Декартов
и цилиндрични координатни системи
Коментар.Цилиндричните координати често се користат кога се разгледуваат телата на ротација, при што оската се наоѓа по должината на оската на ротација.
Сферичен координатен системможе да се конструира на следниов начин. Дозволете ни да ја избереме поларната оска во рамнината. Низ точката цртаме права линија нормална на рамнината (нормална). Тогаш, секоја точка во просторот може да се поврзе со три реални броеви, каде што е растојанието од точката до, е аголот помеѓу оската и проекцијата на отсечката на рамнината и е аголот помеѓу нормалата и отсечката. Забележете дека , , .
Ако ја поставиме рамнината во рамнината и ја избереме поларната оска да се совпаѓа со позитивната насока на оската и ја избереме оската како нормална (слика 2.9), тогаш добиваме формули што ги поврзуваат овие два координатни системи
Слика 2.9. Врска помеѓу сферични и правоаголни Декартови
координатни системи
Скаларни количини,или скаларите целосно се карактеризираат со нивната нумеричка вредност во избраниот систем на единици. Векторски количини или векторите покрај нивната бројна вредност имаат и насока. На пример, ако кажеме дека ветерот дува со брзина од 10 m/s, тогаш ќе воведеме скаларна количинабрзина на ветерот, но ако кажеме дека дува југозападен ветер со брзина од 10 m/sec, тогаш во овој случај брзината на ветерот веќе ќе биде вектор.
Векторнаречена насочена отсечка која има одредена должина, т.е. сегмент со одредена должина, во кој една од ограничувачките точки се зема како почеток, а втората - како крај. Ќе го означиме векторот или или (Слика 2.10).
Должината на векторот се означува со симболот или и се нарекува модул на векторот. Се нарекува вектор чија должина е 1 сингл . Векторот се нарекува нула , ако неговиот почеток и крај се совпаѓаат и се означува со θ или . Нултиот вектор нема специфична насока и има должина еднаква на нула. Се нарекуваат вектори и лоцирани на иста права или на паралелни прави колинеарна . Двата вектори се нарекуваат еднакви , ако се колинеарни, имаат иста должина и иста насока. Сите нула вектори се сметаат за еднакви.
Два колинеарни вектори, различни од нула, со еднакви големини, но спротивни насоки, се нарекуваат спротивно . Векторот спротивен се означува со , за спротивниот вектор.
До бројот линеарни операции над вектори ги вклучуваат операциите на собирање, одземање на вектори и множење на вектор со број, т.е. операции чиј резултат е вектор.
Дозволете ни да ги дефинираме наведените операции на вектори. Нека два вектори и се дадени. Да земеме произволна точка О и да конструираме вектор и да го нацртаме векторот од точката А. Тогаш се нарекува векторот што го поврзува почетокот на првиот член на векторот со крајот на вториот износ овие вектори се означени со . Разгледаното правило за наоѓање на збирот на вектори се нарекува правила на триаголник (Слика 2.11).
Истиот збир на вектори може да се добие на друг начин (слика 2.12). Да ги нацртаме векторот и векторот од точката. Ајде да конструираме паралелограм на овие вектори како на страните. Векторот, кој е дијагонала на паралелограмот извлечен од темето, ќе биде збирот. Ова правило за наоѓање на збирот се нарекува паралелограмски правила .
Било која сума конечен бројвектори може да се добијат со користење на правилото за прекината линија (слика 2.13). Од произволна точка исцртуваме вектор, потоа цртаме вектор итн. Векторот што го поврзува почетокот на првиот со крајот на последниот е збирот
| |
По разлика два вектори и се нарекува таков вектор, чиј збир со одземениот вектор го дава векторот. Од тука правило за конструирање вектор на разлика(Слика 2.14). Од точката ги цртаме векторот и векторот. Разликата е векторот што ги поврзува краевите на векторот минуенд и векторот на субтрахенд и е насочен од субтрахенд кон векторот минуенд.
Производ на векторна реален бројλ е вектор кој е колинеарен со векторот, има должина и иста насока како векторот ако , и спротивна насока на векторот ако .
Внесен линеарни операции над вектори имаат својства :
1 0 . Комутативност на собирањето: .
2 0 . Асоцијативност на додавање: .
3 0 . Постоење на неутрален елемент со собирање: .
4 0 . Постоење на спротивен елемент со собирање:
5 0 . Распределба на множење со број во однос на собирање вектори: .
6 0 . Дистрибутивноста на множење на вектор со збир од два броја:
7 0 . Својството на асоцијативноста во однос на множење на вектор со производ од броеви: .
Нека е даден систем на вектори:
Се повикува изразот каде λ i (i = 1,2,…, n) се некои броеви линеарна комбинација системи на вектори (2.1). Се нарекува системот на вектори (2.1). линеарно зависни , ако нивната линеарна комбинација е еднаква на нула, под услов сите броеви λ 1, λ 2, ..., λ n да не се еднакви на нула. Се нарекува системот на вектори (2.1). линеарно независни , ако нивната линеарна комбинација е еднаква на нула само ако сите броеви λ i = 0 (). Може да се даде друга дефиниција линеарна зависноствектори. Се нарекува системот на вектори (2.1). линеарно зависни , ако некој вектор од овој систем е линеарно изразен во однос на другите, инаку системот на вектори (2.1) линеарно независни .
За векторите што лежат во рамнината, следните тврдења се вистинити.
1 0 . Било кои три вектори на рамнината се линеарно зависни.
2 0 . Ако бројот на овие вектори на рамнината е повеќе од три, тогаш тие се и линеарно зависни.
3 0 . За два вектори на една рамнина да бидат линеарно независни, потребно е и доволно тие да бидат неколинеарни.
Така, максималниот број на линеарно независни вектори на рамнината е два.
Векторите се нарекуваат компланарни , ако лежат во иста рамнина или се паралелни на иста рамнина. Следниве изјави се точни за вектори на просторот.
1 0 . Секои четири вектори на просторот се линеарно зависни.
2 0 . Ако бројот на овие вектори во просторот е повеќе од четири, тогаш тие се и линеарно зависни.
3 0 . За три вектори да бидат линеарно независни, потребно е и доволно тие да бидат некомпланарни.
Така, максималниот број на линеарно независни вектори во просторот е три.
Секој максимален потсистем на линеарно независни вектори преку кој се изразува кој било вектор од овој систем се нарекува основа оној што се разгледува векторски системи . Лесно е да се заклучи дека основата на рамнината се состои од два неколинеарни вектори, а основата во просторот се состои од три некомпланарни вектори. Се нарекува бројот на основни вектори ранг векторски системи. Се нарекуваат коефициентите на проширување на вектор во базични вектори векторски координати во оваа основа.
Нека векторите формираат основа и нека , тогаш броевите λ 1, λ 2, λ 3 се координатите на векторот во основата Во овој случај, запишете Може да се покаже дека разложувањето на векторот во основата е единствено . Главното значење на основата е дека линеарните операции на вектори стануваат обични линеарни операции на броеви - координатите на овие вектори. Користејќи ги својствата на линеарни операции на вектори, можеме да ја докажеме следната теорема.
Теорема. Кога се додаваат два вектори, се додаваат нивните соодветни координати. Кога векторот се множи со број, сите негови координати се множат со тој број.
Така, ако и , тогаш , каде , и каде , λ е одреден број.
Вообичаено, множеството од сите вектори на рамнината, сведено на заедничко потекло, со воведени линеарни операции, се означува со V 2, а множеството од сите вектори во просторот, сведени на заедничко потекло, се означува со V 3. Се повикуваат множествата V 2 и V 3 простори на геометриски вектори.
Агол помеѓу вектории се нарекува најмал агол () со кој еден од векторите мора да се ротира додека не се совпадне со вториот откако овие вектори ќе се доведат до заедничко потекло.
Производ со точкидва вектори е број еднаков на производот на модулите на овие вектори и косинус на аголот меѓу нив. Скаларниот производ на вектори и се означува со , или
Ако аголот помеѓу векторите и е еднаков на , тогаш
СО геометриска точкаВо однос на погледот, скаларниот производ на вектори е еднаков на производот на модулот на еден вектор и проекцијата врз него на друг вектор. Од еднаквоста (2.2) произлегува дека
Од тука услов за ортогоналност на два вектори: два векториИ се ортогонални ако и само ако нивниот скаларен производ е еднаков на нула, т.е. .
Производот со точки на вектори не е линеарна операција, бидејќи неговиот резултат е број, а не вектор.
Својства на скаларниот производ.
1º. – комутативност.
2º. – дистрибутивноста.
3º. – асоцијативност во однос на нумерички фактор.
4º. - својство на скаларен квадрат.
Од својството 4º следи дефиницијата должина на векторот :
Нека се даде основа во просторот V 3, каде што векторите се единечни вектори (тие се нарекуваат единечни вектори), насоката на секој од нив се совпаѓа со позитивната насока на координатните оски Ox, Oy, Oz на правоаголната Декарова координата систем.
Дозволете ни да го прошириме векторот на просторот V 3 според оваа основа (Слика 2.15):
Векторите се нарекуваат векторски компоненти долж координатните оски, или компоненти, броеви a x, a y, a z– правоаголни Декартови координати на векторот А. Насоката на векторот се одредува со аглите α, β, γ формирани од него со координатните линии. Косинусот на овие агли се нарекува вектор на насока. Тогаш косинусите на насоката се одредуваат со формулите:
Лесно е да се покаже тоа
Да го изразиме скаларниот производ во координатна форма.
Нека биде. Множејќи ги овие вектори како полиноми и земајќи предвид дека добиваме израз за наоѓање скаларен производ во координатна форма:
тие. скаларниот производ на два вектори е еднаков на збирот на спарени производи од истоимените координати.
Од (2.6) и (2.4) следи формулата за наоѓање должина на векторот :
Од (2.6) и (2.7) добиваме формула за определување агол помеѓу вектори:
Тројката вектори се нарекува подредена ако се означи кој од нив се смета за прв, кој за втор, а кој за трет.
Нарачано три вектори повикани право , ако по нивното доведување до заедничко потекло од крајот на третиот вектор, најкраткото вртење од првиот кон вториот вектор се прави спротивно од стрелките на часовникот. Во спротивно, се нарекува тројката вектори лево . На пример, на слика 2.15, векторите , , ја формираат десната тројка вектори, а векторите , , ја формираат левата тројка вектори.
На сличен начин се воведува концептот на десни и леви координатни системи во тридимензионален простор.
Векторски уметнички делавектор по вектор е вектор (друга нотација) што:
1) има должина , каде е аголот помеѓу векторите и ;
2) нормално на векторите и (), т.е. е нормална на рамнината во која се наоѓаат векторите и ;
По дефиниција, го наоѓаме векторскиот производ на векторите на координатната единица , , :
Ако , , тогаш координатите на векторскиот производ на вектор и вектор се одредуваат со формулата:
Од дефиницијата следува геометриско значење на векторската уметност : векторски модул еднаква на површинапаралелограм изграден на вектори и .
Својства на векторски производ:
4 0 . , ако векторите и се колинеарни, или еден од овие вектори е нула.
Пример 3.Паралелограмот е изграден на векторите и , каде , , . Пресметајте ја должината на дијагоналите на овој паралелограм, аголот помеѓу дијагоналите и плоштината на паралелограмот.
Решение.Конструкцијата на вектори и е прикажана на слика 2.16, конструкцијата на паралелограм на овие вектори е прикажана на слика 2.17.
Дозволете ни да спроведеме аналитичко решение за овој проблем. Да ги изразиме векторите што ги дефинираат дијагоналите на конструираниот паралелограм преку векторите и , а потоа преку и . Ние наоѓаме,. Следно, ги наоѓаме должините на дијагоналите на паралелограмот како должини на конструираните вектори
Аголот помеѓу дијагоналите на паралелограмот се означува со . Тогаш од формулата за скаларен производ на вектори имаме:
Оттука,.
Користејќи ги својствата на векторскиот производ, ја пресметуваме областа на паралелограмот:
Нека се дадени три вектори , и ,. Да замислиме дека векторот се множи векторски со, а векторот и добиениот вектор се множат скаларно со векторот, со што се одредува бројот. Се нарекува векторско-скаларен или мешана работа три вектори и . Означено со или.
Ајде да дознаеме геометриско значење на мешан производ (Слика 2.18). Нека , , не се компланарни. Ајде да изградиме паралелепипед на овие вектори како на рабовите. Вкрстен производ е вектор чиј модул е еднаков на плоштината на паралелограмот (основата на паралелепипедот), изграден на векторите и е насочен нормално на рамнината на паралелограмот.
Точка производ (еднаков на производот на модулот на векторот и проекцијата на ). Висината на конструираниот паралелепипед е апсолутна вредностоваа проекција. Следствено, апсолутната вредност на измешаниот производ од три вектори е еднаква на волуменот на паралелепипедот изграден на векторите, и т.е. .
Оттука, волуменот на триаголна пирамида изградена на векторите и се пресметува со формулата.
Да забележиме уште нешто својства на мешан производ вектори.
1 o. Знакот на производот е позитивен ако векторите , , и формираат систем со исто име како главниот, а негативен инаку.
Навистина, скаларниот производ е позитивен ако аголот помеѓу и е остар и негативен ако аголот е тап. Со остар агол помеѓу и, векторите и се наоѓаат на едната страна во однос на основата на паралелепипедот, и затоа, од крајот на векторот, ротацијата од до ќе биде видлива на ист начин како и од крајот на векторот. , т.е. во позитивна насока (спротивно од стрелките на часовникот).
На тап аголи вектори и се лоцирани по различни страниво однос на рамнината на паралелограмот што лежи во основата на паралелепипедот, и затоа, од крајот на векторот, ротацијата од k е видлива во негативна насока (во насока на стрелките на часовникот).
2 o Мешаниот производ не се менува кога неговите фактори се преуредуваат кружно: .
3 o При пермутација на кои било два вектори мешана работасамо знакот се менува. На пример, ,. , . - непознати системи.
Систем(3.1) се нарекува хомогена , доколку сите членови се слободни . Систем (3.1) се нарекува хетерогени , ако барем еден од слободни членови.
Системско решениесе нарекува збир на броеви, кога тие се заменуваат во равенките на системот наместо соодветните непознати, секоја равенка на системот се претвора во идентитет. Се нарекува систем кој нема решение некомпатибилни, или контроверзен . Се нарекува систем кој има барем едно решение зглоб .
Зглобниот систем се нарекува одредени ако таа има единственото решение. Ако конзистентен систем има повеќе од едно решение, тогаш тој се нарекува неизвесна . Хомоген систем е секогаш конзистентен, бидејќи има барем нула решение. Се нарекува израз за непознатите од кои може да се добие кое било конкретно решение на системот општа одлука , а секое конкретно решение на системот е негово приватно решение . Два системи со исти непознати еквивалент (еквивалент ), ако секое решение на еден од нив е решение на другиот или двата системи се неконзистентни.
Да ги разгледаме методите за решавање на системи линеарни равенки.
Еден од главните методи за решавање системи на линеарни равенки е Гаусовиот метод, или секвенцијален метод исклучување на непознати. Суштината на овој метод е да се намали системот на линеарни равенки во чекор-степена форма. Во овој случај, треба да се спроведат следните равенки: елементарни трансформации :
1. Преуредување на равенките на системот.
2. Додавање на друга равенка на една равенка.
3. Множење на двете страни на равенката со број различен од нула.
Како резултат на тоа, системот ќе ја добие формата:
Продолжувајќи го овој процес понатаму, ја елиминираме непознатата од сите равенки, почнувајќи од третата. За да го направите ова, помножете ја втората равенка со броеви и додадете ја на 3-та, ..., до --тата равенка на системот. Следниве чекори на методот Гаус се изведуваат слично. Ако како резултат на трансформациите добиеме идентична равенка, тогаш ја бришеме од системот. Ако во некој чекор од Гаусовиот метод се добие равенка на формата:
тогаш системот што се разгледува е неконзистентен и неговото понатамошно решение престанува. Ако не се сретне равенка од формата (3.2) при извршување на елементарни трансформации, тогаш во не повеќе од - чекори системот (3.1) ќе се трансформира во чекор по чекор:
За да се добие одредено решение на системот, ќе биде неопходно да се доделат специфични вредности на слободните променливи во (3.4).
Забележете дека во методот на Гаус сите трансформации се вршат на коефициентите на непознати равенки и слободни членови, во пракса овој метод обично се применува на матрица составена од коефициенти на непознати и колона од слободни членови. Оваа матрица се нарекува проширена. Користејќи елементарни трансформации, оваа матрица е сведена на чекор напред. Потоа, користејќи ја добиената матрица, системот се реконструира и на него се применуваат сите претходни размислувања.
Пример 1.Решете го системот:
Решение.Создаваме проширена матрица и ја сведуваме на чекор по форма:
~ *) ~ **) ~ ***)
*) - вториот ред беше помножен со и третиот ред беше пречкртан.
Во оваа статија ќе разгледаме начини за одредување на растојанието од точка до точка теоретски и користејќи пример за конкретни проблеми. За почеток, да воведеме неколку дефиниции.
Дефиниција 1
Растојание помеѓу точкитее должината на сегментот што ги поврзува, на постоечката скала. Потребно е да се постави скала за да се има единица должина за мерење. Затоа, во основа проблемот со наоѓање на растојанието помеѓу точките се решава со користење на нивните координати на координатната линија, во координатна рамнинаили тродимензионален простор.
Почетен податок: координатна права О x и произволна точка А што лежи на неа Секоја точка на правата има еден реален број: нека биде одреден број за точката А x A,тоа е и координата на точката А.
Генерално, можеме да кажеме дека должината на одреден сегмент се оценува во споредба со отсечка земена како единица должина на дадена скала.
Ако точката А одговара на цел број реален број, со последователно одложување од точката O до точка по права линија O A отсечки - единици за должина, можеме да ја одредиме должината на отсечката O A од вкупниот број на издвоени единечни отсечки.
На пример, точката А одговара на бројот 3 - за да стигнете до неа од точката О, ќе треба да отпуштите три единечни сегменти. Ако точката А има координата - 4, единечните отсечки се поставени на сличен начин, но во различна, негативна насока. Така, во првиот случај, растојанието O A е еднакво на 3; во вториот случај O A = 4.
Ако точката А има за координата рационален број, потоа од потеклото (точка О) издвојуваме цел број единечни отсечки, а потоа неговиот неопходен дел. Но, геометриски не е секогаш можно да се направи мерење. На пример, се чини дека е тешко да се нацрта дропката 4 111 на координатната линија.
Користејќи го горенаведениот метод, сосема е невозможно да се нацрта ирационален број на права линија. На пример, кога координатата на точката А е 11. Во овој случај, можно е да се свртиме кон апстракција: ако дадената координата на точката А е поголема од нула, тогаш O A = x A (бројот се зема како растојание); ако координатата е помала од нула, тогаш O A = - x A . Општо земено, овие изјави се точни за секој реален број x A.
Да резимираме: растојанието од потеклото до точката што одговара на реален број на координатната линија е еднакво на:
- 0 ако точката се совпаѓа со потеклото;
- x A, ако x A > 0;
- - x A ако x A< 0 .
Во овој случај, очигледно е дека должината на самата отсечка не може да биде негативна, затоа, користејќи го знакот за модул, растојанието од точката О до точката А го запишуваме со координатата xA: O A = x A

Следната изјава ќе биде точна: растојанието од една до друга точка ќе биде еднакво на модулот на координатната разлика.Оние. за точките A и B кои лежат на иста координатна права за која било локација и имаат соодветни координати xAИ x B: A B = x B - x A.

Почетни податоци: точките A и B лежат на рамнина во правоаголен координатен систем O x y со дадени координати: A (x A, y A) и B (x B, y B).
Да нацртаме нормални низ точките A и B до координатните оски O x и O y и како резултат да ги добиеме проекционите точки: A x, A y, B x, B y. Врз основа на локацијата на точките А и Б, тогаш се можни следните опции:
Ако точките А и Б се совпаѓаат, тогаш растојанието меѓу нив е нула;
Ако точките A и B лежат на права линија нормална на оската O x (оска на апсциса), тогаш точките се совпаѓаат и | A B | = | A y B y | . Бидејќи растојанието помеѓу точките е еднакво на модулот на разликата на нивните координати, тогаш A y B y = y B - y A, и, според тоа, A B = A y B y = y B - y A.

Ако точките A и B лежат на права линија нормална на оската O y (ординатна оска) - по аналогија со претходниот став: A B = A x B x = x B - x A

Ако точките A и B не лежат на права линија нормална на една од координатните оски, ќе го најдеме растојанието меѓу нив со изведување на формулата за пресметка:

Гледаме дека триаголникот A B C е правоаголен по конструкција. Во овој случај, A C = A x B x и B C = A y B y. Користејќи ја Питагоровата теорема, ја создаваме еднаквоста: A B 2 = A C 2 + B C 2 ⇔ A B 2 = A x B x 2 + A y B y 2 , а потоа ја трансформираме: A B = A x B x 2 + A y B y 2 = x B - x A 2 + y B - y A 2 = (x B - x A) 2 + (y B - y A) 2
Ајде да извлечеме заклучок од добиениот резултат: растојанието од точката А до точката Б на рамнината се одредува со пресметка користејќи ја формулата користејќи ги координатите на овие точки
A B = (x B - x A) 2 + (y B - y A) 2
Резултирачката формула ги потврдува и претходно формираните изјави за случаи на совпаѓање на точки или ситуации кога точките лежат на прави линии нормално на оските. Значи, ако точките A и B се поклопат, еднаквоста ќе биде вистина: A B = (x B - x A) 2 + (y B - y A) 2 = 0 2 + 0 2 = 0
За ситуација кога точките A и B лежат на права линија нормална на оската x:
A B = (x B - x A) 2 + (y B - y A) 2 = 0 2 + (y B - y A) 2 = y B - y A
За случајот кога точките A и B лежат на права линија нормална на оската на ординатите:
A B = (x B - x A) 2 + (y B - y A) 2 = (x B - x A) 2 + 0 2 = x B - x A
Почетен податок: правоаголен координатен систем O x y z со произволни точки што лежат на него со дадени координати A (x A, y A, z A) и B (x B, y B, z B). Неопходно е да се одреди растојанието помеѓу овие точки.
Да го разгледаме општиот случај кога точките A и B не лежат во рамнина паралелна на една од координатните рамнини. Да нацртаме рамнини нормални на координатните оски низ точките A и B и да ги добиеме соодветните проекциони точки: A x , A y , A z , B x , B y , B z

Растојанието помеѓу точките А и Б е дијагоналата на добиениот паралелепипед. Според конструкцијата на мерењата на овој паралелепипед: A x B x , A y B y и A z B z
Од курсот по геометрија знаеме дека квадратот на дијагоналата на паралелепипед е еднаков на збирот на квадратите на неговите димензии. Врз основа на ова тврдење, ја добиваме еднаквоста: A B 2 = A x B x 2 + A y B y 2 + A z B z 2
Користејќи ги заклучоците добиени претходно, го пишуваме следново:
A x B x = x B - x A, A y B y = y B - y A, A z B z = z B - z A
Ајде да го трансформираме изразот:
A B 2 = A x B x 2 + A y B y 2 + A z B z 2 = x B - x A 2 + y B - y A 2 + z B - z A 2 = = (x B - x A) 2 + (y B - y A) 2 + z B - z A 2
Конечно формула за одредување на растојанието помеѓу точките во просторотќе изгледа вака:
A B = x B - x A 2 + y B - y A 2 + (z B - z A) 2
Добиената формула важи и за случаи кога:
Точките се совпаѓаат;
Легнат на еден координатна оскаили права линија паралелна на една од координатните оски.
Примери за решавање проблеми за наоѓање растојание помеѓу точките
Пример 1Почетни податоци: дадена е координатна права и точки што лежат на неа со дадени координати A (1 - 2) и B (11 + 2). Неопходно е да се најде растојанието од почетната точка О до точката А и помеѓу точките А и Б.
Решение
- Растојанието од референтната точка до точката е еднакво на модулот на координатата на оваа точка, соодветно O A = 1 - 2 = 2 - 1
- Растојанието помеѓу точките A и B го дефинираме како модул на разликата помеѓу координатите на овие точки: A B = 11 + 2 - (1 - 2) = 10 + 2 2
Одговор: O A = 2 - 1, A B = 10 + 2 2
Пример 2
Почетни податоци: се дадени правоаголен координатен систем и две точки што лежат на него A (1, - 1) и B (λ + 1, 3). λ е некој реален број. Неопходно е да се најдат сите вредности на овој број на кои растојанието A B ќе биде еднакво на 5.
Решение
За да го пронајдете растојанието помеѓу точките A и B, мора да ја користите формулата A B = (x B - x A) 2 + y B - y A 2
Заменувајќи ги реалните координатни вредности, добиваме: A B = (λ + 1 - 1) 2 + (3 - (- 1)) 2 = λ 2 + 16
Го користиме и постоечкиот услов дека A B = 5 и тогаш еднаквоста ќе биде вистина:
λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3
Одговор: A B = 5 ако λ = ± 3.
Пример 3
Почетни податоци: тродимензионален простор е наведен во правоаголниот координатен систем O x y z и точките A (1, 2, 3) и B - 7, - 2, 4 што лежат во него.
Решение
За да го решиме проблемот, ја користиме формулата A B = x B - x A 2 + y B - y A 2 + (z B - z A) 2
Заменувајќи ги реалните вредности, добиваме: A B = (- 7 - 1) 2 + (- 2 - 2) 2 + (4 - 3) 2 = 81 = 9
Одговор: | A B | = 9
Доколку забележите грешка во текстот, означете ја и притиснете Ctrl+Enter
Решавањето математички задачи за учениците често е придружено со многу тешкотии. Да му се помогне на студентот да се справи со овие тешкотии, како и да го научи да го применува своето постојно теоретско знаење при решавање на конкретни проблеми во сите делови од предметот „Математика“ е главната цел на нашата страница.
Кога започнуваат да решаваат проблеми на темата, учениците треба да бидат способни да конструираат точка на рамнина користејќи ги нејзините координати, како и да ги пронајдат координатите на дадена точка.
Пресметувањето на растојанието помеѓу две точки A(x A; y A) и B(x B; y B) земени на рамнина се врши со помош на формулата d = √((x A – x B) 2 + (y A – y B) 2), каде што d е должината на отсечката што ги поврзува овие точки на рамнината.
Ако еден од краевите на отсечката се совпаѓа со потеклото на координатите, а другиот има координати M(x M; y M), тогаш формулата за пресметување d ќе има форма OM = √(x M 2 + y M 2 ).
1. Пресметување на растојанието помеѓу две точки врз основа на дадените координати на овие точки
Пример 1.
Најдете ја должината на отсечката што ги поврзува точките A(2; -5) и B(-4; 3) на координатната рамнина (сл. 1).
Решение.
Во изјавата за проблемот се наведува: x A = 2; x B = -4; y A = -5 и y B = 3. Најдете d.
Применувајќи ја формулата d = √((x A – x B) 2 + (y A – y B) 2), добиваме:
d = AB = √((2 – (-4)) 2 + (-5 – 3) 2) = 10.
2. Пресметување на координатите на точка која е еднакво оддалечена од три дадени точки
Пример 2.
Најдете ги координатите на точката O 1, која е еднакво оддалечена од три точки A(7; -1) и B(-2; 2) и C(-1; -5).
Решение.
Од формулацијата на проблемските услови произлегува дека O 1 A = O 1 B = O 1 C. Нека саканата точка O 1 има координати (a; b). Користејќи ја формулата d = √((x A – x B) 2 + (y A – y B) 2) наоѓаме:
O 1 A = √((a – 7) 2 + (b + 1) 2);
O 1 B = √((a + 2) 2 + (b – 2) 2);
O 1 C = √((a + 1) 2 + (b + 5) 2).
Ајде да создадеме систем од две равенки:
(√((a – 7) 2 + (b + 1) 2) = √((a + 2) 2 + (b – 2) 2),
(√((a – 7) 2 + (b + 1) 2) = √((a + 1) 2 + (b + 5) 2).
По квадратурата на левата и десната страна на равенките, пишуваме:
((а – 7) 2 + (б + 1) 2 = (а + 2) 2 + (б – 2) 2,
((а – 7) 2 + (б + 1) 2 = (а + 1) 2 + (б + 5) 2.
Поедноставувајќи, ајде да пишуваме
(-3а + б + 7 = 0,
(-2a – b + 3 = 0.
Откако го решивме системот, добиваме: a = 2; b = -1.
Точката O 1 (2; -1) е еднакво оддалечена од трите точки наведени во условот што не лежат на иста права линија. Оваа точка е центар на круг што минува низ три дадени поени (Сл. 2).
3. Пресметување на апсцисата (ординатата) на точка која лежи на оската на апсцисата (ординатата) и се наоѓа на дадено растојаниеод оваа точка
Пример 3.
Растојанието од точката B(-5; 6) до точката А што лежи на оската Ox е 10. Најдете ја точката А.
Решение.
Од формулацијата на проблемските услови произлегува дека ординатата на точката А е еднаква на нула и AB = 10.
Означувајќи ја апсцисата на точката A со a, пишуваме A(a; 0).
AB = √((a + 5) 2 + (0 – 6) 2) = √((a + 5) 2 + 36).
Ја добиваме равенката √((a + 5) 2 + 36) = 10. Поедноставувајќи ја, имаме
a 2 + 10a – 39 = 0.
Корените на оваа равенка се 1 = -13; и 2 = 3.
Добиваме два поени А 1 (-13; 0) и А 2 (3; 0).
Испитување:
A 1 B = √((-13 + 5) 2 + (0 – 6) 2) = 10.
A 2 B = √((3 + 5) 2 + (0 – 6) 2) = 10.
Двете добиени поени се погодни според условите на проблемот (сл. 3).
4. Пресметување на апсцисата (ординатата) на точка која лежи на оската на апсцисата (ординатата) и е на исто растојание од две дадени точки
Пример 4.
Најдете точка на оската Oy што е на исто растојание од точките A (6, 12) и B (-8, 10).
Решение.
Нека координатите на точката што ја бараат условите на задачата, која лежи на оската Oy, се O 1 (0; b) (во точката што лежи на оската Oy, апсцисата е нула). Од условот произлегува дека O 1 A = O 1 B.
Користејќи ја формулата d = √((x A – x B) 2 + (y A – y B) 2) наоѓаме:
O 1 A = √((0 – 6) 2 + (b – 12) 2) = √(36 + (b – 12) 2);
O 1 B = √((a + 8) 2 + (b – 10) 2) = √(64 + (b – 10) 2).
Ја имаме равенката √(36 + (b – 12) 2) = √(64 + (b – 10) 2) или 36 + (b – 12) 2 = 64 + (b – 10) 2.
По поедноставувањето добиваме: b – 4 = 0, b = 4.
Точка O 1 (0; 4) се бара од условите на проблемот (сл. 4).
5. Пресметување на координатите на точка која се наоѓа на исто растојание од координатните оски и некоја дадена точка
Пример 5.
Најдете ја точката М која се наоѓа на координатната рамнина на исто растојание од координатните оски и од точката A(-2; 1).
Решение.
Потребната точка М, како точката A(-2; 1), се наоѓа во вториот координатен агол, бидејќи е еднакво оддалечена од точките A, P 1 и P 2 (сл. 5). Растојанието на точката М од координатните оски се исти, затоа, нејзините координати ќе бидат (-a; a), каде што a > 0.
Од условите на задачата произлегува дека MA = MR 1 = MR 2, MR 1 = a; MP 2 = |-a|,
тие. |-а| = а.
Користејќи ја формулата d = √((x A – x B) 2 + (y A – y B) 2) наоѓаме:
MA = √((-a + 2) 2 + (a – 1) 2).
Ајде да направиме равенка:
√((-а + 2) 2 + (а – 1) 2) = а.
По квадратурата и поедноставувањето имаме: a 2 – 6a + 5 = 0. Решете ја равенката, најдете a 1 = 1; и 2 = 5.
Добиваме две точки M 1 (-1; 1) и M 2 (-5; 5) кои ги задоволуваат условите на проблемот. 
6. Пресметување на координатите на точка која се наоѓа на исто одредено растојание од оската на апсцисата (ординатата) и од дадената точка
Пример 6.
Најдете точка M таква што нејзиното растојание од оската на ординатите и од точката A(8; 6) е еднакво на 5.
Решение.
Од условите на задачата произлегува дека MA = 5 и апсцисата на точката M е еднаква на 5. Нека ординатата на точката M е еднаква на b, тогаш M(5; b) (сл. 6).
Според формулата d = √((x A – x B) 2 + (y A – y B) 2) имаме:
MA = √((5 – 8) 2 + (b – 6) 2).
Ајде да направиме равенка:
√((5 – 8) 2 + (b – 6) 2) = 5. Поедноставувајќи го, добиваме: b 2 – 12b + 20 = 0. Корените на оваа равенка се b 1 = 2; b 2 = 10. Следствено, постојат две точки кои ги задоволуваат условите на проблемот: M 1 (5; 2) и M 2 (5; 10).
Познато е дека многу студенти независна одлукапроблемите бараат постојана консултација за техниките и методите за нивно решавање. Честопати, ученикот не може да најде начин да реши проблем без помош од наставник. Ученикот може да ги добие потребните совети за решавање проблеми на нашата веб-страница.
Сè уште имате прашања? Не знаете како да го најдете растојанието помеѓу две точки на авион?
За да добиете помош од учител, регистрирајте се.
Првата лекција е бесплатна!
веб-страница, при копирање на материјал во целост или делумно, потребна е врска до оригиналниот извор.