Својства на функцијата y sin x. Функции y = sin x, y = cos x, y = mf(x), y = f(kx), y = tg x, y = ctg x. Изразување преку тангента

Функцијаy = гревотx

Графикот на функцијата е синусоид.

Целосниот дел од синусниот бран што не се повторува се нарекува синусен бран.

Половина синусен бран се нарекува полу синусен бран (или лак).

Својства на функцииy = гревотx:

3) Ова е непарна функција. 4) Ова континуирана функција. - со оска на апсциса: (πn; 0), - со ординатна оска: (0; 0). 6) На отсечката [-π/2; π/2] функцијата се зголемува на интервалот [π/2; 3π/2] – се намалува. 7) На интервали функцијата трае позитивни вредности. На интервалите [-π + 2πn; 2πn] функцијата зема негативни вредности. 8) Интервали на зголемување на функцијата: [-π/2 + 2πn; π/2 + 2πn]. Намалувачки интервали на функцијата: [π/2 + 2πn; 3π/2 + 2πn]. 9) Минимални точки на функцијата: -π/2 + 2πn. Максимални точки на функцијата: π/2 + 2πn највисока вредност 1.

Да графирате функција y= грев xУдобно е да се користат следните ваги:

На лист хартија со квадрат ја земаме должината на два квадрати како единица на сегмент.

На оската xДа ја измериме должината π. Во исто време, за погодност, го презентираме 3.14 во форма на 3 - тоа е, без фракција. Потоа на лист хартија во ќелија π ќе има 6 ќелии (три пати по 2 ќелии). И секоја ќелија ќе добие свое природно име (од првата до шестата): π/6, π/3, π/2, 2π/3, 5π/6, π. Ова се значењата x.

На y-оската означуваме 1, која вклучува две ќелии.

Ајде да создадеме табела со вредности на функции користејќи ги нашите вредности x:

			√3 - 2		√3 - 2

Следно, ајде да создадеме распоред. Ќе испадне дека е половина бран, највисоката точкакој (π/2; 1). Ова е графикот на функцијата y= грев xна сегментот. Ајде да додадеме симетричен полубран на конструираниот график (симетричен во однос на потеклото, односно на отсечката -π). Врвот на овој полубран е под х-оската со координати (-1; -1). Резултатот ќе биде бран. Ова е графикот на функцијата y= грев xна сегментот [-π; π].

Можете да го продолжите бранот со тоа што ќе го конструирате на сегментот [π; 3π], [π; 5π], [π; 7π], итн. На сите овие отсечки, графикот на функцијата ќе изгледа исто како на отсечката [-π; π]. Ќе добиете континуирана брановидна линија со идентични бранови.

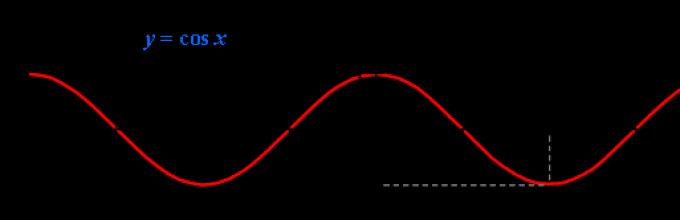
Функцијаy = cosx.

Графикот на функцијата е синусен бран (понекогаш се нарекува и косинус бран).

Својства на функцииy = cosx:

1) Доменот на дефиниција на функцијата е множество од реални броеви. 2) Опсегот на вредности на функцијата е сегментот [–1; 1] 3) Ова е рамномерна функција. 4) Ова е континуирана функција. 5) Координати на пресечните точки на графиконот: - со оската на апсцисата: (π/2 + πn; 0), - со ординатна оска: (0;1). 6) На отсечката функцијата се намалува, на отсечката [π; 2π] – се зголемува. 7) На интервали [-π/2 + 2πn; π/2 + 2πn] функцијата зема позитивни вредности. На интервалите [π/2 + 2πn; Функцијата 3π/2 + 2πn] зема негативни вредности. 8) Зголемување на интервали: [-π + 2πn; 2πn]. Намалувачки интервали: ; 9) Минимални точки на функцијата: π + 2πn. Максимални точки на функцијата: 2πn. 10) Функцијата е ограничена одозгора и долу. Најниска вредностфункции -1, највисоката вредност е 1. 11) Ова периодична функцијасо период 2π (T = 2π)

Функцијаy = мф(x).

Да ја земеме претходната функција y=кос x. Како што веќе знаете, неговиот график е синусен бран. Ако го помножиме косинусот на оваа функција со одреден број m, тогаш бранот ќе се прошири од оската x(или ќе се намали, во зависност од вредноста на m).
Овој нов бран ќе биде графикот на функцијата y = mf(x), каде што m е секој реален број.

Така, функцијата y = mf(x) е познатата функција y = f(x) помножена со m.

Аком< 1, то синусоида сжимается к оси xпо коефициентотм. Акоm > 1, тогаш синусоидот се протега од оскатаxпо коефициентотм.

Кога вршите истегнување или компресија, прво можете да нацртате само еден полубран на синусен бран, а потоа да го комплетирате целиот графикон.

Функцијаy = ѓ(kx).

Доколку функцијата y =мф(x) доведува до истегнување на синусоидот од оската xили компресија кон оската x, тогаш функцијата y = f(kx) води до истегнување од оската yили компресија кон оската y.

Покрај тоа, k е секој реален број.

На 0< к< 1 синусоида растягивается от оси yпо коефициентотк. Акоk > 1, тогаш синусоидот е компресиран кон оскатаyпо коефициентотк.

При графика на оваа функција, прво можете да изградите еден полубран на синусен бран, а потоа да го користите за да го комплетирате целиот график.

Функцијаy = tgx.

График на функции y= tg xе тангента.

Доволно е да се конструира дел од графикот во интервалот од 0 до π/2, а потоа може симетрично да се продолжи во интервалот од 0 до 3π/2.

Својства на функцииy = tgx:

Функцијаy = ctgx

График на функции y=ctg xе исто така тангентоид (понекогаш се нарекува и котангентоид).

Својства на функцииy = ctgx:

Како графички да се направи функцијата y=sin x? Прво, да го погледнеме синусниот график на интервалот.

Во тетратката земаме единечен сегмент 2 ќелии. На оската Oy означуваме еден.

За погодност, го заокружуваме бројот π/2 на 1,5 (а не на 1,6, како што бараат правилата за заокружување). Во овој случај, сегмент со должина π/2 одговара на 3 ќелии.

На оската Ox не означуваме единечни сегменти, туку сегменти со должина π/2 (на секои 3 ќелии). Според тоа, сегмент со должина π одговара на 6 ќелии, а сегмент со должина π/6 одговара на 1 ќелија.

Со овој избор на единична отсечка, графикот прикажан на лист од тетратка во кутија што е можно повеќе одговара на графикот на функцијата y=sin x.

Ајде да направиме табела со вредности на синус на интервалот:

Ние ги означуваме добиените точки на координатната рамнина:

Бидејќи y=sin x е непарна функција, синусниот график е симетричен во однос на потеклото - точката O(0;0). Земајќи го предвид овој факт, да продолжиме да го исцртуваме графикот лево, а потоа точките -π:

Функцијата y=sin x е периодична со период T=2π. Според тоа, графикот на функција земена на интервалот [-π;π] се повторува бесконечен број пати десно и лево.

Назад Напред

Внимание! Прегледите на слајдовите се само за информативни цели и може да не ги претставуваат сите карактеристики на презентацијата. Доколку сте заинтересирани за оваа работа, ве молиме преземете ја целосната верзија.

Железото рѓосува без да најде никаква употреба,
Непојава водаскапува или замрзнува на студ,
а умот на човекот, не наоѓајќи никаква корист за себе, опаѓа.
Леонардо да Винчи

Користени технологии:учење базирано на проблем, критичко размислување, комуникативна комуникација.

Цели:

• Развивање на когнитивен интерес за учење.
• Проучување на својствата на функцијата y = sin x.
• Формирање на практични вештини при конструирање график на функцијата y = sin x врз основа на изучениот теоретски материјал.

Задачи:

1. Користете го постоечкиот потенцијал на знаење за својствата на функцијата y = sin x во конкретни ситуации.

2. Примени свесно воспоставување врски помеѓу аналитичките и геометриските модели на функцијата y = sin x.

Развијте иницијатива, одредена волја и интерес за изнаоѓање решение; способноста да донесувате одлуки, да не застанете тука и да ја браните вашата гледна точка.

Да се ​​поттикне кај учениците когнитивна активност, чувство на одговорност, почит еден кон друг, меѓусебно разбирање, меѓусебна поддршка и самодоверба; култура на комуникација.

Напредокот на лекцијата

Фаза 1. Ажурирање на основни знаења, мотивирање за учење нов материјал

„Влегување во лекцијата“.

На таблата се напишани 3 изјави:

1. Тригонометриски равенка на гревот t = a секогаш има решенија.
2. Графикот на непарна функција може да се конструира со помош на трансформација на симетрија околу оската Oy.
3. Тригонометриска функција може да се прикаже графички со користење на еден главен полубран.

Учениците дискутираат во парови: дали се вистинити изјавите? (1 минута). Резултатите од првичната дискусија (да, не) потоа се внесуваат во табелата во колоната „Пред“.

Наставникот ги поставува целите и задачите на часот.

2. Ажурирање на знаењето (фронтално на модел на тригонометриски круг).

Веќе се запознавме со функцијата s = sin t.

1) Кои вредности може да ги земе променливата t. Кој е опсегот на оваа функција?

2) Во кој интервал се содржани вредностите на изразот sin t? Најдете ги најголемите и најмалите вредности на функцијата s = sin t.

3) Решете ја равенката sin t = 0.

4) Што се случува со ординатата на точка додека се движи по првата четвртина? (ординатата се зголемува). Што се случува со ординатата на точка додека се движи по втората четвртина? (ординатата постепено се намалува). Како се поврзува ова со монотоноста на функцијата? (функцијата s = sin t се зголемува на сегментот и се намалува на сегментот ).

5) Да ја напишеме функцијата s = sin t во форма y = sin x што ни е позната (ќе ја конструираме во вообичаениот координатен систем xOy) и да составиме табела со вредностите на оваа функција.

X	0
на	0			1			0

Фаза 2. Перцепција, разбирање, примарна консолидација, неволно меморирање

Фаза 4. Примарна систематизација на знаењата и методите на активност, нивно пренесување и примена во нови ситуации

6. Бр. 10.18 (б, в)

Фаза 5. Конечна контрола, корекција, оценување и самооценување

7. Вратете се на исказите (почеток на часот), дискутирајте за користење на својствата на тригонометриската функција y = sin x и пополнете ја колоната „По“ во табелата.

8. Д/з: клаузула 10, бр. 10.7(а), 10.8(б), 10.11(б), 10.16(а)

Центрирано во точка А.
α - агол изразен во радијани.

Дефиниција
Синус (грев α)- Ова тригонометриска функција, во зависност од аголот α помеѓу хипотенузата и кракот на правоаголен триаголник, еднаков на односотдолжина на спротивната страна |П.н.е.| до должината на хипотенузата |AC|.

Косинус (cos α)е тригонометриска функција во зависност од аголот α помеѓу хипотенузата и кракот на правоаголен триаголник, еднаков на односот на должината на соседната катета |AB| до должината на хипотенузата |AC|.

Прифатени ознаки

;
;
.

;
;
.

График на синусната функција, y = sin x

График на косинусната функција, y = cos x

Својства на синус и косинус

Периодичноста

Функции y = грев хи y = cos xпериодични со период 2π.

Паритет

Синусната функција е непарна. Косинусот е парен.

Домен на дефиниција и вредности, екстреми, зголемување, намалување

Функциите на синус и косинус се континуирани во нивниот домен на дефиниција, односно за сите x (види доказ за континуитет). Нивните главни својства се претставени во табелата (n - цел број).

	y = грев х	y = cos x
Опсег и континуитет	- ∞ < x < + ∞	- ∞ < x < + ∞
Опсег на вредности	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Зголемување
Опаѓачки
Максима, y = 1
Минимум, y = - 1
Нули, y = 0
Пресечни точки со ординатна оска, x = 0	y = 0	y = 1

Основни формули

Збир на квадрати на синус и косинус

Формули за синус и косинус од збир и разлика

;
;

Формули за производ од синуси и косинуси

Формули за збир и разлика

Изразување синус преку косинус

;
;
;
.

Изразување косинус преку синус

;
;
;
.

Изразување преку тангента

; .

Кога , имаме:
; .

На:
; .

Табела на синуси и косинуси, тангенти и котангенти

Оваа табела ги прикажува вредностите на синусите и косинусите за одредени вредности на аргументот.

Изрази преку сложени променливи

;

Ојлерова формула

Изрази преку хиперболични функции

;
;

Деривати

;

.
{ -∞ < x < +∞ }

Изведување формули > > >

Деривати од n-ти ред:

Секант, косекантИнверзни функции

Инверзни функции

до синус и косинус се арксин и аркозин, соодветно.

Арксин, лаксин
Аркозин, аркос

Користена литература:

И.Н. Бронштајн, К.А. Семендјаев, Прирачник за математика за инженери и студенти, „Лан“, 2009 година., Геометриска дефиниција на синус и косинус

α - агол изразен во радијани.

Синус (грев α)\(\sin \alpha = \dfrac(|BC|)(|AB|) \)

Косинус (cos α)\(\cos \alpha = \dfrac(|AC|)(|AB|) \)

е тригонометриска функција на аголот α помеѓу хипотенузата и кракот на правоаголен триаголник, еднаков на односот на должината на спротивната катета |BC| до должината на хипотенузата |AB|.

е тригонометриска функција на аголот α помеѓу хипотенузата и кракот на правоаголен триаголник, еднаков на односот на должината на соседната катета |AC| до должината на хипотенузата |AB|. Тригонометриска дефиницијаКористејќи ги формулите погоре, можете да ги најдете синусите и косинусите на остар агол. Но, треба да научите како да ги пресметате синусите и косинусите на агол со произволна големина. Правоаголен триаголник не ја дава оваа можност ( тап агол, на пример, не може да биде во него); затоа, потребно е повеќе

општа дефиниција синус и косинус, кои ги содржат овие формули како посебен случај.Доаѓа до спасување

тригонометриски круг

. Нека се даде некој агол; одговара на истоимената точка на тригонометрискиот круг.

Ориз. 2. Тригонометриска дефиниција на синус и косинус Косинусот на аголот е апсциса на точка. Синус на агол е ордината на точка.На сл. 2 аголот е земен акутен, и тоа е лесно да се разбере оваа дефиницијасе поклопува со општото геометриска дефиниција. Всушност, гледаме

правоаголен триаголник

со единица хипотенуза O и остар агол. Соседната катета на овој триаголник е cos (спореди со сл. 1) и во исто време апсцисата на точката; спротивната страна е грев (како на сл. 1) и во исто време ординатата на точката.

Но, сега веќе не сме ограничени од првиот квартал и имаме можност да ја прошириме оваа дефиниција на кој било агол. На сл. Слика 3 покажува колку се синусите и косинусите на аголот во втората, третата и четвртата четвртина.

Ориз. 3. Синус и косинус во II, III и IV четвртини

Табела вредности на синус и косинус

Нулта агол \(\ LARGE 0^(\circ ) \)

Апсцисата на точката 0 е еднаква на 1, ординатата на точката 0 е еднаква на 0. Оттука,

cos 0 = 1 грев 0 = 0

Гледаме правоаголен триаголник со единица хипотенуза и остар агол од 30°. Како што знаете, ногата што лежи спроти аголот 30° е еднаква на половина од хипотенузата 1; со други зборови, вертикалната нога е еднаква на 1/2 и, според тоа,

\[ \sin \frac(\pi)(6) =\frac(1)(2) \]

Ја наоѓаме хоризонталната катета користејќи ја Питагоровата теорема (или, што е исто, го наоѓаме косинусот користејќи ја главната тригонометриски идентитет):

\[ \cos \frac(\pi)(6) = \sqrt(1 - \left(\frac(1)(2) \десно)^(2) =\frac(\sqrt(3))(2 ) \]

1 Зошто се случува ова? Исечете рамностран триаголниксо страна 2 долж неговата висина! Ќе се подели на два правоаголни триаголници со хипотенуза од 2, остар агол од 30° и пократок крак од 1.

Сл 5. Агол π/6

Агол \(\ LARGE \frac(\pi)(4) = 45^(\circ )\)

Во овој случај, правоаголниот триаголник е рамнокрак; Синус и косинус од агол од 45° се еднакви еден на друг. Да ги означиме со x засега. Имаме:

\[ x^(2) + x^(2) = 1 \]

од каде \(x=\frac(\sqrt(2) )(2) \). Оттука,

\[ \cos \frac(\pi)(4) = \sin \frac(\pi)(4) =\frac(\sqrt(2) )(2) \]

Сл 5. Агол π/4

Својства на синус и косинус

Прифатени ознаки

\(\sin^2 x \equiv (\sin x)^2; \)\(\quad \sin^3 x \equiv (\sin x)^3; \)\(\quad \sin^n x \equiv (\sin x)^n \)\(\sin^(-1) x \equiv \arcsin x \)\((\sin x)^(-1) \equiv \dfrac1(\sin x) \equiv \cosec x \).

\(\cos^2 x \equiv (\cos x)^2; \)\(\quad \cos^3 x \equiv (\cos x)^3; \)\(\quad \cos^n x \equiv (\cos x)^n \)\(\cos^(-1) x \equiv \arccos x \)\((\cos x)^(-1) \equiv \dfrac1(\cos x) \equiv \sec x \).

Периодичноста

Функциите y = sin x и y = cos x се периодични со период од 2π.

\(\sin(x + 2\pi) = \sin x; \четири \)\(\cos(x + 2\pi) = \cos x \)

Паритет

Синусната функција е непарна. Косинусот е парен.

\(\sin(-x) = - \sin x; \quad \)\(\cos(-x) = \cos x \)

Области на дефиниција и вредности, екстреми, зголемување, намалување

Основните својства на синус и косинус се претставени во табелата ( n- целина).

	\(\мали< x < \)	\(\small -\pi + 2\pi n \) \(\small< x < \) \(\small 2\pi n \)
Опаѓачки	\(\small \dfrac(\pi)2 + 2\pi n \)\(\мали< x < \) \(\small \dfrac(3\pi)2 + 2\pi n \)	\(\small 2\pi n \) \(\small< x < \) \(\pi + \small 2\pi n \)
Максима, \(\мали x = \) \(\small \dfrac(\pi)2 + 2\pi n \)	\(\мал x = 2\pi n\)
Минимум, \(\мал x = \) \(\small -\dfrac(\pi)2 + 2\pi n \)	\(\мали x = \) \(\мали \pi + 2\pi n \)
Нули, \(\мал x = \pi n\)	\(\small x = \dfrac(\pi)2 + \pi n \)
Пресечни точки на Y-оската, x = 0	y = 0	y = 1

Основни формули кои содржат синус и косинус

Збир на квадрати

\(\sin^2 x + \cos^2 x = 1\)

Формули на синус и косинус за збир и разлика

\(\sin(x + y) = \sin x \cos y + \cos x \sin y \)
\(\sin(x - y) = \sin x \cos y - \cos x \sin y \)
\(\cos(x + y) = \cos x \cos y - \sin x \sin y \)
\(\cos(x - y) = \cos x \cos y + \sin x \sin y \)

\(\sin(2x) = 2 \sin x \cos x \)
\(\cos(2x) = \cos^2 x - \sin^2 x = \)\(2 \cos^2 x - 1 = 1 - 2 \sin^2 x \)
\(\cos\left(\dfrac(\pi)2 - x \десно) = \sin x \) ; \(\sin\left(\dfrac(\pi)2 - x \десно) = \cos x \)
\(\cos(x + \pi) = - \cos x \) ; \(\sin(x + \pi) = - \sin x \)

Формули за производ од синуси и косинуси

\(\sin x \cos y = \) \(\dfrac12 (\Големи [) \sin(x - y) + \sin(x + y) (\Large ]) \)
\(\sin x \sin y = \) \(\dfrac12 (\Големи [) \cos(x - y) - \cos(x + y) (\Големи ]) \)
\(\cos x \cos y = \) \(\dfrac12 (\Големи [) \cos(x - y) + \cos(x + y) (\Големи ]) \)

\(\sin x \cos y = \dfrac12 \sin 2x \)
\(\sin^2 x = \dfrac12 (\Large [) 1 - \cos 2x (\Large ]) \)
\(\cos^2 x = \dfrac12 (\Large [) 1 + \cos 2x (\Large ]) \)

Формули за збир и разлика

\(\sin x + \sin y = 2 \, \sin \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\sin x - \sin y = 2 \, \sin \dfrac(x-y)2 \, \cos \dfrac(x+y)2 \)
\(\cos x + \cos y = 2 \, \cos \dfrac(x+y)2 \, \cos \dfrac(x-y)2 \)
\(\cos x - \cos y = 2 \, \sin \dfrac(x+y)2 \, \sin \dfrac(y-x)2 \)

Изразување синус преку косинус

\(\sin x = \cos\left(\dfrac(\pi)2 - x \десно) = \)\(\cos\left(x - \dfrac(\pi)2 \десно) = - \cos\left(x + \dfrac(\pi)2 \десно) \)\(\sin^2 x = 1 - \cos^2 x\) \(\sin x = \sqrt(1 - \cos^2 x) \) \(\( 2 \pi n \leqslant x \leqslant \pi + 2 \pi n \) \)\(\sin x = - \sqrt(1 - \cos^2 x) \) \(\( -\pi + 2 \pi n \leqslant x \leqslant 2 \pi n \) \).

Изразување косинус преку синус

\(\cos x = \sin\left(\dfrac(\pi)2 - x \десно) = \)\(- \sin\left(x - \dfrac(\pi)2 \десно) = \sin\left(x + \dfrac(\pi)2 \десно) \)\(\cos^2 x = 1 - \sin^2 x \) \(\cos x = \sqrt(1 - \sin^2 x) \) \(\( -\pi/2 + 2 \pi n \leqslant x \leqslant \pi/2 + 2 \pi n \) \)\(\cos x = - \sqrt(1 - \sin^2 x) \) \(\( \pi/2 + 2 \pi n \leqslant x \leqslant 3\pi/2 + 2 \pi n \) \).

Изразување преку тангента

\(\sin^2 x = \dfrac(\tg^2 x)(1+\tg^2 x) \)\(\cos^2 x = \dfrac1(1+\tg^2 x) \).

На \(- \dfrac(\pi)2 + 2 \pi n< x < \dfrac{\pi}2 + 2 \pi n \) \(\sin x = \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = \dfrac1( \sqrt(1+\tg^2 x) ) \).

На \(\dfrac(\pi)2 + 2 \pi n< x < \dfrac{3\pi}2 + 2 \pi n \) :
\(\sin x = - \dfrac(\tg x)( \sqrt(1+\tg^2 x) ) \)\(\cos x = - \dfrac1( \sqrt(1+\tg^2 x) ) \).

Табела на синуси и косинуси, тангенти и котангенти

Оваа табела ги прикажува вредностите на синусите и косинусите за одредени вредности на аргументот.
[ img style="max-width:500px;max-height:1080px;" src="tablitsa.png" alt="Табела на синуси и косинуси" title="Табела на синуси и косинуси" ]!}

Изрази преку сложени променливи

\(i^2 = -1\)
\(\sin z = \dfrac(e^(iz) - e^(-iz))(2i) \)\(\cos z = \dfrac(e^(iz) + e^(-iz))(2) \)

Ојлерова формула

\(e^(iz) = \cos z + i \sin z \)

Изрази преку хиперболични функции

\(\sin iz = i \sh z \) \(\cos iz = \ch z \)
\(\sh iz = i \sin z \) \(\ch iz = \cos z \)

Деривати

\((\sin x)" = \cos x \) \((\cos x)" = - \sin x \) . Изведување формули > > >

.
\(\лево(\sin x \десно)^((n)) = \sin\left(x + n\dfrac(\pi)2 \десно) \)\(\лево(\cos x \десно)^((n)) = \cos\лево(x + n\dfrac(\pi)2 \десно) \).

Интеграли

\(\int \sin x \, dx = - \cos x + C \)\(\int \cos x \, dx = \sin x + C \)
Видете го и делот Табела неопределени интеграли >>>

Проширувања на сериите

\(\sin x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n+1) )( (2n+1)! ) = \)\(x - \dfrac(x^3)(3 + \dfrac{x^5}{5!} - \dfrac{x^7}{7!} + ... \) !} \(\(- \infty< x < \infty \} \)
\(\cos x = \sum_(n=0)^(\infty) \dfrac( (-1)^n x^(2n) )( (2n)! ) = \)\(1 - \dfrac(x^2)(2 + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + ... \) !} \(\( - \infty< x < \infty \} \)

Изведување формули > > >

\(\sec x = \dfrac1( \cos x) ; \) \(\cosec x = \dfrac1( \sin x) \)

Деривати од n-ти ред:

Инверзните функции на синус и косинус се лаксин и аркозин, соодветно.

Инверзни функции

\(y = \arcsin x\) \(\лево\( -1 \leqslant x \leqslant 1; \; - \dfrac(\pi)2 \leqslant y \leqslant \dfrac(\pi)2 \десно\) \)
\(\sin(\arcsin x) = x\)
\(\arcsin(\sin x) = x\) \(\лево\( - \dfrac(\pi)2 \leqslant x \leqslant \dfrac(\pi)2 \десно\) \)

до синус и косинус се арксин и аркозин, соодветно.

\(y = \arccos x\) \(\лево\( -1 \leqslant x \leqslant 1; \; 0 \leqslant y \leqslant \pi \десно\) \)
\(\cos(\arccos x) = x \) \(\( -1 \leqslant x \leqslant 1 \) \)
\(\arccos(\cos x) = x \) \(\( 0 \leqslant x \leqslant \pi \) \)

Арксин, лаксин
Аркозин, аркос

Javascript е оневозможен во вашиот прелистувач.
За да извршите пресметки, мора да овозможите ActiveX контроли!