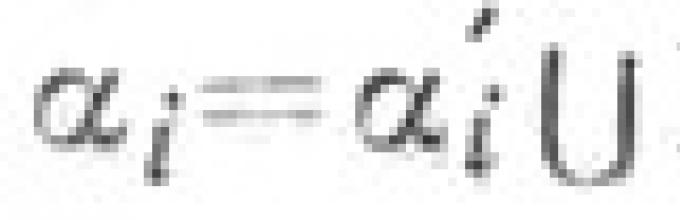Се состои од два различни зраци кои произлегуваат од една точка. Зраците се нарекуваат страни на U., а нивниот заеднички почеток е врвот на U. Нека [ VA),[Сонцето) -
страни на аголот, ВО -неговото теме е рамнина дефинирана со страните U. Фигурата ја дели рамнината на две фигури. ![]() i==l, 2, исто така наречени U. или рамен агол, наречен. внатрешниот регион на станот U.
i==l, 2, исто така наречени U. или рамен агол, наречен. внатрешниот регион на станот U.
Двата агли се нарекуваат еднакви (или складни) ако можат да се порамнат така што нивните соодветни страни и темиња да се совпаѓаат. Од кој било зрак на рамнина, во даден правец од него, може да се нацрта една оска еднаква на дадената оска.Споредбата на оската се врши на два начина. Ако зракот се смета за пар зраци со заедничко потекло, тогаш за да се разјасни прашањето кој од двата зраци е поголем, неопходно е да се комбинираат темињата на зракот и еден пар од нивните страни во една рамнина (види Сл. 1). Ако се покаже дека втората страна на еден U. се наоѓа во друга U., тогаш велат дека првата U. е помала од втората. Вториот метод за споредување на U. се заснова на споредување на секој U. со одреден број. Еднаква U. ќе одговара на истите степени или (види подолу), поголема U. - поголем број, на помалку - помалку.

Се јавиле двајца У. соседни ако имаат заедничко теме и едната страна, а другите две страни формираат права линија (види Сл. 2). Генерално се нарекуваат U. кои имаат заедничко теме и една заедничка страна. соседните. Се јави У вертикална ако страните на едната се продолжетоци надвор од врвот на страните на другата.Вертикални U. се еднакви една со друга. У., чии страни формираат права линија, наречен. проширен. Се јави половина од проширените U. директно U. Директниот U. може еквивалентно да се дефинира поинаку: U. еднаков на неговата соседна, наречена. директно. Внатрешноста на рамна рамнина, која не ја надминува расклопената, е конвексен регион на рамнината. Единицата за мерење на U. се зема како 90-та дропка од директната U., наречена. степен.

Се користи и таканаречената мерка U. Нумеричката вредност на радијанската мерка U. е еднаква на должината на лакот пресечен од страните на U. од единица круг. Еден радијан е доделен на U што одговара на лакот, што е еднакво на неговиот радиус. Раширениот U. е еднаков на радијани.
Кога две прави линии кои лежат во иста рамнина се сечат со трета права линија, се формираат Us (види слика 3): 1 и 5, 2 и 6, 4 и 8, 3 и 7 - т.н. соодветно; 2 и 5, 3 и 8 - внатрешен едностран; 1 и 6, 4 и 7 - надворешен едностран; 3 и 5, 2 и 8 - внатрешно лежи вкрстено; 1 и 7, 4 и 6 - лежи вкрстено однадвор.

Во пракса Во проблемите, препорачливо е да се разгледа ротацијата како мерка за ротација на фиксниот зрак околу неговото потекло до дадена положба. Во зависност од насоката на ротација на сигналите во овој случај, може да се земат предвид и позитивните и негативните. Така, U. во оваа смисла може да има каква било вредност. Во тригонометриската теорија се разгледува ротацијата на зракот. функции: за која било вредност на аргументот (U.), можете да ги одредите вредностите на тригонометрија. функции. Концептот на геометријата во геометријата. системот, кој се заснова на аксиоматика на точка-вектор, суштински се разликува од дефинициите на U. како фигура - во оваа аксиоматика, U. се подразбира како одредена метрика. величина поврзана со два вектори користејќи ја операцијата множење на скаларен вектори. Имено, секој пар вектори a и b дефинира одреден агол - број поврзан со векторите со формулата
![]()
Каде ( а, б) -
скаларен производ на вектори.
Концептот U. како рамна фигура и како одредена нумеричка вредност се користи во различни геометрии. проблеми во кои на посебен начин се определува У. Така, под обликот помеѓу кривите кои се вкрстуваат кои имаат одредени тангенти на точката на вкрстување, ја подразбираме формата формирана од овие тангенти.
Аголот помеѓу права линија и рамнина се зема како агол формиран од правата линија и нејзината правоаголна проекција на рамнината; се мери во опсег од 0
Математичка енциклопедија. - М.: Советска енциклопедија. И.М.Виноградов. 1977-1985 година.
Синоними:Погледнете што е „АГОЛ“ во другите речници:
жар- агол / јок / ... Морфемичко-правописен речник
Маж. фрактура, свиткување, колено, лактот, испакнување или набори (депресија) на едната страна. Линеарен агол, кои било две спротивставени линии и нивниот интервал; аголна рамнина или во рамнини, средба на две рамнини или ѕидови; аголот е густ, тело, средба во едно... РечникДал
Агол, околу агол, на (во) агол и (мат.) во агол, m 1. Дел од рамнина помеѓу две прави што произлегуваат од една точка (мат.). Врвот на аголот. Страни на аголот. Мерење на агол во степени. Прав агол. (90°). Остар агол. (помалку од 90 °). Мал агол…… Објаснувачкиот речник на Ушаков
ЌОШЕ- (1) агол на напад помеѓу насоката на протокот на воздух што тече на крилото на авионот и акордот на делот на крилото. Вредноста на силата на кревање зависи од овој агол. Аголот под кој силата на подигање е максимална се нарекува критичен агол на напад. У... ... Голема политехничка енциклопедија
- (рамно) геометриска фигура, формирани од два зраци (страни на агол) кои излегуваат од една точка (теме на агол). Секој агол со теме во центарот на некој круг ( централен агол) дефинира лак AB на круг, ограничен со точки... ... Голем енциклопедиски речник
Главата на аголот, од зад аголот, мечешкиот агол, недовршениот агол, во сите ќошиња... Речник на руски синоними и изрази слични по значење. под. ед. Н. Абрамова, М.: Руски речници, 1999. агол на врвот, аголна точка; лежиште, засолниште, девијатина, насока,... ... Речник на синоними
агол- агол, прачка. агол; реченица за јаглен, во (на) аголот и во говорот на математичарите во јаглен; pl. агли, прачка. аглите Во предлошки и стабилни комбинации: зад аголот и дозволено е да се оди зад аголот (влезете, свртете итн.), од агол до агол (поместување, позиција итн.), агол... ... Речник на тешкотии во изговорот и стресот на современ руски јазик
АГОЛ, агол, околу аголот, на (во) аголот, маж. 1. (во аголот.). Во геометријата: рамна фигура, формирани од два зраци (во 3 вредности) кои произлегуваат од една точка. Врвот на аголот. Директно y. (90°). Акутна у. (помалку од 90 °). Глупави се. (повеќе од 90 °). Надворешно и внатрешно... ... Објаснувачки речник на Ожегов
агол- АГОЛ, агол, м. Една четвртина од облогот, кога е објавен, работ на картата е преклопен. ◘ Кец и кралица на лопати со агол // Убиен. А.И.Полежаев. Еден ден во Москва, 1832 година. ◘ По вечерата, тој расфрла червонети на масата, ги меша картите; обложувачите ги распукаа своите палуби... ... Терминологија и жаргон за картички од 19 век
Дефиниција
Геометриска фигура која се состои од сите точки на рамнината затворена помеѓу два зраци кои произлегуваат од една точка се нарекува рамен агол.
Дефиниција
Аголот помеѓу двевкрстувајќи се директное вредноста на најмалиот агол на рамнината на пресекот на овие прави. Ако две прави се паралелни, тогаш аголот меѓу нив се зема како нула.
Аголот помеѓу две пресечни линии (ако аглите на рамнината се мерат во радијани) може да има вредности од нула до $\dfrac(\pi)(2)$.
Дефиниција
Аголот помеѓу две вкрстувачки линиие величина еднаква на аголот помеѓу две прави што се сечат паралелни со вкрстувачките. Аголот помеѓу линиите $a$ и $b$ се означува со $\агол (a, b)$.
Точноста на воведената дефиниција произлегува од следната теорема.
Теорема за рамни агли со паралелни страни
Големините на два конвексни рамни агли со соодветно паралелни и идентично насочени страни се еднакви.
Доказ
Ако аглите се прави, тогаш и двата се еднакви на $\pi$. Ако тие не се расклопени, тогаш исцртуваме еднакви отсечки $ON=O_1ON_1$ и $OM=O_1M_1$ на соодветните страни на аглите $\агол AOB$ и $\агол A_1O_1B_1$.
Четириаголникот $O_1N_1NO$ е паралелограм бидејќи неговите спротивни страни $ON$ и $O_1N_1$ се еднакви и паралелни. Исто така, четириаголникот $O_1M_1MO$ е паралелограм. Оттука $NN_1 = OO_1 = MM_1$ и $NN_1 \паралелно OO_1 \паралелно MM_1$, според тоа, $NN_1=MM_1$ и $NN_1 \паралелно MM_1$ по транзитивност. Четириаголникот $N_1M_1MN$ е паралелограм, бидејќи неговите спротивни страни се еднакви и паралелни. Ова значи дека сегментите $NM$ и $N_1M_1$ се еднакви. Триаголниците $ONM$ и $O_1N_1M_1$ се еднакви според третиот критериум за еднаквост на триаголниците, што значи соодветните агли$\аголот NOM$ и $\аголот N_1O_1M_1$ се еднакви.
Нека два не-нула вектори и се дадени на рамнина или во тродимензионален простор. Ајде да одложиме од произволна точка Овектори и . Тогаш важи следнава дефиниција.
Дефиниција.
Агол помеѓу векториа аголот меѓу зраците се вика О.А.И О.Б..
Аголот помеѓу векторите и ќе биде означен како .
Аголот помеѓу векторите може да земе вредности од 0 до или, што е истото, од до.
Кога векторите се и двете насочени, кога векторите се исто така спротивно насочени.
Дефиниција.
Векторите се нарекуваат нормално, ако аголот меѓу нив е еднаков на (радијани).
Ако барем еден од векторите е нула, тогаш аголот не е дефиниран.
Наоѓање на аголот помеѓу вектори, примери и решенија.
Косинусот на аголот помеѓу векторите и , а оттука и самиот агол, во општ случај може да се најде или со користење на скаларниот производ на вектори или со помош на теоремата на косинус за триаголник изграден на векторите и .
Ајде да ги погледнеме овие случаи.
По дефиниција, скаларниот производ на вектори е . Ако векторите и не се нула, тогаш можеме да ги поделиме двете страни на последната еднаквост со производот на должините на векторите и , и ќе добиеме формула за пронаоѓање на косинус на аголот помеѓу вектори кои не се нула: . Оваа формула може да се користи ако се познати должините на векторите и нивниот скаларен производ.
Пример.
Пресметајте го косинусот на аголот помеѓу векторите и , а исто така пронајдете го самиот агол ако должините на векторите и се еднакви 3 И 6 соодветно, а нивниот скаларен производ е еднаков на -9 .
Решение.
Изјавата за проблемот ги содржи сите количини потребни за примена на формулата. Го пресметуваме косинус на аголот меѓу векторите и: .
Сега го наоѓаме аголот помеѓу векторите: .
Одговори:
Има проблеми каде векторите се специфицирани со координати во правоаголен координатен систем на рамнина или во простор. Во овие случаи, за да го пронајдете косинусот на аголот помеѓу векторите, можете да ја користите истата формула, но во координатна форма. Ајде да го добиеме.
Должината на векторот е квадратен корен од збирот на квадратите на неговите координати, скаларниот производ на вектори е еднаков на збирот на производите на соодветните координати. Оттука, формула за пресметување на косинус на аголот помеѓу векторитена рамнината има форма , а за вектори во тродимензионален простор - .
Пример.
Најдете го аголот помеѓу векторите дадени во правоаголен координатен систем.
Решение.
Можете веднаш да ја користите формулата:
Или можете да ја користите формулата за да го пронајдете косинусот на аголот помеѓу векторите, откако претходно ги пресметавме должините на векторите и скаларниот производ над координатите:
Одговор:
Проблемот се сведува на претходниот случај кога се дадени координатите на три точки (на пример А, ВОИ СО) во правоаголен координатен систем и треба да најдете некој агол (на пример, ).
Навистина, аголот е еднаков на аголот помеѓу векторите и . Координатите на овие вектори се пресметуваат како разликата помеѓу соодветните координати на крајните и почетните точки на векторот.
Пример.
На рамнина, координатите на три точки се дадени во Декартовиот координатен систем. Најдете го косинусот на аголот помеѓу векторите и .
Решение.
Да ги одредиме координатите на векторите и координатите на дадените точки:
Сега да ја користиме формулата за да го најдеме косинусот на аголот помеѓу векторите на рамнина во координати:
Одговор:
Аголот помеѓу векторите и исто така може да се пресмета со косинусова теорема. Ако одложиме од поентата Овектори и , потоа со косинусова теорема во триаголник OAVможеме да напишеме, што е еквивалентно на еднаквоста, од која го наоѓаме косинусот на аголот меѓу векторите. За да ја примениме добиената формула, потребни ни се само должините на векторите и , кои лесно може да се најдат од координатите на векторите и . Сепак, овој метод практично не се користи, бидејќи косинусот на аголот помеѓу векторите е полесно да се најде со помош на формулата.
Пресметка ортогонална проекција(сопствена проекција):
Проекцијата на векторот на оската l е еднаква на производот на векторскиот модул и косинусот на аголот φ помеѓу векторот и оската, т.е. pr cosφ.
Доц: Ако φ=< , то пр l =+ = *cos φ.
Ако φ> (φ≤ ), тогаш pr l =- =- * cos( -φ) = cosφ (види Сл.10)
Ако φ= , тогаш pr l = 0 = cos φ.
Последица: Проекцијата на векторот на оската е позитивна (негативна) ако векторот формира остар (тап) агол со оската и е еднаква на нула ако овој агол е прав.
Последица: Проекциите на еднакви вектори на иста оска се еднакви една со друга.
Пресметка на ортогоналната проекција на збирот на вектори (проекциско својство):
Проекцијата на збирот на неколку вектори на иста оска е еднаква на збирот на нивните проекции на оваа оска.
Док: Нека, на пример, = + + . Имаме pr l =+ =+ + - , т.е. pr l ( + + ) = pr l + pr l + pr l (види Сл.11)
ОРИЗ. единаесет
Пресметка на производот на вектор и број:
Кога векторот се множи со број λ, неговата проекција на оската исто така се множи со овој број, т.е. pr l (λ* )= λ* pr l .
Доказ: За λ > 0 имаме pr l (λ* )= *cos φ = λ* φ = λ*pr l
Кога λl (λ* )= *cos( -φ)=- * (-cosφ) = * cosφ= λ *pr l .
Имотот важи и кога
Така, линеарните операции на вектори доведуваат до соодветните линеарни операциинад проекциите на овие вектори.
Овој материјал е посветен на таков концепт како што е аголот помеѓу две пресечни линии. Во првиот пасус ќе објасниме што е тоа и ќе го прикажеме во илустрации. Потоа ќе ги разгледаме начините на кои можете да го пронајдете синусот, косинусот на овој агол и самиот агол (одделно ќе разгледаме случаи со рамнина и тродимензионален простор), ќе ги дадеме потребните формули и ќе покажеме со примери точно како тие се користат во пракса.
За да разбереме каков е аголот формиран кога се сечат две прави, треба да се потсетиме на самата дефиниција на аголот, нормалноста и точката на пресек.
Дефиниција 1
Две прави што се пресекуваат ги нарекуваме ако имаат една заедничка точка. Оваа точка се нарекува точка на пресек на две прави.
Секоја права линија е поделена со пресечна точка на зраци. Двете прави линии формираат 4 агли, од кои два се вертикални, а две се соседни. Ако ја знаеме мерката на еден од нив, тогаш можеме да ги одредиме и останатите.
Да речеме дека знаеме дека еден од аглите е еднаков на α. Во овој случај, аголот што е вертикален во однос на него исто така ќе биде еднаков на α. За да ги пронајдеме преостанатите агли, треба да ја пресметаме разликата 180 ° - α. Ако α е еднаква на 90 степени, тогаш сите агли ќе бидат прави агли. Линиите што се сечат под прав агол се нарекуваат нормални (посебна статија е посветена на концептот на перпендикуларност).
Погледнете ја сликата:
Ајде да продолжиме со формулирање на главната дефиниција.
Дефиниција 2
Аголот формиран од две линии што се пресекуваат е мерка на помалиот од 4-те агли што ги формираат овие две прави.
Од дефиницијата мора да се извлече важен заклучок: големината на аголот во овој случај ќе биде изразена со која било реален бројво интервалот (0, 90]. Ако линиите се нормални, тогаш аголот меѓу нив во секој случај ќе биде еднаков на 90 степени.

Способноста да се најде мерката на аголот помеѓу две линии што се пресекуваат е корисна за решавање на многу практични проблеми. Методот на решение може да се избере од неколку опции.
За почеток, можеме да земеме геометриски методи. Ако знаеме нешто за комплементарните агли, тогаш можеме да ги поврземе со аголот што ни е потребен користејќи ги својствата на еднакви или слични фигури. На пример, ако ги знаеме страните на триаголникот и треба да го пресметаме аголот помеѓу правите на кои се наоѓаат овие страни, тогаш косинусната теорема е погодна за нашето решение. Ако имаме услов правоаголен триаголник, тогаш за пресметки ќе ни требаат и познавање на синус, косинус и тангента на агол.
Координатниот метод е исто така многу удобен за решавање проблеми од овој тип. Дозволете ни да објасниме како правилно да го користите.
Имаме правоаголен (декартов) координатен систем O x y, во кој се дадени две прави. Да ги означиме со буквите a и b. Правите линии може да се опишат со помош на некои равенки. Оригиналните линии имаат пресечна точка М. Како да се одреди потребниот агол (да го означиме α) помеѓу овие прави?
Да почнеме со формулирање на основниот принцип за наоѓање агол под дадени услови.
Знаеме дека концептот на права линија е тесно поврзан со концепти како вектор на насока и нормален вектор. Ако имаме равенка на одредена права, можеме да ги земеме координатите на овие вектори од неа. Можеме да го направиме ова за две линии кои се вкрстуваат одеднаш.
Аголот подвижен од две линии што се пресекуваат може да се најде со помош на:
- агол помеѓу вектори на насока;
- агол помеѓу нормалните вектори;
- аголот помеѓу нормалниот вектор на една права и векторот на насоката на другата права.
Сега да го разгледаме секој метод одделно.
1. Да претпоставиме дека имаме права a со вектор на насока a → = (a x, a y) и права b со вектор на насока b → (b x, b y). Сега да нацртаме два вектори a → и b → од пресечната точка. После ова ќе видиме дека секој од нив ќе биде лоциран на своја права линија. Тогаш имаме четири опции за нив релативна положба. Видете ја илустрацијата:

Ако аголот помеѓу два вектори не е тап, тогаш тоа ќе биде аголот што ни треба помеѓу правата што се вкрстуваат a и b. Ако е тап, тогаш саканиот агол ќе биде еднаков на аголот во непосредна близина на аголот a →, b → ^. Така, α = a → , b → ^ ако a → , b → ^ ≤ 90 ° , и α = 180 ° - a → , b → ^ ако a → , b → ^ > 90 ° .
Врз основа на фактот дека косинусите еднакви аглисе еднакви, добиените еднаквости можеме да ги преработиме на следниов начин: cos α = cos a → , b → ^ , ако a → , b → ^ ≤ 90 ° ; cos α = cos 180 ° - a →, b → ^ = - cos a →, b → ^, ако a →, b → ^ > 90 °.
Во вториот случај, беа користени формули за намалување. Така,
cos α cos a → , b → ^ , cos a → , b → ^ ≥ 0 - cos a → , b → ^ , cos a → , b → ^< 0 ⇔ cos α = cos a → , b → ^
Ајде да ја напишеме последната формула со зборови:
Дефиниција 3
Косинусот на аголот формиран од две вкрстени права ќе биде еднаков на модулот на косинус на аголот помеѓу векторите на неговата насока.
Општата форма на формулата за косинус на аголот помеѓу два вектори a → = (a x , a y) и b → = (b x, b y) изгледа вака:
cos a → , b → ^ = a → , b → ^ a → b → = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
Од него можеме да ја изведеме формулата за косинус на аголот помеѓу две дадени прави:
cos α = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2 = a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
Тогаш самиот агол може да се најде со помош на следнава формула:
α = a r c cos a x b x + a y + b y a x 2 + a y 2 b x 2 + b y 2
Овде a → = (a x , a y) и b → = (b x, b y) се вектори на насоката на дадените линии.
Да дадеме пример за решавање на проблемот.
Пример 1
Во правоаголен координатен систем на рамнина, дадени се две прави што се пресекуваат a и b. Тие можат да се опишат со параметарските равенки x = 1 + 4 · λ y = 2 + λ λ ∈ R и x 5 = y - 6 - 3. Пресметајте го аголот помеѓу овие линии.
Решение
Имаме во наша состојба параметарска равенка, што значи дека за оваа права веднаш можеме да ги запишеме координатите на неговиот вектор на насока. За да го направите ова, треба да ги земеме вредностите на коефициентите за параметарот, т.е. правата x = 1 + 4 · λ y = 2 + λ λ ∈ R ќе има вектор на насока a → = (4, 1).
Втората права линија е опишана со користење канонска равенка x 5 = y - 6 - 3 . Овде можеме да ги земеме координатите од именителот. Така, оваа права има вектор на насока b → = (5 , - 3) .
Следно, се движиме директно кон наоѓање на аголот. За да го направите ова, едноставно заменете ги постојните координати на двата вектори во горната формула α = a r c cos a x · b x + a y + b y a x 2 + a y 2 · b x 2 + b y 2 . Го добиваме следново:
α = a r c cos 4 5 + 1 (- 3) 4 2 + 1 2 5 2 + (- 3) 2 = a r c cos 17 17 34 = a r c cos 1 2 = 45 °
Одговори: Овие прави линии формираат агол од 45 степени.
Можеме да решиме сличен проблем со наоѓање на аголот помеѓу нормалните вектори. Ако имаме права a со нормален вектор n a → = (n a x , n a y) и права b со нормален вектор n b → = (n b x, n b y), тогаш аголот меѓу нив ќе биде еднаков на аголот помеѓу n a → и n b → или аголот што ќе биде во непосредна близина на n a →, n b → ^. Овој метод е прикажан на сликата:

Формулите за пресметување на косинус на аголот помеѓу линиите што се пресекуваат и самиот овој агол користејќи ги координатите на нормалните вектори изгледаат вака:
cos α = cos n a →, n b → ^ = n a x n b x + n a y + n b y n a x 2 + n a y 2 n b x 2 + n b y 2 α = a r c cos n a x n b x + n a y + n b y n a x 2 + n a y 2 n b x 2 + n b y 2
Овде n a → и n b → ги означуваат нормалните вектори на две дадени прави.
Пример 2
Во правоаголен координатен систем, дадени се две прави линии со помош на равенките 3 x + 5 y - 30 = 0 и x + 4 y - 17 = 0. Најдете ги синусот и косинусот на аголот меѓу нив и големината на самиот агол.
Решение
Оригиналните линии се наведени со користење нормални равенкиправа линија од формата A x + B y + C = 0. Нормалниот вектор го означуваме како n → = (A, B). Да ги најдеме координатите на првиот нормален вектор за една права и да ги запишеме: n a → = (3, 5) . За втората линија x + 4 y - 17 = 0, нормалниот вектор ќе има координати n b → = (1, 4). Сега да ги додадеме добиените вредности во формулата и да го пресметаме вкупниот број:
cos α = cos n a → , n b → ^ = 3 1 + 5 4 3 2 + 5 2 1 2 + 4 2 = 23 34 17 = 23 2 34
Ако го знаеме косинусот на аголот, тогаш можеме да го пресметаме неговиот синус користејќи го основниот тригонометриски идентитет. Бидејќи аголот α формиран од прави линии не е тап, тогаш sin α = 1 - cos 2 α = 1 - 23 2 34 2 = 7 2 34.
Во овој случај, α = a r c cos 23 2 34 = a r c sin 7 2 34.
Одговор: cos α = 23 2 34, sin α = 7 2 34, α = a r c cos 23 2 34 = a r c sin 7 2 34
Да го анализираме последниот случај - наоѓање на аголот помеѓу правите ако ги знаеме координатите на векторот на насоката на едната права и нормалниот вектор на другата.
Да претпоставиме дека правата а има вектор на насока a → = (a x , a y) , а правата b има нормален вектор n b → = (n b x , n b y) . Треба да ги оставиме овие вектори настрана од пресечната точка и да ги разгледаме сите опции за нивните релативни позиции. Погледнете на сликата:

Ако аголот помеѓу дадените вектори не е поголем од 90 степени, излегува дека ќе го надополни аголот помеѓу a и b до прав агол.
a → , n b → ^ = 90 ° - α ако a → , n b → ^ ≤ 90 °.
Ако е помало од 90 степени, тогаш го добиваме следново:
a → , n b → ^ > 90 ° , потоа a → , n b → ^ = 90 ° + α
Користејќи го правилото за еднаквост на косинусите со еднакви агли, пишуваме:
cos a → , n b → ^ = cos (90 ° - α) = грев α за a → , n b → ^ ≤ 90 ° .
cos a → , n b → ^ = cos 90 ° + α = - sin α за a → , n b → ^ > 90 ° .
Така,
sin α = cos a → , n b → ^ , a → , n b → ^ ≤ 90 ° - cos a → , n b → ^ , a → , n b → ^ > 90 ° ⇔ sin α = cos a → , n b → ^, a → , n b → ^ > 0 - cos a → , n b → ^ , a → , n b → ^< 0 ⇔ ⇔ sin α = cos a → , n b → ^
Ајде да формулираме заклучок.
Дефиниција 4
За да го пронајдете синусот на аголот помеѓу две прави што се сечат на рамнина, треба да го пресметате модулот на косинус на аголот помеѓу векторот на насоката на првата права и нормалниот вектор на втората.
Ајде да ги запишеме потребните формули. Наоѓање на синус на агол:
sin α = cos a → , n b → ^ = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2
Наоѓање на самиот агол:
α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2
Овде a → е векторот на насоката на првата линија, а n b → е нормалниот вектор на втората.
Пример 3
Две линии кои се пресекуваат се дадени со равенките x - 5 = y - 6 3 и x + 4 y - 17 = 0. Најдете го аголот на пресекот.
Решение
Од дадените равенки ги земаме координатите на водичот и нормалниот вектор. Излегува a → = (- 5, 3) и n → b = (1, 4). Ја земаме формулата α = a r c sin = a x n b x + a y n b y a x 2 + a y 2 n b x 2 + n b y 2 и пресметаме:
α = a r c sin = - 5 1 + 3 4 (- 5) 2 + 3 2 1 2 + 4 2 = a r c sin 7 2 34
Забележете дека ги зедовме равенките од претходниот проблем и го добивме токму истиот резултат, но на поинаков начин.
Одговор:α = a r c sin 7 2 34
Дозволете ни да претставиме друг начин за наоѓање на саканиот агол користејќи ги аголните коефициенти на дадените прави линии.
Имаме права a, која е дефинирана во правоаголен координатен систем користејќи ја равенката y = k 1 x + b 1, и права b, дефинирана како y = k 2 x + b 2. Ова се равенки на линии со падини. За да го пронајдеме аголот на пресек, ја користиме формулата:
α = a r c cos k 1 · k 2 + 1 k 1 2 + 1 · k 2 2 + 1, каде што k 1 и k 2 се наклоните на дадените линии. За да се добие овој запис, користени се формули за одредување на аголот преку координатите на нормалните вектори.
Пример 4
Во една рамнина се сечат две прави, дадени со равенките y = - 3 5 x + 6 и y = - 1 4 x + 17 4. Пресметајте ја вредноста на аголот на пресекот.
Решение
Аголните коефициенти на нашите линии се еднакви на k 1 = - 3 5 и k 2 = - 1 4. Да ги додадеме во формулата α = a r c cos k 1 k 2 + 1 k 1 2 + 1 k 2 2 + 1 и да пресметаме:
α = a r c cos - 3 5 · - 1 4 + 1 - 3 5 2 + 1 · - 1 4 2 + 1 = a r c cos 23 20 34 24 · 17 16 = a r c cos 23 2 34
Одговор:α = a r c cos 23 2 34
Во заклучоците од овој став, треба да се забележи дека формулите за наоѓање на аголот дадени овде не мора да се научат напамет. За да го направите ова, доволно е да ги знаете координатите на водичите и/или нормалните вектори на дадените линии и да можете да ги одредите со различни типовиравенки. Но, подобро е да ги запомните или запишете формулите за пресметување на косинус на аголот.
Како да се пресмета аголот помеѓу линиите што се вкрстуваат во просторот
Пресметката на таков агол може да се сведе на пресметување на координатите на векторите на насоката и одредување на големината на аголот формиран од овие вектори. За такви примери се користи истото резонирање што го наведовме претходно.
Да претпоставиме дека имаме правоаголен координатен систем сместен во тродимензионален простор. Содржи две прави а и б со пресечна точка М. За да ги пресметаме координатите на векторите на насоката, треба да ги знаеме равенките на овие прави. Да ги означиме векторите на насока a → = (a x , a y , a z) и b → = (b x , b y , b z) . За да го пресметаме косинусот на аголот меѓу нив, ја користиме формулата:
cos α = cos a → , b → ^ = a → , b → a → b → = a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2
За да го најдеме самиот агол, потребна ни е оваа формула:
α = a r c cos a x b x + a y b y + a z b z a x 2 + a y 2 + a z 2 b x 2 + b y 2 + b z 2
Пример 5
Имаме линија дефинирана во тродимензионален простор користејќи ја равенката x 1 = y - 3 = z + 3 - 2. Познато е дека се вкрстува со оската O z. Пресметај го аголот на пресекот и косинусот на тој агол.
Решение
Да го означиме аголот што треба да се пресмета со буквата α. Да ги запишеме координатите на векторот на насоката за првата права – a → = (1, - 3, - 2) . За апликативната оска можеме да земеме координатен вектор k → = (0, 0, 1) како водич. Ги добивме потребните податоци и можеме да ги додадеме во саканата формула:
cos α = cos a → , k → ^ = a → , k → a → k → = 1 0 - 3 0 - 2 1 1 2 + (- 3) 2 + (- 2) 2 0 2 + 0 2 + 1 2 = 2 8 = 1 2
Како резултат на тоа, откривме дека аголот што ни треба ќе биде еднаков на r c cos 1 2 = 45 °.
Одговор: cos α = 1 2 , α = 45 ° .
Доколку забележите грешка во текстот, означете ја и притиснете Ctrl+Enter