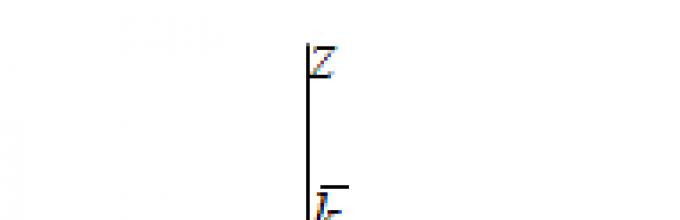тоа се косинусите на аглите што векторот ги формира со позитивните полуоски на координати. Косинусите за насока уникатно ја специфицираат насоката на векторот. Ако векторот има должина 1, тогаш неговите косинуси на насока се еднакви на неговите координати. Општо земено, за вектор со координати ( а; б; в) косинусите на насоката се еднакви:

каде a, b, g се аглите направени од векторот со оските x, y, zсоодветно.

21) Разложување на вектор во единечни вектори. Единечниот вектор на координатната оска се означува со , оските со , а оските со (сл. 1).

За секој вектор што лежи во рамнината, се случува следното проширување:

Ако векторот лоциран во просторот, тогаш проширувањето во единечни вектори на координатните оски има форма:

22)Производ со точкидва вектори не-нула и бројот еднаков на производот на должините на овие вектори и косинусот на аголот меѓу нив се вика:

23) Агол помеѓу два вектори

Ако аголот помеѓу два вектори е акутен, тогаш нивниот скаларен производ е позитивен; ако аголот помеѓу векторите е тап, тогаш скаларниот производ на овие вектори е негативен. Скаларниот производ на два ненулта вектори е еднаков на нула ако и само ако овие вектори се ортогонални.

24) Условот на паралелизам и перпендикуларност на два вектори.

Услов векторите да бидат нормални
Векторите се нормални ако и само ако нивниот скаларен производ е нула Дадени два вектори a(xa;ya) и b(xb;yb). Овие вектори ќе бидат нормални ако изразот xaxb + yayb = 0.

25) Векторски производ на два вектори.

Векторскиот производ на два неколинеарни вектори е вектор c=a×b кој ги задоволува следните услови: 1) |c|=|a| |б| sin(a^b) 2) c⊥a, c⊥b 3) Векторите a, b, c формираат десна тројка вектори.

26) Колинеарни и компланарни вектори..

Векторите се колинеарни ако апсцисата на првиот вектор е поврзана со апсцисата на вториот на ист начин како што е и ординатата на првиот со ординатата на вториот а (xa;да) И б (xb;yb). Овие вектори се колинеарни ако xa = x bИ y a = y b, Каде Р.

Вектори −→ а,−→би −→ все нарекуваат компланарни, ако има рамнина на која се паралелни.

27) Мешан производ од три вектори. Мешан производ на вектори- скаларен производ на векторот a и векторски производвекторите b и c. Најдете го мешаниот производ на векторите a = (1; 2; 3), b = (1; 1; 1), c = (1; 2; 1).



Решение:

1 · 1 · 1 + 1 · 1 · 2 + 1 · 2 · 3 - 1 · 1 · 3 - 1 · 1 · 2 - 1 · 1 · 2 = 1 + 2 + 6 - 3 - 2 - 2 = 2

28) Растојанието помеѓу две точки на рамнина. Растојанието помеѓу две дадени точки е еднакво на квадратниот корен од збирот на квадратните разлики на истите координати на овие точки.

29) Поделба на отсечка во оваа релација. Ако точката M(x; y) лежи на права што минува низ две дадени точки ( , ) и ( , ), и е дадена релација во која точката M ја дели отсечката , тогаш координатите на точката M се одредуваат со формулите

Ако точката М е средната точка на отсечката, тогаш нејзините координати се одредуваат со формулите

30-31. Наклон на права линијасе нарекува тангента на аголот на наклонот на оваа права. Наклонот на права линија обично се означува со буквата к. Потоа по дефиниција

Равенка на права линија со наклонја има формата каде к- права линија наклон, б- некој реален број. Користејќи ја равенката на права линија со коефициент на агол, можете да наведете која било права линија што не е паралелна со оската Ој(за права линија паралелна со оската на ординатите, аголниот коефициент не е дефиниран).

33. Општа равенка на права линија на рамнина. Равенка на формата Постои општа равенка на права Окси. Во зависност од вредностите константа А, Би C се можни следниве посебни случаи:



C = 0, A ≠0, B ≠ 0 - правата линија минува низ потеклото

A = 0, B ≠0, C ≠0 (By + C = 0) - права линија паралелна со оската Ox

B = 0, A ≠0, C ≠ 0 (Ax + C = 0) – права линија паралелна на оската Oy

B = C = 0, A ≠0 - правата линија се совпаѓа со оската Oy

A = C = 0, B ≠0 - правата линија се совпаѓа со оската Ox

34.Равенка на права во отсечкина рамнина во правоаголен координатен систем Оксија има формата каде аИ б- некои не-нула реални броеви. Ова име не е случајно, бидејќи апсолутни вредностиброеви АИ беднакви на должините на отсечките кои правата линија ги отсекува на координатните оски ВолИ Ојсоодветно (сегментите се бројат од потеклото). Така, равенката на права во отсечки го олеснува конструирањето на оваа линија во цртежот. За да го направите ова, треба да ги означите точките со координати и во правоаголен координатен систем на рамнината и да користите линијар за да ги поврзете со права линија.

35. Нормалната равенка на права има форма

каде е растојанието од правата линија до потеклото;  – аголот помеѓу нормалата на правата и оската.

Нормалната равенка може да се добие од општата равенка (1) со множење со факторот за нормализирање, знакот  е спротивен на знакот така што .

Косинусите на аглите помеѓу права линија и координатните оски се нарекуваат косинуси за насока,  – агол помеѓу права линија и оска,  – помеѓу права линија и оска:

Така, нормалната равенка може да се запише во форма

Растојание од точка до права линијаопределена со формулата

36. Растојанието помеѓу точка и права се пресметува со следнава формула:

каде x 0 и y 0 се координатите на точката, а A, B и C се коефициенти од општата равенка на правата

37. Намалување на општата равенка на права во нормала. Равенката и рамнината во овој контекст не се разликуваат едни од други по ништо друго освен по бројот на членовите во равенките и димензијата на просторот. Затоа, прво ќе кажам се за авионот, а на крајот ќе направам резервација за правата линија.
Дадена е општата равенка на рамнината: Ax + By + Cz + D = 0.
;. го добиваме системот: g;Mc=cosb, MB=cosa Да го доведеме во нормална форма. За да го направиме ова, ги множиме двете страни на равенката со нормализирачкиот фактор M. Добиваме: Max+Mvu+MCz+MD=0. Во овој случај MA=cos;.g;Mc=cosb, MB=cosa го добиваме системот:

M2 B2=cos2b
M2 C2=cos2g

Со собирање на сите равенки на системот, добиваме M*(A2 + B2 + C2) = 1 Сега останува само да се изрази М од тука за да се знае со кој фактор за нормализирање мора да се помножи првобитната општа равенка за да се донесе во нормална форма:
M=-+1/ROOT KV A2 +B2 +C2
MD секогаш мора да биде помал од нула, затоа знакот на бројот M се зема спротивно на знакот на бројот D.
Со равенката на права линија, сè е исто, само од формулата за М треба едноставно да го отстраните терминот C2.

Секира + Од страна на + Cz + Д = 0,

38.Општа равенка на рамнината во просторот се нарекува равенка на формата

Каде А 2 + Б 2 + В 2 ≠ 0 .

Во тродимензионалниот простор во Декартовиот координатен систем, секоја рамнина се опишува со равенка од 1 степен (линеарна равенка). И назад, било кој линеарна равенкадефинира рамнина.

40.Равенка на рамнина во отсечки.Во правоаголен координатен систем Оксизво тродимензионален простор равенка на формата , Каде а, бИ в– се повикуваат ненула реални броеви равенка на рамнината во отсечки. Апсолутни вредности на броеви а, бИ веднаква на должините на отсечките што рамнината ги отсекува на координатните оски Вол, ОјИ Озсоодветно, сметајќи од потеклото. Знак на броеви а, бИ впокажува во која насока (позитивна или негативна) се исцртуваат отсечките на координатните оски

41) Равенка на нормална рамнина.

Нормална равенкарамнина се нарекува нејзината равенка, напишана во форма

каде , , се нормални косинусите на насоката на рамнината, д

p е растојанието од потеклото до рамнината. При пресметување на косинусите на насоката на нормалата, треба да се претпостави дека е насочена од почетокот кон рамнината (ако рамнината минува низ потеклото, тогаш изборот на позитивната насока на нормалата е рамнодушен).

42) Растојание од точка до рамнина.Нека рамнината е дадена со равенката и се дава поен. Тогаш растојанието од точката до рамнината се одредува со формулата

Доказ. Растојанието од точка до рамнина е, по дефиниција, должината на нормалната извлечена од точката до рамнината

Агол помеѓу рамнините

Нека рамнините и се специфицирани со равенките и , соодветно. Треба да го пронајдете аголот помеѓу овие рамнини.

Рамнините, кои се сечат, формираат четири диедрални агли: два тапи и два акутни или четири прави, и двата тапи аглисе еднакви едни на други, а и двете акутни се исто така еднакви една на друга. Секогаш ќе бараме остар агол. За да ја одредиме нејзината вредност, земаме точка на линијата на пресек на рамнините и во оваа точка во секоја од

рамнини, цртаме нормални на линијата на пресекот.


Имотот:

cos 2 α + cos 2 β + cos 2 γ = 1

б) дефинирање на линеарни операции

збирот на два неколинеарни вектори е векторот кој доаѓа од заедничкото потекло на векторите долж дијагоналата на паралелограмот конструиран на овие вектори

Векторската разлика е збир на вектор и вектор спротивен на векторот: . Да ги поврземе почетоците на векторите и , тогаш векторот е насочен од крајот на векторот до крајот на векторот.

Работата вектор по број се нарекува вектор со модул , и во и во . Геометриски, множењето со број значи „истегнување“ на векторот за фактор, задржување на насоката и менување на спротивното во .

Од горенаведените правила за собирање вектори и нивно множење со број, следат очигледни изјави:

1. (дополнувањето е комутативно);

2. (дополнувањето е асоцијативно);

3. (постоење на нулта вектор);

4. (постоење на спротивен вектор);

5. (дополнувањето е асоцијативно);

6. (множењето со број е дистрибутивно);

7. (векторското собирање е дистрибутивно);

в) скаларен производ и неговите основни својства

Производ со точкидва вектори не-нула е број еднаков на производот на должините на овие вектори и косинусот на аголот меѓу нив. Ако барем еден од двата вектори е нула, тогаш аголот меѓу нив не е дефиниран, а скаларниот производ се смета за еднаков на нула. Скаларниот производ на вектори и е означен

, каде и се должините на векторите и , соодветно, и е аголот помеѓу векторите и .

Скаларниот производ на векторот со себе се нарекува скаларен квадрат.

Својства на скаларниот производ.

За сите вектори и следново се вистинити: својствата на производот со точки:

комутативното својство на скаларен производ;

дистрибутивна сопственост или ;

асоцијативно својство или , каде што е произволен реален број;

скаларниот квадрат на векторот е секогаш ненегативен ако и само ако векторот е нула.

Г) векторски производ и неговите својства

векторски производвекторот a на векторот b се нарекува вектор c, чија должина е нумерички еднаква на плоштината на паралелограмот конструиран на векторите a и b, нормално на рамнината на овие вектори и насочен така што најмалата ротација од a до b околу векторот c е спротивно од стрелките на часовникот кога се гледа од крајниот вектор c

Формули за пресметување на векторски производ на вектори

Векторски уметнички деладва вектори a = (a x; a y; a z) и b = (b x; b y; b z) во Декартовиот координатен систем е вектор чија вредност може да се пресмета со помош на следните формули:

  • Вкрстениот производ на два ненулта вектори a и b е еднаков на нула ако и само ако векторите се колинеарни.
  • Векторот c, еднаков на вкрстениот производ на ненула вектори a и b, е нормален на овие вектори.
  • a × b = -b × a
  • (k a) × b = a × (k b) = k (a × b)
  • (a + b) × c = a × c + b × c

Равенка на права линија на рамнина

А) равенка на права линија со коефициент на агол

Наклон на права линијасе нарекува тангента на аголот на наклонот на оваа права.

Наклонот на права линија обично се означува со буквата к. Потоа по дефиниција.

Ако правата линија е паралелна со оската на ординатите, тогаш наклонот не постои (во овој случај се вели и дека наклонот оди до бесконечност).

Позитивниот наклон на линијата означува зголемување на нејзиниот график на функцијата, негативниот наклон означува намалување. Равенката на права со аголен коефициент има форма y=kx+b, каде k е аголниот коефициент на правата, b е некој реален број. Користејќи ја равенката на права линија со аголен коефициент, можете да наведете која било права линија што не е паралелна со оската Oy (за права линија паралелна на оската на ординатите, аголниот коефициент не е дефиниран).

Б) видови равенки на права линија

Равенка повикани општа равенкадиректново авион.

Секоја равенка од прв степен со две променливи xИ yљубезен , Каде А, ВОИ СО– некои реални бројки и АИ ВОне се еднакви на нула во исто време, дефинира права линија во правоаголен координатен систем Оксина рамнината, а секоја линија на рамнината е дадена со равенка на формата .

Линиска равенка на формата , каде аИ б– се повикуваат некои реални броеви освен нула равенка на права линија во отсечки. Ова име не е случајно, бидејќи апсолутните вредности на бројките АИ беднакви на должините на отсечките кои правата линија ги отсекува на координатните оски ВолИ Ојсоодветно (сегментите се бројат од потеклото).

Линиска равенка на формата , каде xИ y- променливи, и кИ б– се повикуваат некои реални броеви равенка на права линија со наклон (к- наклон)

Канонска равенка на права на рамнинаво правоаголен Декартов координатен систем Оксиизгледа како , каде и се некои реални броеви, а во исто време тие не се еднакви на нула.

Очигледно, правата линија дефинирана со канонската равенка на правата поминува низ точката. За возврат, броевите и во именителот на дропките ги претставуваат координатите на векторот на насоката на оваа права. Така, канонска равенкадиректно во правоаголен координатен систем Оксина рамнината одговара права линија што минува низ точка и има вектор на насока .

Параметриски равенки на права на рамнинаизгледаат како , каде и се некои реални броеви, а во исто време не се еднакви на нула, и е параметар кој зема какви било реални вредности.

Равенките на параметриските линии воспоставуваат имплицитна врска помеѓу апсцисите и ординатите на точките на права линија користејќи параметар (оттука и името на овој тип на равенка на права).

Пар броеви кои се пресметуваат од параметарските равенки на правата за некоја реална вредност на параметарот претставуваат координати на одредена точка на правата. На пример, кога имаме , односно точката со координати лежи на права линија.

Треба да се напомене дека коефициентите и за параметарот во параметарски равенкиправа се координатите на векторот на насоката на оваа права

Равенка на права што минува низ две точки

Нека две точки M 1 (x 1, y 1, z 1) и M 2 (x 2, y 2, z 2) се дадени во просторот, тогаш равенката на правата што минува низ овие точки е:

Ако некој од именителот е еднаков на нула, соодветниот броител треба да биде еднаков на нула На рамнината, равенката на правата напишана погоре е поедноставена:

ако x 1 ≠ x 2 и x = x 1, ако x 1 = x 2.

Дропката = k се нарекува наклондиректно.

В) пресметување на аголот помеѓу две прави

ако се дадени две прави y = k 1 x + b 1, y = k 2 x + b 2, тогаш акутниот агол помеѓу овие прави ќе се дефинира како

.

Две прави се паралелни ако k 1 = k 2. Две прави се нормални ако k 1 = -1 / k 2.

Теорема.Правите Ax + Bу + C = 0 и A 1 x + B 1 y + C 1 = 0 се паралелни кога коефициентите A 1 = λA, B 1 = λB се пропорционални. Ако исто така C 1 = λC, тогаш линиите се совпаѓаат. Координатите на точката на пресек на две прави се наоѓаат како решение на системот равенки на овие прави.

Г) услови за паралелизам и перпендикуларност на две прави

Услови за паралелизам на две прави:

а) Ако правите се дадени со равенки со аголен коефициент, тогаш неопходен и доволен услов за нивниот паралелизам е еднаквоста на нивните аголни коефициенти:

к 1 = к 2 .

б) За случајот кога правите се дадени со равенки во општ поглед(6), неопходен и доволен услов за нивниот паралелизам е коефициентите за соодветните струјни координати во нивните равенки да бидат пропорционални, т.е.

Услови за перпендикуларност на две прави:

а) Во случај кога правите се дадени со равенки (4) со аголен коефициент, неопходен и доволен услов за нивната перпендикуларност е тие падинисе инверзни по големина и спротивни по знак, т.е.

Оваа состојба може да се напише и во форма

к 1 к 2 = -1.

б) Ако равенките на правите се дадени во општ облик (6), тогаш условот за нивната перпендикуларност (неопходна и доволна) е да се задоволува еднаквоста

А 1 А 2 + Б 1 Б 2 = 0.

Ограничување на функцијата

А) граница на низа

Концептот на граница го користел Њутн во втората половина на 17 век и математичари од 18 век како Ојлер и Лагранж, но тие ја разбрале границата интуитивно. Првите ригорозни дефиниции за границата на низата беа дадени од Болзано во 1816 година и Коши во 1821 година.

Се повикува бројот ограничување броена низа , ако низата е бесконечно мала, т.е. сите нејзини елементи, почнувајќи од одреден, се помали од кој било однапред одреден позитивен број во апсолутна вредност.

Ако бројната низа има ограничување во форма на реален број, таа се нарекува конвергентен на овој број. Во спротивно, се нарекува низата дивергентни . Ако, згора на тоа, тој е неограничен, тогаш се претпоставува дека неговата граница е еднаква на бесконечноста.

Дополнително, ако сите елементи на неограничена низа, почнувајќи од одреден број, имаат позитивен знак, тогаш се вели дека границата на таквата низа е плус бесконечност .

Ако елементите на неограничена низа, почнувајќи од одреден број, имаат негативен знак, тогаш велат дека границата на таквата низа е еднаква на минус бесконечност .

Б) граница на функцијата

Ограничување на функцијата (гранична вредност на функцијата) В дадена точка, ограничување за доменот на дефиниција на функцијата, е вредноста кон која се стреми вредноста на функцијата што се разгледува додека нејзиниот аргумент се стреми кон дадена точка.

Ограничување на функцијатае генерализација на концептот на граница на низа: првично, границата на функцијата во точка беше сфатена како граница на низа елементи од доменот на вредностите на функцијата составена од слики на точки на секвенца на елементи од доменот на дефиниција на функција која се приближува до дадена точка (границата на која се разгледува); ако постои таква граница, тогаш се вели дека функцијата конвергира до одредената вредност; ако таква граница не постои, тогаш се вели дека функцијата се разминува.

Ограничување на функцијата- еден од основните концепти на математичката анализа. Вредноста се нарекува ограничување (гранична вредност) на функција во точка ако за која било низа точки што се конвергира кон, но не содржи еден од нејзините елементи (односно, во пробиено соседство), низата вредности на функцијата конвергира во .

Вредноста се нарекува ограничување (гранична вредност) функционира во точката ако за кој било позитивен број однапред земен има соодветен позитивен број така што за сите аргументи што го задоволуваат условот неравенството е исполнето.

В) две забележителни граници

· Прво прекрасна граница:

Последици

·

·

·

· Втората извонредна граница:

Последици

1.

2.

3.

4.

5. за,

6.

Г) бесконечно мали и бесконечно големи функции

Функција y=f(x)повикани бесконечно малона x→aили кога x→∞, ако или , т.е. бескрајно мала функцијае функција чија граница во дадена точка е нула.

ако функција y=f(x)застапен со x→aкако збир на константен број би бесконечно мала магнитуда α(x): f (x)=b+ α(x)Тоа .

Спротивно на тоа, ако , тогаш f (x)=b+α(x), Каде a (x)– бесконечно мало во x→a.

Заклучок 1.Ако и, тогаш.

Заклучок 2.Доколку и c=конст, тогаш .

Доколку функцијата f(x)е бескрајно голем во x→a, потоа функција 1 /f(x)е бесконечно мало во x→a.

Доколку функцијата f(x)- бесконечно мало во x→a(или x→∞)и не исчезнува, тогаш y= 1/f(x)е бесконечна одлична функција. Наједноставните својства на бесконечно малите и бесконечно големите функции може да се напишат со помош на следните условни односи: А≠ 0

Г) откривање на неизвесности. Правилото на L'Hopital

главни видови на неизвесности: нула поделена со нула ( 0 до 0), бесконечност поделена со бесконечност, нула помножена со бесконечност, бесконечност минус бесконечност, еден до моќта на бесконечноста, нула до моќта на нула, бесконечноста до моќта на нула.

Правилото на L'Hopitalмногу широко се користи за гранични пресметкикога има неизвесност на формата нула поделена со нула, бесконечност поделена со бесконечност.

Овие типови на несигурности ги вклучуваат неизвесностите нула пати бесконечност и бесконечност минус бесконечност.

Ако и ако функционира f(x)И g(x)се диференцијабилни во соседството на точката, тогаш

Во случај кога неизвесноста не исчезне по примената на правилото на L'Hopital, таа може повторно да се примени.

Пресметка на деривати

А) правило за диференцијација комплексна функција

Нека биде комплексна функција , каде што функцијата е среден аргумент. Ќе покажеме како се наоѓа изводот на сложена функција, знаејќи го изводот за функцијата (ќе го означиме со) и изводот за функцијата.

Теорема 1. Ако функцијата има извод во точка x, а функцијата има извод во точката (), потоа сложената функција во точката xима извод, и = .

Во спротивно, изводот на сложената функција е еднаков на производот од изводот на дадената функција во однос на меѓуаргументот и изводот на средниот аргумент.

Б) диференцијација на параметарски одредена функција

Нека функцијата е дадена во параметарска форма, односно во форма:

каде што функциите и се дефинирани и континуирани во одреден интервал на варијација на параметарот . Ајде да ги најдеме диференцијалите на десната и левата страна на секоја од еднаквостите:

За да го пронајдеме вториот извод, ги извршуваме следните трансформации:

Б) концептот на логаритамски извод на функција

Логаритамскиот извод на позитивната функција се нарекува негов извод. Бидејќи , тогаш според правилото за диференцијација на сложена функција ја добиваме следната релација за логаритамскиот извод:

.

Користејќи го логаритамскиот извод, погодно е да се пресмета обичниот извод во случаи кога логаритам ја поедноставува формата на функцијата.

Суштината на оваа диференцијација е како што следува: прво, пронајдете го логаритамот дадена функција, па дури тогаш се пресметува изводот од него. Нека се даде некоја функција. Да ги земеме логаритмите на левата и десната страна на овој израз:

И тогаш, изразувајќи го саканиот дериват, резултатот е:

Г) дериват инверзна функција

Ако y=f(x) и x=g(y) се пар меѓусебно инверзни функции, а функцијата y=f(x) има извод f"(x), тогаш изводот на инверзната функција g"( x)=1/f" (x).

Така, дериватите на заемно инверзните функции се реципрочни величини. Формула за изводот на инверзната функција:

Г) дериват имплицитна функција

Ако со равенката е опишана функција од една променлива y=ѓ(x), каде што променливата yе на левата страна, а десната зависи само од аргументот x, тогаш велат дека функцијата е дадена експлицитно. На пример, следните функции се експлицитно наведени:

y=грев x,y=x 2+2x+5,y=lncos x.

Во многу проблеми, сепак, функцијата може да се специфицира имплицитно, т.е. како равенка

Ф(x,y)=0.

да се најде изводот y′( x) имплицитно одредената функција не треба да се претвора во експлицитна форма. За да го направите ова, знаејќи ја равенката Ф(x,y)=0, само направете го следново:

Прво треба да ги разликувате двете страни на равенката во однос на променливата x, под претпоставка дека y− е диференцијабилна функција xи користење на правилото за пресметување на извод на сложена функција. Во овој случај, изводот на нула (на десната страна) исто така ќе биде еднаков на нула.
Коментар: Ако десната страна е не-нула, т.е. имплицитната равенка е

ѓ(x,y)=е(x,y),

тогаш ги разликуваме левата и десната страна на равенката.

Решете ја добиената равенка за изводот y′( x).

Поим за дериват

А) дефиниција на дериват

Извод на функција диференцијација интеграција.

y xx

Дефиниција на дериват

Размислете за функцијата ѓ(x x 0. Потоа функцијата ѓ(x) е диференцијабилнаво точката x 0, и неа дериватсе одредува со формулата

ѓ′( x 0)=limΔ x→0Δ yΔ x=limΔ x→0ѓ(x 0+Δ x)−ѓ(x 0)Δ x.

Извод на функцијае еден од основните поими на математиката, а во математичка анализадериватот заедно со интегралот зазема централно место. Процесот на пронаоѓање на изводот се нарекува диференцијација. Инверзната операција - враќање на функција од познат извод - се нарекува интеграција.

Изводот на функцијата во одредена точка ја карактеризира брзината на промена на функцијата во таа точка. Проценка на стапката на промена може да се добие со пресметување на односот на промената на функцијата Δ yдо соодветна промена во аргументот Δ x. Во дефиницијата на изводот, таквата врска се разгледува во границата под условот Δ x→0. Ајде да преминеме на построга формулација:

Дефиниција на дериват

Размислете за функцијата ѓ(x), чиј домен содржи некој отворен интервал околу точката x 0. Потоа функцијата ѓ(x) е диференцијабилнаво точката x 0, и неа дериватсе одредува со формулата

ѓ′( x 0)=limΔ x→0Δ yΔ x=limΔ x→0ѓ(x 0+Δ x)−ѓ(x 0)Δ x.

Б) геометриско значењедериват

Изводот на функцијата, пресметан за дадена вредност, е еднаков на тангентата на аголот формиран од позитивната насока на оската и позитивната насока на тангентата нацртана на графикот на оваа функција во точката со апсцисата:

Ако функцијата има конечен извод во точка, тогаш во соседството може да се приближи линеарна функција

Функцијата се нарекува тангента на точката Број.

Г) табела на деривати на наједноставните елементарни функции

Збирот на квадратите на косинусите на насоката е еднаков на еден.

Ако се познати косинусите на насоката на векторот, тогаш неговите координати може да се најдат со помош на формулите: Слични формули се применуваат и во тродимензионалниот случај - ако се познати косинусите на насоката на векторот, тогаш неговите координати можат да се најдат со помош на формулите:

9 Линеарна зависност и линеарна независноствектори. Основа на авион и во вселената

Се нарекува множество вектори систем на вектори.

линеарно зависни, ако има броеви кои не се сите еднакви на нула во исто време, тоа

Се нарекува систем на вектори линеарно независна,ако еднаквоста е можна само за , т.е. кога линеарната комбинација од левата страна на еднаквоста е тривијална.

1. Еден вектор формира и систем: at - линеарно зависен, и at - линеарно независен.

2. Секој дел од системот на вектори се нарекува потсистем.

1. Ако системот на вектори вклучува нула вектор, тогаш тој е линеарно зависен

2. Ако системот на вектори има два еднакви вектори, тогаш тој е линеарно зависен.

3. Ако системот на вектори има два пропорционални вектори, тогаш тој е линеарно зависен.

4. Систем на вектори е линеарно зависен ако и само ако барем еден од векторите е линеарна комбинација на другите.

5. Сите вектори вклучени во линеарно независен систем формираат линеарно независен потсистем.

6. Систем од вектори што содржи линеарно зависен потсистем е линеарно зависен.

7. Ако системот на вектори е линеарно независен, и откако ќе се додаде вектор на него, се покажува дека е линеарно зависен, тогаш векторот може да се прошири во вектори и, згора на тоа, единствениот начин, т.е. коефициентите на проширување може да се најдат уникатно.

Основана рамнина и во простор се нарекува максимален систем на вектори кој е линеарно независен на рамнина или во простор (додавањето на друг вектор на системот го прави линеарно зависен).

Така, основа на рамнината се кои било два неколинеарни вектори земени по одреден редослед, а основа во просторот се трите некомпланарни вектори земени по одреден редослед.

Нека е основа во просторот, тогаш, според Т. 3, секој вектор на простор може да се разложи на единствен начин во вектори на основа: . Коефициентите на проширување се нарекуваат координати на векторот во основата

Запишување линеарни операции на вектори преку координати:

а) собирање и одземање: - основа

б) множење со бројот R:

Формулите произлегуваат од својствата на линеарните операции.

10 Координати на векторот во однос на основата. Орти

Основаво слободен векторски простор V 3е која било подредена тројка од некомпланарни вектори.

Нека ВО :а 1,а 2,а 3– фиксна основа во V 3.

Координативектор бво однос на основата ВО повикана наредена тројка од броеви ( x, y, z), вкл. б=x· а 1 +yа 2 +z· а 3.

Ознака:б={x, y, z} Б Забелешка: Координатите на фиксен вектор значат координати на соодветниот слободен вектор.

Теорема 1:Кореспонденцијата помеѓу V 3 и R 3 за фиксна основа е еден-на-еден, т.е. б V 3 ! {x, y, z) R 3 и ( x, y, z) R 3 ! б V 3,вкл. б={x, y, z} Б

Кореспонденцијата помеѓу векторот и неговите координати во дадена основа ги има следниве својства:

1. Нека b 1 ={x 1, y 1, z 1} Б , b 2 ={x 2, y 2, z 2} Б b 1 + b 2 ={x 1 + x 2, y 1 + y 2, z 1 + z 2} Б

2. Нека б={x, y, z} Б , λR λ б={ λ· x, λ· y, λ· z} Б

3. Нека b 1 || b 2, b 1 = {x 1, y 1, z 1} Б , b 2 ={x 2, y 2, z 2} Б
(Тука: кој било број).

Единица вектор, насочена по оската X, се означува јас, единица вектор, насочена по оската Y, се означува ј, А единица вектор, насочена по оската Z, се означува к. Вектори јас, ј, ксе нарекуваат орти– имаат единечни модули, т.е
i = 1, j = 1, k = 1

11 скаларен производ на вектори. Агол помеѓу вектори. Услов за векторска ортогоналност

Ова е број еднаков на производот од должините на овие вектори и косинусот на аголот меѓу нив.

Точка производ на вектори во однос на нивните координати

Точка производ на вектори X, Y, Z и:

каде е аголот помеѓу векторите и ; ако било, тогаш

Од дефиницијата на скаларниот производ следува дека каде, на пример, е големината на проекцијата на векторот на насоката на векторот.

Скаларен квадрат вектор:

Својства на производот со точки:

Агол помеѓу вектори

Услови за векторска ортогоналност.

Две вектора и б ортогонален (нормален), ако нивниот скаларен производ е еднаков на нула a· b= 0

Така во случајот проблем со авионотвектор

a= (a x ;a y )и b= (b x ;b y )

ортогонален ifa b= a x b x + a y b y = 0

12 векторски производ на вектори, неговите својства. Услов за колинеарност на вектори

Вкрстен производ на вектор и вектор е вектор означен со симбол и дефиниран со следните три услови:

1). Модулот на векторот е еднаков на , каде е аголот помеѓу векторите и ;

2). Векторот е нормален на секој од векторите и ;

3). Насоката на векторот одговара на „правилото на десната рака“. Ова значи дека ако векторите се доведени до заедничко потекло, тогаш векторот треба да биде насочен на ист начин како средниот прст на десната рака, чиј палец е насочен долж првиот фактор (т.е. долж вектор), а показалецот - по вториот (односно, по векторот). Векторскиот производ зависи од редоследот на факторите и тоа: .

Модул за вкрстени производи еднаква на површина S на паралелограм изграден на векторите и : .

Самиот векторски производ може да се изрази со формулата,

каде е единечниот вектор на векторскиот производ.

Вкрстениот производ исчезнува ако и само ако векторите и се колинеарни. Конкретно,.

Ако системот на координатни оски е правилен, а векторите и се наведени во овој систем со нивните координати:

тогаш векторскиот производ на вектор и вектор се одредува со формулата

Векторот е колинеарен со ненулта вектор ако и само ако координатите

векторите се пропорционални на соодветните координати на векторот, т.е.

Линеарни операциинад векторите специфицирани со нивните координати во просторот се изведуваат на сличен начин.

13 мешан производ на вектори. Неговите својства. Услов за компланарност на вектори

Мешан производ од три вектори, , се нарекува број еднаков на скаларен производвектор до вектор:

Својства на мешан производ:

3° Три вектори се компланарни ако и само ако

4° Тројка вектори е правилна ако и само ако . Ако , тогаш векторите , и формирајте ја левата тројка вектори.

10° Јакоби идентитет:

Ако векторите и се дадени со нивните координати, тогаш нивниот измешан производ се пресметува со формулата

Се нарекуваат вектори кои се паралелни на една рамнина или лежат на иста рамнина компланарни вектори.

Услови за компланарност на вектори

Три векторите се компланарниако нивниот измешан производ е нула.

Три векторите се компланарниако се линеарно зависни.

15 различни видови равенки на права и рамнини

Секоја права линија на рамнината може да се определи со равенка од прв ред

Секира + Ву + С = 0,

Покрај тоа, константите A и B не се еднакви на нула во исто време. Оваа равенка од прв ред се нарекува општа равенка на права линија.Во зависност од вредностите на константите A, B и C, можни се следните посебни случаи:

C = 0, A ≠0, B ≠ 0 - правата линија минува низ потеклото

A = 0, B ≠0, C ≠0 (By + C = 0) - права линија паралелна со оската Ox

B = 0, A ≠0, C ≠ 0 (Ax + C = 0) – права линија паралелна на оската Oy

B = C = 0, A ≠0 - правата линија се совпаѓа со оската Oy

A = C = 0, B ≠0 - правата линија се совпаѓа со оската Ox

Равенката на права линија може да се претстави во различни форми во зависност од дадените почетни услови.

Деф. 1.5.6. Косинуси за насокавектор А да ги наречеме косинусите на аглите што овој вектор ги формира со основните вектори, соодветно, јас , ј , к .

Косинуси на насока на вектор А = (X, на, z) се наоѓаат со формулите:

Збирот на квадратите на косинусите на насоката е еднаков на еден:

Косинуси на насока на вектор а се координатите на неговиот единичен вектор: .

Нека основните вектори јас , ј , к одложено од заедничка точка ЗА. Ќе претпоставиме дека ортите ги специфицираат позитивните насоки на оските О, О, Оз. Збир на точки ЗА (потекло) и ортонормална основа јас , ј , к повикани Декартов правоаголен координатен систем во вселената. Нека А– произволна точка во просторот. Вектор А = ОП= x јас + y ј + z к повикани вектор на радиуспоени А, координати на овој вектор ( x, y, z) се нарекуваат и точкести координати А(ознака: А(x, y, z)). Координатни оски О, О, Озисто така наречена, соодветно, оската апсциса, оска ординација, оска аплицираат.

Ако вектор е даден со координатите на неговата почетна точка ВО 1 (x 1 , y 1 , z 1) и крајна точка ВО 2 (x 2 , y 2 , z 2), тогаш координатите на векторот се еднакви на разликата помеѓу координатите на крајот и почетокот: (бидејќи ).

Декартови правоаголни координатни системи на рамнината и на линијатасе одредуваат на ист начин со соодветни квантитативни (во согласност со димензијата) промени.

Решавање на типични проблеми.

Пример 1.Најдете ја должината и насоката на косинусите на векторот А = 6јас – 2ј -3к .

Решение.Векторска должина: . Косинуси на насока: .

Пример 2.Најдете векторски координати А , формирајќи со координатни оскиеднакви остри агли ако должината на овој вектор е .

Решение.Бидејќи , потоа заменувајќи се во формулата (1.6), добиваме . Вектор А формира остри агли со координатните оски, па орт . Затоа, ги наоѓаме координатите на векторот .

Пример 3.Дадени се три некомпланарни вектори д 1 = 2јас – к , д 2 = 3јас + 3ј , д 3 = 2јас + 3к . Рашири го векторот г = јас + 5ј - 2к по основа д 1 , д 2 , д 3 .

ДЕФИНИЦИЈА

Векторсе нарекува подреден пар точки и (односно, точно се знае која од точките во овој пар е прва).

Првата точка се нарекува почеток на векторот, а вториот е негов крајот.

Растојанието помеѓу почетокот и крајот на векторот се нарекува должинаили векторски модул.

Се нарекува вектор чиј почеток и крај се совпаѓаат нулаи се означува со ; неговата должина се смета за нула. Во спротивно, ако должината на векторот е позитивна, тогаш се нарекува не-нула.

Коментар. Ако должината на векторот е еднаква на еден, тогаш тој се нарекува ортомили единица вектори е назначен .

ПРИМЕР

Вежбајте Проверете дали е вектор сингл.
Решение Да ја пресметаме должината на даден вектор, таа е еднаква на квадратниот корен од збирот на квадратите на координатите:

Бидејќи должината на векторот е еднаква на еден, тоа значи дека векторот е правоаголник.
Одговори Единица вектор.

Ненулта вектор може да се дефинира и како насочен сегмент.

Коментар. Насоката на векторот нула не е дефинирана.

Косинуси на насока на вектор

ДЕФИНИЦИЈА

Косинуси за насокана одреден вектор се нарекуваат косинуси на аглите што векторот ги формира со позитивните насоки на координатните оски.

Коментар. Насоката на векторот е уникатно одредена од неговите косинуси на насоката.

За да ги пронајдете косинусите на насоката на векторот, неопходно е да се нормализира векторот (односно, да се подели векторот по неговата должина):

Коментар. Координатите на единечниот вектор се еднакви на косинусите на неговата насока.

ТЕОРЕМА

(Својство на косинусите за насока). Збирот на квадратите на косинусите на насоката е еднаков на еден: