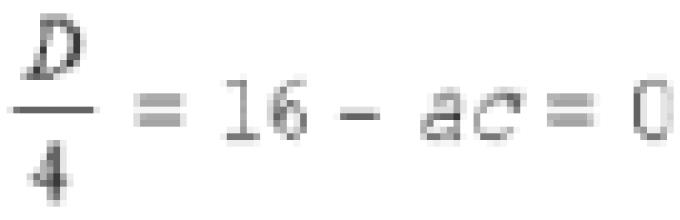Лекција: Како да се конструира парабола или квадратна функција?
ТЕОРЕТСКИ ДЕЛ
Парабола е график на функција опишана со формулата ax 2 +bx+c=0.
За да се конструира парабола треба да се следи едноставен алгоритамакции:
1) Формула за парабола y=ax 2 +bx+c,
Ако a>0тогаш се насочени гранките на параболата нагоре,
во спротивно гранките на параболата се насочени надолу.
Бесплатен член воваа точка ја пресекува параболата со оската OY;
2), се наоѓа со помош на формулата x=(-b)/2a, пронајденото x го заменуваме во равенката на параболата и наоѓаме y;
3)Функција нулиили, со други зборови, точките на пресек на параболата со оската OX, тие се нарекуваат и корени на равенката. За да ги најдеме корените, ја изедначуваме равенката со 0 секира 2 +bx+c=0;
Видови равенки:
а) Целосната квадратна равенка ја има формата секира 2 +bx+c=0а се решава од дискриминаторот;
б) Нецелосна квадратна равенка на формата секира 2 +bx=0.За да го решите, треба да го извадите x од заградите, а потоа да го изедначите секој фактор со 0:
секира 2 +bx=0,
x(ax+b)=0,
x=0 и ax+b=0;
в) Нецелосна квадратна равенка на формата секира 2 +c=0.За да го решите, треба да ги преместите непознатите на едната, а познатите на другата страна. x =±√(c/a);
4) Најдете неколку дополнителни точки за да ја конструирате функцијата.
ПРАКТИЧЕН ДЕЛ
И така, сега, користејќи пример, ќе анализираме сè чекор по чекор:
Пример #1:
y=x 2 +4x+3
c=3 значи параболата се сече на OY во точката x=0 y=3. Гранките на параболата се насочени нагоре бидејќи a=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4- 8+3=-1 теме е во точката (-2;-1)
Да ги најдеме корените на равенката x 2 +4x+3=0
Користејќи го дискриминантот ги наоѓаме корените
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x 1 =(-4+2)/2=-1
x 2 =(-4-2)/2=-3
Да земеме неколку произволни точки кои се наоѓаат во близина на темето x = -2
x -4 -3 -1 0
y 3 0 0 3
Заменете наместо x во равенката y=x 2 +4x+3 вредности
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Од вредностите на функцијата може да се види дека параболата е симетрична во однос на правата x = -2
Пример #2:
y=-x 2 +4x
c=0 значи параболата се сече на OY во точката x=0 y=0. Гранките на параболата гледаат надолу бидејќи a=-1 -1 Да ги најдеме корените на равенката -x 2 +4x=0
Непотполна квадратна равенка од формата ax 2 +bx=0. За да го решите, треба да го извадите x од заградите, а потоа да го изедначите секој фактор со 0.
x(-x+4)=0, x=0 и x=4.
Да земеме неколку произволни точки кои се наоѓаат во близина на темето x=2
x 0 1 3 4
y 0 3 3 0
Заменете наместо x во равенката y=-x 2 +4x вредности
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Од вредностите на функцијата може да се види дека параболата е симетрична во однос на правата линија x = 2
Пример бр. 3
y=x 2 -4
c=4 значи параболата се сече на OY во точката x=0 y=4. Гранките на параболата гледаат нагоре бидејќи a=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 темето е во точката (0;- 4 )
Да ги најдеме корените на равенката x 2 -4=0
Непотполна квадратна равенка од формата ax 2 +c=0. За да го решите, треба да ги преместите непознатите на едната, а познатите на другата страна. x =±√(c/a)
x 2 =4
x 1 =2
x 2 =-2
Да земеме неколку произволни точки кои се наоѓаат во близина на темето x=0
x -2 -1 1 2
y 0 -3 -3 0
Заменете наместо x во равенката y= x 2 -4 вредности
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Од вредностите на функцијата може да се види дека параболата е симетрична во однос на правата x=0
Претплатете се на каналот на YOUTUBEда бидете во тек со сите нови производи и да се подготвите кај нас за испити.
Воведни забелешки и едноставни примери
Пример 1. За кои вредности на a равенката ax 2 + 2x + 1 = 0 има два различни корени?
Решение.
Оваа равенка е квадратна во однос на променливата x за a№ 0 и има различни корени кога е дискриминаторски
т.е. за а< 1.
Дополнително, кога a = 0, се добива равенката 2x + 1 = 0, која има еден корен.
Така, O (– Ґ ; 0) И (0; 1).
Правило 1. Ако коефициентот x 2 на полином од втор степен содржи параметар, потребно е да се анализира случајот кога тој исчезнува.
Пример 2. Равенката ax 2 + 8x + c = 0 има единечен корен еднаков на 1. На што се еднакви a и c?
Решение. Да почнеме да ја решаваме задачата со специјалниот случај a = 0, равенката има форма 8x + c = 0. Оваа линеарна равенка има решение x 0 = 1 за c = – 8.
Кога бр. 0 квадратната равенка има еден корен ако ![]()
Покрај тоа, заменувајќи го коренот x 0 = 1 во равенката, добиваме + 8 + c = 0.
Решавање на системот од два линеарни равенки, наоѓаме a = c = – 4.
Теорема 1.
За намалениот квадратен трином y = x 2 + px + q (претпоставувајќи p 2і
4q)
збир на корени x 1 + x 2 = – p, производ на корени x 1 x 2 = q, разликата на корените е ![]()
а збирот на квадратите на корените x 1 2 + x 2 2 = p 2 – 2q.
Теорема 2.
За квадратен трином y = ax 2 + bx + c со два корени x 1 и x 2, имаме
проширување ax 2 + bx + c = a(x – x 1)(x – x 2), за трином со еден корен x 0 – проширување
секира 2 + bx + c = a(x – x 0) 2 .
Коментар. Често за квадратни равенкисо дискриминант еднаква на нула и има, соодветно, еден корен, се вели дека има два коинцидирачки корени (?). Ова е поврзано со факторизацијата на полиномот даден во теорема 2.(Точниот начин да се каже и разбере во овој случај е „еден корен од повеќе два.“ - Ед.)
Ќе обрнеме внимание на оваа суптилност и ќе го истакнеме случајот на еден корен на мноштво 2.
Пример 3. Во равенката x 2 + ax + 12 = 0, определи a на тој начин што разликата помеѓу корените на равенката е еднаква на еден.
Решение. Корена разлика ![]()
од каде a = ± 7.
Пример 4. За што а збирот на квадратите на корените на равенката 2x 2 + 4x + a = 0 е еднаков на 6?
Решение. Ајде да ја запишеме равенката во форма ![]()
од каде x 1 2 + x 2 2 = 4 – a = 6 и a = – 2.
Пример 5. За сите a, решете ја равенката ax 2 – 2x + 4 = 0.
Решение. Ако a = 0, тогаш x = 2. Ако a№
0, тогаш равенката станува квадратна. Тоа е дискриминаторски
еднакво на D = 4 – 16a. Ако Д< 0, т. е. a > ,
равенката нема решенија. Ако D = 0, т.е. a = ,
x = 4. Ако D > 0, т.е< ,
равенката има два корени![]()
Локација на корените на квадратниот трином
Графикот на квадратна равенка е парабола, а решенијата на квадратната равенка се апсцисите на точките на пресек на оваа парабола со оската Ox. Основата за решавање на сите проблеми во овој дел е да се проучат карактеристиките на локацијата на параболите со дадени својства на координатна рамнина.
Пример 6. За што а корените на равенката x 2 – 2ax + a 2 – a – 6 = 0 имаат различни знаци?
Решение (сл. 1).

Квадратната равенка или нема решенија (графикот е парабола од типот D), или има еден или два позитивни корени (парабола C), или има еден или два негативни корени (парабола А), или има корени со различни знаци (парабола Б).
Лесно е да се разбере дека последниот тип на параболи, за разлика од другите, се карактеризира со тоа што f(0)< 0. Таким образом, f(0) = a 2 – a – 6 < 0, откуда 0 < a < .
Ова решение овозможува генерализација, која ќе ја формулираме како следново правило.
Правило 2. Со цел за равенката ax 2 + bx + c = 0
имаше два различни корени x 1 и x 2 така што x 1< M < x 2 , необходимо и достаточно, чтобы a f(M) < 0.
Пример 7. За што a равенката x 2 – 2ax + a 2 – a – 6 = 0 има два различни корени со ист знак?
Решение. Ние сме заинтересирани за параболи од типот A и C (види Сл. 1). Тие се карактеризираат со тоа што
од каде O (– 6; – 2) И (3; + Ґ ).
Пример 8. За што a равенката x 2 – 2ax + a 2 – a – 6 = 0 има два различни позитивни корени?
Решение. Ние сме заинтересирани за параболите од типот C на сл. 1.
За равенката да има корени, бараме![]()
Бидејќи двата корени на равенката мора да бидат позитивни по услов, апсцисата на темето на параболата што лежи помеѓу корените е позитивна: x 0 = a > 0.
Теме ординати f(x 0)< 0 в силу того, что мы потребовали существование корней, поэтому если, кроме того, потребовать выполнение условия f(x 0) >0, тогаш, поради континуитетот на функцијата што се проучува, постои точка x 1ЗА (0; x 0) така што f(x 1) = 0. Очигледно, ова е помал корен од равенката.
Значи, f(0) = a 2 – a – 6 > 0, и, спојувајќи ги сите услови заедно, го добиваме системот
со растворот a O (3; + Ґ ).
Пример 9. За што a равенката x 2 – 2ax + a 2 – a – 6 има два различни негативни корени?
Решение. Проучувајќи ги параболите од типот А на Сл. 1, го добиваме системот
од каде О (– 6; – 2).
Да го генерализираме решението на претходните проблеми во форма на следново правило.
Правило 3. За да може равенката ax 2 + bx + c = 0 да има два различни корени x 1 и x 2, од кои секој е поголем (помал од) M, потребно е и доволно да
Пример 10. Функцијата f(x) е дадена со формулата
Најдете ги сите вредности на параметарот a за кои равенката f(x) = 0 има најмалку едно решение.
Решение. Сите можни решенија на дадена равенка се добиваат како решенија на квадратна равенка
x 2 – (4a + 14)x + 4a 2 + 33a + 59 = 0
со дополнителен услов барем еден (очигледно поголем) корен x 2јас а.
Секако, за равенката да има корени, таа мора да биде = – 5(a + 2) і
0,
од каде Ј – 2.
Графикот на левата страна на избраната равенка е парабола, чија апсциса на темето е x 0 = 2a + 7. Решението на проблемот е дадено со два вида параболи (сл. 2).
A: x 0 i a, од каде a i – 7. Во овој случај, поголемиот корен на полиномот е x 2јас х 0 и а.
Б: x 0< a, f(a)
Ј
0, од каде  .
.
И во овој случај, поголемиот корен на полиномот е x 2јас а.
Конечно  .
.
Три решенија за една неравенка
Пример 11. Најдете ги сите вредности на параметарот a за кои неравенството x 2 – 2ax + a 2 + 2a – 3 > 0
извршено:
1) за сите вредности на x;
2) пред сите позитивни вредности x;
3) за сите вредности на xО [– 1; 1].
Решение.
Првиот начин.
1) Очигледно, оваа нееднаквост важи за сите x кога дискриминаторот е негативен, т.е.
= a 2 – (a 2 + 2a – 3) = – 2a + 3< 0,
од каде а >.
2) За подобро да разбереме што се бара во изјавата за проблемот, ајде да користиме едноставна техника: нацртајте неколку параболи на координатната рамнина, а потоа земете ја и затворете ја левата полурамнина во однос на оската Oy. Делот од параболата што останува видлив мора да биде над оската Ox.
Состојбата на проблемот е задоволена во два случаи (види Сл. 3):
< 0, откуда a > ;
Б: двата корени (можеби еден, но двојно) од равенката x 2 – 2ax + a 2 + 2a – 3 = 0 се лево од потеклото. Според правилото 3, овој услов е еквивалентен на системот на неравенки Ді 0, x 0 Ј 0 и f(0) і 0.
Меѓутоа, при решавање на овој систем, првата неравенка може да се испушти, бидејќи дури и ако некоја вредност a не го задоволува условот Dі 0, тогаш автоматски паѓа во решението на точката А. Така, го решаваме системот
од каде Ј – 3.
Со комбинирање на решенијата на точките А и Б, добиваме
одговор: ![]()
3) Состојбата на проблемот е задоволена во три случаи (види слика 4):
A: графикот на функцијата y = x 2 – 2ax + a 2 + 2a – 3 лежи над оската Ox, т.е.< 0, откуда a > ;
Б: двата корени (можеби еден од повеќекратните 2) на равенката x 2 – 2ax + a 2 + 2a – 3 = 0 се лево од – 1. Овој услов е еквивалентен, како што знаеме од правилото 3, на системот на неравенки Ді 0, x 0< – 1, f(– 1) > 0;
C: двата корени на равенката x 2 – 2ax + a 2 + 2a – 3 = 0 се десно од 1.
Оваа состојба е еквивалентна на Д i 0, x 0 > 1, f(1) > 0.
Меѓутоа, во точките Б и В, како и при решавањето на претходниот проблем, нееднаквоста поврзана со дискриминаторот може да се изостави.
Според тоа, добиваме два системи на неравенки
Откако ги разгледавме сите случаи, го добиваме резултатот: a >
во точка
во Ц.
Одговорот на проблемот е соединувањето на овие три множества.
Втор начин. За да бидат исполнети условите на секоја од трите точки од задачата, најмала вредностфункции
y = x 2 – 2ax + a 2 + 2a – 3 на секој од соодветните интервали мора да биде позитивен.
1) Темето на параболата y = x 2 – 2ax + a 2 + 2a – 3 е во точката (a; 2a – 3), затоа најмалата вредност на функцијата на целата бројна права е 2a – 3, и a > .
2) на полуоската x i 0 најмалата вредност на функцијата е f(0) = a 2 + 2a – 3, ако a< 0, и f(a) = 2a – 3, если a
і
0. Анализирајќи ги двата случаи, добиваме ![]()
3) Најмалата на сегментот [– 1; 1] вредноста на функцијата е
Бидејќи најмалата вредност мора да биде позитивна, добиваме системи на неравенки
Решението за овие три системи е множество
Трет начин. 1) Теме на параболата y = x 2 – 2ax + a 2 + 2a – 3
се наоѓа во точката (а; 2а – 3).
Да нацртаме множество на координатната рамнина што е формирана од темињата на сите параболи за различни a (сл. 5). Ова е правата y = 2x – 3. Да потсетиме дека секоја точка на оваа права има своја вредност на параметарот, а од секоја точка на оваа права „излегува парабола“, што одговарададена вредност
2) Решенијата на оваа точка се сите решенија на првата точка и, покрај тоа, параболите за кои a се негативни, а f(0) = a 2 + 2a – 3і 0.
3) Од Сл. 5 јасно е дека ние сме заинтересирани за параболи за кои или a е негативен и f(– 1) = a 2 + 4a – 2 > 0,
или a е позитивен и f(1) = a 2 – 2 > 0.
Равенки и неравенки кои се сведуваат на квадратни
Пример 12. За кои вредности на a нема решенија равенката 2x 4 – 2ax 2 + a 2 – 2 = 0?
Решение. Правејќи ја замената y = x 2, ја добиваме квадратната равенка f(y) = 2y 2 – 2ay + a 2 – 2 = 0.
Добиената равенка нема решение кога Д< 0. Кроме того, первоначальное уравнение не имеет решений, когда корни уравнения f(y) = 0 отрицательны.
Овие услови може да се напишат како збир
каде ![]()
Пример 13. За секоја вредност на параметарот a да се реши равенката cos x sin 2x = asin 3x.
Решение. Бидејќи 2cos x sin 2x = sin x + sin 3x и sin 3x = 3sin x – 4sin 3 x,
тогаш равенката ќе се запише како sin x (sin 2 x (4a – 2) – (3a – 2)) = 0.
Од тука добиваме решенија x = p n, n О Z за било кој а. ![]()
Равенка 
има решенија ![]()
не се совпаѓа со решенијата од првата равенка, само под условот
Последните ограничувања се еквивалентни Одговор: x = p n, n О
Z за кое било a; Освен тоа,
Пример 14. Најдете ги сите вредности на параметарот a, од кои секоја неравенка
a 2 + 2a – sin 2 x – 2acos x > 2 важи за кој било број x.
Решение. Да ја трансформираме неравенката во формата cos 2 x – 2acos x + a 2 + 2a – 3 > 0
и направете замена t = cos x.
Важно е да се забележи дека параметарот t се движи од – 1 до 1, така што проблемот може да се преформулира на следниов начин: најдете ги сите такви штоЗА t 2 – 2at + a 2 + 2a – 3 > 0
важи за сите т
[– 1; 1]. Овој проблем веќе го решивме порано.
Пример 15. Определете на кои вредности на равенката log 3 (9 x + 9a 3) = x има решенија и пронајдете ги.
Решение. Да ја трансформираме равенката во форма 9 x – 3 x + 9a 3 = 0
и, правејќи ја замената y = 3 x, добиваме y 2 – y + 9a 3 = 0.
Ако дискриминаторот е негативен, равенката нема решенија. Кога дискриминаторот
D = 1 – 36a 3 = 0, равенката има еден корен,  ,
,
и x = – log 3 2. Конечно, кога дискриминаторот е позитивен, т.е.
првобитната равенка има еден корен ![]() .
.
и ако, дополнително, изразот 1 е позитивен, 
![]() ,
,
тогаш равенката има и втор корен
Значи, конечно добиваме нема решенија за останатите а.Пример 16. За секоја вредност на параметарот a, реши
равенка на гревот
4 x + cos 4 x + sin 2 x + a = 0.
Решение. БидејќиДа ја преработиме равенката во форма sin 2 x – 2sin x – 2a – 2 = 0.
Графикот на функцијата од левата страна на равенката е парабола со теме чија апсциса е y 0 = 1; вредноста на функцијата во точката y = – 1 е 1 – 2a; дискриминантата на равенката е 8a + 12. Тоа значи дека поголемиот корен y 2 од равенката y 2 – 2y – 2a – 2 = 0, дури и да постои, е поголем од 1, а соодветната равенка sin 2x = y 2 нема решенија. 3. За кои вредности на a равенката 2x 2 + (3a + 1)x + a 2 + a + 2 = 0 има барем еден корен?
4. Равенката ax 2 + bx + 5 = 0 има единечен корен еднаков на 1. На што се еднакви a и b?
5. За кои вредности на параметарот a се поврзани корените на квадратната равенка 5x 2 – 7x + a = 0 како 2 до 5?
6. Во равенката ax 2 + 8x + 3 = 0, определи a така што разликата помеѓу корените на равенката е еднаква на еден.
7. За колку a збирот на квадратите на корените на равенката x 2 – 2ax + 2(a + 1) = 0 е еднаков на 20?
8. За кои b и c равенката c + bx – 2x 2 = 0 има еден позитивен и еден негативен корен?
9. Најдете ги сите вредности на параметарот a за кои едниот корен од равенката x 2 – (a + 1)x + 2 = 0 е поголем од a, а другиот е помал од a.
10. Најдете ги сите вредности на параметарот a за кои равенката x 2 + (a + 1)x + 2 = 0 има два различни корени од ист знак.
11. За кои вредности на a се сите добиени корени од равенката (a – 3)x 2 – 2ax + 6a = 0 позитивни?
12. За што a се сите добиени корени од равенката (1 + a)x 2 – 3ax + 4a = 0 поголеми од 1?
13. Најдете ги сите вредности на параметарот a за кои двата различни корени на равенката x 2 + x + a = 0 се поголеми од a.
14. За кои вредности на a се содржани двата корени на равенката 4x 2 – 2x + a = 0 помеѓу – 1 и 1?
15. За кои вредности на a равенката x 2 + 2(a – 1)x + a + 5 = 0 има барем еден позитивен корен?
16. Функцијата f(x) е дадена со формулата
Најдете ги сите вредности на параметарот a за кои равенката f(x) = 0 има барем едно решение.
17. За колку a е неравенството (a 2 – 1)x 2 + 2(a – 1)x + 2 > 0 точно за сите x?
18. За кои вредности на параметарот a важи неравенката ax 2 + 2x > 1 – 3a за сите позитивни x?
19. За кои вредности на a нема решенија равенката x 4 + (1 – 2a)x 2 + a 2 – 1 = 0?
20. За кои вредности на параметарот a равенката 2x 4 – 2ax 2 + a2 – 2 = 0 има едно или две решенија?
21. За секоја вредност на a, решете ја равенката acos x cos 2x = cos 3x.
22. Најдете ги сите вредности на параметарот a, за секоја од нив неравенката cos 2 x + 2asin x – 2a< a 2
– 4 выполняется для любого числа x.
23. За сите a, решете ја равенката log 2 (4 x + a) = x.
24. За секоја вредност на параметарот a, решете ја равенката sin 2 x + asin 2 2x = sin.
График на квадратен трином
2019-04-19
Квадратен трином
Целиот трином го нарековме квадратен трином рационална функцијавтор степен:
$y = ax^2 + bx + c$, (1)
каде $a \nq 0$. Да докажеме дека графикот на квадратен трином е парабола добиена со паралелни поместувања (во насоки координатни оски) од параболата $y = ax^2$. За да го направите ова, го презентираме изразот (1) користејќи едноставни идентитетски трансформациина ум
$y = a(x + \алфа)^2 + \бета$. (2)
Соодветните трансформации, напишани подолу, се познати како „точна екстракција на квадрат“:
$y = x^2 + bx + c = a \лево (x^2 + \frac(b)(a) x \десно) + c = a \лево (x^2 + \frac(b)(a) x + \frac (b^2)(4a^2) \десно) - \frac (b^2)(4a) + c = a \лево (x + \frac(b)(2a) \десно)^2 - \frac (b^2 - 4ac) (4a)$. (2")
Квадратниот трином го намаливме на форма (2); во исто време
$\alpha = \frac(b)(2a), \beta = - \frac (b^2 - 4ac)(4a)$
(овие изрази не треба да се меморираат; попогодно е секој пат директно да се трансформира триномот (1) во форма (2).
Сега е јасно дека графикот на триномот (1) е парабола еднаква на параболата $y = ax^2$ и се добива со поместување на параболата $y = ax^2$ во насоките на координатните оски за $\ alpha$ и $\beta$ (земајќи го предвид знакот $\alpha$ и $\beta$), соодветно. Темето на оваа парабола се наоѓа во точката $(- \alpha, \beta)$, нејзината оска е права линија $x = - \alpha$. За $a > 0$ темето е најниска точкапараболи, за $a
Сега да спроведеме студија за квадратниот трином, т.е., ќе ги дознаеме неговите својства во зависност од нумеричките вредности на коефициентите $a, b, c$ во неговиот израз (1).
Дозволете ни да ја означиме вредноста $b^2- 4ac$ во еднаквост (2") со $d$:
$y = a \лево (x + \frac(b)(2a) \десно)^2 - \frac(d)(4a)$; (4)
$d = b^2 - 4ac$ се нарекува дискриминант на квадратен трином. Својствата на триномот (1) (и локацијата на неговиот график) се одредуваат со знаците на дискриминантната $d$ и водечкиот коефициент $a$.

1) $a > 0, d 0$; бидејќи $a > 0$, тогаш графикот се наоѓа над темето $O^( \prime)$; лежи во горната полурамнина ($y > 0$ - Сл. а.).
2) $a
3) $a > 0, d > 0$. Темето $O^( \prime)$ лежи под оската $Ox$, параболата ја пресекува оската $Ox$ на две точки $x_1, x_2$ (сл. в.).
4) 0 долари. Темето $O^( \prime)$ лежи над оската $Ox$, параболата повторно ја пресекува оската $Ox$ на две точки $x_1, x_2$ (сл. г).
5) $a > 0, d = 0$. Темето лежи на самата оска $Ox$, параболата се наоѓа во горната полурамнина (сл. д).
6) $a
Заклучоци. Ако $d 0$), или пониско (ако $a
Ако $d > 0$, тогаш функцијата е наизменично (графикот делумно лежи под и делумно над оската $Ox$). Квадратен трином со $d > 0$ има два корени (нули) $x_1, x_2$. За $a > 0$ тоа е негативно во интервалот помеѓу корените (сл. в) и позитивно надвор од овој интервал. На $ a
Дефиниција
Параболасе нарекува график на квадратна функција $y = ax^(2) + bx + c$, каде што $a \neq 0$.
График на функцијата $y = x^2$.
За шематски исцртување на графикот на функцијата $y = x^2$, ќе најдеме неколку точки кои ја задоволуваат оваа еднаквост. За погодност, ги запишуваме координатите на овие точки во форма на табела:
График на функцијата $y = ax^2$.
Ако коефициентот $a > 0$, тогаш графикот $y = ax^2$ се добива од графиконот $y = x^2$ или со вертикално истегнување (за $a > 1$) или со компресија на $x$ оска (за $0< a < 1$). Изобразим для примера графики $y = 2x^2$ и $y = \dfrac{x^2}{2}$:
| $y = 2x^2$ | $y = \dfrac(x^2)(2)$ |
|
|
Ако $a< 0$, то график функции $y = ax^2$ можно получить из графика $y = |a|x^2$, отразив его симметрично относительно оси $x$. Построим графики функций $y = - x^2$, $y = -2x^2$ и $y = - \dfrac{x^2}{2}$:
| $y = - x^2$ | $y = -2x^2$ | $y = - \dfrac(x^2)(2)$ |
|
|
|
График на квадратна функција.
За да ја графирате функцијата $y = ax^2 + bx + c$, треба да го изолирате $ax^2 + bx + c$ од квадратниот трином совршен квадрат, односно претстави го во форма $a(x - x_0)^2 + y_0$. Графикот на функцијата $y = a(x - x_0)^2 + y_0$ се добива од соодветниот графикон $y = ax^2$ со поместување за $x_0$ по оската $x$ и за $y_0$ долж оската $y$. Како резултат на тоа, точката $(0;0)$ ќе се премести во точката $(x_0;y_0)$.
Дефиниција
Врвотпараболата $y = a(x - x_0)^2 + y_0$ е точката со координати $(x_0;y_0)$.
Ајде да конструираме парабола $y = 2x^2 - 4x - 6$. Со избирање на целосниот квадрат, добиваме $y = 2(x - 1)^2 - 8$.
| Ајде да зацртаме $y = 2x^2$ | Да го преместиме надесно за 1 | И надолу за 8 |
|
|
|
Резултатот е парабола со нејзиното теме во точката $(1;-8)$.
Графикот на квадратната функција $y = ax^2 + bx + c$ ја пресекува оската $y$ во точката $(0; c)$ и оската $x$ во точките $(x_(1,2) ;0)$, каде што $ x_(1,2)$ се корените на квадратната равенка $ax^2 + bx + c = 0$ (и ако равенката нема корени, тогаш соодветната парабола не го пресекува $ x$ оска).
На пример, параболата $y = 2x^2 - 4x - 6$ ги пресекува оските во точките $(0; -6)$, $(-1; 0)$ и $(3; 0)$.