Zasada najmniejszego działania. Zasada najmniejszego działania Zasada najmniejszego działania w fizyce

Kiedy byłem w szkole, nasz nauczyciel fizyki, Bader, zawołał mnie kiedyś po zajęciach i powiedział: „Wyglądasz, jakbyś był strasznie zmęczony wszystkim; posłuchaj jednej ciekawej rzeczy.” I powiedział mi coś, co wydało mi się naprawdę fascynujące. Nawet teraz, choć minęło już sporo czasu, nadal mnie to fascynuje. I za każdym razem, gdy przypominam sobie, co powiedziałem, wracam do pracy. I tym razem, przygotowując się do wykładu, ponownie analizowałem te same rzeczy. I zamiast przygotowywać się do wykładu, podjąłem się nowego problemu. Temat o którym mówię to zasada najmniejszego działania.

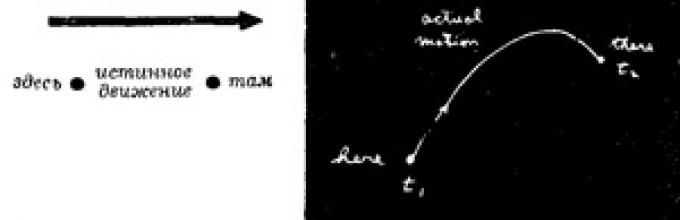
„Tak mi wtedy powiedział mój nauczyciel Bader: «Załóżmy, że masz cząstkę w polu grawitacyjnym; ta cząstka, wychodząc skądś, swobodnie przemieszcza się gdzie indziej do innego punktu. Rzuciłeś go, powiedzmy, w górę, a on poleciał w górę, a potem spadł.

Podróż z miejsca początkowego do końcowego zajęła jej trochę czasu. Teraz spróbuj innego ruchu. Niech porusza się „stąd tu” już nie jak wcześniej, ale w ten sposób:

Ale i tak znalazłem się we właściwym miejscu, w tym samym momencie co wcześniej.”

„I tak” – kontynuował nauczyciel – „jeśli obliczysz energię kinetyczną w każdym momencie drogi cząstki, odejmiesz od niej energię potencjalną i całkujesz różnicę przez cały czas, w którym nastąpił ruch, zobaczysz że numer, który otrzymasz, będzie więcej, niż w przypadku prawdziwego ruchu cząstek.

Innymi słowy, prawa Newtona można sformułować nie jako F=ma, ale w następujący sposób: średnia energia kinetyczna minus średnia energia potencjalna osiąga najniższą wartość na trajektorii, po której obiekt faktycznie przemieszcza się z jednego miejsca do drugiego.

Spróbuję ci to wyjaśnić nieco jaśniej.
Jeśli weźmiemy pole grawitacyjne i wyznaczymy trajektorię cząstki X(T), Gdzie X- wysokość nad ziemią (pomińmy na razie jeden wymiar; niech trajektoria przebiega tylko w górę i w dół, a nie na boki), wówczas energia kinetyczna będzie wynosić y 2 M(dx/ dt) 2 , a energia potencjalna w dowolnym momencie będzie równa mgx.

Teraz przez pewien moment ruchu po trajektorii biorę różnicę pomiędzy energią kinetyczną i potencjalną i całkuję po całym czasie od początku do końca. Niech w początkowej chwili czasu tx ruch rozpoczął się na pewnej wysokości i zakończył w tej chwili T 2 na innej określonej wysokości.

Wtedy całka jest równa ∫ t2 t1 dt

Prawdziwy ruch odbywa się po określonej krzywej (w funkcji czasu jest to parabola) i prowadzi do pewnej wartości całkowej. Ale ty możesz zanimumieścić wyobraźcie sobie inny ruch: najpierw gwałtowny wzrost, a potem dziwne wahania.

Możesz obliczyć różnicę między energią potencjalną i kinetyczną na tej ścieżce... lub na dowolnej innej. A najbardziej zdumiewające jest to, że prawdziwą ścieżką jest ta, wzdłuż której ta całka jest najmniejsza.
Sprawdźmy to. Najpierw spójrzmy na ten przypadek: cząstka swobodna nie ma w ogóle energii potencjalnej. Wtedy reguła mówi, że przy przechodzeniu z jednego punktu do drugiego w danym czasie całka energii kinetycznej powinna być jak najmniejsza. Oznacza to, że cząstka musi poruszać się równomiernie. (I to prawda, ty i ja wiemy, że prędkość takiego ruchu jest stała.) Dlaczego równomiernie? Rozwiążmy to. Gdyby było inaczej, to czasem prędkość cząstki byłaby większa od średniej, czasem niższa od niej, a średnia prędkość byłaby taka sama, bo cząstka musiałaby dostać się „stąd tu” w uzgodniony termin. Przykładowo, jeśli musisz dojechać samochodem z domu do szkoły w określonym czasie, możesz to zrobić na różne sposoby: możesz początkowo jechać jak szalony, a na koniec zwolnić, lub jechać z tą samą prędkością, albo możesz nawet udać się na drugą stronę, a dopiero potem skręcić w stronę szkoły itp. We wszystkich przypadkach średnia prędkość oczywiście powinna być taka sama - iloraz odległości z domu do szkoły podzielonej przez czas. Ale nawet przy tej średniej prędkości czasami poruszałeś się za szybko, a czasami za wolno. I przeciętnie kwadrat coś odbiegającego od średniej jest, jak wiemy, zawsze większe od kwadratu średniej; Oznacza to, że całka energii kinetycznej podczas wahań prędkości ruchu będzie zawsze większa niż podczas poruszania się ze stałą prędkością. Widzisz, że całka osiągnie minimum, gdy prędkość jest stała (przy braku sił). Właściwy sposób jest taki.

Obiekt wyrzucony w górę w polu grawitacyjnym wznosi się początkowo szybko, a potem coraz wolniej. Dzieje się tak, ponieważ ma on również energię potencjalną, a jej minimalna wartość powinna osiągnąć razness pomiędzy energią kinetyczną i potencjalną. Ponieważ energia potencjalna rośnie wraz ze wzrostem, to jest mniejsza różnica To zadziała, jeśli najszybciej jak to możliwe osiągniesz te wysokości, gdzie energia potencjalna jest wysoka. Następnie odejmując ten wysoki potencjał od energii kinetycznej, uzyskujemy spadek średniej. Zatem ścieżka prowadząca w górę i dostarczająca dobry kawałek ujemny kosztem energii potencjalnej jest bardziej opłacalna.

To wszystko, co powiedział mi mój nauczyciel, ponieważ był bardzo dobrym nauczycielem i wiedział, kiedy należy przestać. Ja sam niestety taki nie jestem. Trudno mi zatrzymać się na czas. I tak zamiast tylko zaciekawić moją historią, chcę Cię zastraszyć, chcę, żebyś miał dość złożoności życia – postaram się udowodnić to, o czym Ci mówiłem. Problem matematyczny, który rozwiążemy, jest bardzo trudny i wyjątkowy. Jest pewna ilość S, zwany działanie. Jest równa energii kinetycznej minus energia potencjalna zintegrowana w czasie:

Ale z drugiej strony nie można poruszać się zbyt szybko ani wznosić się zbyt wysoko, ponieważ wymagałoby to zbyt dużej energii kinetycznej. Musisz poruszać się wystarczająco szybko, aby wstać i zejść w wyznaczonym czasie. Nie powinieneś więc próbować latać zbyt wysoko, ale po prostu osiągnąć jakiś rozsądny poziom. W rezultacie okazuje się, że rozwiązaniem jest swego rodzaju równowaga pomiędzy chęcią uzyskania jak największej energii potencjalnej a chęcią maksymalnego zmniejszenia ilości energii kinetycznej – jest to chęć osiągnięcia maksymalnej redukcji różnicy między energią kinetyczną i potencjalną.”

Nie zapomnij o tym p.e. i k.e – obie funkcje czasu. Dla każdej nowej możliwej ścieżki działanie to nabiera specyficznego znaczenia. Problem matematyczny polega na określeniu, która krzywa ma tę liczbę mniejszą niż pozostałe.

Mówicie: „Och, to tylko prosty przykład maksimum i minimum. Musimy obliczyć działanie, rozróżnić je i znaleźć minimum.

Ale poczekaj. Zwykle mamy funkcję jakiejś zmiennej i musimy znaleźć jej wartość zmienny, przy którym funkcja staje się najmniejsza lub największa. Załóżmy, że w środku znajduje się pręt nagrzany. Rozchodzi się po nim ciepło i w każdym punkcie pręta ustala się jego własna temperatura. Musisz znaleźć punkt, w którym jest najwyższy. Ale mówimy o czymś zupełnie innym - każdą ścieżkę w przestrzeni odpowiada na jego numer i ma znaleźć ten numer ścieżka, dla których liczba ta jest minimalna. To zupełnie inny obszar matematyki. To nie jest zwykły rachunek, ale wariacyjny(tak go nazywają).

Ta dziedzina matematyki ma wiele własnych problemów. Powiedzmy, że okrąg jest zwykle definiowany jako zbiór punktów, których odległości od danego punktu są takie same, ale okrąg można zdefiniować inaczej: jest to jedna z krzywych podana długość, który obejmuje największy obszar. Każda inna krzywa o tym samym obwodzie obejmuje obszar mniejszy niż okrąg. Jeśli więc postawimy sobie zadanie: znaleźć krzywą danego obwodu ograniczającą największy obszar, to będziemy mieli problem z rachunku wariacyjnego, a nie z rachunku różniczkowego, do którego jesteś przyzwyczajony.

Chcemy więc przyjąć całkę po drodze przebytej przez ciało. Zróbmy to w ten sposób. Chodzi o to, aby wyobrazić sobie, że istnieje prawdziwa ścieżka i że jakakolwiek inna krzywa, którą narysujemy, nie jest rzeczywistą ścieżką, więc jeśli obliczymy dla niej działanie, otrzymamy liczbę wyższą niż ta, którą otrzymamy dla odpowiadającego działania w prawdziwy sposób.

Zadanie polega więc na odnalezieniu prawdziwej ścieżki. Gdzie to leży? Jednym ze sposobów byłoby oczywiście policzenie działań dla milionów ścieżek i sprawdzenie, na której ścieżce występuje najmniejsze działanie. To ścieżka, na której akcja jest minimalna i będzie prawdziwa.

Ta metoda jest całkiem możliwa. Można to jednak zrobić prościej. Jeśli istnieje wielkość, która ma minimum (ze zwykłych funkcji, powiedzmy, temperaturę), to jedną z właściwości minimum jest to, że podczas oddalania się od niego na odległość Pierwszy rzędu wielkości funkcja odbiega od wartości minimalnej jedynie o kwotę drugi zamówienie. Natomiast w dowolnym innym miejscu krzywej przesunięcie o małą odległość powoduje zmianę wartości funkcji także o wartość pierwszego rzędu małości. Ale przynajmniej niewielkie odchylenia na bok nie prowadzą do zmiany funkcji w pierwszym przybliżeniu.

To właśnie ta właściwość zostanie wykorzystana do obliczenia rzeczywistej ścieżki.

Jeśli ścieżka jest poprawna, to krzywa nieco od niej odmienna nie doprowadzi w pierwszym przybliżeniu do zmiany wielkości działania. Wszelkie zmiany, jeśli rzeczywiście było to minimum, pojawią się dopiero w drugim przybliżeniu.

Łatwo to udowodnić. Jeżeli przy pewnym odchyleniu od krzywej zmiany zachodzą w pierwszej kolejności, to zmiany te obowiązują proporcjonalny odchylenie. Prawdopodobnie wzmocnią efekt; w przeciwnym razie nie byłoby to minimum. Ale kiedy już zmiany proporcjonalny odchylenie, wówczas zmiana znaku odchylenia zmniejszy działanie. Okazuje się, że przy odchyleniu w jednym kierunku efekt wzrasta, a przy odchyleniu w przeciwnym kierunku maleje. Jedyną możliwością, aby było to naprawdę minimum, jest to, że w pierwszym przybliżeniu nie zachodzą żadne zmiany, a zmiany są proporcjonalne do kwadratu odchylenia od rzeczywistej ścieżki.

Pójdziemy więc następującą ścieżką: oznacz przez X(T) (z linią poniżej) prawdziwą ścieżką jest ta, którą chcemy znaleźć. Zróbmy próbę X(T), różni się od pożądanej niewielką ilością, którą oznaczamy η (T).

Pomysł jest taki, że jeśli policzymy akcję S w drodze X(T), wtedy różnica między tym S oraz przez działanie obliczone dla ścieżki X(T) (dla uproszczenia zostanie oznaczony S), lub różnica pomiędzy S_ I S, powinno być pierwszym przybliżeniem η zero. Mogą się różnić w drugim rzędzie, ale w pierwszym różnica musi wynosić zero.

I tego należy przestrzegać dla wszystkich η . Jednak nie do końca dla każdego. Metoda wymaga uwzględnienia tylko tych ścieżek, których wszystkie zaczynają się i kończą w tej samej parze punktów, tzn. każda ścieżka musi zaczynać się w określonym punkcie w czasie T 1 i zakończyć w innym konkretnym momencie w tej chwili T 2 . Te punkty i momenty są rejestrowane. Zatem nasza funkcja d) (odchylenie) musi wynosić zero na obu końcach: η (T 1 )= 0 I η (t2)=0. Pod tym warunkiem nasz problem matematyczny zostaje całkowicie zdefiniowany.

Jeśli nie znasz rachunku różniczkowego, możesz zrobić to samo, aby znaleźć minimum zwykłej funkcji F(X). Czy pomyślałbyś o tym, co by się stało, gdybyś wziął F(X) i dodaj do X mała ilość H, i twierdzi, że poprawka do ust F(X) w pierwszej kolejności H powinna wynosić co najmniej zero. Ustawiłbyś mnie? x+H zamiast X i rozwinie j(x+h) do pierwszej potęgi H. . jednym słowem powtórzylibyśmy wszystko z czym mamy zamiar zrobić η .

Jeśli teraz przyjrzymy się temu uważnie, zobaczymy, że pierwsze dwa zapisane tutaj terminy odpowiadają temu działaniu S, co bym napisał dla poszukiwanej prawdziwej ścieżki X. Chcę skupić Twoją uwagę na zmianie. S, czyli o różnicy pomiędzy S a więc S_, co doprowadziłoby do prawdziwej ścieżki. Zapiszemy tę różnicę jako bS i nazwijmy to odmianą S. Pomijając „rzędy drugie i wyższe”, otrzymujemy dla σS

Teraz zadanie wygląda tak. Tutaj przede mną jest pewna integralność. Jeszcze nie wiem, jak to jest, ale wiem na pewno, że co η Bez względu na wszystko, ta całka musi być równa zeru. „No cóż”, możesz pomyśleć, „jedynym sposobem, aby tak się stało, jest zastosowanie mnożnika η była równa zeru.” Ale co z pierwszym terminem, jeśli istnieje D η / dt? Mówisz: „Jeśli η zamienia się w nic, to jego pochodną jest to samo nic; oznacza to współczynnik przy dw\/ dt musi również wynosić zero.” Cóż, to nie do końca prawda. Nie jest to do końca prawdą, ponieważ pomiędzy odchyleniami η i jego pochodna jest połączeniem; nie są całkowicie niezależne, ponieważ η (T) musi wynosić zero i t 1 i o godz T 2 .

Rozwiązując wszystkie problemy rachunku wariacyjnego, zawsze stosuje się tę samą ogólną zasadę. Lekko przesuwasz to, co chcesz zmienić (podobnie do tego, co zrobiliśmy, dodając η ), spójrz na terminy pierwszego rzędu, Następnie ułóż wszystko tak, aby otrzymać całkę w postaci: „przesunięcie (η ), pomnożona przez to, co się okaże”, ale tak, aby nie zawierała żadnych pochodnych η (NIE D η / dt). Koniecznie trzeba wszystko przemienić, żeby pozostało „coś” pomnożone przez η . Teraz zrozumiesz, dlaczego jest to tak ważne. (Istnieją wzory, które podpowiedzą, jak w niektórych przypadkach można to zrobić bez żadnych obliczeń, ale nie są one na tyle ogólne, aby warto je zapamiętać; najlepiej wykonywać obliczenia w nasz sposób.)

Jak mogę przerobić penisa D η / dt, tak, żeby się pojawiło η ? Mogę to osiągnąć, integrując kawałek po kawałku. Okazuje się, że w rachunku wariacyjnym cała sztuka polega na opisaniu wariacji S a następnie całkuj przez części tak, aby pochodne η zniknął. We wszystkich zadaniach, w których pojawiają się pochodne, stosuje się tę samą sztuczkę.

Przypomnijmy ogólną zasadę całkowania przez części. Jeśli masz dowolną funkcję f pomnożoną przez D η / dt i zintegrowane z T, następnie piszesz pochodną η /T

Granice całkowania należy podstawić do pierwszego członu t 1 I T 2 . Wtedy pod całką otrzymam wyraz z całkowania przez części i ostatni wyraz, który podczas przekształcenia pozostaje niezmieniony.
A teraz dzieje się to, co zawsze się dzieje – zintegrowana część znika. (A jeśli nie zniknie, to należy tę zasadę przeformułować, dodając warunki, które zapewnią takie zniknięcie!) To już powiedzieliśmy η na końcach ścieżki musi wynosić zero. W końcu jaka jest nasza zasada? Faktem jest, że działanie jest minimalne pod warunkiem, że urozmaicona krzywa zaczyna się i kończy w wybranych punktach. To znaczy, że η (t 1)=0 i η (t2)=0. Zatem człon zintegrowany okazuje się wynosić zero. Zbieramy resztę członków i piszemy

Zmiana S uzyskał teraz taką formę, jaką chcieliśmy mu nadać: coś jest w nawiasie (oznaczmy to F), i to wszystko jest mnożone η (T) i zintegrowane z t t zanim T 2 .
Okazało się, że całka jakiegoś wyrażenia pomnożona przez η (T), zawsze równe zeru:

Czy jest jakaś funkcja z T; Mnożę to przez η (T) i zintegrować go od początku do końca. I cokolwiek to jest η, Dostaję zero. Oznacza to, że funkcja F(T) równy zeru. Ogólnie rzecz biorąc, jest to oczywiste, ale na wszelki wypadek pokażę Ci jeden sposób, aby to udowodnić.

Niech jako η (T) Wybiorę coś, co jest równe zeru wszędzie i dla wszystkich T, z wyjątkiem jednej wstępnie wybranej wartości T. Pozostaje zero, dopóki tam nie dotrę T, S Potem na chwilę podskakuje i natychmiast opada. Jeśli weźmiesz całkę z tego m) pomnożoną przez jakąś funkcję F, jedyne miejsce, w którym otrzymasz coś niezerowego, to gdzie η (T) podskoczył; i otrzymasz wartość F w tym momencie całka po skoku. Całka po samym skoku nie jest równa zeru, ale po pomnożeniu przez F powinno dać zero. Oznacza to, że funkcja w miejscu, w którym nastąpił skok, musi okazać się zerowa. Ale skoku można było dokonać gdziekolwiek; Oznacza, F wszędzie musi być zero.

Widzimy, że jeśli nasza całka jest równa zeru dla dowolnego η , wówczas współczynnik przy η powinien wyjść do zera. Całka działania osiąga minimum na drodze, która spełni tak złożone równanie różniczkowe:

Właściwie nie jest to aż tak skomplikowane; spotkałeś go już wcześniej. To po prostu F=ma. Pierwszy człon to masa razy przyspieszenie; druga to pochodna energii potencjalnej, czyli siły.

Pokazaliśmy więc (przynajmniej dla systemu konserwatywnego), że zasada najmniejszego działania prowadzi do prawidłowej odpowiedzi; stwierdza, że ścieżka, na której występuje minimalne działanie, to ścieżka spełniająca prawo Newtona.

Trzeba poczynić jeszcze jedną uwagę. Nie udowodniłem tego minimum. Być może to maksimum. Tak naprawdę nie musi to być minimum. Tutaj wszystko jest tak samo, jak w „zasadzie najkrótszego czasu”, o której mówiliśmy studiując optykę. Tam też po raz pierwszy rozmawialiśmy o „najkrótszym” czasie. Okazało się jednak, że zdarzają się sytuacje, w których czas ten niekoniecznie jest „najkrótszy”. Podstawową zasadą jest to, że dla każdego odchylenia pierwszego rzędu od ścieżki optycznej zmiany w czasie byłoby równe zeru; Tutaj jest ta sama historia. Przez „minimum” właściwie rozumiemy zmianę ilościową pierwszego rzędu wielkości S gdy odchylenia od ścieżki powinny być równe zeru. I niekoniecznie jest to „minimum”.

Teraz chcę przejść do pewnych uogólnień. Po pierwsze, całą tę historię można by opowiedzieć w trzech wymiarach. Zamiast prostego X Wtedy bym to zrobił x, y I z jako funkcje T, i akcja wyglądałaby na bardziej skomplikowaną. Poruszając się w 3D musisz wykorzystać pełną energię kinetyczną): (t/2), pomnożona przez kwadrat całkowitej prędkości. Innymi słowy

Dodatkowo energia potencjalna jest teraz funkcją x, y I z. Co możesz powiedzieć o ścieżce? Ścieżka to pewna ogólna krzywa w przestrzeni; nie jest tak łatwo narysować, ale idea pozostaje ta sama. A co z η? Cóż, η ma również trzy składowe. Ścieżkę można przesuwać zarówno w osi x, jak i w y, i przez z, lub we wszystkich trzech kierunkach jednocześnie. Więc η teraz wektor. Nie powoduje to żadnych większych komplikacji. Tylko odchylenia muszą być równe zeru Pierwsze zamówienie wówczas obliczenia można przeprowadzić sekwencyjnie na trzy zmiany. Najpierw możesz się ruszyć ts tylko w kierunku X i powiedzieć, że współczynnik powinien wynosić zero. Otrzymujesz jedno równanie. Potem się przeniesiemy ts w kierunku Na i dostajemy drugi. Następnie ruszaj we wskazanym kierunku z i dostajemy trzeci. Jeśli chcesz, możesz zrobić wszystko w innej kolejności. Tak czy inaczej, powstaje trzy równania. Ale prawo Newtona to także trzy równania w trzech wymiarach, po jednym dla każdego składnika. Pozostaje Ci przekonać się na własne oczy, że to wszystko działa w trzech wymiarach (pracy nie ma tu zbyt wiele). Nawiasem mówiąc, możesz wziąć dowolny układ współrzędnych, polarny, dowolny i natychmiast uzyskać prawa Newtona w odniesieniu do tego układu, biorąc pod uwagę, co się stanie, gdy nastąpi przesunięcie η wzdłuż promienia lub pod kątem itp.

Metodę można uogólnić na dowolną liczbę cząstek. Jeśli, powiedzmy, masz dwie cząstki i działają między nimi pewne siły i istnieje wzajemna energia potencjalna, to po prostu dodajesz ich energie kinetyczne i odejmujesz od sumy energię potencjalną interakcji. Czym się różnicie? Ścieżki Zarówno cząsteczki. Następnie dla dwóch cząstek poruszających się w trzech wymiarach powstaje sześć równań. Możesz zmieniać położenie cząstki 1 w kierunku X, w kierunku Na i w stronę z, i zrób to samo z cząstką 2, więc jest sześć równań. I tak właśnie powinno być. Trzy równania określają przyspieszenie cząstki 1 pod wpływem działającej na nią siły, a pozostałe trzy określają przyspieszenie cząstki 2 pod wpływem działającej na nią siły. Zawsze postępuj według tych samych zasad gry, a otrzymasz prawo Newtona dla dowolnej liczby cząstek.

Powiedziałem, że dostaniemy prawo Newtona. Nie jest to do końca prawdą, ponieważ prawo Newtona uwzględnia także siły niezachowawcze, takie jak tarcie. Newton to argumentował To równa się dowolnemu F. Zasada najmniejszego działania obowiązuje tylko dla konserwatywny układy, w których wszystkie siły można uzyskać z funkcji potencjalnej. Ale wiesz, że na poziomie mikroskopowym, to znaczy na najgłębszym poziomie fizycznym, siły niezachowawcze nie istnieją. Siły niezachowawcze (takie jak tarcie) powstają tylko dlatego, że zaniedbujemy mikroskopijne efekty złożone: jest po prostu zbyt wiele cząstek do analizy. Fundamentalny te same prawa Móc można wyrazić jako zasadę najmniejszego działania.

Przejdźmy do dalszych uogólnień. Załóżmy, że interesuje nas, co się stanie, gdy cząstka porusza się relatywistycznie. Jak dotąd nie otrzymaliśmy poprawnego relatywistycznego równania ruchu; F=ma jest prawdziwe tylko w ruchach nierelatywistycznych. Powstaje pytanie: czy w przypadku relatywistycznym istnieje odpowiednia zasada najmniejszego działania? Tak, istnieje. Wzór w przypadku relatywistycznym to:

Pierwsza część całki działania jest iloczynem masy spoczynkowej t 0 NA od 2 i do całki funkcji prędkości √ (1- w. 2 /c 2 ). Następnie zamiast odejmować energię potencjalną, mamy całki z potencjału skalarnego φ i potencjału wektorowego A razy v. Oczywiście brane są tutaj pod uwagę tylko siły elektromagnetyczne. Wszystkie pola elektryczne i magnetyczne są wyrażane w postaci φ i A. Ta funkcja działania daje pełną teorię relatywistycznego ruchu pojedynczej cząstki w polu elektromagnetycznym.

Oczywiście musisz zrozumieć, że wszędzie tam, gdzie napisałem v, przed dokonaniem obliczeń należy dokonać podstawienia dx/ dt zamiast vx itp. Ponadto, gdzie po prostu napisałem x, y, z, musisz sobie wyobrazić punkty w tej chwili T: X(T), y(T), z(T). Właściwie dopiero po takich podstawieniach i podstawieniach v otrzymamy wzór na działanie cząstki relatywistycznej. Niech najbardziej doświadczeni spośród was spróbują udowodnić, że ten wzór działania faktycznie daje prawidłowe równania ruchu dla teorii względności. Radzę ci zacząć od odrzucenia A, czyli na razie zrezygnować z pól magnetycznych. Następnie będziesz musiał uzyskać składniki równania ruchu dp/dt=—qVφ, gdzie, jak zapewne pamiętasz, p=mv√(1-v 2 /c 2).

Znacznie trudniej jest uwzględnić potencjał wektorowy A. Różnice stają się wtedy nieporównywalnie bardziej złożone. Ale ostatecznie okazuje się, że siła jest równa: g(E+v × B). Ale pobaw się tym sam.

Chciałbym podkreślić, że w ogólnym przypadku (na przykład we wzorze relatywistycznym) całka w działaniu nie uwzględnia już różnicy między energią kinetyczną i potencjalną. Było to odpowiednie tylko w przybliżeniu nierelatywistycznym. Na przykład członek m o c 2√(1-v 2 /c 2)-To nie jest tak zwana energia kinetyczna. Kwestię, jakie należy podjąć działania w konkretnym przypadku, można rozstrzygnąć po kilku próbach i błędach. Jest to ten sam problem, co określenie, jakie powinny być równania ruchu. Wystarczy pobawić się znanymi równaniami i sprawdzić, czy można je zapisać jako zasadę najmniejszego działania.

Jeszcze jedna uwaga dotycząca terminologii. Funkcja, która jest integrowana w czasie w celu uzyskania działania S, zwany LagrangianaΛ. Jest to funkcja zależna wyłącznie od prędkości i położenia cząstek. Zatem zasada najmniejszego działania jest również zapisana w formie

gdzie pod X I I v ja wszystkie składowe współrzędnych i prędkości są implikowane. Jeśli kiedykolwiek usłyszysz, jak ktoś mówi o „Lagrangianie”, mówi o funkcji stosowanej do uzyskania S. Dla ruchu relatywistycznego w polu elektromagnetycznym

Ponadto należy zauważyć, że najbardziej skrupulatni i pedantyczni ludzie nie dzwonią S działanie. Nazywa się to „pierwszą główną funkcją Hamiltona”. Jednak wygłoszenie wykładu na temat „Zasady najmniejszej pierwszej funkcji głównej Hamiltona” przekraczało moje siły. Nazwałem to „akcją”. A poza tym coraz więcej osób nazywa to „akcją”. Widzisz, historycznie działanie nazywano czymś innym, co nie było tak przydatne dla nauki, ale myślę, że rozsądniej będzie zmienić definicję. Teraz i ty zaczniesz nazywać nową funkcję akcją, a wkrótce wszyscy zaczną nazywać ją tą prostą nazwą.

Teraz chcę powiedzieć coś na nasz temat, co jest podobne do mojego rozumowania na temat zasady najkrótszego czasu. Istnieje różnica w samej istocie prawa, które mówi, że pewna całka wzięta z jednego punktu do drugiego ma minimum - prawo, które mówi nam coś o całej ścieżce od razu, i prawo, które mówi, że kiedy się poruszasz, to Oznacza to, że istnieje siła powodująca przyspieszenie. Drugie podejście informuje Cię o każdym Twoim kroku, śledzi Twoją ścieżkę centymetr po centymetrze, a pierwsze natychmiast podaje ogólne zestawienie całej przebytej ścieżki. Mówiąc o świetle, rozmawialiśmy o związku między tymi dwoma podejściami. Teraz chcę ci wyjaśnić, dlaczego powinny istnieć prawa różniczkowe, jeśli istnieje taka zasada - zasada najmniejszego działania. Powód jest taki: rozważmy faktycznie przebytą drogę w przestrzeni i czasie. Tak jak poprzednio, poprzestaniemy na jednym pomiarze, aby móc narysować wykres zależności X z T. Wzdłuż prawdziwej ścieżki S osiąga minimum. Załóżmy, że mamy tę ścieżkę i że przechodzi ona przez jakiś punkt A przestrzeni i czasu oraz przez inny sąsiedni punkt B.

Teraz, jeśli cała całka z t 1 zanim T 2 osiągnął minimum, konieczne jest całkowanie na małym odcinku od a do B był również minimalny. To nie może być ta część A zanim B przynajmniej trochę więcej niż minimum. W przeciwnym razie można przesuwać krzywą w tę i z powrotem w tej sekcji i nieznacznie zmniejszać wartość całej całki.

Oznacza to, że każda część ścieżki powinna również zapewniać minimum. Dotyczy to wszelkich małych fragmentów ścieżki. Dlatego też zasadę, że cała droga powinna dawać minimum, można sformułować w ten sposób, że nieskończenie mały odcinek ścieżki jest także krzywą, na której działanie jest minimalne. A jeśli weźmiemy wystarczająco krótki odcinek ścieżki - pomiędzy punktami bardzo blisko siebie A I B,- wtedy nie ma znaczenia, jak potencjał zmienia się z punktu na punkt daleko od tego miejsca, ponieważ przechodząc przez cały swój krótki odcinek, prawie nigdy nie ruszasz się z tego miejsca. Jedyną rzeczą, którą musisz wziąć pod uwagę, jest zmiana pierwszego rzędu w małości potencjału. Odpowiedź może zależeć tylko od pochodnej potencjału, a nie od potencjału gdzie indziej. Zatem stwierdzenie o własności całej ścieżki jako całości staje się stwierdzeniem o tym, co dzieje się na krótkim odcinku ścieżki, czyli stwierdzeniem różniczkowym. I to różniczkowe sformułowanie obejmuje pochodne potencjału, czyli siły w danym punkcie. Jest to jakościowe wyjaśnienie związku pomiędzy prawem jako całością a prawem różniczkowym.

Kiedy rozmawialiśmy o świetle, dyskutowaliśmy także o pytaniu: w jaki sposób cząstka znajduje właściwą drogę? Z różnicowego punktu widzenia jest to łatwe do zrozumienia. W każdej chwili cząstka doświadcza przyspieszenia i wie tylko, co w danej chwili ma zrobić. Ale wszystkie twoje instynkty przyczyny i skutku budzą się, gdy słyszysz, że cząstka „decyduje”, którą ścieżkę wybrać, dążąc do minimum działania. Czy nie „obwąchuje” sąsiednich ścieżek, zastanawiając się, do czego doprowadzą - mniej więcej akcji? Kiedy na drodze światła umieściliśmy ekran, tak aby fotony nie mogły wypróbować wszystkich dróg, okazało się, że nie mogą się zdecydować, którą drogę wybrać, i otrzymaliśmy zjawisko dyfrakcji.

Ale czy dotyczy to również mechaniki? Czy to prawda, że cząstka nie tylko „idzie właściwą drogą”, ale ponownie rozważa wszystkie inne możliwe trajektorie? A co jeśli stawiając na jego drodze przeszkody nie pozwolimy mu patrzeć przed siebie, to otrzymamy jakąś analogię do zjawiska dyfrakcji? Najwspanialsze w tym wszystkim jest to, że wszystko naprawdę tak wygląda. Dokładnie to mówią prawa mechaniki kwantowej. Zatem nasza zasada najmniejszego działania nie jest w pełni sformułowana. Nie polega to na tym, że cząstka wybiera drogę najmniejszego działania, ale na tym, że „wyczuwa” wszystkie sąsiednie ścieżki i wybiera tę, na której działanie jest minimalne, a sposób tego wyboru jest podobny do sposób, w jaki światło wybiera najkrótszy czas. Pamiętacie, że światło wybiera najkrótszy czas w następujący sposób: jeśli światło podąża ścieżką wymagającą innego czasu, przybędzie w innej fazie. Całkowita amplituda w pewnym punkcie jest sumą składowych amplitudy dla wszystkich dróg, którymi światło może do niej dotrzeć. Wszystkie te ścieżki, których fazy różnią się znacznie, po dodaniu nic nie dają. Ale jeśli udało ci się znaleźć całą sekwencję ścieżek, których fazy są prawie takie same, wówczas małe wkłady się sumują, a w punkcie przybycia całkowita amplituda otrzyma zauważalną wartość. Najważniejsza ścieżka to ta, w pobliżu której znajduje się wiele bliskich ścieżek dających tę samą fazę.

Dokładnie to samo dzieje się w mechanice kwantowej. Pełna mechanika kwantowa (nierelatywistyczna i zaniedbująca spin elektronu) działa w następujący sposób: prawdopodobieństwo, że cząstka opuści punkt 1 W tym momencie t 1, dotrze do celu 2 W tym momencie T 2 , równy kwadratowi amplitudy prawdopodobieństwa. Całkowitą amplitudę można zapisać jako sumę amplitud dla wszystkich możliwych ścieżek – dla dowolnej ścieżki dotarcia. Dla kazdego X(T), jakie mogłoby wystąpić dla dowolnej wyobrażalnej trajektorii, należy obliczyć amplitudę. Następnie wszystkie należy złożyć. Co przyjmujemy za amplitudę prawdopodobieństwa określonej ścieżki? Nasza całka działania mówi nam, jaka powinna być amplituda pojedynczej ścieżki. Amplituda jest proporcjonalna e tS/h, Gdzie S - działanie na tej ścieżce. Oznacza to, że jeśli przedstawimy fazę amplitudy jako liczbę zespoloną, wówczas kąt fazowy będzie równy S/ H. Działanie S ma wymiar energii w czasie i stała Plancka ma ten sam wymiar. Jest to stała określająca, kiedy potrzebna jest mechanika kwantowa.

I tak to wszystko działa. Niech działanie dla wszystkich ścieżek S będzie bardzo duża w porównaniu z liczbą H. Niech jakaś ścieżka prowadzi do określonej wartości amplitudy. Faza sąsiedniej ścieżki będzie zupełnie inna, bo z ogromną S nawet drobne zmiany S nagle zmienić fazę (w końcu H wyjątkowo mało). Oznacza to, że sąsiednie ścieżki zwykle wygasają po dodaniu. I tylko w jednym obszarze jest to nieprawdą – w tym, gdzie zarówno ścieżka, jak i jej sąsiad – obie w pierwszym przybliżeniu mają tę samą fazę (a dokładniej prawie to samo działanie, różniące się w obrębie H). Tylko takie ścieżki są brane pod uwagę. A w skrajnym przypadku, gdy stała Plancka H dąży do zera, prawidłowe prawa mechaniki kwantowej można podsumować następująco: „Zapomnij o tych wszystkich amplitudach prawdopodobieństwa. Cząstka faktycznie porusza się po specjalnej ścieżce - dokładnie tej, po której S do pierwszego przybliżenia nie ulega zmianie.” Jest to związek pomiędzy zasadą najmniejszego działania a mechaniką kwantową. To, że mechanikę kwantową można tak sformułować, odkrył w 1942 roku uczeń tego samego nauczyciela, pana Badera, o którym Wam mówiłem. [Mechanika kwantowa została pierwotnie sformułowana przy użyciu równania różniczkowego amplitudy (Schrödinger), a także matematyki macierzowej (Heisenberg).]

Teraz chcę porozmawiać o innych zasadach minimum w fizyce. Istnieje wiele ciekawych zasad tego rodzaju. Nie będę ich wszystkich wymieniał, ale wymienię jeszcze tylko jednego. Później, gdy dojdziemy do jednego zjawiska fizycznego, dla którego istnieje doskonała zasada minimum, opowiem ci o tym. Teraz chcę pokazać, że nie ma potrzeby opisywania elektrostatyki za pomocą równania różniczkowego pola; zamiast tego można wymagać, aby jakaś całka miała maksimum lub minimum. Na początek weźmy przypadek, gdy gęstość ładunku jest znana wszędzie, ale musimy znaleźć potencjał φ w dowolnym punkcie przestrzeni. Już wiesz, że odpowiedź powinna brzmieć:

Innym sposobem wyrażenia tego samego jest obliczenie całki U*

jest to całka objętościowa. Jest prowadzony w całej przestrzeni. Przy prawidłowym rozkładzie potencjałów φ (X, takz) to wyrażenie osiąga minimum.

Możemy pokazać, że oba stwierdzenia dotyczące elektrostatyki są równoważne. Załóżmy, że wybraliśmy dowolną funkcję φ. Chcemy pokazać, że jeśli przyjmiemy jako φ poprawną wartość potencjału _φ plus małe odchylenie f, to do pierwszego rzędu małości zmiana U* będzie równa zeru. Więc piszemy

tutaj φ jest tym, czego szukamy; ale będziemy zmieniać φ, aby zobaczyć, jaki musi być, aby wystąpiła zmienność U* okazał się być pierwszego rzędu małości. W pierwszym terminie U* musimy napisać

Należy to zintegrować x, y i przez z. I tutaj sugeruje się ta sama sztuczka: aby się pozbyć zm/ dx, będziemy się integrować X w częściach. Doprowadzi to do dodatkowego zróżnicowania φ w odniesieniu do X. Jest to ta sama podstawowa idea, dzięki której pozbyliśmy się instrumentów pochodnych T. Używamy równości

Człon zintegrowany wynosi zero, ponieważ przyjmujemy, że f wynosi zero w nieskończoności. (Odpowiada to zniknięciu η jako T 1 I T 2 . Zatem nasza zasada jest bardziej precyzyjnie sformułowana w następujący sposób: U* dla prawa φ mniej niż w jakimkolwiek innym φ(x, y,z), mając te same wartości w nieskończoności.) Następnie zrobimy to samo z Na i z z. Nasza całka ΔU* zamieni się w

Aby ta zmiana była równa zero dla dowolnego dowolnego f, współczynnik f musi być równy zero. Oznacza,

Wracamy do naszego starego równania. Oznacza to, że nasza „minimalna” propozycja jest słuszna. Można to uogólnić, jeśli obliczenia zostaną nieznacznie zmodyfikowane. Wróćmy i zintegrujmy część po części, bez opisywania wszystkiego element po komponencie. Zacznijmy od napisania następującej równości:

Różniczkując lewą stronę, mogę wykazać, że jest ona dokładnie równa prawej. To równanie jest odpowiednie do wykonywania całkowania przez części. W naszej całce ΔU* zastępujemy Vφ*Vf n i fV 2 φ+V*(fVφ), a następnie całkuj to po objętości. Wyraz rozbieżności po całkowaniu po objętości zastępuje się całką po powierzchni:

A ponieważ całkujemy po całej przestrzeni, powierzchnia tej całki leży w nieskończoności. Oznacza to f=0 i otrzymujemy ten sam wynik.

Dopiero teraz zaczynamy rozumieć, jak rozwiązywać problemy, w których się znajdujemy nie wiemy gdzie znajdują się wszystkie ładunki. Miejmy przewodniki, w których ładunki są w jakiś sposób rozdzielone. Jeśli potencjały na wszystkich przewodnikach są stałe, wówczas nadal może obowiązywać nasza zasada minimum. Integracja z U* będziemy rysować tylko wzdłuż obszaru leżącego na zewnątrz wszystkich przewodów. Ponieważ jednak nie możemy zmienić (φ) na przewodnikach, to na ich powierzchni f = 0 i całce powierzchniowej

należy wykonać tylko w przestrzeniach pomiędzy przewodnikami. I oczywiście ponownie otrzymujemy równanie Poissona

Pokazaliśmy zatem, że nasza całka pierwotna U* osiąga minimum nawet wtedy, gdy jest liczone w przestrzeni pomiędzy przewodnikami, z których każdy ma stały potencjał [oznacza to, że każda funkcja testowa φ(g, y,z) musi być równy określonemu potencjałowi przewodnika, gdy (x, y,z) - punkty powierzchni przewodnika]. Ciekawym przypadkiem szczególnym jest sytuacja, gdy ładunki znajdują się wyłącznie na przewodnikach. Następnie

a nasza zasada minimum mówi nam, że w przypadku, gdy każdy przewodnik ma swój własny, z góry określony potencjał, potencjały w przestrzeniach między nimi są regulowane w taki sposób, że całka U* okazuje się być tak mały, jak to tylko możliwe. Co to za całka? Termin Vφ oznacza pole elektryczne. Oznacza to, że całka jest energią elektrostatyczną. Prawidłowe pole to jedyne, które spośród wszystkich pól otrzymanych jako gradient potencjału ma najniższą energię całkowitą.

Chciałbym wykorzystać ten wynik do rozwiązania jakiegoś konkretnego problemu i pokazać, że wszystkie te rzeczy mają realne znaczenie praktyczne. Załóżmy, że biorę dwa przewodniki w postaci cylindrycznego kondensatora.

Wewnętrzny przewodnik ma potencjał równy, powiedzmy, V, a dla zewnętrznego - zero. Niech promień wewnętrznego przewodnika będzie równy A, i zewnętrzne - B. Teraz możemy założyć, że rozkład potencjałów między nimi jest każdy. Ale jeśli weźmiemy prawidłowy wartość φ i obliczyć
(ε 0 /2) ∫ (Vφ) 2 dV wtedy energia układu powinna wynosić 1/2CV 2.

Korzystając z naszej zasady, możesz obliczyć pojemność Z. Jeśli przyjmiemy nieprawidłowy rozkład potencjału i spróbujemy oszacować pojemność kondensatora za pomocą tej metody, otrzymamy zbyt dużą wartość pojemności dla ustalonego V. Każdy oszacowany potencjał φ, który nie pokrywa się dokładnie z jego prawdziwą wartością, również doprowadzi do nieprawidłowej wartości C, większej niż to konieczne. Ale jeśli niepoprawnie wybrany potencjał cp jest nadal przybliżonym przybliżeniem, to pojemność Z okaże się z dobrą dokładnością, ponieważ błąd w C jest wartością drugiego rzędu w porównaniu z błędem w φ.

Załóżmy, że nie znam pojemności kondensatora cylindrycznego. Wtedy, aby ją rozpoznać, mogę zastosować tę zasadę. Po prostu będę testował różne funkcje φ jako potencjału, aż osiągnę najniższą wartość Z. Powiedzmy na przykład, że wybrałem potencjał odpowiadający polu stałemu. (Wiesz oczywiście, że pole tutaj nie jest właściwie stałe; zmienia się co 1/r) Jeśli pole jest stałe, oznacza to, że potencjał zależy liniowo od odległości. Aby napięcie na przewodach było zgodne z wymaganiami, funkcja φ musi mieć postać

Ta funkcja jest równa V Na r=a, zero w r =b, a pomiędzy nimi istnieje stałe nachylenie równe - V/(B—A). Zatem, aby wyznaczyć całkę U*, wystarczy pomnożyć kwadrat tego gradientu przez ε o /2 i całkować po całej objętości. Przeprowadźmy to obliczenie dla cylindra o długości jednostkowej. Element objętościowy na promieniu R równa się 2πrdr. Przeprowadzając integrację, stwierdzam, że mój pierwszy test daje następującą pojemność:

Otrzymuję więc wzór na pojemność, który choć niepoprawny, jest pewnym przybliżeniem:

Oczywiście różni się od prawidłowej odpowiedzi C=2πε 0 /ln (b/a), ale ogólnie nie jest tak źle. Spróbujmy porównać to z poprawną odpowiedzią dla kilku wartości b/a. Obliczone przeze mnie liczby przedstawiono w poniższej tabeli.

Nawet kiedy b/a=2(a to już prowadzi do dość dużych różnic między polami stałymi i liniowymi), nadal otrzymuję dość zadowalające przybliżenie. Odpowiedź oczywiście, zgodnie z oczekiwaniami, jest trochę za wysoka. Ale jeśli cienki drut zostanie umieszczony w dużym cylindrze, wszystko wygląda znacznie gorzej. Wtedy pole zmienia się bardzo i zastąpienie go polem stałym nie prowadzi do niczego dobrego. Gdy b/a = 100, zawyżamy odpowiedź prawie dwukrotnie. Dla małych b/a sytuacja wygląda dużo lepiej. W przeciwnej granicy, gdy przerwa między przewodnikami nie jest zbyt duża (powiedzmy dla b/a = 1,1), pole stałe okazuje się bardzo dobrym przybliżeniem, daje wartość Z z dokładnością do dziesiątych procent.

Teraz powiem ci, jak poprawić to obliczenie. (Odpowiedź dla cylindra brzmi oczywiście słynny, ale ta sama metoda działa w przypadku innych nietypowych kształtów kondensatorów, dla których możesz nie znać poprawnej odpowiedzi.) Następnym krokiem jest znalezienie lepszego przybliżenia nieznanego prawdziwego potencjału φ. Powiedzmy, że możesz przetestować stałą plus wykładnik φ itd. Ale skąd wiesz, że masz najlepsze przybliżenie, jeśli nie znasz prawdziwego φ? Odpowiedź: Policz to Z; im niższa, tym bliższa prawdy. Przetestujmy ten pomysł. Niech potencjał nie będzie liniowy, ale powiedzmy kwadratowy w r, a pole elektryczne nie będzie stałe, ale liniowe. Najbardziej ogólny postać kwadratowa, która zamienia się w φ=O, gdy R=b oraz w φ=F w r=a, czy to jest:

gdzie α jest liczbą stałą. Ta formuła jest nieco bardziej skomplikowana niż poprzednia. Zawiera zarówno wyraz kwadratowy, jak i liniowy. Bardzo łatwo jest z niego wydobyć pole. To jest proste

Teraz należy to podnieść do kwadratu i zintegrować po objętości. Ale poczekaj chwilę. Co powinienem wziąć na α? Mogę przyjąć f jako parabolę, ale która? Oto, co zrobię: obliczę pojemność przy dowolne α. wezmę

Wygląda to trochę zagmatwanie, ale tak się okazuje po całkowaniu kwadratu pola. Teraz mogę wybierać dla siebie. Wiem, że prawda leży niżej niż wszystko, co zamierzam obliczyć. Bez względu na to, co wstawię w miejsce a, odpowiedź nadal będzie za duża. Ale jeśli będę kontynuował grę z α i spróbuję osiągnąć najniższą możliwą wartość Z, wówczas ta najniższa wartość będzie bliższa prawdy niż jakakolwiek inna wartość. Dlatego muszę teraz wybrać α, aby wartość Z osiągnął minimum. Wracając do zwykłego rachunku różniczkowego, jestem przekonany, że minimum Z będzie, gdy α =— 2 B/(b+A). Podstawiając tę wartość do wzoru, otrzymuję najmniejszą pojemność

Zorientowałem się, do czego służy ta formuła Z przy różnych wartościach b/a. Nazwałem te liczby Z(kwadratowy). Oto tabela porównująca Z(kwadratowy) z Z(PRAWDA).

Na przykład, gdy stosunek promienia wynosi 2:1, otrzymuję 1,444. Jest to bardzo dobre przybliżenie prawidłowej odpowiedzi, 1,4423. Nawet z dużym Tak przybliżenie pozostaje całkiem dobre — znacznie lepsze niż pierwsze przybliżenie. Pozostaje tolerowane (zawyżone tylko o 10%) nawet przy b/a = 10:1. Duża rozbieżność występuje dopiero przy stosunku 100:1. Dostaję Z równa 0,346 zamiast 0,267. Z drugiej strony dla współczynnika promienia 1,5 zgodność jest doskonała i dla b/a=1,1 odpowiedź to 10,492065 zamiast oczekiwanego 10,492070. Tam, gdzie można się spodziewać dobrej odpowiedzi, okazuje się, że jest ona bardzo, bardzo dobra.

Podałem wszystkie te przykłady, po pierwsze, aby wykazać teoretyczną wartość zasady minimalnego działania i w ogóle wszystkich zasad minimum, a po drugie, aby pokazać ich praktyczną użyteczność, a wcale nie po to, aby obliczyć pojemność które już mamy, wiemy bardzo dobrze. W przypadku dowolnego innego kształtu możesz wypróbować przybliżone pole z kilkoma nieznanymi parametrami (np. α) i dopasować je do minimum. Uzyskasz doskonałe wyniki numeryczne w przypadku problemów, których nie da się rozwiązać w inny sposób.

Przestrzegają go i dlatego zasada ta jest jednym z kluczowych przepisów współczesnej fizyki. Równania ruchu uzyskane za jego pomocą nazywane są równaniami Eulera-Lagrange'a.

Pierwsze sformułowanie zasady podał w roku P. Maupertuis, od razu wskazując na jej uniwersalność, uznając ją za stosowną w optyce i mechanice. Z tej zasady wyprowadził prawa odbicia i załamania światła.

Fabuła

Maupertuis doszedł do tej zasady z poczucia, że doskonałość Wszechświata wymaga pewnej oszczędności w przyrodzie i jest sprzeczna z jakimkolwiek bezużytecznym wydatkowaniem energii. Naturalny ruch musi być taki, aby pewna ilość była minimalna. Jedyne, co musiał zrobić, to znaleźć tę wartość, co kontynuował. Była to iloczyn czasu trwania (czasu) ruchu w układzie o dwukrotność wartości, którą obecnie nazywamy energią kinetyczną układu.

Eulera (w „Refleksje sur quelques loix générales de la nature”, 1748) przyjmuje zasadę najmniejszej ilości działania, nazywając działanie „wysiłkiem”. Jego wyrażenie w statyce odpowiada temu, co teraz nazwalibyśmy energią potencjalną, tak więc jego stwierdzenie najmniejszego działania w statyce jest równoważne minimalnemu warunkowi energii potencjalnej dla konfiguracji równowagowej.

W mechanice klasycznej

Zasada najmniejszego działania służy jako podstawowa i standardowa podstawa sformułowań mechaniki Lagrangianu i Hamiltona.

Najpierw spójrzmy na konstrukcję w następujący sposób: Mechanika Lagrange'a. Na przykładzie układu fizycznego o jednym stopniu swobody przypomnijmy, że działanie jest funkcjonałem względem (uogólnionych) współrzędnych (w przypadku jednego stopnia swobody – jednej współrzędnej), czyli wyraża się poprzez takie, że każda możliwa wersja funkcji jest powiązana z pewną liczbą - akcją (w W tym sensie możemy powiedzieć, że akcja jako funkcjonał to reguła, która pozwala dowolnej funkcji obliczyć dobrze określoną liczbę - zwaną także działanie). Akcja wygląda następująco:

gdzie jest Lagrangianem układu, w zależności od uogólnionej współrzędnej, jego pierwszą pochodną po czasie, a także ewentualnie jawnie po czasie. Jeżeli układ ma większą liczbę stopni swobody, wówczas Lagrangian zależy od większej liczby uogólnionych współrzędnych i ich pierwszych pochodnych po czasie. Zatem działanie jest funkcjonałem skalarnym zależnym od trajektorii ciała.

Fakt, że akcja jest skalarem, ułatwia zapisanie jej w dowolnych uogólnionych współrzędnych, najważniejsze jest to, że położenie (konfiguracja) układu jest przez nie jednoznacznie scharakteryzowane (na przykład zamiast współrzędnych kartezjańskich mogą to być biegunowe współrzędne, odległości między punktami układu, kąty lub ich funkcje itp. .d.).

Akcję można obliczyć dla całkowicie dowolnej trajektorii, niezależnie od tego, jak „dzika” i „nienaturalna” może być. Jednak w mechanice klasycznej spośród całego zestawu możliwych trajektorii istnieje tylko jedna, po której faktycznie porusza się ciało. Zasada stacjonarnego działania precyzyjnie daje odpowiedź na pytanie, jak ciało będzie się faktycznie poruszać:

Oznacza to, że jeśli dany jest Lagrangian układu, to korzystając z rachunku wariacyjnego, możemy dokładnie ustalić, jak ciało będzie się poruszać, najpierw uzyskując równania ruchu - równania Eulera-Lagrange'a, a następnie je rozwiązując. Pozwala to nie tylko poważnie uogólnić sformułowanie mechaniki, ale także wybrać najdogodniejsze współrzędne dla każdego konkretnego problemu, nie ograniczając się do współrzędnych kartezjańskich, co może być bardzo przydatne do uzyskania najprostszych i najłatwiejszych do rozwiązania równań.

gdzie jest funkcja Hamiltona tego układu; - współrzędne (uogólnione), - impulsy sprzężone (uogólnione), które łącznie charakteryzują w każdym danym momencie stan dynamiczny układu i każdy jest funkcją czasu, charakteryzując w ten sposób ewolucję (ruch) układu. W tym przypadku, aby otrzymać równania ruchu układu w postaci równań kanonicznych Hamiltona, konieczne jest różnicowanie zapisanego w ten sposób działania niezależnie dla wszystkich i .

Należy zauważyć, że jeśli z warunków zadania można w zasadzie znaleźć zasadę ruchu, to jest to automatycznie Nie oznacza, że można skonstruować funkcjonał, który w ruchu rzeczywistym przyjmuje wartość stacjonarną. Przykładem jest wspólny ruch ładunków elektrycznych i monopoli – ładunków magnetycznych – w polu elektromagnetycznym. Ich równań ruchu nie można wyprowadzić z zasady działania stacjonarnego. Podobnie niektóre układy Hamiltona mają równania ruchu, których nie można wyprowadzić z tej zasady.

Przykłady

Trywialne przykłady pomagają ocenić zastosowanie zasady działania za pomocą równań Eulera-Lagrange'a. Cząstka swobodna (masa M i prędkość w) w przestrzeni euklidesowej porusza się po linii prostej. Korzystając z równań Eulera-Lagrange'a, można to przedstawić we współrzędnych biegunowych w następujący sposób. W przypadku braku potencjału funkcja Lagrange'a jest po prostu równa energii kinetycznej

w ortogonalnym układzie współrzędnych.

We współrzędnych biegunowych energia kinetyczna, a tym samym funkcja Lagrange'a, staje się

Składowe promieniowe i kątowe równań przyjmują odpowiednio postać:

Rozwiązanie tych dwóch równań

Oto zapis warunkowy nieskończenie wielokrotnej integracji funkcjonalnej po wszystkich trajektoriach x(t) i jest stałą Plancka. Podkreślamy, że w zasadzie działanie w wykładniku pojawia się (lub może pojawić się) samo podczas badania operatora ewolucji w mechanice kwantowej, ale w przypadku układów, które mają dokładny klasyczny (niekwantowy) analog, jest on dokładnie równy zwykłemu klasyczna akcja.

Analiza matematyczna tego wyrażenia w granicy klasycznej – dla dostatecznie dużych, czyli dla bardzo szybkich oscylacji urojonej wykładniczej – pokazuje, że zdecydowana większość wszystkich możliwych trajektorii tej całki znosi się w granicy (formalnie dla ). Dla prawie każdej ścieżki istnieje ścieżka, na której przesunięcie fazowe będzie dokładnie odwrotne i ich udział będzie zerowy. Redukcji nie podlegają tylko te trajektorie, dla których działanie jest bliskie wartości ekstremalnej (dla większości systemów - minimalnej). Jest to fakt czysto matematyczny z teorii funkcji zmiennej zespolonej; Na tym opiera się na przykład metoda fazy stacjonarnej.

W rezultacie cząstka, w pełnej zgodzie z prawami mechaniki kwantowej, porusza się jednocześnie po wszystkich trajektoriach, przy czym w normalnych warunkach do obserwowanych wartości przyczyniają się tylko trajektorie zbliżone do stacjonarnych (czyli klasycznych). Ponieważ mechanika kwantowa w granicach wysokich energii przekształca się w mechanikę klasyczną, można przyjąć, że jest to kwantowo-mechaniczne wyprowadzenie klasycznej zasady stacjonarności działania.

W kwantowej teorii pola

W kwantowej teorii pola z powodzeniem stosowana jest również zasada działania stacjonarnego. Gęstość Lagrangianu obejmuje tutaj operatory odpowiednich pól kwantowych. Chociaż bardziej poprawne jest tutaj w istocie (z wyjątkiem granicy klasycznej i częściowo quasi-klasycznej) mówienie nie o zasadzie stacjonarności działania, ale o całkowaniu Feynmana wzdłuż trajektorii w konfiguracji lub przestrzeni fazowej tych pól - wykorzystując wspomniana właśnie gęstość Lagrangianu.

Dalsze uogólnienia

Szerzej przez akcję rozumie się funkcjonał określający odwzorowanie z przestrzeni konfiguracyjnej na zbiór liczb rzeczywistych i w ogólności nie musi to być całka, gdyż działania nielokalne są w zasadzie możliwe przynajmniej teoretycznie. Co więcej, przestrzeń konfiguracyjna niekoniecznie jest przestrzenią funkcyjną, ponieważ może mieć geometrię nieprzemienną.

Przestrzegają go i dlatego zasada ta jest jednym z kluczowych przepisów współczesnej fizyki. Równania ruchu uzyskane za jego pomocą nazywane są równaniami Eulera-Lagrange'a.

Fabuła

W mechanice klasycznej

Zasada najmniejszego działania służy jako podstawowa i standardowa podstawa sformułowań mechaniki Lagrangianu i Hamiltona.

Przykłady

w ortogonalnym układzie współrzędnych.

We współrzędnych biegunowych energia kinetyczna, a tym samym funkcja Lagrange'a, staje się

Składowe promieniowe i kątowe równań przyjmują odpowiednio postać:

Rozwiązanie tych dwóch równań

W kwantowej teorii pola

Dalsze uogólnienia

Zasada najmniejszego działania, sformułowana po raz pierwszy właśnie przez Jacobiego, jest podobna do zasady Hamiltona, ale mniej ogólna i trudniejsza do udowodnienia. Zasada ta ma zastosowanie tylko w przypadku, gdy połączenia i funkcja siły nie zależą od czasu i dlatego istnieje całka siły życiowej.

Całka ta ma postać:

Zasada Hamiltona podana powyżej stwierdza, że wariacja całki

jest równa zeru po przejściu ruchu rzeczywistego do dowolnego innego ruchu nieskończenie bliskiego, co powoduje przeniesienie układu z tego samego położenia początkowego do tego samego położenia końcowego w tym samym czasie.

Przeciwnie, zasada Jacobiego wyraża właściwość ruchu niezależną od czasu. Jacobi rozważa całkę

określenie działania. Ustalona przez niego zasada głosi, że wariacja tej całki wynosi zero, gdy porównamy rzeczywisty ruch układu z dowolnym innym nieskończenie bliskim ruchem, który przenosi układ z tego samego położenia początkowego do tego samego położenia końcowego. W tym przypadku nie zwracamy uwagi na czas spędzony, ale obserwujemy równanie (1), czyli równanie siły roboczej o tej samej wartości stałej h, co w rzeczywistym ruchu.

Ten warunek konieczny ekstremum prowadzi, ogólnie rzecz biorąc, do minimum całki (2), stąd nazwa zasada najmniejszego działania. Warunek minimalny wydaje się najbardziej naturalny, gdyż wartość T jest zasadniczo dodatnia, a zatem całka (2) musi koniecznie mieć minimum. Istnienie minimum można ściśle udowodnić, jeśli tylko okres czasu jest wystarczająco krótki. Dowód tego stanowiska można znaleźć w słynnym kursie Darboux z teorii powierzchni. Nie będziemy go jednak tutaj przedstawiać i ograniczymy się do wyprowadzenia warunku

432. Dowód zasady najmniejszego działania.

W rzeczywistych obliczeniach napotykamy jedną trudność, która nie występuje w dowodzie twierdzenia Hamiltona. Zmienna t nie pozostaje już niezależna od zmienności; dlatego też odmiany q i oraz q. są powiązane ze zmianą t za pomocą złożonej zależności wynikającej z równania (1). Najprostszym sposobem obejścia tej trudności jest zmiana zmiennej niezależnej, wybierając taką, której wartości mieszczą się w stałych granicach, które nie zależą od czasu. Niech k będzie nową zmienną niezależną, której granice są niezależne od t. Podczas przenoszenia systemu parametry i t będą funkcjami tej zmiennej

Niech litery z liczbami pierwszymi q oznaczają pochodne parametrów q po czasie.

Ponieważ połączenia z założenia nie zależą od czasu, współrzędne kartezjańskie x, y, z są funkcjami q, które nie zawierają czasu. Zatem ich pochodne będą liniowymi jednorodnymi funkcjami q, a 7 będzie jednorodną kwadratową postacią q, której współczynniki są funkcjami q. Mamy

Aby rozróżnić pochodne q po czasie, oznaczamy w nawiasach (q) pochodne q wzięte względem i zapisane zgodnie z tym

wtedy będziemy mieli

i całka (2), wyrażona poprzez nową zmienną niezależną A, przybierze postać;

Pochodną można wyeliminować za pomocą twierdzenia o sile życiowej. Rzeczywiście, całka siły roboczej będzie

Podstawiając to wyrażenie do wzoru na, redukujemy całkę (2) do formy

Całka określająca działanie przyjęła w ten sposób ostateczną formę (3). Funkcja całkowa to pierwiastek kwadratowy z postaci kwadratowej wielkości

Pokażmy, że równania różniczkowe ekstremów całki (3) są dokładnie równaniami Lagrange'a. Równania ekstremów, oparte na ogólnych wzorach rachunku wariacyjnego, będą miały postać:

Pomnóżmy równania przez 2 i wykonajmy różniczkowania cząstkowe, biorąc pod uwagę, że nie zawiera, to otrzymamy, jeśli nie napiszemy indeksu,

Są to równania ekstremów wyrażone w postaci zmiennej niezależnej.Teraz zadaniem jest powrót do zmiennej niezależnej

Ponieważ Γ jest funkcją jednorodną drugiego stopnia i jest funkcją jednorodną pierwszego stopnia, mamy

Z drugiej strony twierdzenie o sile życiowej można zastosować do czynników pochodnych w równaniach ekstremów, co prowadzi, jak widzieliśmy powyżej, do podstawienia

W wyniku wszystkich podstawień równania ekstremów sprowadzają się do postaci

W ten sposób dotarliśmy do równań Lagrange’a.

433. Przypadek braku sił napędowych.

W przypadku, gdy nie ma sił napędowych, istnieje równanie na siłę życiową i mamy

Warunkiem, aby całka była minimalna, jest w tym przypadku to, że odpowiadająca jej wartość -10 musi być najmniejsza. Zatem, gdy nie ma sił napędowych, to spośród wszystkich ruchów, w których siła życiowa utrzymuje tę samą zadaną wartość, właściwym ruchem jest ten, który w najkrótszym czasie przenosi układ z położenia początkowego do położenia końcowego.

Jeśli układ sprowadzić do jednego punktu poruszającego się po nieruchomej powierzchni, wówczas rzeczywistym ruchem spośród wszystkich ruchów na powierzchni występujących z tą samą prędkością jest ruch, w którym punkt przemieszcza się od położenia początkowego do położenia końcowego w układzie najkrótszy

Przedział czasowy. Innymi słowy, punkt opisuje na powierzchni najkrótszą linię pomiędzy jego dwoma pozycjami, czyli linię geodezyjną.

434. Uwaga.

Zasada najmniejszego działania zakłada, że układ ma kilka stopni swobody, gdyż gdyby był tylko jeden stopień swobody, to do określenia ruchu wystarczyłoby jedno równanie. Ponieważ ruch w tym przypadku można całkowicie określić równaniem siły życiowej, to rzeczywisty ruch będzie jedynym, który spełnia to równanie i dlatego nie będzie można go porównać z żadnym innym ruchem.

ZASADA NAJMNIEJ SKUTECZNA

Jedna z wariacyjnych zasad mechaniki, zdaniem Kroma, dla danej klasy ruchów mechanicznych porównywanych między sobą. system, prawidłowy jest ten, dla którego fizyczny. rozmiar, tzw akcja, ma najmniejszą (a dokładniej stacjonarną) wartość. Zwykle N. d. p. jest używany w jednej z dwóch form.

a) N. d. p. w postaci Hamiltona-Ostrogradskiego ustala, że spośród wszystkich kinematycznie możliwych przemieszczeń układu z jednej konfiguracji do drugiej (zbliżonej do pierwszej), dokonanych w tym samym okresie czasu, ważny jest ten, dla którego działanie Hamiltona S będzie najmniejsze. Matematyka. wyrażenie N. d.p. ma w tym przypadku postać: dS = 0, gdzie d jest symbolem zmienności niepełnej (izochronicznej) (tj. w odróżnieniu od zmienności całkowitej czas w niej się nie zmienia).

b) N. d. p. w postaci Maupertuisa-Lagrange'a ustala, że spośród wszystkich kinematycznie możliwych ruchów układu z jednej konfiguracji do innej jej bliskiej, wykonywanych przy zachowaniu tej samej wartości całkowitej energii układu, obowiązuje to, że dla - Zatem działanie Lagrange'a W będzie najmniejsze. Matematyka. wyrażenie N. d.p. ma w tym przypadku postać DW = 0, gdzie D jest symbolem całkowitej zmienności (w odróżnieniu od zasady Hamiltona-Ostrogradskiego zmieniają się tu nie tylko współrzędne i prędkości, ale także czas ruchu systemu z jednej konfiguracji do drugiej). N.d.p.v. W tym przypadku obowiązuje ona tylko dla układów konserwatywnych, a ponadto holonomicznych, przy czym w pierwszym przypadku zasada niezachowawcza jest bardziej ogólna i w szczególności może zostać rozszerzona na układy niekonserwatywne. NDP służą do zestawiania równań ruchu mechanicznego. systemów i badanie ogólnych właściwości tych ruchów. Przy odpowiednim uogólnieniu pojęć NPR znajduje zastosowanie w mechanice ośrodka ciągłego, elektrodynamice i kwantowości. mechanika itp.

- taki sam jak...
Encyklopedia fizyczna
- m-operator, operator minimalizacji, - metoda konstruowania nowych funkcji z innych funkcji, składająca się z następujących...
Encyklopedia matematyczna
- jedna z wariacyjnych zasad mechaniki, według której dla danej klasy ruchów mechanicznych porównuje się ze sobą. system jest wykonywany tak, dla którego działanie jest minimalne...
Naturalna nauka. słownik encyklopedyczny
- jedno z najważniejszych praw mechaniki, ustanowione przez rosyjskiego naukowca M.V. Ostrogradski...
Encyklopedia rosyjska
Słownik terminów prawniczych
- w prawie konstytucyjnym szeregu państw zasada, zgodnie z którą powszechnie uznane zasady i normy prawa międzynarodowego stanowią integralną część systemu prawnego odpowiedniego kraju...
Encyklopedia prawnika
- w prawie konstytucyjnym szeregu państw zasada, zgodnie z którą powszechnie uznane normy prawa międzynarodowego stanowią integralną część krajowego porządku prawnego...
Duży słownik prawniczy
- najkrótsza odległość od środka ładunku wybuchowego do wolnej powierzchni - linia oporu nai-malkoto - křivka nejmenšího odporu - Line der geringsten Festigkeit - robbantás minimális ellenállási tengelyvonala - hamgiin baga...
Słownik konstrukcyjny
- jeśli możliwe jest przesuwanie punktów ciała odkształcalnego w różnych kierunkach, to każdy punkt tego ciała przesuwa się w kierunku najmniejszego oporu...
Encyklopedyczny słownik metalurgii
- zasada, według której istniejące zapasy wycenia się zazwyczaj albo według najniższego kosztu, albo po najniższej cenie sprzedaży...
Słownik terminów biznesowych
– w prawie konstytucyjnym szeregu państw – zasadę, zgodnie z którą powszechnie uznane zasady i normy prawa międzynarodowego stanowią integralną część systemu prawnego danego państwa i działają...
Encyklopedyczny słownik ekonomii i prawa
- jedna z wariacyjnych zasad mechaniki, zgodnie z którą dla danej klasy ruchów układu mechanicznego porównywanych między sobą obowiązuje ta, dla której wielkość fizyczna...
- to samo co zasada Gaussa...
Wielka encyklopedia radziecka
- jedna z wariacyjnych zasad mechaniki; taka sama jak zasada najmniejszego działania...
Wielka encyklopedia radziecka
- jedna z wariacyjnych zasad mechaniki, zgodnie z którą dla danej klasy ruchów układu mechanicznego porównuje się ze sobą ten, dla którego działanie jest minimalne...
Duży słownik encyklopedyczny
- Książka Wybierz najprostszą metodę działania, unikając przeszkód, unikając trudności...
Słownik frazeologiczny rosyjskiego języka literackiego

„ZASADA NAJNIŻSZEJ WARTOŚCI” w książkach

2.5.1. Zasada działania urządzenia

Z książki Entertaining Electronics [Niekonwencjonalna encyklopedia przydatnych obwodów] autor Kaszkarow Andriej Pietrowicz

2.5.1. Zasada działania urządzenia Zasada działania urządzenia jest prosta. Kiedy strumień świetlny emitowany przez diodę HL1 LED odbija się od obiektu i uderza w fotodetektor, jednostka elektroniczna, zaimplementowana na 2 mikroukładach - komparator KR1401SA1 i timer KR1006VI1, wytwarza

Zasada działania terafim

Z książki Tajemna wiedza. Teoria i praktyka Agni Jogi autor Roerich Elena Iwanowna

Zasada działania terafim 24.02.39 Wiesz, że każda świadomość i reprezentacja dowolnego przedmiotu przybliża nas do niego. Jak wiadomo, warstwy psychiczne obiektu można przenieść na jego terafim. Astralne terafimy odległych światów i

Trzy warunki zastosowania prawa najmniejszego wysiłku

Z książki Mądrość Deepaka Chopry [Zdobądź to, czego chcesz, przestrzegając 7 praw Wszechświata] przez Tima Goodmana

Trzy warunki działania Prawa Najmniejszego Wysiłku Zobaczmy, jakie warunki są potrzebne, aby przyciągnąć do Twojego życia ten twórczy przepływ energii z Wszechświata - energię miłości, a co za tym idzie, aby Prawo Najmniejszego Wysiłku zaczęło działać w Twoim życiu .

Rozdział 19 ZASADA najmniejszego efektu

Z księgi 6. Elektrodynamika autor Feynmana Richarda Phillipsa

Rozdział 19 ZASADA najmniejszego efektu Dodatek po wykładzie Kiedy byłem w szkole, nasz nauczyciel fizyki, imieniem Bader, zawołał mnie kiedyś po zajęciach i powiedział: „Wyglądasz, jakbyś był wszystkim strasznie zmęczony; posłuchaj jednej ciekawej rzeczy

5. Zasada najmniejszego działania

Z książki Rewolucja w fizyce przez de Broglie Louisa

5. Zasada najmniejszego działania Równania dynamiki punktu materialnego w polu sił o potencjale można otrzymać w oparciu o zasadę, którą ogólnie nazywamy zasadą Hamiltona lub zasadą działania stacjonarnego. Według tej zasady przede wszystkim

Zasada działania

Z książki Przewodnik ślusarski po zamkach przez Phillipsa Billa

Zasada działania Możliwość obracania wkładki zależy od położenia sworzni, o którym z kolei decyduje siła ciężkości, działanie sprężyn i siła klucza (lub klucza głównego; informacje o kluczach głównych można znaleźć w rozdziale 9) . W przypadku braku klucza naciska grawitacja i sprężyny

Zasada działania stacjonarnego

Z książki Wielka radziecka encyklopedia (ST) autora TSB

Zasada najmniejszego działania

TSB

Zasada najmniejszego przymusu

Z książki Wielkiej Encyklopedii Radzieckiej (NA) autora TSB

2.5.1. Zasada działania

Z książki Ochrona przekaźników w elektrycznych sieciach dystrybucyjnych B90 autor Bułyczow Aleksander Witalijewicz

2.5.1. Zasada działania W sieciach elektrycznych z zasilaniem dwukierunkowym oraz w sieciach pierścieniowych konwencjonalne zabezpieczenie prądowe nie może działać selektywnie. Na przykład w sieci elektrycznej z dwoma źródłami zasilania (ryc. 2.15), gdzie przełączniki i zabezpieczenia są zainstalowane po obu stronach

Zasada działania

Z książki Turbo Suslik. Jak przestać się pierdolić i zacząć żyć autor Leuszkin Dmitrij

Zasada działania „Przetwórz to” to w istocie swego rodzaju „makro”, które jednym zwrotem uruchamia w podświadomości całą masę procesów, których celem jest przetworzenie wybranego materiału mentalnego. Ten moduł obsługi sam w sobie zawiera 7 różnych modułów, z których niektóre

Jak zacząć postępować zgodnie z prawem najmniejszego wysiłku: trzy niezbędne działania

Z książki Przewodnik po rosnącym kapitale autorstwa Josepha Murphy'ego, Dale'a Carnegie, Eckharta Tolle'a, Deepaka Chopry, Barbary Sher, Neila Walsha autora Sterna Valentina

Jak zacząć przestrzegać Prawa Najmniejszego Wysiłku: trzy niezbędne działania Aby Prawo Najmniejszego Wysiłku zaczęło działać, należy nie tylko spełnić trzy wymienione powyżej warunki, ale także wykonać trzy działania.Działanie pierwsze: zacznij akceptować świat takim, jaki jest jest Akceptuj

11. Fizyka i Aikido najmniejszego działania

autor Mindella Arnolda

11. Fizyka i Aikido najmniejszego efektu Kiedy wieje, jest tylko wiatr. Kiedy pada deszcz, jest tylko deszcz. Kiedy chmury przechodzą, słońce przez nie prześwieca. Jeśli otworzysz się na wgląd, wówczas zjednoczysz się z wglądem. I możesz z niego całkowicie skorzystać. Jeśli się otworzysz

Zasada najmniejszego działania Leibniza „Vis Viva”

Z książki Geopsychologia w szamanizmie, fizyce i taoizmie autor Mindella Arnolda

Zasada najmniejszego działania Leibniza „Vis Viva” Wszyscy mamy Wilhelma Gottfrieda Leibniza (1646–1716), któremu możemy podziękować za zasadę najmniejszego działania. Leibniz, jeden z pierwszych „nowoczesnych” fizyków i matematyków, żył w czasach Newtona – epoce, w której naukowcy byli bardziej otwarcie

Aikido - ucieleśnienie zasady najmniejszego działania

Z książki Geopsychologia w szamanizmie, fizyce i taoizmie autor Mindella Arnolda

Aikido - ucieleśnienie zasady najmniejszego działania Nasza psychologia i technologia w dużej mierze kierują się koncepcją bardzo bliską idei najmniejszego działania. Cały czas staramy się ułatwiać nam życie. Dzisiejsze komputery nie są wystarczająco szybkie; Muszą