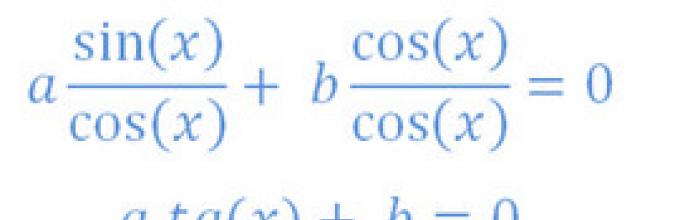Lekcja i prezentacja na temat: „Rozwiązywanie prostych równań trygonometrycznych”
Dodatkowe materiały
Drodzy użytkownicy, nie zapomnijcie zostawić swoich komentarzy, recenzji i życzeń! Wszystkie materiały zostały sprawdzone programem antywirusowym.
Podręczniki i symulatory w sklepie internetowym Integral dla klasy 10 od 1C
Rozwiązujemy problemy z geometrii. Interaktywne zadania do budowania w przestrzeni
Środowisko oprogramowania „1C: Konstruktor matematyczny 6.1”
Co będziemy studiować:
1. Co to są równania trygonometryczne?
3. Dwie główne metody rozwiązania równania trygonometryczne.
4. Równania trygonometryczne jednorodne.
5. Przykłady.
Co to są równania trygonometryczne?
Chłopaki, badaliśmy już arcusinus, arccosinus, arcus tangens i arccotangens. Przyjrzyjmy się teraz ogólnie równaniom trygonometrycznym.
Równania trygonometryczne to równania, w których zmienna jest zawarta pod znakiem funkcji trygonometrycznej.
Powtórzmy formę rozwiązywania najprostszych równań trygonometrycznych:
1)Jeśli |a|≤ 1, to równanie cos(x) = a ma rozwiązanie:
X= ± arccos(a) + 2πk
2) Jeżeli |a|≤ 1, to równanie sin(x) = a ma rozwiązanie:
3) Jeśli |a| > 1, to równanie sin(x) = a i cos(x) = a nie ma rozwiązań 4) Równanie tg(x)=a ma rozwiązanie: x=arctg(a)+ πk
5) Równanie ctg(x)=a ma rozwiązanie: x=arcctg(a)+ πk
Dla wszystkich formuł k jest liczbą całkowitą
Najprostsze równania trygonometryczne mają postać: T(kx+m)=a, T jest jakąś funkcją trygonometryczną.
Przykład.Rozwiąż równania: a) sin(3x)= √3/2
Rozwiązanie:
A) Oznaczmy 3x=t, a następnie przepiszemy nasze równanie do postaci:
Rozwiązaniem tego równania będzie: t=((-1)^n)arcsin(√3 /2)+ πn.
Z tabeli wartości otrzymujemy: t=((-1)^n)×π/3+ πn.
Wróćmy do naszej zmiennej: 3x =((-1)^n)×π/3+ πn,
Wtedy x= ((-1)^n)×π/9+ πn/3
Odpowiedź: x= ((-1)^n)×π/9+ πn/3, gdzie n jest liczbą całkowitą. (-1)^n – minus jeden do potęgi n.
Więcej przykładów równań trygonometrycznych.
Rozwiąż równania: a) cos(x/5)=1 b)tg(3x- π/3)= √3Rozwiązanie:
A) Tym razem przejdźmy od razu do obliczenia pierwiastków równania:
X/5= ± arccos(1) + 2πk. Wtedy x/5= πk => x=5πk
Odpowiedź: x=5πk, gdzie k jest liczbą całkowitą.
B) Zapisujemy to w postaci: 3x- π/3=arctg(√3)+ πk. Wiemy, że: arctan(√3)= π/3
3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3
Odpowiedź: x=2π/9 + πk/3, gdzie k jest liczbą całkowitą.
Rozwiąż równania: cos(4x)= √2/2. I znajdź wszystkie korzenie segmentu.
Rozwiązanie:
Rozwiążmy nasze równanie w postaci ogólnej: 4x= ± arccos(√2/2) + 2πk
4x= ± π/4 + 2πk;
X= ± π/16+ πk/2;
Zobaczmy teraz, jakie korzenie spadają na nasz segment. W k W k=0, x= π/16 jesteśmy w środku dany segment.
Przy k=1, x= π/16+ π/2=9π/16, uderzamy ponownie.
Dla k=2, x= π/16+ π=17π/16, ale tutaj nie trafiliśmy, czyli dla dużego k też oczywiście nie trafimy.
Odpowiedź: x= π/16, x= 9π/16
Dwie główne metody rozwiązania.
Przyjrzeliśmy się najprostszym równaniom trygonometrycznym, ale są też bardziej złożone. Do ich rozwiązania wykorzystuje się metodę wprowadzania nowej zmiennej oraz metodę faktoryzacji. Spójrzmy na przykłady.Rozwiążmy równanie:
Rozwiązanie:
Do rozwiązania naszego równania skorzystamy z metody wprowadzenia nowej zmiennej, oznaczającej: t=tg(x).
W wyniku zamiany otrzymujemy: t 2 + 2t -1 = 0
Znajdźmy pierwiastki równania kwadratowego: t=-1 i t=1/3
Wtedy tg(x)=-1 i tg(x)=1/3, otrzymamy najprostsze równanie trygonometryczne, znajdźmy jego pierwiastki.
X=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.
Odpowiedź: x= -π/4+πk; x=arctg(1/3) + πk.
Przykład rozwiązania równania
Rozwiąż równania: 2sin 2 (x) + 3 cos(x) = 0
Rozwiązanie:
Użyjmy tożsamości: sin 2 (x) + cos 2 (x)=1
Nasze równanie będzie miało postać: 2-2cos 2 (x) + 3 cos (x) = 0
2 cos 2 (x) - 3 cos (x) -2 = 0
Wprowadźmy zamianę t=cos(x): 2t 2 -3t - 2 = 0
Rozwiązaniem naszego równania kwadratowego są pierwiastki: t=2 i t=-1/2
Wtedy cos(x)=2 i cos(x)=-1/2.
Ponieważ cosinus nie może przyjmować wartości większych niż jeden, wówczas cos(x)=2 nie ma pierwiastków.
Dla cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk
Odpowiedź: x= ±2π/3 + 2πk
Równania trygonometryczne jednorodne.
Definicja: Równania w postaci a sin(x)+b cos(x) nazywane są jednorodnymi równaniami trygonometrycznymi pierwszego stopnia.Równania postaci
jednorodne równania trygonometryczne drugiego stopnia.
Aby rozwiązać jednorodne równanie trygonometryczne pierwszego stopnia, podziel je przez cos(x):  Nie można dzielić przez cosinus, jeśli jest równy zero, upewnijmy się, że tak nie jest:
Nie można dzielić przez cosinus, jeśli jest równy zero, upewnijmy się, że tak nie jest:
Niech cos(x)=0, wtedy asin(x)+0=0 => sin(x)=0, ale sinus i cosinus nie są jednocześnie równe zeru, otrzymamy sprzeczność, więc możemy bezpiecznie dzielić o zero.
Rozwiązać równanie:
Przykład: cos 2 (x) + sin(x) cos(x) = 0
Rozwiązanie:
Wyjmijmy wspólny czynnik: cos(x)(c0s(x) + sin (x)) = 0
Następnie musimy rozwiązać dwa równania:
Cos(x)=0 i cos(x)+sin(x)=0
Cos(x)=0 przy x= π/2 + πk;
Rozważmy równanie cos(x)+sin(x)=0. Podzielmy nasze równanie przez cos(x):
1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk
Odpowiedź: x= π/2 + πk i x= -π/4+πk
Jak rozwiązywać jednorodne równania trygonometryczne drugiego stopnia?
Chłopaki, zawsze przestrzegajcie tych zasad!
1. Zobacz, ile wynosi współczynnik a, jeśli a=0 to nasze równanie będzie miało postać cos(x)(bsin(x)+ccos(x)), którego przykład rozwiązania znajduje się na poprzednim slajdzie
2. Jeśli a≠0, to musisz podzielić obie strony równania przez cosinus kwadrat, otrzymamy:

Zmieniamy zmienną t=tg(x) i otrzymujemy równanie:
Rozwiąż przykład nr:3
Rozwiązać równanie:Rozwiązanie:
Podzielmy obie strony równania przez cosinus kwadrat: 
Zmieniamy zmienną t=tg(x): t 2 + 2 t - 3 = 0
Znajdźmy pierwiastki równania kwadratowego: t=-3 i t=1
Wtedy: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk
Tg(x)=1 => x= π/4+ πk
Odpowiedź: x=-arctg(3) + πk i x= π/4+ πk
Rozwiąż przykład nr:4
Rozwiązać równanie:Rozwiązanie:
Przekształćmy nasze wyrażenie:

Potrafimy rozwiązać takie równania: x= - π/4 + 2πk i x=5π/4 + 2πk
Odpowiedź: x= - π/4 + 2πk i x=5π/4 + 2πk
Rozwiąż przykład nr:5
Rozwiązać równanie:Rozwiązanie:
Przekształćmy nasze wyrażenie:

Wprowadźmy podstawienie tg(2x)=t:2 2 - 5t + 2 = 0
Rozwiązaniem naszego równania kwadratowego będą pierwiastki: t=-2 i t=1/2
Wtedy otrzymujemy: tg(2x)=-2 i tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2
2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2
Odpowiedź: x=-arctg(2)/2 + πk/2 i x=arctg(1/2)/2+ πk/2
Problemy do samodzielnego rozwiązania.
1) Rozwiąż równanieA) sin(7x)= 1/2 b) cos(3x)= √3/2 c) cos(-x) = -1 d) tg(4x) = √3 d) ctg(0,5x) = -1,7
2) Rozwiąż równania: sin(3x)= √3/2. I znajdź wszystkie pierwiastki odcinka [π/2; π].
3) Rozwiąż równanie: łóżko 2 (x) + 2 łóżko (x) + 1 =0
4) Rozwiąż równanie: 3 sin 2 (x) + √3sin (x) cos(x) = 0
5) Rozwiąż równanie: 3sin 2 (3x) + 10 sin(3x)cos(3x) + 3 cos 2 (3x) =0
6) Rozwiąż równanie: cos 2 (2x) -1 - cos(x) =√3/2 -sin 2 (2x)
Głównymi metodami rozwiązywania równań trygonometrycznych są: sprowadzanie równań do najprostszych (za pomocą wzorów trygonometrycznych), wprowadzanie nowych zmiennych i rozkład na czynniki. Przyjrzyjmy się ich zastosowaniu na przykładach. Zwróć uwagę na format zapisywania rozwiązań równań trygonometrycznych.
Warunkiem koniecznym pomyślnego rozwiązywania równań trygonometrycznych jest znajomość wzorów trygonometrycznych (temat 13 pracy 6).
Przykłady.
1. Równania zredukowane do najprostszych.
1) Rozwiąż równanie
Rozwiązanie:
Odpowiedź:
2) Znajdź pierwiastki równania
(sinx + cosx) 2 = 1 – sinxcosx, należący do segmentu.
Rozwiązanie:
Odpowiedź:
2. Równania redukujące do kwadratu.
1) Rozwiąż równanie 2 sin 2 x – cosx –1 = 0.
Rozwiązanie: Za pomocą formuła grzechu 2 x = 1 – cos 2 x, otrzymujemy
Odpowiedź:
2) Rozwiąż równanie cos 2x = 1 + 4 cosx.
Rozwiązanie: Korzystając ze wzoru cos 2x = 2 cos 2 x – 1, otrzymujemy
Odpowiedź:
3) Rozwiąż równanie tgx – 2ctgx + 1 = 0
Rozwiązanie:
Odpowiedź:
3. Równania jednorodne
1) Rozwiąż równanie 2sinx – 3cosx = 0
Rozwiązanie: Niech cosx = 0, wtedy 2sinx = 0 i sinx = 0 – sprzeczność z faktem, że sin 2 x + cos 2 x = 1. Oznacza to, że cosx ≠ 0 i możemy podzielić równanie przez cosx. Dostajemy
Odpowiedź:
2) Rozwiąż równanie 1 + 7 cos 2 x = 3 sin 2x
Rozwiązanie:
Używamy wzorów 1 = sin 2 x + cos 2 x i sin 2x = 2 sinxcosx, otrzymujemy
grzech 2 x + sałata 2 x + 7cos 2 x = 6sinxcosx
grzech 2 x – 6sinxcosx+ 8cos 2 x = 0
Niech cosx = 0, następnie sin 2 x = 0 i sinx = 0 – sprzeczność z faktem, że sin 2 x + cos 2 x = 1.
Oznacza to, że cosx ≠ 0 i możemy podzielić równanie przez cos 2 x .
Dostajemy
tg 2 x – 6 tgx + 8 = 0
Oznaczmy tgx = y
y 2 – 6 y + 8 = 0
y1 = 4; y2 = 2
a) tgx = 4, x= arctan4 + 2 k, k
b) tgx = 2, x= arctan2 + 2 k, k .
Odpowiedź: arctg4 + 2 k, arctan2 + 2 k, k
4. Równania postaci A grzech + B cosx = SS≠ 0.
1) Rozwiąż równanie.
Rozwiązanie:
Odpowiedź:
5. Równania rozwiązywane metodą faktoryzacji.
1) Rozwiąż równanie sin2x – sinx = 0.
Pierwiastek równania F (X) = φ ( X) może służyć tylko jako liczba 0. Sprawdźmy to:
cos 0 = 0 + 1 – równość jest prawdziwa.
Liczba 0 jest jedynym pierwiastkiem tego równania.
Odpowiedź: 0.
Temat lekcji: Równania trygonometryczne dające się sprowadzić do kwadratowych, jednorodnych równań trygonometrycznych.
Typ lekcji: Lekcja łączona.
Cele Lekcji:
- Wprowadzenie pojęcia jednorodnych równań trygonometrycznych redukowalnych do równań kwadratowych;
- Wprowadzenie pojęcia równań trygonometrycznych I i II stopnia;
- Wykształcenie u studentów umiejętności rozwiązywania rozważanych równań na poziomie podstawowym.
- Rozwijać umiejętność analizowania i wyciągania wniosków;
- Rozwijaj umiejętność samoanalizy i kontroli.
- Rozwijaj poczucie odpowiedzialności;
- Rozwijaj umiejętności pracy w zespole.
- Wyposażenie lekcji: plakaty, karty, samoocena, zestaw kart do samodzielnej pracy, karty sygnałowe.
Struktura lekcji:
1. Etap organizacyjny.
2. Etap sprawdzania pracy domowej.
3. Etap przygotowania uczniów do aktywnego i świadomego przyswajania nowego materiału. Wprowadzenie do tematu lekcji. Wyznaczanie celów i celów.
4. Etap asymilacji nowej wiedzy.
5. Etap sprawdzania zrozumienia przez uczniów nowego materiału.
6. Etap konsolidacji nowego materiału.
7. Etap informowania uczniów o zadaniach domowych.
8. Etap kompleksowego testowania wiedzy.
9. Podsumowanie. Odbicie.
1. Etap organizacyjny .
- przygotować uczniów do pracy na zajęciach.
2. Etap sprawdzania pracy domowej .
- ustalić obecność i poprawność zadań domowych wszystkich uczniów.
3. Etap przygotowania uczniów do aktywnego i świadomego przyswajania nowego materiału.
- tworząc sytuację problemową, poprowadź uczniów do nowych typów równań trygonometrycznych. Nauczyciel zwraca uwagę uczniów na tablicę magnetyczną, na której znajdują się karty z kilkoma równaniami trygonometrycznymi i prosi o wskazanie sposobu ich rozwiązania.
1) cos (4x-2)=2
3) cos 2 x-2cosx=0
5) 8 grzech 2 x-6 grzech x-5=0
6)8 cos 2 2x+6 grzech 2x-3=0
7)2sin x- 3 cos x=0
9)3 sin 2 x- 4sin x cos x +cos 2 x=0
Uczniowie uważnie przyglądają się tablicy magnetycznej i wyjaśniają, jak rozwiązać to lub inne równanie. Jeżeli nauczyciel nie ma żadnych uwag, kartę z powyższym równaniem usuwa się z tablicy magnetycznej.
W wyniku wykonanej pracy równania pozostały na tablicy magnetycznej, uczniowie nie potrafili znaleźć sposobu na ich rozwiązanie. (nr 5, 7)
4. Etap asymilacji nowej wiedzy.
Wprowadzenie pojęcia „Równania trygonometryczne sprowadzalne do kwadratu”;
- wprowadzić pojęcie „równań trygonometrycznych redukowalnych do kwadratu”;
- wprowadzić pojęcie jednorodnych równań trygonometrycznych;
- analizować metody rozwiązywania jednorodnych równań trygonometrycznych I i II stopnia;
- osiągnąć umiejętność wyznaczania postaci jednorodnych równań trygonometrycznych;
- opanować ogólne techniki rozwiązywania równań trygonometrycznych redukowalnych do równań kwadratowych i jednorodnych równań trygonometrycznych.
Nauczyciel wymienia rodzaje pozostałych równań i prosi uczniów o zapisanie tematu lekcji „Równania trygonometryczne rozwiązywane przez redukcję do równań kwadratowych. Równania trygonometryczne jednorodne I i II stopnia.
Nauczyciel robi notatki na tablicy, a uczniowie w zeszytach zapisują:
Równania trygonometryczne rozwiązywane poprzez redukcję do równań kwadratowych.
1) Równania w postaci A×sin2 t +B×sin t + C = 0, gdzie A ¹ 0, rozwiązuje się poprzez redukcję do kwadratu zastępując sin t = y (równania z kosztem t, tg t, сtg t są rozwiązać podobnie).
2) Równania w postaci A×sin2 t +B×cos t + C = 0. Przy rozwiązywaniu podstawowa tożsamość trygonometryczna sin2 t = 1 - cos2 t.
3) grzech 2 t = a, a= . 4) sałata 2 t = a, a= .
5) tg 2 t = a, a= . 6) łóżeczko 2 t = a, a=
Szczegółowo analizowane jest rozwiązanie równania nr 5, 4. Rozwiązanie równania nr 6 odbywa się przy aktywnym udziale klasy. Aby rozwiązać równanie nr 8, wzywa się ucznia (opcjonalnie).
Równania trygonometryczne jednorodne I i II stopnia.
Równanie, w którym każdy wyraz ma ten sam stopień, nazywa się jednorodnym.
1) Równania w postaci A×sin t +B×cos t = 0, gdzie A ¹ 0, B ¹ 0, nazywane są jednorodnymi równaniami trygonometrycznymi stopnia 1. Rozwiązuje się je dzieląc obie strony przez koszt t ¹ 0. Mamy A× tg t + B = 0.
2) Równania w postaci A×sin2 t +B sin t×cos t + С×cos2 t = 0 nazywane są jednorodnymi równaniami trygonometrycznymi stopnia 2. Rozwiązuje się je dzieląc obie strony przez cos2 t ¹ 0. Mamy A× tg2 t + B× tg t + C = 0.
Nauczyciel rozwiązuje równanie nr 7 wraz ze szczegółowym wyjaśnieniem. Rozwiązując równanie nr 9, za pomocą pytań, łączy uczniów aktywna praca. Po sprowadzeniu równania do postaci 3tg2 t - 4 tg t + 1 = 0, zaprasza uczniów, aby jeśli chcą, podeszli do tablicy i rozwiązali powstałe równanie.
- Etap sprawdzający zrozumienie przez uczniów nowego materiału.
Zadanie: ustalić, czy uczniowie nauczyli się rozwiązywać równania nowego typu.
SFZ ( niezależna praca na temat tworzenia wiedzy).
Określ rodzaj równania i wskaż sposób jego rozwiązania.
2)5 grzech 3x+4cos3x=0 ;
3) grzech 2 x+14sinx*cosx-15cos 2 x=0;
4) 1 + 7cos2 x + 3sin2 x = 0;
5)sin2x+sin 2 x=0 .
6. Etap konsolidacji nowego materiału.
Zadanie: utrwalić w uczniach wiedzę i umiejętności, które zdobyli na lekcji.
Nauczyciel prosi uczniów o rozwiązanie na tablicy następujących równań:
7. Etap informowania uczniów o zadaniach domowych.
Cele: informowanie uczniów Praca domowa, podaj krótkie instrukcje dotyczące jego wdrożenia.
- przeglądaj notatki w swoim notatniku;
- przeanalizuj rozwiązanie przykładów nr 1 - 6 z podręcznika, s. 78 - 79.
- kompletny nr 167a), b); nr 168 b); nr 169a); nr 170v).
- Silni uczniowie zamiast nr 167, 168 potrafią rozwiązać równanie:
15*(sin 2 x+sin x+ cos 2 2x) 2 +17+31sinx
8. Etap kompleksowego testowania wiedzy.
Cele: wszechstronne sprawdzenie wiedzy uczniów w zakresie rozwiązywania równań o charakterze zbliżonym do omawianych na lekcji, rozwinięcie umiejętności samoanalizy i kontroli.
SFN (samodzielna praca nad rozwojem umiejętności).
Rozwiąż równania.
Opcja 1.
Opcja 2
Opcja 3
Opcja 4
9. Zreasumowanie. Odbicie.
Podczas rozwiązywania wielu problemy matematyczne zwłaszcza te, które mają miejsce przed klasą 10, jasno określona jest kolejność wykonywanych działań, które doprowadzą do celu. Takie problemy obejmują na przykład równania liniowe i kwadratowe, liniowe i nierówności kwadratowe, równania ułamkowe i równania redukujące do kwadratu. Zasada pomyślnego rozwiązania każdego z wymienionych problemów jest następująca: należy ustalić, jaki rodzaj problemu jest rozwiązywany, pamiętać o niezbędnej sekwencji działań, które doprowadzą do pożądany rezultat, tj. odpowiedz i wykonaj poniższe kroki.
Oczywiste jest, że sukces lub porażka w rozwiązaniu konkretnego problemu zależy głównie od tego, jak poprawnie zostanie określony rodzaj rozwiązywanego równania, jak poprawnie zostanie odtworzona kolejność wszystkich etapów jego rozwiązania. Oczywiście do wykonania wymagane są umiejętności przemiany tożsamości i informatyka.
Inaczej jest z równania trygonometryczne. Ustalenie faktu, że równanie jest trygonometryczne, wcale nie jest trudne. Trudności pojawiają się przy ustaleniu sekwencji działań, które doprowadziłyby do prawidłowej odpowiedzi.
Przez wygląd równaniu, czasami trudno określić jego rodzaj. A nie znając rodzaju równania, prawie niemożliwe jest wybranie właściwego spośród kilkudziesięciu wzorów trygonometrycznych.
Aby rozwiązać równanie trygonometryczne, musisz spróbować:
1. sprowadzić wszystkie funkcje zawarte w równaniu pod „te same kąty”;
2. doprowadzić równanie do „funkcji identycznych”;
3. uwzględnij lewą stronę równania itp.
Rozważmy podstawowe metody rozwiązywania równań trygonometrycznych.
I. Sprowadzenie do najprostszych równań trygonometrycznych
Schemat rozwiązania
Krok 1. Wyraź funkcję trygonometryczną za pomocą znanych składników.
Krok 2. Znajdź argument funkcji, korzystając ze wzorów:
cos x = a; x = ±arccos a + 2πn, n ЄZ.
grzech x = a; x = (-1) n arcsin a + πn, n Є Z.
tan x = a; x = arctan a + πn, n Є Z.
ctg x = a; x = arcctg a + πn, n Є Z.
Krok 3. Znajdź nieznaną zmienną.
Przykład.
2 cos(3x – π/4) = -√2.
Rozwiązanie.
1) cos(3x – π/4) = -√2/2.
2) 3x – π/4 = ±(π – π/4) + 2πn, n Є Z;
3x – π/4 = ±3π/4 + 2πn, n Є Z.
3) 3x = ±3π/4 + π/4 + 2πn, n Є Z;
x = ±3π/12 + π/12 + 2πn/3, n Є Z;
x = ±π/4 + π/12 + 2πn/3, n Є Z.
Odpowiedź: ±π/4 + π/12 + 2πn/3, n Є Z.
II. Zmienna wymiana
Schemat rozwiązania
Krok 1. Sprowadź równanie do postaci algebraicznej w odniesieniu do jednej z funkcji trygonometrycznych.
Krok 2. Oznacz wynikową funkcję przez zmienną t (jeśli to konieczne, wprowadź ograniczenia na t).
Krok 3. Zapisz i rozwiąż powstałe równanie algebraiczne.
Krok 4. Dokonaj odwrotnej wymiany.
Krok 5. Rozwiąż najprostsze równanie trygonometryczne.
Przykład.
2cos 2 (x/2) – 5sin (x/2) – 5 = 0.
Rozwiązanie.
1) 2(1 – grzech 2 (x/2)) – 5 grzech (x/2) – 5 = 0;
2 grzech 2 (x/2) + 5 grzech (x/2) + 3 = 0.
2) Niech grzech (x/2) = t, gdzie |t| ≤ 1.
3) 2t 2 + 5t + 3 = 0;
t = 1 lub e = -3/2, nie spełnia warunku |t| ≤ 1.
4) grzech(x/2) = 1.
5) x/2 = π/2 + 2πn, n Є Z;
x = π + 4πn, n Є Z.
Odpowiedź: x = π + 4πn, n Є Z.
III. Metoda redukcji rzędu równań
Schemat rozwiązania
Krok 1. Zamień to równanie na liniowe, korzystając ze wzoru na stopień redukcji:
grzech 2 x = 1/2 · (1 – cos 2x);
sałata 2 x = 1/2 · (1 + sałata 2x);
tg 2 x = (1 – cos 2x) / (1 + cos 2x).
Krok 2. Rozwiąż powstałe równanie, stosując metody I i II.
Przykład.
cos 2x + cos 2 x = 5/4.
Rozwiązanie.
1) sałata 2x + 1/2 · (1 + sałata 2x) = 5/4.
2) sałata 2x + 1/2 + 1/2 · sałata 2x = 5/4;
3/2 sałata 2x = 3/4;
2x = ±π/3 + 2πn, n Є Z;
x = ±π/6 + πn, n Є Z.
Odpowiedź: x = ±π/6 + πn, n Є Z.
IV. Równania jednorodne
Schemat rozwiązania
Krok 1. Sprowadź to równanie do postaci
a) a sin x + b cos x = 0 (równanie jednorodne pierwszego stopnia)
lub do widoku
b) a grzech 2 x + b grzech x · cos x + c cos 2 x = 0 (równanie jednorodne drugiego stopnia).
Krok 2. Podziel obie strony równania przez
a) cos x ≠ 0;
b) cos 2 x ≠ 0;
i uzyskaj równanie na tan x:
a) opalenizna x + b = 0;
b) a tan 2 x + b arctan x + c = 0.
Krok 3. Rozwiąż równanie znanymi metodami.
Przykład.
5sin 2 x + 3sin x cos x – 4 = 0.
Rozwiązanie.
1) 5sin 2 x + 3sin x · cos x – 4(sin 2 x + cos 2 x) = 0;
5sin 2 x + 3sin x · cos x – 4sin² x – 4cos 2 x = 0;
grzech 2 x + 3 grzech x · cos x – 4cos 2 x = 0/cos 2 x ≠ 0.
2) tg 2 x + 3tg x – 4 = 0.
3) Niech więc tg x = t
t 2 + 3 t – 4 = 0;
t = 1 lub t = -4, co oznacza
tg x = 1 lub tg x = -4.
Z pierwszego równania x = π/4 + πn, n Є Z; z drugiego równania x = -arctg 4 + πk, k Є Z.
Odpowiedź: x = π/4 + πn, n Є Z; x = -arctg 4 + πk, k Є Z.
V. Metoda przekształcenia równania za pomocą wzorów trygonometrycznych
Schemat rozwiązania
Krok 1. Używanie wszelkiego rodzaju wzory trygonometryczne sprowadź to równanie do równania rozwiązanego metodami I, II, III, IV.
Krok 2. Rozwiąż powstałe równanie, korzystając ze znanych metod.
Przykład.
grzech x + grzech 2x + grzech 3x = 0.
Rozwiązanie.
1) (grzech x + grzech 3x) + grzech 2x = 0;
2sin 2x cos x + grzech 2x = 0.
2) grzech 2x (2cos x + 1) = 0;
grzech 2x = 0 lub 2cos x + 1 = 0;
Z pierwszego równania 2x = π/2 + πn, n Є Z; z drugiego równania cos x = -1/2.
Mamy x = π/4 + πn/2, n Є Z; z drugiego równania x = ±(π – π/3) + 2πk, k Є Z.
W rezultacie x = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.
Odpowiedź: x = π/4 + πn/2, n Є Z; x = ±2π/3 + 2πk, k Є Z.
Zdolność i umiejętność rozwiązywania równań trygonometrycznych jest bardzo duża  Co ważne, ich rozwój wymaga dużego wysiłku, zarówno ze strony ucznia, jak i nauczyciela.
Co ważne, ich rozwój wymaga dużego wysiłku, zarówno ze strony ucznia, jak i nauczyciela.
Z rozwiązywaniem równań trygonometrycznych wiąże się wiele problemów stereometrii, fizyki itp. Proces rozwiązywania takich problemów obejmuje wiele wiedzy i umiejętności, które można zdobyć studiując elementy trygonometrii.
Równania trygonometryczne zajmują ważne miejsce w procesie uczenia się matematyki i rozwoju osobistego w ogóle.
Nadal masz pytania? Nie wiesz jak rozwiązywać równania trygonometryczne?
Aby uzyskać pomoc korepetytora zarejestruj się.
Pierwsza lekcja jest darmowa!
stronie internetowej, przy kopiowaniu materiału w całości lub w części wymagany jest link do źródła.
MOSKWA WYDZIAŁ EDUKACJI
PROFESJONALIZM BUDŻETU PAŃSTWA
INSTYTUCJA EDUKACYJNA w Moskwie
„Politechnika nr 47 imienia V.G. Fiodorowa”
Lekcja
w dyscyplinie Matematyka
„Równania trygonometryczne zredukowane do równań kwadratowych”
Nauczyciel
Protasevich Olga Nikołajewna
ZAWÓD: Inżynier sprzętu i oprogramowania
DYSCYPLINA: Matematyka
DOBRZE : 1
SEMESTR : 2
GRUPA :
Temat lekcji:
„Równania trygonometryczne zredukowane do równań kwadratowych”.
Typ lekcji: lekcja łączona
Forma lekcji: szkolenia zbiorowe według metodologii V.K. Dyaczenko
(Edukacja w systemach małych grup)
Cele Lekcji:
Edukacyjny – rozważyć podejścia ogólne, podsumować informacje o rodzajach i metodach rozwiązywania równań trygonometrycznych, które można sprowadzić do równań kwadratowych; rozwijanie umiejętności i umiejętności stosowania wiedzy przy rozwiązywaniu podstawowych równań i stosowaniu zdobytej wiedzy w działalności zawodowej.
Rozwojowy – promować rozwój logiczne myślenie wśród studentów, rozwijać umiejętność analizowania, rozumowania, porównywania, wyciągania wniosków, rozumienia materiału;
Edukacyjny – rozwijanie zainteresowań poznawczych, elementów kultury komunikowania się, zachęcanie uczniów do pokonywania trudności w procesie aktywności umysłowej, rozwijanie umiejętności pracy w zespole pracy i edukacji.
Cel lekcji:
Zapoznanie studentów z głównymi rodzajami i metodami rozwiązywania równań trygonometrycznych dających się sprowadzić do równań kwadratowych.
Wsparcie (zasoby):
Sprzęt: komputer, projektor multimedialny.
Oprogramowanie:MicrosoftuPrzewyższać.
Podstawowe koncepcje:
Równanie kwadratowe; proste równania trygonometryczne; odwrotne funkcje trygonometryczne; równania trygonometryczne zredukowane do równań kwadratowych.
Literatura:
Bashmakov M.I. Matematyka: podręcznik dla szkół podstawowych i średnich kształcenie zawodowe.- M.; „Akademia”, 2010. - 256 s.
Dyachenko V.K. - M.; „Edukacja publiczna”, 2001. - 496 s.
Bashmakov M.I. Matematyka: książka dla nauczycieli. Podręcznik metodyczny - M.; « Akademia”, 2013 - 224 s.
Materiały witrynyruch społeczno-pedagogiczny na rzecz stworzenia kolektywnego sposobu nauczania:www.kco-kras.ru.
Kroki lekcji
Organizowanie czasu.
Sprawdzanie pracy domowej.
Aktualizacja podstawowej wiedzy.
Nauka nowego materiału.
Utrwalanie i systematyzacja zdobytej wiedzy.
Odbicie. Zreasumowanie. Praca domowa.
Podczas zajęć
Organizowanie czasu.
Nauczyciel wyznacza uczniom cele lekcji:
1) Przedstaw główne typy równań trygonometrycznych, które można sprowadzić do równań kwadratowych;
2) Przedstaw standardowe metody rozwiązywania równań trygonometrycznych dających się sprowadzić do równań kwadratowych.
3) Nauczać, jak zastosować zdobytą wiedzę i umiejętności do rozwiązywania równań standardowych;
4) Naucz, jak pracować z informacjami przedstawionymi w różne formy, sprawować wzajemną kontrolę i samokontrolę, wykorzystywać zdobytą wiedzę w działalności zawodowej.
II . Sprawdzanie pracy domowej.
Nauczyciel przeprowadza prezentację „Zadania domowe”, zgodnie z którą uczniowie samodzielnie sprawdzają swoją pracę domową i w razie potrzeby nanoszą do niej poprawki i poprawki.
Na prośbę uczniów nauczyciel komentuje rozwiązania równań, które sprawiły im trudność, po czym podaje nazwiska uczniów, którzy na koniec lekcji przekazują swoje zeszyty do sprawdzenia.
№ 1
Odpowiedź:
№ 2
Odpowiedź:
№ 3
Odpowiedź:
№ 4
ponieważ wtedy równanie nie ma pierwiastków
Odpowiedź: brak korzeni
№ 5
Odpowiedź:
№ 6
Odpowiedź:
III . Aktualizacja podstawowej wiedzy.
Nauczyciel tworzy grupy/pary studyjne i sugeruje, aby na podstawie dostarczonych formularzy ustalić zgodność równań z odpowiedziami: „Przed tobą slajd z zadaniem edukacyjnym. Połącz równania (lewa strona tabeli) z odpowiedziami (prawa strona tabeli). Zapisz w zeszycie numery odpowiednich par zdań.”
Określone zadania są powielane w dołączonej prezentacji.
Mecz
p/s
Równanie
p/s
Odpowiedź
żadnych korzeni
Na koniec pracy nauczyciel frontalnie przeprowadza wywiad z przedstawicielami grupy, po czym włącza stronę prezentacji z właściwymi rozwiązaniami.
Prawidłowe odpowiedzi
p/s
Równanie
p/s
Odpowiedź
żadnych korzeni
żadnych korzeni
11.
13.
10.
12.
IV . Nauka nowego materiału.
Prowadzący uwzględnia prezentację nowego materiału „Równania trygonometryczne zredukowane do równań kwadratowych. Rodzaje równań i metody ich rozwiązań.”
Zaprasza uczniów do zapisania niezbędnych punktów i rozpoczyna komentowanie każdego slajdu, po czym włączają prezentację.
Przedstawmy koncepcję:
Ogólny widok równania kwadratowego:
1 rodzaj równań trygonometrycznych dających się sprowadzić do równań kwadratowych – równań algebraicznych ze względu na jedną z funkcji trygonometrycznych.
Nauczyciel wyjaśnia rozwiązania.
1. Bezpośrednia substytucja
Wymiana ,
I
żadnych korzeni
Odpowiedź:
Równania postaci mają podobne rozwiązanie
Wymiana
Wymiana
2. Równania wymagające przeliczenia przy użyciu wzoru na jednostkę trygonometryczną
Wymiana , wtedy równanie przyjmuje postać
I
żadnych korzeni
Odpowiedź:
Równania postaci mają podobne rozwiązanie:
zastąpimy , korzystając ze wzoru na jednostkę trygonometryczną
.
Otrzymujemy równanie zawierające tylko jedną funkcję trygonometryczną :
Wymiana
3. Równania wymagające przekształcenia z wykorzystaniem wzoru koneksyjnego tgx I Z tgx
Stosujemy wzór:
Pomnóż równanie przez
Wymiana , wtedy równanie przyjmuje postać
I
Odpowiedź:
Typ 2 równania trygonometryczne sprowadzające się do równań kwadratowych– równania jednorodne, w których każdy wyraz ma ten sam stopień.
Podziel równanie przez
Wymiana , wtedy równanie przyjmuje postać
I
Odpowiedź:
Nauczyciel sugeruje podsumowanie prezentowanego materiału i zadaje pytania: „Na ile typów dzieli się równania trygonometryczne, które można sprowadzić do równań kwadratowych? Ich imię? Wymień sposoby rozwiązywania równań trygonometrycznych, które można sprowadzić do równań kwadratowych.”
Nauczyciel kieruje działaniami uczniów podczas tworzenia algorytmu rozwiązywania tego typu równań.
Równania trygonometryczne redukujące się do równań kwadratowych dzielą się na dwa główne typy:
tgx I Z tgx :
Typ 2 – równania jednorodne, w których każdy wyraz ma ten sam stopień:
Nauczyciel dokonuje korekty Algorytm rozwiązania:
1. Określ typ równania. Jeśli to konieczne, przekształć równanie tak, aby było tylko jedno funkcja trygonometryczna. Aby to zrobić, wybierz żądaną formułę: lub lub podzielić na
2. Wprowadzono zamiennik (np, sinx = T , cosx = T , tgx = T ).
5. Zapisz odpowiedź.
Aby utrwalić zdobytą wiedzę, nauczyciel sugeruje ustalenie zgodności między równaniami a możliwymi sposobami ich rozwiązania: „Przed tobą slajd z zadaniem szkoleniowym.
1. Klasyfikuj równania według metod rozwiązywania zgodnie z poniższą tabelą
(drukowane wersje tabeli znajdują się na Waszych biurkach).
2. Wpisz w odpowiednim polu numer metody rozwiązania.
Wypełnij tabelę”.
Pracę wykonuje się w parach.
p/s
Równanie
metoda
Metody:
1) Wprowadź nową zmienną.
2) Wprowadź nową zmienną
3) Wprowadź nową zmienną.
4) Przekształć równanie korzystając ze wzoru i wprowadź nową zmienną.
5) Przekształć równanie za pomocą wzoru, wprowadź nową zmienną.
6) Podziel każdy wyraz równania przez, wprowadź nową zmienną.
7) Przekształć równanie za pomocą wzoru, pomnóż wyrazy równania przez, wprowadź nową zmienną.
Zadanie sprawdzane jest w formie rozmowy frontalnej.
Nauczyciel: „Przed tobą slajd z poprawnymi odpowiedziami na zadanie edukacyjne. . Sprawdź sprawdzając poprawne odpowiedzi do zadania edukacyjnego. Pracuj nad błędami w swoim notatniku.”
Arkusze zadań zbierane są na koniec lekcji.
p/s
Równanie
metoda
2
4
2
1
7
1
3
5
6
3
6
2
6
VI . Utrwalanie i systematyzacja zdobytej wiedzy.
Nauczyciel zaprasza uczniów do dalszej pracy w grupach.
Nauczyciel: „Rozwiąż równania. Sprawdź wynik w edytorze Microsoftu Przewyższać . Po zakończeniu rozwiązania przedstawiciel grupy podchodzi do tablicy i prezentuje rozwiązanie uzupełnionego przez grupę równania.” Nauczyciel sprawdza rozwiązanie, ocenia pracę grupy i, jeśli to konieczne, wskazuje błędy.”
Nauczyciel:
1 ) Omów rozwiązania w grupie.
2) Zapisz rozwiązanie i otrzymaną odpowiedź w zeszycie.
3) Sprawdź wynik w edytorze Microsoftu Przewyższać .
4) Powiadom nauczyciela, że jesteś gotowy.
5) Wyjaśnij swoją decyzję, zapisując ją na tablicy członkom innych grup.
6) Słuchaj uważnie przemówień swoich towarzyszy, w razie potrzeby zadawaj pytania.
Grupy badawcze, które wykonały w całości zadania, proszone są o wykonanie zadań innych grup. Grupy, które osiągnęły sukces, nagradzane są wzrostem wyniku końcowego o jedną jednostkę.
Pierwsza grupa:
Stosujemy wzór:
I
żadnych korzeni
ponieważ
Odpowiedź:
Druga grupa:
Stosujemy wzór:
Podstawienie, wtedy równanie staje się
I
Odpowiedź: ;
Trzecia grupa:
Stosujemy wzór:
Pomnóż równanie przez
Podstawienie, wtedy równanie staje się
I
Odpowiedź:
Czwarta grupa:
Podziel równanie przez
Podstawienie, wtedy równanie staje się
I
Odpowiedź:
Piąta grupa:
Podstawienie, wtedy równanie staje się
I
Odpowiedź:; .
VII . Odbicie. Zreasumowanie. Praca domowa.
Nauczyciel: Podsumujmy Twoją pracę, korelując rezultaty Twoich działań z Twoim celem.
Powtórzmy koncepcje:
„Równania trygonometryczne, które sprowadza się do równań kwadratowych poprzez transformację i zmianę zmiennej, nazywane są równaniami trygonometrycznymi dającymi się sprowadzić do równań kwadratowych”.
Typ 1 – równania algebraiczne ze względu na jedną z funkcji trygonometrycznych:
- bezpośrednia substytucja - wymiana lub;
- równania wymagające przeliczenia przy użyciu wzoru na jednostkę trygonometryczną;
- równania wymagające przekształcenia zgodnie ze wzorem połączenia tgx i z tgx :
Typ 2 – równania jednorodne, w których każdy wyraz ma ten sam stopień: podziel równanie przez, a następnie zamień.
Algorytm rozwiązania:
1. Określ typ równania. Jeśli to konieczne, przekształć równanie tak, aby zawierało tylko jedną funkcję trygonometryczną.
Aby to zrobić, wybierz żądaną formułę:
Lub lub podzielić na
2. Wprowadzono zamianę (na przykład sinx = T , cosx = T , tgx = T ).
3. Rozwiąż równanie kwadratowe.
4. Dokonano odwrotnego podstawienia i rozwiązano najprostsze równanie trygonometryczne.
5. Zapisz odpowiedź.
Nauczyciel ocenia pracę uczniów, grupy badawcze i ogłasza wyniki.
Nauczyciel: „Zapisz swoją pracę domową: Bashmakov M.I. Matematyka: podręcznik dla profesjonalistów w szkołach podstawowych i średnich. edukacja – M.; „Akademia”, 2010. s. 114-115. W numerze 10 rozwiąż równania numer 4,5,7,9. s. 118. Sprawdź wynik w edytorze Microsoftu Przewyższać ».