Nikołaj kupił ogólny notatnik zawierający 96 kartek. Olimpiady Matematyczne i problemy olimpiad. Życzymy sukcesu

Sekcje: Matematyka

Drogi Uczestniku Olimpiady!

Szkolna Olimpiada Matematyczna odbywa się w jednej rundzie.
Do wykonania jest 5 zadań o różnym stopniu trudności.
Nie stawia się Państwu żadnych specjalnych wymagań odnośnie wykonania pracy. Forma prezentacji rozwiązań problemów, a także sposoby ich rozwiązania mogą być dowolne. Jeśli masz jakieś indywidualne przemyślenia na temat konkretnego zadania, ale nie możesz dokończyć rozwiązania, nie wahaj się wyrazić wszystkich swoich myśli. Nawet częściowo rozwiązane zadania otrzymają odpowiednią liczbę punktów.
Zacznij rozwiązywać problemy, które uważasz za łatwiejsze, a następnie przejdź do reszty. W ten sposób zaoszczędzisz czas pracy.

Życzymy sukcesu!

Etap szkolny Ogólnorosyjska Olimpiada dzieci w wieku szkolnym na matematyce

5 klasa.

Ćwiczenie 1. W wyrażeniu 1*2*3*4*5 zamień „*” na znaki akcji i umieść nawiasy w ten sposób. Aby uzyskać wyrażenie, którego wartość wynosi 100.

Zadanie 2. Wymagane jest rozszyfrowanie zapisu równości arytmetycznej, w której liczby są zastępowane literami, a różne liczby są zastępowane różnymi literami, identyczny - identyczny.

PIĘĆ - TRZY = DWA Wiadomo, że zamiast listu A musisz zastąpić cyfrę 2.

Zadanie 3. Jak za pomocą wagi kubkowej bez odważników podzielić 80 kg gwoździ na dwie części - 15 kg i 65 kg?

Zadanie 4. Przetnij figurę pokazaną na rysunku na dwie równe części, tak aby każda część miała jedną gwiazdkę. Można ciąć tylko wzdłuż linii siatki.

Zadanie 5. Filiżanka i spodek razem kosztują 25 rubli, a 4 filiżanki i 3 spodki kosztują 88 rubli. Znajdź cenę filiżanki i cenę spodka.

6 klasa.

Ćwiczenie 1. Porównuj ułamki zwykłe, nie sprowadzając ich do wspólnego mianownika.

Zadanie 2. Należy rozszyfrować zapis równości arytmetycznej, w której liczby są zastępowane literami, różne liczby zastępowane są różnymi literami, a identyczne zastępowane są identycznymi. Zakłada się, że pierwotna równość jest prawdziwa i zapisana zgodnie ze zwykłymi zasadami arytmetyki.

PRACA
+WOLA
SZCZĘŚCIE

Zadanie 3. W obóz letni Trzej przyjaciele odpoczęli: Misza, Wołodia i Petya. Wiadomo, że każdy z nich ma jedno z następujących nazwisk: Iwanow, Semenow, Gerasimov. Misza to nie Gerasimow. Ojciec Wołodii jest inżynierem. Wołodia jest w szóstej klasie. Gerasimov uczy się w piątej klasie. Ojciec Iwanowa jest nauczycielem. Jak nazywa się każdy z trzech przyjaciół?

Zadanie 4. Podziel figurę wzdłuż linii siatki na cztery równe części, tak aby każda część zawierała jeden punkt.

Zadanie 5. Skacząca ważka spała połowę czasu każdego dnia czerwonego lata, tańczyła przez jedną trzecią każdego dnia i śpiewała przez jedną szóstą czasu. Resztę czasu postanowiła poświęcić na przygotowania do zimy. Ile godzin dziennie Ważka przygotowywała się do zimy?

7. klasa.

Ćwiczenie 1. Rozwiąż zagadkę, jeśli wiesz, że największą cyfrą liczby SILNY jest 5:

DECYDOWAĆ
JEŚLI
MOCNY

Zadanie 2. Rozwiąż równanie│7 - x│ = 9,3

Zadanie 3. Po siedmiu praniach długość, szerokość i grubość mydła zmniejszyła się o połowę. Na ile prań wystarczy pozostałe mydło?

Zadanie 4 . Podziel prostokąt złożony z komórek 4 × 9 wzdłuż boków komórek na dwie równe części, tak aby można było z nich następnie utworzyć kwadrat.

Zadanie 5. Drewniana kostka została pomalowana na biało ze wszystkich stron, a następnie pocięta na 64 identyczne kostki. Ile sześcianów zostało pokolorowanych z trzech stron? Po obu stronach?
Po jednej stronie? Ile kostek nie jest pokolorowanych?

8 klasa.

Ćwiczenie 1. Na jakie dwie cyfry kończy się liczba 13?

Zadanie 2. Zmniejsz ułamek:

Zadanie 3. Szkolne kółko teatralne przygotowuje się do wystawienia fragmentu bajki A.S. Puszkina o carze Saltanie, postanowił podzielić role między uczestnikami.
„Będę Czernomorem” – powiedziała Yura.
„Nie, będę Czernomorem” – powiedział Kola.
„OK” – przyznała Yura. „Umiem zagrać Guidona”.
„Cóż, mogę zostać Saltanem”, Kolya również wykazała zgodność.
- Zgadzam się być tylko Guidonem! - powiedziała Misza.
Życzenia chłopców zostały spełnione. Jak rozdzielono role?

Zadanie 4. W równoramiennych trójkąt ABC przy podstawie AB = 8m wykreślono medianę AD. Obwód trójkąta ACD jest o 2 m większy od obwodu trójkąta ABD. Znajdź AC.

Zadanie 5. Mikołaj kupił zeszyt ogólny zawierający 96 kartek i ponumerował strony od 1 do 192. Bratanek Artur wyrwał z tego zeszytu 35 kartek i dodał wszystkie 70 zapisanych na nich liczb. Czy w 2010 roku mógł odnieść sukces?

9. klasa.

Ćwiczenie 1. Znajdź ostatnią cyfrę roku 1989 1989.

Zadanie 2. Suma pierwiastków niektórych równanie kwadratowe wynosi 1, a suma ich kwadratów wynosi 2. Jaka jest suma ich kostek?

Zadanie 3. Korzystając z trzech median m a, m b i m c ∆ ABC, znajdź długość boku AC = b.

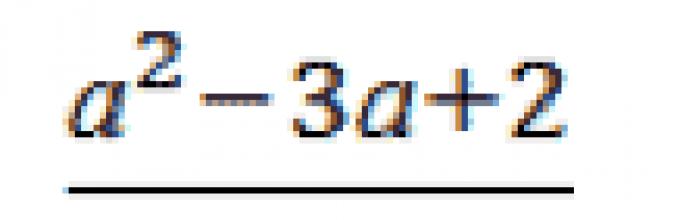
Zadanie 4. Zmniejsz ułamek .

Zadanie 5. Na ile sposobów możesz wybrać samogłoskę i spółgłoskę w słowie „kamzol”?

klasa 10.

Ćwiczenie 1. Obecnie dostępne są monety o nominałach 1, 2, 5, 10 rubli. Wypisz wszystkie sumy pieniędzy, które można zapłacić parzystą i nieparzystą liczbą monet.

Zadanie 2. Udowodnić, że 5 + 5 2 + 5 3 + … + 5 2010 jest podzielne przez 6.

Zadanie 3. W czworokącie ABCD przekątne przecinają się w jednym punkcie M. Wiadomo, że AM = 1,
VM = 2, SM = 4. Przy jakich wartościach DM czworoboczny ABCD czy to trapez?

Zadanie 4. Rozwiązać układ równań

Zadanie 5. Trzydzieścioro uczniów – uczniów dziesiątej i jedenastej klasy – uścisnęło dłonie. Okazało się, że co dziesiąty uczeń uścisnął dłoń ośmiu jedenastoklasistom, a co jedenastoklasista uścisnął dłoń siedmiu dziesiątoklasistom. Ilu było uczniów dziesiątej klasy, a ilu jedenastoklasistów?

Zadanie 16:

Czy można wymienić 25 rubli na 10 banknotów o nominałach 1, 3 i 5 rubli? Rozwiązanie:

Odpowiedź: Nie

Petya kupił notatnik ogólny o objętości 96 kartek i ponumerował wszystkie jego strony liczbami od 1 do 192. Wasia wyrwała z tego notesu 25 kartek i dodała wszystkie 50 zapisanych na nich liczb. Czy w 1990 roku mógł odnieść sukces? Rozwiązanie:

Na każdym arkuszu suma numerów stron jest nieparzysta, a suma 25 liczb nieparzystych jest nieparzysta.

Iloczyn 22 liczb całkowitych wynosi 1. Udowodnij, że ich suma nie wynosi zero. Rozwiązanie:

Wśród tych liczb - Liczba parzysta„jedynki minusowe”, a żeby suma była równa zero, musi ich być dokładnie 11.

Czy można komponować magiczny kwadrat z pierwszych 36 liczb pierwszych? Rozwiązanie:

Spośród tych liczb jedna (2) jest parzysta, a pozostałe są nieparzyste. Dlatego w wierszu, w którym jest dwójka, suma liczb jest nieparzysta, a w innych parzysta.

W rzędzie zapisuje się liczby od 1 do 10. Czy można umieścić między nimi znaki „+” i „-” tak, aby wartość powstałego wyrażenia była równa zero?

Uwaga: proszę o tym pamiętać liczby ujemne są również parzyste i nieparzyste. Rozwiązanie:

Tak naprawdę suma liczb od 1 do 10 wynosi 55, a zmieniając w niej znaki, zmieniamy całe wyrażenie na liczbę parzystą.

Konik polny skacze po linii prostej, a za pierwszym razem skoczył 1 cm w jakimś kierunku, za drugim razem - 2 cm i tak dalej. Udowodnij, że po skokach w 1985 roku nie może skończyć tam, gdzie zaczął. Rozwiązanie:

Uwaga: Suma 1 + 2 + … + 1985 jest nieparzysta.

Na tablicy zapisano liczby 1, 2, 3, ..., 1984, 1985. Można wymazać z tablicy dowolne dwie liczby i zamiast tego zapisać moduł ich różnicy. Ostatecznie na planszy pozostanie tylko jedna liczba. Czy może być zero? Rozwiązanie:

Sprawdź, czy powyższe operacje nie zmieniają parzystości sumy wszystkich liczb zapisanych na tablicy.

Czy da się przykryć szachownicę kostkami domino 1×2 tak, aby wolne były tylko pola a1 i h8? Rozwiązanie:

Każde domino zakrywa jedno czarne i jedno białe pole, a po odrzuceniu kwadratów a1 i h8 zostaje o 2 mniej czarnych kwadratów niż białych.

Do liczby 17-cyfrowej dodaliśmy liczbę zapisaną tymi samymi cyframi, ale w odwrotnej kolejności. Udowodnić, że co najmniej jedna cyfra otrzymanej sumy jest parzysta. Rozwiązanie:

Rozważmy dwa przypadki: suma pierwszej i ostatniej cyfry liczby jest mniejsza niż 10 oraz suma pierwszej i ostatniej cyfry liczby jest nie mniejsza niż 10. Jeśli założymy, że wszystkie cyfry sumy są nieparzyste, to w pierwszym przypadku nie powinno być ani jednego przeniesienia w cyfrach (co jest oczywiste, prowadzi to do sprzeczności), a w drugim przypadku obecność przeniesienia przy przejściu od prawej do lewej lub od lewej do prawej przeplata się z brakiem przeniesienia i w rezultacie otrzymujemy, że cyfra sumy na dziewiątej cyfrze jest z konieczności parzysta.

W oddziale ludowym jest 100 osób, a każdego wieczoru trzy z nich pełnią służbę. Czy może być tak, że po jakimś czasie okazuje się, że każdy miał dyżur z każdym dokładnie raz? Rozwiązanie:

Od każdego obowiązku, w którym uczestniczy ta osoba, pełni służbę z dwoma innymi osobami, wówczas pozostałych można podzielić na pary. Jednak 99 to liczba nieparzysta.

Na prostej znajduje się 45 punktów leżących poza odcinkiem AB. Udowodnij, że suma odległości tych punktów od punktu A nie jest równa sumie odległości tych punktów od punktu B. Rozwiązanie:

Dla dowolnego punktu X leżącego poza AB mamy AX - BX = ± AB. Jeżeli założymy, że sumy odległości są równe, to otrzymamy, że wyrażenie ± AB ± AB ± … ± AB, które obejmuje 45 wyrazów, jest równe zeru. Ale to jest niemożliwe.

W okręgu ułożonych jest 9 liczb - 4 jedyneki i 5 zer. Co sekundę na liczbach wykonywana jest następująca operacja: pomiędzy sąsiadującymi liczbami wstawia się zero, jeśli są różne, i jednostkę, jeśli są równe; następnie stare numery są usuwane. Czy po pewnym czasie wszystkie liczby mogą stać się takie same? Rozwiązanie:

Oczywiste jest, że przed dziewięcioma zerami nie można uzyskać kombinacji dziewięciu jedynek. Jeśli było dziewięć zer, to w poprzednim ruchu zera i jedynki musiały się zmienić, co jest niemożliwe, ponieważ jest ich tylko nieparzysta liczba.

Przy okrągłym stole siedzi 25 chłopców i 25 dziewcząt. Udowodnij, że niektórzy z osób siedzących przy stole mają obu chłopców za sąsiadów. Rozwiązanie:

Przeprowadźmy dowód przez sprzeczność. Ponumerujmy po kolei wszystkich siedzących przy stole, zaczynając od jakiegoś miejsca. Jeśli włączone k-te miejsce siedzi chłopiec, wtedy jasne jest, że dziewczęta siedzą na (k - 2) i (k + 2) miejscach. Ale ponieważ liczba chłopców i dziewcząt jest równa, to w przypadku każdej dziewczyny siedzącej na n-tym miejscu prawdą jest, że na (n - 2) i (n + 2) miejscu są chłopcy. Jeśli teraz weźmiemy pod uwagę tylko te 25 osób, które siedzą na „równych” miejscach, odkryjemy, że wśród nich chłopcy i dziewczęta zmieniają się, jeśli obejdziemy stół w jakimś kierunku. Ale 25 to liczba nieparzysta.

Ślimak czołga się po samolocie ze stałą prędkością, obracając się pod kątem prostym co 15 minut. Udowodnić, że może wrócić do punktu początkowego dopiero po całkowitej liczbie godzin. Rozwiązanie:

Jest oczywiste, że liczba a obszarów, po których ślimak pełzał w górę lub w dół, jest równa liczbie obszarów, po których pełzał w prawo lub w lewo. Pozostaje tylko zauważyć, że a jest parzyste.

Trzy koniki polne grają w żabę skaczącą po linii prostej. Za każdym razem jeden z nich przeskakuje nad drugim (ale nie oba na raz!). Czy po skoku w 1991 roku uda im się znaleźć w tych samych miejscach? Rozwiązanie:

Oznaczmy koniki polne A, B i C. Nazwijmy ułożenie koników polnych ABC, BCA i CAB (od lewej do prawej) prawidłowym, a ACB, BAC i CBA nieprawidłowym. Łatwo zauważyć, że przy każdym skoku zmienia się rodzaj ułożenia.

Monet jest 101, z czego 50 to podróbki, różniące się masą o 1 gram od prawdziwych. Petya wziął jedną monetę i w jednej zważywszy na wadze ze strzałką pokazującą różnicę wag na kubkach, chce ustalić, czy jest to podróbka. Czy uda mu się to zrobić? Rozwiązanie:

Musisz odłożyć tę monetę na bok, a następnie podzielić pozostałe 100 monet na dwa stosy po 50 monet każdy i porównać wagi tych stosów. Jeżeli różnią się one o parzystą liczbę gramów, to interesująca nas moneta jest prawdziwa. Jeśli różnica w wadze jest nieparzysta, moneta jest fałszywa.

Czy można zapisać liczby od 1 do 9 raz pod rząd, tak aby między jednym a dwoma, dwoma i trzema, ..., osiem i dziewięć powstała nieparzysta liczba cyfr? Rozwiązanie:

W przeciwnym razie wszystkie liczby w rzędzie znalazłyby się w miejscach o tej samej parzystości.

Ta praca Petya kupiła ogólny notatnik o objętości 96 arkuszy i ponumerowała wszystkie jego strony numerami od 1 do 192. Vasya wyrwała (Test) na ten temat (ACD i analiza finansowa), została ukończona na indywidualne zamówienie przez specjalistów naszej firmy i zdała egzamin skuteczna obrona. Praca - Petya kupił ogólny notatnik o objętości 96 kartek i ponumerował wszystkie strony w kolejności od 1 do 192. Wasya wyrwał ACD na ten temat, a analiza finansowa odzwierciedla jego temat i logiczny element jego ujawnienia, Ujawnia się istota badanego zagadnienia, uwydatnia się główne postanowienia i wiodące idee tego tematu.
Praca - Petya kupił zeszyt ogólny o objętości 96 kartek i ponumerował wszystkie jego strony numerami od 1 do 192. Wasia go wyrwała, zawiera: tabele, rysunki, najnowsze źródła literackie, rok oddania pracy oraz obroniony - 2017. W pracy Petya kupił ogólny tom zeszytu składający się z 96 arkuszy i ponumerował wszystkie strony w kolejności od 1 do 192. Wyciągnięta Vasya (AHD i analiza finansowa) ujawnia trafność tematu badawczego, odzwierciedla stopień rozwoju problemu, oparty na głębokiej ocenie i analizie wiedzy naukowej i literatura metodologiczna, w pracy nad tematem ACD i analizy finansowej, przedmiot analizy i jego zagadnienia są rozpatrywane kompleksowo, zarówno od strony teoretycznej, jak i praktycznej, formułuje się cel i cele szczegółowe rozpatrywanego tematu, istnieje logika prezentacja materiału i jego kolejności.