W algebrze często konieczne jest nie tylko rozwiązanie układu nierówności, ale wybranie z powstałego zbioru rozwiązań rozwiązań spełniających dodatkowe warunki.
Jednym z tego typu zadań jest znalezienie całkowitych rozwiązań układu nierówności.
1) Znajdź całe rozwiązania układu nierówności:
7x - 5\\ 5 - x
Niewiadome przesuwamy na jedną stronę, znane na drugą z przeciwnym znakiem:
Title="Wyrenderowane przez QuickLaTeX.com">!}
Po uproszczeniu dzielimy obie strony każdej nierówności przez . Przy dzieleniu przez liczbę dodatnią znak nierówności nie zmienia się:
Title="Wyrenderowane przez QuickLaTeX.com">!}
Title="Wyrenderowane przez QuickLaTeX.com">!}
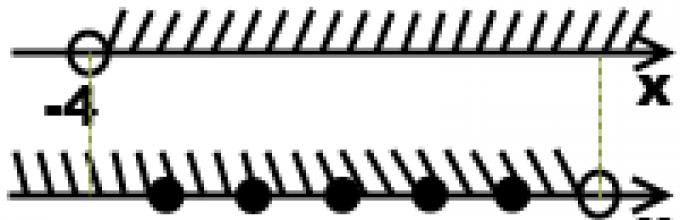
Zaznaczamy rozwiązania nierówności na osiach liczbowych. jest przecięciem rozwiązań (czyli częścią, w której na obu liniach występuje cieniowanie).
Obie nierówności są ścisłe, dlatego -4 i 2 są reprezentowane przez punkty przebite i nie są uwzględniane w rozwiązaniu:

Z przedziału (-4;2) wybieramy całe rozwiązania.
Odpowiedź: -3; -2; -1; 0; 1.
2) Jakie rozwiązania całkowite ma układ nierówności?
Title="Wyrenderowane przez QuickLaTeX.com">!}
Niewiadome przesuwamy w jednym kierunku, znane w drugim, z przeciwnym znakiem
Title="Wyrenderowane przez QuickLaTeX.com">!}
Upraszczamy i dzielimy obie części przez liczbę znajdującą się przed X. Pierwszą nierówność dzielimy przez liczbę dodatnią, więc znak nierówności się nie zmienia, drugi - przez liczba ujemna, więc znak nierówności jest odwrócony:
Title="Wyrenderowane przez QuickLaTeX.com">!}
Zaznaczamy rozwiązania nierówności na osiach liczbowych. Pierwsza nierówność nie jest ścisła, dlatego -2 przedstawiamy jako wypełnioną kropkę. Druga nierówność nie jest ścisła, zatem liczbę 5 reprezentuje przebita kropka:

Rozwiązania całkowite w przedziale [-2;5) to -2; -1; 0; 1; 2; 3; 4.
Odpowiedź: -2; -1; 0; 1; 2; 3; 4.
W niektórych przykładach nie trzeba podawać całych rozwiązań, wystarczy wskazać ich liczbę.
3) Ile rozwiązań całkowitych ma układ nierówności?
![]()
Niewiadome przesuwamy na jedną stronę, wiadome na drugą:
![]()
Title="Wyrenderowane przez QuickLaTeX.com">!}
Obie strony pierwszej nierówności dzielimy przez liczbę ujemną, więc znak nierówności zmienia się na przeciwny. Obie strony drugiej nierówności dzielimy przez liczbę dodatnią, znak nierówności się nie zmienia:
Rozwiązanie nierówności zaznaczamy na osiach liczbowych. Obie nierówności nie są ścisłe, dlatego -3,5 i 1,7 przedstawiamy wypełnionymi kropkami:

Rozwiązaniem układu jest przedział [-3,5; 1,7]. Liczby całkowite mieszczące się w tym zakresie to -3; -2; -1; 0; 1. W sumie jest ich 5.
4) Ile liczb całkowitych jest rozwiązaniami układu nierówności?
Nierówność jest wyrażeniem z, ≤ lub ≥. Na przykład 3x - 5 Rozwiązanie nierówności polega na znalezieniu wszystkich wartości zmiennych, dla których nierówność jest prawdziwa. Każda z tych liczb jest rozwiązaniem nierówności, a zbiór wszystkich takich rozwiązań jest jej rozwiązaniem wiele rozwiązań. Nierówności mające ten sam zbiór rozwiązań nazywane są nierównościami równoważne nierówności.
Nierówności liniowe
Zasady rozwiązywania nierówności są podobne do zasad rozwiązywania równań.Zasady rozwiązywania nierówności
Dla dowolnych liczb rzeczywistych a, b i c:
Zasada dodawania nierówności: Jeśli Zasada mnożenia nierówności: Jeśli 0 jest prawdą, to ac. Jeśli a bc jest również prawdą.
Podobne stwierdzenia dotyczą również a ≤ b.
Gdy obie strony nierówności zostaną pomnożone przez liczbę ujemną, znak nierówności należy odwrócić.
Nazywa się nierówności pierwszego stopnia, jak w przykładzie 1 (poniżej). nierówności liniowe.
Przykład 1 Rozwiąż każdą z poniższych nierówności. Następnie narysuj zestaw rozwiązań.
a) 3x - 5 b) 13 - 7x ≥ 10x - 4
Rozwiązanie
Rozwiązaniem jest każda liczba mniejsza niż 11/5.
Zbiór rozwiązań to (x|x
Aby to sprawdzić, możemy narysować wykres y 1 = 3x - 5 i y 2 = 6 - 2x. Wtedy jest jasne, że dla x 
Zbiór rozwiązań to (x|x ≤ 1) lub (-∞, 1). Wykres zestawu rozwiązań pokazano poniżej. ![]()
Podwójne nierówności
Kiedy dwie nierówności są połączone słowem I, Lub, następnie powstaje podwójna nierówność. Podwójna nierówność, np
-3
I 2x + 5 ≤ 7
zwany połączony, bo używa I. Wpis -3 Nierówności podwójne można rozwiązać stosując zasady dodawania i mnożenia nierówności.
Przykład 2 Rozwiąż -3 Rozwiązanie Mamy
Zbiór rozwiązań (x|x ≤ -1 Lub x > 3). Rozwiązanie możemy również zapisać, korzystając z notacji przedziałowej i symbolu wspomnienia lub włączając oba zbiory: (-∞ -1] (3, ∞) Wykres zbioru rozwiązań pokazano poniżej. 
Aby to sprawdzić, wykreślmy y 1 = 2x - 5, y 2 = -7 i y 3 = 1. Zauważ, że dla (x|x ≤ -1 Lub x > 3), y 1 ≤ y 2 Lub y 1 > y 3 . 
Nierówności o wartości bezwzględnej (moduł)
Nierówności czasami zawierają moduły. Do ich rozwiązania wykorzystywane są następujące właściwości.
Dla a > 0 i wyrażenia algebraicznego x:
|x| |x| > a jest równoważne x lub x > a.
Podobne stwierdzenia dla |x| ≤ a i |x| ≥ a.
Na przykład,
|x| |y| ≥ 1 odpowiada y ≤ -1 Lub y ≥ 1;
i |2x + 3| ≤ 4 odpowiada -4 ≤ 2x + 3 ≤ 4.
Przykład 4 Rozwiąż każdą z poniższych nierówności. Narysuj zbiór rozwiązań.
a) |3x + 2| b) |5 - 2x| ≥ 1
Rozwiązanie
a) |3x + 2|

b) |5 - 2x| ≥ 1
Zbiór rozwiązań to (x|x ≤ 2 Lub x ≥ 3) lub (-∞, 2] .
Cały algorytm opisany powyżej jest zapisany w następujący sposób:
3 x + 12 ≤ 0 ; 3 x ≤ - 12 ; x ≤ - 4 .
Odpowiedź: x ≤ - 4 lub (- ∞, - 4 ] .
Przykład 2
Wskaż wszystkie dostępne rozwiązania nierówności − 2, 7 · z > 0.
Rozwiązanie
Z warunku widzimy, że współczynnik a dla z jest równy - 2,7, a b jest wyraźnie nieobecne lub równe zero. Nie możesz skorzystać z pierwszego kroku algorytmu, ale od razu przejść do drugiego.
Obie strony równania dzielimy przez liczbę - 2, 7. Ponieważ liczba jest ujemna, konieczne jest odwrócenie znaku nierówności. Oznacza to, że otrzymujemy to (− 2, 7 z): (− 2, 7)< 0: (− 2 , 7) , и дальше z < 0 .
Zapiszmy cały algorytm w krótkiej formie:
− 2, 7 z > 0; z< 0 .
Odpowiedź: z< 0 или (− ∞ , 0) .
Przykład 3
Rozwiąż nierówność - 5 x - 15 22 ≤ 0.
Rozwiązanie
Zgodnie z warunkiem widzimy, że konieczne jest rozwiązanie nierówności ze współczynnikiem a dla zmiennej x, która jest równa - 5, ze współczynnikiem b, który odpowiada ułamkowi - 15 22. Należy rozwiązać nierówność postępując zgodnie z algorytmem, czyli: przenieść - 15 22 do innej części o przeciwnym znaku, podzielić obie części przez - 5, zmienić znak nierówności:
5 x ≤ 15 22 ; - 5 x: - 5 ≥ 15 22: - 5 x ≥ - 3 22
Podczas ostatniego przejścia dla prawej strony stosowana jest zasada dzielenia liczby różnymi znakami 15 22: - 5 = - 15 22: 5, po czym wykonujemy dzielenie ułamek wspólny do liczby naturalnej - 15 22: 5 = - 15 22 · 1 5 = - 15 · 1 22 · 5 = - 3 22 .
Odpowiedź: x ≥ - 3 22 i [ - 3 22 + ∞) .
Rozważmy przypadek, gdy a = 0. Wyrażenie liniowe postaci a x + b< 0 является неравенством 0 · x + b < 0 , где на рассмотрение берется неравенство вида b < 0 , после чего выясняется, оно верное или нет.
Wszystko opiera się na wyznaczeniu rozwiązania nierówności. Dla dowolnej wartości x otrzymujemy nierówność liczbowa wpisz b< 0 , потому что при подстановке любого t вместо переменной x , тогда получаем 0 · t + b < 0 , где b < 0 . В случае, если оно верно, то для его решения подходит любое значение. Когда b < 0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Wszystkie oceny rozważymy w formie algorytmu rozwiązania nierówności liniowe 0 x + b< 0 (≤ , > , ≥) :
Definicja 5
Nierówność numeryczna postaci b< 0 (≤ , >, ≥) jest prawdziwa, to pierwotna nierówność ma rozwiązanie dla dowolnej wartości, a jest fałszywa, gdy pierwotna nierówność nie ma rozwiązań.
Przykład 4
Rozwiąż nierówność 0 x + 7 > 0.
Rozwiązanie
Ta nierówność liniowa 0 x + 7 > 0 może przyjmować dowolną wartość x. Otrzymujemy wówczas nierówność postaci 7 > 0. Ostatnią nierówność uważa się za prawdziwą, co oznacza, że jej rozwiązaniem może być dowolna liczba.
Odpowiedź: przedział (− ∞, + ∞) .
Przykład 5
Znajdź rozwiązanie nierówności 0 x − 12, 7 ≥ 0.
Rozwiązanie
Podstawiając zmienną x dowolnej liczby, otrzymujemy, że nierówność przyjmuje postać - 12, 7 ≥ 0. To jest nieprawidłowe. Oznacza to, że 0 x − 12, 7 ≥ 0 nie ma rozwiązań.
Odpowiedź: nie ma rozwiązań.
Rozważmy rozwiązanie nierówności liniowych, w których oba współczynniki są równe zero.
Przykład 6
Znajdź nierozwiązywalną nierówność spośród 0 x + 0 > 0 i 0 x + 0 ≥ 0.
Rozwiązanie
Podstawiając dowolną liczbę zamiast x, otrzymujemy dwie nierówności w postaci 0 > 0 i 0 ≥ 0. Pierwsze jest nieprawidłowe. Oznacza to, że 0 x + 0 > 0 nie ma rozwiązań, a 0 x + 0 ≥ 0 ma nieskończoną liczbę rozwiązań, czyli dowolną liczbę.
Odpowiedź: nierówność 0 x + 0 > 0 nie ma rozwiązań, ale 0 x + 0 ≥ 0 ma rozwiązania.
Metodę tę omówiono w kurs szkolny matematyka. Metoda przedziałowa umożliwia rozwiązywanie różnego rodzaju nierówności, w tym nierówności liniowych.
Metodę przedziałową stosuje się do nierówności liniowych, gdy wartość współczynnika x nie jest równa 0. W przeciwnym razie będziesz musiał obliczyć inną metodą.
Definicja 6
Metoda interwałowa to:
- wprowadzenie funkcji y = a · x + b ;
- poszukiwanie zer w celu podzielenia dziedziny definicji na przedziały;
- definicja znaków dla ich pojęć na przedziałach.
Złóżmy algorytm rozwiązywania równań liniowych a x + b< 0 (≤ , >, ≥) dla ≠ 0 metodą przedziałową:
- znalezienie zer funkcji y = a · x + b aby rozwiązać równanie w postaci a · x + b = 0 . Jeżeli a ≠ 0, to rozwiązaniem będzie pojedynczy pierwiastek, który przyjmie oznaczenie x 0;
- konstrukcja linii współrzędnych z obrazem punktu o współrzędnej x 0, przy nierówności ścisłej punkt oznacza się przebitą, przy nierówności nieścisłej – zacieniowaną;
- określenie znaków funkcji y = a · x + b na przedziałach, w tym celu należy znaleźć wartości funkcji w punktach przedziału;
- rozwiązanie nierówności ze znakami > lub ≥ na osi współrzędnych, dodanie cieniowania na dodatnim przedziale,< или ≤ над отрицательным промежутком.
Przyjrzyjmy się kilku przykładom rozwiązywania nierówności liniowych metodą przedziałową.
Przykład 6
Rozwiąż nierówność − 3 x + 12 > 0.
Rozwiązanie
Z algorytmu wynika, że najpierw trzeba znaleźć pierwiastek równania – 3 x + 12 = 0. Otrzymujemy, że − 3 · x = − 12 , x = 4 . Konieczne jest narysowanie linii współrzędnych w miejscu, w którym zaznaczamy punkt 4. Zostanie przebity, ponieważ nierówność jest ostra. Rozważ poniższy rysunek.
Konieczne jest określenie znaków w odstępach. Aby to wyznaczyć na przedziale (− ∞, 4), należy obliczyć funkcję y = − 3 x + 12 przy x = 3. Stąd otrzymujemy, że − 3 3 + 12 = 3 > 0. Znak na przedziale jest dodatni.
Znak wyznaczamy z przedziału (4, + ∞), następnie podstawiamy wartość x = 5. Mamy to - 3 5 + 12 = - 3< 0 . Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
![]()
Rozwiązujemy nierówność ze znakiem >, a cieniowanie przeprowadzamy na dodatnim przedziale. Rozważ poniższy rysunek.
![]()
Z rysunku jasno wynika, że pożądane rozwiązanie ma postać (− ∞ , 4) lub x< 4 .
Odpowiedź: (− ∞, 4) lub x< 4 .
Aby zrozumieć, jak przedstawić graficznie, należy rozważyć na przykład 4 nierówności liniowe: 0, 5 x − 1< 0 , 0 , 5 · x − 1 ≤ 0 , 0 , 5 · x − 1 >0 i 0, 5 x - 1 ≥ 0. Ich rozwiązaniami będą wartości x< 2 , x ≤ 2 , x >2 i x ≥ 2. Aby to zrobić, narysujmy wykres funkcja liniowa y = 0,5 x - 1 podane poniżej.

Jest oczywiste, że
Definicja 7
- rozwiązanie nierówności 0, 5 x − 1< 0 считается промежуток, где график функции y = 0 , 5 · x − 1 располагается ниже О х;
- za rozwiązanie 0, 5 x − 1 ≤ 0 uważa się przedział, w którym funkcja y = 0, 5 x − 1 jest mniejsza od O x lub pokrywa się;
- rozwiązanie 0, 5 · x − 1 > 0 uważa się za przedział, funkcja znajduje się nad O x;
- za rozwiązanie 0, 5 · x − 1 ≥ 0 uważa się przedział, w którym wykres powyżej O x lub pokrywa się.
Oznaczający rozwiązanie graficzne nierówności polega na znalezieniu przedziałów, które należy przedstawić na wykresie. W tym przypadku odkrywamy, że lewa strona ma y = a · x + b, a prawa strona ma y = 0 i pokrywa się z O x.
Definicja 8Narysujemy wykres funkcji y = a x + b:
- rozwiązując nierówność a x + b< 0 определяется промежуток, где график изображен ниже О х;
- przy rozwiązywaniu nierówności a · x + b ≤ 0 określa się przedział, w którym wykres jest przedstawiony poniżej osi O x lub pokrywa się;
- przy rozwiązywaniu nierówności a · x + b > 0, wyznacza się przedział tam, gdzie wykres jest przedstawiony powyżej O x;
- Rozwiązując nierówność a · x + b ≥ 0, wyznacza się przedział, w którym wykres znajduje się powyżej O x lub pokrywa się.
Przykład 7
Rozwiąż nierówność - 5 · x - 3 > 0 za pomocą wykresu.
Rozwiązanie
Należy skonstruować wykres funkcji liniowej - 5 · x - 3 > 0. Ta prosta jest malejąca, ponieważ współczynnik x jest ujemny. Aby wyznaczyć współrzędne punktu jego przecięcia z O x - 5 · x - 3 > 0, otrzymujemy wartość - 3 5. Przedstawmy to graficznie.

Rozwiązując nierówność ze znakiem >, należy zwrócić uwagę na przedział powyżej O x. Zaznaczmy wymaganą część płaszczyzny na czerwono i zdobądźmy ją

Wymagana szczelina to część O x czerwona. Oznacza to, że rozwiązaniem nierówności będzie otwarty promień liczbowy - ∞ , - 3 5. Jeżeli zgodnie z warunkiem mielibyśmy nieścisłą nierówność, to wartość punktu - 3 5 również byłaby rozwiązaniem nierówności. I zbiegałoby się to z Ox.
Odpowiedź: - ∞ , - 3 5 lub x< - 3 5 .
Metoda graficzna rozwiązanie stosuje się wtedy, gdy lewa strona będzie odpowiadać funkcji y = 0 x + b, czyli y = b. Wtedy linia prosta będzie równoległa do Ox lub zbiega się w punkcie b = 0. Przypadki te pokazują, że nierówność może nie mieć rozwiązań lub rozwiązaniem może być dowolna liczba.
Przykład 8
Wyznacz z nierówności 0 x + 7< = 0 , 0 · x + 0 ≥ 0 то, которое имеет хотя бы одно решение.
Rozwiązanie
Reprezentacja y = 0 x + 7 to y = 7, wtedy zostanie podana płaszczyzna współrzędnych z linią prostą równoległą do Ox i umieszczoną powyżej Ox. Zatem 0 x + 7< = 0 решений не имеет, потому как нет промежутков.
Wykres funkcji y = 0 x + 0 uważa się za y = 0, to znaczy linia prosta pokrywa się z O x. Oznacza to, że nierówność 0 x + 0 ≥ 0 ma wiele rozwiązań.
Odpowiedź: Druga nierówność ma rozwiązanie dla dowolnej wartości x.
Nierówności redukujące się do liniowych
Rozwiązanie nierówności można sprowadzić do rozwiązania równanie liniowe, które nazywane są nierównościami redukującymi do liniowych.
Nierówności te były uwzględniane na lekcjach szkolnych, ponieważ stanowiły szczególny przypadek rozwiązywania nierówności, co prowadziło do otwierania nawiasów i redukcji podobnych wyrazów. Rozważmy na przykład, że 5 − 2 x > 0, 7 (x − 1) + 3 ≤ 4 x − 2 + x, x - 3 5 - 2 x + 1 > 2 7 x.
Podane nierówności zawsze sprowadzamy do postaci równania liniowego. Następnie otwiera się nawiasy i podaje podobne terminy, przenoszone z różnych części, zmieniając znak na przeciwny.
Sprowadzając nierówność 5 − 2 x > 0 do liniowej, przedstawiamy ją tak, aby miała postać − 2 x + 5 > 0, a aby zredukować drugą otrzymujemy, że 7 (x − 1) + 3 ≤ 4 x - 2 + x . Należy otworzyć nawiasy, wprowadzić terminy podobne, przenieść wszystkie terminy na lewą stronę i wprowadzić terminy podobne. To wygląda tak:
7 x − 7 + 3 ≤ 4 x − 2 + x 7 x − 4 ≤ 5 x − 2 7 x − 4 − 5 x + 2 ≤ 0 2 x − 2 ≤ 0
Prowadzi to do rozwiązania nierówności liniowej.
Nierówności te uważa się za liniowe, ponieważ mają tę samą zasadę rozwiązania, po czym można je zredukować do nierówności elementarnych.
Aby rozwiązać ten typ nierówności, należy ją sprowadzić do nierówności liniowej. Należy to zrobić w ten sposób:
Definicja 9
- otwarte nawiasy;
- zbieraj zmienne po lewej stronie i liczby po prawej;
- podać podobne warunki;
- podziel obie strony przez współczynnik x.
Przykład 9
Rozwiąż nierówność 5 · (x + 3) + x ≤ 6 · (x − 3) + 1.
Rozwiązanie
Otwieramy nawiasy i otrzymujemy nierówność postaci 5 x + 15 + x ≤ 6 x − 18 + 1. Po redukcji podobnych wyrazów mamy, że 6 x + 15 ≤ 6 x − 17. Po przeniesieniu wyrazów z lewej strony na prawą okazuje się, że 6 x + 15 − 6 x + 17 ≤ 0. Istnieje zatem nierówność postaci 32 ≤ 0 z nierównością otrzymaną poprzez obliczenie 0 x + 32 ≤ 0. Można zauważyć, że nierówność jest fałszywa, co oznacza, że nierówność wynikająca z warunku nie ma rozwiązań.
Odpowiedź: brak rozwiązań.
Warto zauważyć, że istnieje wiele innych rodzajów nierówności, które można sprowadzić do nierówności liniowych lub typu pokazanego powyżej. Na przykład 5 2 x - 1 ≥ 1 Jest równanie wykładnicze, co sprowadza się do rozwiązania liniowego 2 x - 1 ≥ 0 . Przypadki te będą brane pod uwagę przy rozwiązywaniu nierówności tego typu.
Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter