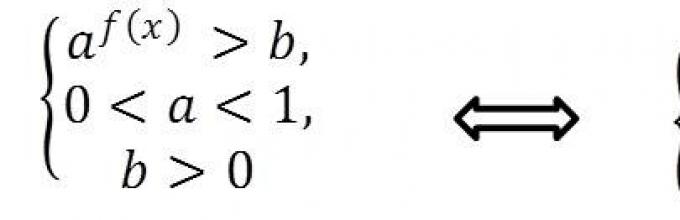Nierówność to zależność liczbowa, która ilustruje wielkość liczb względem siebie. Nierówności są szeroko stosowane w poszukiwaniu wielkości w naukach stosowanych. Nasz kalkulator pomoże Ci uporać się z tak trudnym tematem jak rozwiązanie nierówności liniowe.
Czym jest nierówność
Nierówne proporcje w prawdziwe życie współgrać z czymś ciągłe porównywanie różne przedmioty: wyższe lub niższe, dalsze lub bliższe, cięższe lub lżejsze. Intuicyjnie lub wizualnie możemy zrozumieć, że jeden obiekt jest większy, wyższy lub cięższy od drugiego, ale tak naprawdę zawsze mówimy o porównywaniu liczb charakteryzujących odpowiednie wielkości. Obiekty można porównywać na dowolnej podstawie i w każdym przypadku można stworzyć nierówność numeryczną.
Jeśli nieznane wielkości są równe w określonych warunkach, wówczas tworzymy równanie w celu ich numerycznego określenia. Jeśli nie, to zamiast znaku „równości” możemy wskazać dowolną inną zależność między tymi wielkościami. Dwie liczby lub obiekty matematyczne mogą być większe niż „>”, mniejsze niż „<» или равны «=» относительно друг друга. В этом случае речь идет о строгих неравенствах. Если же в неравных соотношениях присутствует знак равно и числовые элементы больше или равны (a ≥ b) или меньше или равны (a ≤ b), то такие неравенства называются нестрогими.
Znaki nierówności w ich współczesnej formie zostały wynalezione przez brytyjskiego matematyka Thomasa Harriota, który w 1631 roku opublikował książkę o nierównych stosunkach. Znaki większe niż „>” i mniejsze niż „<» представляли собой положенные на бок буквы V, поэтому пришлись по вкусу не только математикам, но и типографам.
Rozwiązywanie nierówności
Nierówności, podobnie jak równania, występują w różnych typach. Nierówności liniowe, kwadratowe, logarytmiczne lub wykładnicze są rozwiązywane różnymi metodami. Jednak niezależnie od metody każdą nierówność należy najpierw sprowadzić do postaci standardowej. W tym celu stosuje się przekształcenia tożsamości, które są tożsame z modyfikacjami równości.
Identyczne przekształcenia nierówności
Takie przekształcenia wyrażeń są bardzo podobne do równań widmowych, ale mają niuanse, które należy wziąć pod uwagę przy rozwiązywaniu nierówności.
Pierwsza transformacja tożsamości jest identyczna z podobną operacją na równościach. Tę samą liczbę lub wyrażenie z nieznanym x można dodać lub odjąć po obu stronach nierównej relacji, podczas gdy znak nierówności pozostaje taki sam. Najczęściej metodę tę stosuje się w uproszczonej formie, jako przeniesienie składników wyrażenia przez znak nierówności ze zmianą znaku liczby na przeciwny. Oznacza to zmianę znaku samego wyrazu, czyli +R po przeniesieniu przez dowolny znak nierówności zmieni się na –R i odwrotnie.
Druga transformacja ma dwa punkty:
- Obie strony nierównego stosunku można mnożyć lub dzielić przez tę samą liczbę dodatnią. Sam znak nierówności nie ulegnie zmianie.
- Obie strony nierówności można podzielić lub pomnożyć przez tę samą rzecz liczba ujemna. Sam znak nierówności zmieni się na przeciwny.
Druga identyczna transformacja nierówności ma poważne różnice w modyfikacji równań. Po pierwsze, przy mnożeniu/dzieleniu przez liczbę ujemną znak nierówności jest zawsze odwracany. Po drugie, części stosunku można dzielić lub mnożyć tylko przez liczbę, a nie przez jakiekolwiek wyrażenie zawierające niewiadomą. Faktem jest, że nie możemy wiedzieć na pewno, czy liczba jest większa, czy mniejsza od zera, ukryta za niewiadomą, dlatego drugą transformację tożsamości stosuje się do nierówności wyłącznie z liczbami. Spójrzmy na te zasady na przykładach.
Przykłady uwalniania nierówności
W zadaniach z algebry istnieje wiele zadań na temat nierówności. Dajmy sobie wyrażenie:
6x - 3(4x + 1) > 6.
Najpierw otwórzmy nawiasy i przesuńmy wszystkie niewiadome w lewo, a wszystkie liczby w prawo.
6x - 12x > 6 + 3
Musimy podzielić obie strony wyrażenia przez -6, więc gdy znajdziemy nieznane x, znak nierówności zmieni się na przeciwny.
Rozwiązując tę nierówność skorzystaliśmy z obu przemiany tożsamości: Przesuń wszystkie liczby na prawo od znaku i podziel obie strony stosunku przez liczbę ujemną.
Nasz program jest kalkulatorem do rozwiązywania nierówności numerycznych niezawierających niewiadomych. Program zawiera następujące twierdzenia dotyczące zależności trzech liczb:
- Jeśli< B то A–C< B–C;
- jeśli A > B, to A–C > B–C.
Zamiast odejmować wyrazy A-C, możesz podać dowolną operację arytmetyczną: dodawanie, mnożenie lub dzielenie. W ten sposób kalkulator automatycznie przedstawi nierówności dla sum, różnic, iloczynów lub ułamków.
Wniosek
W prawdziwym życiu nierówności są tak samo powszechne jak równania. Oczywiście wiedza o rozwiązywaniu nierówności może nie być potrzebna w życiu codziennym. Jednakże w naukach stosowanych nierówności i ich systemy są szeroko stosowane. Na przykład różne badania problemów gospodarki światowej sprowadzają się do zestawienia i oddzielenia systemów liniowych lub nierówności kwadratowe, a niektóre nierówne relacje służą jako jednoznaczny sposób udowodnienia istnienia pewnych obiektów. Skorzystaj z naszych programów do rozwiązywania nierówności liniowych lub sprawdź własne obliczenia.
Cześć! Moi drodzy uczniowie, w tym artykule dowiemy się, jak rozwiązywać nierówności wykładnicze .
Bez względu na to, jak skomplikowana może ci się wydawać nierówność wykładnicza, po pewnych przekształceniach (porozmawiamy o nich nieco później) wszystkie nierówności sprowadzać się do rozwiązania najprostszego nierówności wykładnicze :
a x > b, x< b I a x ≥ b, a x ≤ b.
Spróbujmy dowiedzieć się, jak rozwiązać takie nierówności.
Zastanowimy się nad rozwiązaniem ścisłe nierówności. Jedyna różnica w rozwiązywaniu nieścisłych nierówności polega na tym, że odpowiadające im pierwiastki są uwzględniane w odpowiedzi.
Załóżmy, że musimy rozwiązać nierówność formy oraz f (x) > b, Gdzie a>1 I b>0.
Spójrz na diagram rozwiązywania takich nierówności (rysunek 1):
Spójrzmy teraz na konkretny przykład. Rozwiąż nierówność: 5 x – 1 > 125.
Zatem skoro 5 > 1 i 125 > 0
x – 1 > log 5 125, tj
x – 1 > 3,
x > 4.
Odpowiedź: (4; +∞) .
Jakie będzie rozwiązanie tej samej nierówności? oraz f (x) >b, Jeśli 0
Zatem schemat na rysunku 2

Przykład: Rozwiąż nierówność (1/2) 2x - 2 ≥ 4
Stosując regułę (rysunek 2), otrzymujemy
2х – 2 ≤ log 1/2 4,
2х – 2 ≤ –2,
2x ≤ 0,
x ≤ 0.
Odpowiedź: (–∞; 0] .
Spójrzmy jeszcze raz na tę samą nierówność oraz f (x) > b, Jeśli a>0 I B<0 .
Zatem schemat na rysunku 3:

Przykład rozwiązania nierówności (1/3) x + 2 > –9. Jak zauważamy, niezależnie od tego, jaką liczbę podstawimy za x, (1/3) x + 2 jest zawsze większe od zera.
Odpowiedź: (–∞; +∞) .
Jak rozwiązuje się nierówności postaci? i f(x)< b , Gdzie a>1 I b>0?
Schemat na rysunku 4:

I następujący przykład: 3 3 – x ≥ 8.
Zatem skoro 3 > 1 i 8 > 0
3 – x > log 3 8, tj
–x > log 3 8 – 3,
X< 3 – log
3 8.
Odpowiedź: (0; 3–log 3 8) .
Jak może zmienić się rozwiązanie nierówności? i f(x)< b
, Na 0
Schemat na rysunku 5:

I następujący przykład: Rozwiąż nierówność 0,6 2x – 3< 0,36 .
Postępując zgodnie ze schematem na rysunku 5, otrzymujemy
2x – 3 > log 0,6 0,36,
2х – 3 > 2,
2x > 5,
x > 2,5
Odpowiedź: (2,5; +∞) .
Rozważmy ostatni schemat rozwiązania nierówności formy i f(x)< b , Na a>0 I B<0 , przedstawione na rysunku 6:

Rozwiążmy na przykład nierówność:

Zauważmy, że niezależnie od tego, jaką liczbę podstawimy za x, lewa strona nierówności jest zawsze większa od zera, a w naszym przypadku to wyrażenie jest mniejsze od -8, tj. i zero, co oznacza brak rozwiązań.
Odpowiedź: żadnych rozwiązań.
Wiedząc, jak rozwiązać najprostsze nierówności wykładnicze, możesz przystąpić do rozwiązywanie nierówności wykładniczych.
Przykład 1.
Znajdź największą wartość całkowitą x, która spełnia nierówność

Ponieważ 6 x jest większe od zera (przy żadnym x mianownik nie dąży do zera), mnożąc obie strony nierówności przez 6 x, otrzymujemy:
440 – 2 6 2x > 8, zatem
– 2 6 2x > 8 – 440,
– 2 6 2х > – 332,
6 2x< 216,
2x< 3,
X< 1,5. Наибольшее целое число из помежутка (–∞; 1,5) это число 1.
Odpowiedź 1.
Przykład 2.
Rozwiąż nierówność 2 2 x – 3 2 x + 2 ≤ 0
Oznaczmy 2 x przez y, uzyskajmy nierówność y 2 – 3y + 2 ≤ 0 i rozwiążmy tę nierówność kwadratową.
y 2 – 3 lata +2 = 0,
y 1 = 1 i y 2 = 2.
Gałęzie paraboli są skierowane w górę, narysujmy wykres:

Wtedy rozwiązaniem nierówności będzie nierówność 1< у < 2, вернемся к нашей переменной х и получим неравенство 1< 2 х < 2, решая которое и найдем ответ 0 < x < 1.
Odpowiedź: (0; 1) .
Przykład 3. Rozwiąż nierówność 5 x +1 – 3 x +2< 2·5 x – 2·3 x –1
Zbierzmy wyrażenia o tych samych podstawach w jednej części nierówności
5 x +1 – 2 5 x< 3 x +2 – 2·3 x –1
Weźmy 5 x z nawiasów po lewej stronie nierówności i 3 x po prawej stronie nierówności i otrzymamy nierówność
5x (5 – 2)< 3 х (9 – 2/3),
3,5 x< (25/3)·3 х
Podziel obie strony nierówności przez wyrażenie 3 3 x, znak nierówności się nie zmienia, ponieważ 3 3 x jest liczbą dodatnią, otrzymujemy nierówność:


X< 2 (так как 5/3 > 1).
Odpowiedź: (–∞; 2) .
Jeśli masz pytania dotyczące rozwiązywania nierówności wykładniczych lub chciałbyś poćwiczyć rozwiązywanie podobnych przykładów, zapisz się na moje lekcje. Korepetytor Valentina Galinevskaya.
stronie internetowej, przy kopiowaniu materiału w całości lub w części wymagany jest link do źródła.
Metoda interwałowa– prosty sposób rozwiązywania ułamkowych nierówności wymiernych. Jest to nazwa nierówności zawierających wyrażenia wymierne (lub ułamkowo-wymierne) zależne od zmiennej.
1. Rozważmy na przykład następującą nierówność
Metoda interwałowa pozwala rozwiązać go w ciągu kilku minut.
Po lewej stronie tej nierówności – ułamkowa funkcja wymierna. Racjonalne, ponieważ nie zawiera pierwiastków, sinusów, logarytmów – tylko racjonalne wyrażenia. Po prawej stronie jest zero.
Metoda przedziałowa opiera się na następującej właściwości ułamkowej funkcji wymiernej.
Ułamkowa funkcja wymierna może zmieniać znak tylko w tych punktach, w których jest równy zero lub nie istnieje.
Przypomnijmy, jak rozkładać na czynniki trójmian kwadratowy, czyli wyrażenie formy .
Gdzie i są korzenie równanie kwadratowe.
Rysujemy oś i umieszczamy punkty, w których licznik i mianownik dążą do zera.

Zera mianownika i są punktami przebitymi, ponieważ w tych punktach funkcja po lewej stronie nierówności nie jest zdefiniowana (nie można dzielić przez zero). Zera licznika i - są zacieniowane, ponieważ nierówność nie jest ścisła. Kiedy i nasza nierówność jest spełniona, ponieważ obie jej strony są równe zero.
Punkty te dzielą oś na odstępy.
Wyznaczmy znak ułamkowej funkcji wymiernej po lewej stronie naszej nierówności w każdym z tych przedziałów. Pamiętamy, że ułamkowa funkcja wymierna może zmieniać znak tylko w tych punktach, w których jest równy zero lub nie istnieje. Oznacza to, że w każdym z odstępów między punktami, w których licznik lub mianownik dąży do zera, znak wyrażenia po lewej stronie nierówności będzie stały - „plus” lub „minus”.
Dlatego, aby określić znak funkcji w każdym takim przedziale, bierzemy dowolny punkt należący do tego przedziału. Taki, który jest dla nas wygodny.
. Weźmy na przykład i sprawdź znak wyrażenia po lewej stronie nierówności. Każdy z „nawiasów” jest ujemny. Po lewej stronie znajduje się znak.

Następny interwał: . Sprawdźmy znak na . Zauważamy, że lewa strona zmieniła swój znak na .

Weźmy to. Kiedy wyrażenie jest dodatnie - zatem jest dodatnie w całym przedziale od do.

Gdy lewa strona nierówności jest ujemna.

I na koniec class="tex" alt="x>7"> . Подставим и проверим знак выражения в левой части неравенства. Каждая "скобочка" положительна. Следовательно, левая часть имеет знак .!}

Ustaliliśmy, w jakich odstępach wyrażenie jest dodatnie. Pozostaje tylko zapisać odpowiedź:
Odpowiedź: .
Uwaga: znaki zmieniają się w odstępach czasu. Stało się tak, ponieważ przechodząc przez każdy punkt, dokładnie jeden z czynników liniowych zmieniał znak, a pozostałe pozostawiały go bez zmian.
Widzimy, że metoda przedziałowa jest bardzo prosta. Aby rozwiązać nierówność ułamkowo-wymierną metodą przedziałową, sprowadzamy ją do postaci:
Lub class="tex" alt="\genfrac())()(0)(\displaystyle P\lewo (x \prawo))(\displaystyle Q\lewo(x \prawo)) > 0"> !}, albo albo .
(po lewej stronie znajduje się ułamkowa funkcja wymierna, po prawej stronie jest zero).
Następnie zaznaczamy na osi liczbowej punkty, w których licznik lub mianownik dąży do zera.
Punkty te dzielą całą oś liczbową na przedziały, na każdym z których funkcja ułamkowo-wymierna zachowuje swój znak.
Pozostaje tylko znaleźć jego znak w każdym przedziale.
Robimy to sprawdzając znak wyrażenia w dowolnym punkcie należącym do danego przedziału. Następnie zapisujemy odpowiedź. To wszystko.
Ale pojawia się pytanie: czy znaki zawsze są naprzemienne? Nie, nie zawsze! Należy zachować ostrożność i nie umieszczać znaków mechanicznie i bezmyślnie.
2. Rozważmy inną nierówność.
Class="tex" alt="\genfrac())()(0)(\displaystyle \lewo(x-2 \prawo)^2)(\displaystyle \lewo(x-1 \prawo) \ lewo(x-3 \prawo))>0"> !}
Ponownie umieść punkty na osi. Kropki i są przebijane, ponieważ są zerami mianownika. Ten punkt również zostaje usunięty, ponieważ nierówność jest ścisła.

Gdy licznik jest dodatni, oba czynniki w mianowniku są ujemne. Można to łatwo sprawdzić, biorąc dowolną liczbę z danego przedziału, na przykład . Po lewej stronie znajduje się znak:

Gdy licznik jest dodatni; Pierwszy czynnik w mianowniku jest dodatni, drugi czynnik jest ujemny. Po lewej stronie znajduje się znak:

Sytuacja jest taka sama! Licznik jest dodatni, pierwszy czynnik w mianowniku jest dodatni, drugi jest ujemny. Po lewej stronie znajduje się znak:

Wreszcie z class="tex" alt="x>3">
все множители положительны, и левая часть имеет знак :!} 
Odpowiedź: .
Dlaczego naprzemienność znaków została zakłócona? Bo przechodząc przez punkt, mnożnik jest za to „odpowiedzialny”. nie zmienił znaku. W rezultacie cała lewa strona naszej nierówności nie zmieniła znaku.
Wniosek: jeśli mnożnik liniowy jest potęgą parzystą (na przykład kwadratową), to przy przejściu przez punkt znak wyrażenia po lewej stronie nie zmienia się. W przypadku stopnia nieparzystego znak oczywiście się zmienia.
3. Rozważmy więcej trudny przypadek. Różni się od poprzedniego tym, że nierówność nie jest ścisła:
Lewa strona jest taka sama jak w poprzednim zadaniu. Obraz znaków będzie taki sam:

Może odpowiedź będzie taka sama? NIE! Dodawane jest rozwiązanie Dzieje się tak, ponieważ zarówno lewa, jak i prawa strona nierówności są równe zero - zatem ten punkt jest rozwiązaniem.
Odpowiedź: .
Taka sytuacja często ma miejsce w zadaniach na jednolitym egzaminie państwowym z matematyki. W tym miejscu kandydaci wpadają w pułapkę i tracą punkty. Bądź ostrożny!
4. Co zrobić, jeśli nie można rozłożyć licznika lub mianownika na czynniki liniowe? Rozważmy tę nierówność:
Trójmianu kwadratowego nie można rozłożyć na czynniki: dyskryminator jest ujemny, nie ma pierwiastków. Ale to jest dobre! Oznacza to, że znak wyrażenia dla wszystkich jest taki sam, a konkretnie dodatni. Więcej na ten temat przeczytasz w artykule o właściwościach funkcji kwadratowych.
A teraz możemy podzielić obie strony naszej nierówności przez wartość, która jest dodatnia dla wszystkich. Dochodzimy do równoważnej nierówności:
Które można łatwo rozwiązać za pomocą metody przedziałowej.
Należy pamiętać, że obie strony nierówności podzieliliśmy przez wartość, o której wiedzieliśmy na pewno, że jest dodatnia. Oczywiście, ogólnie rzecz biorąc, nie należy mnożyć ani dzielić nierówności przez zmienną, której znak jest nieznany.
5 . Rozważmy inną nierówność, pozornie całkiem prostą:
Chcę to pomnożyć przez . Ale jesteśmy już mądrzy i nie zrobimy tego. W końcu może być zarówno pozytywny, jak i negatywny. Wiemy też, że jeśli pomnożymy obie strony nierówności przez wartość ujemną, znak nierówności ulegnie zmianie.
My zrobimy to inaczej – zbierzemy wszystko w jedną część i sprowadzimy do wspólnego mianownika. Prawa strona pozostanie zerowa:
Class="tex" alt="\genfrac())()()(0)(\displaystyle x-2)(\displaystyle x)>0"> !}
A potem - aplikuj metoda interwałowa.
Na przykład nierówność jest wyrażeniem \(x>5\).
Rodzaje nierówności:
Jeżeli \(a\) i \(b\) są liczbami lub , to nazywamy nierówność liczbowy. Właściwie to po prostu porównanie dwóch liczb. Takie nierówności dzielą się na wierny I niewierny.
Na przykład:
\(-5<2\) - верное числовое неравенство, ведь \(-5\) действительно меньше \(2\);
\(17+3\geq 115\) jest niepoprawną nierównością liczbową, ponieważ \(17+3=20\), a \(20\) jest mniejsze niż \(115\) (i nie większe lub równe) .
Jeśli \(a\) i \(b\) są wyrażeniami zawierającymi zmienną, to mamy nierówność ze zmienną. Nierówności takie dzielimy na typy w zależności od treści:
|
\(2x+1\geq4(5-x)\) |
Zmienna tylko do pierwszej potęgi |
|||
|
\(3x^2-x+5>0\) |
W drugiej potędze (kwadracie) jest zmienna, ale nie ma wyższych potęg (trzeciej, czwartej itd.) |
|||
|
\(\log_(4)((x+1))<3\) |
||||
|
\(2^(x)\leq8^(5x-2)\) |
Jakie jest rozwiązanie nierówności?
Jeśli zamiast zmiennej zastąpisz nierówność liczbą, zamieni się ona w nierówność numeryczną.
Jeśli dana wartość x zamienia pierwotną nierówność w prawdziwą nierówność liczbową, wówczas nazywa się to rozwiązanie nierówności. Jeśli nie, to ta wartość nie jest rozwiązaniem. I do rozwiązać nierówność– musisz znaleźć wszystkie jego rozwiązania (lub pokazać, że ich nie ma).
Na przykład, jeśli podstawimy liczbę \(7\) do nierówności liniowej \(x+6>10\), otrzymamy poprawną nierówność liczbową: \(13>10\). A jeśli podstawimy \(2\), otrzymamy niepoprawną nierówność liczbową \(8>10\). Oznacza to, że \(7\) jest rozwiązaniem pierwotnej nierówności, ale \(2\) nim nie jest.
Jednak nierówność \(x+6>10\) ma inne rozwiązania. Rzeczywiście, otrzymamy poprawne nierówności numeryczne, podstawiając \(5\), i \(12\), i \(138\)... A jak znaleźć wszystkie możliwe rozwiązania? W tym celu używają W naszym przypadku mamy:
\(x+6>10\) \(|-6\)
\(x>4\)
Oznacza to, że każda liczba większa niż cztery jest dla nas odpowiednia. Teraz musisz zapisać odpowiedź. Rozwiązania nierówności zapisuje się najczęściej cyfrowo, dodatkowo zaznaczając je na osi liczbowej cieniowaniem. Dla naszego przypadku mamy:
Odpowiedź:
\(x\in(4;+\infty)\)
Kiedy zmienia się znak nierówności?
W nierównościach kryje się jedna wielka pułapka, w którą uczniowie naprawdę „uwielbiają” wpadać:
Kiedy mnożymy (lub dzielimy) nierówność przez liczbę ujemną, zostaje ona odwrócona („więcej” przez „mniej”, „więcej lub równa” przez „mniejsze lub równe” itd.)
Dlaczego to się dzieje? Aby to zrozumieć, spójrzmy na transformacje nierówność liczbowa\(3>1\). To prawda, trzy jest rzeczywiście większe niż jeden. Najpierw spróbujmy pomnożyć go przez dowolną liczbę dodatnią, na przykład dwa:
\(3>1\) \(|\cdot2\)
\(6>2\)
Jak widać po pomnożeniu nierówność pozostaje prawdziwa. I bez względu na to, przez jaką liczbę dodatnią pomnożymy, zawsze otrzymamy poprawną nierówność. Spróbujmy teraz pomnożyć przez liczbę ujemną, na przykład minus trzy:
\(3>1\) \(|\cdot(-3)\)
\(-9>-3\)
Rezultatem jest niepoprawna nierówność, ponieważ minus dziewięć jest mniejsze niż minus trzy! Oznacza to, że aby nierówność stała się prawdziwa (a zatem przekształcenie mnożenia przez liczbę ujemną było „legalne”), należy odwrócić znak porównania w następujący sposób: \(−9<− 3\).
Z podziałem wyjdzie to tak samo, możesz to sprawdzić sam.
Zasada napisana powyżej dotyczy wszystkich typów nierówności, nie tylko liczbowych.
Przykład: Rozwiąż nierówność \(2(x+1)-1<7+8x\)Rozwiązanie:
|
\(2x+2-1<7+8x\) |
Przesuńmy \(8x\) w lewo, a \(2\) i \(-1\) w prawo, nie zapominając o zmianie znaków |
|
\(2x-8x<7-2+1\) |
|
|
\(-6x<6\) \(|:(-6)\) |
Podzielmy obie strony nierówności przez \(-6\), nie zapominając o zmianie z „mniej” na „więcej” |
|
Zaznaczmy na osi przedział liczbowy. Nierówność, dlatego „wybijamy” samą wartość \(-1\) i nie bierzemy jej jako odpowiedzi |
|
|
Zapiszmy odpowiedź jako przedział |
Odpowiedź: \(x\in(-1;\infty)\)
Nierówności i niepełnosprawność
Nierówności, podobnie jak równania, mogą mieć ograniczenia co do wartości x. W związku z tym z zakresu rozwiązań należy wyłączyć te wartości, które zdaniem DZ są niedopuszczalne.
Przykład: Rozwiąż nierówność \(\sqrt(x+1)<3\)
Rozwiązanie: Jasne jest, że aby lewa strona była mniejsza niż \(3\), wyrażenie radykalne musi być mniejsze niż \(9\) (w końcu z \(9\) tylko \(3\)). Otrzymujemy:
\(x+1<9\) \(|-1\)
\(X<8\)
Wszystko? Dowolna wartość x mniejsza niż \(8\) będzie nam odpowiadać? NIE! Bo jeśli przyjmiemy np. wartość \(-5\), która wydaje się spełniać warunek, to nie będzie to rozwiązanie pierwotnej nierówności, gdyż doprowadzi nas to do obliczenia pierwiastka z liczby ujemnej.
\(\sqrt(-5+1)<3\)
\(\sqrt(-4)<3\)
Dlatego też musimy wziąć pod uwagę ograniczenia dotyczące wartości X – nie może być tak, że pod pierwiastkiem znajduje się liczba ujemna. Zatem mamy drugi warunek dla x:
\(x+1\geq0\)
\(x\geq-1\)
A żeby x było rozwiązaniem ostatecznym, musi spełniać oba wymagania na raz: musi być mniejsze od \(8\) (aby było rozwiązaniem) i większe od \(-1\) (aby było w zasadzie dopuszczalne). Wykreślając to na osi liczbowej, mamy ostateczną odpowiedź:

Odpowiedź: \(\lewo[-1;8\prawo)\)
Uwaga!
Są dodatkowe
materiały w sekcji specjalnej 555.
Dla tych, którzy są bardzo „nie bardzo…”
A dla tych, którzy „bardzo…”)
Co się stało „nierówność kwadratowa”? Bez dwóch zdań!) Jeśli weźmiesz każdy równanie kwadratowe i zamień w nim znak "=" (równy) dowolnemu znakowi nierówności ( > ≥ < ≤ ≠ ), otrzymujemy nierówność kwadratową. Na przykład:
1. x 2 -8x+12 ≥ 0
2. -x 2 + 3x > 0
3. x 2 ≤ 4
Cóż, rozumiesz...)
Nie bez powodu połączyłem tutaj równania i nierówności. Chodzi o to, że jest to pierwszy krok do rozwiązania każdy nierówność kwadratowa - rozwiązać równanie, z którego wynika ta nierówność. Z tego powodu niemożność rozwiązania równań kwadratowych automatycznie prowadzi do całkowitego niepowodzenia nierówności. Czy wskazówka jest jasna?) Jeśli już, spójrz, jak rozwiązać dowolne równania kwadratowe. Wszystko jest tam szczegółowo opisane. Na tej lekcji zajmiemy się nierównościami.
Gotowa do rozwiązania nierówność ma postać: po lewej stronie znajduje się trójmian kwadratowy topór 2 +bx+c, po prawej - zero. Znak nierówności może być absolutnie dowolny. Pierwsze dwa przykłady znajdziesz tutaj są już gotowi podjąć decyzję. Trzeci przykład nadal wymaga przygotowania.
Jeśli podoba Ci się ta strona...
Przy okazji, mam dla Ciebie jeszcze kilka ciekawych stron.)
Możesz poćwiczyć rozwiązywanie przykładów i sprawdzić swój poziom. Testowanie z natychmiastową weryfikacją. Uczmy się - z zainteresowaniem!)
Można zapoznać się z funkcjami i pochodnymi.