Principen om minsta handling. Principen om minsta verkan Principen om minsta verkan i fysik

När jag gick i skolan kallade vår fysiklärare, som heter Bader, in mig en gång efter lektionen och sa: ”Du ser ut som om du är fruktansvärt trött på allt; lyssna på en intressant sak." Och han berättade något som jag tyckte var riktigt fascinerande. Även nu, även om det har gått mycket tid sedan dess, fortsätter det att fascinera mig. Och varje gång jag kommer ihåg vad jag sa går jag tillbaka till jobbet. Och den här gången, när jag förberedde mig för föreläsningen, kom jag på mig själv med att analysera samma saker igen. Och istället för att förbereda mig för föreläsningen tog jag mig an ett nytt problem. Ämnet jag pratar om är principen om minsta handling.

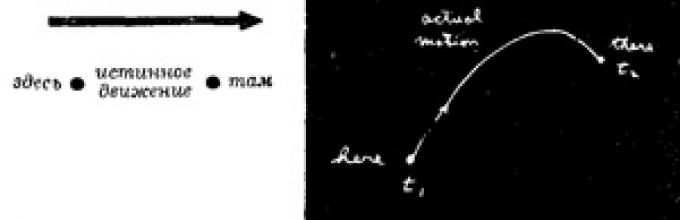
”Det här är vad min lärare Bader sa till mig då: ”Låt dig till exempel ha en partikel i gravitationsfältet; denna partikel, efter att ha kommit ut från någonstans, rör sig fritt någon annanstans till en annan punkt. Du kastade den, säg, upp, och den flög upp och föll sedan.

Det tog henne lite tid att resa från startplatsen till finalplatsen. Prova nu någon annan rörelse. Låt henne flytta "härifrån till här" inte längre som förut, utan så här:

Men jag befann mig ändå på rätt plats i samma ögonblick som tidigare.”

"Och så," fortsatte läraren, "om du beräknar den kinetiska energin vid varje tidpunkt längs partikelns väg, subtraherar den potentiella energin från den och integrerar skillnaden över hela tiden då rörelsen inträffade, kommer du att se att numret du får blir Mer,än för verklig partikelrörelse.

Med andra ord kan Newtons lagar inte formuleras som F=ma, utan som följer: genomsnittlig kinetisk energi minus genomsnittlig potentiell energi når sitt lägsta värde längs den bana längs vilken ett objekt faktiskt rör sig från en plats till en annan.

Jag ska försöka förklara detta för dig lite tydligare.
Om vi tar gravitationsfältet och betecknar partikelns bana x(t), Var X- höjd över marken (låt oss klara oss med en dimension för tillfället; låt banan bara gå upp och ner, och inte åt sidorna), då blir den kinetiska energin y 2 m(dx/ dt) 2, a potentiell energi vid ett godtyckligt ögonblick kommer att vara lika med mgx.

Nu, för ett ögonblick av rörelse längs banan, tar jag skillnaden mellan de kinetiska och potentiella energierna och integrerar över hela tiden från början till slut. Låt vid det första ögonblicket t x rörelsen började på någon höjd och slutade just nu t 2 på en annan viss höjd.

Då är integralen lika med ∫ t2 t1 dt

Sann rörelse sker längs en viss kurva (som en funktion av tiden är det en parabel) och leder till ett visst integralvärde. Men du kan innansätta föreställ dig någon annan rörelse: först en kraftig uppgång och sedan några bisarra fluktuationer.

Du kan beräkna skillnaden mellan potentiella och kinetiska energier på denna väg... eller på någon annan. Och det mest fantastiska är att den verkliga vägen är den längs vilken denna integral är den minsta.
Låt oss kolla upp det. Låt oss först titta på det här fallet: en fri partikel har ingen potentiell energi alls. Sedan säger regeln att när man flyttar från en punkt till en annan under en given tid, ska integralen av den kinetiska energin vara den minsta. Detta innebär att partikeln måste röra sig jämnt. (Och detta är korrekt, du och jag vet att hastigheten i en sådan rörelse är konstant.) Varför enhetligt? Låt oss ta reda på det. Om det var annorlunda, då skulle partikelhastigheten ibland överstiga medelvärdet, och ibland vara under det, och medelhastigheten skulle vara densamma, eftersom partikeln skulle behöva ta sig "härifrån till här" i den överenskomna tiden. Till exempel, om du behöver ta dig hemifrån till skolan i din bil under en viss tid, kan du göra det på olika sätt: du kan köra som en galning först och sakta ner på slutet, eller köra i samma hastighet, eller så kan man till och med gå till motsatt sida, och först då vända mot skolan, etc. I alla fall bör medelhastigheten naturligtvis vara densamma - kvoten av avståndet från hemmet till skolan dividerat med tiden. Men även vid denna medelhastighet rörde du dig ibland för snabbt och ibland för långsamt. Och genomsnittlig fyrkant något som avviker från genomsnittet är som vi vet alltid större än kvadraten på genomsnittet; Detta innebär att integralen av kinetisk energi vid fluktuationer i rörelsehastigheten alltid kommer att vara större än vid rörelse med konstant hastighet. Du ser att integralen når ett minimum när hastigheten är konstant (i frånvaro av krafter). Rätt sätt är detta.

Ett föremål som kastas uppåt i ett gravitationsfält stiger först snabbt och sedan allt långsammare. Detta händer eftersom det också har potentiell energi, och dess lägsta värde bör nå en gångness mellan kinetiska och potentiella energier. Eftersom potentiell energi ökar när du stiger, då mindre skillnad Det kommer att fungera om du når de höjder där den potentiella energin är hög så snabbt som möjligt. Sedan, subtraherar vi denna höga potential från den kinetiska energin, uppnår vi en minskning av medelvärdet. Så vägen som går upp och levererar en bra negativ bit på bekostnad av potentiell energi är mer lönsam.

Det var allt min lärare sa till mig, för han var en väldigt bra lärare och visste när det var dags att sluta. Själv är jag tyvärr inte sådan. Det är svårt för mig att sluta i tid. Och så, istället för att bara väcka ditt intresse med min berättelse, vill jag skrämma dig, jag vill göra dig trött på livets komplexitet - jag ska försöka bevisa det jag berättade om. Det matematiska problemet som vi kommer att lösa är mycket svårt och unikt. Det finns en viss mängd S, kallad handling. Det är lika med kinetisk energi minus potentiell energi integrerad över tiden:

Men å andra sidan kan du inte röra dig för snabbt eller gå för högt, eftersom det skulle kräva för mycket kinetisk energi. Du måste röra dig tillräckligt snabbt för att ta dig upp och ner inom den givna tiden som är tillgänglig för dig. Så du ska inte försöka flyga för högt utan bara nå någon rimlig nivå. Som ett resultat visar det sig att lösningen är en sorts balans mellan önskan att få så mycket potentiell energi som möjligt och önskan att minska mängden kinetisk energi så mycket som möjligt - detta är önskan att uppnå en maximal minskning i skillnaden mellan kinetiska och potentiella energier."

Glöm inte att p.e. och k.e. — båda funktionerna av tiden. För varje ny tänkbar väg får denna handling sin specifika betydelse. Det matematiska problemet är att avgöra vilken kurva som har detta nummer mindre än de andra.

Du säger, "Åh, det här är bara ett enkelt exempel på maximum och minimum. Vi måste beräkna åtgärden, särskilja den och hitta minimum.”

Men vänta. Vanligtvis har vi en funktion av någon variabel och behöver hitta värdet variabel, där funktionen blir minst eller störst. Låt oss säga att det finns en stav uppvärmd i mitten. Värme sprids över den och dess egen temperatur fastställs vid varje punkt på staven. Du måste hitta den punkt där den är högst. Men vi pratar om något helt annat - varje väg i rymden svarar på dess nummer och är tänkt att hitta den väg, för vilket detta antal är minimalt. Detta är ett helt annat område av matematik. Detta är ingen vanlig kalkyl, men variation(det är vad de kallar honom).

Detta område av matematik har många av sina egna problem. Säg att en cirkel vanligtvis definieras som platsen för punkter vars avstånd från en given punkt är desamma, men en cirkel kan definieras annorlunda: det är en av kurvorna given längd, som omsluter det största området. Vilken annan kurva som helst med samma omkrets omsluter ett område som är mindre än cirkeln. Så om vi ställer in uppgiften: att hitta kurvan för en given omkrets som begränsar det största området, så kommer vi att ha ett problem från variationskalkylen, och inte från kalkylen som du är van vid.

Så vi vill ta integralen över vägen som kroppen färdas. Låt oss göra på det här sättet. Hela poängen är att föreställa sig att det finns en sann väg och att vilken annan kurva vi ritar inte är den verkliga vägen, så att om vi beräknar åtgärden för den, kommer vi att få ett högre tal än vad vi får för åtgärden motsvarande till det verkliga sättet.

Så, uppgiften är att hitta den sanna vägen. Var ligger den? Ett sätt skulle naturligtvis vara att räkna handlingen för miljoner och åter miljoner vägar och sedan se vilken väg som har den minsta handlingen. Detta är vägen där handlingen är minimal och kommer att vara verklig.

Denna metod är fullt möjlig. Det kan dock göras enklare. Om det finns en kvantitet som har ett minimum (från vanliga funktioner, t.ex. temperatur), så är en av egenskaperna hos minimum att när man flyttar bort från den på avstånd först av storleksordning avviker funktionen från sitt minimivärde endast med mängden andra beställa. Och på någon annan plats på kurvan ändrar en förskjutning med ett litet avstånd värdet på funktionen också med ett värde av första ordningen av litenhet. Men som ett minimum leder inte små avvikelser åt sidan till en funktionsförändring som en första approximation.

Det är denna egenskap som vi ska använda för att beräkna den verkliga vägen.

Om vägen är korrekt kommer en kurva som är något annorlunda än den inte att leda, som en första approximation, till en förändring av åtgärdens storlek. Alla ändringar, om detta verkligen var minimum, kommer endast att visas i den andra approximationen.

Detta är lätt att bevisa. Om, med viss avvikelse från kurvan, förändringar sker i första ordningen, är dessa ändringar i kraft proportionell avvikelse. De kommer sannolikt att öka effekten; annars skulle det inte vara ett minimum. Men när förändringarna proportionell avvikelse, då ändrar du avvikelsens tecken kommer åtgärden att minska. Det visar sig att när man avviker åt ena hållet så ökar effekten, och när man avviker åt motsatt håll så minskar den. Den enda möjligheten för att detta verkligen ska vara ett minimum är att som en första approximation sker inga förändringar och förändringarna är proportionella mot kvadraten på avvikelsen från den verkliga banan.

Så vi kommer att gå längs följande väg: beteckna med x(t) (med en linje nedan) är den sanna vägen den vi vill hitta. Låt oss provköra x(t), skiljer sig från den önskade med en liten mängd, vilket vi betecknar η (t).

Tanken är att om vi räknar handlingen S på väg x(t), då skillnaden mellan detta S och genom åtgärden som vi beräknat för vägen x(t) (för enkelhetens skull kommer den att utses S), eller skillnaden mellan S_ Och S, bör vara en första uppskattning η noll. De kan skilja sig åt i den andra ordningen, men i den första måste skillnaden vara noll.

Och detta måste observeras för alla η . Dock inte riktigt för alla. Metoden kräver att man endast tar hänsyn till de vägar som alla börjar och slutar vid samma par av punkter, dvs varje väg måste börja vid en viss punkt vid den tidpunkten t 1 och slutar vid en annan specifik punkt för tillfället t 2 . Dessa punkter och ögonblick registreras. Så vår funktion d) (avvikelse) måste vara noll i båda ändar: η (t 1 )= 0 Och η (t2)=0. Under detta tillstånd blir vårt matematiska problem helt definierat.

Om du inte kunde kalkyl kan du göra samma sak för att hitta minimum av en vanlig funktion f(x). Skulle du tänka på vad som skulle hända om du tog f(x) och lägg till X liten mängd h, och vill hävda att ändringen till f(x) i första ordningen h bör vara minst lika med noll. Skulle du ställa upp mig x+h istället för X och skulle expandera j(x+h) upp till första potensen h. . ., med ett ord, skulle upprepa allt som vi tänker göra med η .

Om vi nu tittar noga på detta kommer vi att se att de två första termerna som skrivs här motsvarar den handlingen S, som jag skulle skriva för den sökta sanna vägen X. Jag vill fokusera din uppmärksamhet på förändring. S, dvs på skillnaden mellan S och så S_, vilket skulle resultera för den sanna vägen. Vi kommer att skriva denna skillnad som bS och låt oss kalla det en variant S. Om vi kasserar "andra och högre order", erhåller vi för σS

Nu ser uppgiften ut så här. Här framför mig finns någon integral. Jag vet inte ännu hur det är, men jag vet säkert det, vad η Oavsett vad måste denna integral vara lika med noll. "Tja", kanske du tänker, "det enda sättet för detta att hända är att multiplikatorn gör det η var lika med noll." Men hur är det med den första mandatperioden, där det finns d η / dt? Du säger: "Om η förvandlas till ingenting, då är dess derivata samma ingenting; detta betyder koefficienten vid dv\/ dt måste också vara noll." Tja, det är inte helt sant. Detta är inte helt sant eftersom mellan avvikelsen η och dess derivata där finns ett samband; de är inte helt oberoende pga η (t) måste vara noll och t 1 och kl t 2 .

Vid lösning av alla problem i variationskalkylen används alltid samma allmänna princip. Du ändrar lite vad du vill variera (liknande vad vi gjorde genom att lägga till η ), titta på första ordningens villkor, sedan ordna allt så att du får en integral i följande form: ”shift (η ), multiplicerat med vad det visar sig”, men så att det inte innehåller några derivator av η (Nej d η / dt). Det är absolut nödvändigt att omvandla allt så att "något" finns kvar, multiplicerat med η . Nu kommer du att förstå varför detta är så viktigt. (Det finns formler som berättar hur du i vissa fall kan göra detta utan några beräkningar, men de är inte så generella att de är värda att memorera; det är bäst att göra beräkningarna som vi gör det.)

Hur kan jag göra om en penis d η / dt, så att det dyker upp η ? Jag kan uppnå detta genom att integrera bit för bit. Det visar sig att i variationskalkylen är hela tricket att beskriva variationen S och sedan integrera med delar så att derivatorna av η försvann. I alla problem där derivat förekommer utförs samma trick.

Kom ihåg den allmänna principen om integrering av delar. Om du har en godtycklig funktion f multiplicerat med d η / dt och integrerad med t, sedan skriver du derivatan av η /t

Integrationsgränserna måste bytas in i den första mandatperioden t 1 Och t 2 . Sedan kommer jag under integralen att få termen från integration av delar och den sista termen som förblir oförändrad under omvandlingen.
Och nu händer det som alltid händer – den integrerade delen försvinner. (Och om det inte försvinner, då måste principen omformuleras och lägga till villkor som säkerställer ett sådant försvinnande!) Vi har redan sagt att η vid ändarna av banan måste vara lika med noll. När allt kommer omkring, vad är vår princip? Faktum är att åtgärden är minimal förutsatt att den varierade kurvan börjar och slutar vid utvalda punkter. Det betyder att η (ti)=0 och η (t2)=0. Därför visar sig den integrerade termen vara noll. Vi samlar resten av medlemmarna och skriver

Variation S har nu fått den form som vi ville ge det: något står inom parentes (låt oss beteckna det F), och allt detta multipliceras med η (t) och integrerad från t t innan t 2 .
Det visade sig att integralen av något uttryck multiplicerat med η (t), alltid lika med noll:

Finns det någon funktion från t; Jag multiplicerar det med η (t) och integrera den från början till slut. Och vad det än är η, Jag får noll. Det betyder att funktionen F(t) lika med noll. I allmänhet är detta uppenbart, men för säkerhets skull ska jag visa dig ett sätt att bevisa det.

Låt som η (t) Jag kommer att välja något som är lika med noll överallt, för alla t, förutom ett förvalt värde t. Den förblir noll tills jag kommer dit t, s Sedan hoppar den ett ögonblick och faller genast tillbaka. Om du tar integralen av denna m) multiplicerad med någon funktion F, det enda stället du får något som inte är noll är var η (t) hoppade upp; och du kommer att få värdet F vid denna punkt på integralen över hoppet. Integralen över själva hoppet är inte lika med noll, utan efter multiplikation med F det borde ge noll. Det betyder att funktionen på platsen där det gjordes ett hopp måste visa sig vara noll. Men språnget kunde ha gjorts var som helst; Betyder att, F måste vara noll överallt.

Vi ser att om vår integral är lika med noll för någon η , sedan koefficienten vid η bör gå till noll. Handlingsintegralen når ett minimum längs vägen som kommer att uppfylla en sådan komplex differentialekvation:

Det är faktiskt inte så komplicerat; du har träffat honom förut. Det är bara F=ma. Den första termen är massa gånger acceleration; den andra är derivatan av potentiell energi, dvs kraft.

Så vi har visat (åtminstone för ett konservativt system) att principen om minsta handling leder till det korrekta svaret; han konstaterar att den väg som har minsta verkan är den som uppfyller Newtons lag.

Ytterligare en anmärkning måste göras. Jag har inte bevisat detta minimum. Kanske är detta max. Detta behöver faktiskt inte vara ett minimum. Här är allt detsamma som i "kortaste tidsprincipen", som vi diskuterade när vi studerade optik. Även där pratade vi först om den ”kortaste” tiden. Det visade sig dock att det finns situationer där denna tid inte nödvändigtvis är den "kortaste". Grundprincipen är att för alla första ordningens avvikelser från den optiska vägen ändringar med tiden skulle vara lika med noll; Det är samma historia här. Med "minimum" menar vi faktiskt det till den första ordningen av litenhet av förändringen i kvantitet S när avvikelser från banan ska vara lika med noll. Och detta är inte nödvändigtvis "minimum".

Nu vill jag gå vidare till några generaliseringar. Först och främst kan hela den här historien göras i tre dimensioner. Istället för enkelt X det skulle jag ha då x, y Och z som funktioner t, och handlingen skulle se mer komplicerad ut. När du rör dig i 3D måste du använda full kinetisk energi): (t/2), multiplicerat med kvadraten på den totala hastigheten. Med andra ord

Dessutom är potentiell energi nu en funktion x, y Och z. Vad kan du säga om vägen? En väg är en viss generell kurva i rymden; det är inte så lätt att rita, men idén förblir densamma. Hur är det med η? Tja, η har också tre komponenter. Banan kan skiftas både i x och in y, och genom att z, eller åt alla tre riktningarna samtidigt. Så η nu en vektor. Detta skapar inga större komplikationer. Endast variationer måste vara lika med noll första beställning då kan beräkningen utföras sekventiellt med tre skift. Först kan du flytta ts bara i riktningen X och säg att koefficienten ska gå till noll. Du får en ekvation. Då flyttar vi ts i riktningen på och vi får den andra. Gå sedan i riktningen z och vi får den tredje. Du kan göra allt, om du vill, i en annan ordning. Hur som helst, en trio av ekvationer uppstår. Men Newtons lag är också tre ekvationer i tre dimensioner, en för varje komponent. Du får se själv att allt detta fungerar i tre dimensioner (det finns inte mycket arbete här). Förresten, du kan ta vilket koordinatsystem du vill, polärt, vilket som helst, och omedelbart få Newtons lagar i förhållande till detta system, med tanke på vad som händer när ett skifte inträffar η längs en radie eller längs en vinkel, etc.

Metoden kan generaliseras till ett godtyckligt antal partiklar. Om, säg, du har två partiklar och det finns några krafter som verkar mellan dem och det finns ömsesidig potentiell energi, så adderar du helt enkelt deras kinetiska energier och subtraherar den potentiella interaktionsenergin från summan. Vad varierar du? stigar både partiklar. Sedan uppstår sex ekvationer för två partiklar som rör sig i tre dimensioner. Du kan variera positionen för partikel 1 i riktningen X, i riktningen på och mot z, och gör samma sak med partikel 2, så det finns sex ekvationer. Och det är så det ska vara. Tre ekvationer bestämmer accelerationen av partikel 1 på grund av kraften som verkar på den, och de andra tre bestämmer accelerationen av partikel 2 på grund av kraften som verkar på den. Följ alltid samma spelregler så får du Newtons lag för ett godtyckligt antal partiklar.

Jag sa att vi skulle få Newtons lag. Detta är inte helt sant, eftersom Newtons lag inkluderar även icke-konservativa krafter, såsom friktion. Newton hävdade det den därär lika med alla F. Principen om minsta handling gäller endast för konservativ system, där alla krafter kan erhållas från en potentiell funktion. Men du vet att på den mikroskopiska nivån, det vill säga på den djupaste fysiska nivån, existerar inte icke-konservativa krafter. Icke-konservativa krafter (som friktion) uppstår bara för att vi försummar mikroskopiska komplexa effekter: det finns helt enkelt för många partiklar att analysera. Grundläggande samma lagar burk uttryckas som principen om minsta handling.

Låt mig gå vidare till ytterligare generaliseringar. Antag att vi är intresserade av vad som kommer att hända när partikeln rör sig relativistiskt. Hittills har vi inte erhållit den korrekta relativistiska rörelseekvationen; F=ma är sant endast i icke-relativistiska rörelser. Frågan uppstår: finns det en motsvarande princip om minsta handling i det relativistiska fallet? Ja, det finns. Formeln i det relativistiska fallet är:

Den första delen av aktionsintegralen är produkten av vilomassan t 0 på från 2 och till integralen av hastighetsfunktionen √ (1-v2/c 2 ). Sedan, istället för att subtrahera den potentiella energin, har vi integraler av skalärpotentialen φ och vektorpotentialen A gånger v. Naturligtvis tas här endast hänsyn till elektromagnetiska krafter. Alla elektriska och magnetiska fält uttrycks i termer av φ och A. Denna aktionsfunktion ger en fullständig teori om den relativistiska rörelsen hos en enskild partikel i ett elektromagnetiskt fält.

Naturligtvis måste du förstå att var jag än skrev v, innan du gör beräkningar, bör du ersätta dx/ dt istället för v x etc. Dessutom där jag helt enkelt skrev x, y, z, du måste föreställa dig poängen just nu t: x(t), y(t), z(t). Faktiskt, först efter sådana substitutioner och substitutioner av v kommer du att få en formel för verkan av en relativistisk partikel. Låt de skickligaste bland er försöka bevisa att denna handlingsformel faktiskt ger de korrekta rörelseekvationerna för relativitetsteorin. Låt mig bara råda dig att börja med att slänga A, det vill säga göra utan magnetfält tills vidare. Då måste du få fram komponenterna i rörelseekvationen dp/dt=—qVφ, där, som du säkert minns, p=mv√(1-v 2 /c 2).

Det är mycket svårare att ta hänsyn till vektorpotentialen A. Variationerna blir då ojämförligt mer komplexa. Men i slutändan visar sig kraften vara lika med vad den borde vara: g(E+v × B). Men ha lite kul med det själv.

Jag skulle vilja betona att i det allmänna fallet (till exempel i den relativistiska formeln) inkluderar integralen i handling inte längre skillnaden mellan kinetiska och potentiella energier. Detta var endast lämpligt i en icke-relativistisk approximation. Till exempel medlem m o c 2√(1-v 2 /c 2)-Det här är inte vad som kallas rörelseenergi. Frågan om vad åtgärden ska vara för något särskilt fall kan avgöras efter en del försök och misstag. Detta är samma typ av problem som att bestämma vad rörelseekvationerna ska vara. Du måste bara leka med de ekvationer du känner till och se om de kan skrivas som principen om minsta handling.

Ytterligare en anmärkning om terminologi. Den där funktionen som integreras över tid för att få en åtgärd S, kallad LagrangianΛ. Detta är en funktion som endast beror på partiklarnas hastigheter och positioner. Så principen om minsta handling är också skriven i formen

var under X i Och v i alla komponenter av koordinater och hastigheter är underförstådda. Om du någonsin hör någon prata om "Lagrangian", talar de om funktionen som används för att få S. För relativistisk rörelse i ett elektromagnetiskt fält

Dessutom bör jag notera att de mest noggranna och pedantiska människorna inte ringer S handling. Det kallas "Hamiltons första huvudfunktion". Men att hålla en föreläsning om "Hamiltons princip om minst första huvudfunktion" var över min styrka. Jag kallade det "action". Och dessutom, fler och fler människor kallar det "action". Du förstår, historiskt har handling kallats något annat som inte är lika användbart för vetenskapen, men jag tror att det är mer meningsfullt att ändra definitionen. Nu kommer du också att börja kalla den nya funktionen för en åtgärd, och snart kommer alla att börja kalla den med detta enkla namn.

Nu vill jag berätta något om vårt ämne som liknar det resonemang som jag hade om principen om kortast tid. Det finns en skillnad i själva essensen av lagen som säger att någon integral som tas från en punkt till en annan har ett minimum - lagen som säger oss något om hela vägen på en gång, och lagen som säger att när man rör sig, då Det betyder att det finns en kraft som leder till acceleration. Det andra tillvägagångssättet rapporterar till dig om varje steg, det spårar din väg tum för tum, och den första ger omedelbart ett allmänt uttalande om hela vägen. Medan vi pratade om ljus, pratade vi om kopplingen mellan dessa två tillvägagångssätt. Nu vill jag förklara för dig varför differentiella lagar borde finnas om det finns en sådan princip - principen om minsta handling. Anledningen är denna: låt oss betrakta den väg som faktiskt färdats i rum och tid. Som tidigare nöjer vi oss med en mätning, så att vi kan rita en graf över beroendet X från t. Längs den sanna vägen S når ett minimum. Låt oss anta att vi har denna väg och att den går igenom någon punkt A rum och tid och genom en annan närliggande punkt b.

Nu, om hela integralen av t 1 innan t 2 har nått ett minimum, är det nödvändigt att integralen längs en liten sektion från a till b var också minimal. Det kan inte vara den delen av A innan båtminstone lite mer än minimum. Annars kan du flytta kurvan fram och tillbaka i detta avsnitt och minska värdet på hela integralen något.

Detta innebär att varje del av banan också ska ge ett minimum. Och detta är sant för alla små delar av stigen. Därför kan principen att hela vägen ska ge ett minimum formuleras genom att säga att ett oändligt litet segment av banan också är en kurva på vilken åtgärden är minimal. Och om vi tar ett tillräckligt kort segment av vägen - mellan punkter mycket nära varandra A Och b,- då spelar det ingen roll hur potentialen förändras från punkt till punkt långt från den här platsen, för när du går igenom hela ditt korta segment flyttar du nästan aldrig från den platsen. Det enda du behöver tänka på är den första ordningens förändring i litenhet i potentialen. Svaret beror kanske bara på potentialens derivata och inte på potentialen någon annanstans. Således blir ett uttalande om egenskapen för hela vägen som helhet ett uttalande om vad som händer på en kort del av vägen, det vill säga ett differentiellt uttalande. Och denna differentialformulering inkluderar derivator av potentialen, det vill säga kraften vid en given punkt. Detta är en kvalitativ förklaring av sambandet mellan lagen som helhet och differentiallagen.

När vi pratade om ljus diskuterade vi också frågan: hur hittar en partikel rätt väg? Ur en differentiell synvinkel är detta lätt att förstå. I varje ögonblick upplever partikeln acceleration och vet bara vad den ska göra i det ögonblicket. Men alla dina instinkter av orsak och verkan dyker upp när du hör att en partikel "bestämmer" vilken väg den ska ta och strävar efter ett minimum av åtgärder. "Sniffar" hon inte på närliggande stigar, räknar ut vad de kommer att leda till - mer eller mindre action? När vi placerade en skärm i ljusets väg så att fotonerna inte kunde prova alla vägar, fick vi reda på att de inte kunde bestämma vilken väg de skulle ta, och vi fick fenomenet diffraktion.

Men gäller detta även för mekanik? Är det sant att en partikel inte bara "går rätt väg", utan omprövar alla andra tänkbara banor? Och vad händer om vi, genom att lägga hinder i vägen, inte tillåter det att se framåt, då kommer vi att få någon slags analog av fenomenet diffraktion? Det mest underbara med allt detta är att allt verkligen är så här. Detta är precis vad kvantmekanikens lagar säger. Så vår princip om minsta handling är inte helt formulerad. Det består inte i det faktum att partikeln väljer vägen för minsta verkan, utan i det faktum att den "känner av" alla närliggande vägar och väljer den längs vilken åtgärden är minimal, och metoden för detta val liknar den sätt på vilket ljus väljer den kortaste tiden. Du kommer ihåg att det sätt som ljuset väljer den kortaste tiden är detta: om ljus går längs en väg som kräver en annan tid, kommer det att anlända med en annan fas. Och den totala amplituden vid någon punkt är summan av amplitudbidragen för alla vägar längs vilka ljus kan nå den. Alla de vägar vars faser skiljer sig kraftigt ger inget efter tillsats. Men om du lyckades hitta hela sekvensen av banor, vars faser är nästan desamma, kommer de små bidragen att läggas ihop, och vid ankomstpunkten kommer den totala amplituden att få ett märkbart värde. Den viktigaste vägen är den nära vilken det finns många nära stigar som ger samma fas.

Exakt samma sak händer inom kvantmekaniken. Komplett kvantmekanik (icke-relativistisk och negligerande elektronspin) fungerar så här: sannolikheten att en partikel lämnar en punkt 1 i stunden t 1, kommer att nå poängen 2 i stunden t 2 , lika med kvadraten på sannolikhetsamplituden. Den totala amplituden kan skrivas som summan av amplituderna för alla möjliga vägar—för alla ankomstvägar. För vem som helst x(t), som skulle kunna inträffa för vilken tänkbar imaginär bana som helst, måste amplituden beräknas. Sedan måste de alla vikas. Vad tar vi som sannolikhetsamplituden för en viss väg? Vår handlingsintegral talar om för oss vad amplituden för en individuell väg bör vara. Amplituden är proportionell e tS/h, Var S - åtgärder längs denna väg. Detta betyder att om vi representerar amplitudens fas som ett komplext tal, så blir fasvinkeln lika med S/ h. Handling S har dimensionen energi över tid, och Plancks konstant har samma dimension. Detta är konstanten som avgör när kvantmekanik behövs.

Och det är så det hela fungerar. Låt handling för alla vägar S kommer att vara mycket stort jämfört med antalet h. Låt någon väg leda till ett visst amplitudvärde. Fasen av den intilliggande vägen kommer att vara helt annorlunda, eftersom med en enorm S även små förändringar S byter plötsligt fas (trots allt h extremt lite). Detta innebär att angränsande stigar vanligtvis släcker sina bidrag när de läggs till. Och bara i ett område är detta inte sant - i det där både vägen och dess granne - båda, till en första uppskattning, har samma fas (eller, mer exakt, nästan samma verkan, varierande inom h). Endast sådana vägar beaktas. Och i det begränsade fallet, när Plancks konstant h tenderar mot noll, kan de korrekta kvantmekaniska lagarna sammanfattas genom att säga: "Glöm alla dessa sannolikhetsamplituder. Partikeln rör sig faktiskt längs en speciell bana - exakt den längs vilken S till en första uppskattning ändras inte.” Detta är kopplingen mellan principen om minsta verkan och kvantmekaniken. Det faktum att kvantmekaniken kan formuleras på detta sätt upptäcktes 1942 av en elev till samma lärare, Mr Bader, som jag berättade om. [Kvantmekaniken formulerades ursprungligen med hjälp av en differentialekvation för amplitud (Schrödinger) samt viss matrismatematik (Heisenberg).]

Nu vill jag prata om andra principer om minimum i fysik. Det finns många intressanta principer av detta slag. Jag kommer inte att lista dem alla, men jag kommer bara att nämna en till. Senare, när vi kommer till ett fysiskt fenomen för vilket det finns en utmärkt minimiprincip, kommer jag att berätta om det. Nu vill jag visa att det inte är nödvändigt att beskriva elektrostatik med en differentialekvation för fältet; man kan istället kräva att någon integral har ett maximum eller ett minimum. Till att börja med, låt oss ta fallet när laddningstätheten är känd överallt, men vi måste hitta potentialen φ var som helst i rymden. Du vet redan att svaret borde vara:

Ett annat sätt att säga samma sak är att utvärdera integralen U*

detta är en volymintegral. Det tas i hela utrymmet. Med korrekt potentialfördelning φ (x, y,z) detta uttryck når sitt minimum.

Vi kan visa att båda dessa påståenden om elektrostatik är likvärdiga. Låt oss anta att vi har valt en godtycklig funktion φ. Vi vill visa att när vi tar som φ det korrekta värdet av potentialen _φ plus en liten avvikelse f, så till första ordningen av litenhet ändringen i U* kommer att vara lika med noll. Så vi skriver

här φ är vad vi letar efter; men vi kommer att variera φ för att se vad det måste vara för variationen U* visade sig vara av första ordningen av litenhet. Under första terminen U* vi behöver skriva

Detta måste integreras av x, y och genom att z. Och här antyder samma trick sig själv: för att bli av med df/ dx, vi kommer att integreras över X i delar. Detta kommer att leda till ytterligare differentieringφ med avseende på X. Detta är samma grundidé som vi blev av med derivat med avseende på t. Vi använder jämlikhet

Den integrerade termen är noll eftersom vi tar f för att vara noll i oändligheten. (Detta motsvarar att η försvinner som t 1 Och t 2 . Så vår princip är mer exakt formulerad enligt följande: U* för högern φ mindre än för någon annan φ(x, y,z), har samma värden i oändligheten.) Då kommer vi att göra samma sak med på och med z. Vår integral ΔU* kommer att förvandlas till

För att denna variation ska vara lika med noll för något godtyckligt f måste koefficienten för f vara lika med noll. Betyder att,

Vi är tillbaka till vår gamla ekvation. Det betyder att vårt "minimi" förslag är korrekt. Det kan generaliseras om beräkningarna är något modifierade. Låt oss gå tillbaka och integrera del för del, utan att beskriva allt komponent för komponent. Låt oss börja med att skriva följande likhet:

Genom att särskilja den vänstra sidan kan jag visa att den är exakt lika med den högra. Denna ekvation är lämplig för att utföra integration av delar. I vår integral ΔU* vi byter ut Vφ*Vf n och fV 2 φ+V*(fVφ) och sedan integrera detta över volymen. Divergenstermen efter integration över volymen ersätts av en integral över ytan:

Och eftersom vi integrerar över hela utrymmet, ligger ytan i denna integral i oändlighet. Detta betyder f=0, och vi får samma resultat.

Först nu börjar vi förstå hur vi ska lösa problem där vi vi vet inte där alla avgifter finns. Låt oss ha konduktörer på vilka avgifter på något sätt fördelas. Om potentialerna på alla ledare är fasta, får vår minimiprincip fortfarande gälla. Integration i U* vi ritar endast längs området som ligger utanför alla ledare. Men eftersom vi inte kan ändra (φ) på ledare, då på deras yta f = 0, och ytintegralen

behöver endast göras i utrymmena mellan ledarna. Och vi får såklart Poisson-ekvationen igen

Vi har därför visat att vår ursprungliga integral U* når ett minimum även när det beräknas i utrymmet mellan ledarna, som var och en har en fast potential [det betyder att varje testfunktion φ(g, y,z) måste vara lika med den specificerade ledarpotentialen när (x, y,z) - punkter på ledarytan]. Det finns ett intressant specialfall när laddningar endast finns på ledare. Sedan

och vår minimiprincip säger oss att i det fall varje ledare har sin egen förutbestämda potential, justeras potentialerna i utrymmena mellan dem så att integralen U* visar sig vara så liten som möjligt. Vad är detta för integral? Termen Vφ är det elektriska fältet. Det betyder att integralen är elektrostatisk energi. Det korrekta fältet är det enda som, av alla fält som erhålls som en potentialgradient, har den lägsta totala energin.

Jag skulle vilja använda detta resultat för att lösa något speciellt problem och visa dig att alla dessa saker har verklig praktisk betydelse. Antag att jag tar två ledare i form av en cylindrisk kondensator.

Den inre ledaren har en potential lika med t.ex. V, och för den externa - noll. Låt innerledarens radie vara lika med A, och externa - b. Nu kan vi anta att fördelningen av potentialer mellan dem är några. Men om vi tar korrekt värdet på φ och beräkna
(ε 0 /2) ∫ (Vφ) 2 dV då bör systemets energi vara 1/2CV 2.

Så med hjälp av vår princip kan du beräkna kapaciteten MED. Om vi tar en felaktig potentialfördelning och försöker uppskatta kondensatorns kapacitans med denna metod kommer vi fram till ett alltför stort kapacitansvärde för en fast V. Varje uppskattad potential φ som inte exakt överensstämmer med dess verkliga värde kommer också att leda till ett felaktigt värde på C, större än nödvändigt. Men om den felaktigt valda potentiella cp fortfarande är en grov approximation, då kapacitansen MED kommer att visa sig med god noggrannhet, eftersom felet i C är ett andra ordningens värde jämfört med felet i φ.

Låt oss anta att jag inte vet kapacitansen för den cylindriska kondensatorn. Sedan, för att känna igen henne, kan jag använda den här principen. Jag kommer helt enkelt att testa olika funktioner av φ som potential tills jag uppnår det lägsta värdet MED. Låt oss till exempel säga att jag har valt en potential som motsvarar ett konstant fält. (Du vet förstås att fältet här faktiskt inte är konstant; det varierar som 1/r) Om fältet är konstant betyder det att potentialen beror linjärt på avståndet. För att spänningen på ledarna ska bli som krävs måste funktionen φ ha formen

Denna funktion är lika med V på r=a, noll vid r =b, och mellan dem finns en konstant lutning lika med - V/(b—A). Så, för att bestämma integralen U*, du behöver bara multiplicera kvadraten på denna gradient med ε o /2 och integrera över hela volymen. Låt oss utföra denna beräkning för en cylinder med enhetslängd. Volymelement vid radie rär lika med 2πrdr. När jag genomför integrationen upptäcker jag att mitt första test ger följande kapacitet:

Så jag får en formel för kapacitet, som, även om den är felaktig, är någon form av approximation:

Naturligtvis skiljer det sig från rätt svar C=2πε 0/ln (b/a), men överlag är det inte så illa. Låt oss försöka jämföra det med rätt svar för flera värden b/a. Siffrorna jag beräknade visas i följande tabell.

Även när b/a=2(och detta leder redan till ganska stora skillnader mellan de konstanta och linjära fälten), jag får ändå en ganska acceptabel approximation. Svaret är förstås som väntat lite för högt. Men om en tunn tråd placeras inuti en stor cylinder, så ser allt mycket värre ut. Då förändras fältet väldigt mycket och att ersätta det med ett konstant fält leder inte till något bra. När b/a = 100 överskattar vi svaret med nästan två gånger. För små b/a läget ser mycket bättre ut. I den motsatta gränsen, när gapet mellan ledarna inte är särskilt stort (säg, för b/a = 1,1), visar sig ett konstant fält vara en mycket bra approximation, det ger värdet MED exakt till tiondels procent.

Nu ska jag berätta för dig hur du förbättrar denna beräkning. (Svaret för cylindern är naturligtvis, känd, men samma metod fungerar för vissa andra ovanliga kondensatorformer som du kanske inte vet det rätta svaret på.) Nästa steg är att hitta en bättre approximation för den okända sanna potentialen φ. Låt oss säga att du kan testa konstanten plus exponenten φ, etc. Men hur vet du att du har den bästa approximationen om du inte vet den sanna φ? Svar: Räkna upp det MED; ju lägre den är, desto närmare sanningen. Låt oss testa den här idén. Låt potentialen inte vara linjär, utan säg kvadratisk i r, och det elektriska fältet inte konstant, utan linjärt. Mest allmän kvadratisk form, som övergår till φ=O när r=b och i φ=F at r=a,är detta:

där α är ett konstant tal. Denna formel är lite mer komplicerad än den föregående. Den innehåller både en kvadratisk term och en linjär. Det är väldigt lätt att få ett fält från det. Det är lika med enkelt

Nu måste detta kvadratiseras och integreras över volymen. Men vänta lite. Vad ska jag ta för α? Jag kan ta f för att vara en parabel, men vilken? Så här ska jag göra: beräkna kapaciteten vid godtycklig α. Jag kommer att få

Det här ser lite förvirrande ut, men det är så det blir efter att ha integrerat fältets kvadrat. Nu kan jag välja själv. Jag vet att sanningen ligger lägre än allt jag ska beräkna. Oavsett vad jag sätter i stället för a, kommer svaret fortfarande att vara för stort. Men om jag fortsätter mitt spel med α och försöker uppnå lägsta möjliga värde MED, då kommer detta lägsta värde att vara närmare sanningen än något annat värde. Därför måste jag nu välja α så att värdet MED har nått sitt minimum. När det gäller vanlig differentialkalkyl är jag övertygad om att minimum MED kommer att vara när α =— 2 b/(b+a). Genom att ersätta detta värde i formeln får jag för den minsta kapaciteten

Jag kom på vad den här formeln ger för MED till olika värden b/a. Jag namngav dessa nummer MED(kvadratisk). Här är en tabell som jämför MED(kvadratisk) med MED(Sann).

Till exempel, när radieförhållandet är 2:1 får jag 1,444. Detta är en mycket bra uppskattning av det korrekta svaret, 1,4423. Även med stora Ja approximationen förblir ganska bra - mycket bättre än den första approximationen. Det förblir tolerabelt (överskattat med endast 10%) även med b/a = 10:1. En stor avvikelse uppstår endast vid förhållandet 100:1. Jag får MED lika med 0,346 istället för 0,267. Å andra sidan, för ett radieförhållande på 1,5 är avtalet utmärkt, och för b/a=1,1 svaret är 10,492065 istället för förväntat 10,492070. Där du förväntar dig ett bra svar, visar det sig vara väldigt, väldigt bra.

Jag har gett alla dessa exempel, för det första för att visa det teoretiska värdet av principen om minimal handling och i allmänhet av alla principer om minimum, och för det andra för att visa er deras praktiska användbarhet, och inte alls för att beräkna kapaciteten som vi redan har vet vi mycket väl. För vilken annan form som helst kan du prova ett ungefärligt fält med några okända parametrar (som α) och anpassa dem till ett minimum. Du kommer att få överlägsna numeriska resultat på problem som inte kan lösas på annat sätt.

De lyder det, och därför är denna princip en av nyckelbestämmelserna i modern fysik. De rörelseekvationer som erhålls med dess hjälp kallas Euler-Lagrange-ekvationerna.

Den första formuleringen av principen gavs av P. Maupertuis under året, och påpekade omedelbart dess universella karaktär och ansåg att den var tillämplig på optik och mekanik. Från denna princip härledde han lagarna för reflektion och brytning av ljus.

Berättelse

Maupertuis kom till denna princip från känslan av att universums perfektion kräver en viss ekonomi i naturen och motsäger all värdelös energiförbrukning. Den naturliga rörelsen måste vara sådan att den gör en viss mängd minimum. Allt han behövde göra var att hitta detta värde, vilket han fortsatte att göra. Det var produkten av rörelsens varaktighet (tiden) inom systemet med två gånger värdet, som vi nu kallar systemets kinetiska energi.

Euler (in "Reflexions sur quelques loix générales de la nature", 1748) antar principen om minsta möjliga handling, kallar handling "ansträngning". Dess uttryck i statik motsvarar vad vi nu skulle kalla potentiell energi, så att dess uttalande om minsta verkan i statik är ekvivalent med det minimala potentiella energitillståndet för en jämviktskonfiguration.

I klassisk mekanik

Principen om minsta verkan tjänar som den grundläggande och standardmässiga grunden för mekanikens lagrangska och hamiltonska formuleringar.

Låt oss först titta på konstruktionen så här: Lagrangemekanik. Med hjälp av exemplet med ett fysiskt system med en frihetsgrad, kom ihåg att en handling är en funktion med avseende på (generaliserade) koordinater (i fallet med en frihetsgrad - en koordinat), det vill säga den uttrycks genom att varje tänkbar version av funktionen är associerad med ett visst tal - en handling (i denna mening kan vi säga att en handling som en funktionell är en regel som gör det möjligt för varje given funktion att beräkna ett väldefinierat tal - även kallat en handling). Handlingen ser ut så här:

var är systemets lagrangian, beroende på den generaliserade koordinaten, dess första derivata med avseende på tid, och även, möjligen, explicit på tid. Om systemet har ett större antal frihetsgrader, beror Lagrangian på ett större antal generaliserade koordinater och deras första derivator med avseende på tid. Således är handlingen en skalär funktion beroende på kroppens bana.

Det faktum att handlingen är en skalär gör det lätt att skriva den i alla generaliserade koordinater, huvudsaken är att systemets position (konfiguration) otvetydigt karakteriseras av dem (till exempel, istället för kartesiska koordinater, kan dessa vara polära koordinater, avstånd mellan punkter i systemet, vinklar eller deras funktioner etc. .d.).

Handlingen kan beräknas för en helt godtycklig bana, hur "vild" och "onaturlig" den än kan vara. Men i klassisk mekanik, bland hela uppsättningen av möjliga banor, finns det bara en längs vilken kroppen faktiskt kommer att gå. Principen om stationär handling ger exakt svaret på frågan om hur kroppen faktiskt kommer att röra sig:

Detta betyder att om systemets Lagrangian är given, kan vi med hjälp av variationskalkylen fastställa exakt hur kroppen kommer att röra sig genom att först erhålla rörelseekvationerna - Euler-Lagrange-ekvationerna, och sedan lösa dem. Detta gör det möjligt att inte bara generalisera formuleringen av mekanik på allvar, utan också att välja de mest bekväma koordinaterna för varje specifikt problem, inte begränsat till kartesiska, vilket kan vara mycket användbart för att erhålla de enklaste och lättast lösa ekvationerna.

var är Hamilton-funktionen för detta system; - (generaliserade) koordinater, - konjugera (generaliserade) impulser, som tillsammans vid varje givet tidpunkt kännetecknar systemets dynamiska tillstånd och, var och en som är en funktion av tiden, sålunda karaktäriserar systemets evolution (rörelse). I det här fallet, för att erhålla systemets rörelseekvationer i form av Hamiltons kanoniska ekvationer, är det nödvändigt att variera handlingen skriven på detta sätt oberoende för alla och .

Det bör noteras att om det utifrån villkoren för problemet i princip är möjligt att hitta rörelselagen, så är detta automatiskt Inte innebär att det är möjligt att konstruera en funktion som tar ett stationärt värde under sann rörelse. Ett exempel är den gemensamma rörelsen av elektriska laddningar och monopoler - magnetiska laddningar - i ett elektromagnetiskt fält. Deras rörelseekvationer kan inte härledas från principen om stationär verkan. På samma sätt har vissa Hamiltonska system rörelseekvationer som inte kan härledas från denna princip.

Exempel

Triviala exempel hjälper till att utvärdera användningen av driftsprincipen genom Euler-Lagrange-ekvationerna. Fri partikel (massa m och hastighet v) i det euklidiska rummet rör sig i en rak linje. Med Euler-Lagrange-ekvationerna kan detta visas i polära koordinater enligt följande. I frånvaro av potential är Lagrange-funktionen helt enkelt lika med den kinetiska energin

i ett ortogonalt koordinatsystem.

I polära koordinater blir den kinetiska energin, och därmed Lagrange-funktionen

Ekvationernas radiella och vinkelkomponenter blir respektive:

Lösa dessa två ekvationer

Här är en villkorlig notation för oändligt multipel funktionell integration över alla banor x(t), och är Plancks konstant. Vi betonar att handlingen i exponentialen i princip uppträder (eller kan uppträda) själv när man studerar evolutionsoperatorn i kvantmekanik, men för system som har en exakt klassisk (icke-kvant) analog är den exakt lika med den vanliga klassisk handling.

Matematisk analys av detta uttryck i den klassiska gränsen - för tillräckligt stor , det vill säga för mycket snabba svängningar av den imaginära exponentialen - visar att den överväldigande majoriteten av alla möjliga banor i denna integral upphäver varandra i gränsen (formellt för ). För nästan vilken väg som helst finns det en väg på vilken fasförskjutningen kommer att vara exakt den motsatta, och de kommer att summera till noll bidrag. Endast de banor för vilka åtgärden är nära extremvärdet (för de flesta system - till ett minimum) reduceras inte. Detta är ett rent matematiskt faktum från funktionsteorin för en komplex variabel; Till exempel är den stationära fasmetoden baserad på den.

Som ett resultat rör sig partikeln, i full överensstämmelse med kvantmekanikens lagar, samtidigt längs alla banor, men under normala förhållanden bidrar endast banor nära stationära (det vill säga klassiska) till de observerade värdena. Eftersom kvantmekaniken förvandlas till klassisk mekanik i gränsen för höga energier, kan vi anta att detta är kvantmekanisk härledning av den klassiska principen om verkans stationaritet.

I kvantfältteori

I kvantfältteorin tillämpas även principen om stationär verkan framgångsrikt. Den lagrangiska densiteten inkluderar här operatorerna för motsvarande kvantfält. Även om det är mer korrekt här i huvudsak (med undantag för den klassiska gränsen och delvis kvasi-klassiker) att inte tala om principen om handlingens stationaritet, utan om Feynman-integrering längs banor i dessa fälts konfiguration eller fasutrymme - med hjälp av den nyss nämnda lagrangiska tätheten.

Ytterligare generaliseringar

Mer allmänt förstås en handling som en funktion som definierar en mappning från ett konfigurationsutrymme till en uppsättning reella tal och i allmänhet behöver den inte vara en integral, eftersom icke-lokala åtgärder är möjliga i princip, åtminstone teoretiskt sett. Dessutom är ett konfigurationsutrymme inte nödvändigtvis ett funktionsutrymme eftersom det kan ha icke-kommutativ geometri.

De lyder det, och därför är denna princip en av nyckelbestämmelserna i modern fysik. De rörelseekvationer som erhålls med dess hjälp kallas Euler-Lagrange-ekvationerna.

Berättelse

I klassisk mekanik

Principen om minsta verkan tjänar som den grundläggande och standardmässiga grunden för mekanikens lagrangska och hamiltonska formuleringar.

Exempel

i ett ortogonalt koordinatsystem.

I polära koordinater blir den kinetiska energin, och därmed Lagrange-funktionen

Ekvationernas radiella och vinkelkomponenter blir respektive:

Lösa dessa två ekvationer

I kvantfältteori

Ytterligare generaliseringar

Principen om minsta handling, som först formulerades exakt av Jacobi, liknar Hamiltons princip, men mindre generell och svårare att bevisa. Denna princip är endast tillämplig på fallet när förbindelserna och kraftfunktionen inte beror på tid och när det därför finns en integral av levande kraft.

Denna integral har formen:

Hamiltons princip ovan säger att variationen av integralen

är lika med noll vid övergången av den faktiska rörelsen till någon annan oändligt nära rörelse, som överför systemet från samma initiala position till samma slutliga position under samma tidsperiod.

Jacobis princip uttrycker tvärtom en rörelseegenskap som inte är beroende av tid. Jacobi överväger integralen

beslutande åtgärd. Principen han etablerade säger att variationen av denna integral är noll när vi jämför systemets faktiska rörelse med vilken annan oändligt nära rörelse som helst som tar systemet från samma initiala position till samma slutposition. I det här fallet uppmärksammar vi inte tidsperioden, men vi observerar ekvation (1), dvs ekvationen för arbetskraft med samma värde på konstanten h som i faktisk rörelse.

Detta nödvändiga villkor för ett extremum leder generellt sett till ett minimum av integral (2), därav namnet principen om minsta handling. Minimivillkoret verkar vara det mest naturliga, eftersom värdet på T i huvudsak är positivt, och därför måste integral (2) nödvändigtvis ha ett minimum. Förekomsten av ett minimum kan strikt bevisas om bara tidsperioden är tillräckligt liten. Beviset för denna position finns i Darboux berömda kurs om ytteori. Vi kommer dock inte att presentera det här och kommer att begränsa oss till att härleda villkoret

432. Bevis för principen om minsta handling.

I själva beräkningen stöter vi på en svårighet som inte finns i beviset för Hamiltons sats. Variabeln t förblir inte längre oberoende av variation; därför variationer av q i och q. är relaterade till variationen av t genom ett komplext samband som följer av ekvation (1). Det enklaste sättet att komma runt denna svårighet är att ändra den oberoende variabeln och välja en vars värden ligger mellan konstanta gränser som inte beror på tid. Låt k vara en ny oberoende variabel, vars gränser antas vara oberoende av t. När systemet flyttas kommer parametrarna och t att vara funktioner för denna variabel

Låt bokstäver med primtal q beteckna derivator av parametrar q med avseende på tid.

Eftersom sambanden, enligt antagande, inte är beroende av tid, är de kartesiska koordinaterna x, y, z funktioner av q som inte innehåller tid. Därför kommer deras derivator att vara linjära homogena funktioner av q och 7 kommer att vara en homogen kvadratisk form av q, vars koefficienter är funktioner av q. Vi har

För att särskilja derivatorna av q med avseende på tid, betecknar vi, med hjälp av parentes, (q), derivatorna av q taget med avseende på och satt i enlighet med detta

då har vi

och integral (2), uttryckt genom den nya oberoende variabeln A, kommer att ha formen;

Derivatan kan elimineras med hjälp av levande kraftsatsen. Faktum är att integralen av arbetskraft kommer att vara

Genom att ersätta detta uttryck med formeln reducerar vi integralen (2) till formen

Den integral som definierar handlingen fick alltså sin slutgiltiga form (3). Integrandfunktionen är kvadratroten av kvantiteternas kvadratiska form

Låt oss visa att differentialekvationerna för extremalerna av integralen (3) är exakt Lagrangekvationerna. Ekvationerna för extremal, baserade på de allmänna formlerna för variationskalkylen, kommer att vara:

Låt oss multiplicera ekvationerna med 2 och utföra partiella differentieringar, med hänsyn till att den inte innehåller, då får vi, om vi inte skriver ett index,

Dessa är ekvationer av extremal uttryckta i termer av den oberoende variabeln. Uppgiften är nu att återgå till den oberoende variabeln

Eftersom Γ är en homogen funktion av andra graden av och är en homogen funktion av första graden, har vi

Å andra sidan kan den levande kraftsatsen appliceras på faktorerna för derivator i ekvationerna för extremaler, vilket leder, som vi såg ovan, till substitutionen

Som ett resultat av alla substitutioner reduceras extremalernas ekvationer till formen

Vi har alltså kommit fram till Lagrangekvationerna.

433. Fallet när det inte finns några drivkrafter.

I fallet när det inte finns några drivkrafter finns det en ekvation för levande kraft och det har vi

Villkoret för att integralen ska vara ett minimum är i detta fall att motsvarande värde på -10 måste vara det minsta. Sålunda, när det inte finns några drivkrafter, så är bland alla de rörelser i vilka den levande kraften bibehåller samma givna värde, den faktiska rörelsen den som överför systemet från dess utgångsläge till dess slutliga läge på kortast tid.

Om systemet reduceras till en punkt som rör sig på en stationär yta, så är den faktiska rörelsen, bland alla rörelser på ytan som sker med samma hastighet, den rörelse i vilken punkten rör sig från sin initiala position till den slutliga positionen i kortast

tidsintervall. Med andra ord beskriver en punkt på ytan den kortaste linjen mellan dess två positioner, d.v.s. en geodetisk linje.

434. Anm.

Principen om minsta handling förutsätter att systemet har flera frihetsgrader, eftersom om det bara fanns en frihetsgrad, så skulle en ekvation vara tillräcklig för att bestämma rörelsen. Eftersom rörelsen i detta fall helt kan bestämmas av ekvationen för levande kraft, så kommer den faktiska rörelsen att vara den enda som uppfyller denna ekvation, och kan därför inte jämföras med någon annan rörelse.

MINST EFFEKTIV PRINCIP

En av mekanikens variationsprinciper, enligt Krom, för en given klass av mekaniska rörelser jämfört med varandra. system, det giltiga är det för vilket fysiskt. storlek, kallas action, har det minsta (mer exakt, stationära) värdet. Vanligtvis används N. d. p. i en av två former.

a) N. d. p. i form av Hamilton - Ostrogradsky fastställer att bland alla kinematiskt möjliga rörelser av ett system från en konfiguration till en annan (nära den första), som utförs under samma tidsperiod, är den giltiga den för vilken Hamiltons action S kommer att vara den minsta. Matematik. uttrycket för N. d.p. i detta fall har formen: dS = 0, där d är symbolen för ofullständig (isokron) variation (dvs., till skillnad från fullständig variation, varierar tiden inte i den).

b) N. d. p. i form av Maupertuis - Lagrange fastställer att bland alla kinematiskt möjliga rörelser av ett system från en konfiguration till en annan nära det, utförda samtidigt som man bibehåller samma värde av systemets totala energi, är den giltiga att för - Därför kommer Lagrange-aktionen W att vara den minsta. Matematik. uttrycket av N. d.p. i detta fall har formen DW = 0, där D är symbolen för total variation (till skillnad från Hamilton-Ostrogradsky-principen, här varierar inte bara koordinaterna och hastigheterna, utan också tiden för rörelsen av system från en konfiguration till en annan). N.d.p.v. I det här fallet är det endast giltigt för konservativa och dessutom holonomiska system, medan i det första fallet är den icke-konservativa principen mer generell och i synnerhet kan den utvidgas till icke-konservativa system. N.D.P. används för att sammanställa ekvationer för mekanisk rörelse. system och att studera de allmänna egenskaperna hos dessa rörelser. Med en lämplig generalisering av begrepp, finner NDP tillämpningar i mekaniken i ett kontinuerligt medium, i elektrodynamik och kvant. mekanik osv.

- samma som...
Fysisk uppslagsverk
- m-operator, minimeringsoperatör, - en metod för att konstruera nya funktioner från andra funktioner, bestående av följande...
Matematisk uppslagsverk
- en av mekanikens variationsprinciper, enligt vilken för en given klass av mekaniska rörelser jämfört med varandra. systemet utförs det för vilket åtgärden är minimal...
Naturvetenskap. encyklopedisk ordbok
- en av mekanikens viktigaste lagar, fastställd av den ryska vetenskapsmannen M.V. Ostrogradsky...
Ryska uppslagsverket
Ordbok över juridiska termer
- i ett antal staters författningsrätt principen enligt vilken allmänt erkända folkrättsprinciper och normer är en integrerad del av rättssystemet i motsvarande land...
Encyclopedia of Lawyer
- i ett antal staters författningsrätt principen enligt vilken allmänt erkända folkrättsnormer är en integrerad del av det nationella rättssystemet...
Stor juridisk ordbok
- det kortaste avståndet från mitten av sprängladdningen till den fria ytan - linje på nai-malkoto motstånd - křivka nejmenšího odporu - Line der geringsten Festigkeit - robbantás minimális ellenállási tengelyvonala - hamgiin baga...
Byggordbok
- om det är möjligt att flytta punkter i en deformerbar kropp i olika riktningar, rör sig varje punkt i denna kropp i riktningen för minsta motstånd...
Encyclopedic Dictionary of Metallurgy
- en regel enligt vilken befintliga varulager vanligtvis värderas antingen till den lägsta kostnaden eller till det lägsta försäljningspriset...
Ordbok över affärstermer
- i ett antal staters författningsrätt - principen enligt vilken allmänt erkända folkrättsprinciper och normer är en integrerad del av den relevanta statens rättssystem och verkar...
Encyclopedic Dictionary of Economics and Law
- en av mekanikens variationsprinciper, enligt vilken för en given klass av rörelser i ett mekaniskt system jämfört med varandra, är den giltiga den för vilken den fysiska kvantiteten,...
- samma som Gauss princip...
Stora sovjetiska encyklopedien
- en av mekanikens variationsprinciper; samma som principen om minsta handling...
Stora sovjetiska encyklopedien
- en av mekanikens variationsprinciper, enligt vilken för en given klass av rörelser i ett mekaniskt system jämfört med varandra, den för vilken åtgärden är minimal...
Stor encyklopedisk ordbok
- Bok Välj den enklaste handlingsmetoden, undvik hinder, undvik svårigheter...
Fraseologisk ordbok för det ryska litterära språket

"DEN MINSTA VÄRDEPRINCIPEN" i böcker

2.5.1. Funktionsprincip för enheten

Från boken Entertaining Electronics [Okonventionell encyklopedi av användbara kretsar] författare Kashkarov Andrey Petrovich

2.5.1. Funktionsprincipen för enheten Funktionsprincipen för enheten är enkel. När ljusflödet som emitteras av HL1 LED reflekteras från objektet och träffar fotodetektorn, producerar den elektroniska enheten, implementerad på 2 mikrokretsar - KR1401SA1 komparatorn och KR1006VI1 timern,

Principen för drift av terafim

Från boken Hemlig kunskap. Teori och praktik av Agni Yoga författare Roerich Elena Ivanovna

Terafims funktionsprincip 24.02.39 Du vet att varje medvetenhet och representation av något objekt därigenom för oss närmare det. Som ni vet kan de psykiska lagren av ett föremål överföras till dess terafer. Den astrala terafimen av avlägsna världar och

Tre villkor för att lagen om minsta ansträngning ska tillämpas

Från boken The Wisdom of Deepak Chopra [Få vad du vill genom att följa universums sju lagar] av Tim Goodman

Tre villkor för att lagen om minsta ansträngning ska fungera Låt oss se vilka villkor som krävs för att locka detta kreativa flöde av energi från universum in i ditt liv - kärlekens energi, och därför för att lagen om minsta ansträngning ska börja fungera i ditt liv .

Kapitel 19 PRINCIPEN OM MINSTA EFFEKT

Från bok 6. Elektrodynamik författare Feynman Richard Phillips

Kapitel 19 PRINCIPEN OM MINSTA EFFEKT Tillägg gjort efter en föreläsning När jag gick i skolan kallade vår fysiklärare, som heter Bader, in mig en gång efter lektionen och sa: ”Du ser ut som om du är fruktansvärt trött på allt; lyssna på en intressant sak

5. Principen om minsta åtgärd

Från boken Revolution in Physics av de Broglie Louis

5. Principen för minsta verkan Ekvationerna för dynamiken för en materiell punkt i ett kraftfält med potential kan erhållas utifrån principen, som i allmänna termer kallas Hamiltons princip, eller principen om stationär verkan. Enligt denna princip, av alla

Funktionsprincip

Från boken Locksmith's Guide to Locks av Phillips Bill

Funktionsprincip Förmågan att rotera cylindern beror på tapparnas position, som i sin tur bestäms av tyngdkraften, fjädrarnas verkan och nyckelns (eller huvudnyckeln; för information om huvudnycklar, se kapitel 9) . I avsaknad av nyckel trycker gravitationen och fjädrarna in

Stationär handlingsprincip

Från boken Great Soviet Encyclopedia (ST) av författaren TSB

Principen om minsta handling

TSB

Principen om minsta tvång

Från boken Great Soviet Encyclopedia (NA) av författaren TSB

2.5.1. Funktionsprincip

Ur boken Reläskydd i eldistributionsnät B90 författare Bulychev Alexander Vitalievich

2.5.1. Funktionsprincip I elektriska nät med tvåvägs strömförsörjning och i ringnät kan konventionella strömskydd inte fungera selektivt. Till exempel i ett elektriskt nätverk med två strömkällor (Fig. 2.15), där strömbrytare och skydd är installerade på båda sidor

Funktionsprincip

Från boken Turbo Suslik. Hur man slutar jävla sig själv och börjar leva författare Leushkin Dmitry

Handlingsprincipen "Bearbeta detta" är i själva verket ett slags "makro" som med en fras startar en hel massa processer i det undermedvetna, vars syfte är att bearbeta det valda mentala materialet. Denna hanterare innehåller 7 olika moduler, varav några

Hur man börjar följa lagen om minsta ansträngning: Tre nödvändiga åtgärder

Från boken A Guide to Growing Capital från Joseph Murphy, Dale Carnegie, Eckhart Tolle, Deepak Chopra, Barbara Sher, Neil Walsh författaren Stern Valentin

Hur man börjar följa lagen om minsta ansträngning: tre nödvändiga åtgärder För att lagen om minsta ansträngning ska börja fungera måste du inte bara uppfylla de tre villkoren som nämns ovan, utan också utföra tre åtgärder. Första åtgärden: börja acceptera världen som den är Acceptera

11. Fysik och Aikido av minsta kraft

författare Mindell Arnold

11. Fysik och Aikido av minsta effekt När det blåser är det bara vind. När det regnar är det bara regn. När molnen passerar skiner solen igenom dem. Om du öppnar dig för insikt är du ett med insikten. Och du kan använda den helt. Om du öppnar upp

Leibniz princip om minsta handling "Vis Viva"

Från boken Geopsychology in Shamanism, Physics and Taoism författare Mindell Arnold

Leibniz princip om minsta handling "Vis Viva" Vi har alla Wilhelm Gottfried Leibniz (1646–1716) att tacka för principen om minsta handling. En av de första "moderna" fysikerna och matematikerna, Leibniz levde på Newtons tid - en era då vetenskapsmän var mer öppna

Aikido - förkroppsligandet av principen om minsta handling

Från boken Geopsychology in Shamanism, Physics and Taoism författare Mindell Arnold

Aikido - förkroppsligandet av principen om minsta handling Vår psykologi och teknologi drivs till stor del av ett koncept som ligger mycket nära tanken om minsta handling. Vi försöker hela tiden göra våra liv enklare. Dagens datorer är inte tillräckligt snabba; De måste