Принцип найменшого впливу. Принцип найменшої дії Принцип найменшої дії у фізиці

Коли я навчався в школі, наш учитель фізики, на прізвище Бадер, одного разу закликав мене до себе після уроку і сказав: «У тебе такий вигляд, ніби тобі все страшно набридло; послухай-но про одну цікаву річ». І він розповів мені щось, що мені здалося справді захоплюючим. Навіть зараз, хоча з тих пір пройшла вже безліч часу, це продовжує мене захоплювати. І щоразу, коли я згадую про сказане, я знову беруся до роботи. І цього разу, готуючись до лекції, я спіймав себе на тому, що знову аналізую те саме. І, замість готуватися до лекції, я взявся за вирішення нового завдання. Предмет, про який я говорю,— це принцип найменшого впливу.

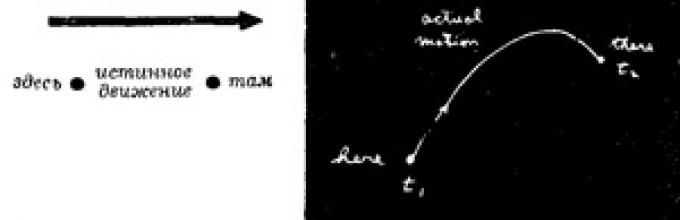
- Ось що сказав мені тоді мій учитель Бадер: «Нехай, наприклад, у тебе є частка в полі тяжкості; ця частка, вийшовши звідкись, вільно кудись рухається в іншу точку. Ти підкинув її, скажімо, вгору, а вона злетіла, а потім упала.

Від вихідного місця до кінцевого часу вона пройшла за якийсь час. Спробуй тепер якийсь інший рух. Нехай для того, щоб перейти звідси сюди, вона рухалася вже не так, як раніше, а ось так:

Але все одно опинилася на потрібному місці в той самий момент часу, що й раніше».

«І ось,— продовжував учитель,— якщо ти підрахуєш кінетичну енергію в кожний момент часу на шляху частки, віднімаєш з неї потенційну енергію і проінтегруєш різницю по всьому тому часу, коли відбувався рух, то побачиш, що число, яке вийде, буде більше,ніж за істинному русі частки.

Іншими словами, закони Ньютона можна сформулювати не у вигляді F=ma, а ось як: середня кінетична енергія мінус середня потенційна енергія досягає свого найменшого значення на тій траєкторії, за якою предмет рухається насправді від одного місця до іншого.

Спробую пояснити тобі трохи зрозуміліше.
Якщо взяти поле тяжіння та позначити траєкторію частки x(t), де х- Висота над землею (покинемося поки одним виміром; нехай траєкторія пролягає тільки вгору і вниз, а не в сторони), то кінетична енергія буде y 2 m(dx/ dt) 2 , aпотенційна енергія в довільний момент часу дорівнюватиме mgx.

Тепер я для якогось моменту руху траєкторією беру різницю кінетичної та потенційної енергій і інтегрую по всьому часу від початку до кінця. Нехай у початковий момент часу t x рух почався на якійсь висоті, а скінчився в мить t 2 на іншій певній висоті.

Тоді інтеграл дорівнює ∫ t2 t1 dt

Справжній рух відбувається за деякою кривою (як функція часу є параболою) і призводить до якогось певного значення інтеграла. Але можна передставитисобі якийсь інший рух: спершу різке піднесення, а потім якісь химерні коливання.

Можна підрахувати різницю потенційної та кінетичної енергій на такому шляху... або на будь-якому іншому. І найдивовижніше — що справжній шлях це той, яким цей інтеграл найменший.
Давайте перевіримо це. Спочатку розберемо такий випадок: у вільної частки зовсім немає потенційної енергії. Тоді правило говорить, що при переході від однієї точки до іншої за заданий час інтеграл від кінетичної енергії має бути найменшим. А це означає, що частка повинна рухатися поступово. (І це правильно, ми ж з тобою знаємо, що швидкість у такому русі постійна.) А чому рівномірно? Розберемося в цьому. Якби було інакше, то часом швидкість частинки перевищила б середню, а часом була б нижчою від неї, а середня швидкість була б однаковою, тому що частинці треба було б дійти «звідси сюди» за обумовлений час. Наприклад, якщо тобі потрібно потрапити з дому в школу на своїй машині за певний час, то зробити це можна по-різному: ти можеш спершу гнати, як божевільний, а в кінці пригальмувати, або їхати з однаковою швидкістю, або спочатку можеш навіть вирушити в зворотний бік, а вже потім повернути до школи, і т. д. У всіх випадках середня швидкість, звичайно, повинна бути однією і тією ж — приватна від поділу відстані від будинку до школи на якийсь час. Але і при цій середній швидкості ти іноді рухався дуже швидко, а іноді занадто повільно. А середній квадратчогось, що відхиляється від середнього, як відомо, завжди більше за квадрат середнього; отже, інтеграл від кінетичної енергії при коливаннях швидкості руху завжди буде більшим, ніж при русі з постійною швидкістю. Ти бачиш, що інтеграл досягне мінімуму, коли швидкість буде постійною (за відсутності сил). Правильний шлях такий.

Предмет же, підкинутий у поле тяжкості вгору, спершу піднімається швидко, а потім дедалі повільніше. Відбувається це тому, що він має і потенційну енергію, а найменшого значення має досягати разністьміж кінетичною та потенційною енергіями.. Якщо потенційна енергія зростає в міру підйому, то менша різницявийде, якщо якнайшвидше досягти тих висот, де потенційна енергія велика. Тоді, віднімаючи з кінетичної енергії цей високий потенціал, ми досягнемо зменшення середнього. Так що вигідніший такий шлях, який йде вгору і постачає добрий негативний шматок за рахунок потенційної енергії.

Ось і все, що сказав мені мій учитель, бо він був дуже добрий учитель і знав, коли настав час зупинитися. Сам я, на жаль, не такий. Мені важко вчасно зупинитися. І тому замість того, щоб просто розпалити у вас інтерес своєю розповіддю, я хочу залякати вас, хочу, щоб вам стало нудно від складності життя, — спробую довести те, про що я розповів. Математичне завдання, яке ми вирішуватимемо, дуже важке і своєрідне. Є деяка величина S, звана дією.Вона дорівнює кінетичній енергії мінус потенційна, проінтегрована за часом:

Але, з іншого боку, не можна ні рухатися дуже швидко, ні піднятися занадто високо, тому що на це потрібно занадто багато кінетичної енергії. Потрібно рухатися досить швидко, щоб піднятися і спуститися за певний час, що є у твоєму розпорядженні. Тож не слід намагатися злетіти надто високо, а просто треба досягти якогось розумного рівня. У результаті виявляється, що рішення є своєрідною рівновагою між бажанням роздобути якнайбільше потенційної енергії та бажанням якнайсильніше зменшити кількість кінетичної енергії — це прагнення домогтися максимального зменшення різниці кінетичної та потенційної енергій».

Не забудьте, що і п. і до. е. - обидві функції часу. Для будь-якого нового мислимого шляху ця дія набуває свого певного значення. Математична задача полягає в тому, щоб визначити, для якої кривої це число менше, ніж для інших.

Ви скажете: «О, це просто звичайний приклад на максимум та мінімум. Треба підрахувати дію, продиференціювати її та знайти мінімум».

Але зачекайте. Зазвичай у нас буває функція якоїсь змінної і потрібно знайти значення змінної,при якому функція стає найменшою чи найбільшою. Скажімо, є стрижень, нагрітий посередині. По ньому розтікається тепло і в кожній точці стрижня встановлюється температура. Потрібно знайти точку, де вона найвища. Але в нас йдеться зовсім про інше. кожному шляху у просторівідповідає своє число, і передбачається знайти той шлях,для якого це число є мінімальним. Це зовсім інша область математики. Це не звичайне обчислення, а варіаційне(Так його називають).

У цій галузі математики є багато своїх завдань. Скажімо, коло зазвичай визначають як геометричне місце точок, відстані яких від цієї точки однакові, але коло можна визначити й інакше: це та з кривих даної довжини,яка обмежує собою найбільшу площу. Будь-яка інша крива такого ж периметра обмежує площу меншу, ніж коло. Так що якщо поставити завдання: знайти криву даного периметра, що обмежує найбільшу площу, то перед нами буде задача з варіаційного обчислення, а не з обчислення, до якого ви звикли.

Отже, ми хочемо взяти інтеграл шляхом, пройденим тілом. Зробимо так. Вся справа в тому, щоб уявити собі, що існує істинний шлях і що будь-яка інша крива, яку ми проведемо,— не справжній шлях, тож якщо підрахувати для неї дію, то вийде число, що перевищує те, що ми отримаємо для дії, що відповідає справжньому шляху.

Отже, завдання: знайти справжній шлях. Де він пролягає? Один з способів звичайно, міг би полягати в тому, щоб підрахувати дію для мільйонів та мільйонів шляхів і потім подивитися, при якому шляху ця найменша дія. Ось той шлях, при якому дія мінімальна, і буде справжньою.

Такий спосіб цілком можливий. Однак, можна зробити простіше. Якщо є величина, що має мінімум (із звичайних функцій, скажімо, температура), то одна з властивостей мінімуму полягає в тому, що при віддаленні від нього на відстань першогопорядку малості функція відхиляється від мінімального значення лише на величину другогопорядку. А в будь-якому іншому місці кривий зрушення на малу відстань змінює значення функції теж на величину першого порядку трішки. Але в мінімумі легкі відходи у бік у першому наближенні не призводять до зміни функції.

Це властивість ми й збираємося використовувати для розрахунку справжнього шляху.

Якщо шлях правильний, то крива, трохи відмінна від нього, не приведе в першому наближенні до зміни у величині дії. Усі зміни, якщо це був справді мінімум, виникнуть лише у другому наближенні.

Це легко довести. Якщо при якомусь відхиленні від кривої виникають зміни у першому порядку, то ці зміни у дії пропорційнівідхилення. Вони, ймовірно, збільшать дію; інакше це не був би мінімум. Але коли зміни пропорційнівідхилення, зміна знака відхилення зменшить дію. Виходить, що при відхиленні і один бік дія зростає, а при відхиленні у зворотний бік – зменшується. Єдина можливість того, щоб це дійсно був мінімум,— щоб у першому наближенні жодних змін не відбувалося і зміни були б пропорційні квадрату відхилення від справжнього шляху.

Отже, ми підемо наступним шляхом: позначимо через x(t) (з межею внизу) істинний шлях - той, який ми хочемо знайти. Візьмемо деякий пробний шлях x(t), відрізняється від шуканого на невелику величину, яку ми позначимо η (t).

Ідея полягає в тому, що якщо ми підрахуємо дію S на шляху x(t), то різниця між цим S і тією дією, яку ми вирахували на шляху x(t) (для простоти воно буде позначено S), або різниця між S_ і S, має бути в першому наближенні по η нулем. Вони можуть відрізнятися у другому порядку, але у першому різницю має бути банкрутом.

І це має дотримуватися для будь-якої η . Втім, не зовсім для будь-якої. Метод вимагає брати до уваги лише ті шляхи, які всі починаються і закінчуються в одній і тій же парі точок, тобто кожен шлях повинен починатися в певній точці в момент t 1 і закінчуватися в іншій точці в момент t 2 . Ці точки та моменти фіксуються. Так що наша функція г) (відхилення) повинна дорівнювати нулю на обох кінцях: η (t 1 )= 0 і η (T 2) = 0. При цій умові наше математичне завдання стає цілком певним.

Якби ви не знали диференціального обчислення, ви могли б зробити таку саму річ для пошуку мінімуму нормальної функції f(x). Ви б задумалися над тим, що станеться, якщо взяти f(x) і додати до хмалу величину h, і доводили б, що поправка до f(x) у першому порядку за h повинна в мінімумі дорівнювати нулю. Ви б підставили x+h замість хі розклали б j(x+h) з точністю до першого ступеня h. . ., словом, повторили б все те, що ми маємо намір зробити з η .

Якщо ми тепер уважно поглянемо на це, то побачимо, що два перші написані тут члени відповідають цій дії S, яке я написав би для шуканого істинного шляху х.Я хочу зосередити вашу увагу на зміні S, тобто на різниці між S і тим S_, яке вийшло б для справжнього шляху. Цю різницю ми записуватимемо як bS і назвемо її варіацією S. Відкидаючи «другий та вищі порядки», отримуємо для σS

Тепер завдання має такий вигляд. Ось переді мною якийсь інтеграл. Я не знаю ще, як це ж, але я твердо знаю, що, яку η я не візьму, цей інтеграл повинен дорівнювати нулю. «Ну що ж,— подумаєте ви,— єдина можливість для цього — це щоб множник при η дорівнював нулю». Але як бути з першим доданком, де є d η / dt? Ви скажете: «Якщо η звертається до ніщо, те й її похідна таке ж ніщо; значить, коефіцієнт при dv\/ dt повинен також бути банкрутом». Ну це не зовсім правильно. Це не зовсім правильно тому, що між відхиленням η та його похідний є зв'язок; вони не повністю незалежні, тому що η (t) має бути нулем і при t 1 і при t 2 .

При вирішенні всіх завдань варіаційного обчислення завжди користуються одним і тим самим загальним принципом. Ви трохи зрушуєте те, що хочете варіювати (подібно до того, як це зробили ми, додаючи η ), кидаєте погляд на члени першого порядку, потімрозставляєте все так, щоб вийшов інтеграл у такому вигляді: «зсув (η ), помножений на що вийде», але щоб у ньому не було жодних похідних від η (ніяких d η / dt). Неодмінно потрібно так все перетворити, щоб залишилося щось, помножене на η . Тепер ви зрозумієте, чому це так важливо. (Існують формули, які підкажуть вам, як у деяких випадках можна це зробити без будь-яких викладок; але вони не такі вже спільні, щоб варто було заучувати їх; найкраще робити викладки так, як це робимо ми.)

Як же я можу переробити член d η / dt, щоб у ньому з'явилося η ? Я можу досягти цього, інтегруючи частинами. Виявляється, що у варіаційному обчисленні весь фокус у тому й полягає, щоб розписати варіацію S і потім проінтегрувати частинами так, щоб похідні від η зникли. У всіх завданнях, у яких з'являються похідні, проходить такий самий фокус.

Пригадайте загальний принцип інтегрування частинами. Якщо у вас є довільна функція f, помножена на d η / dt і проінтегрована по t, то ви розписуєте похідну від η /t

У перший член мають бути підставлені межі інтегрування t 1 і t 2 . Тоді я отримаю під інтегралом член від інтегрування частинами і останній член, що залишився при перетворенні незмінним.
А тепер відбувається те, що буває завжди, проінтегрована частина зникає. (А якщо не зникає, то потрібно переформулювати принцип, додавши умови, що забезпечують таке зникнення!) Ми вже казали, що η на кінцях шляху повинна дорівнювати нулю. Адже в чому полягає наш принцип? У тому, що дія мінімальна за умови, що крива, що варіюється, починається і закінчується в обраних точках. Це означає що η (t 1) = 0 і η (T 2) = 0. Тому проінтегрований член виходить рівним нулю. Ми збираємо докупи інші члени і пишемо

Варіація S тепер набула такого вигляду, який ми хотіли їй надати: щось стоїть у дужках (позначимо його F), і все це помножено на η (t) та проінтегровано від t t до t 2 .
У нас вийшло, що інтеграл від якогось виразу, помноженого на η (t), завжди дорівнює нулю:

Коштує якась функція від t; множу її на η (t) та інтегрую її від початку до кінця. І яка б не була η, я отримую нуль. Це означає, що функція F(t) дорівнює нулю. Загалом це очевидно, але я про всяк випадок покажу вам один із способів доказу.

Нехай як η (t) я виберу щось, що одно нулю всюди, при всіх t, крім одного, заздалегідь обраного значення t. Воно залишається нулем, поки я не дійду до цього t, зпотім воно підскакує на мить і відразу ж тримає в облогу назад. Якщо ви берете інтеграл від цієї т), помноженої на якусь функцію F, то єдине місце, в якому ви отримаєте щось ненульове, це там, де η (t) підскакувало; і у вас вийде значення F тут на інтеграл по стрибку. Сам собі інтеграл по стрибку не дорівнює нулю, але після множення на F він має дати нуль. Значить, функція там, де був стрибок, має виявитися нулем. Але стрибок можна було зробити в будь-якому місці; значить, F має бути нулем усюди.

Ми бачимо, що якщо наш інтеграл дорівнює нулю за будь-якої η , то коефіцієнт при η повинен звернутися в нуль. Інтеграл дії досягає мінімуму на тому шляху, який задовольнятиме такому складному диференціальному рівнянню:

Насправді вона не така вже й складна; ви його вже зустрічали раніше. Це просто F=ma. Перший член - це маса, помножена на прискорення; другий - це похідна від потенційної енергії, тобто сила.

Отже, ми показали (принаймні для консервативної системи), що принцип найменшої дії призводить до правильної відповіді; він стверджує, що шлях, що володіє мінімумом дії, це шлях, що задовольняє закону Ньютона.

Потрібно зробити ще одне зауваження. Я не довів, що це мінімум.Можливо, це максимум. Насправді це і не обов'язково має бути мінімум. Тут так само, як у «принципі найкоротшого часу», який ми обговорювали, вивчаючи оптику. Там теж ми спершу говорили про найкоротший час. Однак з'ясувалося, що бувають положення, в яких цей час не обов'язково найкоротший. Фундаментальний принцип полягає в тому, щоб для будь-яких відхилень першого порядкувід оптичного шляху зміниу часі дорівнювали б нулю; тут та сама історія. Під «мінімумом» ми насправді маємо на увазі, що в першому порядку трохи зміни величини Sпри відхиленнях від шляху повинні дорівнювати нулю. І це не обов'язково "мінімум".

Тепер я хочу перейти до деяких узагальнень. Насамперед усю цю історію можна було б зробити й у трьох вимірах. Замість простого хя тоді мав би х, уі zяк функції t,і дія виглядала б складніше. При тривимірному русі ви повинні використовувати повну кінетичну енергію): (т/2),помножене на квадрат усієї швидкості. Інакше кажучи

Крім того, потенційна енергія тепер є функцією х, уі z.А що можна сказати про шлях? Шлях є деяка крива загального вигляду у просторі; її не так легко накреслити, але ідея залишається незмінною. А як справи з η? Що ж, і має три компоненти. Шлях можна зрушувати і x, і по у,і по z,або у всіх трьох напрямках одночасно. Так що η тепер вектор. Від цього сильних ускладнень не виходить. Якщо нулю повинні дорівнювати лише варіації першого порядку,можна провести розрахунок послідовно з трьома зрушеннями. Спершу можна зрушити цтільки у напрямку хі сказати, що коефіцієнт повинен звернутися на нуль. Вийде одне рівняння. Потім ми зрушимо цв напрямку ута отримаємо друге. Потім ссунемо в напрямку zта отримаємо третє. Можна все, якщо завгодно, зробити в іншому порядку. Як би там не було, виникає трійка рівнянь. Але закон Ньютона — це теж три рівняння у трьох вимірах, по одному для кожної компоненти. Вам надається самим переконатися, що це діє і в трьох вимірах (роботи тут не так багато). Між іншим, можна взяти будь-яку систему координат, полярну, будь-яку, і відразу отримати закони Ньютона стосовно цієї системи, розглядаючи, що вийде, коли станеться зрушення η вздовж радіусу або по кутку, і т.д.

Метод може бути узагальнений і довільне число частинок. Якщо, скажімо, у вас є дві частинки і між ними діють якісь сили і є взаємна потенційна енергія, то ви просто складаєте їх кінетичні енергії та віднімаєте із суми потенційну енергію взаємодії. А що ви варіюєте? Шляхи обохчастинок. Тоді для двох частинок, що рухаються у трьох вимірах, виникає шість рівнянь. Ви можете варіювати положення частинки 1 у напрямку х,в напрямку ута у напрямку z,і те саме зробити з часткою 2, так що існує шість рівнянь. І так і має бути. Три рівняння визначають прискорення частки 1 через силу, що діє на неї, а три інших - прискорення частки 2 через силу, що діє на неї. Дотримуйтесь завжди тих же правил гри, і ви отримаєте закон Ньютона для довільної кількості частинок.

Я сказав, що ми отримаємо закон Ньютона. Це не зовсім правильно, тому що до закону Ньютона входять і неконсервативні сили, наприклад тертя. Ньютон стверджував, що таі всякої F. Принцип ж найменшої дії справедливий тільки для консервативнихсистем, де всі сили можуть бути отримані з потенційної функції. Але ж ви знаєте, що на мікроскопічному рівні, тобто на глибинному фізичному рівні, неконсервативних сил не існує. Неконсервативні сили (такі, як тертя) з'являються лише від того, що ми нехтуємо складними мікроскопічними ефектами: просто занадто багато частинок доводиться аналізувати. Фундаментальніж закони можутьбути виражені у вигляді принципу найменшої дії.

Дозвольте перейти до подальших узагальнень. Припустимо, нас цікавить, що буде, коли частка рухається релятивістською. Поки що ми не отримали правильного релятивістського рівняння руху; F=ma вірно лише у нерелятивістських рухах. Постає питання: чи існує у релятивістському випадку відповідний принцип найменшої дії? Так, існує. Формула у релятивістському випадку така:

Перша частина інтеграла дії - це твір маси спокою т 0на з 2та на інтеграл від функції швидкості √ (1- v 2 /c 2 ). Потім замість того, щоб віднімати потенційну енергію, ми маємо інтеграли від скалярного потенціалу і від векторного потенціалу А, помноженого на v. Звісно, тут прийнято до уваги лише електромагнітні сили. Усі електричні та магнітні поля виражені в термінах φ та А. Така функція дії дає повну теорію релятивістського руху окремої частки в електромагнітному полі.

Звичайно, ви повинні розуміти, що всюди, де я написав v, перш ніж робити викладки, слід підставити dx/ dt замість v x і т. д. Крім того, там, де я писав просто х, у, z,ви повинні уявити собі точки в момент t: x(t), y(t), z(t). Власне, тільки після таких підстановок та замін v у вас вийде формула для дії релятивістської частки. Нехай найуміліші з вас спробують довести, що ця формула для дії справді дає правильні рівняння руху теорії відносності. Дозвольте лише порадити для початку відкинути А, тобто обійтися поки що без магнітних полів. Тоді ви повинні будете отримати компоненти рівняння руху dp/dt=-qVφ,де, як ви, мабуть, пам'ятаєте, p=mv√(1-v 2 /c 2).

Включити до розгляду векторний потенціал А набагато складніше. Варіації тоді стають незрівнянно складнішими. Але в кінці сила виявляється рівною тому, чому слідує: g(E+v × B). Але побавтеся з цим самі.

Мені хотілося б наголосити, що в загальному випадку (наприклад, у релятивістській формулі) під інтегралом у дії вже не стоїть різниця кінетичної та потенційної енергій. Це годилося лише у нерелятивістському наближенні. Наприклад, член m o c 2√(1-v 2 /c 2)-Це не те, що називають кінетичною енергією. Питання, яким має бути дія для довільного окремого випадку, може бути вирішено після деякої кількості проб і помилок. Це завдання того ж типу, що і визначення, якими мають бути рівняння руху. Ви просто повинні пограти з відомими вам рівняннями та подивитися, чи можна їх написати у вигляді принципу найменшої дії.

Ще одне зауваження щодо термінології. Ту функцію, яку інтегрують за часом, щоб діяти S,називають лагранжіаномΛ. Це функція, яка залежить тільки від швидкостей та положень частинок. Отже, принцип найменшої дії записується також у вигляді

де під х iі v i маються на увазі всі компоненти координат та швидкостей. Якщо ви коли-небудь почуєте, що хтось говорить про «лагранжіану», знайте, що йдеться про функцію, яка використовується для отримання S. Для релятивістського руху в електромагнітному полі

Крім того, я повинен відзначити, що найприскіпливіші і педантичні люди не називають Sдією. Його називають «першою основною функцією Гамільтона». Але читати лекцію про «принцип найменшої першої головної функції Гамільтона» було понад мої сили. Я назвав це «дією». До того ж, все більше і більше людей називають це «дією». Чи бачите, історично дією було названо щось інше, не таке корисне для науки, але я думаю, що розумніше змінити визначення. Тепер і ви почнете називати нову функцію дією, а незабаром і всі взагалі називатимуть її цим простим ім'ям.

Тепер я хочу повідомити вас про нашу тему дещо, схоже на ті міркування, які я вів з приводу принципу найкоротшого часу. Існує різниця в самій суті закону, який стверджує, що деякий інтеграл, взятий від однієї точки до іншої, має мінімум — закону, який повідомляє нам щось про весь шлях відразу, і закону, який говорить, що коли ви рухаєтеся, то, отже, є сила, яка веде до прискорення. Другий підхід повідомляє вам про кожен ваш крок, він простежує ваш шлях п'ядь за п'яддю, а перший видає відразу якесь загальне твердження про весь пройдений шлях. Толкуючи про світло, ми говорили про зв'язок цих двох підходів. Тепер я хочу пояснити вам, чому мають існувати диференціальні закони, якщо є такий принцип — принцип найменшої дії. Причина ось у чому: розглянемо справді пройдений у просторі та часі шлях. Як і раніше обійдемося одним виміром, так що можна буде накреслити графік залежності хвід t. Вздовж істинного шляху S досягає мінімуму. Припустимо, що ми маємо цей шлях і що він проходить через деяку точку апростору та часу та через іншу сусідню точку b.

Тепер, якщо весь інтеграл від t 1 до t 2 досяг мінімуму, необхідно, щоб інтеграл уздовж маленької ділянки від а до b також був мінімальним. Не може бути, щоб частина від адо bхоч трохи перевищувала мінімум. Інакше ви могли б спонукати туди-сюди криву на цій ділянці і знизити трохи значення всього інтеграла.

Отже, будь-яка частина шляху теж має давати мінімум. Та це справедливо для будь-яких малих часточок дороги. Тому той принцип, що весь шлях має давати мінімум, можна сформулювати, сказавши, що нескінченно мала часточка колії — це теж така крива, на якій дія мінімальна. І якщо ми візьмемо досить короткий відрізок шляху між дуже близькими один до одного точками аі b,— то вже неважливо, як змінюється потенціал від точки до точки далеко від цього місця, тому що, проходячи весь ваш коротенький відрізок, ви майже не сходите з місця. Єдине, що вам потрібно враховувати, це зміна першого порядку малості в потенціалі. Відповідь може залежати лише від похідної потенціалу, а чи не від потенціалу інших місцях. Так, твердження про властивість всього шляху загалом стає твердженням про те, що відбувається на короткій ділянці шляху, тобто диференціальним твердженням. І це диференціальне формулювання включає похідні від потенціалу, тобто силу в даній точці. Таке якісне пояснення зв'язку між законом загалом та диференціальним законом.

Коли ми говорили про світло, то обговорювали також питання: як усе-таки частка знаходить правильний шлях? З диференціальної точки зору це легко зрозуміти. У кожен момент частка відчуває прискорення і знає тільки те, що їй належить робити цієї миті. Але всі ваші інстинкти причин і наслідків встають дибки, коли ви чуєте, що частка «вирішує», який їй вибрати шлях, прагнучи до мінімуму дії. Чи не «обнюхує» вона сусідні шляхи, прикидаючи, до чого вони приведуть — до більшої чи меншої дії? Коли ми на шляху світла ставили екран так, щоб фотони не могли перепробувати всі шляхи, ми з'ясували, що вони не можуть вирішити яким шляхом йти, і отримали явище дифракції.

Але чи це правильно і для механіки? Чи правда, що частка не просто «йде вірним шляхом», а переглядає всі інші мислимі траєкторії? І що якщо, ставлячи перепони її шляху, ми дамо їй заглядати вперед, ми отримаємо якийсь аналог явища дифракції? Найдивовижніше в усьому цьому — те, що справді так. Саме це затверджують закони квантової механіки. Отже, наш принцип найменшої дії сформульований не повністю. Він полягає не в тому, що частка обирає шлях найменшої дії, а в тому, що вона «чує» всі сусідні шляхи і вибирає той, уздовж якого дія мінімальна, і спосіб цього вибору подібний до того, яким світло відбирає найкоротший час. Ви пам'ятаєте, що спосіб, яким світло відбирає найкоротший час, такий: якщо світло піде шляхом, що вимагає іншого часу, то прийде воно з іншою фазою. А повна амплітуда в деякій точці є сумою вкладів амплітуд для всіх шляхів, якими світло може її досягти. Всі шляхи, у яких фази різко різняться, нічого після складання не дають. Але якщо вам удалося знайти всю послідовність шляхів, фази яких майже однакові, то дрібні вклади складуться, і в точці прибуття повна амплітуда набуде помітного значення. Найважливішим шляхом стає той, біля якого є багато близьких шляхів, що дають ту саму фазу.

В точності те саме відбувається і в квантовій механіці. Закінчена квантова механіка (нерелятивістська і нехтує спином електрона) працює так: ймовірність того, що частка, вийшовши з точки 1 в момент t 1, досягне точки 2 в момент t 2 , дорівнює квадрату амплітуди ймовірності. Повна амплітуда може бути записана у вигляді суми амплітуд для всіх можливих шляхів для будь-якого шляху прибуття. Для будь-кого x(t), яке могло б виникнути для будь-якої уявної траєкторії, потрібно підрахувати амплітуду. Потім їх треба скласти. Що ми приймемо за амплітуду ймовірності деякого шляху? Наш інтеграл дії говорить нам, якою має бути амплітуда окремого шляху. Амплітуда пропорційна e tS/h, де S - Дія на цьому шляху. Це означає, що якщо ми представимо фазу амплітуди у вигляді комплексного числа, то фазовий кут дорівнюватиме S/ h. Дія S має розмірність енергії на якийсь час, і у постійної Планка розмірність така ж. Це стала, яка визначає, коли потрібна квантова механіка.

І ось як усе це спрацьовує. Нехай для всіх шляхів дія S буде дуже великим у порівнянні з числом h. Нехай якийсь шлях призвів до певної величини амплітуди. Фаза поруч прокладеного шляху виявиться зовсім іншою, тому що при величезному S навіть незначні зміни S різко змінюють фазу (адже hнадзвичайно мало). Значить, поруч шляхи, що лежать, при складанні зазвичай гасять свої вклади. І тільки в одній області це не так - у тій, де і шлях і його сусід - обидва в першому наближенні мають одну і ту ж фазу (або, точніше, майже однією і тією ж дією, що змінюється в межах h).Тільки такі шляхи і беруться до уваги. А в граничному випадку, коли постійна Планка hпрагне до нуля, правильні квантовомеханічні закони можна підсумувати, сказавши: «Забудьте про всі ці амплітуди ймовірностей. Частка і справді рухається особливим шляхом — саме тим, яким S у першому наближенні не змінюється». Такий зв'язок між принципом найменшої дії та квантовою механікою. Та обставина, що у такий спосіб можна сформулювати квантову механіку, було відкрито 1942 р. учнем того самого вчителя, містера Бадера, про якого я вам розповідав. [Спочатку квантова механіка була сформульована за допомогою диференціального рівняння для амплітуди (Шредінгер), а також за допомогою деякої матричної математики (Гейзенберг).]

Тепер я хочу поговорити про інші принципи мінімуму у фізиці. Є багато цікавих принципів такого роду. Я не буду їх все перераховувати, а назву ще один. Пізніше, коли ми дістанемося одного фізичного явища, для якого існує чудовий принцип мінімуму, я розповім вам про нього. А зараз хочу показати, що необов'язково описувати електростатику за допомогою диференціального рівняння для поля; можна замість цього вимагати, щоб деякий інтеграл мав максимум або мінімум. Для початку візьмемо випадок, коли щільність зарядів відома ловсюди, а потрібно знайти потенціал у будь-якій точці простору. Ви вже знаєте, що відповідь має бути такою:

Інший спосіб стверджувати те саме полягає в наступному: треба обчислити інтеграл U*

це об'ємний інтеграл. Він береться у всьому просторі. При правильному розподілі потенціалу? (x, у,z) цей вираз сягає мінімуму.

Ми можемо показати, що ці твердження щодо електростатики еквівалентні. Припустимо, що ми вибрали довільну функцію. Ми хочемо показати, що коли як φ ми візьмемо правильне значення потенціалу _φ плюс мале відхилення f, то в першому порядку трохи зміни в U* дорівнюватиме нулю. Тож ми пишемо

тут φ це те, що ми шукаємо; але ми проварюємо φ, щоб побачити, яким він має бути для того, щоб варіація U* виявилася першого порядку малості. У першому члені U* нам потрібно написати

Це потрібно проінтегрувати за х, уі по z. І тут напрошується той же фокус: щоб позбутися df/ dx, ми проінтегруємо по хпо частинах. Це призведе до додаткового диференціювання? х.Це та ж основна ідея, за допомогою якої ми позбулися похідних по t. Ми користуємось рівністю

Проінтегрований член дорівнює нулю, оскільки ми вважаємо f рівним нулю на нескінченності. (Це відповідає обігу η в нуль при t 1 і t 2 . Тож наш принцип більш точно формулюється так: U* для правильного φ менше, ніж для будь-якого іншого φ(х, у,z), що володіє тими ж значеннями на нескінченності.) Потім ми зробимо те ж з ута з z. Наш інтеграл ΔU* звернеться до

Щоб ця варіація дорівнювала нулю при будь-якому довільному f, коефіцієнт при f повинен дорівнювати нулю. Значить,

Ми повернулися до нашого старого рівняння. Отже, наша «мінімальна» пропозиція вірна. Його можна узагальнити, якщо трохи змінити викладки. Повернемося назад і проінтегруємо частинами, не розписуючи все покомпонентно. Почнемо з того, що напишемо таку рівність:

Продиференціювавши ліву частину, я можу показати, що вона точно дорівнює правій. Це рівняння підходить для того, щоб провести інтегрування частинами. У нашому інтегралі ΔU* ми замінюємо Vφ*Vf на fV 2 φ+V*(fVφ) і потім інтегруємо це за обсягом. Член із дивергенцією після інтегрування за обсягом замінюється інтегралом по поверхні:

А оскільки ми інтегруємо по всьому простору, то поверхня у цьому інтегралі лежить на нескінченності. Значить f = 0, і ми отримуємо колишній результат.

Тільки тепер ми починаємо розуміти, як вирішувати завдання, у яких ми не знаємо,де розташовані усі заряди. Нехай ми маємо провідники, на яких якось розподілено заряди. Якщо потенціали на всіх провідниках зафіксовані, наш принцип мінімуму все ще дозволяється застосовувати. Інтегрування в U* ми проведемо лише по області, що лежить зовні всіх провідників. Але якщо ми не можемо на провідниках змінювати (φ, то на їх поверхні f=0, і поверхневий інтеграл

потрібно робити лише у проміжках між провідниками. І ми, звичайно, знову отримуємо рівняння Пуассона

Ми показали, що наш початковий інтеграл U* досягає мінімуму і тоді, коли він обчислюється у просторі між провідниками, кожен з яких знаходиться при фіксованому потенціалі [це означає, що кожна пробна функція φ(ж, у,z) повинна дорівнювати заданому потенціалу провідника, коли (х, у,z) - Точки поверхні провідника]. Існує цікавий окремий випадок, коли заряди розташовані тільки на провідниках. Тоді

і наш принцип мінімуму говорить нам, що у випадку, коли кожен провідник має свій заздалегідь заданий потенціал, потенціали в проміжках між ними приганяються так, що інтеграл U* виявляється якнайменше. А що то за інтеграл? Член Vφ – це електричне поле. Отже, інтеграл це електростатична енергія. Правильне поле і є єдиним, яке з усіх полів, одержуваних як градієнт потенціалу, відрізняється найменшою повною енергією.

Я хотів би скористатися цим результатом, щоб вирішити якесь приватне завдання і показати вам, що всі ці речі мають реальне практичне значення. Припустимо, що я взяв два провідники у формі циліндричного конденсатора.

У внутрішнього провідника потенціал дорівнює, скажімо, V, а у зовнішнього – нулю. Нехай радіус внутрішнього провідника дорівнюватиме а,а зовнішнього - b.Тепер ми можемо припустити, що розподіл потенціалів між ними будь-яке.Але якщо ми візьмемо правильнезначення φ та обчислимо
(ε 0 /2) ∫ (Vφ) 2 dVто має вийти енергія системи 1/2CV 2 .

Отже, за допомогою нашого принципу можна підрахувати і ємність З.Якщо ж ми візьмемо неправильне розподілення потенціалу і спробуємо цим методом прикинути ємність конденсатора, то прийдемо до надто великого значення ємності при фіксованому V. Будь-який передбачуваний потенціал φ, який не точно збігається з істинним його значенням, призведе і до невірної величини, більшої, ніж потрібно. Але якщо невірно обраний потенціал СР є ще грубим наближенням, то ємність Звийде вже з хорошою точністю, тому що похибка С - величина другого порядку в порівнянні з похибкою в φ.

Припустимо, що мені невідома ємність циліндричного конденсатора. Тоді, щоб дізнатися про неї, я можу скористатися цим принципом. Я просто відчуватиму в якості потенціалу різні функції φ до тих пір, поки не досягну нижчого значення З.Допустимо, наприклад, що я вибрав потенціал, що відповідає постійному полю. (Ви, звичайно, знаєте, що насправді поле тут не завжди; воно змінюється як 1/r) Якщо поле постійно, то це означає, що потенціал лінійно залежить від відстані. Щоб напруга на провідниках була якою потрібно, функція φ повинна мати вигляд

Ця функція дорівнює V при r=а,нулю при r =b,а між ними є постійний нахил, рівний V/(b—а).Отже, щоб визначити інтеграл U*, треба тільки помножити квадрат цього градієнта на ε /2 і проінтегрувати по всьому об'єму. Проведемо цей розрахунок для циліндра одиничної довжини. Елемент об'єму при радіусі rдорівнює 2πrdr. Проводячи інтегрування, я вважаю, що моя перша проба дає таку ємність:

Так я отримую формулу для ємності, яка хоч і неправильна, але є якимось наближенням:

Звичайно, вона відрізняється від правильної відповіді С=2πε 0 /ln (b/а),але загалом вона не така вже й погана. Давайте спробуємо порівняти її з правильною відповіддю для кількох значень b/a.Обчислені мною числа наведені у таблиці.

Навіть коли b/а=2(а це призводить до досить великих відмінностей між постійним і лінійним полем), я все ще отримую досить стерпне наближення. Відповідь, звичайно, як і очікувалося, трохи завищена. Але якщо тонкий зволікання помістити всередині великого циліндра, то все виглядає вже набагато гірше. Тоді поле змінюється дуже сильно і заміна його постійним полем нічого хорошого не призводить. При b/а=100 ми завищуємо відповідь майже вдвічі. Для малих b/астановище виглядає набагато краще. У протилежній межі, коли проміжок між провідниками не дуже широкий (скажімо, при b/а=1,1), постійне поле виявляється добрим наближенням, воно дає значення Зз точністю до десятих відсотка.

А тепер я розповім вам, як удосконалити цей розрахунок. (Відповідь для циліндра вам, зрозуміло, відомий,але той самий спосіб підходить і для деяких інших незвичайних форм конденсаторів, для яких правильна відповідь вам може бути і не відома.) Наступним кроком буде пошук кращого наближення для невідомого нам істинного потенціалу φ. Скажімо, можна випробувати константу плюс експоненту і т. д. Але як ви дізнаєтеся, що у вас вийшло краще наближення, якщо ви не знаєте істинного? Відповідь:Підрахуйте З;чим вона нижча, тим до істини ближче. Давайте перевіримо цю ідею. Нехай потенціал буде не лінійним, а, скажімо, квадратичним r, а електричне поле не постійним, а лінійним. Сама загальнаквадратична форма, яка звертається до φ=О при r=bі в φ=F при r=а,така:

де α - Постійне число. Ця формула трохи складніша за колишню. До неї входить і квадратичний член, і лінійний. З неї легко отримати поле. Воно одно просто

Тепер це потрібно звести у квадрат та проінтегрувати за обсягом. Але зачекайте хвилинку. Що мені прийняти за α? За ф я можу прийняти параболу, але яку? Ось що я зроблю: підрахую ємність при довільному α.Я отримаю

Це виглядає трохи заплутано, але так виходить після інтегрування квадрата поля. Тепер я можу вибирати собі а. Я знаю, що правда лежить нижче, ніж усе, що я збираюся обчислити. Що б я не поставив замість а, відповідь все одно вийде занадто великою. Але якщо я продовжу свою гру з α і постараюся досягти найнижчого можливого значення З,то це найнижче значення буде ближчим до правди, ніж будь-яке інше значення. Отже, мені тепер треба підібрати α так, щоб значення Здосягло свого мінімуму. Звертаючись до звичайного диференціального числення, я переконуюсь, що мінімум Збуде тоді, коли α = - 2 b/(b+a). Підставляючи це значення у формулу, я отримую для найменшої ємності

Я прикинув, що дає ця формула для Зпри різних значеннях b/а.Ці числа я назвав З(квадратичні). Наводжу таблицю, в якій порівнюються З(квадратичні) з З(Істинними).

Наприклад, коли відношення радіусів дорівнює 2:1, я отримую 1,444. Це дуже добре наближення до правильної відповіді, 1,4423. Навіть за великих Ыанаближення залишається досить хорошим - воно набагато краще першого наближення. Воно залишається стерпним (завищення лише на 10%) навіть при b/а=10: 1.Велика розбіжність настає тільки при відношенні 100: 1. Я отримую Зрівним 0,346 замість 0,267. З іншого боку, для відношення радіусів 1,5 збіг чудовий, а при b/а=1,1відповідь виходить 10,492065 замість належного 10,492070. Там, де слід очікувати хорошої відповіді, він виявляється дуже хорошим.

Я навів усі ці приклади, по-перше, щоб продемонструвати теоретичну цінність принципу мінімальної дії і взагалі будь-яких принципів мінімуму, і, по-друге, щоб показати вам їхню практичну корисність, а зовсім не для того, щоб підрахувати ємність, яку ми й так чудово знаємо. Для будь-якої іншої форми ви можете випробувати наближене поле з кількома невідомими параметрами (на зразок α) та підігнати їх під мінімум. Ви отримаєте чудові чисельні результати у завданнях, які в інший спосіб не вирішуються.

Йому підкоряються, у зв'язку з чим цей принцип одна із ключових положень сучасної фізики. Одержувані з його допомогою рівняння руху мають назву рівнянь Ейлера-Лагранжа.

Перше формулювання принципу дав П. Мопертюї (P. Maupertuis) у році, відразу ж вказавши на його універсальну природу, вважаючи його придатним до оптики та механіки. З цього принципу він вивів закони відображення та заломлення світла.

Історія

Мопертюї прийшов до цього принципу з відчуття, що досконалість Всесвіту потребує певної економії в природі та суперечить будь-яким марним витратам енергії. Природний рух має бути таким, щоб зробити певну величину мінімальною. Треба було тільки знайти цю величину, що він і продовжував робити. Вона була добутком тривалості (час) руху в межах системи на подвоєну величину, яку ми тепер називаємо кінетичною енергією системи.

Ейлер (в «Reflexions sur quelques loix générales de la nature», 1748) приймає принцип найменшої кількості дії, називаючи дію "зусиллям". Його вираз у статиці відповідає тому, що ми тепер назвали б потенційною енергією, так що його затвердження найменшої дії у статиці еквівалентне умові мінімуму потенційної енергії для конфігурації рівноваги.

У класичній механіці

Принцип найменшої дії служить фундаментальною та стандартною основою лагранжевої та гамільтонової формулювань механіки.

Спочатку розглянемо побудову таким чином лагранжової механіки. На прикладі фізичної системи з одним ступенем свободи, нагадаємо, що дія - це функціонал щодо (узагальнених) координат (у разі одного ступеня свободи - однієї координати), тобто виражається через так, що кожному мислимому варіанту функції зіставляється деяка кількість - дія (у цьому сенсі можна сказати, що дія як функціонал є правило, що дозволяє для будь-якої заданої функції обчислити цілком певну кількість - також називається дією). Дія має вигляд:

де є лагранжіан системи, що залежить від узагальненої координати, її першої похідної за часом, а також, можливо, і явно від часу. Якщо система має більшу кількість ступенів свободи, то лагранжіан залежить від більшої кількості узагальнених координат та їх перших похідних за часом. Таким чином, дія є скалярним функціоналом, що залежить від траєкторії тіла.

Те, що дія є скаляром, дозволяє легко записати його в будь-яких узагальнених координатах, головне тільки, щоб положення (конфігурація) системи однозначно ними характеризувалося (наприклад, замість декартових це можуть бути полярні координати, відстані між точками системи, кути або їх функції тощо) д.).

Дію можна обчислити для абсолютно довільної траєкторії, якою б «дикою» та «неприродною» вона не була б. Однак у класичній механіці серед усього набору можливих траєкторій існує одна-єдина, якою тіло дійсно піде. Принцип стаціонарності дії якраз і дає відповідь на питання, як дійсно рухатиметься тіло:

Це означає, що якщо заданий лагранжіан системи, то ми за допомогою варіаційного обчислення можемо встановити, як саме рухатиметься тіло, спочатку отримавши рівняння руху – рівняння Ейлера – Лагранжа, а потім вирішивши їх. Це дозволяє не тільки серйозно узагальнити формулювання механіки, але й вибирати найбільш зручні координати для кожної певної задачі, не обмежуючись декартовими, що може бути дуже корисно для отримання найпростіших рівнянь, що легко вирішуються.

де – функція Гамільтона даної системи; - (узагальнені) координати, - пов'язані ним (узагальнені) імпульси, що характеризують разом у кожний момент часу динамічний стан системи і, будучи кожним функцією часу, характеризуючи, в такий спосіб, еволюцію (рух) системи. У цьому випадку для отримання рівнянь руху системи у формі канонічних рівнянь Гамільтона треба проваріювати записану так дію незалежно по всіх і .

Слід зазначити, що з умов завдання принципово можна знайти закон руху, це автоматично неозначає, що можна побудувати функціонал, що набуває стаціонарного значення при істинному русі. Прикладом може служити спільний рух електричних зарядів і монополій - магнітних зарядів - в електромагнітному полі. Їхні рівняння руху неможливо вивести з принципу стаціонарності дії. Аналогічно деякі гамільтонові системи мають рівняння руху, які не виводяться з цього принципу.

Приклади

Тривіальні приклади допомагають оцінювати використання принципу дії через рівняння Ейлера-Лагранжа. Вільна частка (маса mта швидкість v) в Евклідовому просторі переміщається прямою лінією. Використовуючи рівняння Ейлера Лагранжа, це можна показати в полярних координатах наступним чином. За відсутності потенціалу функція Лагранжа просто дорівнює кінетичній енергії

в ортогональній системі координат.

У полярних координатах кінетична енергія, отже, функція Лагранжа стає

Радіальна та кутова компонента рівнянь стають, відповідно:

Розв'язання цих двох рівнянь

Тут - це умовний запис нескінченно функціонального інтегрування по всіх траєкторіях x(t), а - постійна Планка. Підкреслимо, що в принципі дія в експоненті з'являється (або може з'являтися) сама, при вивченні оператора еволюції в квантовій механіці, проте для систем, що мають точний класичний (неквантовий) аналог, воно точно дорівнює звичайному класичному дії.

Математичний аналіз цього висловлювання у класичному межі - за досить великих , тобто за дуже швидких осциляціях уявної експоненти - показує, що переважна більшість усіляких траєкторій у тому інтегралі взаємозменшуються у своїй межі (формально при ). Для майже будь-якого шляху знайдеться такий шлях, на якому набіг фази буде протилежним, і вони в сумі дадуть нульовий внесок. Не скорочуються ті траєкторії, котрим дія близька до екстремального значення (для більшості систем - мінімуму). Це - суто математичний факт з теорії функцій комплексного змінного; на ньому, наприклад, заснований метод стаціонарної фази.

В результаті частка в повній згоді з законами квантової механіки рухається одночасно по всіх траєкторіях, але в звичайних умовах в значення, що спостерігаються, дають вклад тільки траєкторії, близькі до стаціонарних (тобто класичних). Оскільки квантова механіка перетворюється на класичну межі великих енергій, можна вважати, що це - квантовомеханічне виведення класичного принципу стаціонарності дії.

У квантовій теорії поля

У квантовій теорії поля принцип стаціонарності дії також успішно застосовується. У лагранжеву густину тут входять оператори відповідних квантових полів. Хоча правильніше тут по суті (за винятком класичної межі і частково квазікласики) говорити не про принцип стаціонарності дії, а про фейнманівське інтегрування по траєкторіях у конфігураційному або фазовому просторі цих полів - з використанням згаданої щойно лагранжової щільності.

Подальші узагальнення

Найбільш широко, під впливом розуміють функціонал, що задає відображення з конфігураційного простору на безліч речових чисел і, загалом, він не повинен бути інтегралом, тому що нелокальні події в принципі можливі, принаймні, теоретично. Понад те, конфігураційний простір необов'язково є функціональним простором, оскільки може мати некомутативну геометрію.

Історія

У класичній механіці

Приклади

в ортогональній системі координат.

У полярних координатах кінетична енергія, отже, функція Лагранжа стає

Радіальна та кутова компонента рівнянь стають, відповідно:

Розв'язання цих двох рівнянь

У квантовій теорії поля

Подальші узагальнення

Принцип найменшої дії, вперше точно сформульований Якобі, аналогічний принципу Гамільтона, але менш загальний і важчий для доказу. Цей принцип застосовується тільки до того випадку, коли зв'язки та силова функція не залежать від часу і, отже, існує інтеграл живої сили.

Цей інтеграл має вигляд:

Принцип Гамільтона, викладений вище, стверджує, що варіація інтеграла

дорівнює нулю при переході дійсного руху до будь-якого іншого нескінченно близького руху, який переводить систему з того самого початкового положення в той же кінцевий стан за той самий проміжок часу.

Принцип Якобі, навпаки, виражає властивість, рухи, що не залежить від часу. Якобі розглядає інтеграл

визначальний дію. Встановлений ним принцип стверджує, що варіація цього інтеграла дорівнює нулю, коли ми порівнюємо дійсний рух системи з будь-яким іншим нескінченно близьким рухом, що переводить систему з того самого початкового положення в той же кінцевий стан. При цьому ми не звертаємо уваги на проміжок часу, що витрачається, але дотримуємось рівняння (1), тобто рівняння живої сили з тим же значенням постійної h, що і в дійсному русі.

Ця необхідна умова екстремуму приводить, взагалі кажучи, до мінімуму інтеграла (2), звідки і походить назва принцип найменшої дії. Умова мінімуму є найбільш природною, оскільки величина Т істотно позитивна, і тому інтеграл (2) необхідно мати мінімум. Існування мінімуму може бути суворо доведено, якщо проміжок часу - досить малий. Доказ цього можна знайти у відомому курсі Дарбу з теорії поверхонь. Ми, однак, не наводитимемо його тут і обмежимося виведенням умови

432. Доказ принципу найменшої дії.

При дійсному обчисленні ми зустрічаємося з одним складним трудом, якого немає в доказі теореми Гамільтона. Змінна t не залишається більш незалежною від варіацій; тому варіації q i та q. пов'язані з варіацією t складним співвідношенням, яке випливає з рівняння (1). Найпростіший спосіб обійти це утруднення полягає в тому, щоб змінити незалежну змінну, вибравши таку, значення якої розташовувалися б між постійними межами, що не залежать від часу. Нехай є нова незалежна змінна, межі якої і передбачаються не залежать від t. При переміщенні системи параметри та t будуть функціями від цієї змінної

Нехай літери зі штрихами q позначатимуть похідні від параметрів q за часом.

Оскільки зв'язку, за припущенням, не залежить від часу, то декартові координати х, у, z є функціями від q, які містять час. Тому їх похідні будуть однорідними лінійними функціями від q і 7 буде однорідною квадратичною формою від q, коефіцієнти якої суть функції від q. Маємо

Щоб відрізняти похідні q за часом, позначимо за допомогою дужок, (q), похідні від q, взяті за і покладемо відповідно до цього

тоді матимемо

і інтеграл (2), виражений через нову незалежну змінну А, набуде вигляду;

Похідну можна виключити з допомогою теореми живої сили. Справді, інтеграл живої сили буде

Підставивши цей вираз у формулу для наведемо інтеграл (2) до виду

Інтеграл, що визначає дію, набув, таким чином, остаточного вигляду (3). Підінтегральна функція є квадратний корінь із квадратичної форми від величин

Покажемо, що диференціальні рівняння екстремалей інтеграла (3) є точності рівняння Лагранжа. Рівняння екстремалей на підставі загальних формул варіаційного обчислення будуть:

Помножимо рівняння на 2 і виконаємо приватні диференціювання, зважаючи на те, що не містить тоді отримаємо, якщо не писати індексу ,

Це рівняння екстремалей, виражені через незалежну змінну. Завдання полягає тепер у тому, щоб повернутися до незалежної змінної.

Оскільки Г є однорідна функція другого ступеня від - однорідна функція першого ступеня, то маємо

З іншого боку, до множників при похідних у рівняннях екстремалей можна застосувати теорему живої сили, яка призводить, як ми бачили вище, до підстановки

В результаті всіх підстановок рівняння екстремалей наводяться до вигляду

Таким чином, ми прийшли до рівнянь Лагранжа.

433. Випадок, коли немає рушійних сил.

У випадку, коли рушійних сил немає, рівняння живої сили є і ми маємо

Умова, що інтеграл є мінімум, полягає в даному випадку в тому, що відповідне значення -10 має бути найменшим. Таким чином, коли рушійних сил немає, то серед усіх рухів, при яких жива сила зберігає одне й те саме дане значення, дійсний рух є те, що переводить систему з її початкового положення в кінцеве положення в найкоротший час.

Якщо система зводиться до однієї точки, що рухається нерухомою поверхнею, то дійсний рух, серед усіх рухів по поверхні, що відбуваються з тією ж швидкістю, є такий рух, при якому точка переходить зі свого початкового положення в кінцеве положення в найкоротший

проміжок часу. Інакше висловлюючись, точка описує лежить на поверхні найкоротшу лінію між двома її положеннями, т. е. геодезичну лінію.

434. Зауваження.

Принцип найменшої дії передбачає, що система має кілька ступенів свободи, оскільки якби була лише одна ступінь свободи, то одного рівняння було б достатньо для визначення руху. Так як рух може бути в даному випадку цілком визначено рівнянням живої сили, то дійсний рух буде єдиним, що задовольняє цього рівняння, і тому не може бути порівнюваним з іншим рухом.

НАЙМЕНШОГО ДІЇ ПРИНЦИП

Один з варіаційних принципів механіки, згідно до якого для даного класу порівнюваних один з одним рухів механіч. системи дійсним є те, для якого фіз. величина, зв. дією, має найменше (точніше, стаціонарне) значення. Зазвичай Н. д. п. застосовується в одній із двох форм.

а) М. буд. дія за Гамільтоном S буде найменшою. Матем. вираз Н. д. п. має в цьому випадку вид: dS = 0, де d - символ неповної (ізохронної) варіації (тобто на відміну від повної варіації в ній час не варіюється).

б) Н. буд. рого дія по Лагранжу W буде найменшою. Матем. вираз Н. д. п. у цьому випадку має вигляд DW=0, де D - символ повної варіації (на відміну від принципу Гамільтона - Остроградського, тут варіюються не тільки координати та швидкості, але й час переміщення системи з однієї конфігурації до іншої) . Н. д. п. в. цьому випадку справедливий тільки для консервативних і притому голономних систем, у той час як у першому випадку Н. д. п. є більш загальним і, зокрема, може бути поширений на неконсервативні системи. Н. д. п. користуються для складання ур-ний руху механіч. систем й у дослідження загальних св-в цих рухів. При відповідному узагальненні понять Н. д. п. знаходить додатки в механіці безперервного середовища, електродинаміки, квант. механіки та ін.

- те саме, що...
Фізична енциклопедія
- m-оператор, оператор мінімізації та,- спосіб побудови нових функцій з інших функцій, що полягає в наступному...
Математична енциклопедія
- один з варіаційних принципів механіки, згідно до якого для даного класу порівнюваних один з одним рухів механіч. системи здійснюється те, для якого дія мінімально...
Природознавство. Енциклопедичний словник
- одне із найважливіших законів механіки, встановлений російським ученим М.В. Остроградським...
Російська енциклопедія
Словник юридичних термінів
- у конституційному праві низки держав принцип, за яким загальновизнані принципи та норми міжнародного права є складовою правової системи відповідної країни.
Енциклопедія юриста
- у конституційному праві низки держав принцип, за яким загальновизнані норми міжнародного права є складовою національної правової системи.
Великий юридичний словник
- найкоротша відстань від центру заряду вибухової речовини до вільної поверхні - лінія на найменше опір - křivka найменшого odporу;
Будівельний словник
- при можливості переміщення точок деформованого тіла в різних напрямках кожна точка цього тіла переміщується у напрямку найменшого опору.
Енциклопедичний словник з металургії
- правило, за яким наявні запаси прийнято оцінювати або за найменшою собівартістю або за найменшою ціною продажу...
Словник бізнес термінів
- у конституційному праві низки держав - принцип, згідно з яким загальновизнані принципи та норми міжнародного права є складовою правової системи відповідної держави та діють...
Енциклопедичний словник економіки та права
- один з варіаційних принципів механіки, згідно з яким для даного класу рухів механічної системи, що порівнюються один з одним, дійсним є те, для якого фізична величина,...
- те ж, що Гауса принцип...
Велика Радянська Енциклопедія
- один із варіаційних принципів механіки; те ж, що найменшої дії є принцип...
Велика Радянська Енциклопедія
- один з варіаційних принципів механіки, згідно з яким для даного класу рухів механічної системи, що порівнюються один з одним, здійснюється те, для якого дія мінімально...
Великий енциклопедичний словник
- Книжковий. Вибирати найлегший спосіб дії, уникаючи перешкод, ухиляючись від труднощів.
Фразеологічний словник української літературної мови

"НАМЕНШОГО ДІЇ ПРИНЦИП" у книгах

2.5.1. Принцип дії пристрою

З книги Цікава електроніка [Нешаблонна енциклопедія корисних схем] автора Кашкаров Андрій Петрович

2.5.1. Принцип дії пристрою Принцип дії пристрою простий. Коли світловий потік, що випромінюється світлодіодом HL1, відбивається від об'єкта та потрапляє на фотоприймач, електронний вузол, реалізований на 2 мікросхемах – компараторі КР1401СА1 та таймері КР1006ВІ1, виробляє

Принцип дії терафіму

З книги Потаємне знання. Теорія та практика Агні Йоги автора Реріх Олена Іванівна

Принцип дії терафіма 24.02.39 Ви знаєте, що кожне усвідомлення та уявлення будь-якого об'єкта тим самим наближає нас до нього. Як Ви знаєте, психічні нашарування об'єкта можуть бути перенесені на його терафім. Особливо важливі астральні терафими далеких світів та

Три умови для дії Закону Найменшого Зусилля

З книги Мудрість Діпака Чопри [Знайди бажане, дотримуючись 7 законів Всесвіту] автора Гудмен Тім

Три умови для дії Закону Найменшого Зусилля Давайте подивимося, які умови потрібні для залучення у ваше життя цього творчого потоку енергії Всесвіту - енергії кохання, а значить, і для того, щоб Закон Найменшого Зусилля почав працювати у вашому

Глава 19 ПРИНЦИП НАЙМЕНШОЇ ДІЇ

З книги 6. Електродинаміка автора Фейнман Річард Філліпс

Розділ 19 ПРИНЦИП НАЙМЕНШОЇ ДІЇ Додавання, зроблене після лекції Коли я навчався в школі, наш учитель фізики, на прізвище Бадер, одного разу закликав мене до себе після уроку і сказав: «У тебе вигляд такий, ніби тобі все страшно набридло; послухай-но про одну цікаву

5. Принцип найменшої дії

З книги Революція у фізиці автора де Бройль Луї

5. Принцип найменшої дії Рівняння динаміки матеріальної точки в полі сил, що володіють потенціалом, можна отримати, виходячи з принципу, який у загальному вигляді називається принципом Гамільтона, або принципом стаціонарної дії. Відповідно до цього принципу, з усіх

Принцип дії

З книги Керівництво слюсаря по замках автора Філіпс Білл

Принцип дії Можливість повороту циліндра залежить від положення пінів, яке в свою чергу визначається силою тяжіння, дією пружин та зусиллям ключа (або відмички; інформацію про відмички див. розділ 9). За відсутності ключа сила тяжкості та пружини вдавлюють

Стаціонарного дії принцип

З книги Велика Радянська Енциклопедія (СТ) автора Вікіпедія

Найменшої дії принцип

Вікіпедія

Найменшого примусу принцип

З книги Велика Радянська Енциклопедія (НА) автора Вікіпедія

2.5.1. Принцип дії

З книги Релейний захист у розподільних електричних мережах Б90 автора Буличов Олександр Віталійович

2.5.1. Принцип дії В електричних мережах із двостороннім живленням та в кільцевих мережах звичайні струмові захисту не можуть діяти селективно. Наприклад, в електричній мережі з двома джерелами живлення (рис. 2.15), де вимикачі та захист встановлені з обох сторін

Принцип дії

З книги Турбо-Суслік. Як припинити трахкати собі мозок і почати жити автора Леушкін Дмитро

Принцип дії «Оброби це» - це, фактично, своєрідний «макрос», який однією фразою запускає цілу купу процесів у підсвідомості, метою яких є обробка обраного ментального матеріалу. У сам цей обробник входить 7 різних модулів, частина з яких

Як почати слідувати Закону Найменшого Зусилля: три необхідні дії

З книги Посібник з вирощування капіталу від Джозефа Мерфі, Дейла Карнегі, Екхарта Толле, Діпака Чопри, Барбари Шер, Ніла Уолша автора Штерн Валентин

Як почати слідувати Закону Найменшого Зусилля: три необхідні дії Щоб Закон Найменшого Зусилля почав працювати, потрібно не тільки дотримуватися названих вище трьох умов, але ще й виконати три дії.

11. Фізика та айкідо найменшої дії

автора Мінделл Арнольд

11. Фізика та айкідо найменшої дії Коли дме, тобто лише вітер. Коли йде дощ, то є лише дощ. Коли хмари йдуть, крізь них світить сонце. Якщо ти відкриваєшся прозрінню, то ти заразом із прозрінням. І можеш використати його повністю. Якщо ти відкриваєшся

Принцип найменшої дії Лейбниця Vis Viva

З книги Геопсихологія в шаманізму, фізиці та даосизмі автора Мінделл Арнольд

Принцип найменшої дії Лейбниця Vis Viva За принцип найменшої дії ми всі повинні бути вдячні Вільгельму Готфріду Лейбніцу (1646–1716). Один із перших «сучасних» фізиків і математиків, Лейбніц жив у часи Ньютона - в епоху, коли вчені відкрито

Айкідо – втілення принципу найменшої дії

З книги Геопсихологія в шаманізму, фізиці та даосизмі автора Мінделл Арнольд

Айкідо - втілення принципу найменшої дії Наші психологія та технологія значною мірою керуються концепцією, дуже близькою до ідеї найменшої дії. Ми постійно намагаємось полегшити собі життя. Сьогоднішні комп'ютери недостатньо швидкі; вони повинні