Eng kam harakat tamoyili. Eng kam harakat printsipi Fizikada eng kam harakat printsipi

Maktabda o‘qib yurgan paytlarim, Beyder ismli fizika o‘qituvchimiz darsdan so‘ng meni chaqirib: “Siz hamma narsadan juda charchaganga o‘xshaysiz; bitta qiziqarli narsani tinglang." Va u menga haqiqatan ham hayratlanarli deb o'ylagan narsani aytdi. Hozir ham, o'shandan beri ko'p vaqt o'tgan bo'lsa-da, bu meni hayratda qoldirishda davom etmoqda. Va har safar aytganlarimni eslaganimda, ishga qaytaman. Bu gal esa ma’ruzaga tayyorgarlik ko‘rayotganimda yana o‘sha narsalarni tahlil qilib ko‘rdim. Va ma'ruzaga tayyorgarlik ko'rish o'rniga men yangi muammoni oldim. Men gapirayotgan mavzu eng kam harakat tamoyili.

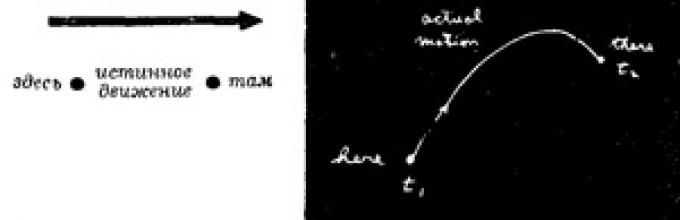
“O'shanda ustozim Bader menga shunday degan edi: “Masalan, sizda tortishish maydonida zarracha bor; bu zarra bir joydan chiqib, boshqa joydan boshqa nuqtaga erkin harakat qiladi. Siz uni, aytaylik, yuqoriga tashladingiz va u yuqoriga uchib ketdi va keyin yiqildi.

Unga boshlang'ich joydan yakuniy joyga borish uchun biroz vaqt kerak bo'ldi. Endi boshqa harakatni sinab ko'ring. Unga avvalgidek emas, balki “bu yerdan bu yerga” harakat qilsin:

Ammo men hali ham avvalgidek o'zimni kerakli joyda topdim."

- Shunday qilib, - davom etdi o'qituvchi, - agar siz zarrachaning yo'li bo'ylab har bir vaqtning kinetik energiyasini hisoblab chiqsangiz, undan potentsial energiyani ayirsangiz va harakat sodir bo'lgan butun vaqt davomida farqni integrallasangiz, ko'rasiz siz olgan raqam bo'ladi Ko'proq, haqiqiy zarrachalar harakatidan ko'ra.

Boshqacha qilib aytganda, Nyuton qonunlarini F=ma shaklida emas, balki quyidagicha shakllantirish mumkin: o'rtacha kinetik energiya minus o'rtacha potentsial energiya ob'ekt haqiqatda bir joydan ikkinchi joyga o'tadigan traektoriya bo'ylab eng past qiymatga etadi.

Men buni sizga biroz aniqroq tushuntirishga harakat qilaman.
Agar biz tortishish maydonini olsak va zarrachaning traektoriyasini belgilasak x(t), Qayerda X- erdan balandlik (hozircha bir o'lchov bilan harakat qilaylik; traektoriya faqat yuqoriga va pastga harakat qilsin, yon tomonga emas), shunda kinetik energiya bo'ladi. y 2 m(dx/ dt) 2, a vaqtning ixtiyoriy momentidagi potentsial energiya teng bo'ladi mgx.

Endi, traektoriya bo'ylab harakatlanishning bir lahzasi uchun men kinetik va potentsial energiyalar o'rtasidagi farqni olaman va boshidan oxirigacha butun vaqt davomida birlashaman. Vaqtning dastlabki daqiqalarida ruxsat bering t x harakat qandaydir balandlikda boshlandi va ayni paytda tugadi t 2 boshqa ma'lum balandlikda.

U holda integral ∫ t2 t1 dt ga teng

Haqiqiy harakat ma'lum bir egri chiziq bo'ylab sodir bo'ladi (vaqt funksiyasi sifatida u parabola) va ma'lum bir integral qiymatga olib keladi. Lekin qila olasiz oldinqo'yish boshqa harakatni tasavvur qiling: birinchi navbatda keskin ko'tarilish, keyin esa g'alati tebranishlar.

Siz bu yo'lda potentsial va kinetik energiya o'rtasidagi farqni hisoblashingiz mumkin ... yoki boshqa har qanday yo'lda. Va eng ajablanarlisi shundaki, haqiqiy yo'l bu integral eng kichik bo'lgan yo'ldir.
Keling, buni tekshirib ko'ramiz. Birinchidan, bu holatni ko'rib chiqaylik: erkin zarrachaning potentsial energiyasi umuman yo'q. Keyin qoida ma'lum bir vaqt ichida bir nuqtadan ikkinchisiga o'tishda kinetik energiyaning integrali eng kichik bo'lishi kerakligini aytadi. Bu zarrachaning bir tekis harakatlanishi kerakligini anglatadi. (Va bu to'g'ri, siz va men bunday harakatdagi tezlik doimiy ekanligini bilamiz.) Nima uchun bir xil? Keling, buni aniqlaylik. Agar boshqacha bo'lganida, zarrachaning tezligi ba'zan o'rtachadan oshib, ba'zida undan past bo'lar va o'rtacha tezlik bir xil bo'lar edi, chunki zarracha "bu erdan bu erga" borishi kerak edi. kelishilgan vaqt. Misol uchun, agar siz uydan maktabga ma'lum bir vaqtda mashinangizda borishingiz kerak bo'lsa, unda siz buni turli yo'llar bilan qilishingiz mumkin: siz boshida aqldan ozgandek haydashingiz va oxirida sekinlashishingiz yoki bir xil tezlikda haydashingiz mumkin. yoki siz hatto qarama-qarshi tomonga borishingiz mumkin va shundan keyingina maktab tomon burilishingiz mumkin va hokazo. Barcha holatlarda o'rtacha tezlik, albatta, bir xil bo'lishi kerak - uydan maktabgacha bo'lgan masofaning vaqtga bo'lingan qismi. Ammo bu o'rtacha tezlikda ham siz ba'zan juda tez va ba'zan juda sekin harakat qildingiz. Va o'rtacha kvadrat o'rtachadan chetga chiqadigan narsa, biz bilganimizdek, har doim o'rtacha kvadratdan kattaroqdir; Bu shuni anglatadiki, harakat tezligining tebranishlari paytida kinetik energiyaning integrali doimo doimiy tezlikda harakat qilgandan ko'ra katta bo'ladi. Tezlik doimiy bo'lganda (kuchlar bo'lmaganda) integral minimal darajaga yetishini ko'rasiz. To'g'ri yo'l shu.

Og'irlik maydonida yuqoriga tashlangan jism avvaliga tez ko'tariladi, keyin esa tobora sekinroq ko'tariladi. Buning sababi shundaki, u ham potentsial energiyaga ega va uning minimal qiymatiga erishish kerak bir martaness kinetik va potentsial energiyalar o'rtasida.. Potentsial energiya siz ko'tarilgan sayin ortib borgani uchun, keyin kamroq farq Agar siz potentsial energiya yuqori bo'lgan balandliklarga imkon qadar tezroq erishsangiz, u ishlaydi. Keyin, bu yuqori potentsialni kinetik energiyadan chiqarib tashlasak, biz o'rtacha qiymatning pasayishiga erishamiz. Shunday qilib, yuqoriga ko'tariladigan va potentsial energiya hisobiga yaxshi salbiy qismni ta'minlaydigan yo'l yanada foydali bo'ladi.

Ustozim menga shuni aytdi, chunki u juda yaxshi o'qituvchi edi va qachon to'xtash kerakligini bilardi. Men o'zim, afsuski, bunday emasman. O'z vaqtida to'xtash menga qiyin. Shunday qilib, mening hikoyam bilan qiziqishingizni uyg'otish o'rniga, men sizni qo'rqitmoqchiman, sizni hayotning murakkabligidan xafa qilmoqchiman - men sizga aytganlarimni isbotlashga harakat qilaman. Biz hal qiladigan matematik masala juda qiyin va noyobdir. Muayyan miqdor mavjud S, chaqirdi harakat. Bu vaqt davomida integrallashgan kinetik energiya minus potentsial energiyaga teng:

Ammo boshqa tomondan, siz juda tez harakat qila olmaysiz yoki juda baland ko'tarila olmaysiz, chunki bu juda ko'p kinetik energiya talab qiladi. Sizga berilgan vaqt ichida yuqoriga va pastga tushish uchun etarlicha tez harakat qilishingiz kerak. Shunday qilib, siz juda baland uchishga harakat qilmasligingiz kerak, faqat o'rtacha darajaga erishing. Natijada, yechim imkon qadar ko'proq potentsial energiya olish istagi va kinetik energiya miqdorini imkon qadar kamaytirish istagi o'rtasidagi o'ziga xos muvozanat ekanligi ma'lum bo'ldi - bu maksimal pasayishga erishish istagi. kinetik va potentsial energiyalar o'rtasidagi farqda.

Shuni unutmangki, p.e. va k.e - vaqtning ikkala funktsiyasi. Har qanday yangi yo'l uchun bu harakat o'ziga xos ma'noga ega bo'ladi. Matematik muammo qaysi egri chiziqda bu raqam boshqalarga qaraganda kamroq ekanligini aniqlashdir.

Siz shunday deysiz: “Oh, bu maksimal va minimalning oddiy misoli. Biz harakatni hisoblashimiz, uni farqlashimiz va minimalni topishimiz kerak”.

Lekin kuting. Odatda bizda qandaydir o'zgaruvchining funksiyasi bor va qiymatni topishimiz kerak o'zgaruvchan, bunda funksiya eng kichik yoki eng katta bo'ladi. Aytaylik, o'rtada isitiladigan novda bor. Issiqlik uning ustiga tarqaladi va tayoqning har bir nuqtasida o'z harorati o'rnatiladi. Siz eng yuqori nuqtani topishingiz kerak. Ammo biz butunlay boshqacha narsa haqida gapirayapmiz - kosmosdagi har bir yo'l uning raqamiga javob beradi va uni topishi kerak yo'l, ular uchun bu raqam minimaldir. Bu matematikaning mutlaqo boshqa sohasi. Bu oddiy hisob emas, balki o'zgaruvchan(Ular uni shunday deyishadi).

Matematikaning bu sohasining o'ziga xos muammolari ko'p. Aytaylik, aylana odatda berilgan nuqtadan masofalari bir xil bo'lgan nuqtalarning joylashuvi sifatida belgilanadi, lekin aylana boshqacha belgilanishi mumkin: u egri chiziqlardan biridir. berilgan uzunlik, eng katta maydonni o'rab oladi. Xuddi shu perimetrning boshqa har qanday egri chizig'i aylanadan kichikroq maydonni o'rab oladi. Shunday qilib, agar biz vazifani qo'ysak: berilgan perimetrning eng katta maydonni chegaralovchi egri chizig'ini topish, u holda bizda siz o'rgangan hisobdan emas, balki variatsiyalar hisobi bo'yicha muammo paydo bo'ladi.

Shunday qilib, biz integralni tananing bosib o'tgan yo'lidan o'tkazmoqchimiz. Keling, buni shunday qilaylik. Gap shundaki, haqiqiy yo'l borligini va biz chizgan boshqa har qanday egri chiziq haqiqiy yo'l emasligini tasavvur qilishdir, shuning uchun agar biz uning uchun harakatni hisoblasak, biz mos keladigan harakat uchun olganimizdan yuqori raqamga ega bo'lamiz. haqiqiy yo'lga.

Demak, vazifa to‘g‘ri yo‘lni topishdir. Qayerda yotadi? Buning bir usuli, albatta, harakatni millionlab va millionlab yo'llar uchun hisoblash va keyin qaysi yo'lda eng kichik harakatga ega ekanligini ko'rishdir. Bu harakat minimal bo'lgan va haqiqiy bo'ladigan yo'ldir.

Bu usul juda mumkin. Biroq, buni oddiyroq qilish mumkin. Agar minimal (oddiy funktsiyalardan, aytaylik, harorat) bo'lgan miqdor mavjud bo'lsa, u holda minimalning xususiyatlaridan biri undan uzoqroqda uzoqlashganda. birinchi kichiklik tartibi bo'yicha, funktsiya o'zining minimal qiymatidan faqat miqdorga qarab chetlanadi ikkinchi buyurtma. Va egri chiziqning boshqa har qanday joyida kichik masofaga siljish funktsiya qiymatini birinchi darajali kichiklik qiymatiga ham o'zgartiradi. Ammo, hech bo'lmaganda, yon tomonga engil og'ishlar birinchi taxminiylik sifatida funktsiyaning o'zgarishiga olib kelmaydi.

Aynan shu xususiyat biz haqiqiy yo'lni hisoblash uchun foydalanamiz.

Agar yo'l to'g'ri bo'lsa, undan bir oz farq qiladigan egri chiziq, birinchi taxmin sifatida, harakatning kattaligi o'zgarishiga olib kelmaydi. Barcha o'zgarishlar, agar bu haqiqatan ham minimal bo'lsa, faqat ikkinchi yaqinlashishda paydo bo'ladi.

Buni isbotlash oson. Agar egri chiziqdan biroz og'ish bilan birinchi tartibda o'zgarishlar ro'y bersa, u holda bu o'zgarishlar kuchga kiradi mutanosib og'ish. Ular ta'sirni kuchaytirishi mumkin; aks holda bu minimal bo'lmaydi. Ammo bir marta o'zgarishlar mutanosib og'ish, keyin og'ish belgisini o'zgartirish harakatni kamaytiradi. Ma’lum bo‘lishicha, bir tomonga og‘ishda effekt kuchayadi, teskari tomonga og‘ishda esa pasayadi. Buning haqiqatan ham minimal bo'lishining yagona imkoniyati shundan iboratki, birinchi taxminga ko'ra, hech qanday o'zgarishlar yuz bermaydi va o'zgarishlar haqiqiy yo'ldan og'ish kvadratiga proportsionaldir.

Shunday qilib, biz quyidagi yo'ldan boramiz: belgilang x(t) (pastdagi chiziq bilan) haqiqiy yo'l biz topmoqchi bo'lgan yo'ldir. Keling, bir oz sinovdan o'taylik x(t), biz belgilagan kichik miqdor bilan istalganidan farq qiladi η (t).

Fikr shundan iboratki, agar biz harakatni hisoblasak S yo'lda x(t), keyin bu o'rtasidagi farq S va biz yo'l uchun hisoblagan harakat bilan x(t) (oddiylik uchun u belgilanadi S), yoki orasidagi farq S_ Va S, birinchi taxminiy bo'lishi kerak η nol. Ular ikkinchi tartibda farq qilishi mumkin, lekin birinchisida farq nolga teng bo'lishi kerak.

Va bu hamma uchun kuzatilishi kerak η . Biroq, hamma uchun unchalik emas. Usul faqat bitta juft nuqtada boshlanadigan va tugaydigan yo'llarni hisobga olishni talab qiladi, ya'ni har bir yo'l ma'lum bir vaqtning o'zida boshlanishi kerak. t 1 va ayni paytda boshqa aniq nuqtada tugaydi t 2 . Bu nuqtalar va daqiqalar yozib olinadi. Shunday qilib, bizning d) funktsiyamiz (og'ish) ikkala uchida ham nolga teng bo'lishi kerak: η (t 1 )= 0 Va η (t 2)=0. Bunday sharoitda bizning matematik muammomiz to'liq aniqlangan bo'ladi.

Agar siz hisob-kitobni bilmasangiz, oddiy funktsiyaning minimalini topish uchun ham xuddi shunday qilishingiz mumkin edi f(x). Olsangiz nima bo'lishini o'ylab ko'rasizmi f(x) va qo'shing X kichik miqdor h, va o'zgartirishlar kiritilishini ta'kidlaydilar f(x) birinchi tartibda h minimal nolga teng bo'lishi kerak. Meni sozlay olasizmi? x+h o'rniga X va j(x+h) ni birinchi darajagacha kengaytiradi h. . ., bir so'z bilan aytganda, biz qilmoqchi bo'lgan hamma narsani takrorlaymiz η .

Agar biz buni diqqat bilan ko'rib chiqsak, bu erda yozilgan dastlabki ikki atama o'sha harakatga mos kelishini ko'ramiz S, Men qidirilgan to'g'ri yo'l uchun yozgan bo'lardim X. Men sizning e'tiboringizni o'zgarishlarga qaratmoqchiman. S, ya'ni orasidagi farq haqida S va hokazo S_, natijada haqiqiy yo'l paydo bo'ladi. Bu farqni quyidagicha yozamiz bS va keling, uni variatsiya deb ataymiz S. "Ikkinchi va undan yuqori buyurtmalar" dan voz kechib, biz olamiz s S

Endi vazifa shunday ko'rinadi. Mana, mening oldimda qandaydir integral bor. Men bu qanday ekanligini hali bilmayman, lekin men buni aniq bilaman, nima η Nima bo'lishidan qat'iy nazar, bu integral nolga teng bo'lishi kerak. "Xo'sh," deb o'ylashingiz mumkin, "buning sodir bo'lishining yagona yo'li - bu multiplikator η nolga teng edi." Lekin birinchi muddat haqida nima deyish mumkin, qaerda bor d η / dt? Siz aytasiz: "Agar η hech narsaga aylanadi, keyin uning hosilasi bir xil hech narsa; bu at koeffitsientini bildiradi dv\/ dt ham nolga teng bo'lishi kerak." Xo'sh, bu mutlaqo to'g'ri emas. Bu butunlay to'g'ri emas, chunki og'ish o'rtasida η va uning hosilasi bog'lanish mavjud; ular butunlay mustaqil emas, chunki η (t) nol bo'lishi kerak va t 1 va da t 2 .

O'zgarishlarni hisoblashning barcha masalalarini echishda doimo bir xil umumiy printsip qo'llaniladi. Siz o'zgartirmoqchi bo'lgan narsani biroz o'zgartirasiz (qo'shish orqali qilganimizga o'xshash). η ), birinchi tartib shartlariga qarash, keyin Quyidagi shaklda integral olish uchun hamma narsani tartibga soling: "shift (η ), chiqadigan narsaga ko'paytiriladi", lekin unda hech qanday hosila bo'lmasligi uchun η (yo'q d η / dt). Hamma narsani o'zgartirish kerak, shunda "bir narsa" qoladi, ko'paytiriladi η . Endi nima uchun bu juda muhimligini tushunasiz. (Ba'zi hollarda buni qanday qilib hech qanday hisob-kitoblarsiz amalga oshirishingiz mumkinligini aytadigan formulalar mavjud; lekin ular eslab qolishga arziydigan darajada umumiy emas; eng yaxshisi hisob-kitoblarni o'zimiz qilgandek qilishdir.)

Qanday qilib jinsiy olatni qayta tiklashim mumkin d η / dt, paydo bo'lishi uchun η ? Men buni parcha-parcha birlashtirish orqali erisha olaman. Ma'lum bo'lishicha, o'zgarishlarni hisoblashda butun hiyla o'zgaruvchanlikni tasvirlashdir S va keyin qismlar bo'yicha integrallashing, shunday qilib hosilalari η G'oyib bo'lgan. Losmalar paydo bo'lgan barcha masalalarda bir xil hiyla bajariladi.

Qismlar bo'yicha integratsiyaning umumiy tamoyilini eslang. Agar ixtiyoriy f funktsiyaga ko'paytirilsa d η / dt va bilan birlashtirilgan t, keyin hosilasini yozasiz η /t

Integratsiya chegaralari birinchi muddatga almashtirilishi kerak t 1 Va t 2 . Keyin integral ostida men qismlar bo'yicha integrallashdan atamani va transformatsiya paytida o'zgarmagan oxirgi hadni olaman.
Va endi har doim sodir bo'ladigan narsa sodir bo'ladi - integratsiyalashgan qism yo'qoladi. (Va agar u yo'qolmasa, unda printsipni qayta shakllantirish, bunday yo'qolishni ta'minlaydigan shartlarni qo'shish kerak!) Biz allaqachon aytdik. η yo'lning oxirida nolga teng bo'lishi kerak. Axir bizning printsipimiz nima? Haqiqat shundaki, turli xil egri chiziq tanlangan nuqtalarda boshlanib, tugasa, harakat minimal bo'ladi. Bu shuni anglatadiki η (t 1)=0 va η (t 2)=0. Shuning uchun integrallashgan atama nolga aylanadi. Qolgan a'zolarni yig'amiz va yozamiz

Variatsiya S endi biz bermoqchi bo'lgan shaklni oldi: qavs ichida biror narsa bor (uni belgilaymiz F), va bularning barchasi ko'paytiriladi η (t) va dan integratsiyalashgan t t oldin t 2 .
Ma'lum bo'ldiki, qandaydir ifodaning integrali ē ga ko'paytiriladi (t), har doim nolga teng:

dan qandaydir funksiya bormi t; ga ko'paytiraman η (t) va uni boshidan oxirigacha birlashtiring. Va nima bo'lishidan qat'iy nazar η, Men nol olaman. Bu funktsiyani anglatadi F(t) nolga teng. Umuman olganda, bu aniq, lekin har qanday holatda, men sizga buni isbotlashning bir usulini ko'rsataman.

ē bo'lsin (t) Men hamma joyda, hamma uchun nolga teng bo'lgan narsani tanlayman t, oldindan tanlangan bitta qiymatdan tashqari t. Men u erga borgunimcha u nol bo'lib qoladi t, s Keyin u bir lahzaga sakrab tushadi va darhol orqaga tushadi. Agar bu m) integralini qandaydir funktsiyaga ko'paytirsangiz F, nolga teng bo'lmagan narsani oladigan yagona joy - bu qaerda η (t) sakrab tushdi; va siz qiymatga ega bo'lasiz F bu nuqtada integral ustida sakrash ustida. O'tish ustidagi integralning o'zi nolga teng emas, lekin ko'paytirilgandan keyin F nol berishi kerak. Bu sakrash sodir bo'lgan joydagi funktsiya nolga aylanishi kerakligini anglatadi. Ammo sakrash har qanday joyda amalga oshirilishi mumkin edi; Ma'nosi, F hamma joyda nolga teng bo'lishi kerak.

Biz shuni ko'ramizki, agar bizning integralimiz har qanday uchun nolga teng bo'lsa η , keyin koeffitsient at η nolga tushishi kerak. Harakat integrali shunday murakkab differensial tenglamani qanoatlantiradigan yo'l bo'ylab minimal darajaga etadi:

Bu aslida unchalik murakkab emas; siz u bilan oldin uchrashgansiz. Bu shunchaki F = ma. Birinchi a'zo - massalar sonining tezlanishi; ikkinchisi - potentsial energiyaning hosilasi, ya'ni kuch.

Shunday qilib, biz (hech bo'lmaganda konservativ tizim uchun) eng kam harakat tamoyili to'g'ri javobga olib kelishini ko'rsatdik; u minimal harakatga ega bo'lgan yo'l Nyuton qonunini qanoatlantiradigan yo'l ekanligini aytadi.

Yana bir eslatmani aytish kerak. Men buni isbotlaganim yo'q eng kam. Ehtimol, bu maksimaldir. Aslida, bu minimal bo'lishi shart emas. Bu erda hamma narsa optikani o'rganayotganda muhokama qilgan "eng qisqa vaqt printsipi" bilan bir xil. U erda ham biz birinchi navbatda "eng qisqa" vaqt haqida gaplashdik. Biroq, ma'lum bo'lishicha, bu vaqt "eng qisqa" bo'lishi shart bo'lmagan holatlar mavjud. Asosiy tamoyil - bu har qanday kishi uchun birinchi tartibli og'ishlar optik yo'ldan o'zgarishlar vaqt ichida nolga teng bo'ladi; Bu erda ham xuddi shunday hikoya. “Minimal” deganda, aslida miqdor o‘zgarishining kichikligining birinchi tartibini nazarda tutamiz S yo'ldan og'ishlar nolga teng bo'lishi kerak bo'lganda. Va bu "minimal" bo'lishi shart emas.

Endi men ba'zi umumlashmalarga o'tmoqchiman. Birinchidan, bu butun hikoyani uch o'lchovda qilish mumkin edi. Oddiy o'rniga X O'shanda bo'lardim x, y Va z funktsiyalar sifatida t, va harakat yanada murakkab ko'rinadi. 3D rejimida harakatlanayotganda siz to'liq kinetik energiyadan foydalanishingiz kerak): (t/2), umumiy tezlikning kvadratiga ko'paytiriladi. Boshqa so'zlar bilan aytganda

Bundan tashqari, potentsial energiya endi funktsiyaga aylandi x, y Va z. Yo'l haqida nima deya olasiz? Yo'l - fazodagi ma'lum bir umumiy egri chiziq; chizish unchalik oson emas, lekin g'oya bir xil bo'lib qoladi. ē-chi? Xo'sh, ē ham uchta komponentga ega. Yo'lni ham x, ham ichida o'zgartirish mumkin y, va tomonidan z, yoki bir vaqtning o'zida barcha uch yo'nalishda. Shunday qilib η endi vektor. Bu hech qanday jiddiy asoratlarni keltirib chiqarmaydi. Faqat o'zgarishlar nolga teng bo'lishi kerak birinchi buyurtma keyin hisoblash uch smenada ketma-ket amalga oshirilishi mumkin. Avval siz harakat qilishingiz mumkin ts faqat yo'nalishda X va koeffitsient nolga borishi kerakligini ayting. Siz bitta tenglamani olasiz. Keyin harakat qilamiz ts yo'nalishda da va biz ikkinchisini olamiz. Keyin yo'nalishda harakatlaning z va uchinchisini olamiz. Agar xohlasangiz, hamma narsani boshqa tartibda qilishingiz mumkin. Qanday bo'lmasin, tenglamalar uchligi paydo bo'ladi. Ammo Nyuton qonuni har bir komponent uchun bittadan uchta o'lchovli uchta tenglamadir. Bularning barchasi uch o'lchovda ishlayotganini o'zingiz ko'rasiz (bu erda ko'p ish yo'q). Aytgancha, siz o'zingizga yoqqan har qanday koordinata tizimini, qutbli yoki istalgan koordinata tizimini olishingiz va siljish sodir bo'lganda nima sodir bo'lishini hisobga olgan holda ushbu tizimga nisbatan Nyuton qonunlarini darhol olishingiz mumkin. η radius yoki burchak bo'ylab va hokazo.

Usul ixtiyoriy zarrachalar soniga umumlashtirilishi mumkin. Aytaylik, sizda ikkita zarra bo'lsa va ular o'rtasida qandaydir kuchlar harakat qilsa va o'zaro potentsial energiya mavjud bo'lsa, unda siz shunchaki ularning kinetik energiyalarini qo'shib, o'zaro ta'sir potentsial energiyasini yig'indidan ayirasiz. Siz nima bilan farq qilasiz? Yo'llar ikkalasi ham zarralar. Keyin uch o'lchamda harakatlanadigan ikkita zarra uchun oltita tenglama paydo bo'ladi. 1-zarrachaning o'rnini yo'nalishda o'zgartirishingiz mumkin X, yo'nalishda da va tomon z, va 2-zarra bilan ham xuddi shunday qiling, shuning uchun oltita tenglama mavjud. Va shunday bo'lishi kerak. Uchta tenglama 1-zarrachaning unga ta’sir etuvchi kuch ta’sirida tezlanishini, qolgan uchtasi esa 2-zarrachaning unga ta’sir etuvchi kuch ta’sirida tezlanishini aniqlaydi. Har doim bir xil o'yin qoidalariga rioya qiling va siz ixtiyoriy miqdordagi zarralar uchun Nyuton qonunini olasiz.

Men Nyuton qonunini olamiz dedim. Bu mutlaqo to'g'ri emas, chunki Nyuton qonuni ishqalanish kabi konservativ bo'lmagan kuchlarni ham o'z ichiga oladi. Nyuton buni ta'kidladi bu har qanday F ga teng. Eng kam harakat tamoyili faqat uchun amal qiladi konservativ potentsial funktsiyadan barcha kuchlarni olish mumkin bo'lgan tizimlar. Ammo siz mikroskopik darajada, ya'ni eng chuqur jismoniy darajada konservativ bo'lmagan kuchlar mavjud emasligini bilasiz. Konservativ bo'lmagan kuchlar (masalan, ishqalanish) biz mikroskopik murakkab effektlarni e'tiborsiz qoldirganimiz uchun paydo bo'ladi: tahlil qilish uchun juda ko'p zarrachalar mavjud. Asosiy bir xil qonunlar mumkin eng kam harakat tamoyili sifatida ifodalanadi.

Keling, keyingi umumlashmalarga o'tmoqchiman. Aytaylik, bizni zarracha nisbiy harakat qilganda nima sodir bo'lishi qiziqtiradi. Hozircha biz harakatning to'g'ri relativistik tenglamasini ololmadik; F=ma faqat relyativistik bo'lmagan harakatlarda to'g'ri bo'ladi. Savol tug'iladi: relativistik holatda eng kam harakatning tegishli printsipi bormi? Ha, mavjud. Relyativistik holatda formula:

Harakat integralining birinchi qismi qolgan massaning mahsulotidir t 0 yoqilgan 2 dan va tezlik funksiyasining integrali √ (1-v 2 /c 2 ). Keyin, potentsial energiyani ayirish o'rniga, bizda skalyar potentsial ph va vektor potensialining A marta v integrallari mavjud. Albatta, bu erda faqat elektromagnit kuchlar hisobga olinadi. Barcha elektr va magnit maydonlar ph va A bilan ifodalanadi. Bu harakat funksiyasi alohida zarrachaning elektromagnit maydondagi relyativistik harakatining to'liq nazariyasini beradi.

Albatta, siz tushunishingiz kerakki, men v ni yozgan har bir joyda hisob-kitob qilishdan oldin, uni almashtirish kerak dx/ dt o'rniga v x va hokazo. Bundan tashqari, men oddiygina yozgan joy x, y, z, siz ayni damdagi nuqtalarni tasavvur qilishingiz kerak t: x(t), y(t), z(t). Haqiqatan ham, v ni shunday almashtirish va almashtirishlardan keyingina relyativistik zarrachaning ta'siri formulasini olasiz. Sizning orangizdagi eng malakalilar ushbu harakat formulasi nisbiylik nazariyasi uchun to'g'ri harakat tenglamalarini berishini isbotlashga harakat qilsin. Sizga faqat A ni tashlab boshlashni maslahat beraman, ya'ni hozircha magnit maydonlarsiz ishla. Keyin harakat tenglamasining komponentlarini olishingiz kerak bo'ladi dp/dt=—qVph, Bu erda, ehtimol, esingizda bo'lsa, p=mv√(1-v 2 /c 2).

A vektor potensialini hisobga olish ancha qiyinroq. Variatsiyalar keyinchalik taqqoslanmaydigan darajada murakkablashadi. Lekin oxir-oqibat kuch qanday bo'lishi kerak bo'lganiga teng bo'lib chiqadi: g (E+v × B). Lekin o'zingiz bilan biroz zavqlaning.

Shuni ta'kidlashni istardimki, umumiy holatda (masalan, relyativistik formulada) harakatdagi integral endi kinetik va potentsial energiyalar orasidagi farqni o'z ichiga olmaydi. Bu faqat relyativistik bo'lmagan yaqinlashuvda mos edi. Masalan, a'zo m o c 2√(1-v 2 /c 2)- Bu kinetik energiya deb ataladigan narsa emas. Har qanday muayyan ish uchun harakat qanday bo'lishi kerakligi haqidagi savol, ba'zi sinov va xatolardan so'ng hal qilinishi mumkin. Bu harakat tenglamalari qanday bo'lishi kerakligini aniqlash bilan bir xil turdagi masala. Siz shunchaki o'zingiz bilgan tenglamalar bilan o'ynashingiz va ularni eng kam harakat tamoyili sifatida yozish mumkinligini ko'rishingiz kerak.

Terminologiya haqida yana bir eslatma. Harakatni olish uchun vaqt o'tishi bilan birlashtirilgan bu funktsiya S, chaqirdi Lagrangian s. Bu faqat zarrachalarning tezligi va pozitsiyalariga bog'liq bo'lgan funktsiyadir. Demak, eng kam harakat tamoyili ham shaklda yoziladi

qaerda ostida X i Va v i koordinatalar va tezliklarning barcha komponentlari nazarda tutilgan. Agar kimdir "Lagrangian" haqida gapirayotganini eshitsangiz, ular olish uchun ishlatiladigan funktsiya haqida gapirishadi S. Elektromagnit maydonda relyativistik harakat uchun

Bundan tashqari, shuni ta'kidlash kerakki, eng sinchkov va pedantik odamlar qo'ng'iroq qilmaydi S harakat. Bu "Gamiltonning birinchi asosiy funktsiyasi" deb ataladi. Ammo “Gemiltonning eng kichik birinchi asosiy funktsiya printsipi” mavzusida ma'ruza o'qish mening kuchimdan tashqarida edi. Men buni "harakat" deb atadim. Bundan tashqari, tobora ko'proq odamlar buni "harakat" deb atashadi. Ko'ryapsizmi, tarixan harakat ilm-fan uchun unchalik foydali bo'lmagan boshqa narsa deb nomlangan, ammo menimcha, ta'rifni o'zgartirish mantiqiyroq. Endi siz ham yangi funksiyani harakat deb atay boshlaysiz va tez orada hamma uni shu oddiy nom bilan chaqira boshlaydi.

Endi men sizga eng qisqa vaqt tamoyili haqidagi mulohazalarga o'xshash mavzuimiz haqida gapirmoqchiman. Bir nuqtadan ikkinchi nuqtaga olingan ba'zi bir integral minimal darajaga ega ekanligini aytadigan qonunning mohiyatida farq bor - bu bizga bir vaqtning o'zida butun yo'l haqida nimanidir aytib beradigan qonun va harakat qilganingizda, keyin Bu tezlashuvga olib keladigan kuch borligini anglatadi. Ikkinchi yondashuv sizning har bir qadamingiz haqida sizga xabar beradi, u sizning yo'lingizni dyuym-dyuym bilan kuzatib boradi va birinchisi darhol bosib o'tgan butun yo'l haqida umumiy ma'lumot beradi. Nur haqida gapirganda, biz bu ikki yondashuv o'rtasidagi bog'liqlik haqida gapirdik. Endi men sizga nima uchun differensial qonunlar mavjud bo'lishi kerakligini tushuntirmoqchiman, agar shunday printsip mavjud bo'lsa - eng kam harakat tamoyili. Buning sababi shundaki: keling, fazoda va vaqt ichida aslida bosib o'tgan yo'lni ko'rib chiqaylik. Avvalgidek, biz bitta o'lchovni bajaramiz, shunda biz qaramlikning grafigini chizishimiz mumkin X dan t. Haqiqiy yo'lda S minimal darajaga etadi. Faraz qilaylik, bizda bu yo'l bor va u qaysidir nuqtadan o'tadi A makon va vaqt va boshqa qo'shni nuqta orqali b.

Endi, agar butun integrali bo'lsa t 1 oldin t 2 minimal darajaga yetgan bo'lsa, integral a dan kichik kesim bo'ylab bo'lishi kerak b ham minimal edi. Bu qismi bo'lishi mumkin emas A oldin b hech bo'lmaganda minimaldan bir oz ko'proq. Aks holda, siz ushbu bo'limda egri chiziqni oldinga va orqaga siljitishingiz va butun integralning qiymatini biroz kamaytirishingiz mumkin.

Bu shuni anglatadiki, yo'lning har qanday qismi ham minimalni ta'minlashi kerak. Va bu yo'lning har qanday kichik qismlari uchun amal qiladi. Shuning uchun, butun yo'l minimal berishi kerakligi tamoyilini, yo'lning cheksiz kichik segmenti ham harakat minimal bo'lgan egri chiziq ekanligini aytish orqali shakllantirish mumkin. Va agar biz yo'lning etarlicha qisqa qismini olsak - bir-biriga juda yaqin nuqtalar orasida A Va b,- keyin bu joydan uzoqroqda potentsial qanday o'zgarishi muhim emas, chunki butun qisqa segmentingizdan o'tib, siz deyarli hech qachon bu joydan harakatlanmaysiz. Siz e'tiborga olishingiz kerak bo'lgan yagona narsa - bu potentsialdagi kichiklikning birinchi navbatdagi o'zgarishi. Javob boshqa potentsialga emas, balki faqat potentsial hosilasiga bog'liq bo'lishi mumkin. Shunday qilib, butun yo'lning mulki to'g'risidagi bayonot yo'lning qisqa qismida nima sodir bo'lishi haqidagi bayonotga, ya'ni differentsial bayonotga aylanadi. Va bu differentsial formulaga potentsialning hosilalari, ya'ni ma'lum bir nuqtadagi kuch kiradi. Bu butun huquq va differensial qonun o'rtasidagi bog'liqlikni sifatli tushuntirishdir.

Biz yorug'lik haqida gapirganda, biz savolni ham muhokama qildik: zarracha qanday qilib to'g'ri yo'lni topadi? Differensial nuqtai nazardan, buni tushunish oson. Har lahzada zarracha tezlanishni boshdan kechiradi va faqat o'sha paytda nima qilishi kerakligini biladi. Ammo zarracha qaysi yo'ldan borishni "hal qilishini", minimal harakatga intilishini eshitganingizda, barcha sabab va ta'sir instinktlaringiz kuchayadi. U qo'shni yo'llarni "hidlamaydi", ular nimaga olib kelishini - ozmi-ko'pmi harakatni tushunmayaptimi? Fotonlar barcha yo'llarni sinab ko'ra olmasligi uchun yorug'lik yo'liga ekran o'rnatganimizda, ular qaysi yo'lni tanlashni hal qila olmasligini bilib oldik va biz diffraktsiya hodisasini oldik.

Ammo bu mexanikaga ham tegishlimi? Zarracha nafaqat "to'g'ri yo'ldan boradi", balki boshqa barcha mumkin bo'lgan traektoriyalarni qayta ko'rib chiqadimi? Va agar uning yo'liga to'siqlar qo'yish orqali biz uning oldinga qarashiga yo'l qo'ymasak, unda biz diffraktsiya hodisasining qandaydir o'xshashini olamiz? Bularning eng ajoyib tomoni shundaki, hamma narsa haqiqatan ham shunday. Kvant mexanikasi qonunlari aynan shunday deydi. Shunday qilib, bizning eng kam harakat tamoyilimiz to'liq shakllantirilgan emas. Bu zarrachaning eng kam harakat yo'lini tanlashida emas, balki u barcha qo'shni yo'llarni "sezishi" va harakat minimal bo'lganini tanlashi va bu tanlash usuli yorug'lik eng qisqa vaqtni tanlash usuli. Yodingizda bo'lsin, yorug'lik eng qisqa vaqtni tanlaydi: agar yorug'lik boshqa vaqtni talab qiladigan yo'l bo'ylab ketsa, u boshqa faza bilan keladi. Va bir nuqtada umumiy amplituda yorug'lik unga etib borishi mumkin bo'lgan barcha yo'llar uchun amplituda hissalarining yig'indisidir. Fazalari keskin farq qiladigan barcha yo'llar qo'shilgandan keyin hech narsa bermaydi. Ammo agar siz fazalari deyarli bir xil bo'lgan barcha yo'llar ketma-ketligini topa olgan bo'lsangiz, unda kichik hissalar qo'shiladi va kelish nuqtasida umumiy amplituda sezilarli qiymatga ega bo'ladi. Eng muhim yo'l - bu bir xil fazani beradigan ko'plab yaqin yo'llar mavjud.

Aynan shu narsa kvant mexanikasida sodir bo'ladi. To'liq kvant mexanikasi (relativistik bo'lmagan va e'tiborsiz elektron spin) quyidagicha ishlaydi: zarrachaning nuqtadan chiqib ketish ehtimoli 1 hozirda t 1, nuqtaga yetadi 2 hozirda t 2 , ehtimollik amplitudasining kvadratiga teng. Umumiy amplitudani barcha mumkin bo'lgan yo'llar uchun - har qanday kelish yo'li uchun amplitudalarning yig'indisi sifatida yozish mumkin. Har kim uchun x(t), Har qanday tasavvur qilinadigan traektoriya uchun sodir bo'lishi mumkin bo'lgan amplitudani hisoblash kerak. Keyin ularning barchasi katlanmalıdır. Muayyan yo'lning ehtimollik amplitudasi sifatida biz nimani olamiz? Bizning harakat integrali bizga individual yo'lning amplitudasi qanday bo'lishi kerakligini aytadi. Amplituda proportsionaldir e tS/s, Qayerda S - bu yo'lda harakat. Bu shuni anglatadiki, agar biz amplitudaning fazasini kompleks son sifatida ifodalasak, u holda faza burchagi teng bo'ladi. S/ h. Harakat S vaqt davomida energiya o'lchamiga ega va Plank doimiysi bir xil o'lchamga ega. Bu kvant mexanikasi qachon kerakligini aniqlaydigan doimiydir.

Va hammasi shunday ishlaydi. Barcha yo'llar uchun harakatga ruxsat bering S soniga nisbatan juda katta bo'ladi h. Ba'zi yo'l ma'lum bir amplituda qiymatiga olib kelsin. Qo'shni yo'lning bosqichi butunlay boshqacha bo'ladi, chunki ulkan bilan S hatto kichik o'zgarishlar S fazani keskin o'zgartirish (axir h juda oz). Bu shuni anglatadiki, qo'shni yo'llar qo'shilganda odatda o'z hissalarini o'chiradi. Va faqat bitta sohada bu to'g'ri emas - yo'l ham, uning qo'shnisi ham, birinchi taxminga ko'ra, bir xil fazaga ega (yoki, aniqrog'i, deyarli bir xil harakat, ichida o'zgarib turadi) h). Faqat shunday yo'llar hisobga olinadi. Va cheklovchi holatda, Plank doimiy bo'lganda h nolga moyil bo'lsa, to'g'ri kvant mexanik qonunlarini quyidagicha umumlashtirish mumkin: "Bu barcha ehtimollik amplitudalarini unuting. Zarracha aslida maxsus yo'l bo'ylab harakatlanadi - aynan qaysi yo'l bo'ylab S birinchi taxminga ko'ra o'zgarmaydi." Bu eng kam harakat tamoyili va kvant mexanikasi o'rtasidagi bog'liqlikdir. Kvant mexanikasini shu tarzda shakllantirish mumkinligini 1942 yilda men sizga aytib bergan o'sha o'qituvchining shogirdi janob Bader kashf etgan. [Kvant mexanikasi dastlab amplituda uchun differensial tenglama (Shrödinger) va ba'zi matritsalar matematikasi (Geyzenberg) yordamida tuzilgan.]

Endi men fizikadagi minimumning boshqa tamoyillari haqida gapirmoqchiman. Bunday ko'plab qiziqarli tamoyillar mavjud. Men ularning barchasini sanab o'tmayman, lekin yana bittasini aytaman. Keyinchalik, biz mukammal minimal printsipga ega bo'lgan bitta jismoniy hodisaga kelganimizda, men bu haqda sizga aytib beraman. Endi men maydon uchun differentsial tenglama yordamida elektrostatikani tasvirlash shart emasligini ko'rsatmoqchiman; Buning o'rniga ba'zi bir integral maksimal yoki minimumga ega bo'lishini talab qilish mumkin. Boshlash uchun, zaryad zichligi hamma joyda ma'lum bo'lgan holatni olaylik, lekin biz fazoning istalgan nuqtasida ph potentsialini topishimiz kerak. Javob bo'lishi kerakligini allaqachon bilasiz:

Xuddi shu narsani aytishning yana bir usuli - integralni baholash U*

bu hajm integralidir. U butun kosmosda olinadi. To'g'ri potentsial taqsimot bilan ph (x, y,z) bu ifoda minimal darajaga etadi.

Elektrostatikaga oid ushbu ikkala bayonot ham ekvivalent ekanligini ko'rsatishimiz mumkin. Faraz qilaylik, biz ixtiyoriy ph funksiyasini tanladik. Biz ko'rsatmoqchimizki, biz ph sifatida _ph potentsialining to'g'ri qiymatini plyus kichik f og'ishini qabul qilsak, u holda kichiklikning birinchi tartibiga o'zgarish bo'ladi. U* nolga teng bo'ladi. Shunday qilib, biz yozamiz

bu erda ph biz qidirayotgan narsa; lekin biz o'zgarish uchun nima bo'lishi kerakligini ko'rish uchun ph ni o'zgartiramiz U* kichiklikning birinchi tartibida bo'lib chiqdi. Birinchi muddatda U* yozishimiz kerak

Bu bilan birlashtirilishi kerak x, y va tomonidan z. Va bu erda xuddi shu hiyla o'zini taklif qiladi: qutulish uchun df/ dx, ustidan integratsiya qilamiz X qismlarda. Bu nisbatan qo'shimcha farqlashga olib keladiph X. Bu xuddi shu asosiy g'oya bo'lib, biz hosilalardan xalos bo'ldik t. Biz tenglikdan foydalanamiz

Integratsiyalashgan atama nolga teng, chunki biz f ni cheksizlikda nol deb olamiz. (Bu ē yo'qolib ketishga mos keladi t 1 Va t 2 . Shunday qilib, bizning printsipimiz quyidagicha aniqroq tuzilgan: U* o'ng uchun φ boshqalarga qaraganda kamroq ph(x, y,z), cheksizlikda bir xil qiymatlarga ega bo'lish.) Keyin biz bilan ham xuddi shunday qilamiz da va z bilan. Bizning integral DU* ga aylanadi

Bu o'zgarish har qanday ixtiyoriy f uchun nolga teng bo'lishi uchun f koeffitsienti nolga teng bo'lishi kerak. Ma'nosi,

Biz eski tenglamamizga qaytdik. Bu bizning "minimal" taklifimiz to'g'ri ekanligini anglatadi. Agar hisob-kitoblar biroz o'zgartirilsa, uni umumlashtirish mumkin. Keling, orqaga qaytaylik va hamma narsani komponent-komponentni tavsiflamasdan, qisman birlashaylik. Keling, quyidagi tenglikni yozishdan boshlaylik:

Chap tomonni farqlash orqali men uning o'ngga to'liq teng ekanligini ko'rsata olaman. Ushbu tenglama qismlar bo'yicha integratsiyani amalga oshirish uchun javob beradi. Bizning integralimizda DU* almashtiramiz Vph*Vf n va fV 2 ph+V*(fVph) va keyin buni hajm bo'yicha integrallang. Hajm bo'yicha integrallashdan keyin farqlanish atamasi sirt ustidagi integral bilan almashtiriladi:

Va biz butun fazoda integrallashganimiz sababli, bu integraldagi sirt cheksizlikda yotadi. Bu f=0 degan ma'noni anglatadi va biz bir xil natijaga erishamiz.

Endigina biz o'zimiz bo'lgan muammolarni qanday hal qilishni tushuna boshlaymiz biz bilmaymiz barcha to'lovlar qaerda joylashgan. Keling, zaryadlar qandaydir tarzda taqsimlangan o'tkazgichlarga ega bo'lsin. Agar barcha o'tkazgichlardagi potentsiallar sobit bo'lsa, bizning minimal printsipimiz hali ham qo'llanilishi mumkin. Integratsiya U* biz faqat barcha o'tkazgichlardan tashqarida joylashgan maydon bo'ylab chizamiz. Ammo biz o'tkazgichlarda (ph) ni o'zgartira olmasligimiz sababli, ularning yuzasida f = 0 va sirt integrali

faqat o'tkazgichlar orasidagi bo'shliqlarda bajarilishi kerak. Va biz, albatta, yana Puasson tenglamasini olamiz

Shuning uchun biz asl integralimiz ekanligini ko'rsatdik U* har biri sobit potentsialda bo'lgan o'tkazgichlar orasidagi bo'shliqda hisoblanganda ham minimal darajaga etadi [bu shuni anglatadiki, har bir sinov funktsiyasi ph (g, y,z) qachon belgilangan o'tkazgich potentsialiga teng bo'lishi kerak (x, y,z) - o'tkazgich sirtining nuqtalari]. Zaryadlar faqat o'tkazgichlarda joylashganida qiziqarli alohida holat mavjud. Keyin

va bizning minimal printsipimiz shuni aytadiki, har bir o'tkazgich o'zining oldindan belgilangan potentsialiga ega bo'lsa, ular orasidagi bo'shliqlardagi potentsiallar integral bo'lishi uchun o'rnatiladi. U* imkon qadar kichik bo'lib chiqadi. Bu qanday integral? Vph atamasi elektr maydonidir. Bu integral elektrostatik energiya ekanligini anglatadi. To'g'ri maydon potentsial gradient sifatida olingan barcha maydonlar ichida eng kam umumiy energiyaga ega bo'lgan yagona maydondir.

Men ushbu natijadan muayyan muammoni hal qilish uchun foydalanmoqchiman va bularning barchasi haqiqiy amaliy ahamiyatga ega ekanligini ko'rsatmoqchiman. Aytaylik, men silindrsimon kondansatör shaklida ikkita o'tkazgichni olaman.

Ichki o'tkazgich, aytaylik, teng potentsialga ega. V, va tashqi uchun - nolga teng. Ichki o'tkazgichning radiusi teng bo'lsin A, va tashqi - b. Endi biz ular orasidagi potentsiallarning taqsimlanishini taxmin qilishimiz mumkin har qanday. Ammo olsak to'g'ri ph qiymati va hisoblang
(e 0 /2) ∫ (Vph) 2 dV u holda tizimning energiyasi 1/2CV 2 bo'lishi kerak.

Shunday qilib, bizning printsipimizdan foydalanib, siz quvvatni hisoblashingiz mumkin BILAN. Agar biz noto'g'ri potentsial taqsimotni olsak va ushbu usul yordamida kondansatkichning sig'imini baholashga harakat qilsak, biz qattiq quvvat uchun haddan tashqari katta sig'im qiymatiga erishamiz. V. Haqiqiy qiymatiga to'liq mos kelmaydigan har qanday taxmin qilingan potentsial ph ham C ning noto'g'ri qiymatiga olib keladi, zarur bo'lganidan kattaroqdir. Ammo noto'g'ri tanlangan potentsial cp hali ham taxminan taxminiy bo'lsa, u holda sig'im BILAN yaxshi aniqlik bilan chiqadi, chunki C dagi xato ph dagi xatoga nisbatan ikkinchi tartibli qiymatdir.

Keling, silindrsimon kondansatkichning sig'imini bilmayman deb faraz qilaylik. Keyin uni tanib olish uchun men ushbu printsipdan foydalanishim mumkin. Men eng past qiymatga erishgunimcha ph ning turli funktsiyalarini potentsial sifatida sinab ko'raman BILAN. Aytaylik, men doimiy maydonga mos keladigan potentsialni tanladim. (Bilasizmi, albatta, bu yerdagi maydon aslida doimiy emas; u 1/r sifatida o'zgaradi) Agar maydon doimiy bo'lsa, bu potentsial chiziqli masofaga bog'liqligini anglatadi. Supero'tkazuvchilardagi kuchlanish talab qilinadigan darajada bo'lishi uchun ph funktsiyasi shaklga ega bo'lishi kerak

Bu funksiya ga teng V da r=a, r da nol =b, va ular orasida - ga teng doimiy qiyalik mavjud. V/(b—A). Shunday qilib, integralni aniqlash U*, siz shunchaki bu gradient kvadratini e o /2 ga ko'paytirishingiz va butun hajm bo'ylab integrallashingiz kerak. Keling, birlik uzunlikdagi silindr uchun ushbu hisobni amalga oshiramiz. Radiusdagi hajm elementi r 2pr ga teng. Integratsiyani amalga oshirar ekanman, mening birinchi sinovim quyidagi imkoniyatlarni beradi:

Shunday qilib, men sig'im uchun formulani olaman, bu noto'g'ri bo'lsa ham, qandaydir taxminiydir:

Albatta, bu to'g'ri javobdan farq qiladi C=2pi 0 /ln (b/a), lekin umuman olganda bu unchalik yomon emas. Keling, uni bir nechta qiymatlar uchun to'g'ri javob bilan solishtirishga harakat qilaylik b/a. Men hisoblagan raqamlar quyidagi jadvalda ko'rsatilgan.

Hatto qachon b/a=2(va bu doimiy va chiziqli maydonlar o'rtasida juda katta farqlarga olib keladi), men hali ham juda mos keladigan taxminni olaman. Javob, albatta, kutilganidek, biroz balandroq. Ammo katta tsilindrning ichiga yupqa sim qo'yilgan bo'lsa, unda hamma narsa ancha yomonroq ko'rinadi. Keyin maydon juda o'zgaradi va uni doimiy maydon bilan almashtirish yaxshi narsaga olib kelmaydi. b/a = 100 bo'lsa, biz javobni deyarli ikki baravar oshirib yuboramiz. Kichiklar uchun b/a vaziyat ancha yaxshi ko'rinadi. Qarama-qarshi chegarada, o'tkazgichlar orasidagi bo'shliq unchalik keng bo'lmaganda (aytaylik, b/a = 1,1 uchun) doimiy maydon juda yaxshi yaqinlik bo'lib chiqadi, u qiymatni beradi. BILAN foizning o'ndan bir qismigacha aniq.

Endi men sizga bu hisobni qanday yaxshilashni aytaman. (Tsilindr uchun javob, albatta, mashhur, lekin to'g'ri javobni bilmasligingiz mumkin bo'lgan boshqa noodatiy kondansatör shakllari uchun ham xuddi shu usul ishlaydi.) Keyingi qadam noma'lum haqiqiy potentsial ph uchun yaxshiroq yaqinlashuvni topishdir. Aytaylik, siz doimiy va ph ko'rsatkichini va hokazolarni sinab ko'rishingiz mumkin. Lekin haqiqiy ph ni bilmasangiz, eng yaxshi taxminiy qiymatga ega ekanligingizni qayerdan bilasiz? Javob: Hisoblang BILAN; qanchalik past bo'lsa, haqiqatga yaqinroq bo'ladi. Keling, bu fikrni sinab ko'raylik. Potensial chiziqli emas, aytaylik, r da kvadratik va elektr maydoni doimiy emas, balki chiziqli bo'lsin. Eng umumiy qachon ph=O ga aylanadigan kvadratik shakl r=b va ph=F da at r=a, bu .. mi:

bu yerda a doimiy son. Ushbu formula avvalgisiga qaraganda biroz murakkabroq. U kvadratik va chiziqli hadni o'z ichiga oladi. Undan dala olish juda oson. Bu oddiyga teng

Endi bu kvadratga aylantirilishi va hajm bo'yicha birlashtirilishi kerak. Lekin bir daqiqa kuting. a uchun nimani olishim kerak? Men f ni parabola deb olishim mumkin, ammo qaysi biri? Mana men nima qilaman: quvvatni hisoblang ixtiyoriy a. olaman

Bu biroz chalkash ko'rinadi, lekin maydon kvadratini birlashtirgandan keyin shunday bo'ladi. Endi men o'zim uchun tanlashim mumkin. Men haqiqat men hisoblamoqchi bo'lgan hamma narsadan pastroq ekanligini bilaman. A o'rniga nima qo'ysam ham, javob juda katta bo'ladi. Ammo men o'yinimni a bilan davom ettirsam va mumkin bo'lgan eng past qiymatga erishishga harakat qilsam BILAN, u holda bu eng past qiymat boshqa qiymatlarga qaraganda haqiqatga yaqinroq bo'ladi. Shuning uchun, men endi a ni tanlashim kerak, shuning uchun qiymat BILAN minimal darajaga yetdi. Oddiy differensial hisob-kitoblarga murojaat qiladigan bo'lsak, men minimal ekanligiga aminman BILAN a =— bo‘lganda bo‘ladi 2 b/(b+a). Ushbu qiymatni formulaga almashtirib, men eng kichik quvvatni olaman

Men bu formula nimani anglatishini tushundim BILAN turli qiymatlarda b/a. Men bu raqamlarni nomladim BILAN(kvadrat). Mana taqqoslanadigan jadval BILAN(kvadrat) bilan BILAN(to'g'ri).

Misol uchun, radius nisbati 2: 1 bo'lsa, men 1,444 ni olaman. Bu to'g'ri javobga juda yaxshi yaqinlik, 1.4423. Hatto katta bo'lsa ham Ya yaqinlashuv ancha yaxshi bo'lib qolmoqda - birinchi taxminiylikdan ancha yaxshi. Hatto b/a = 10: 1 bilan ham chidash mumkin bo'lib qoladi (faqatgina 10% ga oshirib yuborilgan): 1. Katta nomuvofiqlik faqat 100 nisbatda yuzaga keladi: 1. Men olaman BILAN 0,267 o‘rniga 0,346 ga teng. Boshqa tomondan, 1,5 radius nisbati uchun kelishuv juda yaxshi va uchun b/a=1,1 javob kutilgan 10.492070 oʻrniga 10.492065. Qaerda siz yaxshi javob kutsangiz, u juda yaxshi bo'lib chiqadi.

Men bu misollarning barchasini, birinchidan, minimal harakat tamoyilining nazariy ahamiyatini va umuman, minimalning barcha tamoyillarini ko'rsatish uchun, ikkinchidan, ularning amaliy foydaliligini ko'rsatish uchun keltirdim, lekin imkoniyatlarni hisoblash uchun umuman emas. Biz allaqachon borligini juda yaxshi bilamiz. Boshqa har qanday shakl uchun siz bir nechta noma'lum parametrlarga ega (masalan, a) taxminiy maydonni sinab ko'rishingiz va ularni minimal darajaga moslashingiz mumkin. Boshqa yo'l bilan hal qilib bo'lmaydigan muammolar bo'yicha yuqori raqamli natijalarga erishasiz.

Ular unga bo'ysunadilar va shuning uchun bu tamoyil zamonaviy fizikaning asosiy qoidalaridan biridir. Uning yordami bilan olingan harakat tenglamalari Eyler-Lagranj tenglamalari deyiladi.

Printsipning birinchi formulasi yili P. Maupertuis tomonidan berilgan bo'lib, uni optika va mexanikaga taalluqli deb hisoblab, uning universal tabiatiga darhol ishora qildi. Bu tamoyildan u yorug'likning aks etishi va sinishi qonunlarini chiqardi.

Hikoya

Maupertuis bu tamoyilga Olamning mukammalligi tabiatda ma'lum bir iqtisodni talab qiladi va har qanday foydasiz energiya sarfiga zid keladi, degan tuyg'udan kelib chiqqan. Tabiiy harakat shunday bo'lishi kerakki, ma'lum bir miqdor minimal bo'ladi. U qilish kerak bo'lgan narsa bu qiymatni topish edi, u buni davom ettirdi. Bu tizim ichidagi harakat davomiyligining (vaqtning) ikki baravar qiymatga mahsuloti edi, biz buni endi tizimning kinetik energiyasi deb ataymiz.

Eyler (in "Tabiatdagi g'oyalar", 1748) harakatning eng kam miqdori tamoyilini qabul qilib, harakatni "harakat" deb ataydi. Uning statikadagi ifodasi biz hozir potentsial energiya deb ataydigan narsaga to'g'ri keladi, shuning uchun uning statikada eng kam ta'sir ko'rsatishi muvozanat konfiguratsiyasi uchun minimal potentsial energiya shartiga ekvivalent bo'ladi.

Klassik mexanikada

Eng kam harakat tamoyili mexanikaning Lagranj va Gamilton formulalarining asosiy va standart asosi bo'lib xizmat qiladi.

Birinchidan, keling, bunday qurilishni ko'rib chiqaylik: Lagranj mexanikasi. Bir erkinlik darajasiga ega bo'lgan jismoniy tizim misolidan foydalanib, harakat (umumlashtirilgan) koordinatalarga (bir darajadagi erkinlik holatida - bitta koordinata) nisbatan funktsional ekanligini eslang, ya'ni u shunday ifodalanadi: Funktsiyaning har bir taxminiy versiyasi ma'lum bir raqam - harakat bilan bog'liq (shu ma'noda, biz funktsiya sifatida harakatni har qanday berilgan funktsiyaga aniq belgilangan sonni hisoblash imkonini beradigan qoida deb aytishimiz mumkin - bu ham deyiladi. harakat). Amal quyidagicha ko'rinadi:

umumiylashtirilgan koordinataga, uning vaqtga nisbatan birinchi hosilasiga, shuningdek, ehtimol, aniq vaqtga bog'liq bo'lgan tizimning Lagrangiani qayerda. Agar tizimning erkinlik darajasi ko'proq bo'lsa, u holda Lagrangian ko'proq umumiylashtirilgan koordinatalar va ularning vaqtga nisbatan birinchi hosilalariga bog'liq. Shunday qilib, harakat tananing traektoriyasiga qarab skalyar funktsionaldir.

Harakatning skalyar ekanligi uni har qanday umumlashtirilgan koordinatalarda yozishni osonlashtiradi, asosiysi, tizimning holati (konfiguratsiyasi) ular bilan bir ma'noda tavsiflanadi (masalan, Dekart koordinatalari o'rniga ular qutbli bo'lishi mumkin). koordinatalar, tizim nuqtalari orasidagi masofalar, burchaklar yoki ularning funktsiyalari va boshqalar. .d.).

Harakat, qanchalik "yovvoyi" va "g'ayritabiiy" bo'lishidan qat'i nazar, butunlay o'zboshimchalik bilan traektoriya uchun hisoblanishi mumkin. Biroq, klassik mexanikada, mumkin bo'lgan traektoriyalarning butun to'plami orasida, tananing haqiqatda ketadigan faqat bittasi bor. Statsionar harakat tamoyili tananing aslida qanday harakatlanishi haqidagi savolga aniq javob beradi:

Bu shuni anglatadiki, agar tizimning Lagrangiani berilgan bo'lsa, u holda variatsiyalar hisobi yordamida biz birinchi navbatda harakat tenglamalarini - Eyler-Lagranj tenglamalarini olish va keyin ularni yechish orqali tananing qanday harakat qilishini aniq aniqlashimiz mumkin. Bu nafaqat mexanika formulasini jiddiy umumlashtirishga, balki har bir aniq muammo uchun eng qulay koordinatalarni tanlashga imkon beradi, faqat Dekart bilan cheklanmaydi, bu eng oddiy va eng oson echilgan tenglamalarni olish uchun juda foydali bo'lishi mumkin.

bu sistemaning Gamilton funksiyasi qayerda; - (umumlashtirilgan) koordinatalar - konjugat (umumlashtirilgan) impulslar, ular birgalikda vaqtning har bir ma'lum momentida tizimning dinamik holatini tavsiflaydi va har biri vaqtning funktsiyasi bo'lib, shu bilan tizimning evolyutsiyasini (harakatini) tavsiflaydi. Bunda sistemaning harakat tenglamalarini Gamiltonning kanonik tenglamalari ko'rinishida olish uchun shu tarzda yozilgan harakatni hamma va uchun mustaqil ravishda o'zgartirish kerak bo'ladi.

Shuni ta'kidlash kerakki, agar muammoning shartlaridan printsipial ravishda harakat qonunini topish mumkin bo'lsa, u holda bu avtomatik ravishda Yo'q haqiqiy harakat vaqtida statsionar qiymat qabul qiluvchi funksionalni qurish mumkinligini bildiradi. Misol tariqasida elektromagnit maydonda elektr zaryadlari va monopollar - magnit zaryadlarning birgalikda harakatlanishini keltirish mumkin. Ularning harakat tenglamalarini statsionar harakat tamoyilidan kelib chiqib bo‘lmaydi. Xuddi shunday, ba'zi Gamilton tizimlarida bu printsipdan kelib chiqib bo'lmaydigan harakat tenglamalari mavjud.

Misollar

Arzimas misollar Eyler-Lagranj tenglamalari orqali ishlash printsipidan foydalanishni baholashga yordam beradi. Erkin zarracha (massa m va tezlik v) Evklid fazosida to'g'ri chiziq bo'ylab harakatlanadi. Eyler-Lagranj tenglamalaridan foydalanib, buni qutb koordinatalarida quyidagicha ko'rsatish mumkin. Potensial bo'lmasa, Lagrange funktsiyasi oddiygina kinetik energiyaga teng

ortogonal koordinatalar tizimida.

Qutb koordinatalarida kinetik energiya, demak, Lagranj funksiyasi bo'ladi

Tenglamalarning radial va burchakli komponentlari mos ravishda:

Bu ikki tenglamani yechish

Bu erda barcha traektoriyalar bo'yicha cheksiz ko'p funktsional integratsiyaning shartli belgisi mavjud x(t) va Plank doimiysi. Biz ta'kidlaymizki, printsipial jihatdan, eksponensialdagi harakat kvant mexanikasida evolyutsiya operatorini o'rganishda o'zi paydo bo'ladi (yoki paydo bo'lishi mumkin), ammo aniq klassik (kvant bo'lmagan) analogga ega bo'lgan tizimlar uchun u odatdagiga to'liq tengdir. klassik harakat.

Klassik chegaradagi ushbu ifodaning matematik tahlili - etarlicha katta, ya'ni xayoliy eksponentning juda tez tebranishlari uchun - bu integraldagi barcha mumkin bo'lgan traektoriyalarning mutlaq ko'pchiligi chegarada bir-birini bekor qilishini ko'rsatadi (rasmiy ravishda ). Deyarli har qanday yo'l uchun faza almashinuvi mutlaqo teskari bo'ladigan yo'l bor va ular nolga teng hissa qo'shadi. Faqat harakat ekstremal qiymatga yaqin bo'lgan traektoriyalar (ko'pchilik tizimlar uchun - minimal darajaga) kamaytirilmaydi. Bu murakkab o'zgaruvchining funktsiyalari nazariyasidan sof matematik fakt; Masalan, statsionar faza usuli unga asoslanadi.

Natijada, zarracha kvant mexanikasi qonunlariga to'liq mos ravishda barcha traektoriyalar bo'ylab bir vaqtning o'zida harakat qiladi, lekin normal sharoitda faqat statsionarga yaqin (ya'ni klassik) traektoriyalar kuzatilgan qiymatlarga hissa qo'shadi. Kvant mexanikasi yuqori energiyalar chegarasida klassik mexanikaga aylanganligi sababli, biz buni taxmin qilishimiz mumkin. harakatning statsionarligining klassik printsipining kvant mexanik hosilasi.

Kvant maydon nazariyasida

Kvant maydon nazariyasida statsionar harakat tamoyili ham muvaffaqiyatli qo'llaniladi. Bu yerdagi Lagranj zichligi tegishli kvant maydonlarining operatorlarini o'z ichiga oladi. Garchi bu erda (klassik chegara va qisman kvaziklassiklar bundan mustasno) harakatning statsionarligi printsipi haqida emas, balki Feynmanning ushbu maydonlarning konfiguratsiyasi yoki fazaviy fazosida traektoriyalar bo'ylab integratsiyasi haqida gapirish to'g'riroq bo'lsa-da. yuqorida aytib o'tilgan Lagrangian zichligi.

Qo'shimcha umumlashtirishlar

Kengroq ma'noda, harakat deganda konfiguratsiya maydonidan haqiqiy sonlar to'plamiga xaritalashni belgilaydigan funktsional tushuniladi va umuman olganda, u integral bo'lishi shart emas, chunki mahalliy bo'lmagan harakatlar printsipial jihatdan mumkin, hech bo'lmaganda. nazariy jihatdan. Bundan tashqari, konfiguratsiya maydoni funktsiya maydoni bo'lishi shart emas, chunki u kommutativ bo'lmagan geometriyaga ega bo'lishi mumkin.

Ular unga bo'ysunadilar va shuning uchun bu tamoyil zamonaviy fizikaning asosiy qoidalaridan biridir. Uning yordami bilan olingan harakat tenglamalari Eyler-Lagranj tenglamalari deyiladi.

Hikoya

Klassik mexanikada

Eng kam harakat tamoyili mexanikaning Lagranj va Gamilton formulalarining asosiy va standart asosi bo'lib xizmat qiladi.

Misollar

ortogonal koordinatalar tizimida.

Qutb koordinatalarida kinetik energiya, demak, Lagranj funksiyasi bo'ladi

Tenglamalarning radial va burchakli komponentlari mos ravishda:

Bu ikki tenglamani yechish

Kvant maydon nazariyasida

Qo'shimcha umumlashtirishlar

Dastlab Yakobi tomonidan aniq shakllantirilgan eng kam harakat printsipi Gamilton printsipiga o'xshaydi, ammo kamroq umumiy va isbotlash qiyinroq. Bu tamoyil faqat bog'lanishlar va kuch funktsiyasi vaqtga bog'liq bo'lmagan va shuning uchun tirik kuchning integrali mavjud bo'lgan hollarda qo'llaniladi.

Ushbu integral quyidagi shaklga ega:

Yuqorida aytilgan Gamilton printsipi integralning o'zgarishini bildiradi

haqiqiy harakatning boshqa cheksiz yaqin harakatga o'tishida nolga teng bo'lib, bu tizimni bir xil vaqt oralig'ida bir xil boshlang'ich holatidan bir xil yakuniy holatga o'tkazadi.

Yakobi printsipi, aksincha, vaqtga bog'liq bo'lmagan harakat xususiyatini ifodalaydi. Yakobi integralni ko'rib chiqadi

harakatni aniqlash. U o'rnatgan printsip shuni ko'rsatadiki, biz tizimning haqiqiy harakatini tizimni bir xil boshlang'ich holatdan bir xil yakuniy holatga olib keladigan boshqa cheksiz yaqin harakat bilan solishtirganda, bu integralning o'zgarishi nolga teng. Bu holda biz sarflangan vaqt davriga e'tibor bermaymiz, lekin biz (1) tenglamani, ya'ni haqiqiy harakatdagi kabi h doimiy qiymatining bir xil qiymatiga ega bo'lgan ishchi kuchi tenglamasini kuzatamiz.

Ekstremum uchun bu zaruriy shart, umuman olganda, minimal integralga (2) olib keladi, shuning uchun eng kichik harakat printsipi nomi. Minimal shart eng tabiiy bo'lib tuyuladi, chunki T ning qiymati asosan ijobiydir va shuning uchun integral (2) albatta minimal bo'lishi kerak. Minimalning mavjudligi, agar vaqt oralig'i etarlicha kichik bo'lsa, qat'iy isbotlanishi mumkin. Bu pozitsiyaning isbotini Darbouxning sirt nazariyasi bo'yicha mashhur kursida topish mumkin. Biroq, biz buni bu erda taqdim etmaymiz va shartni keltirib chiqarish bilan cheklanamiz

432. Eng kam harakat tamoyilining isboti.

Haqiqiy hisoblashda biz Gamilton teoremasini isbotlashda mavjud bo'lmagan bitta qiyinchilikka duch kelamiz. t o'zgaruvchisi endi o'zgaruvchanlikdan mustaqil bo'lib qolmaydi; shuning uchun q i va q ning o'zgarishlari. t ning (1) tenglamadan kelib chiqadigan murakkab munosabat bilan o'zgarishi bilan bog'liq. Ushbu qiyinchilikni engib o'tishning eng oddiy usuli - mustaqil o'zgaruvchini o'zgartirish, qiymatlari vaqtga bog'liq bo'lmagan doimiy chegaralar orasiga tushadigan birini tanlash. Chegaralari t dan mustaqil deb qabul qilingan yangi mustaqil o‘zgaruvchi bo‘lsin. Tizimni ko'chirishda parametrlar va t bu o'zgaruvchining funktsiyalari bo'ladi

q tub sonli harflar q parametrlarning vaqtga nisbatan hosilalarini bildirsin.

Bog'lanishlar, farazga ko'ra, vaqtga bog'liq emasligi sababli, Dekart koordinatalari x, y, z q ning vaqtni o'z ichiga olmaydi. Shuning uchun ularning hosilalari q ning chiziqli bir jinsli funktsiyalari va 7 q ning bir jinsli kvadrat shakli bo'ladi, koeffitsientlari q ning funksiyalari. Bizda ... bor

q ning vaqtga nisbatan hosilalarini farqlash uchun (q) qavslar yordamida q ning hosilalarini (q) belgilaymiz.

keyin bizda bo'ladi

va yangi mustaqil o'zgaruvchi A orqali ifodalangan integral (2) shaklni oladi;

Hosilni tirik kuch teoremasi yordamida yo'q qilish mumkin. Darhaqiqat, ishchi kuchining ajralmas qismi bo'ladi

Bu ifodani formulaga almashtirib, (2) integralni shaklga keltiramiz

Harakatni belgilovchi integral shu tariqa yakuniy shaklni oldi (3). Integratsiya funksiyasi kattaliklarning kvadrat shaklining kvadrat ildizidir

(3) integral ekstremallarining differensial tenglamalari aynan Lagranj tenglamalari ekanligini ko'rsatamiz. O'zgarishlarni hisoblashning umumiy formulalariga asoslangan ekstremal tenglamalar quyidagicha bo'ladi:

Keling, tenglamalarni 2 ga ko'paytiramiz va unda yo'qligini hisobga olib, qisman differentsiatsiya qilamiz, agar biz indeks yozmasak,

Bular mustaqil oʻzgaruvchida ifodalangan ekstremal tenglamalar.Endi vazifa mustaqil oʻzgaruvchiga qaytishdir.

D ikkinchi darajali bir jinsli funktsiya bo'lgani uchun va birinchi darajali bir hil funktsiya bo'lgani uchun bizda

Boshqa tomondan, tirik kuch teoremasi ekstremallar tenglamalarida hosila omillariga nisbatan qo'llanilishi mumkin, bu biz yuqorida ko'rganimizdek, almashtirishga olib keladi.

Barcha almashtirishlar natijasida ekstremallarning tenglamalari shaklga keltiriladi

Shunday qilib, biz Lagrange tenglamalariga keldik.

433. Harakatlanuvchi kuchlar bo'lmagan holat.

Agar harakatlantiruvchi kuchlar bo'lmasa, tirik kuch uchun tenglama mavjud va bizda mavjud

Integralning minimal bo'lishi sharti, bu holda -10 ning mos keladigan qiymati eng kichik bo'lishi kerak. Shunday qilib, harakatlantiruvchi kuchlar mavjud bo'lmaganda, tirik kuch bir xil qiymatni saqlaydigan barcha harakatlar orasida, eng qisqa vaqt ichida tizimni dastlabki holatidan yakuniy holatiga o'tkazadigan haqiqiy harakatdir.

Agar tizim statsionar yuzada harakatlanadigan bir nuqtaga qisqartirilsa, u holda bir xil tezlikda sodir bo'ladigan sirtdagi barcha harakatlar orasida haqiqiy harakat nuqtaning boshlang'ich holatidan oxirgi holatiga o'tishidagi harakatdir. eng qisqasi

vaqt oralig'i. Boshqacha qilib aytganda, nuqta sirtda o'zining ikkita pozitsiyasi orasidagi eng qisqa chiziqni, ya'ni geodezik chiziqni tasvirlaydi.

434. Eslatma.

Eng kam harakat printsipi tizimning bir necha erkinlik darajasiga ega ekanligini nazarda tutadi, chunki agar faqat bitta erkinlik darajasi mavjud bo'lsa, harakatni aniqlash uchun bitta tenglama etarli bo'ladi. Bu holda harakatni tirik kuch tenglamasi bilan to'liq aniqlash mumkin bo'lganligi sababli, haqiqiy harakat ushbu tenglamani qondiradigan yagona harakat bo'ladi va shuning uchun boshqa harakat bilan solishtirib bo'lmaydi.

ENG KAM SAMARALI PRINSİP

Mexanikaning o'zgaruvchan tamoyillaridan biri, Kromga ko'ra, ma'lum bir mexanik harakatlar sinfi uchun bir-biri bilan taqqoslangan. Jismoniy tizim uchun to'g'ri bo'lgan tizim hisoblanadi. hajmi, deyiladi harakat, eng kichik (aniqrog'i, statsionar) qiymatga ega. Odatda N. d. p. ikki shakldan birida ishlatiladi.

a) N. d. p. Gamilton shaklida - Ostrogradskiy tizimning bir konfiguratsiyadan ikkinchisiga (birinchisiga yaqin) barcha kinematik mumkin bo'lgan harakatlari orasida bir xil vaqt oralig'ida amalga oshirilgani tegishli ekanligini aniqlaydi. Gamilton harakati S eng kichik bo'ladi. Matematika. bu holda N. d.p.ning ifodasi quyidagi shaklga ega: dS = 0, bu erda d - to'liq bo'lmagan (izoxron) o'zgaruvchanlik belgisi (ya'ni, to'liq o'zgaruvchanlikdan farqli o'laroq, vaqt unda o'zgarmaydi).

b) Maupertuis ko'rinishida N. d. p. - Lagrange, tizimning umumiy energiyasining bir xil qiymatini saqlab qolgan holda amalga oshiriladigan tizimning bir konfiguratsiyadan unga yaqin bo'lgan boshqa konfiguratsiyaga kinematik jihatdan mumkin bo'lgan barcha harakatlari orasida haqiqiy ekanligini aniqlaydi. for - Shuning uchun, Lagrange harakati W eng kichik bo'ladi. Matematika. bu holda N. d.p.ning ifodasi DW = 0 koʻrinishga ega boʻlib, bu yerda D toʻliq oʻzgaruvchanlik belgisidir (Gamilton-Ostrogradskiy prinsipidan farqli oʻlaroq, bu yerda nafaqat koordinatalar va tezliklar, balki harakatlanish vaqti ham oʻzgaradi. tizim bir konfiguratsiyadan ikkinchisiga). N.d.p.v. Bunday holda, u faqat konservativ va, bundan tashqari, golonomik tizimlar uchun amal qiladi, birinchi holatda esa, konservativ bo'lmagan tamoyil umumiyroq va ayniqsa, konservativ bo'lmagan tizimlarga ham kengaytirilishi mumkin. N.D.P. mexanik harakat tenglamalarini tuzish uchun ishlatiladi. tizimlar va bu harakatlarning umumiy xususiyatlarini o'rganish. Tushunchalarni tegishli umumlashtirish bilan NDP uzluksiz muhit mexanikasida, elektrodinamikada va kvantda qo'llanmalarni topadi. mexanika va boshqalar.

- xuddi shunday...
Jismoniy ensiklopediya
- m-operator, minimizatsiya operatori, - boshqa funksiyalardan yangi funksiyalar qurish usuli, quyidagi...
Matematik entsiklopediya
- mexanikaning variatsion tamoyillaridan biri, unga ko'ra ma'lum bir mexanik harakatlar sinfi uchun bir-biri bilan taqqoslangan. tizim harakat minimal bo'lgan narsa amalga oshiriladi ...
Tabiatshunoslik. ensiklopedik lug'at
- mexanikaning eng muhim qonunlaridan biri, rus olimi M.V. Ostrogradskiy...
Rus entsiklopediyasi
Yuridik atamalar lug'ati
- bir qator davlatlarning konstitutsiyaviy huquqida xalqaro huquqning umume'tirof etilgan tamoyillari va normalari tegishli mamlakat huquqiy tizimining ajralmas qismi bo'lgan tamoyil...
Yurist ensiklopediyasi
- bir qator davlatlarning konstitutsiyaviy huquqida xalqaro huquqning umume'tirof etilgan normalari milliy huquq tizimining ajralmas qismi bo'lgan prinsip...
Katta yuridik lug'at
- portlovchi zaryad markazidan erkin sirtgacha bo'lgan eng qisqa masofa - nai-malkoto qarshiligidagi chiziq - křivka nejmenšího odporu - Line der geringsten Festigkeit - robbantás minimális ellenállási tengelyvonala - hamgiin baga...
Qurilish lug'ati
- agar deformatsiyalanuvchi jismning nuqtalarini turli yo'nalishlarda siljitish mumkin bo'lsa, bu jismning har bir nuqtasi eng kichik qarshilik yo'nalishi bo'yicha harakat qiladi...
Metallurgiya ensiklopedik lug'ati
- mavjud tovar-moddiy boyliklar odatda eng past narxda yoki eng past sotish bahosida baholanadigan qoida...
Biznes atamalari lug'ati
- bir qator davlatlarning konstitutsiyaviy huquqida - xalqaro huquqning umume'tirof etilgan tamoyillari va normalari tegishli davlat huquqiy tizimining ajralmas qismi bo'lgan va amal qiladigan printsip...
Iqtisodiyot va huquqning entsiklopedik lug'ati
- mexanikaning o'zgaruvchan tamoyillaridan biri, unga ko'ra mexanik tizimning harakatlarning ma'lum bir sinfi uchun bir-biri bilan solishtirganda, jismoniy miqdor, ...
- Gauss printsipi bilan bir xil ...
Buyuk Sovet Entsiklopediyasi
- mexanikaning variatsion tamoyillaridan biri; eng kam harakat tamoyili bilan bir xil ...
Buyuk Sovet Entsiklopediyasi
- mexanikaning variatsion tamoyillaridan biri, unga ko'ra mexanik tizimning harakatlarning ma'lum bir sinfi uchun bir-biri bilan solishtirganda, harakat minimal bo'lgan ...
Katta ensiklopedik lug'at
- Kitob Harakat qilishning eng oson usulini tanlang, to'siqlardan qoching, qiyinchiliklardan qoching ...
Rus adabiy tilining frazeologik lug'ati

Kitoblarda "ENG KIM QIYMAT PRINSIBI"

2.5.1. Qurilmaning ishlash printsipi

Ko'ngilochar elektronika kitobidan [Foydali sxemalarning noan'anaviy ensiklopediyasi] muallif Kashkarov Andrey Petrovich

2.5.1. Qurilmaning ishlash printsipi Qurilmaning ishlash printsipi oddiy. HL1 LED tomonidan chiqariladigan yorug'lik oqimi ob'ektdan aks ettirilganda va fotodetektorga tushganda, 2 mikrosxemada o'rnatilgan elektron blok - KR1401SA1 komparatori va KR1006VI1 taymerida hosil bo'ladi.

Terafimning ishlash printsipi

"Yashirin bilim" kitobidan. Agni Yoga nazariyasi va amaliyoti muallif Rerich Elena Ivanovna

Terafimning ishlash printsipi 24.02.39 Siz bilasizki, har qanday ob'ektning har bir tushunchasi va tasviri shu orqali bizni unga yaqinlashtiradi. Ma'lumki, ob'ektning ruhiy qatlamlari uning terafimiga o'tkazilishi mumkin. Uzoq olamlarning astral terafimi va

Eng kam harakat qonunini qo'llash uchun uchta shart

"Dipak Chopraning donoligi" kitobidan [Olamning 7 qonuniga rioya qilib, xohlagan narsangizga erishing] Tim Gudman tomonidan

Eng kam harakat qonunining ishlashi uchun uchta shart Keling, koinotdan energiyaning ijodiy oqimini hayotingizga jalb qilish uchun qanday shartlar kerakligini ko'rib chiqaylik - sevgi energiyasi va shuning uchun hayotingizda eng kam harakat qonuni ishlay boshlashi uchun. .

19-bob Eng kam ta'sir printsipi

6-kitobdan. Elektrodinamika muallif Feynman Richard Phillips

19-bob Ma'ruzadan so'ng qo'shilgan eng kam ta'sir printsipi Maktabda o'qib yurgan paytimda fizika o'qituvchimiz Beyder meni darsdan keyin chaqirib dedi: "Siz hamma narsadan juda charchaganga o'xshaysiz; bitta qiziqarli narsani tinglang

5. Eng kam harakat tamoyili

"Fizikadagi inqilob" kitobidan de Brogli Lui tomonidan

5. Eng kam harakat tamoyili Potensialli kuchlar sohasidagi moddiy nuqtaning dinamikasi uchun tenglamalarni umumiy ma'noda Gamilton printsipi yoki statsionar ta'sir printsipi deb ataladigan printsip asosida olish mumkin. Ushbu tamoyilga ko'ra, hammadan

Ishlash printsipi

"Locksmith's Guide of Locks" kitobidan Phillips Bill tomonidan

Ishlash printsipi Tsilindrni aylantirish qobiliyati pinlarning holatiga bog'liq bo'lib, ular o'z navbatida tortishish kuchi, kamonlarning harakati va kalitning kuchi bilan belgilanadi (yoki asosiy kalit; asosiy kalitlar haqida ma'lumot uchun 9-bobga qarang). . Kalit bo'lmasa, tortishish kuchi va buloqlar ichkariga kiradi

Statsionar harakat tamoyili

Muallifning Buyuk Sovet Entsiklopediyasi (ST) kitobidan TSB

Eng kam harakat tamoyili

TSB

Eng kam majburlash printsipi

Muallifning Buyuk Sovet Entsiklopediyasi (NA) kitobidan TSB

2.5.1. Ishlash printsipi

B90 elektr taqsimlash tarmoqlarida o'rni himoyasi kitobidan muallif Bulychev Aleksandr Vitaliyevich

2.5.1. Ishlash printsipi Ikki tomonlama quvvat manbai bo'lgan elektr tarmoqlarida va halqali tarmoqlarda an'anaviy oqim muhofazasi tanlab ishlay olmaydi. Masalan, ikkita quvvat manbai bo'lgan elektr tarmog'ida (2.15-rasm), bu erda har ikki tomonda kalitlar va himoya o'rnatiladi.

Ishlash printsipi

Turbo Suslik kitobidan. Qanday qilib o'zingizni xafa qilishni to'xtatish va yashashni boshlash kerak muallif Leushkin Dmitriy

"Buni qayta ishlash" harakat tamoyili, aslida, bir ibora bilan ongsizda bir qator jarayonlarni ishga tushiradigan o'ziga xos "makro" dir, uning maqsadi tanlangan aqliy materialni qayta ishlashdir. Ushbu ishlov beruvchining o'zi 7 xil modulni o'z ichiga oladi, ulardan ba'zilari

Eng kam harakat qonuniga amal qilishni qanday boshlash kerak: uchta zarur harakat

Jozef Merfi, Deyl Karnegi, Ekxart Tolle, Dipak Chopra, Barbara Sher, Nil Uolshdan "Kapitalni o'stirish bo'yicha qo'llanma" kitobidan muallif Stern Valentin

Eng kam harakat qonuniga amal qilishni qanday boshlash kerak: uchta zarur harakat Eng kam harakat qonuni ish boshlash uchun siz nafaqat yuqorida qayd etilgan uchta shartga rioya qilishingiz, balki uchta harakatni ham bajarishingiz kerak.Birinchi harakat: dunyoni xuddi shunday qabul qilishni boshlang. Qabul qilinadi

11. Fizika va eng kam harakatning aykidosi

muallif Mindell Arnold

11. Fizika va eng kichik effekt Aykido U esganda faqat shamol bor. Yomg'ir yog'sa, faqat yomg'ir yog'adi. Bulutlar o'tib ketganda, ular orasidan quyosh porlaydi. Agar siz o'zingizni tushunchaga ochsangiz, demak, siz tushuncha bilan birlashasiz. Va siz uni to'liq ishlatishingiz mumkin. Agar ochsangiz

Leybnitsning eng kam harakat printsipi "Vis Viva"

Shamanizm, fizika va daosizmda geopsixologiya kitobidan muallif Mindell Arnold

Leybnitsning eng kam harakat tamoyili "Vis Viva" Biz hammamiz Vilgelm Gotfrid Leybnitsga (1646–1716) eng kam harakat tamoyili uchun minnatdorchilik bildiramiz. Birinchi "zamonaviy" fizik va matematiklardan biri bo'lgan Leybnits Nyuton davrida - olimlar ochiqroq bo'lgan davrda yashagan.

Aykido - eng kam harakat tamoyilining timsolidir

Shamanizm, fizika va daosizmda geopsixologiya kitobidan muallif Mindell Arnold

Aykido - eng kam harakat tamoyilining timsolidir. Bizning psixologiyamiz va texnologiyamiz asosan eng kam harakat g'oyasiga juda yaqin bo'lgan kontseptsiyaga asoslangan. Biz doimo hayotimizni osonlashtirishga harakat qilamiz. Hozirgi kompyuterlar yetarlicha tez emas; Ular majbur