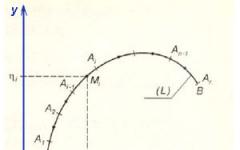
Определение: Пусть в каждой точки гладкой кривой L = AB в плоскости Oxy задана непрерывная функция двух переменных f(x,y) . Произвольно разобьем кривую L на n частей точками A = М 0 , М 1 , М 2 , ... М n = B. Затем на каждой из полученых частей \(\bar{{M}_{i-1}{M}_{i}}\) выберем любую точку \(\bar{{M}_{i}}\left(\bar{{x}_{i}},\bar{{y}_{i}}\right)\)и составим сумму $${S}_{n}=\sum_{i=1}^{n}f\left(\bar{{x}_{i}},\bar{{y}_{i}}\right)\Delta {l}_{i}$$ где \(\Delta{l}_{i}={M}_{i-1}{M}_{i}\) - дуга дуги \(\bar{{M}_{i-1}{M}_{i}}\). Полученная сумма называется интегральной суммой первого рода для функции f(x,y) , заданой на кривой L.
Обозначим через d наибольшую из длин дуг \(\bar{{M}_{i-1}{M}_{i}}\) (таким образом, d = \(max_{i}\Delta{l}_{i}\)). Если при d ? 0 существует предел интегральных сумм S n (не зависящих от способа разбиения кривой L на части и выбора точек \(\bar{{M}_{i}}\)), то этот предел называется криволинейным интегралом первого порядка от функции f(x,y) по кривой L и обозначается $$\int_{L}f(x,y)dl$$
Можно доказать, что если функция f(x,y) непрерывна, то криволинейный интеграл \(\int_{L}f(x,y)dl\) существует.
Свойства криволинейного интеграла 1 рода
Криволинейный интеграл первого рода обладает свойствами, аналогичными соответствующим свойства определеннного интеграла:
- аддитивность,
- линейность,
- оценка модуля,
- теорема о среднем.
Однако есть отличие: $$\int_{AB}f(x,y)dl=\int_{BA}f(x,y)dl$$ т.е. криволинейный интеграл первого рода не зависит от направления интегрирования.
Вычисление криволинейных интегралов первого рода
Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла. А именно:
- Если кривая L задана непрерывно дифференцируемой функцией y=y(x), x \(\in \) , то $${\int\limits_L {f\left({x,y} \right)dl} } = {\int\limits_a^b {f\left({x,y\left(x \right)} \right)\sqrt {1 + {{\left({y"\left(x \right)} \right)}^2}} dx} ;}$$ при этом выражение \(dl=\sqrt{{1 + {{\left({y"\left(x \right)} \right)}^2}}} dx \) называется дифференциалом длины дуги.
- Если крива L задана параметрически, т.е. в виде x=x(t), y=y(t), где x(t), y(t) - непрерывно дифференцируемые функции на некотором отрезке \(\left [ \alpha ,\beta \right ]\), то $$ {\int\limits_L {f\left({x,y} \right)dl} } = {\int\limits_\alpha ^\beta {f\left ({x\left(t \right),y\left(t \right)} \right)\sqrt {{{\left({x"\left(t \right)} \right)}^2} + {{\left({y"\left(t \right)} \right)}^2}} dt}} $$ Это равенство распространяется на случай пространственной кривой L, заданной параметрически: x=x(t), y=y(t), z=z(t), \(t\in \left [ \alpha ,\beta \right ]\). В этом случае, если f(x,y,z) - непрерывная функция вдоль кривой L, то $$ {\int\limits_L {f\left({x,y,z} \right)dl} } = {\int\limits_\alpha ^\beta {f\left [ {x\left(t \right),y\left(t \right),z\left(t \right)} \right ]\sqrt {{{\left({x"\left(t \right)} \right)}^2} + {{\left({y"\left(t \right)} \right)}^2} + {{\left({z"\left(t \right)} \right)}^2}} dt}} $$
- Если плоская кривая L задана полярным уравнением r=r(\(\varphi \)), \(\varphi \in\left [ \alpha ,\beta \right ] \), то $$ {\int\limits_L {f\left({x,y} \right)dl} } = {\int\limits_\alpha ^\beta {f\left({r\cos \varphi ,r\sin \varphi } \right)\sqrt {{r^2} + {{{r}"}^2}} d\varphi}} $$
Криволинейные интегралы 1 рода - примеры
Пример 1
Вычислить криволинейный интеграл первого рода
$$ \int_{L}\frac{x}{y}dl $$ где L дуга параболы y 2 =2x, заключенная между точками (2,2) и (8,4).
Решение: Найдем дифференциал дуги dl для кривой \(y=\sqrt{2x}\). Имеем:
\({y}"=\frac{1}{\sqrt{2x}} \) $$ dl=\sqrt{1+\left ({y}" \right)^{2}} dx= \sqrt{1+\left (\frac{1}{\sqrt{2x}} \right)^{2}} dx = \sqrt{1+ \frac{1}{2x}} dx $$ Следовательно данный интеграл равен: $$\int_{L}\frac{x}{y}dl=\int_{2}^{8}\frac{x}{\sqrt{2x}}\sqrt{1+\frac{1}{2x}}dx= \int_{2}^{8}\frac{x\sqrt{1+2x}}{2x}dx= $$ $$ \frac{1}{2}\int_{2}^{8}\sqrt{1+2x}dx = \frac{1}{2}.\frac{1}{3}\left (1+2x \right)^{\frac{3}{2}}|_{2}^{8}= \frac{1}{6}(17\sqrt{17}-5\sqrt{5}) $$
Пример 2
Вычислить криволинейный интеграл первого рода \(\int_{L}\sqrt{x^2+y^2}dl \), где L - окружность x 2 +y 2 =ax (a>0).
Решение: Введем полярные координаты: \(x = r\cos \varphi \), \(y=r\sin \varphi \). Тогда поскольку x 2 +y 2 =r 2 , уравнение окружности имеет вид: \(r^{2}=arcos\varphi \), то есть \(r=acos\varphi \), а дифференциал дуги $$ dl = \sqrt{r^2+{2}"^2}d\varphi = $$ $$ =\sqrt{a^2cos^2\varphi=a^2sin^2\varphi }d\varphi=ad\varphi $$.
При этом \(\varphi\in \left [- \frac{\pi }{2} ,\frac{\pi }{2} \right ] \). Следовательно, $$ \int_{L}\sqrt{x^2+y^2}dl=a\int_{-\frac{\pi }{2}}^{\frac{\pi }{2}}acos\varphi d\varphi =2a^2 $$
На случай, когда областью интегрирования является отрезок некоторой кривой, лежащий в плоскости. Общая запись криволинейного интеграла следующая:
где f (x , y ) - функция двух переменных, а L - кривая, по отрезку AB которой происходит интегрирование. Если подынтегральная функция равна единице, то криволинейный интеграл равен длине дуги AB .
Как всегда в интегральном исчислении, криволинейный интеграл понимается как предел интегральных сумм каких-то очень маленьких частей чего-то очень большого. Что же суммируется в случае криволинейных интегралов?
Пусть на плоскости расположен отрезок AB некоторой кривой L , а функция двух переменных f (x , y ) определена в точках кривой L . Пусть мы выполняем с этим отрезком кривой следующий алгоритм.
- Разделить кривую AB на части точками (рисунки ниже).
- В каждой части свободно выбрать точку M .
- Найти значение функции в выбранных точках.
- Значения функции умножить на
- длины частей в случае криволинейного интеграла первого рода ;
- проекции частей на ось координат в случае криволинейного интеграла второго рода .
- Найти сумму всех произведений.
- Найти предел найденной интегральной суммы при условии, что длина самой длинной части кривой стремится к нулю.
Если упомянутый предел существует, то этот предел интегральной суммы и называется криволинейным интегралом от функции f (x , y ) по кривой AB .
первого рода

Случай криволинейного интеграла
второго рода

Введём следующие ообозначения.
M i (ζ i ; η i ) - выбранная на каждом участке точка с координатами.
f i (ζ i ; η i ) - значение функции f (x , y ) в выбранной точке.
Δs i - длина части отрезка кривой (в случае криволинейного интеграла первого рода).
Δx i - проекция части отрезка кривой на ось Ox (в случае криволинейного интеграла второго рода).
d = maxΔs i - длина самой длинной части отрезка кривой.
Криволинейные интегралы первого рода
Исходя из вышеизложенного о пределе интегральных сумм, криволинейный интеграл первого рода записывается так:
![]() .
.
Криволинейный интеграл первого рода обладает всеми свойствами, которыми обладает определённый интеграл . Однако есть одно важное различие. У определённого интеграла при перемене местами пределов интегрирования знак меняется на противоположный:
В случае же криволинейного интеграла первого рода не имеет значения, какую из точек кривой AB (A или B ) считать началом отрезка, а какую концом, то есть
![]() .
.
Криволинейные интегралы второго рода
Исходя из изложенного о пределе интегральных сумм, криволинейный интеграл второго рода записывается так:
![]() .
.
В случае криволинейного интеграла второго рода при перемене местами начала и конца отрезка кривой знак интеграла меняется:
![]() .
.
При составлении интегральной суммы криволинейного интеграла второго рода значения функции f i (ζ i ; η i ) можно умножать также на проекции частей отрезка кривой на ось Oy . Тогда получим интеграл
![]() .
.
На практике обычно используется объединение криволинейных интегралов второго рода, то есть две функции f = P (x , y ) и f = Q (x , y ) и интегралы
![]() ,
,
а сумма этих интегралов
![]()
называется общим криволинейным интегралом второго рода .
Вычисление криволинейных интегралов первого рода
Вычисление криволинейных интегралов первого рода сводится к вычислению определённых интегралов. Рассмотрим два случая.
Пусть на плоскости задана кривая y
= y
(x
)
и отрезку кривой AB
соответствует изменение переменной x
от a
до b
.
Тогда в точках кривой подынтегральная функция f
(x
, y
) = f
(x
, y
(x
))
("игрек" должен быть выражен через "икс"),
а дифференциал дуги ![]() и
криволинейный интеграл можно вычислить по формуле
и
криволинейный интеграл можно вычислить по формуле
![]() .
.
Если интеграл проще интегрировать по y , то из уравнения кривой нужно выразить x = x (y ) ("икс" через "игрек"), где и интеграл вычисляем по формуле
![]() .
.
Пример 1.
где AB - отрезок прямой между точками A (1; −1) и B (2; 1) .
Решение. Составим уравнение прямой AB
, используя
формулу ![]() (уравнение прямой,
проходящей через две данные точки A
(x
1
; y
1
)
и
B
(x
2
; y
2
)
):
(уравнение прямой,
проходящей через две данные точки A
(x
1
; y
1
)
и
B
(x
2
; y
2
)
):
Из уравнения прямой выразим y через x :
Тогда и теперь можем вычислять интеграл, так как у нас остались одни "иксы":

Пусть в пространстве задана кривая

Тогда в точках кривой функцию нужно выразить через параметр
t
()
а дифференциал дуги ![]() ,
поэтому криволинейный интеграл можно вычислить по формуле
,
поэтому криволинейный интеграл можно вычислить по формуле

Аналогично, если на плоскости задана кривая
 ,
,
то криволинейный интеграл вычисляется по формуле
 .
.
Пример 2. Вычислить криволинейный интеграл
где L - часть линии окружности
находящаяся в первом октанте.
Решение. Данная кривая - четверть линии окружности, расположенная в плоскости z = 3 . Она соответствует значениям параметра . Так как
то дифференциал дуги

Подынтегральную функцию выразим через параметр t :
Теперь, когда у нас всё выражено через параметр t , можем свести вычисление данного криволинейного интеграла к определённому интегралу:

Вычисление криволинейных интегралов второго рода
Так же, как и в случае криволинейных интегралов первого рода, вычисление интегралов второго рода сводится к вычислению определённых интегралов.
Кривая дана в декартовых прямоугольных координатах
Пусть дана кривая на плоскости уравнением функции "игрек", выраженной через "икс": y = y (x ) и дуге кривой AB соответствует изменение x от a до b . Тогда в подынтегральную функцию подставим выражение "игрека" через "икс" и определим дифференциал этого выражения "игрека" по "иксу": . Теперь, когда всё выражено через "икс", криволинейный интеграл второго рода вычисляется как определённый интеграл:

Аналогично вычисляется криволинейный интеграл второго рода, когда кривая дана уравнением функции "икс", выраженной через "игрек": x = x (y ) , . В этом случае формула для вычисления интеграла следующая:

Пример 3. Вычислить криволинейный интеграл
![]() , если
, если
а) L - отрезок прямой OA , где О (0; 0) , A (1; −1) ;
б) L - дуга параболы y = x ² от О (0; 0) до A (1; −1) .
а) Вычислим криволинейный интеграл по отрезку прямой (на рисунке - синяя). Напишем уравнение прямой и выразим "игрек" через "икс":
![]() .
.
Получаем dy = dx . Решаем данный криволинейный интеграл:

б) если L - дуга параболы y = x ² , получим dy = 2xdx . Вычисляем интеграл:

В только что решённом примере получили в двух случаях один и тот же результат. И это не совпадение, а результат закономерности, так как данный интеграл удовлетворяет условиям следующей теоремы.
Теорема . Если функции P (x ,y ) , Q (x ,y ) и их частные производные , - непрерывные в области D функции и в точках этой области частные производные равны, то криволинейный интеграл не зависит от пути интегрирования по линии L , находящейся в области D .
Кривая дана в параметрической форме
Пусть в пространстве дана кривая
 .
.
а в подынтегральные функции подставим
выражения этих функций через параметр t . Получаем формулу для вычисления криволинейного интеграла:

Пример 4. Вычислить криволинейный интеграл
![]() ,
,
если L - часть эллипса
отвечающая условию y ≥ 0 .
Решение. Данная кривая - часть эллипса, находящаяся в плоскости z = 2 . Она соответствует значению параметра .
можем представить криволинейный интеграл в виде определённого интеграла и вычислить его:

Если дан криволинейный интеграл и L - замкнутая линия, то такой интеграл называется интегралом по замкнутому контуру и его проще вычислить по формуле Грина .
Больше примеров вычисления криволинейных интегралов
Пример 5. Вычислить криволинейный интеграл
где L - отрезок прямой между точками её пересечения с осями координат.
Решение. Определим точки пересечения прямой с осями координат. Подставив в уравнение прямой y = 0 , получим , . Подставив x = 0 , получим , . Таким образом, точка пересечения с осью Ox - A (2; 0) , с осью Oy - B (0; −3) .
Из уравнения прямой выразим y :
![]() .
.
,
![]() .
.
Теперь можем представить криволинейный интеграл в виде определённого интеграла и начать вычислять его:

В подынтегральном выражении выделяем множитель , выносим его за знак интеграла. В получившемся после этого подынтегральном выражении применяем подведение под знак дифференциала и окончательно получаем.
Вычисление объема удобнее вести в цилиндрических координатах. Уравнение окружности, ограничивающей областьD , конуса и параболоида
соответственно принимают вид ρ = 2, z = ρ , z = 6 − ρ 2 . С учетом того, что данное тело симметрично относительно плоскостей xOz и yOz . имеем
6− ρ 2 |
||||
V = 4 ∫ 2 dϕ ∫ ρ dρ ∫ dz = 4 ∫ 2 dϕ ∫ ρ z |
6 ρ − ρ 2 d ρ = |
|||
4 ∫ d ϕ∫ (6 ρ − ρ3 − ρ2 ) d ρ =
2 d ϕ = |
|||||||||||||||||
4 ∫ 2 (3 ρ 2 − |
∫ 2 d ϕ = |
32π |
|||||||||||||||
Если не учитывать симметрию, то |
|||||||||||||||||
6− ρ 2 |
32π |
||||||||||||||||
V = ∫ |
dϕ ∫ ρ dρ ∫ dz = |
||||||||||||||||
3. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Обобщим понятие определенного интеграла на случай, когда областью интегрирования является некоторая кривая. Интегралы такого рода называются криволинейными. Различают два типа криволинейных интегралов: криволинейные интегралы по длине дуги и криволинейные интегралы по координатам.
3.1. Определение криволинейного интеграла первого типа (по длине дуги). Пусть функция f (x, y) определена вдоль плоской кусочно-
гладкой1 кривой L , концами которой будут точки A и B . Разобьем кривую L произвольным образом на n частей точками M 0 = A , M 1 ,... M n = B . На
каждой из частичных дуг M i M i + 1 выберем произвольную точку (x i , y i ) и вычислим значения функции f (x, y) в каждой из этих точек. Сумма
1 Кривая называется гладкой, если в каждой ее точке существует касательная, непрерывно изменяющаяся вдоль кривой. Кусочногладкой кривой называется кривая, состоящая из конечного числа гладких кусков.
n− 1 |
|
σ n = ∑ f (x i , y i ) ∆ l i , |
i = 0
где∆ l i – длина частичной дуги M i M i + 1 , называется интегральной суммой
для функции f (x , y ) по кривой L . Обозначим наибольшую из длин |
|||
частичных дуг M i M i + 1 , i = |
|||
0 ,n − 1 черезλ , то есть λ = max ∆ l i . |
|||
0 ≤i ≤n −1 |
|||
Если существует конечный предел I интегральной суммы (3.1) |
|||
стремлении к нулю наибольшей из длин частичных дугM i M i + 1 , |
|||
зависящий ни от способа разбиения кривой L на частичные дуги, ни от |
|||
выбора точек (x i , y i ) , то этот предел называется криволинейным интегралом первого типа (криволинейным интегралом по длине дуги) от функции f (x , y ) по кривой L и обозначается символом ∫ f (x , y ) dl .
Таким образом, по определению |
||
n− 1 |
||
I = lim ∑ f (xi , yi ) ∆ li = ∫ f (x, y) dl. |
||
λ → 0 i = 0 |
||
Функция f (x , y ) называется в этом случае интегрируемой вдоль кривой L ,
кривая L = AB - контуром интегрирования, А – начальной, а В - конечной точками интегрирования, dl - элементом длины дуги.
Замечание 3.1. Если в (3.2) положить f (x , y ) ≡ 1 для (x , y ) L , то
получим выражение длины дуги L в виде криволинейного интеграла первого типа
l = ∫ dl.
Действительно, из определения криволинейного интеграла следует, |
||||
dl = lim n − 1 |
||||
∆l |
Lim l = l . |
|||
λ → 0 ∑ |
λ→ 0 |
|||
i = 0 |
||||
3.2. Основные свойства криволинейного интеграла первого типа |
||||
аналогичны свойствам определенного интеграла: |
||||
1 о . ∫ [ f1 (x, y) ± f2 (x, y) ] dl = ∫ f1 (x, y) dl ± ∫ f2 (x, y) dl. |
||||
2 о . ∫ cf (x , y ) dl = c ∫ f (x , y ) dl , где с - константа. |
||||
и L , не |
||||
3 о . Если контур интегрирования L разбит на две части L |
||||
имеющие общих внутренних точек, то

∫ f (x, y)dl = ∫ f (x, y)dl + ∫ f (x, y)dl.
4 о .Отметим особо, что величина криволинейного интеграла первого типа не зависит от направления интегрирования, так как в формировании интегральной суммы (3.1) участвуют значения функции f (x , y ) в
произвольных точках и длины частичных дуг ∆ l i , которые положительны,
независимо от того, какую точку кривой AB считать начальной, а какую – конечной, то есть
f (x, y) dl = ∫ f (x, y) dl . |
|||
3.3. Вычисление криволинейного интеграла первого типа |
|||
сводится к вычислению определенных интегралов. |
|||
x= x(t) |
|||
Пусть кривая L задана параметрическими уравнениями |
y= y(t) |
||
Пустьα и β – значения параметра t , соответствующие началу (точка А ) и |
|||||||||||||||||||||||||||||||||
концу (точка В ) |
[α , β ] |
||||||||||||||||||||||||||||||||
x (t ), y (t ) и |
производные |
x (t), y (t) |
Непрерывны, |
f (x , y ) - |
|||||||||||||||||||||||||||||
непрерывна вдоль кривой L . Из курса дифференциального исчисления |
|||||||||||||||||||||||||||||||||
функций одной переменной известно, что |
|||||||||||||||||||||||||||||||||
dl = (x (t)) |
+ (y (t )) |
||||||||||||||||||||||||||||||||
∫ f (x, y) dl = ∫ f (x(t), y(t)) |
|||||||||||||||||||||||||||||||||
(x (t ) |
+ (y (t )) |
||||||||||||||||||||||||||||||||
∫ x2 dl, |
|||||||||||||||||||||||||||||||||
Пример 3.1. |
Вычислить |
окружности |
|||||||||||||||||||||||||||||||
x= a cos t |
|||||||||||||||||||||||||||||||||
0 ≤ t ≤ |
|||||||||||||||||||||||||||||||||
y= a sin t |
|||||||||||||||||||||||||||||||||
Решение. Так как x (t ) = − a sin t , y (t ) = a cos t , то |
|||||||||||||||||||||||||||||||||
dl = |
(− a sin t) 2 + (a cos t) 2 dt = a2 sin 2 t + cos 2 tdt = adt |
||||||||||||||||||||||||||||||||
и по формуле (3.4) получаем |
|||||||||||||||||||||||||||||||||
Cos 2t )dt = |
sin 2t |
||||||||||||||||||||||||||||||||
∫ x2 dl = ∫ a2 cos 2 t adt = a |
3 ∫ |
||||||||||||||||||||||||||||||||
πa 3 |
|||||||||||||||||||||||||||||||||
sin π |
|||||||||||||||||||||||||||||||||

L задана |
уравнением |
y = y(x) , |
a ≤ x ≤ b |
y(x) |
||||||||||||||||
непрерывна вместе со своей производной y |
(x ) при a ≤ x ≤ b , то |
|||||||||||||||||||
dl = |
||||||||||||||||||||
1+ (y (x )) |
||||||||||||||||||||
и формула (3.4) принимает вид |
||||||||||||||||||||
∫ f (x, y) dl = ∫ f (x, y(x)) |
||||||||||||||||||||
(y (x )) |
||||||||||||||||||||
L задана |
x = x(y), c ≤ y ≤ d |
x (y ) |
||||||||||||||||||
уравнением |
||||||||||||||||||||
непрерывна вместе со своей производной x (y ) при c ≤ y ≤ d , то |
||||||||||||||||||||
dl = |
||||||||||||||||||||
1+ (x (y )) |
||||||||||||||||||||
и формула (3.4) принимает вид |
||||||||||||||||||||
∫ f (x, y) dl = ∫ f (x(y), y) |
||||||||||||||||||||
1 + (x (y )) |
||||||||||||||||||||
Пример 3.2. Вычислить ∫ ydl, где L – дуга параболы |
2 x от |
|||||||||||||||||||
точки А (0,0) до точки В (2,2). |
||||||||||||||||||||
Решение . Вычислим интеграл двумя способами, применяя |
||||||||||||||||||||
формулы (3.5) и(3.6) |
||||||||||||||||||||
1)Воспользуемся формулой (3.5). Так как |
||||||||||||||||||||
2x (y ≥ 0), y ′ |
||||||||||||||||||||
2 x = |
2 x , |
dl = |
1+ 2 x dx , |
|||||||||||||||||
3 / 2 2 |
||||||||||||||||||||
1 (5 |
3 2 − 1) . |
|||||||||||||||||||
∫ ydl = ∫ |
2 x + 1 dx = ∫ (2 x + 1) 1/ 2 dx = |
1 (2x + 1) |
||||||||||||||||||
2)Воспользуемся формулой (3.6). Так как |
||||||||||||||||||||
x = 2 , x |
Y, dl |
1 + y |
||||||||||||||||||
y 1 + y 2 dy = |
(1 + y |
/ 2 2 |
||||||
∫ ydl = ∫ |
||||||||
3 / 2 |
||||||||
1 3 (5 5 − 1).
Замечание 3.2. Аналогично рассмотренному, можно ввести понятие криволинейного интеграла первого типа от функции f (x , y , z ) по
пространственной кусочно-гладкой кривой L :

Если кривая L задана параметрическими уравнениями
α ≤ t ≤ β , то
dl = |
||||||||||||||||
(x (t )) |
(y (t )) |
(z (t )) |
||||||||||||||
∫ f (x, y, z) dl = |
||||||||||||||||
= ∫ |
dt . |
|||||||||||||||
f (x (t ), y (t ), z (t )) (x (t )) |
(y (t )) |
(z (t )) |
||||||||||||||
x= x(t) , y= y(t)
z= z(t)
Пример 3.3. Вычислить∫ (2 z − x 2 + y 2 ) dl , где L – дуга кривой
x= t cos t |
0 ≤ t ≤ 2 π. |
|
y = t sin t |
||
z = t |
||
x′ = cost − t sint, y′ = sint + t cost, z′ = 1 , |
||
dl = |
(cos t − t sin t)2 + (sin t + t cos t)2 + 1 dt = |
|
Cos2 t − 2 t sin t cos t + t2 sin2 t + sin2 t + 2 t sin t cos t + t2 cos2 t + 1 dt =
2 + t2 dt .
Теперь по формуле (3.7) имеем
∫ (2z − |
x2 + y2 ) dl = ∫ (2 t − |
t 2 cos 2 t + t 2 sin 2 t ) |
2 + t 2 dt = |
|||||||||||||||||||
T 2 ) |
||||||||||||||||||||||
= ∫ |
t 2 + t |
dt = |
4 π |
− 2 2 |
||||||||||||||||||
цилиндрической |
поверхности, |
|||||||||||||||||||||
которая составлена из перпендикуляров к |
||||||||||||||||||||||
плоскости xOy , |
восстановленных в точках |
|||||||||||||||||||||
(x , y ) |
L = AB |
и имеющих |
||||||||||||||||||||
представляет собой массу кривой L , имеющей переменную линейную плотность ρ (x , y )
линейная плотность которой меняется по закону ρ (x , y ) = 2 y .
Решение. Для вычисления массы дуги AB воспользуемся формулой (3.8). Дуга AB задана параметрически, поэтому для вычисления интеграла (3.8) применяем формулу (3.4). Так как
1+ t |
dt , |
|||||||||||||
x (t) = 1, y (t) = t , dl = |
||||||||||||||
3/ 2 1 |
||||||||||||||
1 (1+ t |
||||||||||||||
m = ∫ 2 ydl = ∫ |
1 2 + t2 dt = ∫ t 1 + t2 dt = |
|||||||||||||
(2 3 / 2 − |
1) = |
2 2 − 1. |
||||||||||||
3.4. Определение криволинейного интеграла второго типа (по |
||||||||||||||
координатам ). Пусть функция |
f (x , y ) определена вдоль плоской |
|||||||||||||
кусочно-гладкой кривойL , концами которой будут точки А и В . Опять |
||||||||||||||
произвольным |
разобьем |
кривую L |
||||||||||||
M 0 = A , M 1 ,... M n = B Так же выберем в пределах |
каждой частичной |
|||||||||||||
дуги M i M i + 1 |
произвольную точку |
(xi , yi ) |
и вычислим |
16.3.2.1. Определение криволинейного интеграла первого рода. Пусть в пространстве переменных x,y,z задана кусочно-гладкая кривая , на которой определена функция f (x ,y ,z ).Разобьём кривую точками на частей, на каждой из дуг выберем произвольную точку , найдём и длину дуги , и составим интегральную сумму . Если существует предел последовательности интегральных сумм при , не зависящий ни от способа разбиения кривой на дуги , ни от выбора точек , то функция f (x ,y ,z ) называется интегрируемой по кривой , а значение этого предела называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги от функции f (x ,y ,z ) по кривой , и обозначается (или ). Теорема существования. Если функция f (x ,y ,z ) непрерывна на кусочно-гладкой кривой , то она интегрируема по этой кривой. Случай замкнутой кривой. В этом случае в качестве начальной и конечной точки можно взять произвольную точку кривой. Замкнутую кривую в дальнейшем будем называть контуром и обозначать буквой С . То, что кривая, по которой вычисляется интеграл, замкнута, принято обозначать кружочком на знаке интеграла: . 16.3.2.2. Свойства криволинейного интеграла первого рода. Для этого интеграла имеют место все шесть свойств, справедливых для определённого, двойного, тройного интеграла, от линейности до теоремы о среднем . Сформулировать и доказать их самостоятельно . Однако для этого интеграла справедливо и седьмое, персональное свойство: Независимость криволинейного интеграла первого рода от направления прохождения кривой: . Доказательство. Интегральные суммы для интегралов, стоящих в правой и левой частях этого равенства, при любом разбиении кривой и выборе точек совпадают (всегда длина дуги ), поэтому равны их пределы при . 16.3.2.3. Вычисление криволинейного интеграла первого рода. Примеры. Пусть кривая задана параметрическими уравнениями , где - непрерывно дифференцируемые функции, и пусть точкам , которые задают разбиение кривой, соответствуют значения параметра , т.е. . Тогда (см. раздел 13.3. Вычисление длин кривых) . По теореме о среднем, существует точка такая, что . Выберем точки , получающиеся при этом значении параметра: . Тогда интегральная сумма для криволинейного интеграла будет равна интегральной сумме для определенного интеграла . Так как , то, переходя к пределу при в равенстве , получим Таким образом, вычисление криволинейного интеграла первого рода сводится к вычислению определённого интеграла по параметру. Если кривая задана параметрически, то этот переход не вызывает трудностей; если дано качественное словесное описание кривой, то основной трудностью может быть введение параметра на кривой. Ещё раз подчеркнём, что интегрирование всегда ведётся в сторону возрастания параметра. Примеры. 1. Вычислить , где - один виток спирали Здесь переход к определённому интегралу проблем не вызывает: находим , и . 2. Вычислить тот же интеграл по отрезку прямой, соединяющей точки и . Здесь прямого параметрического задания кривой нет, поэтому на АВ необходимо ввести параметр. Параметрические уравнения прямой имеют вид где - направляющий вектор, - точка прямой. В качестве точки берем точку , в качестве направляющего вектора - вектор : . Легко видеть, что точка соответствует значению , точка - значению , поэтому . 3. Найти, где - часть сечения цилиндра плоскостью z =x +1, лежащая в первом октанте. Решение: Параметрические уравнения окружности - направляющей цилиндра имеют вид x =2cosj, y =2sinj, и так как z=x +1, то z = 2cosj+1. Итак, поэтому 16.3.2.3.1. Вычисление криволинейного интеграла первого рода. Плоский случай. Если кривая лежит на какой-либо координатной плоскости, например, плоскости Оху , и задаётся функцией , то, рассматривая х как параметр, получаем следующую формулу для вычисления интеграла: . Аналогично, если кривая задаётся уравнением , то . Пример. Вычислить , где - четверть окружности , лежащая в четвёртом квадранте. Решение. 1. Рассматривая х как параметр, получаем , поэтому 2. Если за параметр взять переменную у , то и . 3. Естественно, можно взять обычные параметрические уравнения окружности : . Если кривая задана в полярных координатах , то , и . 1 рода. 1.1.1. Определение криволинейного интеграла 1 рода Пусть на плоскости Оxy задана кривая (L). Пусть для любой точки кривой (L) определена непрерывная функция f(x;y). Разобьем дугу АВ линии (L) точками А=P 0 , P 1 , P n = В на n произвольных дуг P i -1 P i с длинами (i = 1, 2, n ) (рис.27) Выберем на каждой дуге P i -1 P i произвольную точку M i (x i ; y i) , вычислим значение функции f(x;y) в точке M i . Составим интегральную сумму Пусть , где . λ→0 (n→∞ ), не зависящий ни от способа разбиения кривой (L )на элементарные части, ни от выбора точек M i криволинейным интегралом 1 рода от функции f(x;y) (криволинейным интегралом по длине дуги) и обозначают: Замечание . Аналогично вводиться определение криволинейного интеграла от функции f(x;y;z) по пространственной кривой (L). Физический смысл криволинейного интеграла 1 рода: Если (L)- плоская кривая с линейной плоскостью , то массу кривой находят по формуле: 1.1.2. Основные свойства криволинейного интеграла 1 рода: 3. Если путь интегрирования разбит на части такие что , и имеют единственную общую точку, то . 4. Криволинейный интеграл 1 рода не зависит от направления интегрирования: 5. , где - длина кривой. 1.1.3. Вычисление криволинейного интеграла 1 рода. Вычисление криволинейного интеграла сводят к вычислению определенного интеграла. 1. Пусть кривая (L) задана уравнением . Тогда То есть дифференциал дуги вычисляют по формуле . Пример Вычислить массу отрезка прямой от точки А(1;1) до точки В(2;4), если . Решение Уравнение прямой проходящей через две точки: . Тогда уравнение прямой (АВ ): , . Найдём производную . Тогда . = . 2. Пусть кривая (L) задана параметрически : . Тогда , то есть дифференциал дуги вычисляют по формуле . Для пространственного случая задания кривой: .Тогда То есть дифференциал дуги вычисляют по формуле . Пример Найти длину дуги кривой , . Решение Длину дуги найдём по формуле : . Для этого найдём дифференциал дуги . Найдём производные , , .Тогда и длина дуги: . 3. Пусть кривая (L) задана в полярной системе координат: . Тогда То есть дифференциал дуги вычислют по формуле . Пример Вычислить массу дуги линии , 0≤ ≤ , если . Решение Массу дуги найдём по формуле: Для этого найдёмдифференциал дуги . Найдём производную . 1.2. Криволинейный интеграл 2 рода 1.2.1. Определение криволинейного интеграла 2 рода Пусть на плоскости Оxy задана кривая (L) . Пусть на (L) задана непрерывная функция f (x;y). Разобьем дугу АВ линии (L) точками А = P 0 ,P 1 , P n = В в направлении от точки А к точке В на n произвольных дуг P i -1 P i с длинами (i = 1, 2, n ) (рис.28). Выберем на каждой дуге P i -1 P i произвольную точку M i (x i ; y i) , вычислим значение функции f(x;y) в точке M i . Составим интегральную сумму , где - длина проекции дуги P i -1 P i на ось Оx . Если направление движения вдоль проекции совпадает с положительным направлением оси Оx , то проекцию дуг считают положительной , иначе - отрицательной . Пусть , где . Если существует предел интегральной суммы при λ→0 (n→∞ ), не зависящий ни от способа разбиения кривой (L) на элементарные части, ни от выбора точек M i в каждой элементарной части, то этот предел называют криволинейным интегралом 2 рода от функции f(x;y) (криволинейным интегралом по координате х ) и обозначают: Замечание. Аналогично вводится криволинейный интеграл по координате у: Замечание. Если (L) - замкнутая кривая, то интеграл по ней обозначают Замечание. Если на (L ) задано сразу три функции и от этих функций существуют интегралы , , , то выражение: + + называют общим криволинейным интегралом 2 рода и записывают: 1.2.2. Основные свойства криволинейного интеграла 2 рода: 3. При изменении направления интегрирования криволинейный интеграл 2 рода изменяет свой знак . 4. Если путь интегрирования разбит на части такие что , и имеют единственную общую точку, то 5. Если кривая (L ) лежит в плоскости: Перпендикулярной оси Ох , то =0 ; Перпендикулярной оси Oy , то ; Перпендикулярной оси Oz , то =0. 6. Криволинейный интеграл 2 рода по замкнутой кривой не зависит от выбора начальной точки (зависит только от направления обхода кривой). 1.2.3. Физический смысл криволинейного интеграла 2 рода. Работа А силы при перемещении материальной точки единичной массы из точки М в точку N вдоль (MN ) равна: 1.2.4. Вычисление криволинейного интеграла 2 рода. Вычисление криволинейного интеграла 2 рода сводят к вычислению определенного интеграла. 1. Пусть кривая (L ) задана уравнением . Пример Вычислить, где (L )- ломаная OAB : O(0;0), A(0;2), B(2;4). Решение Так как (рис.29), то 1)Уравнение (OA) : , , 2) Уравнение прямой (AB ): . 2. Пусть кривая (L) задана параметрически: . Замечание. В пространственном случае: Пример Вычислить Где (АВ)- отрезок от А(0;0;1) до B(2;-2;3). Решение Найдём уравнение прямой (АВ ): Перейдём к параметрической записи уравнения прямой (АВ) . Тогда . Точке A(0;0;1) соответствует параметр t равный: следовательно, t=0. Точке B(2;-2;3) соответствует параметр t , равный: следовательно, t=1. При перемещении от А к В ,параметр t меняется от 0 до 1 . 1.3. Формула Грина . L ) в т. М(х;у;z) с осями Оx, Оy, Oz | ||||||||||