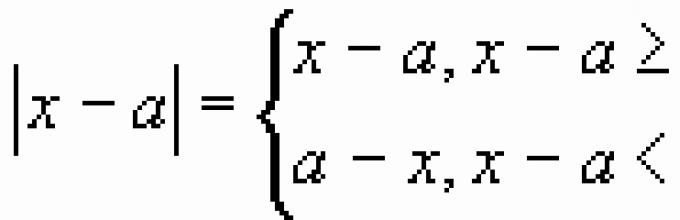ΣΕ τα τελευταία χρόνιαεπί εισαγωγικές εξετάσεις, στην τελική δοκιμή στο Έντυπο Ενιαίας Κρατικής Εξέτασηςπροσφέρονται εργασίες με παραμέτρους. Αυτές οι εργασίες καθιστούν δυνατή τη διάγνωση του επιπέδου των μαθηματικών και, το πιο σημαντικό, λογική σκέψητων αιτούντων, η ικανότητα διεξαγωγής ερευνητικών δραστηριοτήτων, καθώς και η απλή γνώση των κύριων ενοτήτων του σχολικού μαθήματος των μαθηματικών.
Η άποψη μιας παραμέτρου ως ίσης μεταβλητής αντικατοπτρίζεται σε γραφικές μεθόδους. Στην πραγματικότητα, εφόσον η παράμετρος είναι «ίση σε δικαιώματα» με τη μεταβλητή, τότε, φυσικά, μπορεί να «κατανεμηθεί» στη δική της άξονα συντεταγμένων. Έτσι, προκύπτει επίπεδο συντεταγμένων. Η άρνηση της παραδοσιακής επιλογής γραμμάτων για τον προσδιορισμό αξόνων καθορίζει μια από τις πιο αποτελεσματικές μεθόδους για την επίλυση προβλημάτων με παραμέτρους - «μέθοδος περιοχής». Μαζί με άλλες μεθόδους που χρησιμοποιούνται για την επίλυση προβλημάτων με παραμέτρους, εισάγω τους μαθητές μου σε γραφικές τεχνικές, δίνοντας προσοχή στο πώς να αναγνωρίζουν «τέτοια» προβλήματα και πώς φαίνεται η διαδικασία επίλυσης ενός προβλήματος.
Το περισσότερο γενικά σημάδια, το οποίο θα σας βοηθήσει να αναγνωρίσετε εργασίες κατάλληλες για την υπό εξέταση μέθοδο:
Πρόβλημα 1. "Για ποιες τιμές της παραμέτρου ισχύει η ανισότητα για όλες;"
Λύση. 1).
Ας επεκτείνουμε τις ενότητες λαμβάνοντας υπόψη το πρόσημο της υπομονάδας έκφρασης: 
2). Ας γράψουμε όλα τα συστήματα των ανισοτήτων που προκύπτουν:
ΕΝΑ) 
σι) 
V) 
ΣΟΛ) 
3). Ας δείξουμε το σύνολο των σημείων που ικανοποιούν κάθε σύστημα ανισοτήτων (Εικ. 1α).
4). Συνδυάζοντας όλες τις περιοχές που φαίνονται στο σχήμα με σκίαση, μπορείτε να δείτε ότι η ανισότητα δεν ικανοποιείται από τα σημεία που βρίσκονται μέσα στις παραβολές.
Το σχήμα δείχνει ότι για οποιαδήποτε τιμή της παραμέτρου είναι δυνατό να βρεθεί μια περιοχή όπου υπάρχουν σημεία των οποίων οι συντεταγμένες ικανοποιούν την αρχική ανισότητα. Η ανισότητα ισχύει για όλους αν . Απάντηση: στο .
Το εξεταζόμενο παράδειγμα είναι ένα "ανοιχτό πρόβλημα" - μπορείτε να εξετάσετε τη λύση σε μια ολόκληρη κατηγορία προβλημάτων χωρίς να αλλάξετε την έκφραση που εξετάζεται στο παράδειγμα 
, στην οποία έχουν ήδη ξεπεραστεί οι τεχνικές δυσκολίες δημιουργίας γραφημάτων.
Εργο. Για ποιες τιμές της παραμέτρου δεν έχει λύσεις η εξίσωση; Απάντηση: στο .
Εργο. Για ποιες τιμές της παραμέτρου έχει δύο λύσεις η εξίσωση; Καταγράψτε και τις δύο λύσεις που βρέθηκαν.
Απάντηση: τότε 
, 
;
Επειτα 
; , Επειτα 
, .
Εργο. Για ποιες τιμές της παραμέτρου η εξίσωση έχει μία ρίζα; Βρείτε αυτή τη ρίζα. Απάντηση: πότε πότε .
Εργο. Λύστε την ανισότητα.
(«Τα σημεία που βρίσκονται μέσα στις παραβολές λειτουργούν»).
, ; , δεν υπάρχουν λύσεις?
Εργασία 2. Βρείτε όλες τις τιμές της παραμέτρου ΕΝΑ, για καθένα από τα οποία το σύστημα των ανισοτήτων 
σχηματίζει ένα τμήμα μήκους 1 στην αριθμητική γραμμή.
Λύση. Ας ξαναγράψουμε το αρχικό σύστημα με αυτή τη μορφή 
Όλες οι λύσεις αυτού του συστήματος (ζεύγη της μορφής ) σχηματίζουν μια ορισμένη περιοχή που περιορίζεται από παραβολές 
Και 
(Φιγούρα 1).
Προφανώς, η λύση στο σύστημα των ανισοτήτων θα είναι ένα τμήμα μήκους 1 στο και στο . Απάντηση: ; .
Εργασία 3. Βρείτε όλες τις τιμές της παραμέτρου για τις οποίες το σύνολο των λύσεων της ανισότητας 
περιέχει τον αριθμό και επίσης περιέχει δύο τμήματα μήκους, τα οποία δεν έχουν κοινά σημεία.
Λύση. Σύμφωνα με την έννοια της ανισότητας. Ας ξαναγράψουμε την ανισότητα πολλαπλασιάζοντας και τις δύο πλευρές με (), παίρνουμε την ανισότητα:
, ,
(1)
Η ανισότητα (1) είναι ισοδύναμη με το συνδυασμό δύο συστημάτων:
(Εικ. 2).
Προφανώς, το διάστημα δεν μπορεί να περιέχει τμήμα μήκους . Αυτό σημαίνει ότι δύο μη τέμνοντα τμήματα μήκους περιέχονται στο διάστημα.Αυτό είναι δυνατό για , δηλ. στο . Απάντηση: .
Πρόβλημα 4. Βρείτε όλες τις τιμές της παραμέτρου, για καθεμία από τις οποίες υπάρχουν πολλές λύσεις στην ανισότητα 
περιέχει ένα τμήμα μήκους 4 και περιέχεται σε κάποιο τμήμα μήκους 7.
Λύση. Ας πραγματοποιήσουμε ισοδύναμους μετασχηματισμούς, λαμβάνοντας υπόψη ότι και .
, ,
; η τελευταία ανισότητα είναι ισοδύναμη με το συνδυασμό δύο συστημάτων:
Ας δείξουμε τις περιοχές που αντιστοιχούν σε αυτά τα συστήματα (Εικ. 3).
1) Όταν ένα σύνολο λύσεων είναι ένα διάστημα μήκους μικρότερο από 4. Όταν ένα σύνολο λύσεων είναι ένωση δύο διαστημάτων. Μόνο ένα διάστημα μπορεί να περιέχει ένα τμήμα μήκους 4. Αλλά τότε , και η ένωση δεν περιέχεται πλέον σε κανένα τμήμα μήκους 7. Αυτό σημαίνει ότι αυτά δεν ικανοποιούν την προϋπόθεση.
2) το σύνολο των λύσεων είναι ένα διάστημα. Περιέχει ένα τμήμα μήκους 4 μόνο εάν το μήκος του είναι μεγαλύτερο από 4, δηλ. στο . Περιέχεται σε ένα τμήμα μήκους 7 μόνο εάν το μήκος του δεν είναι μεγαλύτερο από 7, δηλαδή για , τότε . Απάντηση: .
Πρόβλημα 5. Βρείτε όλες τις τιμές της παραμέτρου για τις οποίες το σύνολο των λύσεων της ανισότητας 
περιέχει τον αριθμό 4 και περιέχει επίσης δύο ασύνδετα τμήματα μήκους 4 το καθένα.
Λύση. Σύμφωνα με τις προϋποθέσεις. Ας πολλαπλασιάσουμε και τις δύο πλευρές της ανισότητας επί (). Λαμβάνουμε μια ισοδύναμη ανισότητα στην οποία ομαδοποιούμε όλους τους όρους στην αριστερή πλευρά και τη μετατρέπουμε σε γινόμενο:
, ,
, 
.
Από την τελευταία ανισότητα προκύπτει:
1) 
2)
Ας δείξουμε τις περιοχές που αντιστοιχούν σε αυτά τα συστήματα (Εικ. 4).
α) Στο παίρνουμε ένα διάστημα που δεν περιέχει τον αριθμό 4. Στο παίρνουμε ένα διάστημα που επίσης δεν περιέχει τον αριθμό 4.
β) Στο παίρνουμε την ένωση δύο διαστημάτων. Τα μη τέμνοντα τμήματα μήκους 4 μπορούν να εντοπιστούν μόνο στο διάστημα . Αυτό είναι δυνατό μόνο εάν το μήκος του διαστήματος είναι μεγαλύτερο από 8, δηλαδή εάν . Με αυτά ικανοποιείται και μια άλλη προϋπόθεση: . Απάντηση: .
Πρόβλημα 6. Βρείτε όλες τις τιμές της παραμέτρου για τις οποίες το σύνολο των λύσεων της ανισότητας 
περιέχει κάποιο τμήμα μήκους 2, αλλά Δεν περιέχει
κανένα τμήμα μήκους 3.
Λύση. Σύμφωνα με το νόημα της ανάθεσης, πολλαπλασιάζουμε και τις δύο πλευρές της ανίσωσης με , ομαδοποιούμε όλους τους όρους στην αριστερή πλευρά της ανίσωσης και τη μετατρέπουμε σε γινόμενο:
, 
. Από την τελευταία ανισότητα προκύπτει:
1) 
2) 
Ας δείξουμε την περιοχή που αντιστοιχεί στο πρώτο σύστημα (Εικ. 5).
Προφανώς η συνθήκη του προβλήματος ικανοποιείται αν 
. Απάντηση: .
Πρόβλημα 7. Βρείτε όλες τις τιμές της παραμέτρου για τις οποίες το σύνολο λύσεων στην ανισότητα 1+ 
περιέχεται σε κάποιο τμήμα μήκους 1 και ταυτόχρονα περιέχει κάποιο τμήμα μήκους 0,5.
Λύση. 1). Ας υποδείξουμε το ODZ της μεταβλητής και της παραμέτρου: 
2). Ας ξαναγράψουμε την ανισότητα στη μορφή
, 
,
(1). Η ανισότητα (1) είναι ισοδύναμη με το συνδυασμό δύο συστημάτων:
1) 
2) 
Λαμβάνοντας υπόψη το ODZ, οι λύσεις συστήματος μοιάζουν με αυτό:
ΕΝΑ) 
σι) 
(Εικ. 6).
ΕΝΑ) 
σι)
Ας δείξουμε την περιοχή που αντιστοιχεί στο σύστημα α) (Εικ. 7).Απάντηση: .
Πρόβλημα 8. Έξι αριθμοί σχηματίζουν μια αυξανόμενη αριθμητική πρόοδο. Ο πρώτος, ο δεύτερος και ο τέταρτος όρος αυτής της εξέλιξης είναι λύσεις για την ανισότητα 
, και το υπόλοιπο
δεν είναι λύσεις σε αυτή την ανισότητα. Βρείτε το σύνολο όλων των πιθανών τιμών του πρώτου όρου τέτοιων προόδων.
Λύση. I. Βρείτε όλες τις λύσεις στην ανισότητα
ΕΝΑ). ODZ: 
, δηλ.
(λάβαμε υπόψη στη λύση ότι η συνάρτηση αυξάνεται κατά ).
σι). Ανισότητες στην υγεία των παιδιών 
ισοδυναμεί με ανισότητα 
, δηλ. 
, τι δίνει:
1). 
2). 
Προφανώς, η λύση στην ανισότητα εξυπηρετεί πολλές έννοιες 
.
II. Ας επεξηγήσουμε το δεύτερο μέρος του προβλήματος σχετικά με τους όρους μιας αυξανόμενης αριθμητικής προόδου με το σχήμα ( ρύζι. 8 , όπου είναι ο πρώτος όρος, είναι ο δεύτερος κ.λπ.). Σημειώσε ότι:
Ή έχουμε ένα σύστημα γραμμικών ανισοτήτων:
ας το λύσουμε γραφικά. Χτίζουμε ευθείες γραμμές και , καθώς και ευθείες γραμμές
Τότε, .. Ο πρώτος, ο δεύτερος και ο έκτος όρος αυτής της προόδου είναι λύσεις για την ανισότητα 
, και τα υπόλοιπα δεν είναι λύσεις σε αυτήν την ανισότητα. Βρείτε το σύνολο όλων των πιθανών τιμών της διαφοράς αυτής της προόδου.
Εξίσωση της φόρμας φά(Χ; ένα) = 0 καλείται εξίσωση με μεταβλητή Χκαι παράμετρος ΕΝΑ.
Επίλυση εξίσωσης με παράμετρο ΕΝΑ– αυτό σημαίνει για κάθε τιμή ΕΝΑβρείτε αξίες Χ, ικανοποιώντας αυτή την εξίσωση.
Παράδειγμα 1. Ω= 0
Παράδειγμα 2. Ω = ΕΝΑ
Παράδειγμα 3.
x + 2 = αχ
x – ah = -2
x(1 – a) = -2
Αν 1 - ΕΝΑ= 0, δηλ. ΕΝΑ= 1, λοιπόν Χ 0 = -2 χωρίς ρίζες
Αν 1 - ΕΝΑ 0, δηλ. ΕΝΑ 1, λοιπόν Χ =
Παράδειγμα 4.
(ΕΝΑ 2 – 1) Χ = 2ΕΝΑ 2 + ΕΝΑ – 3
(ΕΝΑ – 1)(ΕΝΑ + 1)Χ = 2(ΕΝΑ – 1)(ΕΝΑ – 1,5)
(ΕΝΑ – 1)(ΕΝΑ + 1)Χ = (1ΕΝΑ – 3)(ΕΝΑ – 1)
Αν ΕΝΑ= 1 και μετά 0 Χ = 0
Χ- όποιος πραγματικός αριθμός
Αν ΕΝΑ= -1, μετά 0 Χ = -2
χωρίς ρίζες
Αν ΕΝΑ 1, ΕΝΑ-1, λοιπόν Χ = (μόνη απόφαση).
Αυτό σημαίνει ότι για κάθε έγκυρη τιμή ΕΝΑταιριάζει με μία μόνο τιμή Χ.
Για παράδειγμα:
Αν ΕΝΑ= 5, λοιπόν Χ = = ;
Αν ΕΝΑ= 0, λοιπόν Χ= 3, κ.λπ.
Διδακτικό υλικό
1. Ω = Χ + 3
2. 4 + Ω = 3Χ – 1
3. ΕΝΑ = +
στο ΕΝΑ= 1 χωρίς ρίζες.
στο ΕΝΑ= 3 χωρίς ρίζες.
στο ΕΝΑ = 1 Χ– οποιοδήποτε πραγματικό αριθμό εκτός Χ = 1
στο ΕΝΑ = -1, ΕΝΑ= 0 χωρίς λύσεις.
στο ΕΝΑ = 0, ΕΝΑ= 2 χωρίς λύσεις.
στο ΕΝΑ = -3, ΕΝΑ = 0, 5, ΕΝΑ= -2 χωρίς λύσεις
στο ΕΝΑ = -Με, Με= 0 χωρίς λύσεις.
Τετραγωνικές εξισώσεις με παράμετρο
Παράδειγμα 1.Λύστε την εξίσωση
(ΕΝΑ – 1)Χ 2 = 2(2ΕΝΑ + 1)Χ + 4ΕΝΑ + 3 = 0
Στο ΕΝΑ = 1 6Χ + 7 = 0
Οταν ΕΝΑ 1, επισημαίνουμε εκείνες τις τιμές παραμέτρων στις οποίες ρεπάει στο μηδέν.
D = (2(2 ΕΝΑ + 1)) 2 – 4(ΕΝΑ – 1)(4ΕΝΑ + 30 = 16ΕΝΑ 2 + 16ΕΝΑ + 4 – 4(4ΕΝΑ 2 + 3ΕΝΑ – 4ΕΝΑ – 3) = 16ΕΝΑ 2 + 16ΕΝΑ + 4 – 16ΕΝΑ 2 + 4ΕΝΑ + 12 = 20ΕΝΑ + 16
20ΕΝΑ + 16 = 0
20ΕΝΑ = -16
Αν ΕΝΑ < -4/5, то ρε < 0, уравнение имеет действительный корень.
Αν ΕΝΑ> -4/5 και ΕΝΑ 1, λοιπόν ρε > 0,
Χ = 
Αν ΕΝΑ= 4/5, λοιπόν ρε = 0,
Παράδειγμα 2.Σε ποιες τιμές της παραμέτρου a κάνει η εξίσωση
x 2 + 2( ΕΝΑ + 1)Χ + 9ΕΝΑ– 5 = 0 έχει 2 διαφορετικές αρνητικές ρίζες;
D = 4( ΕΝΑ + 1) 2 – 4(9ΕΝΑ – 5) = 4ΕΝΑ 2 – 28ΕΝΑ + 24 = 4(ΕΝΑ – 1)(ΕΝΑ – 6)
4(ΕΝΑ – 1)(ΕΝΑ – 6) > 0
μέσω t. Vieta: Χ 1 + Χ 2 = -2(ΕΝΑ + 1)
Χ 1 Χ 2 = 9ΕΝΑ – 5
Κατά συνθήκη Χ 1 < 0, Χ 2 < 0 то –2(ΕΝΑ + 1) < 0 и 9ΕΝΑ – 5 > 0
| Τελικά | 4(ΕΝΑ – 1)(ΕΝΑ – 6) > 0 - 2(ΕΝΑ + 1) < 0 9ΕΝΑ – 5 > 0 |
ΕΝΑ < 1: а > 6 ΕΝΑ > - 1 ΕΝΑ > 5/9 |
 (Ρύζι. 1) < ένα < 1, либо ένα > 6 |
Παράδειγμα 3.Βρείτε τις τιμές ΕΝΑ, για το οποίο αυτή η εξίσωση έχει λύση.
x 2 – 2( ΕΝΑ – 1)Χ + 2ΕΝΑ + 1 = 0
D = 4( ΕΝΑ – 1) 2 – 4(2ΕΝΑ + 10 = 4ΕΝΑ 2 – 8ΕΝΑ + 4 – 8ΕΝΑ – 4 = 4ΕΝΑ 2 – 16ΕΝΑ
4ΕΝΑ 2 – 16 0
4ΕΝΑ(ΕΝΑ – 4) 0
ΕΝΑ( ΕΝΑ – 4)) 0
ΕΝΑ( ΕΝΑ – 4) = 0
a = 0 ή ΕΝΑ – 4 = 0
ΕΝΑ = 4
(Ρύζι. 2)
Απάντηση: ΕΝΑ 0 και ΕΝΑ 4
Διδακτικό υλικό
1. Σε ποια τιμή ΕΝΑτην εξίσωση Ω 2 – (ΕΝΑ + 1) Χ + 2ΕΝΑ– 1 = 0 έχει μία ρίζα;
2. Σε ποια τιμή ΕΝΑη εξίσωση ( ΕΝΑ + 2) Χ 2 + 2(ΕΝΑ + 2)Χ+ 2 = 0 έχει μία ρίζα;
3. Για ποιες τιμές του a είναι η εξίσωση ( ΕΝΑ 2 – 6ΕΝΑ + 8) Χ 2 + (ΕΝΑ 2 – 4) Χ + (10 – 3ΕΝΑ – ΕΝΑ 2) = 0 έχει περισσότερες από δύο ρίζες;
4. Για ποιες τιμές του a, η εξίσωση 2 Χ 2 + Χ – ΕΝΑ= 0 έχει τουλάχιστον μία κοινή ρίζα με την εξίσωση 2 Χ 2 – 7Χ + 6 = 0?
5. Για ποιες τιμές α η εξίσωση Χ 2 +Ω+ 1 = 0 και Χ 2 + Χ + ΕΝΑ= 0 έχουν τουλάχιστον μία κοινή ρίζα;
1. Πότε ΕΝΑ = - 1/7, ΕΝΑ = 0, ΕΝΑ = 1
2. Πότε ΕΝΑ = 0
3. Πότε ΕΝΑ = 2
4. Πότε ΕΝΑ = 10
5. Πότε ΕΝΑ = - 2
Εκθετικές εξισώσεις με παράμετρο
Παράδειγμα 1.Βρείτε όλες τις τιμές ΕΝΑ, για την οποία η εξίσωση
9 x – ( ΕΝΑ+ 2)*3 x-1/x +2 ΕΝΑ*3 -2/x = 0 (1) έχει ακριβώς δύο ρίζες.
Λύση. Πολλαπλασιάζοντας και τις δύο πλευρές της εξίσωσης (1) με 3 2/x, παίρνουμε την ισοδύναμη εξίσωση
3 2(x+1/x) – ( ΕΝΑ+ 2)*3 x+1/x + 2 ΕΝΑ = 0 (2)
Έστω 3 x+1/x = στο, τότε η εξίσωση (2) θα πάρει τη μορφή στο 2 – (ΕΝΑ + 2)στο + 2ΕΝΑ= 0, ή
(στο – 2)(στο – ΕΝΑ) = 0, από όπου στο 1 =2, στο 2 = ΕΝΑ.
Αν στο= 2, δηλ. 3 x+1/x = 2 τότε Χ + 1/Χ= log 3 2 , ή Χ 2 – Χημερολόγιο 3 2 + 1 = 0.
Αυτή η εξίσωση δεν έχει πραγματικές ρίζες, αφού ρε= ημερολόγιο 2 3 2 – 4< 0.
Αν στο = ΕΝΑ, δηλ. 3 x+1/x = ΕΝΑΟτι Χ + 1/Χ= ημερολόγιο 3 ΕΝΑ, ή Χ 2 –Χ log 3 a + 1 = 0. (3)
Η εξίσωση (3) έχει ακριβώς δύο ρίζες αν και μόνο αν
D = log 2 3 2 – 4 > 0, ή |log 3 a| > 2.
Εάν το αρχείο καταγραφής 3 a > 2, τότε ΕΝΑ> 9, και αν log 3 a< -2, то 0 < ΕΝΑ < 1/9.
Απάντηση: 0< ΕΝΑ < 1/9, ΕΝΑ > 9.
Παράδειγμα 2. Σε ποιες τιμές του a είναι η εξίσωση 2 2x – ( ΕΝΑ - 3) 2 x – 3 ΕΝΑ= 0 έχει λύσεις;
Ωστε να δεδομένη εξίσωσηέχει λύσεις, είναι απαραίτητο και επαρκές ότι η εξίσωση t 2 – (ένα - 3) t – 3ένα= 0 είχε τουλάχιστον μία θετική ρίζα. Ας βρούμε τις ρίζες χρησιμοποιώντας το θεώρημα του Vieta: Χ 1 = -3, Χ 2 = ΕΝΑ = >
Το α είναι θετικός αριθμός.
Απάντηση: πότε ΕΝΑ > 0
Διδακτικό υλικό
1. Βρείτε όλες τις τιμές του a για τις οποίες η εξίσωση
25 x – (2 ΕΝΑ+ 5)*5 x-1/x + 10 ΕΝΑ* 5 -2/x = 0 έχει ακριβώς 2 λύσεις.
2. Για ποιες τιμές του a είναι η εξίσωση
2 (a-1)x?+2(a+3)x+a = 1/4 έχει μία ρίζα;
3. Σε ποιες τιμές της παραμέτρου a κάνει η εξίσωση
4 x - (5 ΕΝΑ-3)2 x +4 ΕΝΑ 2 – 3ΕΝΑ= 0 έχει μοναδική λύση;
Λογαριθμικές εξισώσεις με παράμετρο
Παράδειγμα 1.Βρείτε όλες τις τιμές ΕΝΑ, για την οποία η εξίσωση
ημερολόγιο 4x (1 + Ω) = 1/2 (1)
έχει μια μοναδική λύση.
Λύση. Η εξίσωση (1) είναι ισοδύναμη με την εξίσωση
1 + Ω = 2Χστο Χ > 0, Χ 1/4 (3)
Χ = στο
αι 2 - στο + 1 = 0 (4)
Η προϋπόθεση (2) από (3) δεν ικανοποιείται.
Αφήνω ΕΝΑ 0, λοιπόν AU 2 – 2στο+ 1 = 0 έχει πραγματικές ρίζες αν και μόνο αν ρε = 4 – 4ΕΝΑ 0, δηλ. στο ΕΝΑ 1. Για να λύσουμε την ανισότητα (3), ας σχεδιάσουμε τις συναρτήσεις Galitsky M.L., Moshkovich M.M., Shvartsburd S.I.Σε βάθος μελέτη του μαθήματος της άλγεβρας και της μαθηματικής ανάλυσης. – Μ.: Εκπαίδευση, 1990
1. Συστήματα γραμμικές εξισώσειςμε παράμετρο
Τα συστήματα γραμμικών εξισώσεων με μια παράμετρο επιλύονται με τις ίδιες βασικές μεθόδους με τα συνηθισμένα συστήματα εξισώσεων: τη μέθοδο αντικατάστασης, τη μέθοδο προσθήκης εξισώσεων και τη γραφική μέθοδο. Γνώση γραφικής ερμηνείας γραμμικά συστήματακαθιστά εύκολη την απάντηση στην ερώτηση σχετικά με τον αριθμό των ριζών και την ύπαρξή τους.
Παράδειγμα 1.
Βρείτε όλες τις τιμές για την παράμετρο α για την οποία το σύστημα εξισώσεων δεν έχει λύσεις.
(x + (a 2 – 3)y = a,
(x + y = 2.
Λύση.
Ας δούμε διάφορους τρόπους επίλυσης αυτής της εργασίας.
1 τρόπος.Χρησιμοποιούμε την ιδιότητα: το σύστημα δεν έχει λύσεις εάν η αναλογία των συντελεστών μπροστά από το x είναι ίση με την αναλογία των συντελεστών μπροστά από το y, αλλά όχι ίση με την αναλογία ελεύθερα μέλη(a/a 1 = b/b 1 ≠ c/c 1). Τότε έχουμε:
1/1 = (a 2 – 3)/1 ≠ a/2 ή σύστημα
(και 2 – 3 = 1,
(α ≠ 2.
Από την πρώτη εξίσωση a 2 = 4, λοιπόν, λαμβάνοντας υπόψη την συνθήκη ότι a ≠ 2, παίρνουμε την απάντηση.
Απάντηση: a = -2.
Μέθοδος 2.Λύνουμε με τη μέθοδο αντικατάστασης.
(2 – y + (a 2 – 3)y = a,
(x = 2 – y,
((a 2 – 3)y – y = a – 2,
(x = 2 – y.
Αφού αφαιρέσουμε τον κοινό παράγοντα y από αγκύλες στην πρώτη εξίσωση, παίρνουμε:
((a 2 – 4)y = a – 2,
(x = 2 – y.
Το σύστημα δεν έχει λύσεις αν η πρώτη εξίσωση δεν έχει λύσεις, δηλαδή
(και 2 – 4 = 0,
(α – 2 ≠ 0.
Προφανώς, a = ±2, αλλά λαμβάνοντας υπόψη τη δεύτερη συνθήκη, η απάντηση έρχεται μόνο με αρνητική απάντηση.
Απάντηση: a = -2.
Παράδειγμα 2.
Βρείτε όλες τις τιμές για την παράμετρο α για την οποία το σύστημα εξισώσεων έχει άπειρο αριθμό λύσεων.
(8x + ay = 2,
(ax + 2y = 1.
Λύση.
Σύμφωνα με την ιδιότητα, αν η αναλογία των συντελεστών των x και y είναι η ίδια και ισούται με την αναλογία των ελεύθερων μελών του συστήματος, τότε έχει άπειρο αριθμό λύσεων (δηλ. a/a 1 = b/ b 1 = c/c 1). Επομένως 8/a = a/2 = 2/1. Λύνοντας καθεμία από τις εξισώσεις που προκύπτουν, βρίσκουμε ότι a = 4 είναι η απάντηση σε αυτό το παράδειγμα.
Απάντηση:α = 4.
2. Συστήματα ορθολογικές εξισώσειςμε παράμετρο
Παράδειγμα 3.
(3|x| + y = 2,
(|x| + 2y = α.
Λύση.
Ας πολλαπλασιάσουμε την πρώτη εξίσωση του συστήματος επί 2:
(6|x| + 2y = 4,
(|x| + 2y = α.
Αφαιρώντας τη δεύτερη εξίσωση από την πρώτη, παίρνουμε 5|x| = 4 – α. Αυτή η εξίσωση θα έχει μια μοναδική λύση για a = 4. Σε άλλες περιπτώσεις, αυτή η εξίσωση θα έχει δύο λύσεις (για ένα< 4) или ни одного (при а > 4).
Απάντηση: α = 4.
Παράδειγμα 4.
Βρείτε όλες τις τιμές της παραμέτρου a για τις οποίες το σύστημα εξισώσεων έχει μοναδική λύση.
(x + y = a,
(y – x 2 = 1.
Λύση.
Θα λύσουμε αυτό το σύστημα χρησιμοποιώντας τη γραφική μέθοδο. Έτσι, η γραφική παράσταση της δεύτερης εξίσωσης του συστήματος είναι μια παραβολή υψωμένη κατά μήκος του άξονα Oy προς τα πάνω κατά μία μονάδα τμήματος. Η πρώτη εξίσωση καθορίζει ένα σύνολο γραμμών παράλληλων στην ευθεία y = -x (εικόνα 1). Από το σχήμα φαίνεται καθαρά ότι το σύστημα έχει λύση αν η ευθεία y = -x + a εφάπτεται στην παραβολή σε σημείο με συντεταγμένες (-0,5, 1,25). Αντικαθιστώντας αυτές τις συντεταγμένες στην ευθεία εξίσωση αντί των x και y, βρίσκουμε την τιμή της παραμέτρου a: 
1,25 = 0,5 + a;
Απάντηση: α = 0,75.
Παράδειγμα 5.
Χρησιμοποιώντας τη μέθοδο αντικατάστασης, μάθετε σε ποια τιμή της παραμέτρου a, το σύστημα έχει μια μοναδική λύση.
(ax – y = a + 1,
(ax + (a + 2)y = 2.
Λύση.
Από την πρώτη εξίσωση εκφράζουμε το y και το αντικαθιστούμε στη δεύτερη:
(y = τσεκούρι – a – 1,
(ax + (a + 2)(ax – a – 1) = 2.
Ας ανάγουμε τη δεύτερη εξίσωση στη μορφή kx = b, η οποία θα έχει μοναδική λύση για k ≠ 0. Έχουμε:
ax + a 2 x – a 2 – a + 2ax – 2a – 2 = 2;
a 2 x + 3ax = 2 + a 2 + 3a + 2.
Αντιπροσωπεύουμε το τετράγωνο τριώνυμο a 2 + 3a + 2 ως γινόμενο αγκύλων
(a + 2)(a + 1), και στα αριστερά βγάζουμε x από αγκύλες:
(a 2 + 3a)x = 2 + (a + 2)(a + 1).
Προφανώς, ένα 2 + 3a δεν πρέπει να είναι ίσο με μηδέν, επομένως,
a 2 + 3a ≠ 0, a(a + 3) ≠ 0, που σημαίνει a ≠ 0 και ≠ -3.
Απάντηση: a ≠ 0; ≠ -3.
Παράδειγμα 6.
Χρησιμοποιώντας τη μέθοδο γραφικής λύσης, προσδιορίστε σε ποια τιμή της παραμέτρου a το σύστημα έχει μια μοναδική λύση.
(x 2 + y 2 = 9,
(y – |x| = α.
Λύση.
Με βάση την συνθήκη, κατασκευάζουμε έναν κύκλο με κέντρο στην αρχή και ακτίνα 3 μονάδων τμημάτων, αυτό ορίζεται από την πρώτη εξίσωση του συστήματος
x 2 + y 2 = 9. Η δεύτερη εξίσωση του συστήματος (y = |x| + a) είναι μια διακεκομμένη γραμμή. Με τη χρήση Σχήμα 2Εξετάζουμε όλες τις πιθανές περιπτώσεις θέσης του σε σχέση με τον κύκλο. Είναι εύκολο να δούμε ότι a = 3. 
Απάντηση: α = 3.
Έχετε ακόμα ερωτήσεις; Δεν ξέρετε πώς να λύσετε συστήματα εξισώσεων;
Για να λάβετε βοήθεια από έναν δάσκαλο, εγγραφείτε.
Το πρώτο μάθημα είναι δωρεάν!
ιστοσελίδα, όταν αντιγράφετε υλικό εν όλω ή εν μέρει, απαιτείται σύνδεσμος προς την πηγή.
