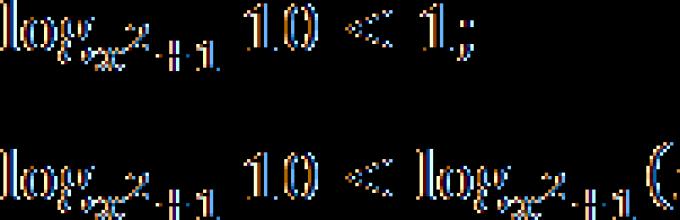Μεταξύ όλης της ποικιλίας των λογαριθμικών ανισώσεων, οι ανισώσεις με μεταβλητή βάση μελετώνται χωριστά. Επιλύονται χρησιμοποιώντας μια ειδική φόρμουλα, η οποία για κάποιο λόγο σπάνια διδάσκεται στο σχολείο:
log k (x) f (x) ∨ log k (x) g (x) ⇒ (f (x) − g (x)) (k (x) − 1) ∨ 0
Αντί για το πλαίσιο ελέγχου "∨", μπορείτε να βάλετε οποιοδήποτε σύμβολο ανισότητας: περισσότερο ή λιγότερο. Το κυριότερο είναι ότι και στις δύο ανισότητες τα ζώδια είναι ίδια.
Έτσι απαλλαγούμε από τους λογάριθμους και ανάγουμε το πρόβλημα σε μια ορθολογική ανισότητα. Το τελευταίο είναι πολύ πιο εύκολο να λυθεί, αλλά κατά την απόρριψη λογαρίθμων, μπορεί να εμφανιστούν επιπλέον ρίζες. Για να τα κόψετε, αρκεί να βρείτε το εύρος των αποδεκτών τιμών. Εάν έχετε ξεχάσει το ODZ ενός λογάριθμου, συνιστώ ανεπιφύλακτα να το επαναλάβετε - δείτε «Τι είναι ο λογάριθμος».
Όλα όσα σχετίζονται με το εύρος των αποδεκτών τιμών πρέπει να γράφονται και να επιλύονται ξεχωριστά:
f(x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1.
Αυτές οι τέσσερις ανισότητες αποτελούν ένα σύστημα και πρέπει να ικανοποιούνται ταυτόχρονα. Όταν βρεθεί το εύρος των αποδεκτών τιμών, το μόνο που μένει είναι να το τέμνουμε με τη λύση της ορθολογικής ανισότητας - και η απάντηση είναι έτοιμη.
Εργο. Λύστε την ανισότητα:
Αρχικά, ας γράψουμε το ODZ του λογαρίθμου:
Οι δύο πρώτες ανισότητες ικανοποιούνται αυτόματα, αλλά η τελευταία θα πρέπει να διαγραφεί. Εφόσον το τετράγωνο ενός αριθμού είναι μηδέν αν και μόνο αν ο ίδιος ο αριθμός είναι μηδέν, έχουμε:
x 2 + 1 ≠ 1;
x2 ≠ 0;
x ≠ 0.
Αποδεικνύεται ότι το ODZ του λογάριθμου είναι όλοι οι αριθμοί εκτός από το μηδέν: x ∈ (−∞ 0)∪(0; +∞). Τώρα λύνουμε την κύρια ανισότητα:

Κάνουμε τη μετάβαση από τη λογαριθμική ανισότητα στην ορθολογική. Η αρχική ανισότητα έχει πρόσημο "λιγότερο από", που σημαίνει ότι η προκύπτουσα ανισότητα πρέπει επίσης να έχει πρόσημο "λιγότερο από". Εχουμε:
(10 − (x 2 + 1)) · (x 2 + 1 − 1)< 0;
(9 − x 2) x 2< 0;
(3 − x) · (3 + x) · x 2< 0.
Τα μηδενικά αυτής της έκφρασης είναι: x = 3; x = −3; x = 0. Επιπλέον, το x = 0 είναι ρίζα της δεύτερης πολλαπλότητας, που σημαίνει ότι κατά τη διέλευση από αυτήν, το πρόσημο της συνάρτησης δεν αλλάζει. Εχουμε:

Παίρνουμε x ∈ (−∞ −3)∪(3; +∞). Αυτό το σύνολο περιέχεται πλήρως στο ODZ του λογαρίθμου, που σημαίνει ότι αυτή είναι η απάντηση.
Μετατροπή λογαριθμικών ανισώσεων
Συχνά η αρχική ανισότητα είναι διαφορετική από την παραπάνω. Αυτό μπορεί εύκολα να διορθωθεί χρησιμοποιώντας τους τυπικούς κανόνες για την εργασία με λογάριθμους - βλέπε «Βασικές ιδιότητες των λογαρίθμων». Και συγκεκριμένα:
- Οποιοσδήποτε αριθμός μπορεί να αναπαρασταθεί ως λογάριθμος με δεδομένη βάση.
- Το άθροισμα και η διαφορά λογαρίθμων με τις ίδιες βάσεις μπορούν να αντικατασταθούν από έναν λογάριθμο.
Ξεχωριστά, θα ήθελα να σας υπενθυμίσω το εύρος των αποδεκτών τιμών. Δεδομένου ότι μπορεί να υπάρχουν αρκετοί λογάριθμοι στην αρχική ανισότητα, απαιτείται να βρεθεί η VA καθενός από αυτούς. Ετσι, γενικό σχέδιοΟι λύσεις των λογαριθμικών ανισώσεων είναι οι εξής:
- Βρείτε το VA κάθε λογάριθμου που περιλαμβάνεται στην ανισότητα.
- Μειώστε την ανισότητα σε τυπική χρησιμοποιώντας τους τύπους για την πρόσθεση και την αφαίρεση λογαρίθμων.
- Λύστε την προκύπτουσα ανισότητα χρησιμοποιώντας το σχήμα που δίνεται παραπάνω.
Εργο. Λύστε την ανισότητα:
Ας βρούμε το πεδίο ορισμού (DO) του πρώτου λογάριθμου:
Λύνουμε με τη μέθοδο του διαστήματος. Βρίσκοντας τα μηδενικά του αριθμητή:
3x − 2 = 0;
x = 2/3.
Τότε - τα μηδενικά του παρονομαστή:
x − 1 = 0;
x = 1.
Σημειώνουμε μηδενικά και σημάδια στο βέλος συντεταγμένων:

Παίρνουμε x ∈ (−∞ 2/3)∪(1; +∞). Ο δεύτερος λογάριθμος θα έχει το ίδιο VA. Αν δεν το πιστεύετε, μπορείτε να το ελέγξετε. Τώρα μετασχηματίζουμε τον δεύτερο λογάριθμο έτσι ώστε η βάση να είναι δύο:
Όπως βλέπετε, τα τριάρια στη βάση και μπροστά από τον λογάριθμο έχουν μειωθεί. Πήραμε δύο λογάριθμους με την ίδια βάση. Ας τα αθροίσουμε:

log 2 (x − 1) 2< 2;
log 2 (x − 1) 2< log 2 2 2 .
Λάβαμε την τυπική λογαριθμική ανισότητα. Απαλλαγούμε από τους λογάριθμους χρησιμοποιώντας τον τύπο. Δεδομένου ότι η αρχική ανισότητα περιέχει ένα πρόσημο «λιγότερο από», το αποτέλεσμα ορθολογική έκφρασηπρέπει επίσης να είναι μικρότερο από το μηδέν. Εχουμε:
(f (x) − g (x)) (k (x) − 1)< 0;
((x − 1) 2 − 2 2)(2 − 1)< 0;
x 2 − 2x + 1 − 4< 0;
x 2 − 2x − 3< 0;
(x − 3)(x + 1)< 0;
x ∈ (−1; 3).
Έχουμε δύο σετ:
- ODZ: x ∈ (−∞ 2/3)∪(1; +∞);
- Απάντηση υποψηφίου: x ∈ (−1; 3).
Απομένει να διασταυρωθούν αυτά τα σύνολα - παίρνουμε την πραγματική απάντηση:

Μας ενδιαφέρει η τομή των συνόλων, επομένως επιλέγουμε διαστήματα που είναι σκιασμένα και στα δύο βέλη. Παίρνουμε x ∈ (−1; 2/3)∪(1; 3) - όλα τα σημεία είναι τρυπημένα.
Μαζί τους είναι μέσα σε λογάριθμους.
Παραδείγματα:
\(\log_3x≥\log_39\)
\(\log_3 ((x^2-3))< \log_3{(2x)}\)
\(\log_(x+1)((x^2+3x-7))>2\)
\(\lg^2((x+1))+10≤11 \lg((x+1))\)
Πώς να λύσετε λογαριθμικές ανισώσεις:
Θα πρέπει να προσπαθήσουμε να μειώσουμε οποιαδήποτε λογαριθμική ανισότητα στη μορφή \(\log_a(f(x)) ˅ \log_a(g(x))\) (το σύμβολο \(˅\) σημαίνει οποιοδήποτε από ). Αυτός ο τύπος σάς επιτρέπει να απαλλαγείτε από τους λογάριθμους και τις βάσεις τους, κάνοντας τη μετάβαση στην ανισότητα των παραστάσεων κάτω από τους λογάριθμους, δηλαδή στη μορφή \(f(x) ˅ g(x)\).
Αλλά όταν κάνετε αυτή τη μετάβαση, υπάρχει ένα πολύ σημαντική λεπτότητα:
\(-\) αν είναι αριθμός και είναι μεγαλύτερος από 1, το πρόσημο της ανισότητας παραμένει το ίδιο κατά τη μετάβαση,
\(-\) εάν η βάση είναι ένας αριθμός μεγαλύτερος από 0 αλλά μικρότερος από 1 (βρίσκεται μεταξύ μηδέν και ενός), τότε το πρόσημο της ανισότητας θα πρέπει να αλλάξει στο αντίθετο, δηλ.
|
\(\log_2((8-x))<1\) Λύση: |
\(\log\)\(_(0,5)\) \((2x-4)\)≥\(\log\)\(_(0,5)\) \(((x+ 1))\) Λύση: |
Πολύ σημαντικό!Σε οποιαδήποτε ανισότητα, η μετάβαση από τη μορφή \(\log_a(f(x)) ˅ \log_a(g(x))\) στη σύγκριση παραστάσεων κάτω από λογάριθμους μπορεί να γίνει μόνο εάν:
Παράδειγμα . Επίλυση ανισότητας: \(\log\)\(≤-1\)
Λύση:
|
\(\κούτσουρο\) \(_(\frac(1)(3))(\frac(3x-2)(2x-3))\)\(≤-1\) |
Ας γράψουμε το ODZ. |
|
ODZ: \(\frac(3x-2)(2x-3)\) \(>0\) |
|
|
\(\frac(3x-2-3(2x-3))(2x-3)\)\(≥\) \(0\) |
Ανοίγουμε τις αγκύλες και φέρνουμε . |
|
\(\frac(-3x+7)(2x-3)\) \(≥\) \(0\) |
Πολλαπλασιάζουμε την ανισότητα με \(-1\), χωρίς να ξεχνάμε να αντιστρέψουμε το πρόσημο σύγκρισης. |
|
\(\frac(3x-7)(2x-3)\) \(≤\) \(0\) |
|
|
\(\frac(3(x-\frac(7)(3)))(2(x-\frac(3)(2)))\)\(≤\) \(0\) |
Ας κατασκευάσουμε μια αριθμητική γραμμή και ας σημειώσουμε τα σημεία \(\frac(7)(3)\) και \(\frac(3)(2)\) πάνω της. Σημειώστε ότι η τελεία αφαιρείται από τον παρονομαστή, παρά το γεγονός ότι η ανισότητα δεν είναι αυστηρή. Γεγονός είναι ότι αυτό το σημείο δεν θα είναι λύση, αφού όταν αντικατασταθεί με ανισότητα θα μας οδηγήσει στη διαίρεση με το μηδέν. |
|
|
Τώρα σχεδιάζουμε το ODZ στον ίδιο αριθμητικό άξονα και γράφουμε ως απόκριση το διάστημα που εμπίπτει στο ODZ. |
|
|
Καταγράφουμε την τελική απάντηση. |
Παράδειγμα . Λύστε την ανισότητα: \(\log^2_3x-\log_3x-2>0\)
Λύση:
|
\(\log^2_3x-\log_3x-2>0\) |
Ας γράψουμε το ODZ. |
|
ODZ: \(x>0\) |
Πάμε στη λύση. |
|
Λύση: \(\log^2_3x-\log_3x-2>0\) |
Εδώ έχουμε μια τυπική τετραγωνική-λογαριθμική ανισότητα. Ας το κάνουμε. |
|
\(t=\log_3x\) |
Επεκτείνουμε την αριστερή πλευρά της ανισότητας σε . |
|
\(D=1+8=9\) |
|
|
Τώρα πρέπει να επιστρέψουμε στην αρχική μεταβλητή - x. Για να το κάνουμε αυτό, ας πάμε στο , το οποίο έχει την ίδια λύση, και ας κάνουμε την αντίστροφη αντικατάσταση. |
|
|
\(\αριστερά[ \αρχή(συγκεντρώθηκε) t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2\\\log_3x<-1 \end{gathered} \right.\) |
Μετασχηματισμός \(2=\log_39\), \(-1=\log_3\frac(1)(3)\). |
|
\(\left[ \begin(gathered) \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) |
Ας προχωρήσουμε στη σύγκριση επιχειρημάτων. Οι βάσεις των λογαρίθμων είναι μεγαλύτερες από \(1\), οπότε το πρόσημο των ανισώσεων δεν αλλάζει. |
|
\(\αριστερά[ \αρχή(συγκεντρώθηκε) x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) |
Ας συνδυάσουμε τη λύση της ανισότητας και το ODZ σε ένα σχήμα. |
|
|
Ας γράψουμε την απάντηση. |
Μεταξύ όλης της ποικιλίας των λογαριθμικών ανισώσεων, οι ανισώσεις με μεταβλητή βάση μελετώνται χωριστά. Επιλύονται χρησιμοποιώντας μια ειδική φόρμουλα, η οποία για κάποιο λόγο σπάνια διδάσκεται στο σχολείο. Η παρουσίαση παρουσιάζει λύσεις σε εργασίες Γ3 της Ενιαίας Κρατικής Εξέτασης - 2014 στα μαθηματικά.
Κατεβάστε:
Προεπισκόπηση:
Για να χρησιμοποιήσετε προεπισκοπήσεις παρουσίασης, δημιουργήστε έναν λογαριασμό Google και συνδεθείτε σε αυτόν: https://accounts.google.com
Λεζάντες διαφάνειας:
Επίλυση λογαριθμικών ανισώσεων που περιέχουν μια μεταβλητή στη βάση του λογαρίθμου: μέθοδοι, τεχνικές, ισοδύναμες μεταβάσεις, καθηγητής μαθηματικών, Γυμνάσιο Νο. 143 Knyazkina T. V.
Μεταξύ όλης της ποικιλίας των λογαριθμικών ανισώσεων, οι ανισώσεις με μεταβλητή βάση μελετώνται χωριστά. Επιλύονται χρησιμοποιώντας έναν ειδικό τύπο, ο οποίος για κάποιο λόγο σπάνια διδάσκεται στο σχολείο: log k (x) f (x) ∨ log k (x) g (x) ⇒ (f (x) − g (x)) ( k ( x) − 1) ∨ 0 Αντί για το πλαίσιο ελέγχου «∨», μπορείτε να βάλετε οποιοδήποτε πρόσημο ανισότητας: περισσότερο ή λιγότερο. Το κυριότερο είναι ότι και στις δύο ανισότητες τα ζώδια είναι ίδια. Έτσι απαλλαγούμε από τους λογάριθμους και ανάγουμε το πρόβλημα σε μια ορθολογική ανισότητα. Το τελευταίο είναι πολύ πιο εύκολο να λυθεί, αλλά κατά την απόρριψη λογαρίθμων, μπορεί να εμφανιστούν επιπλέον ρίζες. Για να τα κόψετε, αρκεί να βρείτε το εύρος των αποδεκτών τιμών. Μην ξεχνάτε το ODZ του λογαρίθμου! Όλα όσα σχετίζονται με το εύρος των αποδεκτών τιμών πρέπει να γράφονται και να επιλύονται ξεχωριστά: f (x) > 0; g(x) > 0; k(x) > 0; k(x) ≠ 1. Αυτές οι τέσσερις ανισότητες αποτελούν ένα σύστημα και πρέπει να ικανοποιούνται ταυτόχρονα. Όταν βρεθεί το εύρος των αποδεκτών τιμών, το μόνο που μένει είναι να το τέμνουμε με τη λύση της ορθολογικής ανισότητας - και η απάντηση είναι έτοιμη.
Λύστε την ανισότητα: Λύση Αρχικά, ας γράψουμε το OD του λογάριθμου Οι δύο πρώτες ανισώσεις ικανοποιούνται αυτόματα, αλλά η τελευταία θα πρέπει να γραφτεί. Εφόσον το τετράγωνο ενός αριθμού είναι ίσο με μηδέν αν και μόνο αν ο ίδιος ο αριθμός είναι ίσος με μηδέν, έχουμε: x 2 + 1 ≠ 1; x2 ≠ 0; x ≠ 0. Αποδεικνύεται ότι το ODZ ενός λογάριθμου είναι όλοι οι αριθμοί εκτός από το μηδέν: x ∈ (−∞0)∪(0 ;+ ∞). Τώρα λύνουμε την κύρια ανισότητα: Κάνουμε τη μετάβαση από τη λογαριθμική ανισότητα στην ορθολογική. Η αρχική ανισότητα έχει πρόσημο "λιγότερο από", που σημαίνει ότι η προκύπτουσα ανισότητα πρέπει επίσης να έχει πρόσημο "λιγότερο από".
Έχουμε: (10 − (x 2 + 1)) · (x 2 + 1 − 1)
Μετασχηματισμός λογαριθμικών ανισοτήτων Συχνά η αρχική ανισότητα είναι διαφορετική από την παραπάνω. Αυτό μπορεί εύκολα να διορθωθεί χρησιμοποιώντας τυπικούς κανόνες για την εργασία με λογάριθμους. Δηλαδή: Οποιοσδήποτε αριθμός μπορεί να αναπαρασταθεί ως λογάριθμος με δεδομένη βάση. Το άθροισμα και η διαφορά λογαρίθμων με τις ίδιες βάσεις μπορούν να αντικατασταθούν από έναν λογάριθμο. Ξεχωριστά, θα ήθελα να σας υπενθυμίσω το εύρος των αποδεκτών τιμών. Δεδομένου ότι μπορεί να υπάρχουν αρκετοί λογάριθμοι στην αρχική ανισότητα, απαιτείται να βρεθεί η VA καθενός από αυτούς. Έτσι, το γενικό σχήμα για την επίλυση λογαριθμικών ανισώσεων είναι το εξής: Βρείτε το VA κάθε λογάριθμου που περιλαμβάνεται στην ανισότητα. Μειώστε την ανισότητα σε τυπική χρησιμοποιώντας τους τύπους για την πρόσθεση και την αφαίρεση λογαρίθμων. Λύστε την προκύπτουσα ανισότητα χρησιμοποιώντας το σχήμα που δίνεται παραπάνω.
Λύστε την ανίσωση: Λύση Ας βρούμε το πεδίο ορισμού (DO) του πρώτου λογάριθμου: Λύστε με τη μέθοδο των διαστημάτων. Να βρείτε τα μηδενικά του αριθμητή: 3 x − 2 = 0; x = 2/3. Τότε - τα μηδενικά του παρονομαστή: x − 1 = 0; x = 1. Σημειώστε μηδενικά και σημάδια στη γραμμή συντεταγμένων:
Παίρνουμε x ∈ (−∞ 2/3) ∪ (1; +∞). Ο δεύτερος λογάριθμος θα έχει το ίδιο VA. Αν δεν το πιστεύετε, μπορείτε να το ελέγξετε. Τώρα ας μετατρέψουμε τον δεύτερο λογάριθμο έτσι ώστε να υπάρχει ένα δύο στη βάση: Όπως μπορείτε να δείτε, τα τρία στη βάση και μπροστά από τον λογάριθμο έχουν ακυρωθεί. Πήραμε δύο λογάριθμους με την ίδια βάση. Προσθέστε τα: log 2 (x − 1) 2
(f (x) − g (x)) (k (x) − 1)
Μας ενδιαφέρει η τομή των συνόλων, επομένως επιλέγουμε διαστήματα που είναι σκιασμένα και στα δύο βέλη. Παίρνουμε: x ∈ (−1; 2/3) ∪ (1; 3) - όλα τα σημεία είναι τρυπημένα. Απάντηση: x ∈ (−1; 2/3)∪(1; 3)
Επίλυση εργασιών USE-2014 τύπου C3
Λύστε το σύστημα των ανισοτήτων Λύση. ODZ: 1) 2)
Λύστε το σύστημα των ανισώσεων 3) -7 -3 - 5 x -1 + + + − − (συνέχεια)
Λύστε το σύστημα των ανισώσεων 4) Κοινή απόφαση: και -7 -3 - 5 x -1 -8 7 log 2 129 (συνέχεια)
Λύστε την ανίσωση (συνέχεια) -3 3 -1 + − + − x 17 + -3 3 -1 x 17 -4
Λύστε την ανισότητα Λύση. ODZ:
Λύστε την ανισότητα (συνέχεια)
Λύστε την ανισότητα Λύση. ODZ: -2 1 -1 + − + − x + 2 -2 1 -1 x 2
Πιστεύετε ότι υπάρχει ακόμα χρόνος μέχρι τις εξετάσεις του Ενιαίου Κράτους και θα έχετε χρόνο να προετοιμαστείτε; Ίσως είναι έτσι. Αλλά σε κάθε περίπτωση, όσο πιο νωρίς ξεκινήσει ένας μαθητής την προετοιμασία, τόσο πιο επιτυχημένα περνάει τις εξετάσεις. Σήμερα αποφασίσαμε να αφιερώσουμε ένα άρθρο στις λογαριθμικές ανισότητες. Αυτό είναι ένα από τα καθήκοντα, που σημαίνει μια ευκαιρία να λάβετε επιπλέον πίστωση.
Γνωρίζετε ήδη τι είναι λογάριθμος; Το ελπίζουμε πραγματικά. Αλλά ακόμα κι αν δεν έχετε απάντηση σε αυτή την ερώτηση, δεν είναι πρόβλημα. Η κατανόηση του τι είναι ένας λογάριθμος είναι πολύ απλή.

Γιατί 4; Πρέπει να αυξήσετε τον αριθμό 3 σε αυτήν την ισχύ για να πάρετε το 81. Μόλις κατανοήσετε την αρχή, μπορείτε να προχωρήσετε σε πιο περίπλοκους υπολογισμούς.
Πέρασες από ανισότητες πριν από μερικά χρόνια. Και από τότε τα συναντάς συνεχώς στα μαθηματικά. Εάν αντιμετωπίζετε προβλήματα με την επίλυση ανισοτήτων, ελέγξτε την κατάλληλη ενότητα.
Τώρα που εξοικειωθήκαμε με τις έννοιες μεμονωμένα, ας προχωρήσουμε στην εξέταση τους γενικά.
Η απλούστερη λογαριθμική ανισότητα.

Οι απλούστερες λογαριθμικές ανισότητες δεν περιορίζονται σε αυτό το παράδειγμα· υπάρχουν άλλες τρεις, μόνο με διαφορετικά πρόσημα. Γιατί είναι απαραίτητο αυτό; Για να κατανοήσουμε καλύτερα πώς να λύνουμε ανισώσεις με λογάριθμους. Ας δώσουμε τώρα ένα πιο εφαρμόσιμο παράδειγμα, ακόμα αρκετά απλό· θα αφήσουμε τις σύνθετες λογαριθμικές ανισότητες για αργότερα.

Πώς να το λύσετε αυτό; Όλα ξεκινούν με το ODZ. Αξίζει να μάθετε περισσότερα για αυτό εάν θέλετε να λύνετε πάντα εύκολα οποιαδήποτε ανισότητα.
Τι είναι το ODZ; ODZ για λογαριθμικές ανισώσεις
Η συντομογραφία σημαίνει το εύρος των αποδεκτών τιμών. Συχνά εμφανίζεται σε εργασίες για την Ενιαία Κρατική Εξέταση. αυτή η διατύπωση. Το ODZ θα σας είναι χρήσιμο όχι μόνο στην περίπτωση των λογαριθμικών ανισοτήτων.
Κοιτάξτε ξανά το παραπάνω παράδειγμα. Θα εξετάσουμε το ODZ με βάση αυτό, έτσι ώστε να κατανοήσετε την αρχή, και η επίλυση λογαριθμικών ανισοτήτων δεν εγείρει ερωτήματα. Από τον ορισμό του λογάριθμου προκύπτει ότι το 2x+4 πρέπει να είναι μεγαλύτερο από το μηδέν. Στην περίπτωσή μας αυτό σημαίνει το εξής.

Αυτός ο αριθμός, εξ ορισμού, πρέπει να είναι θετικός. Λύστε την ανισότητα που παρουσιάζεται παραπάνω. Αυτό μπορεί να γίνει ακόμη και προφορικά· εδώ είναι σαφές ότι το X δεν μπορεί να είναι μικρότερο από 2. Η λύση στην ανισότητα θα είναι ο ορισμός του εύρους των αποδεκτών τιμών.
Τώρα ας προχωρήσουμε στην επίλυση της απλούστερης λογαριθμικής ανισότητας.

Απορρίπτουμε τους ίδιους τους λογάριθμους και από τις δύο πλευρές της ανισότητας. Τι μας μένει ως αποτέλεσμα; Απλή ανισότητα.

Δεν είναι δύσκολο να λυθεί. Το X πρέπει να είναι μεγαλύτερο από -0,5. Τώρα συνδυάζουμε τις δύο λαμβανόμενες τιμές σε ένα σύστημα. Ετσι,

Αυτό θα είναι το εύρος των αποδεκτών τιμών για την υπό εξέταση λογαριθμική ανισότητα.
Γιατί χρειαζόμαστε καθόλου το ODZ; Αυτή είναι μια ευκαιρία να εξαλειφθούν λανθασμένες και αδύνατες απαντήσεις. Εάν η απάντηση δεν είναι εντός του εύρους των αποδεκτών τιμών, τότε η απάντηση απλά δεν έχει νόημα. Αυτό αξίζει να το θυμόμαστε για πολύ καιρό, αφού στις εξετάσεις του Ενιαίου Κράτους υπάρχει συχνά ανάγκη αναζήτησης για ODZ και δεν αφορά μόνο λογαριθμικές ανισότητες.
Αλγόριθμος επίλυσης λογαριθμικής ανισότητας
Η λύση αποτελείται από πολλά στάδια. Αρχικά, πρέπει να βρείτε το εύρος των αποδεκτών τιμών. Θα υπάρχουν δύο έννοιες στο ODZ, το συζητήσαμε παραπάνω. Στη συνέχεια, πρέπει να λύσετε την ίδια την ανισότητα. Οι μέθοδοι επίλυσης είναι οι εξής:
- μέθοδος αντικατάστασης πολλαπλασιαστή.
- αποσύνθεση;
- μέθοδος εξορθολογισμού.
Ανάλογα με την κατάσταση, αξίζει να χρησιμοποιήσετε μία από τις παραπάνω μεθόδους. Ας περάσουμε κατευθείαν στη λύση. Ας αποκαλύψουμε την πιο δημοφιλή μέθοδο, η οποία είναι κατάλληλη για την επίλυση εργασιών Ενοποιημένης Κρατικής Εξέτασης σε όλες σχεδόν τις περιπτώσεις. Στη συνέχεια θα δούμε τη μέθοδο αποσύνθεσης. Μπορεί να βοηθήσει αν συναντήσετε μια ιδιαίτερα δύσκολη ανισότητα. Λοιπόν, ένας αλγόριθμος για την επίλυση λογαριθμικής ανισότητας.
Παραδείγματα λύσεων :

Δεν είναι τυχαίο που πήραμε ακριβώς αυτήν την ανισότητα! Δώστε προσοχή στη βάση. Θυμηθείτε: εάν είναι μεγαλύτερο από ένα, το πρόσημο παραμένει το ίδιο όταν βρίσκετε το εύρος των αποδεκτών τιμών. Διαφορετικά, πρέπει να αλλάξετε το πρόσημο της ανισότητας.
Ως αποτέλεσμα, παίρνουμε την ανισότητα:

Τώρα μειώνουμε την αριστερή πλευρά στη μορφή της εξίσωσης ίση με το μηδέν. Αντί για το σύμβολο «λιγότερο από» βάζουμε «ίσον» και λύνουμε την εξίσωση. Έτσι, θα βρούμε το ODZ. Ελπίζουμε ότι με μια λύση σε αυτό απλή εξίσωσηδεν θα εχεις κανενα προβλημα. Οι απαντήσεις είναι -4 και -2. Δεν είναι μόνο αυτό. Πρέπει να εμφανίσετε αυτά τα σημεία στο γράφημα, τοποθετώντας τα «+» και «-». Τι πρέπει να γίνει για αυτό; Αντικαταστήστε τους αριθμούς από τα διαστήματα στην παράσταση. Όπου οι τιμές είναι θετικές, βάζουμε «+».
Απάντηση: Το x δεν μπορεί να είναι μεγαλύτερο από -4 και μικρότερο από -2.
Βρήκαμε το εύρος των αποδεκτών τιμών μόνο για την αριστερή πλευρά· τώρα πρέπει να βρούμε το εύρος των αποδεκτών τιμών για τη δεξιά πλευρά. Αυτό είναι πολύ πιο εύκολο. Απάντηση: -2. Τέμνουμε και τις δύο περιοχές που προκύπτουν.
Και μόλις τώρα αρχίζουμε να αντιμετωπίζουμε την ίδια την ανισότητα.

Ας το απλοποιήσουμε όσο το δυνατόν περισσότερο για να το λύσουμε πιο εύκολα.

Χρησιμοποιούμε ξανά τη μέθοδο του διαστήματος στη λύση. Ας παραλείψουμε τους υπολογισμούς· όλα είναι ήδη ξεκάθαρα με αυτό από το προηγούμενο παράδειγμα. Απάντηση.

Αλλά αυτή η μέθοδος είναι κατάλληλη εάν η λογαριθμική ανισότητα έχει τις ίδιες βάσεις.
Η επίλυση λογαριθμικών εξισώσεων και ανισώσεων με διαφορετικές βάσεις απαιτεί αρχική αναγωγή στην ίδια βάση. Στη συνέχεια, χρησιμοποιήστε τη μέθοδο που περιγράφεται παραπάνω. Αλλά υπάρχουν περισσότερα δύσκολη υπόθεση. Ας εξετάσουμε ένα από τα πιο πολύπλοκα είδηλογαριθμικές ανισότητες.
Λογαριθμικές ανισώσεις με μεταβλητή βάση
Πώς να λύσετε ανισότητες με τέτοια χαρακτηριστικά; Ναι, και τέτοια άτομα μπορούν να βρεθούν στην Ενιαία Κρατική Εξέταση. Η επίλυση των ανισοτήτων με τον ακόλουθο τρόπο θα σας ωφελήσει επίσης εκπαιδευτική διαδικασία. Ας δούμε αναλυτικά το θέμα. Ας απορρίψουμε τη θεωρία και ας πάμε κατευθείαν στην πράξη. Για να λύσετε λογαριθμικές ανισότητες, αρκεί να εξοικειωθείτε με το παράδειγμα μία φορά.

Για να λυθεί μια λογαριθμική ανισότητα της μορφής που παρουσιάζεται, είναι απαραίτητο να αναχθεί η δεξιά πλευρά σε έναν λογάριθμο με την ίδια βάση. Η αρχή μοιάζει με ισοδύναμες μεταβάσεις. Ως αποτέλεσμα, η ανισότητα θα μοιάζει με αυτό.

Στην πραγματικότητα, το μόνο που μένει είναι να δημιουργηθεί ένα σύστημα ανισοτήτων χωρίς λογάριθμους. Χρησιμοποιώντας τη μέθοδο εξορθολογισμού, προχωράμε σε ένα ισοδύναμο σύστημα ανισοτήτων. Θα κατανοήσετε τον ίδιο τον κανόνα όταν αντικαταστήσετε τις κατάλληλες τιμές και παρακολουθήσετε τις αλλαγές τους. Το σύστημα θα έχει τις ακόλουθες ανισότητες.

Όταν χρησιμοποιείτε τη μέθοδο εξορθολογισμού κατά την επίλυση ανισώσεων, πρέπει να θυμάστε τα εξής: ένα πρέπει να αφαιρεθεί από τη βάση, το x, εξ ορισμού του λογαρίθμου, αφαιρείται και από τις δύο πλευρές της ανισότητας (δεξιά από αριστερά), πολλαπλασιάζονται δύο εκφράσεις και ορίστε κάτω από το αρχικό πρόσημο σε σχέση με το μηδέν.
Η περαιτέρω λύση πραγματοποιείται χρησιμοποιώντας τη μέθοδο του διαστήματος, όλα είναι απλά εδώ. Είναι σημαντικό για εσάς να κατανοήσετε τις διαφορές στις μεθόδους λύσης, τότε όλα θα αρχίσουν να λειτουργούν εύκολα.
Υπάρχουν πολλές αποχρώσεις στις λογαριθμικές ανισότητες. Τα πιο απλά από αυτά είναι αρκετά εύκολο να λυθούν. Πώς μπορείτε να λύσετε το καθένα από αυτά χωρίς προβλήματα; Έχετε ήδη λάβει όλες τις απαντήσεις σε αυτό το άρθρο. Τώρα έχετε μια μακρά πρακτική μπροστά σας. Εξασκηθείτε συνεχώς στην επίλυση ποικίλων προβλημάτων στις εξετάσεις και θα μπορέσετε να τα καταφέρετε υψηλότερο σκόρ. Καλή επιτυχία στο δύσκολο έργο σας!