ΓΕΩΜΕΤΡΙΑ
Σχέδια μαθήματος για 10 βαθμούς
Μάθημα 56
Θέμα. Περιοχή ορθογραφικής προβολής πολυγώνου
Ο σκοπός του μαθήματος: μελέτη του θεωρήματος στην περιοχή της ορθογώνιας προβολής ενός πολυγώνου, η διαμόρφωση των δεξιοτήτων των μαθητών για την εφαρμογή του μελετημένου θεώρηματος για την επίλυση προβλημάτων.
Εξοπλισμός: στερεομετρικό σετ, μοντέλο κύβου.
Κατά τη διάρκεια των μαθημάτων
I. Έλεγχος εργασίας
1. Δύο μαθητές αναπαράγουν λύσεις στα προβλήματα αρ. 42, 45 στον πίνακα.
2. Μετωπική ψηφοφορία.
1) Δώστε τον ορισμό της γωνίας μεταξύ δύο επιπέδων που τέμνονται.
2) Ποια είναι η γωνία μεταξύ:
α) παράλληλα επίπεδα ·
β) κάθετα επίπεδα;
3) Σε ποιο βαθμό μπορεί να αλλάξει η γωνία μεταξύ δύο επιπέδων;
4) Είναι αλήθεια ότι ένα επίπεδο που τέμνει παράλληλα επίπεδα τα τέμνει στις ίδιες γωνίες;
5) Είναι αλήθεια ότι ένα επίπεδο που τέμνει κάθετα επίπεδα τα τέμνει στις ίδιες γωνίες;
3. Έλεγχος της ορθότητας της λύσης στα προβλήματα αρ. 42, 45, που οι μαθητές δημιούργησαν ξανά στο ταμπλό.
ΙΙ. Αντίληψη και ευαισθητοποίηση για νέο υλικό
Εργασία σε μαθητές
1. Αποδείξτε ότι η περιοχή προβολής ενός τριγώνου με τη μία πλευρά στο επίπεδο προβολής είναι ίση με το προϊόν της περιοχής του και το συνημίτονο της γωνίας μεταξύ του επιπέδου πολυγώνου και του επιπέδου προβολής.
2. Αποδείξτε το θεώρημα για την περίπτωση όταν υπάρχει ένα τρίγωνο δικτυωτού πλέγματος με μία πλευρά παράλληλη προς το επίπεδο προβολής.
3. Αποδείξτε το θεώρημα για την περίπτωση όταν υπάρχει ένα τρίγωνο πλέγματος με καμία από τις πλευρές του παράλληλη με το επίπεδο προβολής.
4. Αποδείξτε το θεώρημα για οποιοδήποτε πολύγωνο.
Λύνοντας προβλήματα
1. Βρείτε την περιοχή της ορθογώνιας προβολής ενός πολυγώνου της οποίας η περιοχή είναι 50 cm2 και η γωνία μεταξύ του επιπέδου του πολυγώνου και της προβολής του είναι 60 °.
2. Βρείτε την περιοχή ενός πολυγώνου εάν η περιοχή της ορθογώνιας προβολής αυτού του πολυγώνου είναι 50 cm2 και η γωνία μεταξύ του επιπέδου του πολυγώνου και της προβολής του είναι 45 °.
3. Η επιφάνεια του πολυγώνου είναι 64 cm2 και η περιοχή της ορθογώνιας προβολής είναι 32 cm2. Βρείτε τη γωνία μεταξύ των επιπέδων του πολυγώνου και της προβολής του.
4. Ή μήπως η περιοχή της ορθογώνιας προβολής ενός πολυγώνου είναι ίση με την περιοχή αυτού του πολυγώνου;
5. Το άκρο του κύβου είναι ίσο με το α. Βρείτε την περιοχή διατομής του κύβου από ένα επίπεδο που διέρχεται από την κορυφή της βάσης υπό γωνία 30 ° προς αυτή τη βάση και τέμνει όλες τις πλευρικές άκρες. (Απάντηση.)
6. Πρόβλημα αριθμός 48 (1, 3) από το βιβλίο (σελ. 58).
7. Πρόβλημα αριθμός 49 (2) από το βιβλίο (σελ. 58).
8. Οι πλευρές του ορθογωνίου είναι 20 και 25 εκ. Η προβολή του στο επίπεδο είναι παρόμοια με αυτήν. Βρείτε την περίμετρο της προβολής. (Απάντηση. 72 cm ή 90 cm.)
III. Εργασία για το σπίτι
§4, παράγραφος 34 · ερώτηση ασφαλείας αριθμός 17; αρ. 48 (2), 49 (1) (σελ. 58).
IV. Περίληψη μαθήματος
Ερώτηση στην τάξη
1) Διατυπώστε το θεώρημα στην περιοχή της ορθογώνιας προβολής ενός πολυγώνου.
2) Μπορεί η περιοχή μιας ορθογώνιας προβολής ενός πολυγώνου να είναι μεγαλύτερη από την περιοχή ενός πολυγώνου;
3) Μέσω της υπόνοιας AB ορθογώνιο τρίγωνο Το ABC τραβά το επίπεδο α σε γωνία 45 ° προς το επίπεδο του τριγώνου και το κάθετο CO στο επίπεδο α. AC \u003d 3 cm, BC \u003d 4 cm. Αναφέρετε ποιες από τις ακόλουθες δηλώσεις είναι σωστές και ποιες είναι λανθασμένες:
α) η γωνία μεταξύ των επιπέδων ABC και α ίσο με τη γωνία CMO, όπου το σημείο H είναι η βάση του ύψους CM τρίγωνο ABC;
β) CO \u003d 2,4 cm.
γ) το τρίγωνο ABC είναι μια ορθογώνια προβολή του τριγώνου ABC στο επίπεδο α ·
δ) η επιφάνεια του τριγώνου AOB είναι 3 cm2.
(Απάντηση. Α) Σωστό; β) λάθος · γ) λάθος · δ) σωστό.)
Θυμηθείτε ότι η γωνία μεταξύ μιας ευθείας γραμμής και ενός επιπέδου είναι η γωνία μεταξύ μιας δεδομένης ευθείας γραμμής και της προβολής της σε ένα επίπεδο (Εικ. 164)
Θεώρημα. Η περιοχή της ορθογώνιας προβολής του πολυγώνου στο επίπεδο είναι ίση με την περιοχή του προβαλλόμενου πολυγώνου πολλαπλασιαζόμενη με το συνημίτονο της γωνίας που σχηματίζεται από το επίπεδο του πολυγώνου και το επίπεδο της προβολής.
Κάθε πολύγωνο μπορεί να χωριστεί σε τρίγωνα, το άθροισμα των περιοχών των οποίων είναι ίσο με την περιοχή του πολυγώνου. Επομένως, αρκεί να αποδειχθεί το θεώρημα για ένα τρίγωνο.
Αφήστε \\ (\\ Delta \\) ABC να προβάλλεται στο αεροπλάνο Ρ... Εξετάστε δύο περιπτώσεις:
a) μία από τις πλευρές \\ (\\ Delta \\) ABC είναι παράλληλη με το επίπεδο Ρ;
β) καμία από τις πλευρές \\ (\\ Delta \\) ABC δεν είναι παράλληλη Ρ.
Σκεφτείτε πρώτη περίπτωση: ας [AB] || Ρ.

Ας σχεδιάσουμε το αεροπλάνο μέσω (AB) Ρ 1 || Ρ και προβάλλετε ορθογώνια \\ (\\ Delta \\) ABC Ρ 1 και μετά Ρ (εικ. 165); παίρνουμε \\ (\\ Delta \\) ABC 1 και \\ (\\ Delta \\) A'B'S '.
Από την ιδιότητα προβολής, έχουμε \\ (\\ Delta \\) ABC 1 \\ (\\ cong \\) \\ (\\ Delta \\) A'B'C 'και επομένως
S \\ (\\ Delta \\) ABC1 \u003d S \\ (\\ Delta \\) A'B'C '
Σχέδιο ⊥ και το τμήμα D 1 C 1. Στη συνέχεια ⊥, a \\ (\\ widehat (CD_ (1) C_ (1)) \\) \u003d φ είναι η γωνία μεταξύ του επιπέδου \\ (\\ Delta \\) ABC και του επιπέδου Ρ ένας . επομένως
S \\ (\\ Delta \\) ABC1 \u003d 1/2 | AB | | C 1 D 1 | \u003d 1/2 | ΑΒ | | CD 1 | cos φ \u003d S \\ (\\ Delta \\) ABC cos φ
και επομένως S \\ (\\ Delta \\) A'B'C '\u003d S \\ (\\ Delta \\) ABC cos φ.
Ας προχωρήσουμε στη σκέψη δεύτερη περίπτωση... Ας σχεδιάσουμε ένα αεροπλάνο Ρ 1 || Ρ μέσω αυτής της κορυφής \\ (\\ Delta \\) ABC, η απόσταση από την οποία στο επίπεδο Ρ το μικρότερο (ας είναι η κορυφή Α).
Ας σχεδιάσουμε το ABC στο αεροπλάνο Ρ 1 και Ρ (εικ. 166); ας είναι οι προβολές του, αντίστοιχα, \\ (\\ Delta \\) AB 1 C 1 και \\ (\\ Delta \\) A'B'S '.

Αφήστε (ВС) \\ (\\ cap \\) Π 1 \u003d D. Τότε
S \\ (\\ Delta \\) A'B'C '\u003d S \\ (\\ Delta \\) AB1 C1 \u003d S \\ (\\ Delta \\) ADC1 - S \\ (\\ Delta \\) ADB1 \u003d (S \\ (\\ Delta \\) ADC - S \\ (\\ Delta \\) ADB) cos φ \u003d S \\ (\\ Delta \\) ABC cos φ
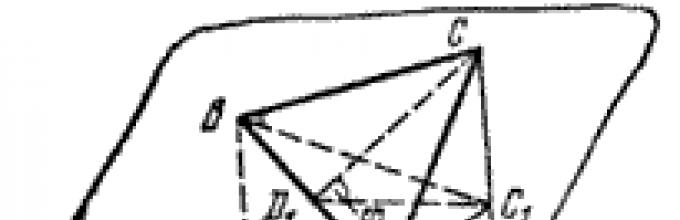
Μια εργασία. Ένα επίπεδο τραβιέται μέσω της πλευράς της βάσης ενός κανονικού τριγωνικού πρίσματος υπό γωνία φ \u003d 30 ° προς το επίπεδο της βάσης του. Βρείτε την περιοχή του τμήματος που προκύπτει εάν η πλευρά της βάσης του πρίσματος ένα \u003d 6 εκ.

Ας σχεδιάσουμε μια διατομή αυτού του πρίσματος (Εικ. 167). Δεδομένου ότι το πρίσμα είναι σωστό, οι πλευρικές άκρες του είναι κάθετες στο επίπεδο της βάσης. Επομένως, το \\ (\\ Delta \\) ABC είναι η προβολή του \\ (\\ Delta \\) ADC
$$ S _ (\\ Delta ADC) \u003d \\ frac (S _ (\\ Delta ABC)) (cos \\ phi) \u003d \\ frac (a \\ cdot a \\ sqrt3) (4cos \\ phi) $$
ή
$$ S _ (\\ Delta ADC) \u003d \\ frac (6 \\ cdot 6 \\ cdot \\ sqrt3) (4 \\ cdot \\ frac (\\ sqrt3) (2)) \u003d 18 (cm ^ 2) $$
Θα εξετάσω το ζήτημα του τύπου για τις προβολές των όψεων ενός ορθογώνιου τετραέδρου. Προκαταρκτικά, θα εξετάσω την ορθογώνια προβολή ενός τμήματος που βρίσκεται στο επίπεδο α, επισημαίνοντας δύο περιπτώσεις της θέσης αυτού του τμήματος σε σχέση με την ευθεία γραμμή l \u003d α∩π.
Περίπτωση 1.
AB∥l (εικ. 8). Το τμήμα Α 1 Β 1, που είναι η ορθογώνια προβολή του τμήματος ΑΒ, είναι ίσο και παράλληλο με το τμήμα ΑΒ.
Φιγούρα: 8
Περίπτωση 2.
CD⊥l (εικ. 8). Με το τρεις κάθετο θεώρημα, η γραμμή C1 D1, η οποία είναι η ορθογώνια προβολή της γραμμής CD, είναι επίσης κάθετη προς τη γραμμή l. Επομένως, το ∠CEC 1 είναι η γωνία μεταξύ του επιπέδου α και του επιπέδου προβολής π, δηλαδή, όπου C 0 D \u003d C 1 D 1... Επομένως, | C 1 D 1 | \u003d | CD | ∙ cosφ
Τώρα θα εξετάσω το ζήτημα του ορθογώνιου τριγώνου.
Η περιοχή μιας ορθογώνιας προβολής ενός τριγώνου σε ένα επίπεδο είναι ίση με την περιοχή του προβαλλόμενου τριγώνου πολλαπλασιασμένη επί το συνημίτονο της γωνίας μεταξύ του επιπέδου του τριγώνου και του επιπέδου των προεξοχών.
Απόδειξη.Η προβαλλόμενη περιοχή του τριγώνου. Σύμφωνα με το θεώρημα σε τρεις κάθετες, η γραμμή B 1 H 1 - η ορθογώνια προβολή της γραμμής BH - είναι κάθετη προς τη γραμμή l, επομένως, το τμήμα B 1 H 1 είναι το ύψος του τριγώνου A 1 B 1 C 1 . Επομένως . Με αυτόν τον τρόπο, .
α) Αφήστε μια από τις πλευρές, για παράδειγμα AC, του προβαλλόμενου τριγώνου ABC να είναι παράλληλη με την ευθεία γραμμή l \u003d α∩π (Εικ. 9) ή να βρίσκεται πάνω του.
Στη συνέχεια, το ύψος του VN είναι κάθετο προς την ευθεία γραμμή l, και η περιοχή είναι ίση, δηλαδή

Φιγούρα: εννέα
![]()
β) Καμία από τις πλευρές του προβαλλόμενου τριγώνου ABC δεν είναι παράλληλη με τη γραμμή l (Εικ. 10). Σχεδιάστε μια ευθεία γραμμή μέσω κάθε κορυφής του τριγώνου παράλληλη προς την ευθεία γραμμή l. Μία από αυτές τις γραμμές βρίσκεται μεταξύ δύο άλλων (στο σχήμα είναι η γραμμή m) και, επομένως, χωρίζει το τρίγωνο ABC σε τρίγωνα ABD και ACD με ύψη, αντίστοιχα, BH και CE, που σύρονται στην κοινή πλευρά AD (ή τη συνέχισή του) , που είναι παράλληλο l. Η γραμμή m 1 - ορθογώνια προβολή της γραμμής m - διαχωρίζει επίσης το τρίγωνο A 1 B 1 C 1 - ορθογώνια προβολή του τριγώνου ABC - σε τρίγωνα A 1 B 1 D 1 και A 1 C 1 D 1, όπου. Λαμβάνοντας υπόψη (9) και (10), παίρνω
Πρόσφατα, στην εργασία C2, υπάρχουν προβλήματα στα οποία είναι απαραίτητο να κατασκευαστεί ένα τμήμα ενός πολυεδρού από ένα αεροπλάνο και να βρεθεί η περιοχή του. Αυτή η εργασία προτείνεται στην έκδοση επίδειξης. Συχνά είναι βολικό να βρείτε την περιοχή μιας τομής μέσω της περιοχής της ορθογώνιας προβολής της. Η παρουσίαση παρέχει έναν τύπο για μια τέτοια λύση και λεπτομερή ανάλυση έργο, το οποίο συνοδεύεται από μια σειρά σχεδίων.
Κατεβάστε:
Προεπισκόπηση:
Για να χρησιμοποιήσετε την προεπισκόπηση των παρουσιάσεων, δημιουργήστε έναν λογαριασμό Google (λογαριασμός) και συνδεθείτε σε αυτόν: https://accounts.google.com
Λεζάντες διαφανειών:
Προετοιμασία για τις εξετάσεις - 2014 στα μαθηματικά. Εύρεση της διατομής μέσω της περιοχής της ορθογώνιας προβολής του. Εργασία C2 καθηγητής μαθηματικών MBOU δευτεροβάθμιας εκπαίδευσης № 143 στο Krasnoyarsk Knyazkina T. V.
Εξετάστε τη λύση στο ακόλουθο πρόβλημα: Σε ορθογώνιο παραλληλεπίπεδο ,. Το τμήμα του παραλλήλου διέρχεται από τα σημεία B και D και σχηματίζει μια γωνία με το επίπεδο ABC. Βρείτε την περιοχή διατομής. Συχνά είναι βολικό να βρείτε την περιοχή μιας τομής μέσω της περιοχής της ορθογώνιας προβολής της. Η εύρεση της περιοχής ενός τριγώνου μέσω της περιοχής της ορθογώνιας προβολής του απεικονίζεται εύκολα από το ακόλουθο σχήμα:
Το CH είναι το ύψος του τριγώνου ABC, το C 'H είναι το ύψος του τριγώνου ABC ", το οποίο είναι η ορθογώνια προβολή του τριγώνου ABC. Από το ορθογώνιο τρίγωνο CHC": Η περιοχή του τριγώνου ABC "είναι ίση με την περιοχή του Το τρίγωνο ABC είναι Επομένως, η περιοχή του τριγώνου ABC είναι ίση με την περιοχή του τριγώνου ABC «διαιρεμένη με συνημίτονο της γωνίας μεταξύ των επιπέδων του τριγώνου ABC και του τριγώνου ABC», που είναι η ορθογώνια προβολή του τριγώνου ABC.
Δεδομένου ότι η περιοχή οποιουδήποτε πολυγώνου μπορεί να αναπαρασταθεί ως το άθροισμα των περιοχών των τριγώνων, η περιοχή ενός πολυγώνου είναι ίση με την περιοχή της ορθογωνικής προβολής του στο επίπεδο διαιρούμενο με το συνημίτονο της γωνίας μεταξύ του επίπεδα του πολυγώνου και την προβολή του. Χρησιμοποιούμε αυτό το γεγονός για να λύσουμε το πρόβλημά μας (βλ. Διαφάνεια 2) Το σχέδιο λύσης έχει ως εξής: Α) Δημιουργήστε μια ενότητα. Β) Βρείτε την ορθογώνια προβολή του στο επίπεδο βάσης. Γ) Βρείτε την περιοχή της ορθογώνιας προβολής. Δ) Βρείτε την περιοχή διατομής.
1. Πρώτα πρέπει να δημιουργήσουμε αυτήν την ενότητα. Προφανώς, το τμήμα BD ανήκει στο επίπεδο τομής και στο επίπεδο βάσης, δηλαδή ανήκει στη γραμμή τομής των επιπέδων:
Η γωνία μεταξύ δύο επιπέδων είναι η γωνία μεταξύ δύο κάθετων που σύρονται στη γραμμή τομής των επιπέδων και βρίσκονται σε αυτά τα επίπεδα. Αφήστε το σημείο O να είναι το σημείο τομής των διαγώνιων βάσεων. OC - \u200b\u200bκάθετα προς τη γραμμή τομής των επιπέδων, η οποία βρίσκεται στο επίπεδο της βάσης:
2. Προσδιορίστε τη θέση της κάθετης, που βρίσκεται στο επίπεδο τομής. (Να θυμάστε ότι εάν μια ευθεία γραμμή είναι κάθετη προς την κεκλιμένη προβολή, τότε είναι κάθετη προς την πιο κεκλιμένη. Ψάχνουμε για μια κεκλιμένη από την προβολή της (OC) και τη γωνία μεταξύ της προβολής και της κεκλιμένης). Βρείτε την εφαπτομένη της γωνίας COC ₁ μεταξύ OC ₁ και OC
Κατά συνέπεια, η γωνία μεταξύ του επιπέδου τομής και του επιπέδου βάσης είναι μεγαλύτερη από ό, τι μεταξύ OC ₁ και OC. Δηλαδή, η ενότητα βρίσκεται κάπως έτσι: K είναι το σημείο τομής των OP και A ₁C₁, LM || B₁D₁.
Ορίστε λοιπόν η ενότητα μας: 3. Βρείτε την προβολή της ενότητας BLMD στο επίπεδο της βάσης. Για να γίνει αυτό, βρίσκουμε τις προβολές των σημείων L και M.
Τετράγωνο BL ₁M₁D - προβολή τομής στο επίπεδο βάσης. 4. Βρείτε την περιοχή του τετράπλευρου BL ₁M₁D. Για να το κάνετε αυτό, αφαιρέστε την περιοχή του τριγώνου L ₁CM₁ από την περιοχή του τριγώνου BCD. Βρείτε την περιοχή του τριγώνου L CM₁. Το τρίγωνο L CM₁ είναι παρόμοιο με το τρίγωνο BCD. Ας βρούμε τον συντελεστή ομοιότητας.
Για να το κάνετε αυτό, λάβετε υπόψη τα t reangles OPC και OKK₁: Επομένως, η περιοχή του τριγώνου L₁CM₁ είναι 4/25 της περιοχής του τριγώνου BCD (ο λόγος των περιοχών παρόμοιων αριθμών είναι ίσος με το τετράγωνο του ο συντελεστής ομοιότητας). Στη συνέχεια, η περιοχή του τετράπλευρου BL₁M₁D είναι ίση με 1-4 / 25 \u003d 21/25 της περιοχής του τριγώνου BCD και είναι ίση με
5. Τώρα βρίσκουμε 6. Και τέλος παίρνουμε: Απάντηση: 112
Σχετικά με το θέμα: μεθοδολογικές εξελίξεις, παρουσιάσεις και σημειώσεις
Η δοκιμαστική εργασία στον κλάδο "Μηχανική Computer Graphics" αποτελείται από τέσσερα αντικείμενα δοκιμής για να διαπιστωθεί η συμμόρφωση. Χρειάζονται 15-20 λεπτά για να ολοκληρωθούν οι εργασίες ...
Παρουσίαση με σύντομο μάθημα θεωρία και λύσεις διαφόρων πρωτοτύπων του Β8 από την ανοιχτή τράπεζα εργασιών USE. Μπορεί να χρησιμοποιηθεί για διαδραστικό πίνακα ή υπολογιστή σπουδαστή για αυτο-μελέτη ....
Προετοιμασία για τις εξετάσεις-2014 στα μαθηματικά. Λύση της εργασίας C1.
Το υλικό περιέχει λύσεις στην εργασία C1 (τριγωνομετρική εξίσωση) και 4 τρόπους επιλογής ριζών που ανήκουν στο διάστημα: χρήση τριγωνομετρικός κύκλος, χρησιμοποιώντας ένα γράφημα μιας συνάρτησης, ωμή δύναμη ...