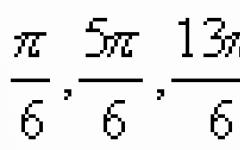Solving tasks B8. Preparation for the Unified State Exam in mathematics. Solving problems B8 I. Organizational moment

Solving tasks B8 using materials open bank Unified State Exam problems in mathematics 2012 The line y = 4x + 11 is parallel to the tangent to the graph of the function y = x2 + 8x + 6. Find the abscissa of the point of tangency. No. 1 Solution: If the line is parallel to the tangent to the graph of the function at some point (let's call it xo), then its the angular coefficient (in our case k = 4 from the equation y = 4x +11) is equal to the value of the derivative of the function at the point xo: k = f ′(xo) = 4 Derivative of the function f′(x) = (x2+8x + 6)′= 2x +8. This means that to find the desired tangent point it is necessary that 2xo + 8 = 4, from which xo = – 2. Answer: – 2. The line y = 3x + 11 is tangent to the graph

functions y = x3−3x2− 6x + 6.

Find the abscissa of the tangent point.

No. 2 Solution: Note that if the line is tangent to the graph, then its slope (k = 3) must be equal to the derivative of the function at the point of tangency, from which we have Zx2 − 6x − 6 = 3, that is, Zx2 − 6x − 9 = 0 or x2 − 2x − 3 = 0. This is quadratic equation has two roots: −1 and 3. Thus, there are two points at which the tangent to the graph of the function y = x3 − 3x2 − 6x + 6 has a slope equal to 3. In order to determine which of these two points the straight line y = 3x + 11 touches the graph of the function, let's calculate the values ​​of the function at these points and check whether they satisfy the tangent equation. The value of the function at point −1 is y(−1) = −1 − 3 + 6 + 6 = 8, and the value at point 3 is y(3) = 27 − 27 − 18 + 6 = −12. Note that the point with coordinates (−1; 8) satisfies the tangent equation, since 8 = −3 + 11. But the point (3; −12) does not satisfy the tangent equation, since −12 ≠ 9 + 11. This means that the required The abscissa of the tangency point is −1. Answer: −1. The figure shows a graph of y = f ′(x) – the derivative of the function f(x), defined on the interval (–10; 8). At what point of the segment [–8; –4] function f(x) takes smallest value.№3 Solution: Note that on the segment [–8; –4] the derivative of the function is negative, which means that the function itself is decreasing, which means that it takes the smallest value on this segment at the right end of the segment, that is, at the point –4.у = f ′(x) f(x) –Answer: –4 .The figure shows a graph of y = f ′(x) – the derivative of the function f(x), defined on the interval (–8; 8). Find the number of extremum points of the function f(x), belonging to the segment [– 6; 6].No. 4Solution: At the extremum point, the derivative of the function is equal to 0 or does not exist. It can be seen that there are such points belonging to the segment [–6; 6] three. In this case, at each point the derivative changes sign either from “+” to “–”, or from “–” to “+”.у = f ′(x) ++––Answer: 3. The figure shows the graph of у = f ′(x) – derivative of the function f(x), defined on the interval (–8; 10). Find the extremum point of the function f(x) on the interval (– 4; 8). No. 5. Solution: Note that on the interval (–4; 8) the derivative at the point xo = 4 turns to 0 and when passing through this point changes sign derivative from “–” to “+”, point 4 is the desired extremum point of the function on a given interval. y = f ′(x) +–Answer: 4. The figure shows a graph of y = f ′(x) – the derivative of the function f(x), defined on the interval (–8; 8). Find the number of points at which the tangent to the graph of the function f(x) is parallel to the line y = –2x + 2 or coincides with it. No. 6 Solution: If the tangent to the graph of the function f(x) is parallel to the line y = –2x+ 2 or coincides with it, then its slope k = –2, which means we need to find the number of points at which the derivative of the function f ′(x) = –2. To do this, draw a straight line y = –2 on the derivative graph and count the number of points on the derivative graph lying on this line. There are 4 such points. y = f ′(x) y = –2Answer: 4. The figure shows a graph of the function y = f(x), defined on the interval (–6; 5). Determine the number of integer points at which the derivative of the function is negative. No. 7y Solution: Note that the derivative of a function is negative if the function f(x) itself is decreasing, which means it is necessary to find the number of integer points included in the intervals of decreasing function. There are 6 such points: x = −4, x = −3, x = −2, x = −1, x = 0, x = 3.y = f(x) x–6–45–1–20–33 Answer: 6. The figure shows graph of the function y = f(x), defined on the interval (–6; 6). Find the number of points at which the tangent to the graph of the function is parallel to the straight line y = –5. No. 8ySolution: The straight line y = −5 is horizontal, which means that if the tangent to the graph of a function is parallel to it, then it is also horizontal. Consequently, the angular coefficient at the required points k = f′(x)= 0. In our case, these are extremum points. There are 6 such points. him at the abscissa point xo. Find the value of the derivative of the function f(x) at the point xo. No. 9 Solution: The value of the derivative of the function f′(хo) = tanα = k to the equiangular coefficient of the tangent drawn to the graph of this function at a given point. In our case k > 0, since α– acute angle(tgα > 0).To find the slope, we choose two points A and B lying on the tangent, the abscissas and ordinates of which are integers. Now let's determine the modulus of the angular coefficient. For this we will build triangle ABC. tgα =ВС: AC = 5: 4 = 1.25 у = f(x) Вα5хоαС4АAnswer: 1.25. The figure shows a graph of the function у = f(x), defined on the interval (–10; 2) and the tangent to it in point with abscissa xo. Find the value of the derivative of the function f(x) at point xo. No. 10Solution: The value of the derivative of the function f′(хo) = tanα = k to the equiangular coefficient of the tangent drawn to the graph of this function at a given point. In our case k< 0, так как α– obtuse angle(tgα< 0).Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых − целые числа. Теперь определим модуль углового коэффициента. Для этого построим треугольник ABC. tg(180°−α) = ВС: АС = 6: 8 = 0,75 tgα = − tg (180°−α) = −0,75Ву = f(x) α6хо180°− αСА8Ответ: −0,75.На рисунке изображен график производной у = f ′(x) –функции f(x), определенной на интервале (–11; 11). Найдите количество точек максимума функции f(x) на отрезке [−10; 10]. №11.Решение: В точке экстремума производная функции равна 0 либо не существует. Видно, что таких точек принадлежащих отрезку [−10; 10] пять. В точках х2и х4 производная меняет знак с «+» на «−» – это точки максимума.уу = f ′(x) +++–100–––х10f(x) х3х5х2х4х1maxmaxОтвет: 2.Прямая у = 4х – 4является касательной к графику функции ах2+ 34х + 11. Найдите а.№12Решение:Производная функции в точке касания должна совпадать с угловым коэффициентом прямой. Откуда, если за хo принять абсциссу точки касания, имеем: 2ахo+ 34 = 4. То есть ахo =–15. Найдем значение исходной функции в точке касания:ахo2 + 34хo + 11 = –15xo+ 34хo + 11 = 19хo + 11.Так как прямая у = 4х – 4– касательная, имеем: 19хo + 11 =4хo–4, откуда хo = –1. А значитa = 15. Ответ: 15.Прямая у = –4х – 5 является касательной к графику функции 9х2+bх + 20. Найдите b,учитывая, что абсцисса точки касания больше 0.№13Решение. Если хо– абсцисса точки касания, то 18xo+ b = –4, откуда b = –4 –18хо. Аналогично задаче№12 найдем хо:9xo2+ (–4 –18хо)xo+20 = – 4хo – 5, 9xo2–4xo –18хо2+20 + 4хo + 5 = 0,–9xo2+25 = 0,хо2 = 25/9. Откуда xo = 5/3или xo = –5/3. Условию задачи соответствует только положительный корень, значит xo = 5/3, следовательно b = –4 –18∙ 5/3, имеем b = –34. Ответ: –34.Прямая у = 2х – 6является касательной к графику функции х2+ 12х + с. Найдите с.№14Решение. Аналогично предыдущим задачам обозначим абсциссу точки касания хо и приравняем значение производной функции в точке хо угловому коэффициенту касательной. 2хо + 12 = 2, откуда xo= –5. Значение исходной функции в точке –5 равно: 25 – 60 + с = с – 35, значит с – 35 = 2∙(–5) – 6, откуда с = 19. Ответ: 19.Материальная точка движется прямолинейно по закону x(t) = 0,5t2 – 2t – 6, где x – расстояние от точки отсчета в метрах, t– время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6с.№15Решение. Так как мгновенная скорость точки в момент времени to, rectilinear motion performed according to the law x = x(t), is equal to the value of the derivative of the function xnput = to, the desired speed will be x ′(t) = 0.5 ∙ 2t – 2 = t – 2.x ′(6) = 6 – 2 = 4 m/s. Answer: 4. A material point moves rectilinearly according to the law x(t) = 0.5t2 – 2t – 22, where x is the distance from the reference point in meters, t is the time in seconds, measured from the beginning of the movement. At what point in time (in seconds) was its speed equal to 4 m/s? No. 16 Solution. Since the instantaneous speed of a point at time to, rectilinear motion performed according to the law x = x(t), is equal to the value of the derivative of the function xnput = to, the desired speed will be x ′(to) = 0.5 ∙ 2to – 2 = to – 2, Because by condition, x ′(to) = 4, then to – 2 = 4, whence to = 4 + 2 = 6 m/s. Answer: 6. The figure shows a graph of the function y = f(x), defined on the interval (– 8; 6).Find the sum of the extremum points of the function f(x).No. 17Solution: The extremum points are the minimum and maximum points. It can be seen that there are five such points belonging to the interval (–8; 6). Let's find the sum of their abscissas: -6 + (-4) + (-2) + 2 + 4 = 6.у = f ′(x) Answer: 6. The figure shows a graph of the derivative y = f ′(x) – function f (x), defined on the interval (–10; 8). Find the intervals of increasing function f(x). In your answer, indicate the sum of integer points included in these intervals. Solution: Note that the function f(x) increases if the derivative of the function is positive; which means it is necessary to find the sum of integer points included in the intervals of increasing function. There are 7 such points: x = −3, x = −2, x = 3, x = 4, x = 5, x = 6, x = 7. Their sum: −3+(−2)+3+4+5+6+7 = 20у = f ′(x) ++3-357Answer: 20. Materials used

Unified State Exam 2012. Mathematics. Problem B8. Geometric meaning of derivative. Workbook/ Ed. A.L. Semenov and I.V. Yashchenko. 3rd ed. stereotype. − M.: MTsNMO, 2012. − 88 p.

http://mathege.ru/or/ege/Main− Materials of the open bank of tasks in mathematics 2012

“B8 in the Unified State Exam in Mathematics” - Minimum points. The derivative of the function is negative. Find the value of the derivative of the function. Find the abscissa of the tangent point. Speed. The value of the derivative of the function. Derivative. Time. Graph of the derivative of a function. Find the derivative of the function. Intervals of increasing function. Solving B8 Unified State Examination tasks in mathematics.

“B3 in mathematics” - Memo to the student. CT skills. Task prototype. Contents of task B3. Prototype of task B3. Prototype of task B3. Equation. Basic properties of roots. Find the root of the equation. Logarithms. Logarithms with on the same grounds. Degree. Preparation for the Unified State Exam in mathematics. Tasks for independent decision.

“Solving tasks B11” - Tasks. Beginnings mathematical analysis. Find highest value functions on a segment. Formulas. Find the largest value of the function. CT skills. Tasks for independent solution. Find the smallest value of the function on the segment. Find the smallest value of the function. Examination. Solution. Memo to the student.

“B1 in the Unified State Exam in Mathematics” - The smallest number. Bun. Ticket. American car. Electric kettle. Promotion. Day. Payment terminal. Medicine. Tasks B1. Client. Motor ship. General notebook. Hot water flow meter. Train ticket. Pensioners.

“Unified State Examination tasks in mathematics” - Task B 13. We need to solve a couple more examples. Task B 6. Find the speed of the motorcyclist. Task B 1. How much should the water level rise after rain? Find the area. After rain, the water level in the well may rise. Task B 5. Task B 12. Independent work. Preparation for the Unified State Exam. Task B 3.

“B1 in mathematics” - Marmalade. Promotion. Discount on sale day. Ampoule. Washing machine. Bus. Income tax. Shampoo bottle. Notebook. Smallest number. Mobile phone. Intercity bus ticket. Taxi driver. Shop. Ticket. A stick of butter. Rose. Tasks B1 Unified State Examination in mathematics. Solution.

There are a total of 33 presentations in the topic

Solving tasks B8 Unified State Exam in mathematics The figure shows a graph functions y = f(x), defined on the interval (−5; 5). Find the number of points at which the derivative f'(x) equal to 0

• Answer: 4

f(x), defined on the interval (−10; 8). Find the number of maximum points of the function f(x) on the segment [−9;6].

• Solution. The maximum points correspond to the points where the sign of the derivative changes from plus to minus. On the segment [−9;6] the function has two maximum points x= − 4 and x= 4. Answer: 2.

The figure shows a graph of the function y=f(x), defined on the interval (−1; 12). Determine the number of integer points at which the derivative of the function is negative.

• Solution.

The derivative of the function is negative on those intervals on which the function decreases, i.e. on the intervals (0.5; 3), (6; 10) and (11; 12). They contain whole points 1, 2, 7, 8 and 9. There are 5 points in total. Answer: 5.

The figure shows a graph of the derivative of the function f(x), defined on the interval (−10; 4). Find the intervals of decrease of the function f(x). In your answer, indicate the length of the largest of them.

• Solution. Decreasing intervals of a function f(x) correspond to intervals on which the derivative of the function is negative, that is, the interval (−9; −6) of length 3 and the interval (−2; 3) of length 5. The length of the largest of them is 5. Answer: 5.

The figure shows a graph of the derivative of the function f(x), defined on the interval (−7; 14). Find the number of maximum points of the function f(x) on the interval [−6; 9].

• Solution. The maximum points correspond to the points where the derivative sign changes from positive to negative. On the segment [−6; 9] the function has one maximum point x= 7. Answer: 1.

The figure shows a graph of the derivative of the function f(x), defined on the interval (−8; 6). Find the intervals of increase of the function f(x). In your answer, indicate the length of the largest of them.

• Solution. Intervals of increasing function f(x) correspond to intervals on which the derivative of the function is positive, that is, to the intervals (−7; −5), (2; 5). The largest of them is the interval (2; 5), whose length is 3.

The figure shows a graph of the derivative of the function f(x), defined on the interval (−7; 10). Find the number of minimum points of the function f(x) on the interval [−3; 8].

• Solution. The minimum points correspond to the points where the sign of the derivative changes from minus to plus. On the segment [−3; 8] the function has one minimum point x= 4. Answer: 1.

The figure shows a graph of the derivative of the function f(x), defined on the interval (−16; 4). Find the number of extremum points of the function f(x) on the segment [−14; 2].

• Solution. The extremum points correspond to the points where the sign of the derivative changes - the zeros of the derivative shown on the graph. The derivative vanishes at points −13, −11, −9, −7. On the segment [−14; 2] the function has 4 extremum points. Answer: 4.

The figure shows the graph of the function y=f(x), defined on the interval (−2; 12). Find the sum of the extremum points of the function f(x).

• Solution. The given function has maxima at points 1, 4, 9, 11 and minima at points 2, 7, 10. Therefore, the sum of the extremum points is 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44. Answer: 44.

The figure shows the graph of the function y=f(x) and the tangent to it at the abscissa point x 0. Find the value of the derivative of the function f(x) at the point x 0 .

• Solution. The value of the derivative at the point of tangency is equal to the slope of the tangent, which in turn is equal to the tangent of the angle of inclination of this tangent to the abscissa axis. Let's construct a triangle with vertices at points A (2; −2), B (2; 0), C (−6; 0). The angle of inclination of the tangent to the abscissa axis will be equal to angle, adjacent to angle ACB

The figure shows a graph of the function y = f(x) and a tangent to this graph at the abscissa point equal to 3. Find the value of the derivative of this function at the point x = 3.

To solve we use geometric meaning derivative: the value of the derivative of a function at a point is equal to the slope of the tangent to the graph of this function drawn at that point. Slope factor tangent is equal to the tangent of the angle between the tangent and the positive direction of the x-axis (tg α). Angle α = β, as crosswise angles with parallel lines y=0, y=1 and a secant-tangent. For triangle ABC

The figure shows the graph of the function y=f(x) and the tangent to it at the point with the abscissa xo. Find the value of the derivative of the function f(x) at the point xо.

• According to the properties of the tangent, the formula for the tangent to the function f(x) at the point x 0 is equal to
• y=f ′ (x 0)⋅x+b, b=const
• The figure shows that the tangent to the function f(x) at the point x0 passes through the points (-3;2), (5,4). Therefore, we can create a system of equations

The figure shows a graph y=f’(x)- derivative of a function f(x), defined on the interval (−6; 6). Find the number of points at which the tangent to the graph f(x) is parallel to or coincides with the straight line y = -3x-11.

• Answer: 4

f’(x0)=-3

Sources

• http://reshuege.ru/
• http://egemat.ru/prepare/B8.html
• http://bankege.ru/

Goals:

• Educational: repeat the basic formulas and rules of differentiation, the geometric meaning of the derivative; to develop the ability to comprehensively apply knowledge, skills, abilities and their transfer to new conditions; test students’ knowledge, skills and abilities on this topic in preparation for the Unified State Exam.
• Developmental: promote development mental operations: analysis, synthesis, generalization; formation of self-esteem skills.
• Educational: promote the desire for continuous improvement of one’s knowledge

Equipment:

• Multimedia projector.

Lesson type: systematization and generalizations.
Scope of knowledge: two lessons (90 min.)
Expected result: teachers use the acquired knowledge in practical application, while developing communication, creative and search skills, and the ability to analyze the task received.

Lesson structure:

1. Org. Moment, updating the knowledge necessary for the solution practical tasks from Unified State Examination materials.
2. Practical part (testing students' knowledge).
3. Reflection, creative homework

Consultation progress

I. Organizational moment.

Message of the lesson topic, lesson goals, motivation educational activities(through the creation of a problematic theoretical knowledge base).

II. Updating the subjective experience of students and their knowledge.

Review the rules and definitions.

1) if at a point the function is continuous and at it the derivative changes sign from plus to minus, then it is a maximum point;

2) if at a point the function is continuous and at it the derivative changes sign from minus to plus, then it is a minimum point.

• Critical points – these are internal points of the domain of definition of a function at which the derivative does not exist or is equal to zero.
• A sufficient sign of increase, descending functions .
• If f "(x)>0 for all x from the interval (a; b), then the function increases on the interval (a; b).
• If f "(x)<0 для всех х из промежутка (а; в), то функция убывает на промежутке (а; в).

• Algorithm for finding the largest and the smallest values ​​of a function on the segment [a;b], if a graph of the derivative of the function is given:

If the derivative on a segment is positive, then a is the smallest value, b is the largest value.

If the derivative on a segment is negative, then a is the largest and b is the smallest value.

The geometric meaning of the derivative is as follows. If it is possible to draw a tangent to the graph of the function y = f(x) at the point with the abscissa x0 that is not parallel to the y-axis, then f "(x0) expresses the slope of the tangent: κ = f "(x0). Since κ = tanα, the equality f "(x0) = tanα is true

Let's consider three cases:

1. The tangent drawn to the graph of the function formed an acute angle with the OX axis, i.e. α< 90º. Производная положительная.
2. The tangent formed an obtuse angle with the OX axis, i.e. α > 90º. The derivative is negative.
3. The tangent is parallel to the OX axis. The derivative is zero.

Task 1. The figure shows a graph functions y = f(x) and the tangent to this graph drawn at the point with abscissa -1. Find the value of the derivative of the function f(x) at the point x0 = -1

Solution: a) The tangent drawn to the graph of the function forms an obtuse angle with the OX axis. Using the reduction formula, we find the tangent of this angle tg(180º - α) = - tanα. This means f "(x) = - tanα. From what we studied earlier, we know that the tangent is equal to the ratio of the opposite side to the adjacent side.

To do this, we build a right triangle so that the vertices of the triangle are at the vertices of the cells. We count the cells of the opposite side and the adjacent one. Divide the opposite side by the adjacent side. (Slide 44)

b) The tangent drawn to the graph of the function forms an acute angle with the OX axis.

f "(x)= tgα. The answer will be positive. (Slide 30)

Exercise 2. The figure shows a graph derivative function f(x), defined on the interval (-4; 13). Find the intervals of decreasing function. In your answer, indicate the length of the largest of them.

Solution: f "(x)< 0 функция убывает. Находим длину,который имеет наибольший участок.(Слайд 34)

Practical part.
35 min. The prepared slides require theoretical knowledge on the topic of the lesson. The purpose of the slides is to enable students to improve and practically apply knowledge.
Using slides you can:
- frontal survey (individual characteristics of students are taken into account);
- the information formulation of the main concepts, properties, definitions is clarified;
- algorithm for solving problems. Students must answer the slides.

IV. Individual work. Solving problems using slides.

V. Summing up the lesson, reflection.

CT skills Determine the value of a function by the value of the argument when
different ways of specifying a function; describe according to schedule
behavior and properties of functions, find functions from graphs
highest and lowest values; build graphs
functions studied
Calculate derivatives and antiderivatives of elementary
functions
Investigate functions for monotonicity in the simplest cases,
find the largest and smallest values ​​of functions
Contents of assignment B8 on IES
Function Research
4.2.1 Application of the derivative to the study of functions and
plotting
4.2.2 Examples of using the derivative to find
the best solution in applied, including socio-economic, problems

Memo to the student

Task B8 to calculate the derivative. For
student must be able to solve a task
calculate the value of a function from a known one
argument for different ways of specifying
functions and find derivatives and
antiderivatives of elementary functions.

Table
derivatives
f' (x)
formulas
WITH"
0
(x)"
1
(xa)"
sin"x
ax a 1
when a≠1
cos x
сos"x
sin x
tg"x
1
cos 2 x
1
sin 2 x
ctg"x
(ex)"
ex
(ax)"
a x ln a
ln"x
1
x
loga"x
1
x ln a
(f+g)"
f"g"
(f∙g)"
f "g fg"
(cf)"
cf"
f`
g
(f "g fg")
g2
(f(kx+b)) "
kf " (kx b)
(f(g(x))) "
f " (g(x)) g" (x)

Prototype of task B8 (No. 27485)

The straight line y=7x-5 is parallel to the tangent to the graph of the function y=x2+6x-8
. Find the abscissa of the tangent point.
k=7 , then f "(x0)=7
find the derivative of the function y=x2+6x-8,
we get:
f "(x)=2x+6; f "(x0)= 2x0+6
f "(x0)=7
2x0+6=7
2x0=1
x0=0.5
Solution
Answer:x0=0.5

Task B8 (No. 6009)
The straight line y=6x+8 is parallel to the tangent to the graph of the function y=x2-3x+5. Find the abscissa of the point
touch.
Task B8 (No. 6011)
The straight line y=7x+11 is parallel to the tangent to the graph of the function y=x2+8x+6. Find the abscissa of the point
touch.
Task B8 (No. 6013)
The line y=4x+8 is parallel to the tangent to the graph of the function y=x2-5x+7. Find the abscissa of the tangent point.
Task B8 (No. 6015)
The straight line y=3x+6 is parallel to the tangent to the graph of the function y=x2-5x+8. Find the abscissa of the point
touch.
Task B8 (No. 6017)
The straight line y=8x+11 is parallel to the tangent to the graph of the function y=x2+5x+7. Find the abscissa of the point
touch.
Task B8 (No. 6019)
The straight line y=-5x+4 is parallel to the tangent to the graph of the function y=x2+3x+6. Find the abscissa of the point
touch.
Examination
ANSWERS: No. 6009: 4.5
№ 6011: -0,5
№ 6013: 4,5
№ 6015: 4
№ 6017: 1,5
№ 6019: -4

Prototype of task B8 (No. 27487)

The figure shows a graph of the function y=f(x), defined on the interval (-6;8). Define
function is positive.
f(x) increases by [-3;0] and by .
This means that the derivative of the function is positive on
these segments, the number of integer points is 4
Answer: 4
Solution

Tasks for independent solution

Task B8 (No. 6399)

defined on the interval (-9;8). Define
number of integer points at which the derivative
function f(x) is positive.
Task B8 (No. 6869)
The figure shows a graph of the function y=f(x),
defined on the interval (-5;6). Define
number of integer points at which the derivative
function is positive.
ANSWERS: No. 6399: 7
№ 6869: 5
Examination

Prototype of task B8 (No. 27488)
The figure shows a graph of the function y=f(x) defined on the interval (-5;5) Determine the number
integer points at which the derivative of the function f(x) is negative.
f(x) decreases by [-4;1] and by .
This means the derivative of the function is negative
on these segments. Number of whole points 4
Solution
ANSWER:4

Tasks for independent solution

Task B8 (No. 6871)
The figure shows a graph of the function y=f(x),
defined on the interval (-1;12). Define
number of integer points at which the derivative
function is negative.
Task B8 (No. 6873)
The figure shows a graph of the function y=f(x),
defined on the interval (-7;7). Define
number of integer points at which the derivative
function is negative.
ANSWERS: No. 6771: 3
№ 6873: 3
Examination

Prototype of task B8 (No. 27489)

The figure shows a graph of the function y=f(x), defined on the interval (-5;5). Find the number of points
in which the tangent to the graph of the function is parallel to the straight line y=6 or coincides with it.
K=0
Answer: 4 points
Solution

Tasks for independent solution

Task B8 (No. 6401)
The figure shows a graph of the function y=f(x),
defined on the interval (-9;8). Find
number of points at which the tangent to the graph
function parallel to the line y=10
Task B8 (No. 6421)
The figure shows a graph of the function y=f(x),
defined on the interval (-5;5)Find
number of points at which the tangent to
graph of the function is parallel to the straight line y=6
ANSWERS: No. 6401: 6
№ 6421: 4
Examination

Prototype of task B8 (No. 27490)

The figure shows a graph of the function y=f(x), defined on the interval (-2;12).
Find the sum of the extremum points of the function f(x).
The function has 7 extremum points; 1, 2, 4, 7, 9, 10,
11.
Let's find their sum 1+2+4+7+9+10+11=44
Solution
ANSWER:44

Tasks for independent solution

Task B8 (No. 7329)


extremum points of the function f(x).
Examination
Task B8 (No. 7331)
The figure shows the graph of the function y=f(x),
defined on the interval (-7;5). Find the amount
extremum points of the function f(x).
ANSWERS: No. 7329: 0
№ 7331: -10

Prototype of task B8 (No. 27491)

The figure shows a graph of the derivative of the function f(x), defined on the interval (-8;3). At what point
segment [-3;2] f(x) takes the greatest value.
On the segment [-3;2] f(x) takes the greatest
value equal to 0 at x= -3.
ANSWER: -3
Solution

Tasks for independent solution

Task B8 (No. 6413)

function f(x), defined on the interval (-6;6). IN
what point [-5;-1] of the segment f(x) takes
greatest value.
Task B8 (No. 6415)
The figure shows a graph of the derivative
function f(x) defined on the interval (-6:6). IN
what point of the segment f(x) takes
greatest value.
ANSWERS: #6413: -5
№6415: 3
Examination

Prototype of task B8 (No. 27492)

The figure shows a graph of the derivative of the function f(x), defined on the interval (-8;4). At what point
segment [-7;-3] f(x) takes the smallest value.
On the segment [-7;-3] f(x) takes
the smallest value is 0 at x= -7.
ANSWER: -7
Solution

Tasks for independent solution

Task B8 (No. 6403)

f(x) defined on the interval (-9;8) . Which
point of the segment [-8;-4] f(x) takes the smallest
meaning.
Task B8 (No. 6405)
The figure shows a graph of the derivative
function f(x), defined on the interval (-9;8). IN
what point of the segment f(x) takes
lowest value.
ANSWERS: No. 6403: -4
№6405: 3
Examination

Prototype of task B8 (No. 27503)

The figure shows a graph of the function y=f(x) and a tangent to it at the point with the abscissa x0. Find

α
f(x0)= k= tgA
Consider a right triangle. IN
German tgα= 2/1 = 2
f(x0)=2
Solution
ANSWER:2

Tasks for independent solution

Task B8 (No. 9051)
The figure shows a graph of the function y=f(x) and
tangent to it at the point with abscissa x0. Find
the value of the derivative of the function f(x) at the point x0.
Task B8 (No. 9055)
The figure shows the graph of the function and
tangent to it at the abscissa point. Find
the value of the derivative of a function at a point.
ANSWERS: #9051: -0.25
№9055: 0,5
Examination

Prototype of task B8 (No. 27494)

The figure shows a graph of the derivative of the function f(x), defined on the interval (-7;14). Find
number of maximum points of the function f(x) on the segment [-6;9]
On the segment [-6;9] the function f(x) changes 5 times
character of monotony, from increasing to
decreasing, which means it has 5 maximum points.
Solution
ANSWER:4

Tasks for independent solution

Task B8 (No. 7807)
The figure shows a graph of the derivative of the function
f(x), defined on the interval (-4;16). Find
number of maximum points of the function f(x) on
segment.
Task B8 (No. 7817)
The figure shows a graph of the derivative
function f(x), defined on the interval (13;8). Find the number of maximum points
function f(x) on the interval [-8;6].
ANSWERS: No. 6413: 4
№6415: 4
Examination

List of recommended literature
The most complete edition of standard versions of real Unified State Examination tasks: 2010: Mathematics / author's compilation. I.R. Vysotsky, D.D. Gushchin, P.I. Zakharov and others; edited by A.L. Semenova, I.V. Yashchenko. –
M.:AST:Astrel, 2010. – 93, (3) p. – (Federal Institute of Pedagogical Measurements)
Mathematics: thematic planning of lessons in preparation for the exam / Beloshistaya.V.
A. – M: Publishing house “Exam”, 2007. – 478 (2) p. (Series “Unified State Exam 2007. Lesson
planning")
Mathematics: independent preparation for the Unified State Exam / L.D. Lappo, M.A. Popov. – 3rd ed.,
reworked And additional - M.: Publishing house “Exam”, 2009. – 381, (3) p. (Series “Unified State Exam.
Intensive")
Mathematics. Solving group B problems / Yu.A. Glazkov, I.A. Varshavsky, M.Ya. Gaiashvilli.
– M.: Publishing house “Exam”, 2009. – 382 (2) p. (Series “Unified State Exam. 100 points”)
Mathematics: training thematic tasks of increased difficulty with answers
for preparation for the Unified State Exam and other forms of final and entrance examinations /comp.
G.I. Kovaleva, T.I. Buzulina, O.L. Bezrukova, Yu.A. Rose. _ Volgograd: Teacher, 20089, 494 p.
Shabunin M.I. and others. Algebra and the beginnings of analysis: Didactic materials for grades 10-11. –
3rd ed. – M.: Mnemosyne, 2000. – 251 p.: ill.

Internet site addresses
www.fipi.ru – Federal Institute of Pedagogical Measurements (FIPI). Pay special attention
attention to the section “Open segment of FBTZ” - this is a system for preparing for the Unified State Exam - online. You can answer questions from the Unified State Exam task bank in various subjects, as well as
selected topic.
http://mathege.ru -Open bank of Unified State Exam problems in mathematics. The main task of an open bank
Unified State Exam assignments in mathematics - give an idea of ​​what tasks will be included in the options
Unified State Examination in Mathematics in 2010, and help graduates
to help you prepare for the exam. Here you can find all the test exams for the Unified State Examination
mathematics that have already been completed.
http://egetrener.ru/ - mathematics: video lessons, solving Unified State Exam problems.
http://ege-trener.ru/ - very exciting and effective preparation for the Unified State Exam in mathematics.
Register and try to get into the top 30!
uztest.ru - free materials for preparing for the Unified State Exam (and not only the Unified State Exam) in mathematics:
interactive thematic simulators, the ability to enroll in free on-line courses on
preparation for the Unified State Exam.
www.ege.edu.ru is the official information portal of the unified state exam.
On-line video lectures "Consultations on the Unified State Exam" in all subjects.
Videos of the Unified State Exam category. Lectures on mathematics
http://www.alexlarin.narod.ru/ege.html - materials for preparing for the Unified State Exam in mathematics (website
Larin Alexander Alexandrovich).
http://www.diary.ru/~eek/ - a community that provides assistance in solving problems in mathematics,
Here you can download many useful books on mathematics, including those for preparing for the Unified State Exam.
http://4ege.ru/ - Unified State Exam portal, everything latest for the Unified State Exam. All information about the exam. Unified State Exam 2010.