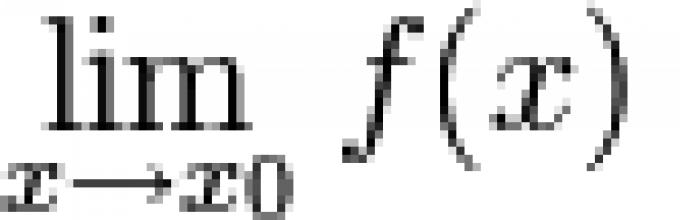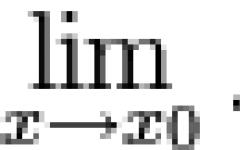Արդյո՞ք ֆունկցիան անվերջ փոքր է. Անսահման մեծ ֆունկցիայի սահմանում: Սահմանափակ հաջորդականության սահմանում

Անվերջ փոքրերի և մեծերի հաշվարկ

Անսահման փոքր հաշվարկ- անվերջ փոքր մեծություններով կատարված հաշվարկներ, որոնցում ստացված արդյունքը համարվում է անվերջ փոքրերի գումար. Անվերջ փոքրերի հաշվարկը դիֆերենցիալ և ինտեգրալ հաշվարկի ընդհանուր հասկացություն է, որը կազմում է ժամանակակից բարձրագույն մաթեմատիկայի հիմքը։ Անսահման փոքր մեծության հասկացությունը սերտորեն կապված է սահման հասկացության հետ։

Անսահման փոքր

Հաջորդականություն ա nկանչեց անսահման փոքր, Եթե . Օրինակ՝ թվերի հաջորդականությունը անվերջ փոքր է։

Ֆունկցիան կոչվում է անսահման փոքր՝ կետի մոտակայքում x 0 եթե .

Ֆունկցիան կոչվում է անսահման փոքր անսահմանության մեջ, Եթե կամ .

Նաև անվերջ փոքր է ֆունկցիան, որը ֆունկցիայի և նրա սահմանի տարբերությունն է, այսինքն՝ եթե , Դա զ(x) − ա = α( x) , .

Անսահման մեծ քանակությամբ

Ստորև բերված բոլոր բանաձևերում անսահմանությունը հավասարության աջ կողմում ենթադրվում է ունենալ որոշակի նշան (կամ «գումարած» կամ «մինուս»): Դա, օրինակ, ֆունկցիան է xմեղք x, անսահմանափակ երկու կողմից, անսահման մեծ չէ .

Հաջորդականություն ա nկանչեց անսահման մեծ, Եթե .

Ֆունկցիան կոչվում է անսահման մեծ կետի մոտակայքում x 0 եթե .

Ֆունկցիան կոչվում է անսահման մեծ անսահմանության մեջ, Եթե կամ .

Անսահման փոքրի և անսահման մեծի հատկությունները

Անսահման փոքր մեծությունների համեմատություն

Ինչպե՞ս համեմատել անսահման փոքր մեծությունները:
Անվերջ փոքր մեծությունների հարաբերակցությունը ձևավորում է այսպես կոչված անորոշություն։

Սահմանումներ

Ենթադրենք, որ մենք ունենք անվերջ փոքր արժեքներ α( x) և β( x) (կամ, որը սահմանման համար կարևոր չէ, անվերջ փոքր հաջորդականություններ)։

Նման սահմանները հաշվարկելու համար հարմար է օգտագործել L'Hopital-ի կանոնը։

Համեմատության օրինակներ

Օգտագործելով ՄԱՍԻՆ-սիմվոլիզմ, ստացված արդյունքները կարելի է գրել հետեւյալ ձեւով x 5 = o(x 3). Այս դեպքում ճշմարիտ են հետևյալ գրառումները. 2x 2 + 6x = Օ(x) Եվ x = Օ(2x 2 + 6x).

Համարժեք արժեքներ

Սահմանում

Եթե ​​, ապա կոչվում են α և β անվերջ փոքր մեծությունները համարժեք ().
Ակնհայտ է, որ համարժեք մեծությունները նույն փոքրության կարգի անվերջ փոքր մեծությունների հատուկ դեպք են։

Երբ վավեր են հետևյալ համարժեքության հարաբերությունները (որպես այսպես կոչված նշանակալի սահմանների հետևանք).

Թեորեմ

Երկու անվերջ փոքր մեծությունների գործակցի (հարաբերակցության) սահմանը չի փոխվի, եթե դրանցից մեկը (կամ երկուսը) փոխարինվի համարժեք մեծությամբ..

Այս թեորեմը գործնական նշանակություն ունի սահմաններ գտնելիս (տե՛ս օրինակ):

Օգտագործման օրինակ

Փոխարինելով սեսn 2x համարժեք արժեք 2 x, ստանում ենք

Պատմական ուրվագիծ

«Անվերջ փոքր» հասկացությունը քննարկվել է դեռևս հին ժամանակներում՝ կապված անբաժանելի ատոմների հայեցակարգի հետ, բայց դասական մաթեմատիկայի մեջ չի ներառվել։ Այն կրկին վերածնվեց 16-րդ դարում «անբաժանելիների մեթոդի» հայտնվելով՝ ուսումնասիրվող պատկերը բաժանելով անվերջ փոքր հատվածների։

17-րդ դարում տեղի է ունեցել անվերջ փոքր հաշվարկների հանրահաշիվը։ Դրանք սկսեցին սահմանվել որպես թվային մեծություններ, որոնք փոքր են ցանկացած վերջավոր (ոչ զրոյական) մեծությունից և դեռևս հավասար չեն զրոյի։ Վերլուծության արվեստը բաղկացած էր անվերջ փոքրեր (դիֆերենցիալներ) պարունակող հարաբերություն կազմելուց և այնուհետև ինտեգրելուց:

Հին դպրոցի մաթեմատիկոսները հայեցակարգը փորձության ենթարկեցին անսահման փոքրկոշտ քննադատություն. Միշել Ռոլեն գրել է, որ նոր հաշվարկը « հնարամիտ սխալների հավաքածու«; Վոլտերը կաուստիկ կերպով նկատեց, որ հաշվարկը այն իրերը հաշվարկելու և ճշգրիտ չափելու արվեստ է, որոնց գոյությունն ապացուցված չէ: Նույնիսկ Հյուգենսը խոստովանեց, որ չի հասկանում ավելի բարձր կարգի դիֆերենցիալների իմաստը:

Որպես ճակատագրի հեգնանք կարելի է համարել դարի կեսերին ոչ ստանդարտ վերլուծության ի հայտ գալը, որն ապացուցեց, որ սկզբնական տեսակետը` փաստացի անվերջ փոքրերը, նույնպես համահունչ էր և կարող էր օգտագործվել որպես վերլուծության հիմք:

տես նաեւ

Վիքիմեդիա հիմնադրամ. 2010 թ.

Տեսեք, թե ինչ է «Անվերջ փոքր քանակությունը» այլ բառարաններում.

ԱՆՍԱՀՄԱՆ ՓՈՔՐ ՔԱՆԱԿ- փոփոխական մեծություն որոշակի գործընթացում, եթե այս գործընթացում այն ​​անսահմանորեն մոտենում է (հակվում է) զրոյի... Մեծ պոլիտեխնիկական հանրագիտարան

Անսահման փոքր- ■ Անհայտ բան, բայց կապված հոմեոպաթիայի հետ... Ընդհանուր ճշմարտությունների բառարան

Գործառույթ y=f(x)կանչեց անսահման փոքրժամը x→aկամ երբ x→∞, եթե կամ, այսինքն. անվերջ փոքր ֆունկցիան այն ֆունկցիան է, որի սահմանը տվյալ կետում զրո է:

Օրինակներ.

1. Գործառույթ f(x)=(x-1) 2-ը անվերջ փոքր է x→1, քանի որ (տե՛ս նկարը):

2. Գործառույթ f(x)= tg x– անսահման փոքր ժամը x→0.

3. f(x)= տեղեկամատյան (1+ x) – անսահման փոքր ժամը x→0.

4. f(x) = 1/x– անսահման փոքր ժամը x→∞.

Եկեք հաստատենք հետևյալ կարևոր հարաբերությունները.

Թեորեմ.Եթե ​​ֆունկցիան y=f(x)հետ ներկայացվող x→aորպես հաստատուն թվի գումար բև անսահման փոքր մեծություն α(x): f (x)=b+ α(x)որ .

Եվ հակառակը, եթե, ապա f (x)=b+α(x), Որտեղ կացին)– անսահման փոքր ժամը x→a.

Ապացույց.

1. Փաստենք հայտարարության առաջին մասը. Հավասարությունից f(x)=b+α(x)պետք է |f(x) – b|=| α|. Բայց քանի որ կացին)անվերջ փոքր է, ապա կամայական ε-ի համար կա δ – կետի հարևանություն ա,բոլորի աչքի առաջ xորից՝ արժեքներ կացին)բավարարել հարաբերությունները |α(x)|< է. Հետո |f(x) – բ|< է. Եվ սա նշանակում է, որ.

2. Եթե , ապա ցանկացած ε >0 բոլորի համար Xորոշ δ – կետի հարևանությամբ ակամք |f(x) – բ|< է. Բայց եթե նշենք f(x) – b= α, Դա |α(x)|< ε, ինչը նշանակում է, որ ա- անսահման փոքր:

Դիտարկենք անվերջ փոքր ֆունկցիաների հիմնական հատկությունները։

Թեորեմ 1.Երկու, երեք և ընդհանրապես անվերջ փոքրերի ցանկացած վերջավոր թվի հանրահաշվական գումարը անվերջ փոքր ֆունկցիա է։

Ապացույց. Եկեք ապացույցներ տանք երկու ժամկետով. Թող f(x)=α(x)+β(x), որտեղ և. Մենք պետք է ապացուցենք, որ ցանկացած կամայական փոքր ε > Գտնվել է 0 δ> 0, այնպիսին, որ համար x, բավարարելով անհավասարությունը |x – ա|<δ , կատարվեց |զ(x)|< ε.

Այսպիսով, եկեք ամրագրենք կամայական ε > 0. Քանի որ ըստ թեորեմի պայմանների α(x)անվերջ փոքր ֆունկցիա է, ուրեմն կա այդպիսի δ 1 > 0, որը |x – ա|< δ 1 ունենք |α(x)|< ε / 2. Նմանապես, քանի որ β(x)անվերջ փոքր է, ուրեմն կա այդպիսի δ 2 > 0, որը |x – ա|< δ 2 ունենք | β(x)|< ε / 2.

Վերցնենք δ=min(δ 1 , δ2 } .Այնուհետև կետի մոտակայքում աշառավիղը δ անհավասարություններից յուրաքանչյուրը կբավարարվի |α(x)|< ε / 2 և | β(x)|< ε / 2. Հետեւաբար, այս հարեւանությամբ կլինի

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

դրանք. |զ(x)|< ε, ինչը պետք է ապացուցվեր:

Թեորեմ 2.Անվերջ փոքր ֆունկցիայի արտադրյալ կացին)սահմանափակ գործառույթի համար f(x)ժամը x→a(կամ երբ x→∞) անվերջ փոքր ֆունկցիա է։

Ապացույց. Քանի որ գործառույթը f(x)սահմանափակ է, ապա կա քանակ Մայնպես, որ բոլոր արժեքների համար xկետի ինչ-որ հարևանությամբ a|f(x)|≤M.Ավելին, քանի որ կացին)ժամը անվերջ փոքր ֆունկցիա է x→a, ապա կամայական ε > 0 կա կետի հարևանություն ա, որում կպահպանվի անհավասարությունը |α(x)|< ε /Մ. Հետո այս թաղամասերից ավելի փոքրում մենք ունենք | αf|< ε /Մ= է. Իսկ սա նշանակում է, որ աֆ- անսահման փոքր: Առիթով x→∞ապացույցն իրականացվում է նույն կերպ.

Ապացուցված թեորեմից հետևում է.

Եզրակացություն 1.Եթե ​​և, ապա.

Եզրակացություն 2.Եթե գ= const, ապա .

Թեորեմ 3.Անվերջ փոքր ֆունկցիայի հարաբերակցությունը α(x)ըստ գործառույթի f(x), որի սահմանը տարբերվում է զրոյից, անվերջ փոքր ֆունկցիա է։

Ապացույց. Թող . Հետո 1 /f(x)սահմանափակ գործառույթ կա. Հետևաբար, կոտորակը անվերջ փոքր ֆունկցիայի և սահմանափակ ֆունկցիայի արտադրյալն է, այսինքն. ֆունկցիան անսահման փոքր է:

Def:Ֆունկցիան կոչվում է անսահման փոքրժամը , եթե .

« » նշումով մենք կենթադրենք, որ x 0որպես վերջնական արժեք կարող է ընդունվել՝ x 0= Սոնստ, և անսահման: x 0= ∞.

Անվերջ փոքր ֆունկցիաների հատկությունները.

1) Անվերջ թվով անվերջ փոքր ֆունկցիաների հանրահաշվական գումարը ֆունկցիաների անվերջ փոքր գումար է:

2) Անվերջ թվով անվերջ փոքր ֆունկցիաների արտադրյալը անվերջ փոքր ֆունկցիա է:

3) Սահմանափակված ֆունկցիայի և անվերջ փոքր ֆունկցիայի արտադրյալը անվերջ փոքր ֆունկցիա է:

4) Անվերջ փոքր ֆունկցիան բաժանելու գործակիցը, որի սահմանը ոչ զրոյական է, անվերջ փոքր ֆունկցիա է:

Օրինակ: Գործառույթ y = 2 + xանսահման փոքր է, քանի որ .

Def:Ֆունկցիան կոչվում է անսահման մեծժամը , եթե .

Անսահման մեծ ֆունկցիաների հատկությունները.

1) Անսահման մեծ ֆունկցիաների գումարը անսահման մեծ ֆունկցիա է:

2) Անսահման մեծ ֆունկցիայի և ֆունկցիայի արտադրյալը, որի սահմանը զրոյական չէ, անսահման մեծ ֆունկցիա է:

3) Անսահման մեծ ֆունկցիայի և սահմանափակված ֆունկցիայի գումարը անսահման մեծ ֆունկցիա է:

4) Անսահման մեծ ֆունկցիան վերջավոր սահման ունեցող ֆունկցիայի վրա բաժանելու գործակիցը անսահման մեծ ֆունկցիա է:

Օրինակ: Գործառույթ y= անսահման մեծ է , քանի որ .

Թեորեմ.Անսահման փոքր և անսահման մեծ քանակությունների փոխհարաբերությունները. Եթե ​​ֆունկցիան անվերջ փոքր է ժամը , ապա ֆունկցիան անսահման մեծ է ժամը . Եվ հակառակը, եթե ֆունկցիան անսահման մեծ է , ապա ֆունկցիան անվերջ փոքր է .

Երկու անվերջ փոքրերի հարաբերակցությունը սովորաբար նշվում է խորհրդանիշով, իսկ երկու անվերջ փոքրերի հարաբերակցությունը՝ նշանով։ Երկու հարաբերություններն էլ անորոշ են այն իմաստով, որ դրանց սահմանը կարող է լինել կամ չլինել, հավասար լինել որոշակի թվի կամ լինել անսահման՝ կախված անորոշ արտահայտություններում ներառված կոնկրետ ֆունկցիաների տեսակից։

Տիպի և անորոշությունների անորոշություններից բացի, հետևյալ արտահայտություններն են.

Նույն նշանի անսահման մեծերի տարբերությունը.

Անվերջ փոքրի արտադրյալը անսահման մեծով;

Էքսպոնենցիալ ֆունկցիա, որի հիմքը հակված է 1-ի, իսկ աստիճանը՝ դեպի ;

Էքսպոնենցիալ ֆունկցիա, որի հիմքը անվերջ փոքր է, իսկ աստիճանը՝ անսահման մեծ;

Էքսպոնենցիալ ֆունկցիա, որի հիմքը և աստիճանը անվերջ փոքր են.

Էքսպոնենցիալ ֆունկցիա, որի հիմքը անսահման մեծ է, իսկ աստիճանը՝ անվերջ փոքր։

Ասում են՝ կա համապատասխան տեսակի անորոշություն։ Սահմանաչափի հաշվարկը կոչվում է այս դեպքերում անորոշության բացահայտում. Անորոշությունը բացահայտելու համար սահմանային նշանի տակ գտնվող արտահայտությունը վերածվում է մի ձևի, որը չի պարունակում անորոշություն:

Սահմանները հաշվարկելիս օգտագործվում են սահմանների հատկությունները, ինչպես նաև անվերջ փոքր և անսահման մեծ ֆունկցիաների հատկությունները։

Դիտարկենք տարբեր սահմանաչափերի հաշվարկների օրինակներ։

1) . 2) .

4) , որովհետեւ ժամը և սահմանափակ ֆունկցիայի անվերջ փոքր ֆունկցիայի արտադրյալ անսահման փոքր է.

5) . 6) .

7) = =

. Տվյալ դեպքում առկա էր տիպի անորոշություն, որը լուծվում էր բազմանդամները գործակցելով և դրանք հասցնելով ընդհանուր գործոնի։

= .

Այս դեպքում կար տիպի անորոշություն, որը լուծվում էր համարիչն ու հայտարարը բազմապատկելով արտահայտությամբ, բանաձևով, այնուհետև կոտորակը կրճատելով (+1-ով):

9)
. Այս օրինակում տիպային անորոշությունը բացահայտվեց կոտորակի համարիչն ու հայտարարը առաջատար հզորության վրա բաժանելով։

Հրաշալի սահմաններ

Առաջին հրաշալի սահմանը : .

Ապացույց.Դիտարկենք միավորի շրջանագիծը (նկ. 3):

Նկ.3. Միավոր շրջանակ

Թող X– կենտրոնական անկյան ճառագայթային չափումը MOA(), Հետո ՕԱ = Ռ= 1, ՄԿ= մեղք x, AT= tg x. Եռանկյունների մակերեսների համեմատություն ՕՄԱ, OTAև ոլորտները ՕՄԱ, ստանում ենք.

,

.

Վերջին անհավասարությունը բաժանեք մեղքի վրա x, ստանում ենք.

.

Քանի որ ժամը , ապա ըստ սեփականության 5) սահմանները

Հենց այստեղից է գալիս հակադարձ արժեքը, ինչը պետք է ապացուցվեր:

Մեկնաբանություն:Եթե ​​ֆունկցիան անվերջ փոքր է, այսինքն. , ապա առաջին ուշագրավ սահմանը ունի ձևը.

.

Դիտարկենք սահմանաչափի հաշվարկների օրինակներ՝ օգտագործելով առաջին ուշագրավ սահմանը:

Այս սահմանը հաշվարկելիս մենք օգտագործել ենք եռանկյունաչափական բանաձևը. .

.

Դիտարկենք սահմանաչափի հաշվարկների օրինակներ՝ օգտագործելով երկրորդ ուշագրավ սահմանը:

2) .

3) . Տիպային անորոշություն կա. Եկեք փոխարինում անենք, ուրեմն; ժամը .

Անվերջ փոքրերի և մեծերի հաշվարկ

Անսահման փոքր հաշվարկ- անվերջ փոքր մեծություններով կատարված հաշվարկներ, որոնցում ստացված արդյունքը համարվում է անվերջ փոքրերի գումար. Անվերջ փոքրերի հաշվարկը դիֆերենցիալ և ինտեգրալ հաշվարկի ընդհանուր հասկացություն է, որը կազմում է ժամանակակից բարձրագույն մաթեմատիկայի հիմքը։ Անսահման փոքր մեծության հասկացությունը սերտորեն կապված է սահման հասկացության հետ։

Անսահման փոքր

Հաջորդականություն ա nկանչեց անսահման փոքր, Եթե . Օրինակ՝ թվերի հաջորդականությունը անվերջ փոքր է։

Ֆունկցիան կոչվում է անսահման փոքր՝ կետի մոտակայքում x 0 եթե .

Ֆունկցիան կոչվում է անսահման փոքր անսահմանության մեջ, Եթե կամ .

Նաև անվերջ փոքր է ֆունկցիան, որը ֆունկցիայի և նրա սահմանի տարբերությունն է, այսինքն՝ եթե , Դա զ(x) − ա = α( x) , .

Անսահման մեծ քանակությամբ

Հաջորդականություն ա nկանչեց անսահման մեծ, Եթե .

Ֆունկցիան կոչվում է անսահման մեծ կետի մոտակայքում x 0 եթե .

Ֆունկցիան կոչվում է անսահման մեծ անսահմանության մեջ, Եթե կամ .

Բոլոր դեպքերում, հավասարության իրավունքի անսահմանությունը ենթադրվում է ունենալ որոշակի նշան (կամ «գումարած» կամ «մինուս»): Դա, օրինակ, ֆունկցիան է xմեղք xանսահման մեծ չէ ժամը .

Անսահման փոքրի և անսահման մեծի հատկությունները

Անսահման փոքր մեծությունների համեմատություն

Ինչպե՞ս համեմատել անսահման փոքր մեծությունները:
Անվերջ փոքր մեծությունների հարաբերակցությունը ձևավորում է այսպես կոչված անորոշություն։

Սահմանումներ

Ենթադրենք, որ մենք ունենք անվերջ փոքր արժեքներ α( x) և β( x) (կամ, որը սահմանման համար կարևոր չէ, անվերջ փոքր հաջորդականություններ)։

Նման սահմանները հաշվարկելու համար հարմար է օգտագործել L'Hopital-ի կանոնը։

Համեմատության օրինակներ

Օգտագործելով ՄԱՍԻՆ-սիմվոլիզմ, ստացված արդյունքները կարելի է գրել հետեւյալ ձեւով x 5 = o(x 3). Այս դեպքում ճշմարիտ են հետևյալ գրառումները. 2x 2 + 6x = Օ(x) Եվ x = Օ(2x 2 + 6x).

Համարժեք արժեքներ

Սահմանում

Եթե ​​, ապա կոչվում են α և β անվերջ փոքր մեծությունները համարժեք ().
Ակնհայտ է, որ համարժեք մեծությունները նույն փոքրության կարգի անվերջ փոքր մեծությունների հատուկ դեպք են։

Երբ վավեր են հետևյալ համարժեքության հարաբերությունները. .

Թեորեմ

Երկու անվերջ փոքր մեծությունների գործակցի (հարաբերակցության) սահմանը չի փոխվի, եթե դրանցից մեկը (կամ երկուսը) փոխարինվի համարժեք մեծությամբ..

Այս թեորեմը գործնական նշանակություն ունի սահմաններ գտնելիս (տե՛ս օրինակ):

Օգտագործման օրինակ

Փոխարինելով սեսn 2x համարժեք արժեք 2 x, ստանում ենք

Պատմական ուրվագիծ

«Անվերջ փոքր» հասկացությունը քննարկվել է դեռևս հին ժամանակներում՝ կապված անբաժանելի ատոմների հայեցակարգի հետ, բայց դասական մաթեմատիկայի մեջ չի ներառվել։ Այն կրկին վերածնվեց 16-րդ դարում «անբաժանելիների մեթոդի» հայտնվելով՝ ուսումնասիրվող պատկերը բաժանելով անվերջ փոքր հատվածների։

17-րդ դարում տեղի է ունեցել անվերջ փոքր հաշվարկների հանրահաշիվը։ Դրանք սկսեցին սահմանվել որպես թվային մեծություններ, որոնք փոքր են ցանկացած վերջավոր (ոչ զրոյական) մեծությունից և դեռևս հավասար չեն զրոյի։ Վերլուծության արվեստը բաղկացած էր անվերջ փոքրեր (դիֆերենցիալներ) պարունակող հարաբերություն կազմելուց և այնուհետև ինտեգրելուց:

Հին դպրոցի մաթեմատիկոսները հայեցակարգը փորձության ենթարկեցին անսահման փոքրկոշտ քննադատություն. Միշել Ռոլեն գրել է, որ նոր հաշվարկը « հնարամիտ սխալների հավաքածու«; Վոլտերը կաուստիկ կերպով նկատեց, որ հաշվարկը այն իրերը հաշվարկելու և ճշգրիտ չափելու արվեստ է, որոնց գոյությունն ապացուցված չէ: Նույնիսկ Հյուգենսը խոստովանեց, որ չի հասկանում ավելի բարձր կարգի դիֆերենցիալների իմաստը:

Որպես ճակատագրի հեգնանք կարելի է համարել դարի կեսերին ոչ ստանդարտ վերլուծության ի հայտ գալը, որն ապացուցեց, որ սկզբնական տեսակետը` փաստացի անվերջ փոքրերը, նույնպես համահունչ էր և կարող էր օգտագործվել որպես վերլուծության հիմք:

տես նաեւ

Վիքիմեդիա հիմնադրամ. 2010 թ.

Տեսեք, թե ինչ է «Անսահման մեծ» բառը այլ բառարաններում.

Y փոփոխական մեծությունը X անվերջ փոքր մեծության հակադարձն է, այսինքն՝ Y = 1/X... Մեծ Հանրագիտարանային բառարան

y փոփոխականը անվերջ փոքր x-ի հակադարձն է, այսինքն՝ y = 1/x: * * * ԱՆՎԵՐՋ ՄԵԾ ԱՆՎԵՐՋ ՄԵԾ, փոփոխական մեծություն Y, հակադարձ անվերջ փոքր X մեծությանը, այսինքն՝ Y = 1/X ... Հանրագիտարանային բառարան

Մաթեմատիկայի մեջ փոփոխական մեծություն, որը փոփոխության տվյալ գործընթացում դառնում և մնում է բացարձակ արժեքով ավելի մեծ, քան ցանկացած կանխորոշված ​​թիվ։ Բ.-ի ուսումնասիրություն. քանակները կարող են կրճատվել մինչև անվերջ փոքրերի ուսումնասիրությունը (Տես... ... Խորհրդային մեծ հանրագիտարան

Ֆունկցիան կոչվում է անսահման փոքր ժամը
կամ երբ
, Եթե
կամ
.

Օրինակ՝ ֆունկցիա
անսահման փոքր ժամը
; ֆունկցիան
անսահման փոքր ժամը
.

Ծանոթագրություն 1. Առանց փաստարկի փոփոխության ուղղությունը նշելու՝ ոչ մի ֆունկցիա չի կարելի անվանել անվերջ փոքր։ Այո, գործառույթը
ժամը
անսահման փոքր է, և երբ
դա այլևս անսահման փոքր չէ (
).

Ծանոթագրություն 2. Մի կետում ֆունկցիայի սահմանի սահմանումից անվերջ փոքր ֆունկցիաների համար գործում է հետևյալ անհավասարությունը.
Այս փաստը մենք հետագայում կօգտագործենք մեկից ավելի անգամ։

Սահմանենք մի քանի կարևոր անվերջ փոքր ֆունկցիաների հատկությունները.

Թեորեմ (ֆունկցիայի, դրա սահմանի և անվերջ փոքրի միջև կապի մասին). Եթե ֆունկցիան
կարող է ներկայացվել որպես հաստատուն թվի գումար Աև անսահման փոքր ֆունկցիա
ժամը
, ապա համարը

Ապացույց:

Թեորեմի պայմաններից հետևում է, որ ֆունկցիան
.

Այստեղից արտահայտվենք
:
. Քանի որ գործառույթը
անվերջ փոքր, անհավասարությունը պահպանվում է դրա համար
, ապա արտահայտության համար (
) անհավասարությունը նույնպես պահպանվում է

Իսկ սա նշանակում է, որ
.

Թեորեմ (հակադարձ). Եթե
, ապա ֆունկցիան
կարող է ներկայացվել որպես թվի գումար Աեւ անսահման փոքր ժամը
գործառույթները
, այսինքն.
.

Ապացույց:

Որովհետեւ
, ապա համար
անհավասարությունը պահպանվում է
(*) Դիտարկենք ֆունկցիան
որպես մեկ և վերագրեք անհավասարությունը (*) ձևով

Վերջին անհավասարությունից հետևում է, որ արժեքը (
) անսահման փոքր է
. Նշանակենք
.

Որտեղ
. Թեորեմն ապացուցված է.

Թեորեմ 1 . Անվերջ թվով անվերջ փոքր ֆունկցիաների հանրահաշվական գումարը անվերջ փոքր ֆունկցիա է։

Ապացույց:

Ապացուցումն իրականացնենք երկու անդամի համար, քանի որ ցանկացած վերջավոր թվով անդամների համար այն տրված է նույն ձևով։

Թող
Եվ
անսահման փոքր ժամը
գործառույթներ և
- այս գործառույթների գումարը: Եկեք ապացուցենք դա
, նման բան կա
դա բոլորի համար է X, բավարարելով անհավասարությունը
, անհավասարությունը պահպանվում է
.

Քանի որ գործառույթը
անսահման փոքր ֆունկցիա
դա բոլորի համար է
անհավասարությունը պահպանվում է
.

Քանի որ գործառույթը
անսահման փոքր ֆունկցիա
, և հետևաբար կա այդպիսին դա բոլորի համար է
անհավասարությունը պահպանվում է
.

Վերցնենք հավասար է փոքր թվին Եվ , ապա ներս - կետի հարևանությունը Աանհավասարությունները կբավարարվեն
,
.

Եկեք ստեղծենք ֆունկցիոնալ մոդուլ
և գնահատել դրա նշանակությունը։

Այն է
, ապա ֆունկցիան անվերջ փոքր է, ինչն էլ պետք է ապացուցել։

Թեորեմ 2. Անվերջ փոքր ֆունկցիայի արտադրյալ
ժամը
սահմանափակ գործառույթի համար
անվերջ փոքր ֆունկցիա է։

Ապացույց:

Քանի որ գործառույթը
սահմանափակված, ապա կա դրական թիվ
դա բոլորի համար է անհավասարությունը պահպանվում է
.

Քանի որ գործառույթը
անսահման փոքր ժամը
, ապա կա այդպիսին - կետի հարևանություն դա բոլորի համար է այս հարևանությամբ անհավասարությունը պահպանվում է
.

Հաշվի առեք գործառույթը
և գնահատել դրա մոդուլը

Այսպիսով
, եւ հետո
- անսահման փոքր:

Թեորեմն ապացուցված է.

Սահմանային թեորեմներ.

Թեորեմ 1. Վերջավոր թվով ֆունկցիաների հանրահաշվական գումարի սահմանը հավասար է այս ֆունկցիաների սահմանների հանրահաշվական գումարին.

Ապացույց:

Դա ապացուցելու համար բավական է դիտարկել երկու գործառույթ՝ սա չի խախտի պատճառաբանության ընդհանրությունը։

Թող
,
.

Համաձայն ֆունկցիայի, նրա սահմանի և անվերջ փոքր ֆունկցիայի կապի թեորեմի
Եվ
կարող է ներկայացվել ձևով
Որտեղ
Եվ
– անսահման փոքր ժամը
.

Գտնենք ֆունկցիաների գումարը
Եվ

Մեծություն
կա հաստատուն արժեք
- քանակը անսահման փոքր է: Այսպիսով, գործառույթը
ներկայացված է որպես հաստատուն արժեքի և անվերջ փոքր ֆունկցիայի գումար:

Հետո համարը
ֆունկցիայի սահմանն է
, այսինքն.

Թեորեմն ապացուցված է.

Թեորեմ 2 . Վերջավոր թվով ֆունկցիաների արտադրյալի սահմանը հավասար է այս ֆունկցիաների սահմանների արտադրյալին

Ապացույց:

Չկորցնելով պատճառաբանության ընդհանրությունը, մենք կիրականացնենք ապացուցումը երկու գործառույթի համար
Եվ
.

Թող այդպես լինի
,

Գտնենք ֆունկցիաների արտադրյալը
Եվ

Մեծություն
հաստատուն մեծություն է, անվերջ փոքր ֆունկցիա։ Հետեւաբար, թիվը
ֆունկցիայի սահմանն է
, այսինքն՝ հավասարությունը ճշմարիտ է

Հետևանք.
.

Թեորեմ 3. Երկու ֆունկցիաների քանորդի սահմանը հավասար է այս ֆունկցիաների սահմանների քանորդին, եթե հայտարարի սահմանը զրոյական չէ.

.

Ապացույց՝ թող
,

Հետո
,
.

Գտնենք գործակիցը և դրա վրա կատարել մի քանի նույնական փոխակերպումներ

Մեծություն հաստատուն, կոտորակ
անսահման փոքր: Հետեւաբար, գործառույթը ներկայացված է որպես հաստատուն թվի և անվերջ փոքր ֆունկցիայի գումար:

Հետո
.

Մեկնաբանություն. Գործի համար 1–3 թեորեմներն ապացուցված են
. Այնուամենայնիվ, դրանք կարող են կիրառվել, երբ
, քանի որ թեորեմների ապացուցումն այս դեպքում կատարվում է նույն կերպ։

Օրինակ. Գտեք սահմանները.

Առաջինն ու երկրորդը հրաշալի սահմաններ են։

Գործառույթ սահմանված չէ
. Այնուամենայնիվ, դրա արժեքները զրոյական կետի մոտակայքում գոյություն ունեն: Հետևաբար, մենք կարող ենք դիտարկել այս ֆունկցիայի սահմանը ժամը
. Այս սահմանը կոչվում է առաջին հրաշալի սահման .

Կարծես թե.
.

Օրինակ . Գտեք սահմանները՝ 1.
. Նշանակել
, Եթե
, Դա
.
; 2.
. Եկեք փոխակերպենք այս արտահայտությունն այնպես, որ սահմանը կրճատվի մինչև առաջին նշանակալի սահմանը:
; 3..

Եկեք դիտարկենք ձևի փոփոխականը
, որտեղ ընդունում է բնական թվերի արժեքները աճման կարգով. Եկեք տանք տարբեր իմաստներ՝ եթե

Տալ հետևյալ արժեքները հավաքածուից
, հեշտ է տեսնել, որ արտահայտությունը
ժամը
կամք
. Ավելին, ապացուցված է, որ
սահման ունի. Այս սահմանը նշվում է տառով :
.

Թիվ իռացիոնալ:
.

Հիմա հաշվի առեք ֆունկցիայի սահմանը
ժամը
. Այս սահմանը կոչվում է երկրորդ ուշագրավ սահմանը

Կարծես թե
.

Օրինակ.

Ա)
. Արտահայտություն
փոխարինեք այն ապրանքով նույնական գործոններ
, մենք կիրառում ենք արտադրանքի սահմանային թեորեմը և երկրորդ ուշագրավ սահմանը. բ)
. դնենք
, Հետո
,
.

Երկրորդ ուշագրավ սահմանն օգտագործվում է շարունակական բարդացման խնդիր

Ավանդներից կանխիկ եկամուտը հաշվարկելիս հաճախ օգտագործվում է բարդ տոկոսադրույքի բանաձևը, որն ունի հետևյալ տեսքը.

,

Որտեղ - նախնական ներդրում,

- տարեկան բանկային տոկոսներ,

- տարեկան տոկոսագումարների քանակը,

- ժամանակ, տարիներով:

Այնուամենայնիվ, տեսական ուսումնասիրություններում ներդրումային որոշումները հիմնավորելիս հաճախ օգտագործում են էքսպոնենցիալ (էքսպոնենցիալ) աճի օրենքի բանաձևը.

.

Էքսպոնենցիալ աճի օրենքի բանաձևը ստացվել է բաղադրյալ տոկոսադրույքի բանաձևի երկրորդ ուշագրավ սահմանի կիրառման արդյունքում.

Գործառույթների շարունակականություն.

Հաշվի առեք գործառույթը
ինչ-որ պահի սահմանվում է և կետի որոշ հարևանություն . Թող ֆունկցիան ունենա նշված կետի արժեքը
.

Սահմանում 1. Ֆունկցիա
կանչեց շարունակական մի կետում , եթե այն սահմանվում է կետի հարևանությամբ, ներառյալ բուն կետը և
.

Շարունակականության սահմանումը կարելի է տարբեր կերպ ձևակերպել.

Թող գործառույթը
որոշված ​​արժեքով ,
. Եթե ​​փաստարկը ավելացում տալ
, ապա ֆունկցիան կստանա ավելացում

Թողեք ֆունկցիան կետում շարունակական (մի կետում ֆունկցիայի շարունակականության առաջին սահմանմամբ),

Այսինքն, եթե ֆունկցիան կետում շարունակական է , ապա արգումենտի անվերջ փոքր աճ
այս պահին համապատասխանում է ֆունկցիայի անվերջ փոքր աճը:

Ճիշտ է նաև հակառակը. եթե փաստարկի անվերջ փոքր աճը համապատասխանում է ֆունկցիայի անվերջ փոքր աճին, ապա ֆունկցիան շարունակական է:

Սահմանում 2. Ֆունկցիա
կոչվում է շարունակական ժամը
(կետում ), եթե այն սահմանվում է այս կետում և դրա շրջակայքի որոշ մասերում և եթե
.

Հաշվի առնելով կետում ֆունկցիայի շարունակականության առաջին և երկրորդ սահմանումները՝ կարող ենք ստանալ հետևյալ պնդումը.

կամ
, Բայց
, Հետո
.

Հետևաբար, շարունակական ֆունկցիայի սահմանը գտնելու համար ժամը
բավական է արգումենտի փոխարեն օգտագործել վերլուծական ֆունկցիայի արտահայտություն փոխարինել դրա արժեքը .

Սահմանում 3. Այն ֆունկցիան, որը շարունակական է որոշակի շրջանի յուրաքանչյուր կետում, կոչվում է շարունակական այս տարածքում.

Օրինակ:

Օրինակ 1. Ապացուցեք, որ ֆունկցիան
շարունակական է սահմանման տիրույթի բոլոր կետերում:

Եկեք օգտագործենք կետում ֆունկցիայի շարունակականության երկրորդ սահմանումը: Դա անելու համար վերցրեք փաստարկի ցանկացած արժեք և ավելացրեք այն
. Գտնենք ֆունկցիայի համապատասխան աճը

Օրինակ 2. Ապացուցեք, որ ֆունկցիան
շարունակական բոլոր կետերում -ից
.

Եկեք փաստարկենք ավելացում
, ապա ֆունկցիան կավելացվի

Եկեք գտնենք, քանի որ գործառույթը
, այսինքն՝ սահմանափակ։

Նմանապես, կարելի է ապացուցել, որ բոլոր հիմնական տարրական ֆունկցիաները շարունակական են իրենց սահմանման տիրույթի բոլոր կետերում, այսինքն՝ տարրական ֆունկցիայի սահմանման տիրույթը համընկնում է նրա շարունակականության տիրույթի հետ։

Սահմանում 4. Եթե ֆունկցիան
շարունակական որոշակի ընդմիջման յուրաքանչյուր կետում
, ապա ասում ենք, որ ֆունկցիան այս միջակայքում շարունակական է։