Проект по алгебре «Решение тригонометрических неравенств» Выполнила ученица 10 «Б» класса Казачкова Юлия Руководитель: учитель математики Кочакова Н.Н.
Цель Закрепить материал по теме «Решение тригонометрических неравенств» и создать памятку ученикам для подготовки к предстоящему экзамену.
Задачи Обобщить материал по данной теме. Систематизировать полученную информацию. Рассмотреть данную тему в ЕГЭ.
Актуальность Актуальность выбранной мною темы заключается в том, что задания на тему «Решение тригонометрических неравенств» входят в задания ЕГЭ.
Тригонометрические неравенства Неравенство - это отношение, связывающее два числа или выражения посредством одного из знаков: (больше); ≥ (больше или равно). Тригонометрическое неравенство – это неравенство, содержащее тригонометрические функции.
Тригонометрические неравенства Решение неравенств, содержащих тригонометрические функции, сводится, как правило, к решению простейших неравенств вида: sin x>a, sin xa, cos x a, tg x a, ctg x
Алгоритм решения тригонометрических неравенств На оси, соответствующей заданной тригонометрической функции, отметить данное числовое значение этой функции. Провести через отмеченную точку прямую, пересекающую единичную окружность. Выделить точки пересечения прямой и окружности с учетом строгого или нестрогого знака неравенства. Выделить дугу окружности, на которой расположены решения неравенства. Определить значения углов в начальной и конечной точках дуги окружности. Записать решение неравенства с учетом периодичности заданной тригонометрической функции.
Формулы решения тригонометрических неравенств sinx >a; x (arcsin a + 2πn; π- arcsin a + 2πn). sinx a; x (- arccos a + 2πn; arccos a + 2πn). cosx a; x (arctg a + πn ; + πn). tgx a; x (πn ; arctg + πn). ctgx
Графическое решение основных тригонометрическх неравенств sinx >a
Графическое решение основных тригонометрическх неравенств sinx Графическое решение основных тригонометрическх неравенств cosx >a Графическое решение основных тригонометрическх неравенств cosx Графическое решение основных тригонометрическх неравенств tgx >a Графическое решение основных тригонометрическх неравенств tgx Графическое решение основных тригонометрическх неравенств ctgx >a
Неравенства – это соотношения вида a › b, где a и b – есть выражения, содержащие как минимум одну переменную. Неравенства могут быть строгими — ‹, › и нестрогими — ≥, ≤.
Тригонометрические неравенства представляют собой выражения вида: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, в которых F(x) представлено одной или несколькими тригонометрическими функциями.
Примером простейшего тригонометрического неравенства является: sin x ‹ 1/2. Решать подобные задачи принято графически, для этого разработаны два способа.
Способ 1 — Решение неравенств с помощью построения графика функции
Чтобы найти промежуток, удовлетворяющий условиям неравенство sin x ‹ 1/2, необходимо выполнить следующие действия:
- На координатной оси построить синусоиду y = sin x.
- На той же оси начертить график числового аргумента неравенства, т. е. прямую, проходящую через точку ½ ординаты ОY.
- Отметить точки пересечения двух графиков.
- Заштриховать отрезок являющийся, решением примера.
Когда в выражении присутствуют строгие знаки, точки пересечения не являются решениями. Так как наименьший положительный период синусоиды равен 2π, то запишем ответ следующим образом:
![]()
Если знаки выражения нестрогие, то интервал решений необходимо заключить в квадратные скобки — . Ответ задачи можно также записать в виде очередного неравенства: ![]()
Способ 2 — Решение тригонометрических неравенств с помощью единичной окружности
Подобные задачи легко решаются и с помощью тригонометрического круга. Алгоритм поиска ответов очень прост:
- Сначала стоит начертить единичную окружность.
- Затем нужно отметить значение аркфункции аргумента правой части неравенства на дуге круга.
- Нужно провести прямую проходящую через значение аркфункции параллельно оси абсциссы (ОХ).
- После останется только выделить дугу окружности, являющуюся множеством решений тригонометрического неравенства.
- Записать ответ в требуемой форме.
Разберем этапы решения на примере неравенства sin x › 1/2. На круге отмечены точки α и β – значения
![]()
Точки дуги, расположенные выше α и β, являются интервалом решения заданного неравенства.

Если нужно решить пример для cos, то дуга ответов будет располагаться симметрично оси OX, а не OY. Рассмотреть разницу между интервалами решений для sin и cos можно на схемах приведенных ниже по тексту.

Графические решения для неравенств тангенса и котангенса будут отличаться и от синуса, и от косинуса. Это обусловлено свойствами функций.

Арктангенс и арккотангенс представляют собой касательные к тригонометрической окружности, а минимальный положительный период для обеих функций равняется π. Чтобы быстро и правильно пользоваться вторым способом, нужно запомнить на какой из оси откладываются значения sin, cos, tg и ctg.
Касательная тангенс проходит параллельно оси OY. Если отложить значение arctg a на единичном круге, то вторая требуемая точка будет расположено в диагональной четверти. Углы
Являются точками разрыва для функции, так как график стремится к ним, но никогда не достигает.

В случае с котангенсом касательная проходит параллельно оси OX, а функция прерывается в точках π и 2π.

Сложные тригонометрические неравенства
Если аргумент функции неравенства представлен не просто переменной, а целым выражением содержащим неизвестную, то речь уже идет о сложном неравенстве. Ход и порядок его решения несколько отличаются от способов описанных выше. Допустим необходимо найти решение следующего неравенства:

Графическое решение предусматривает построение обычной синусоиды y = sin x по произвольно выбранным значениям x. Рассчитаем таблицу с координатами для опорных точек графика:

В результате должна получиться красивая кривая.
Для простоты поиска решения заменим сложный аргумент функции

Пересечение двух графиков позволяет определить область искомых значений, при которых выполняется условие неравенства.

Найденный отрезок является решением для переменной t:

Однако, цель задания найти все возможные варианты неизвестной x:

Решить двойное неравенство достаточно просто, нужно перенести π/3 в крайние части уравнения и произвести требуемые вычисления:

Ответ на задание будет выглядеть как интервал для строгого неравенства:

Подобные задачи потребует опыта и сноровки учащихся в обращении с тригонометрическими функциями. Чем больше тренировочных заданий будет решено в процессе подготовке, тем проще и быстрее школьник найдет ответ на вопрос ЕГЭ теста.
ОПРЕДЕЛЕНИЕ
Тригонометрическими неравенствами называются неравенства, которые содержат переменную под знаком тригонометрической функции.
Решение тригонометрических неравенств
Решение тригонометрических неравенств зачастую сводится к решению простейших тригонометрических неравенств вида: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname{tg} x > a \), \(\ \operatorname{ctg} x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \operatorname{tg} x \leq a \), \(\ \operatorname{ctg} x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatorname{tg} x \geq a \), \(\ \operatorname{tg} x \geq a \)
Решаются простейшие тригонометрические неравенства графически или с помощью единичной тригонометрической окружности.
По определению, синусом угла \(\ \alpha \) есть ординатой точки \(\ P_{\alpha}(x, y) \) единичного круга (рис. 1), а косинусом – абсцисса этой точки. Этот факт используется при решении простейших тригонометрических неравенств с косинусом и синусом с помощью единичного круга.
Примеры решения тригонометрических неравенств
Решить неравенство \(\ \sin x \leq \frac{\sqrt{3}}{2} \)
Поскольку \(\ \left|\frac{\sqrt{3}}{2}\right| , то это неравенство имеет решение и его можно решить двумя способами
Первый способ. Решим это неравенство графически. Для этого построим в одной системе координат график синуса \(\ y=\sin x \) (рис. 2) и прямой \(\ y=\frac{\sqrt{3}}{2} \)
Выделим промежутки, на которых синусоида расположена ниже графика прямой \(\ y=\frac{\sqrt{3}}{2} \) . Найдем абсциссы \(\ x_{1} \) и \(\ x_{2} \) точек пересечения этих графиков: \(\ x_{1}=\pi-\arcsin \frac{\sqrt{3}}{2}=\pi-\frac{\pi}{3}=\frac{2 \pi}{3} x_{2}=\arcsin \frac{\sqrt{3}}{2}+2 \pi=\frac{\pi}{3}+2 \pi=\frac{7 \pi}{3} \)
Получили интервал \(\ \left[-\frac{4 \pi}{3} ; \frac{\pi}{3}\right] \) но так как функцию \(\ y=\sin x \) периодическая и имеет период \(\ 2 \pi \) , то ответом будет объединение интервалов: \(\ \left[\frac{2 \pi}{3}+2 \pi k ; \frac{7 \pi}{3}+2 \pi k\right] \), \(\ k \in Z \)
Второй способ. Построим единичную окружность и прямую \(\ y=\frac{\sqrt{3}}{2} \) , точки их пересечения обозначим \(\ P_{x_{1}} \) и \(\ P_{x_{2}} \) (рис. 3). Решением исходного неравенства будет множество точек ординаты, которых меньше \(\ \frac{\sqrt{3}}{2} \) . Найдем значение \(\ \boldsymbol{I}_{1} \) и \(\ \boldsymbol{I}_{2} \) , совершая обход против часовой стрелки, \(\ x_{1} Рис. 3
\(\ x_{1}=\pi-\arcsin \frac{\sqrt{3}}{2}=\pi-\frac{\pi}{3}=\frac{2 \pi}{3} x_{2}=\arcsin \frac{\sqrt{3}}{2}+2 \pi=\frac{\pi}{3}+2 \pi=\frac{7 \pi}{3} \)
Учитывая периодичность функции синус, окончательно получим интервалы \(\ \left[\frac{2 \pi}{3}+2 \pi k ; \frac{7 \pi}{3}+2 \pi\right] \), \(\ k \in Z \)
Решить неравенство \(\ \sin x>2 \)
Синус – функция ограниченная: \(\ |\sin x| \leq 1 \) , а правая часть данного неравенства больше единицы, поэтому решений нет.
Решить неравенство \(\ \cos x>\frac{1}{2} \)
Данное неравенство можно решить двумя способами: графически и с помощью единичного круга. Рассмотрим каждый из способов.
Первый способ. Изобразим в одной системе координат функции, описывающие левую и правую части неравенства, то есть \(\ y=\cos x \) и \(\ y=\frac{1}{2} \) . Выделим промежутки, на которых график функции косинус \(\ y=\cos x \) расположен выше графика прямой \(\ y=\frac{1}{2} \) (рис. 4).
Найдем абсциссы точек \(\ \boldsymbol{x}_{1} \) и \(\ x_{2} \) – точек пересечения графиков функций \(\ y=\cos x \) и \(\ y=\frac{1}{2} \) , которые являются концами одного из промежутков, на котором выполняется указанное неравенство. \(\ x_{1}=-\arccos \frac{1}{2}=-\frac{\pi}{3} \); \(\ x_{1}=\arccos \frac{1}{2}=\frac{\pi}{3} \)
Учитывая, что косинус – функция периодическая, с периодом \(\ 2 \pi \) , ответом будет значения \(\ x \) из промежутков \(\ \left(-\frac{\pi}{3}+2 \pi k ; \frac{\pi}{3}+2 \pi k\right) \), \(\ k \in Z \)
Второй способ. Построим единичную окружность и прямую \(\ x=\frac{1}{2} \) (так как на единичной окружности косинусам отвечает ось абсцисс). Обозначим \(\ P_{x_{1}} \) и \(\ P_{x_{2}} \) (рис. 5) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше \(\ \frac{1}{2} \) . Найдем значение \(\ x_{1} \) и \(\ 2 \) , совершая обход против часовой стрелки так, чтобы \(\ x_{1} Учитывая периодичность косинуса, окончательно получим интервалы \(\ \left(-\frac{\pi}{3}+2 \pi k ; \frac{\pi}{3}+2 \pi k\right) \),\(\ k \in Z \)
Решить неравенство \(\ \operatorname{ctg} x \leq-\frac{\sqrt{3}}{3} \)
Построим в одной системе координат графики функций \(\ y=\operatorname{ctg} x \), \(\ y=-\frac{\sqrt{3}}{3} \)
Выделим промежутки, на которых график функции \(\ y=\operatorname{ctg} x \) расположен не выше графика прямой \(\ y=-\frac{\sqrt{3}}{3} \) (рис. 6).
Найдем абсциссу точки \(\ x_{0} \) , которая является концом одного из промежутков, на котором неравенство \(\ x_{0}=\operatorname{arcctg}\left(-\frac{\sqrt{3}}{3}\right)=\pi-\operatorname{arcctg}\left(\frac{\sqrt{3}}{3}\right)=\pi-\frac{\pi}{3}=\frac{2 \pi}{3} \)
Другим концом этого промежутка есть точка \(\ \pi \) , а функция \(\ y=\operatorname{ctg} x \) в этой точке неопределенна. Таким образом, одним из решением данного неравенства является промежуток \(\ \frac{2 \pi}{3} \leq x
Тригонометрические неравенства со сложным аргументом
Тригонометрические неравенства со сложным аргументом можно свести к простейшим тригонометрическим неравенствам с помощью замены. После его решения делается обратная замена и выражается исходная неизвестная.
Решить неравенство \(\ 2 \cos \left(2 x+100^{\circ}\right) \leq-1 \)
Выразим в правой части данного неравенства косинус: \(\ \cos \left(2 x+100^{\circ}\right) \leq-\frac{1}{2} \)
Ведем замену \(\ t=2 x+100^{\circ} \) , после чего данное неравенство преобразуется к простейшему неравенству \(\ \cos t \leq-\frac{1}{2} \)
Решим его, используя единичную окружность. Построим единичный круг и прямую \(\ x=-\frac{1}{2} \) . Обозначим \(\ P_{1} \) и \(\ P_{2} \) – точки пересечения прямой и единичной окружности (рис. 7).
Решением исходного неравенства будет множество точек абсциссы, которых не больше \(\ -\frac{1}{2} \). Точке \(\ P_{1} \) соответствует угол \(\ 120^{\circ} \) , а точке \(\ P_{2} \) . Таким образом, учитывая период косинуса, получим \(\ 120^{\circ}+360^{\circ} \cdot n \leq t \leq 240^{\circ}+360^{\circ} \cdot n \), \(\ n \in Z \)
Сделаем обратную замену \(\ t=2 x+100^{\circ} 120^{\circ}+360^{\circ} \cdot n \leq 2 x+100^{\circ} \leq 240^{\circ}+360^{\circ} \cdot n \), \(\ n \in Z \)
Выразим \(\ \mathbf{x} \), для сначала этого из каждой части неравенства вычтем \(\ 100^{\circ} 120^{\circ}-100^{\circ}+360^{\circ} \cdot n \leq 2 x+100^{\circ}-100^{\circ} \leq 240^{\circ}-100^{\circ}+360^{\circ} \cdot n \), \(\ n \in Z \); \(\ 20^{\circ}+360^{\circ} \cdot n \leq 2 x \leq 140^{\circ}+360^{\circ} \cdot n \), \(\ n \in Z \)
а затем, разделим на 2 \(\ \frac{20^{\circ}+360^{\circ} \cdot n}{2} \leq \frac{2 x}{2} \leq \frac{140^{\circ}+360^{\circ} \cdot n}{2} \), \(\ n \in Z \); \(\ 10^{\circ}+180^{\circ} \cdot n \leq x \leq 70^{\circ}+180^{\circ} \cdot n \), \(\ n \in Z \)
Двойные тригонометрические неравенства
Решить двойное тригонометрическое неравенство \(\ \frac{1}{2}
Введем замену \(\ t=\frac{x}{2} \) , тогда исходное неравенство примет вид \(\ \frac{1}{2}
Решим его, используя единичную окружность. Так как на единичной окружности синусу соответствует ось ординат, выделим на ней множество ординаты которых больше \(\ x=\frac{1}{2} \) и меньше или равно \(\ \frac{\sqrt{2}}{2} \) . На рисунке 8 эти точки будут расположены на дугах \(\ P_{t_{1}} \), \(\ P_{t_{2}} \) и \(\ P_{t_{3}} \), \(\ P_{t_{4}} \) . Найдем значение \(\ t_{1} \), \(\ t_{2} \), \(\ t_{3} \), \(\ t_{4} \) , совершая обход против часовой стрелки, причем \(\ t_{1} \(\ t_{3}=\pi-\arcsin \frac{\sqrt{2}}{2}=\pi-\frac{\pi}{4}=\frac{3 \pi}{4} \); \(\ t_{4}=\pi-\arcsin \frac{1}{2}=\pi-\frac{\pi}{6}=\frac{5 \pi}{6} \)
Таким образом, получаем два интервала, которые, учитывая периодичность функции синус, можно записать следующим образом \(\ \frac{\pi}{6}+2 \pi k \leq t \frac{\pi}{4}+2 \pi k \quad \frac{3 \pi}{4}+2 \pi k Сделаем обратную замену \(\ t=\frac{x}{2} \frac{\pi}{6}+2 \pi k \leq \frac{x}{2} \frac{\pi}{4}+2 \pi k \), \(\ \frac{3 \pi}{4}+2 \pi kВыразим \(\ \mathbf{x} \), для этого умножим все стороны обои неравенств на 2, получим \(\ \frac{\pi}{3}+4 \pi k \leq x
На практическом занятии мы повторим основные типы заданий из темы «Тригонометрия», дополнительно разберем задачи повышенной сложности и рассмотрим примеры решения различных тригонометрических неравенств и их систем.
Данный урок поможет Вам подготовиться к одному из типов заданий В5, В7, С1 и С3.
Начнем с повторения основных типов заданий, которые мы рассмотрели в теме «Тригонометрия» и решим несколько нестандартных задач.
Задача №1 . Выполнить перевод углов в радианы и градусы: а) ; б) .
а) Воспользуемся формулой перевода градусов в радианы
![]()
Подставим в нее указанное значение .
б) Применим формулу перевода радиан в градусы
![]()
Выполним подстановку ![]() .
.
Ответ. а) ; б) .
Задача №2 . Вычислить: а) ; б) .
а) Поскольку угол далеко выходит за рамки табличного, уменьшим его с помощью вычитания периода синуса. Т.к. угол указан в радианах, то и период будем рассматривать как .
б) В данном случае ситуация аналогичная. Поскольку угол указан в градусах, то и период тангенса будем рассматривать как .
Полученный угол хоть и меньше периода, но больше , а это значит, что он относится уже не к основной, а к расширенной части таблицы. Чтобы не тренировать лишний раз свою память запоминанием расширенной таблицы значений тригофункций, вычтем период тангенса еще раз:
Воспользовались нечетностью функции тангенс.
Ответ. а) 1; б) .
Задача №3
. Вычислить ![]() , если .
, если .
Приведем все выражение к тангенсам, разделив числитель и знаменатель дроби на . При этом, можем не бояться, что , т.к. в таком случае значения тангенса не существовало бы.
Задача №4 . Упростить выражение .
Указанные выражения преобразовываются с помощью формул приведения. Просто они непривычно записаны с использованием градусов. Первое выражение вообще представляет собой число. Упростим все тригофункции по очереди:
Т.к. , то функция меняется на кофункцию, т.е. на котангенс, и угол попадает во вторую четверть, в которой у исходного тангенса знак отрицательный.

По тем же причинам, что и предыдущем выражении, функция меняется на кофункцию, т.е. на котангенс, а угол попадает в первую четверть, в которой у исходного тангенса знак положительный.
Подставим все в упрощаемое выражение:
Задача №5 . Упростить выражение .
Распишем тангенс двойного угла по соответствующей формуле и упростим выражение:
Последнее тождество является одной из формул универсальной замены для косинуса.
Задача №6 . Вычислить .
Главное, это не сделать стандартной ошибки и не дать ответ, что выражение равно . Воспользоваться основным свойством арктангенса нельзя пока возле него присутствует множитель в виде двойки. Чтобы от него избавиться распишем выражение по формуле тангенса двойного угла , при этом относимся к , как к обыкновенному аргументу.
![]()
Теперь уже можно применять основное свойство арктангенса, вспомним, что на его численный результат ограничений нет.
Задача №7 . Решить уравнение .
При решении дробного уравнения, которое приравнивается к нулю, всегда указывается, что числитель равен нулю, а знаменатель нет, т.к. на ноль делить нельзя.

Первое уравнение представляет собой частный случай простейшего уравнения, которое решается с помощью тригонометрической окружности. Вспомните самостоятельно этот способ решения. Второе неравенство решается как простейшее уравнение по общей формуле корней тангенса, но только с записью знака неравно.

Как видим, одно семейство корней исключает другое точно такое же по виду семейство не удовлетворяющих уравнению корней. Т.е. корней нет.
Ответ. Корней нет.
Задача №8 . Решить уравнение .
Сразу заметим, что можно вынести общий множитель и проделаем это:
Уравнение свелось к одной из стандартных форм, когда произведение нескольких множителей равно нулю. Мы уже знаем, что в таком случае или один из них равен нулю или другой, или третий. Запишем это в виде совокупности уравнений:

Первые два уравнения являются частными случаями простейших, с подобными уравнениями мы уже многократно встречались, поэтому сразу укажем их решения. Третье уравнение приведем к одной функции с помощью формулы синуса двойного угла.

Решим отдельно последнее уравнение:
![]()
Данное уравнение не имеет корней, т.к. значение синуса не могут выходить за пределы ![]() .
.
Таким образом, решением является только два первых семейства корней, их можно объединить в одно, что легко показать на тригонометрической окружности:
 |
Это семейство всех половин , т.е.
Перейдем к решению тригонометрических неравенств. Сначала разберем подход к решению примера без использования формул общих решений, а с помощью тригонометрической окружности.
Задача №9 . Решить неравенство .
Изобразим на тригонометрической окружности вспомогательную линию, соответствующую значению синуса равному , и покажем промежуток углов, удовлетворяющих неравенству.
 |
Очень важно понять, как именно указывать полученный промежуток углов, т.е. что является его началом, а что концом. Началом промежутка будет угол, соответствующей точке, в которую мы войдем в самом начале промежутка, если будем двигаться против часовой стрелки. В нашем случае это точка, которая находится слева, т.к. двигаясь против часовой стрелки и проходя правую точку, мы наоборот выходим из необходимого промежутка углов. Правая точка будет, следовательно, соответствовать концу промежутка.
Теперь необходимо понять значения углов начала и конца нашего промежутка решений неравенства. Типичная ошибка - это указать сразу, что правой точке соответствует угол , левой и дать ответ . Это неверно! Обратите внимание, что мы только что указали промежуток, соответствующий верхней части окружности, хотя нас интересует нижняя, иными словами, мы перепутали начало и конец необходимого нам интервала решений.
Чтобы интервал начинался с угла правой точки, а заканчивался углом левой точки, необходимо, чтобы первый указанный угол был меньше второго. Для этого угол правой точки нам придется отмерять в отрицательном направлении отсчета, т.е. по часовой стрелке и он будет равен . Тогда, начиная движение с него в положительном направлении по часовой стрелке, мы попадем в правую точку уже после левой точки и получим для нее значение угла . Теперь начало промежутка углов меньше конца , и мы можем записать промежуток решений без учета периода:
Учитывая, что такие промежутки будут повторяться бесконечное количество раз после любого целого количества поворотов, получим общее решение с учетом периода синуса :
Круглые скобки ставим из-за того, что неравенство строгое, и точки на окружности, которые соответствуют концам промежутка, мы выкалываем.
Сравните полученный ответ с формулой общего решения, которую мы приводили на лекции.
Ответ.![]() .
.
Указанный способ хорош для понимания того, откуда берутся формулы общих решений простейших тригонеравенств. Кроме того, он полезен для тех, кому лень учить все эти громоздкие формулы. Однако сам по себе способ тоже непростой, выберете, какой подход к решению вам наиболее удобен.
Для решения тригонометрических неравенств можно использовать и графики функций, на которых строится вспомогательная линия аналогично показанному способу с использованием единичной окружности. Если вам интересно, попробуйте самостоятельно разобраться с таким подходом к решению. В дальнейшем будем использовать общие формулы для решения простейших тригонометрических неравенств.
Задача №10 . Решить неравенство .
Воспользуемся формулой общего решения с учетом того, что неравенство нестрогое:
Получаем в нашем случае:
Ответ. ![]()
Задача №11 . Решить неравенство .
Воспользуемся формулой общего решения для соответствующего строго неравенства:
Ответ.![]() .
.
Задача №12 . Решить неравенства: а) ; б) .
В указанных неравенствах не надо спешить использовать формулы общих решений или тригонометрическую окружность, достаточно просто вспомнить об области значений синуса и косинуса.
а) Поскольку ![]() , то неравенство не имеет смысла. Следовательно, решений нет.
, то неравенство не имеет смысла. Следовательно, решений нет.
б) Т.к. аналогично , то синус от любого аргумента всегда удовлетворяет указанному в условии неравенству . Следовательно неравенству удовлетворяют все действительные значения аргумента .
Ответ. а) решений нет; б) .
Задача 13
. Решить неравенство ![]() .
.
Решение простейших тригонометрических уравнений
Для начала вспомним формулы для решения простейших тригонометрических уравнений .
- $sinx=a$
- $cosx=a$
- $tgx=a$
- $ctgx=a$
Решение простейших тригонометрических неравенств.
Для решения простейших тригонометрических неравенств нам вначале необходимо решить соответствующее уравнение, а затем, используя тригонометрическую окружность , найти решение неравенства . Рассмотрим решения простейших тригонометрических неравенств на примерах.
Пример 1
$sinx\ge \frac{1}{2}$
Найдем решение тригонометрического неравенства $sinx=\frac{1}{2}$
\ \
Рисунок 1. Решение неравенства $sinx\ge \frac{1}{2}$.
Так как неравенство имеет знак «больше или равно», то решение лежит на верхней дуге окружности (относительно решения уравнения).
Ответ: $\left[\frac{\pi }{6}+2\pi n,\frac{5\pi }{6}+2\pi n\right]$.
Пример 2
Найдем решение тригонометрического неравенства $cosx=\frac{\sqrt{3}}{2}$
\ \
Отметим решение на тригонометрической окружности
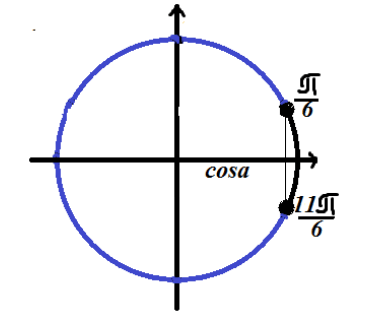
Так как неравенство имеет знак «меньше», то решение лежит на дуге окружности, расположенной слева (относительно решения уравнения).
Ответ: $\left(\frac{\pi }{6}+2\pi n,\frac{11\pi }{6}+2\pi n\right)$.
Пример 3
$tgx\le \frac{\sqrt{3}}{3}$
Найдем решение тригонометрического неравенства $tgx=\frac{\sqrt{3}}{3}$
\ \
Здесь также нам понадобится область определения. Как мы помним у функции тангенса $x\ne \frac{\pi }{2}+\pi n,n\in Z$
Отметим решение на тригонометрической окружности
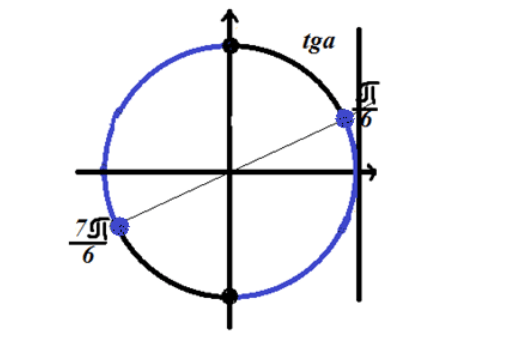
Рисунок 3. Решение неравенства $tgx\le \frac{\sqrt{3}}{3}$.
Так как неравенство имеет знак «меньше или равно», то решение лежит на дугах окружности, отмеченных синим на рисунке 3.
Ответ:$\ \left(-\frac{\pi }{2}+2\pi n\right.,\left.\frac{\pi }{6}+2\pi n\right]\cup \left(\frac{\pi }{2}+2\pi n,\right.\left.\frac{7\pi }{6}+2\pi n\right]$
Пример 4
Найдем решение тригонометрического неравенства $ctgx=\sqrt{3}$
\ \
Здесь также нам понадобится область определения. Как мы помним у функции тангенса $x\ne \pi n,n\in Z$
Отметим решение на тригонометрической окружности

Рисунок 4. Решение неравенства $ctgx\le \sqrt{3}$.
Так как неравенство имеет знак «больше», то решение лежит на дугах окружности, отмеченных синим на рисунке 4.
Ответ:$\ \left(2\pi n,\frac{\pi }{6}+2\pi n\right)\cup \left(\pi +2\pi n,\frac{7\pi }{6}+2\pi n\right)$








