Тригонометрические функции числового и углового аргументов. Формулы приведения Вычислить тригон выражение числового аргумента

Тригонометрические функции числового аргумента.

Тригонометрические функции числового аргумента t – это функции вида y = cos t,
y = sin t, y = tg t, y = ctg t.

С помощью этих формул через известное значение одной тригонометрической функции можно найти неизвестные значения других тригонометрических функций.

Пояснения .

1) Возьмем формулу cos 2 t + sin 2 t = 1 и выведем с ее помощью новую формулу.

Для этого разделим обе части формулы на cos 2 t (при t ≠ 0, то есть t ≠ π/2 + πk ). Итак:

cos 2 t sin 2 t 1
--- + --- = ---
cos 2 t cos 2 t cos 2 t

Первое слагаемое равно 1. Мы знаем, что отношение синуса к конисусу – это тангенс, значит, второе слагаемое равно tg 2 t. В результате мы получаем новую (и уже известную вам) формулу:

2) Теперь разделим cos 2 t + sin 2 t = 1 на sin 2 t (при t ≠ πk ):

cos 2 t sin 2 t 1
--- + --- = ---, где t ≠ πk + πk , k – целое число
sin 2 t sin 2 t sin 2 t

Отношение косинуса к синусу – это котангенс. Значит:

Зная элементарные основы математики и выучив основные формулы тригонометрии, вы легко сможете самостоятельно выводить большинство остальных тригонометрических тождеств. И это даже лучше, чем просто зазубривать их: выученное наизусть быстро забывается, а понятое запоминается надолго, если не навсегда. К примеру, необязательно зазубривать, чему равна сумма единицы и квадрата тангенса. Забыли – можно легко вспомнить, если вы знаете самую простую вещь: тангенс – это отношение синуса к косинусу. Примените вдобавок простое правило сложения дробей с разными знаменателями – и получите результат:

sin 2 t 1 sin 2 t cos 2 t + sin 2 t 1
1 + tg 2 t = 1 + --- = - + --- = ------ = ---
cos 2 t 1 cos 2 t cos 2 t cos 2 t

Точно так же легко можно найти сумму единицы и квадрата котангенса, как и многие другие тождества.

Тригонометрические функции углового аргумента.

В функциях у = cos t , у = sin t , у = tg t , у = ctg t переменная t может быть не только числовым аргументом. Ее можно считать и мерой угла – то есть угловым аргументом.

С помощью числовой окружности и системы координат можно легко найти синус, косинус, тангенс, котангенс любого угла. Для этого должны быть соблюдены два важных условия:
1) вершиной угла должен быть центр окружности, который одновременно является центром оси координат;

2) одной из сторон угла должен быть положительный луч оси x .

В этом случае ордината точки, в которой пересекаются окружность и вторая сторона угла, является синусом этого угла, а абсцисса этой точки – косинусом данного угла.

Пояснение . Нарисуем угол, одна сторона которого – положительный луч оси x , а вторая сторона выходит из начала оси координат (и из центра окружности) под углом 30º (см.рисунок). Тогда точка пересечения второй стороны с окружностью соответствует π/6. Нам известны ордината и абсцисса этой точки. Они же являются косинусом и синусом нашего угла:

√3 1
--; --
2 2

А зная синус и косинус угла, вы уже легко сможете найти его тангенс и котангенс.

Таким образом, числовая окружность, расположенная в системе координат, является удобным способом найти синус, косинус, тангенс или котангенс угла.

Но есть более простой способ. Можно и не рисовать окружность и систему координат. Можно воспользоваться простыми и удобными формулами:

Пример : найти синус и косинус угла, равного 60º.

Решение :

π · 60 π √3
sin 60º = sin --- = sin -- = --
180 3 2

π 1
cos 60º = cos -- = -
3 2

Пояснение : мы выяснили, что синус и косинус угла 60º соответствуют значениям точки окружности π/3. Далее просто находим в таблице значения этой точки – и таким образом решаем наш пример. Таблица синусов и косинусов основных точек числовой окружности – в предыдущем разделе и на странице «Таблицы».

В настоящей главе мы введем тригонометрические функции числового аргумента. Многие вопросы математики, механики, физики и других наук приводят к тригонометрическим функциям не только угла (дуги), но и аргументов совершенно различной природы (длина, время, температура и т. д.). До сих пор под аргументом тригонометрической функции понимался угол, измеренный в градусах или радианах. Теперь мы обобщим понятия синуса, косинуса, тангенса, котангенса, секанса и косеканса, введя их как функции числового аргумента.

Определение. Тригонометрическими функциями числового аргумента называются одноименные тригонометрические функции угла, равного радианам.

Поясним это определение на конкретных примерах.

Пример 1. Вычислим значенйе . Здесь под мы понимаем отвлеченное иррациональное число. Согласно определению . Итак, .

Пример 2. Вычислим значение . Здесь под 1,5 мы понимаем отвлеченное число. Согласно определению (см. приложение II).

Пример 3. Вычислим значение Аналогично предыдущему получаем (см. приложение II).

Итак, в дальнейшем под аргументом тригонометрических функций мы будем понимать угол (дугу) или просто число в зависимости от той задачи, которую решаем. А в ряде случаев аргументом может служить величина, имеющая и другую размерность, например время и т. д. Называя аргумент углом (дугой), мы можем подразумевать под ним число, с помощью которого он измерен в радианах.

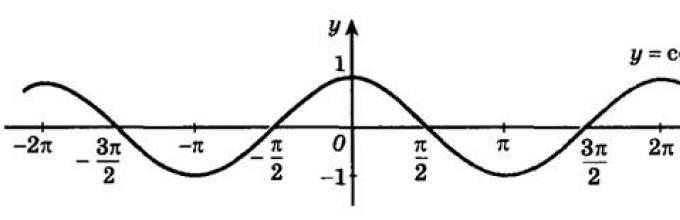
Определение1: Числовая функция, заданная формулой y=sin x называется синусом.

Данная кривая имеет название – синусоида.

Свойства функции y=sin x

2. Область значения функции: E(y)=[-1; 1]

3. Четность функции:

y=sin x – нечетная,.

4. Периодичность: sin(x+2πn)=sin x, где n – целое число.

Данная функция через определенный промежуток принимает одинаковые значения. Такое свойство функции называют периодичностью. Промежуток – периодом функции.

Для функции y=sin x период составляет 2π.

Функция y=sin x – периодическая, с периодом Т=2πn, n – целое число.

Наименьший положительный период Т=2π.

Математически это можно записать так: sin(x+2πn)=sin x, где n – целое число.

Определение2: Числовая функция, заданная формулой y=cosx называется косинусом.

Свойства функции y=cos x

1. Область определения функции: D(y)=R

2. Область значения функции: E(y)=[-1;1]

3. Четность функции:

y=cos x –четная.

4. Периодичность: cos(x+2πn)=cos x, где n – целое число.

Функция y=cos x – периодическая, с периодом Т=2π.

Определение 3: Числовая функция, заданная формулой y=tg x, называется тангенсом.

Свойства функции y=tg x

1. Область определения функции: D(y) - все действительные числа, кроме π/2+πk, k – целое число. Потому что в этих точках тангенс не определен.

3. Четность функции:

y=tg x – нечетная.

4. Периодичность: tg(x+πk)=tg x, где k – целое число.

Функция y=tg x – периодическая с периодом π.

Определение 4: Числовая функция, заданная формулой y=ctg x, называется котангенсом.

Свойства функции y=ctg x

1. Область определения функции: D(y) - все действительные числа, кроме πk, k– целое число. Потому что в этих точках котангенс не определен.

2. Область значения функции: E(y)=R.

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели урока:

1. Выработка умений и навыков применения тригонометрических формул для упрощения тригонометрических выражений.
2. Реализация принципа деятельностного подхода в обучении учащихся, развитие коммуникабельности и толерантности учащихся, умения слушать и слышать других и высказывать своё мнение.
3. Повышение интереса учащихся к математике.

Тип урока: тренировочный.

Вид урока: урок отработки навыков и умений.

Форма обучения: групповая.

Тип групп : группа, сидящая вместе. Ученики разного уровня обученности, информированности по данному предмету, совместимые учащиеся, что позволяет им взаимно дополнять и обогащать друг друга.

Оборудование: доска; мел; таблица «Тригонометр»; маршрутные листы; карточки с буквами (А, В, С.) для выполнения теста; таблички с названиями экипажей; оценочные листы; таблицы с названиями этапов пути; магниты, мультимедийный комплекс.

Ход урока

Ученики сидят по группам: 4 группы по 5-6 человек. Каждая группа – это экипаж машины с названиями, соответствующими названиям тригонометрических функций, во главе с рулевым. Каждому экипажу выдаётся маршрутный лист и определяется цель: пройти заданный маршрут успешно, без ошибок. Урок сопровождается презентацией.

I. Организационный момент.

Учитель сообщает тему урока, цель урока, ход урока, план работы групп, роль рулевых.

Вступительное слово учителя:

– Ребята! Запишите число и тему урока:«Тригонометрические функции числового аргумента».

Сегодня на уроке мы буде учиться:

1. Вычислять значения тригонометрических функций;
2. Упрощать тригонометрические выражения.

Для этого нужно знать:

1. Определения тригонометрических функций
2. Тригонометрические соотношения (формулы).

Известно давно, что одна голова хорошо, а две лучше, поэтому вы сегодня работаете в группах. Известно также, что дорогу осилит идущий. Но мы живём в век скоростей и время дорого, а значит можно сказать так: «Дорогу осилит едущий», поэтому сегодня урок у нас пройдёт в виде игры «Математическое ралли». Каждая группа – это экипаж машины, во главе с рулевым.

Цель игры:

• успешно пройти маршрут каждому экипажу;
• выявить чемпионов ралли.

Название экипажей соответствует марке машины, на которой вы совершаете пробег.

Представляются экипажи и их рулевые:

• Экипаж – «синус»
• Экипаж – «косинус»
• Экипаж – «тангенс»
• Экипаж – «котангенс»

Девиз гонки: «Торопись медленно!»

Вам предстоит совершить пробег по «математической местности» со множеством препятствий.

Маршрутные листы каждому экипажу выданы. Преодолеть препятствия смогут экипажи, которые знают определения и тригонометрические формулы.

Во время пробега каждый рулевой руководит экипажем, помогая, и оценивая вклад каждого члена экипажа в преодоление маршрута в виде «плюсов» и «минусов» в оценочном листе. За каждый правильный ответ группа получает «+», неправильный «-».

Вам предстоит преодолеть следующие этапы пути:

I этап. ПДД (правила дорожного движения).
II этап. Техосмотр.
III этап. Гонка по пересечённой местности.
IV этап. Внезапная остановка – авария.
V этап. Привал.
VI этап. Финиш.
VII этап. Итоги.

И так в путь!

I этап. ПДД (правила дорожного движения).

1) В каждом экипаже рулевые раздают каждому члену экипажа билеты с теоретическими вопросами:

1. Расскажите определение синуса числа t и его знаки по четвертям.
2. Расскажите определение косинуса числа t и его знаки по четвертям.
3. Назовите наименьшее и наибольшее значения sin t и cos t.
4. Расскажите определение тангенса числа t и его знаки по четвертям.
5. Расскажите определение котангенса числа t и его знаки по четвертям.
6. Расскажите, как найти значение функции sin t по известному числу t.

2) Соберите «рассыпавшиеся» формулы. На тайной доске таблица (см. ниже). Экипажи должны привести в соответствие формулы. Ответ каждая команда записывает на доске в виде строки соответствующих букв (парами).

а	tg 2 t + 1	е	1
в	tg t	ж	cos t / sin t, t ≠ к, кZ.
д	sin 2 t + cos 2 t	и	1/ sin 2 t, t ≠ к, кZ.
ё	ctg t	к	1,t ≠ к / 2, кZ.
з	1 + ctg 2 t	г	sin t /cos t, t ≠ /2 + к, кZ.
й	tg t ∙ctg t	б	1/ cos 2 t, t ≠ /2 + к, кZ.

Ответ: аб, вг, де, ёж, зи, йк.

II этап. Техосмотр.

Устная работа: тест.

На тайной доске написано: задание: упростить выражение.

Рядом записаны варианты ответов. Экипажи определяют правильные ответы за1 мин. и поднимают соответствующий набор букв.

№	Выражение	Варианты ответов
		А	В	С
1.	1 – cos 2 t	cos 2 t	- sin 2 t	sin 2 t
2.	sin 2 t – 1	cos 2 t	- cos 2 t	2 cos 2 t
3.	(cos t – 1)(1+ cos t)	-sin 2 t	(1+ cos t) 2	(cos t – 1) 2

Ответ: С В А.

III этап. Гонка по пересечённой местности.

3 минуты экипажам на совещание по решению задания, а далее представители экипажей пишут решение на доске. Когда представители экипажей закончат записывать решение первого задания, все ученики (вместе с учителем) проверяют правильность и рациональность решений и записывают в тетрадь. Рулевые оценивают вклад каждого члена экипажа знаками « + » и « – » в оценочных листах.

Задания из учебника:

• Экипаж – «синус»: № 118 г;
• Экипаж – «косинус»: № 122 а;
• Экипаж – «тангенс»: № 123 г;
• Экипаж – «котангенс»: № 125 г.

IV этап. Внезапная остановка – авария.

– Ваш автомобиль сломался. Необходимо устранить неисправность вашего автомобиля.

Для каждого экипажа приведены высказывания, но в них допущены ошибки. Найдите эти ошибки и объясните, почему они были допущены. В высказываниях используются тригонометрические функции, соответствующие маркам ваших машин.

V этап. Привал.

Вы устали и должны отдохнуть. Пока экипаж отдыхает рулевые подводят предварительные итоги: считают «плюсы» и «минусы» у членов экипажа и в целом у экипажа.

Для учеников:

3 и более «+» – оценка «5»;
2 «+» – оценка «4»;
1 «+» – оценка «3».

Для экипажей: «+» и «-» взаимно уничтожаются. Считаются только оставшиеся знаки.

Отгадайте шараду .

Из чисел вы мой первый слог возьмите,
Второй – из слова «гордецы».
А третьим лошадей вы погоните,
Четвёртым будет блеянье овцы.
Мой пятый слог такой же, как и первый,
Последней буквой в алфавите является шестой,
А если отгадаешь ты всё верно,
То в математике раздел получишь ты такой.
(Три-го-но-ме-три-я)

Слово «тригонометрия» (от греческих слов «тригонон» – треугольник и «метрео» – измеряю) означает «измерение треугольников». Возникновение тригонометрии связано с развитием географии и астрономии – науки о движении небесных тел, о строении и развитии Вселенной.

В результате произведённых астрономических наблюдений возникла необходимость определения положения светил, вычисления расстояний и углов. Так как некоторые расстояния, например, от Земли до других планет, нельзя было измерить непосредственно, то учёные стали разрабатывать приёмы нахождения взаимосвязей между сторонами и углами треугольника, у которого две вершины расположены на земле, а третью представляет планета или звезда. Такие соотношения можно вывести, изучая различные треугольники и их свойства. Вот почему астрономические вычисления привели к решению (т. е. нахождению элементов) треугольника. Этим и занимается тригонометрия.

Зачатки тригонометрии были обнаружены в древнем Вавилоне. Вавилонские учёные умели предсказывать солнечные и лунные затмения. Некоторые сведения тригонометрического характера встречаются в старинных памятниках других народов древности.

VI этап. Финиш.

Чтобы успешно пересечь линию финиша осталось поднапрячься и совершить «рывок». Очень важно в тригонометрии уметь быстро определять значения sin t, cost, tgt, ctg t, где 0 ≤ t ≤ . Учебники закрыть.

Экипажи поочерёдно называют значения функций sin t, cost, tgt, ctg t , если:

VII этап. Итоги.

Итоги игры.

Рулевые сдают оценочные листы. Определяется экипаж, ставший чемпионом «Математического ралли» и характеризуется работа остальных групп. Далее называются фамилии тех, кто получил оценки «5» и «4».

Итоги урока.

– Ребята! Чему вы сегодня научились на уроке? (упрощать тригонометрические выражения; находить значения тригонометрических функций). А что для этого нужно знать?

• определения и свойства sin t, cos t, tg t, ctg t;
• соотношения, связывающие значения различных тригонометрических функций;
• знаки тригонометрических функций по четвертям числовой окружности.
• значения тригонометрических функций первой четверти числовой окружности.

– Я думаю, что вы поняли, что формулы нужно хорошо знать, чтобы их правильно применять. Вы также поняли, что тригонометрия очень важная часть математики, так как она применяется в других науках: астрономии, географии, физике и др.

Домашнее задание:

• для учеников получивших «5» и «4»: §6, №128а, 130а, 134а.
• для остальных учеников: §6, №119г, №120г, №121г.

Видеоурок «Тригонометрические функции числового аргумента» представляет наглядный материал для обеспечения наглядности при объяснении темы на уроке. В ходе демонстрации рассматривается принцип формирования значения тригонометрических функций от числа, описывается ряд примеров, обучающих вычислению значений тригонометрических функций от числа. С помощью данного пособия легче сформировать навыки в решении соответствующих задач, добиться запоминания материала. Использование пособия повышает эффективность урока, способствует быстрому достижению целей обучения.

В начале урока демонстрируется название темы. Затем ставится задача нахождения соответствующего косинуса некоторому числовому аргументу. Отмечается, что данная задача решается просто и это можно наглядно продемонстрировать. На экране изображается единичная окружность с центром в начале координат. При этом замечено, что точка пересечения окружности с положительной полуосью оси абсцисс располагается в точке А(1;0). Приводится пример точки М, которая представляет аргумент t=π/3. Данная точка отмечается на единичной окружности, и от нее опускается перпендикуляр к оси абсцисс. Найденная абсцисса точки и является косинусом cos t. В данном случае абсциссой точки будет х=1/2. Поэтому cos t=1/2.

Обобщая рассмотренные факты, отмечается, что имеет смысл говорить о функции s=cos t. Отмечается, что некоторые знания об этой функции уже имеются у учеников. Вычислены некоторые значения косинуса cos 0=1, cos π/2=0, cos π/3=1/2. Также связанными к данной функцией являются функции s=sin t, s=tg t, s=ctg t. Отмечается, что они имеют общее для всех название - тригонометрические функции.

Демонстрируются важные соотношения, которые используются в решении задач с тригонометрическими функциями: основное тождество sin 2 t+ cos 2 t=1, выражение тангенса и котангенса через синус и косинус tg t=sin t/cos t, где t≠π/2+πk для kϵZ, ctg t= cos t/sin t, где t≠πk для kϵZ, а также соотношение тангенса к котангенсу tg t·ctg t=1 где t≠πk/2 для kϵZ.

Далее предлагается рассмотреть доказательство соотношения 1+ tg 2 t=1/ cos 2 t, при t≠π/2+πk для kϵZ. Чтобы доказать тождество, необходимо представить tg 2 t в виде соотношения синуса и косинуса, а после слагаемые в левой части привести к общему знаменателю 1+ tg 2 t=1+sin 2 t/cos 2 t = (sin 2 t+cos 2 t)/ cos 2 t. Используя основное тригонометрическое тождество, получаем в числителе 1, то есть конечное выражение 1/ cos 2 t. Что и требовалось доказать.

Аналогично доказывается тождество 1+ ctg 2 t=1/ sin 2 t, при t≠πk для kϵZ. Так же, как и в предыдущем доказательстве, котангенс заменяется соответствующим соотношением косинуса и синуса, и оба слагаемых в левой части приводятся к общему знаменателю 1+ ctg 2 t=1+ cos 2 t/sin 2 t= (sin 2 t+cos 2 t)/sin 2 t. После применения основного тригонометрического тождества к числителю получаем 1/ sin 2 t. Это и есть искомое выражение.

Рассматривается решение примеров, в котором применяются полученные знания. В первом задании необходимо найти значения cost, tgt, ctgt, если известен синус числа sint=4/5, а t принадлежит промежутку π/2< t<π. Для нахождения косинуса в данном примере рекомендуется использовать тождество sin 2 t+ cos 2 t=1, из которого следует cos 2 t=1-sin 2 t. Зная значение синуса, можно найти косинус cos 2 t=1-(4/5) 2 =9/25. То есть значение косинуса cost=3/5 и cost=-3/5. В условии указано, что аргумент принадлежит второй четверти координатной плоскости. В этой четверти значение косинуса отрицательное. С учетом данного ограничения находим cost=-3/5. Для нахождения тангенса числа пользуемся его определением tgt= sint/cost. Подставив известные значения синуса и косинуса, получаем tgt=4/5:(-3/5)=-4/3. Чтобы найти значение котангенса, также используется определение котангенса ctgt= cost/sint. Подставив известные значения синуса и косинуса в отношение, получаем ctgt=(-3/5):4/5=-3/4.

Далее рассматривается решение аналогичной задачи, в которой известен тангенс tgt=-8/15, а аргумент ограничен значениями 3π/2

Чтобы найти значение синуса, используем определение тангенса tgt= sint/cost. Из него находим sint= tgt·cost=(-8/15)·(15/17)=-8/17. Зная, что котангенс - функция, обратная тангенсу, находим ctgt=1/(-8/15)=-15/8.

Видеоурок «Тригонометрические функции числового аргумента» применяется для повышения эффективности урока математики в школе. В ходе дистанционного обучения данный материал может использоваться как наглядное пособие для формирования навыков решения задач, где есть тригонометрические функции от числа. Для приобретения этих навыков ученику может рекомендовано самостоятельное рассмотрение наглядного материала.

ТЕКСТОВАЯ РАСШИФРОВКА:

Тема урока «Тригонометрические функции числового аргумента».

Любому действительному числу t можно поставить в соответствие однозначно определенное число cos t. Для этого необходимо выполнить следующие действия:

1) на координатной плоскости расположить числовую окружность так, чтобы центр окружности совпал с началом координат, а начальная точка А окружности попала в точку (1;0);

2) на окружности найти точку, которая соответствует числу t;

3) найти абсциссу этой точки. Это и есть cos t.

Поэтому речь пойдет о функции s= cos t (эс равно косинус тэ), где t - любое действительное число. Некоторое представление о этой функции мы уже получили:

• научились вычислять некоторые значения, например cos 0=1, cos = 0, cos = и т.д.(косинус нуля равен единице, косинус пи на два равен нулю, косинус пи на три равен одной второй и так далее).
• а так как значения синуса, косинуса, тангенса и котангенса взаимосвязаны, то получили некоторое представление еще о трех функциях: s= sint; s= tgt; s= ctgt. (эс равно синус тэ, эс равно тангенс тэ, эс равно котангенс тэ)

Все эти функции называются тригонометрическими функциями числового аргумента t.

Из определений синуса, косинуса, тангенса и котангенса следуют некоторые соотношения:

1)sin 2 t + cos 2 t = 1(синус квадрат тэ плюс косинус квадрат тэ равно одному)

2)tgt = при t ≠ + πk, kϵZ(тангенс тэ равно отношению синуса тэ к косинусу тэ при тэ не равном пи на два плюс пи ка, ка принадлежит зэт)

3)ctgt = при t ≠ πk, kϵZ(котангенс тэ равно отношению косинуса тэ к синусу тэ при тэ не равном пи ка, ка принадлежит зэт).

4)tgt ∙ ctgt = 1 при t ≠ , kϵZ (произведение тангенса тэ на котангенс тэ равно одному при тэ не равном пи ка, деленное на два, ка принадлежит зэт)

Докажем еще две важные формулы:

Один плюс тангенс квадрат тэ равно отношению единицы к косинусу квадрату тэ при тэ не равном пи на два плюс пи ка.

Доказательство. Выражение единица плюс тангенс квадрат тэ, приведем к общему знаменателю косинус квадрат тэ. Получим в числителе сумму квадратов косинуса тэ и синуса тэ, что равно одному. А знаменатель остается квадрат косинуса тэ.

Сумма единицы и квадрата котангенса тэ равна отношению единицы к квадрату синуса тэ при тэ не равном пи ка.

Доказательство. Выражение единица плюс котангенс квадрат тэ, аналогично приведем к общему знаменателю и применим первое соотношение.

Рассмотрим примеры.

ПРИМЕР1. Найти cost, tgt, ctgt , если sint = и < t < π.(если синус тэ равен четырем пятым и тэ из промежутка от пи на два до пи)

Решение. Из первого соотношения найдем косинус квадрат тэ равен единица минус синус квадрат тэ: cos 2 t = 1 - sin 2 t.

Значит, cos 2 t = 1 -() 2 = (косинус квадрат тэ равен девяти двадцать пятым), то есть cost= (косинус тэ равен трем пятым) или cost = - (косинус тэ равен минус трем пятым). По условию аргумент t принадлежит второй четверти, а в ней cos t < 0 (косинус тэ отрицательный).

Значит косину тэ равен минус трем пятым, cost = - .

Вычислим тангенс тэ:

tgt = = ׃ (-)= - ;(тангенс тэ равен отношению синуса тэ к косинусу тэ, а значит, четырех пятых к минус трем пятым и равно минус четырем третьим)

Соответственно вычисляем (котангенс числа тэ. так как котангенс тэ равен отношению косинуса тэ к синусу тэ,) ctgt = = - .

(котангенс тэ равен минус трем четвертым).

Ответ: cost = - , tgt= - ; ctgt = - . (ответ заполняем по мере решения)

ПРИМЕР 2. Известно, что tgt = - и < t < 2π(тангенс тэ равен минус восемь пятнадцатых и тэ принадлежит промежутку от трех пи на два до двух пи). Найти значения cost, sint, ctgt.

Решение. Воспользуемся данным соотношением, подставив значение в эту формулу получим:

1 + (-) 2 = (единица на косинус квадрат тэ равно сумме единицы и квадрата минус восьми пятнадцатых). Отсюда находим cos 2 t =

(косинус квадрат тэ равен двести двадцать пять двести восемьдесят девятых). Значит, cost = (косинус тэ равен пятнадцать семнадцатых) или

cost = . По условию аргумент t принадлежит четвертой четверти, где cost>0. Поэтому cost = .(косенус тэ равен пятнадцать семнадцатых)

Найдем значение аргумента синус тэ. Так как из соотношения (показать соотношение tgt = при t ≠ + πk, kϵZ) синус тэ равен произведению тангенса тэ на косинус тэ, то подставив значение аргумента тэ..тангенс тэ равен минус восемь пятнадцатых.. по условию, а косинус тэ равен из решенного ранее, получаем

sint = tgt ∙ cost = (-) ∙ = - , (синус тэ равен минус восемь семнадцатых)

ctgt = = - . (так как котангенс тэ, есть величина обратная тангенсу, значит, котангенс тэ равен минус пятнадцать восемнадцатых)