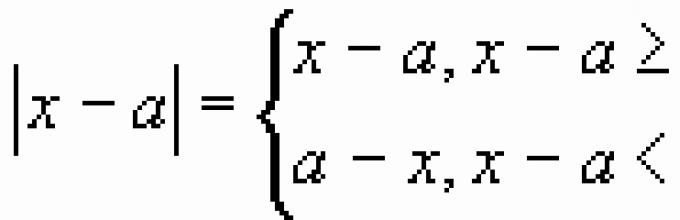В последние годы на вступительных экзаменах, на итоговом тестировании в форме ЕГЭ предлагаются задачи с параметрами. Эти задачи позволяют диагностировать уровень математического и, главное, логического мышления абитуриентов, способность осуществлять исследовательскую деятельность, а также просто знание основных разделов школьного курса математики.
Взгляд на параметр как на равноправную переменную находит своё отражение в графических методах. В самом деле, поскольку параметр “равен в правах” с переменной, то ему, естественно, можно “выделить” и свою координатную ось. Таким образом, возникает координатная плоскость . Отказ от традиционного выбора букв и для обозначения осей, определяет один из эффективнейших методов решения задач с параметрами – “метод областей”. Наряду с другими методами, применяемыми при решении задач с параметрами, я знакомлю своих учеников и с графическими приёмами, обращая внимание на то, как распознать “такие” задачи и как выглядит процесс решения задачи.
Самые общие признаки, которые помогут узнавать задачи, подходящие под рассматриваемый метод:
Задача 1. “При каких значениях параметра неравенство выполняется при всех ?”
Решение. 1).
Раскроем модули с учётом знака
подмодульного выражения: 
2). Запишем все системы получившихся неравенств:
а) 
б) 
в) 
г) 
3). Покажем множество точек, удовлетворяющих каждой системе неравенств (рис.1а).
4). Объединяя все области, показанные на рисунке штриховкой, можно заметить, что неравенству не удовлетворяют точки , лежащие внутри парабол.
На рисунке видно, что при любом значении параметра можно найти область, где лежат точки, координаты которых удовлетворяют исходному неравенству. Неравенство выполняется при всех , если . Ответ: при .
Рассмотренный пример представляет собой
“открытую задачу” - можно рассмотреть решение
целого класса задач, не изменяя рассмотренное в
примере выражение
, в которых технические
трудности построения графиков уже преодолены.
Задача. При каких значениях параметра уравнение не имеет решений? Ответ: при .
Задача. При каких значениях параметра уравнение имеет два решения? Запишите оба найденных решения.
Ответ: , тогда 
, 
;
Тогда 
; , тогда 
, .
Задача. При каких значениях параметра уравнение имеет один корень? Найдите этот корень. Ответ: при при .
Задача. Решите неравенство .
(“Работают” точки, лежащие внутри парабол).
, ; , решений нет;
Задача 2.Найдите все значения параметра а
,
при каждом из которых система неравенств
образует на числовой прямой отрезок длины 1.
Решение. Перепишем исходную систему в таком
виде 
Все решения этой системы (пары вида )
образуют некоторую область, ограниченную
параболами 
и 
(рис 1).
Очевидно, решением системы неравенств будет отрезок длины 1 при и при . Ответ: ; .
Задача 3.Найдите все значения параметра , при которых
множество решений неравенства 
содержит число , а так же содержит два отрезка длиной , не
имеющие общих точек.
Решение. По смыслу неравенства ; перепишем неравенство, умножив обе его части на (), получаем неравенство:
, ,
(1)
Неравенство (1) равносильно совокупности двух систем:
(рис. 2).
Очевидно, интервал не может содержать отрезка длины . Значит, два непересекающихся отрезка длины содержатся в интервале Это возможно при , т.е. при . Ответ: .
Задача 4.Найдите все значения параметра , при каждом из
которых множество решений неравенства 
содержит отрезок длиной 4 и при этом содержится в
некотором отрезке длиной 7.
Решение. Проведём равносильные преобразования, учитывая, что и .
, ,
;
последнее неравенство равносильно совокупности
двух систем:
Покажем области, которые соответствуют этим системам (рис. 3).
1) При множество решений – это интервал длиной, меньшей 4. При множество решений – это объединение двух интервалов .Содержать отрезок длиной 4 может только интервал . Но тогда , и объединение уже не содержится ни в каком отрезке длиной 7. Значит, такие не удовлетворяют условию.
2) множество решений – это интервал . Он содержит отрезок длиной 4, только если его длина больше 4, т.е. при . Он содержится в отрезке длиной 7, только если его длина не больше 7, т. е. при , тогда . Ответ: .
Задача 5. Найдите все значения параметра , при
которых множество решений неравенства 
содержит число 4, а также содержит два
непересекающихся отрезка длиной 4 каждый.
Решение. По условия . Домножим обе части неравенства на (). Получим равносильное неравенство, в котором сгруппируем все члены в левой части и преобразуем её в произведение:
, ,
, 
.
Из последнего неравенства следует:
1) 
2)
Покажем области, которые соответствуют этим системам (рис. 4).
а) При получаем интервал , не содержащий числа 4. При получаем интервал , также не содержащий числа 4.
б) При получаем объединение двух интервалов. Непересекающиеся отрезки длиной 4 могут располагаться только в интервале . Это возможно только в том случае, если длина интервала больше 8, т. е. если . При таких выполнено и другое условие: . Ответ: .
Задача 6. Найдите все значения параметра , при которых
множество решений неравенства 
содержит какой-нибудь отрезок длиной 2, но не
содержит
никакого отрезка длиной 3.
Решение. По смыслу задания , умножим обе части неравенства на , сгруппируем все члены в левой части неравенства и преобразуем её в произведение:
, 
. Из
последнего неравенства следует:
1) 
2) 
Покажем область, которая соответствует первой системе (рис. 5).
Очевидно, что условие задачи выполняется, если 
. Ответ:
.
Задача 7. Найдите все значения параметра , при
которых множество решений неравенства 1+
содержится в некотором отрезке длиной 1 и при
этом содержит какой-нибудь отрезок длиной 0,5.
Решение. 1). Укажем ОДЗ переменной и параметра:
2). Перепишем неравенство в виде
, 
,
(1).
Неравенство (1) равносильно совокупности двух
систем:
1) 
2) 
С учётом ОДЗ решения систем выглядят так:
а) 
б)
(рис. 6).
а) 
б)
Покажем область, соответствующую системе а) (рис. 7). Ответ: .
Задача 8. Шесть чисел образуют возрастающую
арифметическую прогрессию. Первый, второй и
четвертый члены этой прогрессии являются
решениями неравенства 
, а остальные
не являются решениями этого неравенства. Найдите множество всех возможных значений первого члена таких прогрессий.
Решение. I. Найдём все решения неравенства
а). ОДЗ: 
, т.е.
(учли в решении, что функция возрастает на ).
б). На ОДЗ неравенство 
равносильно неравенству 
, т.е. 
, что
даёт:
1). 
2). 
Очевидно, решением неравенства служит
множество значений 
.
II. Проиллюстрируем вторую часть задачи о членах возрастающей арифметической прогрессии рисунком (рис. 8 , где - первый член, - второй и т.д.). Заметим, что:
Или имеем систему линейных неравенств:
решим её графическим способом. Строим прямые и , а
также прямые
То, ..
Первый, второй и шестой члены этой прогрессии
являются решениями неравенства 
, а
остальные не являются решениями этого
неравенства. Найдите множество всех возможных
значений разности этой прогрессии.
Уравнение вида f (x ; a ) = 0 называется уравнением с переменной х и параметром а .
Решить уравнение с параметром а – это значит, для каждого значения а найти значения х , удовлетворяющие этому уравнению.
Пример 1. ах = 0
Пример 2. ах = а
Пример 3.
х + 2 = ах
х – ах = -2
х(1 – а) = -2
Если 1 – а = 0, т.е. а = 1, то х 0 = -2 корней нет
Если 1 – а 0, т.е. а 1, то х =
Пример 4.
(а 2 – 1) х = 2а 2 + а – 3
(а – 1)(а + 1)х = 2(а – 1)(а – 1,5)
(а – 1)(а + 1)х = (1а – 3)(а – 1)
Если а
= 1, то 0х
= 0
х
– любое действительное число
Если а
= -1, то 0х
= -2
Корней нет
Если а 1, а -1, то х = (единственное решение).
Это значит, что каждому допустимому значению а соответствует единственное значение х .
Например:
если а = 5, то х = = ;
если а = 0, то х = 3 и т. д.
Дидактический материал
1. ах = х + 3
2. 4 + ах = 3х – 1
3. а = +
при а = 1 корней нет.
при а = 3 корней нет.
при а = 1 х – любое действительное число, кроме х = 1
при а = -1, а = 0 решений нет.
при а = 0, а = 2 решений нет.
при а = -3, а = 0, 5, а = -2 решений нет
при а = -с , с = 0 решений нет.
Квадратные уравнения с параметром
Пример 1. Решить уравнение
(а – 1)х 2 = 2(2а + 1)х + 4а + 3 = 0
При а = 1 6х + 7 = 0
В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.
Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16
20а + 16 = 0
20а = -16
Если а < -4/5, то Д < 0, уравнение имеет действительный корень.
Если а > -4/5 и а 1, то Д > 0,
х
= 
Если а = 4/5, то Д = 0,
Пример 2. При каких значениях параметра а уравнение
х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?
Д = 4(а + 1) 2 – 4(9а – 5) = 4а 2 – 28а + 24 = 4(а – 1)(а – 6)
4(а – 1)(а – 6) > 0
по т. Виета: х
1 + х
2 = -2(а
+ 1)
х
1 х
2 = 9а
– 5
По условию х 1 < 0, х 2 < 0 то –2(а + 1) < 0 и 9а – 5 > 0
| В итоге | 4(а
– 1)(а
– 6) > 0 - 2(а + 1) < 0 9а – 5 > 0 |
а
< 1: а > 6 а > - 1 а > 5/9 |
 (Рис. 1 ) < a < 1, либо a > 6 |
Пример 3. Найдите значения а , при которых данное уравнение имеет решение.
х 2 – 2(а – 1)х + 2а + 1 = 0
Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а
4а 2 – 16 0
4а (а – 4) 0
а(а – 4)) 0
а(а – 4) = 0
а = 0 или а – 4 = 0
а = 4
(Рис. 2 )
Ответ: а 0 и а 4
Дидактический материал
1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?
2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?
3. При каких значениях а уравнение (а 2 – 6а + 8) х 2 + (а 2 – 4) х + (10 – 3а – а 2) = 0 имеет более двух корней?
4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?
5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?
1. При а = - 1/7, а = 0, а = 1
2. При а = 0
3. При а = 2
4. При а = 10
5. При а = - 2
Показательные уравнения с параметром
Пример 1 .Найти все значения а , при которых уравнение
9 х – (а + 2)*3 х-1/х +2а *3 -2/х = 0 (1) имеет ровно два корня.
Решение. Умножив обе части уравнения (1) на 3 2/х, получим равносильное уравнение
3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)
Пусть 3 х+1/х = у , тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или
(у – 2)(у – а ) = 0, откуда у 1 =2, у 2 = а .
Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log 3 2 , или х 2 – х log 3 2 + 1 = 0.
Это уравнение не имеет действительных корней, так как его Д = log 2 3 2 – 4 < 0.
Если у = а , т.е. 3 х+1/х = а то х + 1/х = log 3 а , или х 2 – х log 3 а + 1 = 0. (3)
Уравнение (3) имеет ровно два корня тогда и только тогда, когда
Д = log 2 3 2 – 4 > 0, или |log 3 а| > 2.
Если log 3 а > 2, то а > 9, а если log 3 а < -2, то 0 < а < 1/9.
Ответ: 0 < а < 1/9, а > 9.
Пример 2 . При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?
Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х 1 = -3, х 2 = а = >
а – положительное число.
Ответ: при а > 0
Дидактический материал
1. Найти все значения а, при которых уравнение
25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.
2. При каких значениях а уравнение
2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?
3. При каких значениях параметра а уравнение
4 х - (5а -3)2 х +4а 2 – 3а = 0 имеет единственное решение?
Логарифмические уравнения с параметром
Пример 1. Найти все значения а , при которых уравнение
log 4x (1 + ах ) = 1/2 (1)
имеет единственное решение.
Решение. Уравнение (1) равносильно уравнению
1 + ах = 2х при х > 0, х 1/4 (3)
х = у
ау 2 –у + 1 = 0 (4)
Не выполняется (2) условие из (3).
Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.Чтобы решить неравенство (3), построим графики функций Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение курса алгебры и математического анализа. – М.: Просвещение, 1990
1. Системы линейных уравнений с параметром
Системы линейных уравнений с параметром решаются теми же основными методами, что и обычные системы уравнений: метод подстановки, метод сложения уравнений и графический метод. Знание графической интерпретации линейных систем позволяет легко ответить на вопрос о количестве корней и их существовании.
Пример 1.
Найти все значения для параметра а, при которых система уравнений не имеет решений.
{х + (а 2 – 3)у = а,
{х + у = 2.
Решение.
Рассмотрим несколько способов решения данного задания.
1 способ . Используем свойство: система не имеет решений, если отношение коэффициентов перед х равно отношению коэффициентов перед у, но не равно отношению свободных членов (а/а 1 = b/b 1 ≠ c/c 1). Тогда имеем:
1/1 = (а 2 – 3)/1 ≠ а/2 или систему
{а 2 – 3 = 1,
{а ≠ 2.
Из первого уравнения а 2 = 4, поэтому с учетом условия, что а ≠ 2, получаем ответ.
Ответ: а = -2.
2 способ . Решаем методом подстановки.
{2 – у + (а 2 – 3)у = а,
{х = 2 – у,
{(а 2 – 3)у – у = а – 2,
{х = 2 – у.
После вынесения в первом уравнении общего множителя у за скобки, получим:
{(а 2 – 4)у = а – 2,
{х = 2 – у.
Система не имеет решений, если первое уравнение не будет иметь решений, то есть
{а 2 – 4 = 0,
{а – 2 ≠ 0.
Очевидно, что а = ±2, но с учетом второго условия в ответ идет только ответ с минусом.
Ответ: а = -2.
Пример 2.
Найти все значения для параметра а, при которых система уравнений имеет бесконечное множество решений.
{8х + ау = 2,
{ах + 2у = 1.
Решение.
По свойству, если отношение коэффициентов при х и у одинаковое, и равно отношению свободных членов системы, то она имеет бесконечное множество решений (т. е. а/а 1 = b/b 1 = c/c 1). Следовательно 8/а = а/2 = 2/1. Решая каждое из полученных уравнений находим, что а = 4 – ответ в данном примере.
Ответ: а = 4.
2. Системы рациональных уравнений с параметром
Пример 3.
{3|х| + у = 2,
{|х| + 2у = a.
Решение.
Умножим первое уравнение системы на 2:
{6|х| + 2у = 4,
{|х| + 2у = a.
Вычтем из первого второе уравнение, получим 5|х| = 4 – а. Это уравнение будет иметь единственное решение при а = 4. В других случаях это уравнение будет иметь два решения (при а < 4) или ни одного (при а > 4).
Ответ: а = 4.
Пример 4.
Найти все значения параметра а, при которых система уравнений имеет единственное решение.
{х + у = а,
{у – х 2 = 1.
Решение.
Данную систему решим с использованием графического метода. Так, графиком второго уравнения системы является парабола, поднятая по оси Оу вверх на один единичный отрезок. Первое уравнение задает множество прямых, параллельных прямой y = -x (рисунок 1)
. Из рисунка хорошо видно, что система имеет решение, если прямая у = -х + а является касательной к параболе в точке с координатами (-0,5; 1,25). Подставив в уравнение прямой вместо х и у эти координаты, находим значение параметра а:
1,25 = 0,5 + а;
Ответ: а = 0,75.
Пример 5.
Используя метод подстановки, выясните, при каком значении параметра а, система имеет единственное решение.
{ах – у = а + 1,
{ах + (а + 2)у = 2.
Решение.
Из первого уравнения выразим у и подставим во второе:
{у = ах – а – 1,
{ах + (а + 2)(ах – а – 1) = 2.
Приведем второе уравнение к виду kx = b, которое будет иметь единственное решение при k ≠ 0. Имеем:
ах + а 2 х – а 2 – а + 2ах – 2а – 2 = 2;
а 2 х + 3ах = 2 + а 2 + 3а + 2.
Квадратный трехчлен а 2 + 3а + 2 представим в виде произведения скобок
(а + 2)(а + 1), а слева вынесем х за скобки:
(а 2 + 3а)х = 2 + (а + 2)(а + 1).
Очевидно, что а 2 + 3а не должно быть равным нулю, поэтому,
а 2 + 3а ≠ 0, а(а + 3) ≠ 0, а значит а ≠ 0 и ≠ -3.
Ответ: а ≠ 0; ≠ -3.
Пример 6.
Используя графический метод решения, определите, при каком значении параметра а, система имеет единственное решение.
{х 2 + у 2 = 9,
{у – |х| = а.
Решение.
Исходя из условия, строим окружность с центром в начале координат и радиусом 3 единичных отрезка, именно ее задает первое уравнение системы
х 2 + у 2 = 9. Второе уравнение системы (у = |х| + а) – ломаная. С помощью рисунка 2
рассматриваем все возможные случаи ее расположения относительно окружности. Легко видеть, что а = 3.
Ответ: а = 3.
Остались вопросы? Не знаете, как решать системы уравнений?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
