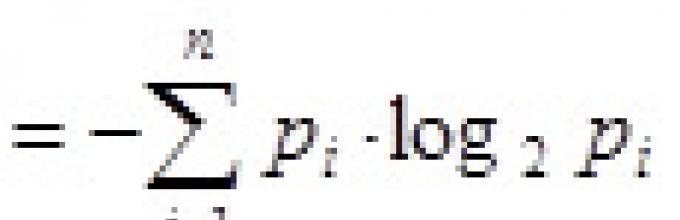Εννοια Εντροπία εισήχθη για πρώτη φορά το 1865 από τον R. Clausius στη θερμοδυναμική για να καθορίσει το μέτρο της μη αναστρέψιμης διασποράς ενέργειας. Η εντροπία χρησιμοποιείται σε διάφορους κλάδους της επιστήμης, συμπεριλαμβανομένης της θεωρίας πληροφοριών, ως μέτρο της αβεβαιότητας οποιασδήποτε εμπειρίας, δοκιμής, η οποία μπορεί να έχει διαφορετικά αποτελέσματα. Αυτοί οι ορισμοί της εντροπίας έχουν βαθιά ενδοεπικοινωνία. Έτσι, με βάση τις ιδέες σχετικά με τις πληροφορίες, μπορούν να συναχθούν όλες οι πιο σημαντικές διατάξεις στατιστική φυσική. [BES. Η φυσικη. Μ: Μεγάλη Ρωσική Εγκυκλοπαίδεια, 1998].

Δυαδική εντροπία πληροφοριών για ανεξάρτητα (άνισα πιθανά) τυχαία συμβάντα ΧΜε nπιθανές καταστάσεις (από 1 έως n, Π- συνάρτηση πιθανότητας) υπολογίζεται από Η φόρμουλα του Shannon:

Αυτή η ποσότητα ονομάζεται επίσης μέση εντροπίαμηνύματα. Η εντροπία στον τύπο του Shannon είναι μέσο χαρακτηριστικό – μαθηματική προσδοκίακατανομές μιας τυχαίας μεταβλητής.
Για παράδειγμα, στην ακολουθία των γραμμάτων που συνθέτουν μια πρόταση στα ρωσικά, διαφορετικά γράμματαεμφανίζονται με διαφορετικές συχνότητες, επομένως η αβεβαιότητα εμφάνισης είναι μικρότερη για ορισμένα γράμματα παρά για άλλα.
Το 1948, ενώ διερευνούσε το πρόβλημα της ορθολογικής μετάδοσης πληροφοριών μέσω ενός θορυβώδους κανάλι επικοινωνίας, ο Claude Shannon πρότεινε μια επαναστατική πιθανολογική προσέγγιση για την κατανόηση των επικοινωνιών και δημιούργησε την πρώτη πραγματικά μαθηματική θεωρία της εντροπίας. Οι συγκλονιστικές ιδέες του λειτούργησαν γρήγορα ως βάση για την ανάπτυξη της θεωρίας της πληροφορίας, η οποία χρησιμοποιεί την έννοια της πιθανότητας. Η έννοια της εντροπίας ως μέτρο της τυχαιότητας εισήχθη από τον Shannon στο άρθρο του "A Mathematical Theory of Communication", που δημοσιεύτηκε σε δύο μέρη στο Bell System Technical Journal το 1948.

Σε περίπτωση εξίσου πιθανών γεγονότων ( ειδική περίπτωση), όταν όλες οι επιλογές είναι εξίσου πιθανές, η εξάρτηση παραμένει μόνο από τον αριθμό των επιλογών που εξετάζονται και ο τύπος του Shannon απλοποιείται σημαντικά και συμπίπτει με τον τύπο του Hartley, ο οποίος προτάθηκε για πρώτη φορά από έναν Αμερικανό μηχανικό Ραλφ Χάρτλεϊτο 1928, ως μία από τις επιστημονικές προσεγγίσεις για την αξιολόγηση των μηνυμάτων:

, όπου I είναι η ποσότητα των πληροφοριών που μεταδίδονται, p είναι η πιθανότητα του συμβάντος, N είναι ο πιθανός αριθμός διαφορετικών (εξίσου πιθανών) μηνυμάτων.

Εργασία 1. Για εξίσου πιθανά γεγονότα.
Υπάρχουν 36 φύλλα στην τράπουλα. Πόσες πληροφορίες περιέχονται στο μήνυμα ότι μια κάρτα με πορτρέτο «άσου» λήφθηκε από την τράπουλα; "άσος μπαστούνι"?

Πιθανότητα p1 = 4/36 = 1/9 και p2 = 1/36. Χρησιμοποιώντας τον τύπο του Hartley έχουμε:

Απάντηση: 3,17; 5,17 bit
Σημειώστε (από το δεύτερο αποτέλεσμα) ότι για την κωδικοποίηση όλων των καρτών χρειάζονται 6 bit.
Είναι επίσης σαφές από τα αποτελέσματα ότι όσο μικρότερη είναι η πιθανότητα ενός γεγονότος, τόσο περισσότερες πληροφορίες περιέχει. (Αυτή η ιδιότητα ονομάζεται μονοτονία)

Εργασία 2. Για άνισα πιθανά γεγονότα
Υπάρχουν 36 φύλλα στην τράπουλα. Από αυτές, οι 12 είναι κάρτες με «πορτρέτα». Μία προς μία, μία από τις κάρτες λαμβάνεται από την τράπουλα και εμφανίζεται για να καθοριστεί εάν απεικονίζει ένα πορτρέτο. Η κάρτα επιστρέφεται στην τράπουλα. Προσδιορίστε τον όγκο των πληροφοριών που μεταδίδονται κάθε φορά που εμφανίζεται μία κάρτα.

Claude Elwood Shannon (1916-2001) -
Αμερικανός μηχανικός και μαθηματικός
ιδρυτής της θεωρίας της πληροφορίας,
εκείνοι. θεωρίες επεξεργασίας, μετάδοσης
και αποθήκευση πληροφοριών

Κλοντ Σάνονήταν ο πρώτος που ερμήνευσε τα μεταδιδόμενα μηνύματα και τον θόρυβο στα κανάλια επικοινωνίας από στατιστική άποψη, λαμβάνοντας υπόψη τόσο πεπερασμένα όσο και συνεχή σύνολα μηνυμάτων. Ο Claude Shannon ονομάζεται "πατέρας της θεωρίας της πληροφορίας".

Ένα από τα πιο διάσημα επιστημονικές εργασίεςΟ Claude Shannon είναι το άρθρο του «Μαθηματική θεωρία της επικοινωνίας», που δημοσιεύτηκε το 1948.

Σε αυτό το έργο, ο Shannon, διερευνώντας το πρόβλημα της ορθολογικής μετάδοσης πληροφοριών μέσω ενός θορυβώδους καναλιού επικοινωνίας, πρότεινε μια πιθανολογική προσέγγιση για την κατανόηση των επικοινωνιών, δημιούργησε την πρώτη πραγματικά μαθηματική θεωρία της εντροπίας ως μέτρο τυχαίας και εισήγαγε ένα μέτρο διακριτής κατανομής. Ππιθανότητες σε ένα σύνολο εναλλακτικών καταστάσεων του πομπού και του δέκτη μηνυμάτων.

Ο Shannon έθεσε τις απαιτήσεις για τη μέτρηση της εντροπίας και εξήγαγε έναν τύπο που έγινε η βάση της ποσοτικής θεωρίας πληροφοριών:

Ιπποδύναμη).

Εδώ n- τον αριθμό των χαρακτήρων από τους οποίους μπορεί να συντεθεί ένα μήνυμα (αλφάβητο), H - δυαδική εντροπία πληροφοριών .

Στην πράξη, οι τιμές πιθανότητας πιστον παραπάνω τύπο αντικαθίστανται από στατιστικές εκτιμήσεις: πι - σχετική συχνότητα Εγώο χαρακτήρας στο μήνυμα, όπου Ν- τον αριθμό όλων των χαρακτήρων στο μήνυμα, N i- απόλυτη συχνότητα Εγώο χαρακτήρας στο μήνυμα, δηλ. αριθμός περιστατικού Εγώο χαρακτήρας στο μήνυμα.

Στην εισαγωγή του άρθρου του «A Mathematical Theory of Communication», ο Shannon σημειώνει ότι σε αυτό το άρθρο επεκτείνει τη θεωρία της επικοινωνίας, οι κύριες διατάξεις της οποίας περιέχονται στο σημαντικά έργα NyquistΚαι Χάρτλεϋ.

Harry Nyquist (1889-1976) -
Αμερικανός Σουηδός μηχανικός
καταγωγής, ένας από τους πρωτοπόρους
θεωρία πληροφοριών

Τα πρώτα αποτελέσματα του Nyquist στον προσδιορισμό του πλάτους του εύρους συχνοτήτων που απαιτείται για τη μετάδοση πληροφοριών έθεσαν τα θεμέλια για τις μετέπειτα επιτυχίες του Claude Shannon στην ανάπτυξη της θεωρίας της πληροφορίας.

Το 1928, ο Hartley εισήγαγε το λογαριθμικό μέτρο της πληροφορίας H = κημερολόγιο 2 Ν, η οποία συχνά ονομάζεται ποσότητα πληροφοριών Hartley.

Ο Hartley έχει το ακόλουθο σημαντικό θεώρημα σχετικά με την απαιτούμενη ποσότητα πληροφοριών: εάν σε ένα δεδομένο σύνολο Μ, που αποτελείται από Νστοιχεία, περιέχει ένα στοιχείο Χ, για το οποίο είναι γνωστό μόνο ότι ανήκει σε αυτό το σύνολο Μ, μετά να βρεις Χ, είναι απαραίτητο να αποκτήσετε μια ποσότητα πληροφοριών για αυτό το σύνολο ίσο με το log 2 Νκομμάτι.

Με την ευκαιρία, σημειώστε ότι ο τίτλος ΚΟΜΜΑΤΙπροέρχεται από την αγγλική συντομογραφία BIT - Δυαδικό ψηφίο. Αυτός ο όρος προτάθηκε για πρώτη φορά από έναν Αμερικανό μαθηματικό Τζον Τούκιτο 1946. Οι Hartley και Shannon χρησιμοποίησαν το bit ως μονάδα πληροφοριών.

Γενικά, η εντροπία Shannon είναι η εντροπία ενός συνόλου πιθανοτήτων Π 1 , Π 2 ,…, p n.

Ralph Vinton Lyon Hartley (1888-1970)
- Αμερικανός επιστήμονας ηλεκτρονικών

Αυστηρά μιλώντας, αν Χ Π 1 , Π 2 ,…, p n- η πιθανότητα όλων των πιθανών τιμών του, μετά η συνάρτηση H (Χ)καθορίζει την εντροπία αυτής της τυχαίας μεταβλητής, σε αυτήν την περίπτωση, αν και Χκαι δεν είναι όρισμα εντροπίας, μπορούμε να γράψουμε H (Χ).

Ομοίως, αν Υείναι μια πεπερασμένη διακριτή τυχαία μεταβλητή, και q 1 , q 2 ,…, q m είναι η πιθανότητα όλων των πιθανών τιμών του, τότε για αυτήν την τυχαία μεταβλητή μπορούμε να γράψουμε H (Υ).

John Wilder Tukey (1915-2000) -
Αμερικανός μαθηματικός. Ο Τούκι εξελέγη
bit για να υποδείξει ένα ψηφίο
σε δυαδικό σύστημα αριθμών

Ο Σάνον κάλεσε τη συνάρτηση H(Χ)εντροπία κατόπιν συμβουλής Τζον φον Νόιμαν.

Ο Neumann πεπεισμένος: αυτή η συνάρτηση πρέπει να ονομάζεται εντροπία «για δύο λόγους. Πρώτα απ 'όλα, η συνάρτηση αβεβαιότητας χρησιμοποιήθηκε στη στατιστική μηχανική με αυτό το όνομα, επομένως έχει ήδη ένα όνομα. Δεύτερον, και το πιο σημαντικό, κανείς δεν ξέρει τι είναι στην πραγματικότητα η εντροπία, οπότε θα έχετε πάντα το πλεονέκτημα στη συζήτηση»..

Πρέπει να υποθέσει κανείς ότι αυτή η συμβουλή του Neumann δεν ήταν ένα απλό αστείο. Πιθανότατα, τόσο ο John von Neumann όσο και ο Claude Shannon γνώριζαν για την ερμηνεία πληροφοριών της εντροπίας Boltzmann ως ποσότητα που χαρακτηρίζει την ατελή πληροφόρηση για το σύστημα.

Κατά τον ορισμό του Shannon εντροπία- αυτή είναι η ποσότητα πληροφοριών ανά ένα στοιχειώδες μήνυμα από μια πηγή που παράγει στατιστικά ανεξάρτητα μηνύματα.

7. Εντροπία Κολμογκόροφ

Αντρέι Νικολάεβιτς
Kolmogorov (1903-1987) -
Σοβιετικός επιστήμονας, ένας από τους μεγαλύτερους
μαθηματικοί του 20ου αιώνα

ΕΝΑ. ΚολμογκόροφΕπιτεύχθηκαν θεμελιώδη αποτελέσματα σε πολλούς τομείς των μαθηματικών, συμπεριλαμβανομένης της θεωρίας της πολυπλοκότητας των αλγορίθμων και της θεωρίας πληροφοριών.

Συγκεκριμένα, έπαιξε βασικό ρόλο στη μετατροπή της θεωρίας της πληροφορίας, που διατυπώθηκε από τον Claude Shannon ως τεχνική πειθαρχία, σε μια αυστηρή μαθηματική επιστήμη, και στην οικοδόμηση της θεωρίας της πληροφορίας σε μια θεμελιωδώς διαφορετική βάση από αυτή του Shannon.

Στα έργα του για τη θεωρία της πληροφορίας και στον τομέα της θεωρίας των δυναμικών συστημάτων, ο Α.Ν. Ο Kolmogorov γενίκευσε την έννοια της εντροπίας σε εργοδικές τυχαίες διεργασίες μέσω της οριακής κατανομής πιθανότητας. Για να κατανοήσουμε το νόημα αυτής της γενίκευσης, είναι απαραίτητο να γνωρίζουμε τους βασικούς ορισμούς και τις έννοιες της θεωρίας των τυχαίων διεργασιών.

Η τιμή της εντροπίας Kolmogorov (ονομάζεται επίσης Κ-εντροπία) καθορίζει μια εκτίμηση του ρυθμού απώλειας πληροφοριών και μπορεί να ερμηνευθεί ως μέτρο της «μνήμης» του συστήματος ή ως μέτρο του ρυθμού «λήθης» των αρχικών συνθηκών. Μπορεί επίσης να θεωρηθεί ως μέτρο του χάους του συστήματος.

8. Εντροπία Renyi

Alfred Renyi (1921-1970) -
Ούγγρος μαθηματικός, δημιουργός
Μαθηματικό Ινστιτούτοστη Βουδαπέστη,
που τώρα φέρει το όνομά του

Παρουσίασε το φάσμα εντροπίας Renyi μιας παραμέτρου.

Από τη μία πλευρά, η εντροπία Rényi είναι μια γενίκευση της εντροπίας Shannon. Από την άλλη πλευρά, ταυτόχρονα αντιπροσωπεύει μια γενίκευση της απόστασης (απόκλιση) Κούλμπακ-Λάιμπλερ. Σημειώνουμε επίσης ότι ο Rényi ήταν υπεύθυνος για την πλήρη απόδειξη του θεωρήματος του Hartley σχετικά με τον απαιτούμενο όγκο πληροφοριών.

Απόσταση Kullback-Leibler(απόκλιση πληροφοριών, σχετική εντροπία) είναι ένα ασύμμετρο μέτρο της απόστασης μεταξύ δύο κατανομών πιθανοτήτων.

Συνήθως, μία από τις κατανομές που συγκρίνονται είναι η «αληθινή» κατανομή και η δεύτερη κατανομή είναι η εκτιμώμενη (δοκιμασμένη) κατανομή, η οποία είναι κατά προσέγγιση της πρώτης.

Αφήνω Χ, Υ- αυτές είναι πεπερασμένες διακριτές τυχαίες μεταβλητές για τις οποίες οι περιοχές των πιθανών τιμών ανήκουν σε ένα δεδομένο σύνολο και οι συναρτήσεις πιθανότητας είναι γνωστές: Π (Χ = ένα i) = πιΚαι Π (Υ = ένα i) = τσι.

Στη συνέχεια, η τιμή DKL της απόστασης Kullback-Leibler υπολογίζεται χρησιμοποιώντας τους τύπους

D KL (Χ, Υ) =, D KL (Υ, Χ) = .

Στην περίπτωση απολύτως συνεχών τυχαίων μεταβλητών Χ, Υ, που δίνονται από τις πυκνότητες κατανομής τους, στους τύπους για τον υπολογισμό της τιμής της απόστασης Kullback-Leibler, τα αθροίσματα αντικαθίστανται από τα αντίστοιχα ολοκληρώματα.

Η απόσταση Kullback-Leibler είναι πάντα ένας μη αρνητικός αριθμός και ισούται με μηδέν D KL(Χ, Υ) = 0 αν και μόνο αν για δεδομένες τυχαίες μεταβλητές η ισότητα ισχύει σχεδόν παντού Χ = Υ.

Το 1960, ο Alfred Rényi πρότεινε τη γενίκευση της εντροπίας.

Εντροπία Reny αντιπροσωπεύει μια οικογένεια λειτουργιών για την ποσοτική ποικιλία της τυχαιότητας ενός συστήματος. Ο Rényi όρισε την εντροπία του ως τη στιγμή της τάξης α του μέτρου του ε-διαμερίσματος (κάλυψης).

Έστω το α δεδομένο πραγματικός αριθμός, ικανοποιώντας τις απαιτήσεις α ≥ 0, α ≠ 1. Τότε η εντροπία Rényi τάξης α προσδιορίζεται από τον τύπο H α = H α ( Χ), Οπου πι = Π (Χ = x i) είναι η πιθανότητα ενός γεγονότος που συνίσταται στο γεγονός ότι μια διακριτή τυχαία μεταβλητή Χθα ισούται με την αντίστοιχη πιθανή τιμή του, n- ο συνολικός αριθμός των διαφορετικών δυνατών τιμών της τυχαίας μεταβλητής Χ.

Για ομοιόμορφη διανομή όταν Π 1 = Π 2 =…= p n =1/n, όλες οι εντροπίες Reny είναι ίσες H α ( Χ) = κούτσουρο n.

Διαφορετικά, οι τιμές των εντροπιών Renyi μειώνονται ελαφρώς όσο αυξάνονται οι τιμές της παραμέτρου α. Οι εντροπίες Rényi παίζουν σημαντικό ρόλο στην οικολογία και τις στατιστικές ως δείκτες ποικιλότητας.

Η εντροπία Rényi είναι επίσης σημαντική στις κβαντικές πληροφορίες και μπορεί να χρησιμοποιηθεί ως μέτρο πολυπλοκότητας.

Ας εξετάσουμε μερικές ειδικές περιπτώσεις εντροπίας Rényi για συγκεκριμένες τιμές τάξης α:

1. Εντροπία Hartley : H 0 = H 0 (Χ) = κούτσουρο n, Οπου n- ισχύς της περιοχής των πιθανών τιμών μιας πεπερασμένης τυχαίας μεταβλητής Χ, δηλ. τον αριθμό των διαφορετικών στοιχείων που ανήκουν σε ένα σύνολο πιθανών τιμών·

2. Εντροπία πληροφοριών Shannon : H 1 = H 1 (Χ) = H 1 (Π) (ορίζεται ως το όριο ως α → 1, το οποίο είναι εύκολο να βρεθεί, για παράδειγμα, χρησιμοποιώντας τον κανόνα του L'Hopital).

3. Εντροπία συσχέτισης ή σύγκρουση εντροπίας: H 2 = H 2 (Χ)= - ln ( Χ = Υ);

4. Ελάχιστη εντροπία : H ∞ = H ∞ (Χ).

Σημειώστε ότι για οποιαδήποτε τιμή μη αρνητικής τάξης (α ≥ 0) οι ανισώσεις ισχύουν πάντα: H ∞ (Χ) ≤ H α ( Χ). Εκτός, H 2 (Χ) ≤ H 1 (Χ) Και H ∞ (Χ) ≤ H 2 (Χ) ≤ 2· H ∞ (Χ).

Ο Alfred Rényi εισήγαγε όχι μόνο τις απόλυτες εντροπίες του (1.15), αλλά όρισε επίσης ένα φάσμα μετρήσεων απόκλισης που γενικεύουν τις αποκλίσεις Kullback-Leibner.

Έστω α ένας δεδομένος πραγματικός αριθμός που ικανοποιεί τις απαιτήσεις α > 0, α ≠ 1. Στη συνέχεια στη σημείωση που χρησιμοποιείται για τον προσδιορισμό της τιμής D KLΑποστάσεις Kullback-Leibler, η τιμή της απόκλισης Rényi της τάξης α καθορίζεται από τους τύπους

ρε α ( Χ, Υ), ρε α ( Χ, Υ).

Η απόκλιση Renyi ονομάζεται επίσης άλφα-απόκλιση ή α-απόκλιση. Ο ίδιος ο Rényi χρησιμοποίησε τον λογάριθμο βάσης 2, αλλά όπως πάντα, η τιμή της βάσης του λογάριθμου είναι εντελώς ασήμαντη.

9. Εντροπία Τσάλλη

Κωνσταντίνος Τσάλλης (γεν. 1943) -
Βραζιλιάνος φυσικός
Ελληνικής καταγωγής

Το 1988, πρότεινε μια νέα γενίκευση της εντροπίας, η οποία είναι βολική για χρήση στην ανάπτυξη της θεωρίας της μη γραμμικής θερμοδυναμικής.

Η γενίκευση της εντροπίας που πρότεινε μπορεί, ίσως, να παίξει σημαντικό ρόλο στη θεωρητική φυσική και την αστροφυσική στο εγγύς μέλλον.

Εντροπία Τσάλληπλ, που συχνά ονομάζεται μη εκτεταμένη (μη προσθετική) εντροπία, ορίζεται για nμικροκαταστάσεις σύμφωνα με τον ακόλουθο τύπο:

πλ = πλ (Χ) = πλ (Π) = κ· , .

Εδώ κ- σταθερά διαστάσεων εάν η διάσταση παίζει σημαντικό ρόλο για την κατανόηση του προβλήματος.

Ο Τσάλλης και οι υποστηρικτές του προτείνουν την ανάπτυξη «μη εκτεταμένης στατιστικής μηχανικής και θερμοδυναμικής» ως γενίκευση αυτών των κλασικών επιστημών στην περίπτωση συστημάτων με μακριές μνήμες και/ή δυνάμεις μεγάλης εμβέλειας.

Από όλους τους άλλους τύπους εντροπίας, συμπ. και από την εντροπία Ρένυη, η εντροπία Τσάλλη διαφέρει στο ότι δεν είναι προσθετική. Αυτή είναι μια θεμελιώδης και σημαντική διαφορά.

Ο Τσάλλης και οι υποστηρικτές του πιστεύουν ότι αυτό το χαρακτηριστικό καθιστά δυνατή τη δημιουργία μιας νέας θερμοδυναμικής και μιας νέας στατιστικής θεωρίας που μπορεί απλά και σωστά να περιγράψει συστήματα με μακριές μνήμες και συστήματα στα οποία κάθε στοιχείο αλληλεπιδρά όχι μόνο με τους άμεσους γείτονές του, αλλά με ολόκληρο το σύστημα. στο σύνολό του.ή τα μεγάλα μέρη του.

Ένα παράδειγμα τέτοιων συστημάτων, και επομένως ένα πιθανό αντικείμενο έρευνας με χρήση νέα θεωρία, είναι κοσμικά βαρυτικά συστήματα: αστρικά σμήνη, νεφελώματα, γαλαξίες, σμήνη γαλαξιών κ.λπ.

Από το 1988, όταν ο Κωνσταντίνος Τσάλλης πρότεινε την εντροπία του, εμφανίστηκε ένας σημαντικός αριθμός εφαρμογών της θερμοδυναμικής ανώμαλων συστημάτων (με μήκος μνήμης ή/και δυνάμεις μεγάλης εμβέλειας), συμπεριλαμβανομένου του τομέα της θερμοδυναμικής των βαρυτικών συστημάτων.

10. Κβαντική εντροπία Von Neumann

John (Janos) von Neumann (1903-1957) -
Αμερικανός μαθηματικός και φυσικός
Ουγγρικής καταγωγής

Η εντροπία Von Neumann παίζει σημαντικό ρόλο σε κβαντική φυσικήκαι στην αστροφυσική έρευνα.

Τζον φον Νόιμανσυνέβαλε σημαντικά στην ανάπτυξη τέτοιων κλάδων της επιστήμης όπως η κβαντική φυσική, η κβαντική λογική, η λειτουργική ανάλυση, η θεωρία συνόλων, η επιστήμη των υπολογιστών και τα οικονομικά.

Ήταν μέλος του Manhattan Project to develop πυρηνικά όπλα, ένας από τους δημιουργούς της μαθηματικής θεωρίας παιγνίων και της έννοιας των κυψελωτών αυτόματα, καθώς και ο ιδρυτής της σύγχρονης αρχιτεκτονικής υπολογιστών.

Η εντροπία Von Neumann, όπως κάθε εντροπία, σχετίζεται με πληροφορίες: σε αυτήν την περίπτωση, με πληροφορίες σχετικά με κβαντικό σύστημα. Και από αυτή την άποψη, παίζει το ρόλο μιας θεμελιώδους παραμέτρου που χαρακτηρίζει ποσοτικά την κατάσταση και την κατεύθυνση της εξέλιξης ενός κβαντικού συστήματος.

Επί του παρόντος, η εντροπία von Neumann χρησιμοποιείται ευρέως σε διάφορες μορφές(εντροπία υπό όρους, σχετική εντροπία κ.λπ.) εντός κβαντική θεωρίαπληροφορίες.

Τα διάφορα μέτρα εμπλοκής σχετίζονται άμεσα με την εντροπία von Neumann. Ωστόσο, πρόσφατα εμφανίστηκε μια σειρά από έργα αφιερωμένα στην κριτική της εντροπίας Shannon ως μέτρου πληροφοριών και της πιθανής ανεπάρκειάς της, και, κατά συνέπεια, της ανεπάρκειας της εντροπίας von Neumann ως γενίκευσης της εντροπίας Shannon.

Μια ανασκόπηση (δυστυχώς, πρόχειρη και μερικές φορές όχι αρκετά αυστηρή μαθηματικά) της εξέλιξης επιστημονικές απόψειςσχετικά με την έννοια της εντροπίας μας επιτρέπει να δώσουμε απαντήσεις σε σημαντικά ερωτήματα που σχετίζονται με την πραγματική ουσία της εντροπίας και τις προοπτικές χρήσης της προσέγγισης της εντροπίας στην επιστημονική και πρακτική έρευνα. Ας περιοριστούμε στο να εξετάσουμε τις απαντήσεις σε δύο τέτοιες ερωτήσεις.

Πρώτη ερώτηση: Οι πολυάριθμοι τύποι εντροπίας, που εξετάζονται και δεν εξετάζονται παραπάνω, έχουν κάτι κοινό εκτός από το ίδιο όνομα;

Αυτό το ερώτημα προκύπτει φυσικά αν λάβουμε υπόψη την ποικιλομορφία που χαρακτηρίζει τις διάφορες υπάρχουσες ιδέες για την εντροπία.

Σήμερα, η επιστημονική κοινότητα δεν έχει αναπτύξει μια ενιαία, καθολικά αποδεκτή απάντηση σε αυτό το ερώτημα: ορισμένοι επιστήμονες απαντούν σε αυτήν την ερώτηση καταφατικά, άλλοι - αρνητικά, και άλλοι αντιμετωπίζουν την κοινότητα των εντροπιών διαφορετικών τύπων με αξιοσημείωτο βαθμό αμφιβολίας. .

Ο Clausius, προφανώς, ήταν ο πρώτος επιστήμονας που πείστηκε για την καθολική φύση της εντροπίας και πίστευε ότι σε όλες τις διεργασίες που συμβαίνουν στο Σύμπαν, παίζει σημαντικό ρόλο, ιδίως καθορίζοντας την κατεύθυνση ανάπτυξής τους στο χρόνο.

Παρεμπιπτόντως, ήταν ο Ρούντολφ Κλαούσιους που κατέληξε σε μια από τις διατυπώσεις του δεύτερου νόμου της θερμοδυναμικής: «Μια διαδικασία είναι αδύνατη, το μόνο αποτέλεσμα της οποίας θα ήταν η μεταφορά θερμότητας από ένα ψυχρότερο σώμα σε ένα πιο ζεστό».

Αυτή η διατύπωση του δεύτερου νόμου της θερμοδυναμικής ονομάζεται Το αξίωμα του Clausius , και η μη αναστρέψιμη διαδικασία που συζητείται σε αυτό το αξίωμα είναι διαδικασία Clausius .

Από την ανακάλυψη του δεύτερου νόμου της θερμοδυναμικής, οι μη αναστρέψιμες διεργασίες έχουν παίξει μοναδικό ρόλο στη φυσική εικόνα του κόσμου. Έτσι, το περίφημο άρθρο του 1849 Ουίλιαμ Τόμσον, που περιείχε μία από τις πρώτες διατυπώσεις του δεύτερου νόμου της θερμοδυναμικής, ονομαζόταν «Σχετικά με την καθολική τάση στη φύση να διασκορπίζει τη μηχανική ενέργεια».

Σημειώστε επίσης ότι ο Clausius αναγκάστηκε να χρησιμοποιήσει κοσμολογική γλώσσα: «Η εντροπία του Σύμπαντος τείνει στο μέγιστο».

Ilya Romanovich Prigogine (1917-2003) -
Βέλγο-Αμερικανός φυσικός και
χημικός ρωσικής καταγωγής,
δαφνοστεφής βραβείο Νόμπελ
στη Χημεία 1977

Κατέληξαν σε παρόμοια συμπεράσματα Ilya Prigozhin. Ο Prigogine πιστεύει ότι η αρχή της εντροπίας είναι υπεύθυνη για τη μη αναστρέψιμη διάρκεια του χρόνου στο Σύμπαν και ίσως παίζει σημαντικό ρόλο στην κατανόηση της έννοιας του χρόνου ως φυσικού φαινομένου.

Μέχρι σήμερα, πολλές μελέτες και γενικεύσεις της εντροπίας έχουν πραγματοποιηθεί, μεταξύ άλλων από την άποψη της αυστηρής μαθηματικής θεωρίας. Ωστόσο, η αξιοσημείωτη δραστηριότητα των μαθηματικών σε αυτόν τον τομέα δεν είναι ακόμη σε ζήτηση σε εφαρμογές, με πιθανή εξαίρεση τα έργα Κολμογκόροφ, RenyiΚαι Τσάλλης.

Αναμφίβολα, η εντροπία είναι πάντα μέτρο (βαθμός) χάους, αταξίας. Είναι η ποικιλομορφία των εκδηλώσεων του φαινομένου του χάους και της αταξίας που καθορίζει το αναπόφευκτο της ποικιλομορφίας των τροποποιήσεων της εντροπίας.

Δεύτερη ερώτηση: Μπορεί το πεδίο εφαρμογής της προσέγγισης της εντροπίας να θεωρηθεί εκτεταμένο ή όλες οι εφαρμογές της εντροπίας και του δεύτερου νόμου της θερμοδυναμικής περιορίζονται στην ίδια τη θερμοδυναμική και σε συναφείς τομείς της φυσικής επιστήμης;

Ιστορία επιστημονική έρευναΗ εντροπία δείχνει ότι η εντροπία είναι ένα επιστημονικό φαινόμενο που ανακαλύφθηκε στη θερμοδυναμική και στη συνέχεια μετανάστευσε με επιτυχία σε άλλες επιστήμες και, πάνω απ 'όλα, στη θεωρία της πληροφορίας.

Αναμφίβολα, η εντροπία παίζει σημαντικό ρόλο σε όλους σχεδόν τους τομείς σύγχρονη φυσική επιστήμη: στη θερμοφυσική, τη στατιστική φυσική, τη φυσική και χημική κινητική, τη βιοφυσική, την αστροφυσική, την κοσμολογία και τη θεωρία πληροφοριών.

Μιλώντας για τα εφαρμοσμένα μαθηματικά, δεν μπορούμε να μην αναφέρουμε εφαρμογές της αρχής της μέγιστης εντροπίας.

Όπως έχει ήδη σημειωθεί, σημαντικοί τομείς εφαρμογής της εντροπίας είναι τα κβαντομηχανικά και τα σχετικιστικά αντικείμενα. Στην κβαντική φυσική και την αστροφυσική, τέτοιες εφαρμογές της εντροπίας παρουσιάζουν μεγάλο ενδιαφέρον.

Ας αναφέρουμε μόνο ένα αρχικό αποτέλεσμα της θερμοδυναμικής των μαύρων οπών: εντροπία μαύρη τρύπαίσο με το ένα τέταρτο της επιφάνειάς του (εμβαδόν ορίζοντα γεγονότων).

Στην κοσμολογία, πιστεύεται ότι η εντροπία του Σύμπαντος είναι ίση με τον αριθμό των κβαντών ακτινοβολίας ανά νουκλεόνιο.

Έτσι, το πεδίο εφαρμογής της προσέγγισης της εντροπίας είναι πολύ εκτεταμένο και περιλαμβάνει μια μεγάλη ποικιλία κλάδων γνώσης, ξεκινώντας από τη θερμοδυναμική, άλλους τομείς της φυσικής επιστήμης, την επιστήμη των υπολογιστών και τελειώνοντας, για παράδειγμα, με την ιστορία και τα οικονομικά.

A.V. Seagal, γιατρός οικονομικές επιστήμες, Πανεπιστήμιο της Κριμαίας με το όνομα V.I. Βερνάντσκι

Πληροφορίες και εντροπία

Όταν συζητάμε την έννοια της πληροφορίας, είναι αδύνατο να μην αγγίξουμε μια άλλη σχετική έννοια – την εντροπία. Οι έννοιες της εντροπίας και της πληροφορίας συνδέθηκαν για πρώτη φορά από τον K. Shannon.

Claude Elwood Shannon ( Κλοντ Έλγουντ Σάνον), 1916-2001 - μακρινός συγγενής του Thomas Edison, Αμερικανού μηχανικού και μαθηματικού, ήταν υπάλληλος των εργαστηρίων Bell από το 1941 έως το 1972. Στο έργο του "Mathematical Theory of Communications" (http://cm.bell-labs.com Το /cm/ms /what/shannonday/), που δημοσιεύτηκε το 1948, ήταν ο πρώτος που καθόρισε το μέτρο του περιεχομένου πληροφοριών οποιουδήποτε μηνύματος και την έννοια του κβαντικού όγκου πληροφοριών - λίγο. Αυτές οι ιδέες αποτέλεσαν τη βάση της θεωρίας των σύγχρονων ψηφιακών επικοινωνιών. Το άλλο έργο του Shannon, Communication Theory of Secrecy Systems, που δημοσιεύτηκε το 1949, συνέβαλε στην ανάπτυξη της κρυπτογραφίας σε επιστημονική πειθαρχία. Είναι ο ιδρυτής θεωρία πληροφοριών, που έχει βρει εφαρμογή στα σύγχρονα συστήματα επικοινωνίας υψηλής τεχνολογίας. Ο Shannon έκανε τεράστια συμβολή στη θεωρία των πιθανοτικών κυκλωμάτων, στη θεωρία των αυτομάτων και στη θεωρία των συστημάτων ελέγχου - επιστήμες που ενώνονται με την έννοια της «κυβερνητικής».

Φυσικός ορισμός της εντροπίας

Η έννοια της εντροπίας εισήχθη για πρώτη φορά από τον Clausius το 1865 ως συνάρτηση της θερμοδυναμικής κατάστασης του συστήματος

όπου Q είναι θερμότητα, T είναι θερμοκρασία.

Η φυσική έννοια της εντροπίας εκδηλώνεται ως μέρος της εσωτερικής ενέργειας του συστήματος, η οποία δεν μπορεί να μετατραπεί σε έργο. Ο Clausius απέκτησε εμπειρικά αυτή τη συνάρτηση πειραματιζόμενος με αέρια.

Ο L. Boltzmann (1872), χρησιμοποιώντας τις μεθόδους της στατιστικής φυσικής, εξήγαγε μια θεωρητική έκφραση για την εντροπία

όπου το Κ είναι σταθερά. W – θερμοδυναμική πιθανότητα (ο αριθμός των αναδιατάξεων των ιδανικών μορίων αερίου που δεν επηρεάζει τη μακροκατάσταση του συστήματος).

Η εντροπία Boltzmann προήλθε για ένα ιδανικό αέριο και ερμηνεύεται ως μέτρο αταξίας, μέτρο του χάους ενός συστήματος. Για ένα ιδανικό αέριο, οι εντροπίες Boltzmann και Clausius είναι πανομοιότυπες. Η φόρμουλα του Boltzmann έγινε τόσο διάσημη που γράφτηκε ως επιτάφιος στον τάφο του. Υπάρχει η άποψη ότι η εντροπία και το χάος είναι ένα και το αυτό. Παρά το γεγονός ότι η εντροπία περιγράφει μόνο ιδανικά αέρια, έχει αρχίσει χωρίς κριτική να χρησιμοποιείται για την περιγραφή πιο πολύπλοκων αντικειμένων.

Ο ίδιος ο Boltzmann το 1886 προσπάθησε να χρησιμοποιήσει την εντροπία για να εξηγήσει τι είναι ζωή. Σύμφωνα με τον Boltzmann, η ζωή είναι ένα φαινόμενο ικανό να μειώσει την εντροπία της. Σύμφωνα με τον Boltzmann και τους οπαδούς του, όλες οι διαδικασίες στο Σύμπαν αλλάζουν προς την κατεύθυνση του χάους. Το σύμπαν οδεύει προς τον θερμικό θάνατο. Αυτή η ζοφερή πρόβλεψη κυριάρχησε στην επιστήμη για πολύ καιρό. Ωστόσο, η εμβάθυνση της γνώσης για τον περιβάλλοντα Κόσμο υπονόμευσε σταδιακά αυτό το δόγμα.

Οι κλασικοί δεν συνέδεαν την εντροπία με την πληροφορία.

Η εντροπία ως μέτρο πληροφοριών

Σημειώστε ότι η έννοια της «πληροφορίας» συχνά ερμηνεύεται ως «πληροφορία» και η μεταφορά πληροφοριών πραγματοποιείται μέσω επικοινωνίας. Ο K. Shannon θεώρησε την εντροπία ως μέτρο ΧΡΗΣΙΜΕΣ ΠΛΗΡΟΦΟΡΙΕΣστις διαδικασίες μετάδοσης σημάτων μέσω καλωδίων.

Για τον υπολογισμό της εντροπίας, ο Shannon πρότεινε μια εξίσωση που θυμίζει την κλασική έκφραση της εντροπίας που βρέθηκε από τον Boltzmann. Ένα ανεξάρτητο τυχαίο συμβάν θεωρείται Χμε Ν δυνατές καταστάσεις και p i -πιθανότητα της i-ης κατάστασης. Στη συνέχεια η εντροπία του γεγονότος Χ

Αυτή η ποσότητα ονομάζεται επίσης μέση εντροπία. Για παράδειγμα, μπορεί να μιλάμε για μετάδοση ενός μηνύματος σε φυσική γλώσσα. Όταν μεταδίδουμε διαφορετικά γράμματα μεταδίδουμε διαφορετικές ποσότητεςπληροφορίες. Ο όγκος των πληροφοριών ανά γράμμα σχετίζεται με τη συχνότητα χρήσης αυτού του γράμματος σε όλα τα μηνύματα που σχηματίζονται στη γλώσσα. Όσο πιο σπάνιο είναι το γράμμα που μεταδίδουμε, τόσο περισσότερες πληροφορίες περιέχει.

Μέγεθος

H i = P i log 2 1/P i = -P i log 2 P i ,

ονομάζεται μερική εντροπία, χαρακτηρίζοντας μόνο την κατάσταση i-e.

Ας εξηγήσουμε με παραδείγματα. Όταν ρίχνετε ένα κέρμα, εμφανίζονται κεφάλια ή ουρές, αυτές είναι ορισμένες πληροφορίες σχετικά με τα αποτελέσματα της εκτίναξης.

Για ένα νόμισμα, ο αριθμός των εξίσου πιθανών πιθανοτήτων είναι N = 2. Η πιθανότητα να πέσουν τα κεφάλια (ουρές) είναι 1/2.

Όταν ρίχνουμε ένα ζάρι, λαμβάνουμε πληροφορίες για έναν συγκεκριμένο αριθμό πόντων (για παράδειγμα, τρεις). Σε ποια περίπτωση παίρνουμε περισσότερες πληροφορίες;

Για ένα ζάρι, ο αριθμός των εξίσου πιθανών πιθανοτήτων είναι N = 6. Η πιθανότητα να ληφθούν τρία σημεία ζαριών είναι 1/6. Η εντροπία είναι 2,58. Η πραγματοποίηση ενός λιγότερο πιθανού γεγονότος παρέχει περισσότερες πληροφορίες. Όσο μεγαλύτερη είναι η αβεβαιότητα πριν από τη λήψη ενός μηνύματος για ένα γεγονός (ρίψη νομίσματος, ζαριών), τόσο μεγαλύτερη είναι η ποσότητα των πληροφοριών που λαμβάνονται κατά τη λήψη του μηνύματος.

Αυτή η προσέγγιση στην ποσοτική έκφραση της πληροφορίας απέχει πολύ από το να είναι καθολική, καθώς οι ενότητες που υιοθετήθηκαν δεν λαμβάνουν υπόψη τόσο σημαντικές ιδιότητες της πληροφορίας όπως η αξία και το νόημά τους. Η αφαίρεση από τις συγκεκριμένες ιδιότητες των πληροφοριών (το νόημά τους, η αξία τους) σχετικά με πραγματικά αντικείμενα, όπως αποδείχθηκε αργότερα, κατέστησε δυνατό τον εντοπισμό γενικών προτύπων πληροφοριών. Οι μονάδες (bits) που προτείνει ο Shannon για τη μέτρηση του όγκου των πληροφοριών είναι κατάλληλες για την αξιολόγηση τυχόν μηνυμάτων (γέννηση ενός γιου, αποτελέσματα αθλητικού αγώνα κ.λπ.). Στη συνέχεια, έγιναν προσπάθειες να βρεθούν μέτρα για την ποσότητα των πληροφοριών που θα λάμβαναν υπόψη την αξία και το νόημά τους. Ωστόσο, η καθολικότητα χάθηκε αμέσως: διαφορετικές διαδικασίες έχουν διαφορετικά κριτήρια αξίας και νοήματος. Επιπλέον, οι ορισμοί της σημασίας και της αξίας της πληροφορίας είναι υποκειμενικοί και το μέτρο των πληροφοριών που προτείνει ο Shannon είναι αντικειμενικό. Για παράδειγμα, η όσφρηση μεταφέρει έναν τεράστιο όγκο πληροφοριών για ένα ζώο, αλλά είναι άπιαστη για τον άνθρωπο. Το ανθρώπινο αυτί δεν αντιλαμβάνεται υπερηχητικά σήματα, αλλά μεταφέρει πολλές πληροφορίες για ένα δελφίνι κ.λπ. Επομένως, το μέτρο των πληροφοριών που προτείνει ο Shannon είναι κατάλληλο για τη μελέτη όλων των τύπων διαδικασιών πληροφοριών, ανεξάρτητα από τα «γούστα» των πληροφοριών καταναλωτής.

Πληροφορίες μέτρησης

Από ένα μάθημα φυσικής το ξέρετε πριν μετρήσετε την αξία οποιουδήποτε φυσική ποσότητα, πρέπει να εισαγάγετε τη μονάδα μέτρησης. Οι πληροφορίες έχουν επίσης μια τέτοια ενότητα - λίγο, αλλά το νόημά τους είναι διαφορετικό με διαφορετικές προσεγγίσεις για τον ορισμό της έννοιας της "πληροφορίας".

Υπάρχουν πολλές διαφορετικές προσεγγίσεις στο πρόβλημα της μέτρησης των πληροφοριών.

Εντροπία (θεωρία πληροφοριών)

Εντροπία (πληροφοριακή)- ένα μέτρο του χάους πληροφοριών, η αβεβαιότητα της εμφάνισης οποιουδήποτε συμβόλου του πρωτεύοντος αλφαβήτου. Εάν δεν υπάρχουν απώλειες πληροφοριών, είναι αριθμητικά ίσο με την ποσότητα πληροφοριών ανά σύμβολο του μεταδιδόμενου μηνύματος.

Για παράδειγμα, στην ακολουθία των γραμμάτων που συνθέτουν μια πρόταση στα ρωσικά, εμφανίζονται διαφορετικά γράμματα με διαφορετικές συχνότητες, επομένως η αβεβαιότητα εμφάνισης για ορισμένα γράμματα είναι μικρότερη από ό,τι για άλλα. Αν λάβουμε υπόψη ότι κάποιοι συνδυασμοί γραμμάτων (στην προκειμένη περίπτωση μιλάμε για εντροπία n-η τάξη, βλ.) είναι πολύ σπάνιες, τότε η αβεβαιότητα μειώνεται περαιτέρω.

Για να επεξηγήσει την έννοια της εντροπίας πληροφοριών, μπορεί κανείς επίσης να καταφύγει σε ένα παράδειγμα από το πεδίο της θερμοδυναμικής εντροπίας, που ονομάζεται δαίμονας του Μάξγουελ. Οι έννοιες της πληροφορίας και της εντροπίας έχουν βαθιές συνδέσεις μεταξύ τους, αλλά παρόλα αυτά, η ανάπτυξη των θεωριών στη στατιστική μηχανική και τη θεωρία της πληροφορίας χρειάστηκε πολλά χρόνια για να γίνουν συνεπείς μεταξύ τους.

Τυπικοί ορισμοί

Αποφασιστικότητα χρησιμοποιώντας τις δικές σας πληροφορίες

Μπορείτε επίσης να προσδιορίσετε την εντροπία μιας τυχαίας μεταβλητής εισάγοντας πρώτα την έννοια της κατανομής μιας τυχαίας μεταβλητής Χέχοντας τελικός αριθμόςαξίες:

Εγώ(Χ) = − ημερολόγιο Π Χ (Χ).

Τότε η εντροπία θα οριστεί ως:

Η μονάδα μέτρησης της πληροφορίας και της εντροπίας εξαρτάται από τη βάση του λογάριθμου: bit, nat ή hartley.

Εντροπία πληροφοριώνγια ανεξάρτητα τυχαία συμβάντα ΧΜε nπιθανές καταστάσεις (από 1 έως n) υπολογίζεται με τον τύπο:

Αυτή η ποσότητα ονομάζεται επίσης μέση εντροπία μηνύματος. Η ποσότητα ονομάζεται ιδιωτική εντροπία, χαρακτηρίζοντας μόνο Εγώ-e κατάσταση.

Έτσι, η εντροπία του γεγονότος Χείναι το άθροισμα με το αντίθετο πρόσημο όλων των γινομένων των σχετικών συχνοτήτων εμφάνισης του γεγονότος Εγώ, πολλαπλασιαζόμενοι με τους δικούς τους δυαδικούς λογάριθμους (η βάση 2 επιλέχθηκε μόνο για την ευκολία της εργασίας με πληροφορίες που παρουσιάζονται σε δυαδική μορφή). Αυτός ο ορισμός για διακριτά τυχαία συμβάντα μπορεί να επεκταθεί σε μια συνάρτηση κατανομής πιθανότητας.

Γενικά σι-αριακή εντροπία(Οπου σιισούται με 2, 3, ...) πηγή με το αρχικό αλφάβητο και διακριτή κατανομή πιθανοτήτων όπου Π Εγώείναι η πιθανότητα ένα Εγώ (Π Εγώ = Π(ένα Εγώ) ) καθορίζεται από τον τύπο:

Ο ορισμός της εντροπίας Shannon σχετίζεται με την έννοια της θερμοδυναμικής εντροπίας. Οι Boltzmann και Gibbs έκαναν πολλή δουλειά στη στατιστική θερμοδυναμική, γεγονός που συνέβαλε στην υιοθέτηση της λέξης «εντροπία» στη θεωρία πληροφοριών. Υπάρχει μια σύνδεση μεταξύ της θερμοδυναμικής και της εντροπίας πληροφοριών. Για παράδειγμα, ο δαίμονας του Maxwell αντιπαραβάλλει επίσης τη θερμοδυναμική εντροπία με την πληροφορία και η απόκτηση οποιουδήποτε όγκου πληροφοριών ισοδυναμεί με χαμένη εντροπία.

Εναλλακτικός ορισμός

Ένας άλλος τρόπος ορισμού της συνάρτησης εντροπίας είναι Hείναι απόδειξη ότι Hκαθορίζεται μοναδικά (όπως αναφέρθηκε προηγουμένως) εάν και μόνο εάν Hπληροί τις προϋποθέσεις:

Ιδιότητες

Είναι σημαντικό να θυμόμαστε ότι η εντροπία είναι μια ποσότητα που ορίζεται στο πλαίσιο ενός πιθανολογικού μοντέλου για μια πηγή δεδομένων. Για παράδειγμα, η ρίψη ενός νομίσματος έχει εντροπία − 2(0,5log 2 0,5) = 1 bit ανά εκτίναξη (υποθέτοντας ότι είναι ανεξάρτητο). Μια πηγή που δημιουργεί μια συμβολοσειρά που αποτελείται μόνο από τα γράμματα "A" έχει μηδενική εντροπία: . Έτσι, για παράδειγμα, μπορεί να διαπιστωθεί πειραματικά αυτή η εντροπία Αγγλικό κείμενοείναι ίσο με 1,5 bit ανά χαρακτήρα, το οποίο φυσικά θα διαφέρει για διαφορετικά κείμενα. Ο βαθμός εντροπίας μιας πηγής δεδομένων σημαίνει τον μέσο αριθμό bit ανά στοιχείο δεδομένων που απαιτείται για την κρυπτογράφηση της χωρίς απώλεια πληροφοριών, με βέλτιστη κωδικοποίηση.

  1. Ορισμένα bit δεδομένων ενδέχεται να μην φέρουν πληροφορίες. Για παράδειγμα, οι δομές δεδομένων συχνά αποθηκεύουν περιττές πληροφορίες ή έχουν πανομοιότυπες ενότητες ανεξάρτητα από τις πληροφορίες στη δομή δεδομένων.
  2. Το ποσό της εντροπίας δεν εκφράζεται πάντα ως ακέραιος αριθμός bit.

Μαθηματικές ιδιότητες

Αποδοτικότητα

Το αρχικό αλφάβητο που συναντάται στην πράξη έχει κατανομή πιθανοτήτων που απέχει πολύ από τη βέλτιστη. Αν το αρχικό αλφάβητο είχε nχαρακτήρες, τότε μπορεί να συγκριθεί με ένα «βελτιστοποιημένο αλφάβητο» του οποίου η κατανομή πιθανοτήτων είναι ομοιόμορφη. Η αναλογία εντροπίας του αρχικού και του βελτιστοποιημένου αλφαβήτου είναι η αποτελεσματικότητα του αρχικού αλφαβήτου, η οποία μπορεί να εκφραστεί ως ποσοστό.

Από αυτό προκύπτει ότι η αποτελεσματικότητα του αρχικού αλφαβήτου με nτα σύμβολα μπορούν να οριστούν απλά ως ίσα με αυτό n-αριακή εντροπία.

Η εντροπία περιορίζει τη μέγιστη δυνατή συμπίεση χωρίς απώλειες (ή σχεδόν χωρίς απώλειες) που μπορεί να πραγματοποιηθεί χρησιμοποιώντας θεωρητικά τυπικό σύνολο ή, στην πράξη, κωδικοποίηση Huffman, κωδικοποίηση Lempel–Ziv–Welch ή αριθμητική κωδικοποίηση.

Παραλλαγές και γενικεύσεις

Εντροπία υπό όρους

Εάν η ακολουθία των χαρακτήρων του αλφαβήτου δεν είναι ανεξάρτητη (για παράδειγμα, σε γαλλική γλώσσατο γράμμα "q" ακολουθείται σχεδόν πάντα από ένα "u", και η λέξη "συντακτική" στις σοβιετικές εφημερίδες ακολουθείται συνήθως από τη λέξη "παραγωγή" ή "εργασία"), την ποσότητα των πληροφοριών που μεταφέρεται από μια ακολουθία τέτοιων συμβόλων (και επομένως η εντροπία) είναι προφανώς μικρότερη. Για να ληφθούν υπόψη τέτοια γεγονότα, χρησιμοποιείται εντροπία υπό όρους.

Η εντροπία υπό όρους πρώτης τάξης (παρόμοια με το μοντέλο Markov πρώτης τάξης) είναι η εντροπία για ένα αλφάβητο όπου είναι γνωστές οι πιθανότητες να εμφανίζεται το ένα γράμμα μετά το άλλο (δηλαδή, οι πιθανότητες συνδυασμών δύο γραμμάτων):

Οπου Εγώείναι μια κατάσταση που εξαρτάται από τον προηγούμενο χαρακτήρα και Π Εγώ (ι) - αυτή είναι η πιθανότητα ι, υπό την προϋπόθεση ότι Εγώήταν ο προηγούμενος χαρακτήρας.

Έτσι, για τη ρωσική γλώσσα χωρίς το γράμμα "".

Οι απώλειες πληροφοριών κατά τη μετάδοση δεδομένων σε ένα θορυβώδες κανάλι περιγράφονται πλήρως μέσω ιδιωτικών και γενικών εντροπιών υπό όρους. Για το σκοπό αυτό, τα λεγόμενα πίνακες καναλιών. Έτσι, για να περιγράψουμε απώλειες από την πλευρά της πηγής (δηλαδή, το απεσταλμένο σήμα είναι γνωστό), λαμβάνεται υπόψη η υπό όρους πιθανότητα λήψης του συμβόλου από τον δέκτη. σι ιυπό την προϋπόθεση ότι ο χαρακτήρας στάλθηκε ένα Εγώ. Σε αυτήν την περίπτωση, ο πίνακας καναλιών έχει την ακόλουθη μορφή:

σι 1 σι 2 … σι ι … σι Μ
ένα 1 … …
ένα 2 … …
… … … … … … …
ένα Εγώ … …
… … … … … … …
ένα Μ … …

Προφανώς, οι πιθανότητες που βρίσκονται κατά μήκος της διαγώνιου περιγράφουν την πιθανότητα σωστής λήψης και το άθροισμα όλων των στοιχείων της στήλης θα δώσει την πιθανότητα να εμφανιστεί το αντίστοιχο σύμβολο στην πλευρά του δέκτη - Π(σι ι) . Απώλειες ανά μεταδιδόμενο σήμα ένα Εγώ, περιγράφονται μέσω μερικής εντροπίας υπό όρους:

Για τον υπολογισμό των απωλειών μετάδοσης όλων των σημάτων, χρησιμοποιείται η γενική εντροπία υπό όρους:

Σημαίνει εντροπία στην πλευρά της πηγής· η εντροπία στην πλευρά του δέκτη θεωρείται με παρόμοιο τρόπο: αντί για παντού υποδεικνύεται (αθροίζοντας τα στοιχεία της γραμμής μπορείτε να πάρετε Π(ένα Εγώ) , και τα διαγώνια στοιχεία σημαίνουν την πιθανότητα να στάλθηκε ο ακριβής χαρακτήρας που ελήφθη, δηλαδή η πιθανότητα σωστής μετάδοσης).

Αμοιβαία εντροπία

Αμοιβαία εντροπία, ή εντροπία της ένωσης, προορίζεται για τον υπολογισμό της εντροπίας διασυνδεδεμένων συστημάτων (η εντροπία της κοινής εμφάνισης στατιστικά εξαρτημένων μηνυμάτων) και συμβολίζεται H(ΕΝΑσι) , Οπου ΕΝΑ, όπως πάντα, χαρακτηρίζει τον πομπό, και σι- δέκτης.

Η σχέση μεταξύ των μεταδιδόμενων και των λαμβανόμενων σημάτων περιγράφεται από τις πιθανότητες κοινών γεγονότων Π(ένα Εγώ σι ι) , και για πλήρης περιγραφήχαρακτηριστικά καναλιού, απαιτείται μόνο ένας πίνακας:

Π(ένα 1 σι 1) Π(ένα 1 σι 2) … Π(ένα 1 σι ι) … Π(ένα 1 σι Μ)
Π(ένα 2 σι 1) Π(ένα 2 σι 2) … Π(ένα 2 σι ι) … Π(ένα 2 σι Μ)
… … … … … …
Π(ένα Εγώ σι 1) Π(ένα Εγώ σι 2) … Π(ένα Εγώ σι ι) … Π(ένα Εγώ σι Μ)
… … … … … …
Π(ένα Μ σι 1) Π(ένα Μ σι 2) … Π(ένα Μ σι ι) … Π(ένα Μ σι Μ)

Για μια γενικότερη περίπτωση, όταν δεν περιγράφεται ένα κανάλι, αλλά απλά συστήματα αλληλεπίδρασης, ο πίνακας δεν χρειάζεται να είναι τετράγωνος. Προφανώς, το άθροισμα όλων των στοιχείων της στήλης με τον αριθμό ιθα δώσω Π(σι ι) , το άθροισμα του αριθμού γραμμής ΕγώΥπάρχει Π(ένα Εγώ) , και το άθροισμα όλων των στοιχείων του πίνακα είναι ίσο με 1. Από κοινού πιθανότητα Π(ένα Εγώ σι ι) εκδηλώσεις ένα ΕγώΚαι σι ιυπολογίζεται ως το γινόμενο της αρχικής και υπό όρους πιθανότητας,

Οι υπό όρους πιθανότητες παράγονται χρησιμοποιώντας τον τύπο του Bayes. Έτσι, υπάρχουν όλα τα δεδομένα για τον υπολογισμό των εντροπιών της πηγής και του δέκτη:

Η αμοιβαία εντροπία υπολογίζεται αθροίζοντας διαδοχικά σε γραμμές (ή στήλες) όλες τις πιθανότητες του πίνακα, πολλαπλασιαζόμενες με τον λογάριθμό τους:

H(ΕΝΑσι) = − ∑ ∑ Π(ένα Εγώ σι ι)κούτσουρο Π(ένα Εγώ σι ι).
Εγώ ι

Η μονάδα μέτρησης είναι bit/δύο σύμβολα, αυτό εξηγείται από το γεγονός ότι η αμοιβαία εντροπία περιγράφει την αβεβαιότητα ανά ζεύγος συμβόλων - που αποστέλλονται και λαμβάνονται. Με απλούς μετασχηματισμούς παίρνουμε επίσης

Η αμοιβαία εντροπία έχει την ιδιότητα πληρότητα πληροφοριών- από αυτό μπορείτε να πάρετε όλες τις υπό εξέταση ποσότητες.

Ιστορία

Σημειώσεις

δείτε επίσης

Συνδέσεις

  • Claude E. Shannon. Μια Μαθηματική Θεωρία της Επικοινωνίας
  • S. M. Korotaev.

«Η ενημέρωση είναι μια μορφή ζωής», έγραψε Αμερικανός ποιητήςκαι ο δοκιμιογράφος John Perry Barlow. Πράγματι, συναντάμε συνεχώς τη λέξη "πληροφορίες" - λαμβάνεται, μεταδίδεται και αποθηκεύεται. Μάθετε την πρόγνωση του καιρού ή το αποτέλεσμα ενός ποδοσφαιρικού αγώνα, το περιεχόμενο μιας ταινίας ή βιβλίου, μιλήστε στο τηλέφωνο - είναι πάντα σαφές με τι είδους πληροφορίες έχουμε να κάνουμε. Κανείς, όμως, συνήθως δεν σκέφτεται τι είναι η ίδια η πληροφορία, και το πιο σημαντικό, πώς μπορεί να μετρηθεί. Εν τω μεταξύ, οι πληροφορίες και οι μέθοδοι μετάδοσής τους είναι ένα σημαντικό πράγμα που καθορίζει σε μεγάλο βαθμό τη ζωή μας, της οποίας έχουμε γίνει αναπόσπαστο κομμάτι. ΤΕΧΝΟΛΟΓΙΑ της ΠΛΗΡΟΦΟΡΙΑΣ. Ο επιστημονικός συντάκτης της έκδοσης Laba.Media Vladimir Gubailovsky εξηγεί τι είναι η πληροφορία, πώς να τις μετρήσετε και γιατί το πιο δύσκολο πράγμα είναι η μετάδοση πληροφοριών χωρίς παραμόρφωση.

Χώρος τυχαίων γεγονότων

Το 1946, ο Αμερικανός στατιστικολόγος John Tukey πρότεινε το όνομα BIT (BINary digiT - "δυαδικός αριθμός" - "High-Tech") - μια από τις κύριες έννοιες του 20ου αιώνα. Ο Tukey επέλεξε ένα bit για να υποδηλώσει ένα δυαδικό ψηφίο ικανό να πάρει την τιμή 0 ή 1. Ο Claude Shannon, στο θεμελιώδες άρθρο του «Mathematical Theory of Communication», πρότεινε τη μέτρηση της ποσότητας πληροφοριών σε bit. Αλλά αυτή δεν είναι η μόνη έννοια που εισήγαγε και εξερευνά ο Shannon στο άρθρο του.

Ας φανταστούμε έναν χώρο τυχαίων γεγονότων που αποτελείται από τη ρίψη ενός πλαστού νομίσματος με κεφαλές και στις δύο πλευρές. Πότε έρχεται στο μυαλό; Σαφώς, πάντα. Το γνωρίζουμε εκ των προτέρων, γιατί έτσι είναι δομημένος ο χώρος μας. Η προσγείωση των κεφαλιών είναι ένα ορισμένο γεγονός, δηλαδή η πιθανότητα του είναι ίση με 1. Πόσες πληροφορίες θα μεταφέρουμε αν μιλάμε για τις κεφαλές που πέφτουν; Οχι. Θα θεωρήσουμε ότι ο όγκος των πληροφοριών σε ένα τέτοιο μήνυμα είναι 0.

Τώρα ας ρίξουμε το σωστό νόμισμα: έχει κεφάλια στη μία πλευρά και ουρές στην άλλη, όπως αναμενόταν. Οι κεφαλές ή οι ουρές προσγείωσης θα είναι δύο διαφορετικά γεγονότα που συνθέτουν τον χώρο των τυχαίων γεγονότων μας. Αν αναφέρουμε το αποτέλεσμα μιας εκτίναξης, τότε όντως θα είναι ΝΕΑ ΠΛΗΡΟΦΟΡΙΑ. Εάν πέσουν οι κεφαλές, θα αναφέρουμε 0, και αν οι ουρές είναι 1. Για να αναφέρουμε αυτές τις πληροφορίες, χρειαζόμαστε μόνο 1 bit.

Τι άλλαξε; Η αβεβαιότητα εμφανίστηκε στον χώρο εκδηλώσεών μας. Έχουμε κάτι να πούμε για αυτό σε κάποιον που δεν πετάει μόνος του ένα νόμισμα και δεν βλέπει το αποτέλεσμα της εκτίναξης. Αλλά για να κατανοήσει σωστά το μήνυμά μας, πρέπει να γνωρίζει ακριβώς τι κάνουμε, τι σημαίνουν το 0 και το 1. Οι χώροι συμβάντων μας πρέπει να ταιριάζουν και η διαδικασία αποκωδικοποίησης πρέπει να ανακατασκευάσει μοναδικά το αποτέλεσμα της ρίψης. Εάν ο χώρος συμβάντων του πομπού και του δέκτη δεν συμπίπτει ή δεν υπάρχει δυνατότητα ξεκάθαρης αποκωδικοποίησης του μηνύματος, οι πληροφορίες θα παραμείνουν μόνο θόρυβος στο κανάλι επικοινωνίας.

Αν δύο νομίσματα πεταχτούν ανεξάρτητα και ταυτόχρονα, τότε θα υπάρξουν τέσσερα διαφορετικά εξίσου πιθανά αποτελέσματα: κεφαλές-κεφαλές, κεφαλές-ουρές, ουρές-κεφαλές και ουρές-ουρές. Για να μεταδώσουμε πληροφορίες, θα χρειαστούμε 2 bit και τα μηνύματά μας θα είναι τα εξής: 00, 01, 10 και 11. Υπάρχουν διπλάσιες πληροφορίες. Αυτό συνέβη επειδή η αβεβαιότητα αυξήθηκε. Αν προσπαθήσουμε να μαντέψουμε το αποτέλεσμα μιας τέτοιας ζευγαρωμένης εκτίναξης, έχουμε διπλάσιες πιθανότητες να κάνουμε λάθος.

Όσο μεγαλύτερη είναι η αβεβαιότητα του χώρου γεγονότων, τόσο περισσότερες πληροφορίες περιέχει το μήνυμα για την κατάστασή του.

Ας περιπλέκουμε λίγο τον χώρο των εκδηλώσεών μας. Μέχρι στιγμής όλα τα γεγονότα που έχουν συμβεί ήταν εξίσου πιθανά. Αλλά σε πραγματικούς χώρους, δεν έχουν όλα τα γεγονότα ίσες πιθανότητες. Ας πούμε ότι η πιθανότητα το κοράκι που βλέπουμε να είναι μαύρο είναι κοντά στο 1. Η πιθανότητα ο πρώτος περαστικός που θα συναντήσουμε στο δρόμο να είναι άντρας είναι περίπου 0,5. Αλλά η συνάντηση με έναν κροκόδειλο στους δρόμους της Μόσχας είναι σχεδόν αδύνατο. Διαισθητικά, καταλαβαίνουμε ότι μια αναφορά για μια συνάντηση με έναν κροκόδειλο έχει πολύ μεγαλύτερη πληροφοριακή αξία από ότι για ένα μαύρο κοράκι. Όσο μικρότερη είναι η πιθανότητα ενός συμβάντος, τόσο περισσότερες πληροφορίες υπάρχουν στο μήνυμα για ένα τέτοιο συμβάν.

Ας μην είναι τόσο εξωτικός ο χώρος εκδηλώσεων. Απλώς στεκόμαστε στο παράθυρο και κοιτάμε τα διερχόμενα αυτοκίνητα. Υπάρχουν τέσσερα διαφορετικά χρώματα αυτοκινήτων που κινούνται με τα οποία πρέπει να αναφέρουμε. Για να γίνει αυτό, κωδικοποιούμε τα χρώματα: μαύρο - 00, λευκό - 01, κόκκινο - 10, μπλε - 11. Για να αναφέρουμε ποιο αυτοκίνητο πέρασε, χρειάζεται μόνο να μεταδώσουμε 2 bit πληροφοριών.

Αλλά παρακολουθώντας τα αυτοκίνητα για αρκετό καιρό, παρατηρούμε ότι το χρώμα των αυτοκινήτων κατανέμεται άνισα: μαύρο - 50% (κάθε δευτερόλεπτο), λευκό - 25% (κάθε τέταρτο), κόκκινο και μπλε - 12,5% το καθένα (κάθε όγδοο). Στη συνέχεια, μπορείτε να βελτιστοποιήσετε τις μεταδιδόμενες πληροφορίες.

Η πλειονότητα των αυτοκινήτων είναι μαύρα, οπότε ας υποδηλώσουμε το μαύρο - 0 - τον συντομότερο κωδικό και ας αφήσουμε τον κωδικό όλων των υπολοίπων να ξεκινά από το 1. Από τα υπόλοιπα μισά, το λευκό - 10, και τα υπόλοιπα χρώματα ξεκινούν από το 11. Εν κατακλείδι, ας υποδηλώσουμε κόκκινο - 110 και μπλε - 111.

Τώρα, μεταδίδοντας πληροφορίες για το χρώμα των αυτοκινήτων, μπορούμε να το κωδικοποιήσουμε πιο πυκνά.

Εντροπία Shannon

Αφήστε τον χώρο εκδηλώσεών μας να αποτελείται από n διαφορετικά συμβάντα. Όταν ρίχνετε ένα νόμισμα με δύο κεφαλές, υπάρχει ακριβώς ένα τέτοιο γεγονός, όταν ρίχνετε ένα σωστό νόμισμα - 2, όταν ρίχνετε δύο νομίσματα ή παρακολουθείτε αυτοκίνητα - 4. Κάθε γεγονός έχει μια αντίστοιχη πιθανότητα να συμβεί. Κατά τη ρίψη ενός νομίσματος με δύο κεφαλές, υπάρχει ένα γεγονός (πτώση κεφαλιών) και η πιθανότητα του είναι p1 = 1. Όταν ρίχνετε ένα δίκαιο νόμισμα, υπάρχουν δύο γεγονότα, είναι εξίσου πιθανά και η πιθανότητα καθενός είναι 0,5: p1 = 0,5, p2 = 0,5. Κατά τη ρίψη δύο δίκαιων νομισμάτων, υπάρχουν τέσσερα γεγονότα, όλα είναι εξίσου πιθανά και η πιθανότητα καθενός είναι 0,25: p1 = 0,25, p2 = 0,25, p3 = 0,25, p4 = 0,25. Κατά την παρατήρηση των αυτοκινήτων, υπάρχουν τέσσερα συμβάντα και έχουν διαφορετικές πιθανότητες: μαύρο - 0,5, λευκό - 0,25, κόκκινο - 0,125, μπλε - 0,125: p1 = 0,5, p2 = 0,25, p3 = 0,125, p4 = 0,125.

Αυτό δεν είναι τυχαίο. Ο Shannon επέλεξε την εντροπία (ένα μέτρο αβεβαιότητας στον χώρο των γεγονότων) έτσι ώστε να πληρούνται τρεις προϋποθέσεις:

  • Η εντροπία δύο ανεξάρτητων γεγονότων είναι ίση με το άθροισμα των εντροπιών αυτών των γεγονότων.
  • Η εντροπία είναι μέγιστη εάν όλα τα γεγονότα είναι εξίσου πιθανά.

Όλες αυτές οι απαιτήσεις συνάδουν πλήρως με τις ιδέες μας σχετικά με την αβεβαιότητα του χώρου εκδηλώσεων. Εάν υπάρχει μόνο ένα γεγονός (το πρώτο παράδειγμα), δεν υπάρχει αβεβαιότητα. Εάν τα γεγονότα είναι ανεξάρτητα - η αβεβαιότητα του αθροίσματος ισούται με το άθροισμα των αβεβαιοτήτων - απλώς αθροίζονται (ένα παράδειγμα με τη ρίψη δύο νομισμάτων). Και τέλος, αν όλα τα γεγονότα είναι εξίσου πιθανά, τότε ο βαθμός αβεβαιότητας του συστήματος είναι μέγιστος. Όπως στην περίπτωση της ρίψης δύο νομισμάτων, και τα τέσσερα γεγονότα είναι εξίσου πιθανά και η εντροπία είναι 2, είναι μεγαλύτερη από ό,τι στην περίπτωση των αυτοκινήτων, όταν υπάρχουν επίσης τέσσερα γεγονότα, αλλά έχουν διαφορετικές πιθανότητες - σε αυτήν την περίπτωση η εντροπία είναι 1,75.

Η ποσότητα Η παίζει κεντρικό ρόλο στη θεωρία πληροφοριών ως μέτρο της πληροφορίας, της επιλογής και της αβεβαιότητας.

Κλοντ Σάνον

Κλοντ Έλγουντ Σάνον- Αμερικανός μηχανικός, κρυπτοαναλυτής και μαθηματικός. Θεωρείται ο «πατέρας» εποχή της πληροφορίας" Ιδρυτής της θεωρίας της πληροφορίας, που έχει βρει εφαρμογή στα σύγχρονα συστήματα επικοινωνίας υψηλής τεχνολογίας. Παρέχονται θεμελιώδεις έννοιες, ιδέες και οι μαθηματικές τους διατυπώσεις που σήμερα αποτελούν τη βάση για τις σύγχρονες τεχνολογίες επικοινωνίας.

Το 1948, πρότεινε τη χρήση της λέξης "bit" για να δηλώσει τη μικρότερη μονάδα πληροφοριών. Απέδειξε επίσης ότι η εντροπία που εισήγαγε είναι ισοδύναμη με ένα μέτρο της αβεβαιότητας των πληροφοριών στο μεταδιδόμενο μήνυμα. Τα άρθρα του Shannon "Mathematical Theory of Communication" και "Theory of Communication in μυστικά συστήματα" θεωρούνται θεμελιώδεις για τη θεωρία της πληροφορίας και την κρυπτογραφία.

Κατά τη διάρκεια του Β 'Παγκοσμίου Πολέμου, ο Shannon εργάστηκε στα Bell Laboratories για να αναπτύξει κρυπτογραφικά συστήματα, τα οποία αργότερα τον βοήθησαν να ανακαλύψει μεθόδους κωδικοποίησης διόρθωσης σφαλμάτων.

Ο Shannon συνέβαλε σημαντικά στη θεωρία των πιθανοτικών κυκλωμάτων, στη θεωρία παιγνίων, στη θεωρία των αυτομάτων και στη θεωρία συστημάτων ελέγχου - πεδία της επιστήμης που περιλαμβάνονται στην έννοια της «κυβερνητικής».

Κωδικοποίηση

Τόσο η ρίψη νομισμάτων όσο και τα αυτοκίνητα που περνούν δεν είναι σαν τους αριθμούς 0 και 1. Για να επικοινωνήσετε σχετικά με γεγονότα που συμβαίνουν σε χώρους, πρέπει να βρείτε έναν τρόπο να περιγράψετε αυτά τα γεγονότα. Αυτή η περιγραφή ονομάζεται κωδικοποίηση.

Τα μηνύματα μπορούν να κωδικοποιηθούν με άπειρους διαφορετικούς τρόπους. Αλλά ο Shannon έδειξε ότι ο συντομότερος κώδικας δεν μπορεί να είναι μικρότερος σε bit από την εντροπία.

Αυτός είναι ο λόγος για τον οποίο η εντροπία ενός μηνύματος είναι ένα μέτρο των πληροφοριών στο μήνυμα. Εφόσον σε όλες τις εξεταζόμενες περιπτώσεις ο αριθμός των bit κατά την κωδικοποίηση είναι ίσος με την εντροπία, σημαίνει ότι η κωδικοποίηση ήταν βέλτιστη. Με λίγα λόγια, δεν είναι πλέον δυνατή η κωδικοποίηση μηνυμάτων για γεγονότα στους χώρους μας.

Με τη βέλτιστη κωδικοποίηση, δεν μπορεί να χαθεί ή να παραμορφωθεί ούτε ένα bit που μεταδίδεται στο μήνυμα. Εάν χαθεί έστω και ένα bit, οι πληροφορίες θα παραμορφωθούν. Αλλά όλα τα πραγματικά κανάλια επικοινωνίας δεν παρέχουν 100 τοις εκατό εμπιστοσύνη ότι όλα τα κομμάτια του μηνύματος θα φτάσουν στον παραλήπτη χωρίς παραμόρφωση.

Για να εξαλειφθεί αυτό το πρόβλημα, είναι απαραίτητο να γίνει ο κώδικας όχι βέλτιστος, αλλά περιττός. Για παράδειγμα, μεταδώστε μαζί με το μήνυμα το άθροισμα ελέγχου του - μια ειδικά υπολογισμένη τιμή που λαμβάνεται κατά τη μετατροπή του κωδικού του μηνύματος και η οποία μπορεί να ελεγχθεί με επανυπολογισμό κατά τη λήψη του μηνύματος. Εάν το μεταδιδόμενο άθροισμα ελέγχου ταιριάζει με το υπολογιζόμενο, η πιθανότητα η μετάδοση να ήταν χωρίς σφάλματα θα είναι αρκετά υψηλή. Και αν το άθροισμα ελέγχου δεν ταιριάζει, τότε πρέπει να ζητηθεί αναμετάδοση. Αυτός είναι περίπου ο τρόπος με τον οποίο λειτουργούν τα περισσότερα κανάλια επικοινωνίας σήμερα, για παράδειγμα, κατά τη μετάδοση πακέτων πληροφοριών μέσω του Διαδικτύου.

Μηνύματα φυσικής γλώσσας

Σκεφτείτε έναν χώρο εκδηλώσεων που αποτελείται από μηνύματα σε φυσική γλώσσα. Αυτή είναι μια ειδική περίπτωση, αλλά μια από τις πιο σημαντικές. Τα συμβάντα εδώ θα μεταδίδονται με χαρακτήρες (γράμματα ενός σταθερού αλφαβήτου). Αυτά τα σύμβολα εμφανίζονται στη γλώσσα με διαφορετικές πιθανότητες.

Ο πιο συνηθισμένος χαρακτήρας (δηλαδή αυτός που εμφανίζεται πιο συχνά σε όλα τα κείμενα που είναι γραμμένα στα ρωσικά) είναι το διάστημα: από τους χίλιους χαρακτήρες, κατά μέσο όρο, το διάστημα εμφανίζεται 175 φορές. Το δεύτερο πιο κοινό σύμβολο είναι το "o" - 90, ακολουθούμενο από άλλα φωνήεντα: "e" (ή "e" - δεν θα διακρίνουμε μεταξύ τους) - 72, "a" - 62, "i" - 62 και μόνο εμφανίζεται περαιτέρω το πρώτο σύμφωνο "t" είναι 53. Και το πιο σπάνιο "f" - αυτό το σύμβολο εμφανίζεται μόνο δύο φορές ανά χίλιους χαρακτήρες.

Θα χρησιμοποιήσουμε το αλφάβητο των 31 γραμμάτων της ρωσικής γλώσσας (δεν κάνει διάκριση μεταξύ "e" και "ё", καθώς και "ъ" και "ь"). Εάν όλα τα γράμματα εμφανίζονταν σε μια γλώσσα με την ίδια πιθανότητα, τότε η εντροπία ανά χαρακτήρα θα ήταν H = 5 bit, αλλά αν λάβουμε υπόψη τις πραγματικές συχνότητες των συμβόλων, τότε η εντροπία θα είναι μικρότερη: H = 4,35 bit. (Αυτό είναι σχεδόν δύο φορές λιγότερο από ό,τι με την παραδοσιακή κωδικοποίηση, όταν ένας χαρακτήρας μεταδίδεται ως byte - 8 bit).

Αλλά η εντροπία ενός συμβόλου στη γλώσσα είναι ακόμη χαμηλότερη. Η πιθανότητα εμφάνισης του επόμενου χαρακτήρα δεν καθορίζεται εξ ολοκλήρου από τη μέση συχνότητα του χαρακτήρα σε όλα τα κείμενα. Ποιος χαρακτήρας ακολουθεί εξαρτάται από τους χαρακτήρες που έχουν ήδη μεταδοθεί. Για παράδειγμα, στα σύγχρονα ρωσικά το σύμβολο «ъ» δεν μπορεί να ακολουθείται από σύμφωνο σύμφωνο. Μετά από δύο φωνήεντα «ε» στη σειρά, ένα τρίτο φωνήεν «ε» ακολουθεί εξαιρετικά σπάνια, εκτός από τη λέξη «μακρυλαιμός». Δηλαδή, ο επόμενος χαρακτήρας είναι σε κάποιο βαθμό προκαθορισμένος. Αν λάβουμε υπόψη αυτόν τον προκαθορισμό του επόμενου συμβόλου, η αβεβαιότητα (δηλαδή η πληροφορία) του επόμενου συμβόλου θα είναι ακόμη μικρότερη από 4,35. Σύμφωνα με ορισμένες εκτιμήσεις, ο επόμενος χαρακτήρας στη ρωσική γλώσσα προκαθορίζεται από τη δομή της γλώσσας κατά περισσότερο από 50%, δηλαδή, με τη βέλτιστη κωδικοποίηση, όλες οι πληροφορίες μπορούν να μεταφερθούν διαγράφοντας τα μισά γράμματα από το μήνυμα.

Ένα άλλο πράγμα είναι ότι δεν μπορεί να διαγραφεί κάθε γράμμα ανώδυνα. Το "o" υψηλής συχνότητας (και τα φωνήεντα γενικά), για παράδειγμα, είναι εύκολο να διαγραφούν, αλλά τα σπάνια "f" ή "e" είναι αρκετά προβληματικά.

Η φυσική γλώσσα στην οποία επικοινωνούμε μεταξύ μας είναι εξαιρετικά περιττή, και επομένως αξιόπιστη· εάν κάτι δεν ακούσαμε σωστά, δεν πειράζει, οι πληροφορίες θα εξακολουθήσουν να μεταδίδονται.

Αλλά έως ότου η Shannon εισήγαγε ένα μέτρο πληροφοριών, δεν μπορούσαμε να καταλάβουμε ότι η γλώσσα είναι περιττή ή σε ποιο βαθμό μπορούμε να συμπιέσουμε μηνύματα (ή γιατί τα αρχεία κειμένου συμπιέζονται τόσο καλά από τον αρχειοθέτη).

Πλεονασμός φυσικής γλώσσας

Στο άρθρο «Πώς γράφουμε το κείμενο» (ο τίτλος ακούγεται ακριβώς έτσι!), ένα κομμάτι του μυθιστορήματος του Ιβάν Τουργκένεφ «Η φωλιά των ευγενών» λήφθηκε και υποβλήθηκε σε κάποια μεταμόρφωση: το 34% των γραμμάτων διαγράφηκαν από το θραύσμα, αλλά όχι τυχαία. Τα πρώτα και τα τελευταία γράμματα στις λέξεις έμειναν, μόνο φωνήεντα διαγραμμίστηκαν και όχι όλα. Ο στόχος δεν ήταν απλώς να μπορέσουμε να ανακτήσουμε όλες τις πληροφορίες από το κείμενο που μετατράπηκε, αλλά και να διασφαλίσουμε ότι το άτομο που διαβάζει αυτό το κείμενο δεν θα αντιμετωπίσει ιδιαίτερες δυσκολίες λόγω έλλειψης γραμμάτων.

Γιατί είναι σχετικά εύκολο να διαβάσετε αυτό το κατεστραμμένο κείμενο; Στην πραγματικότητα περιέχει τις απαραίτητες πληροφορίες για την ανασύσταση ολόκληρων λέξεων. Ένας μητρικός ομιλητής των Ρωσικών έχει ένα συγκεκριμένο σύνολο γεγονότων (λέξεις και ολόκληρες προτάσεις) που χρησιμοποιεί ως αναγνώριση. Επιπλέον, ο ομιλητής έχει επίσης τυποποιημένες γλωσσικές δομές στη διάθεσή του που τον βοηθούν να ανακτήσει πληροφορίες. Για παράδειγμα, «Είναι τόσο ευαίσθητη»- με μεγάλη πιθανότητα μπορεί να διαβαστεί ως «Ήταν πιο ευαίσθητη». Λαμβάνονται όμως χωριστά "Είναι μπλα μπλα", μάλλον, θα αποκατασταθεί ως «Ήταν πιο λευκή». Εφόσον στην καθημερινή επικοινωνία ασχολούμαστε με κανάλια στα οποία υπάρχει θόρυβος και παρεμβολές, είμαστε αρκετά καλοί στην επαναφορά πληροφοριών, αλλά μόνο ό,τι γνωρίζουμε ήδη εκ των προτέρων. Για παράδειγμα, η φράση «Στον διάβολο δεν άρεσαν οι απολαύσεις της, παρόλο που ξέσπασε σε κλάματα και διαλύθηκε»διαβάζει καλά εκτός από την τελευταία λέξη "πλημμύρισε" - "πλημμύρισε". Αυτή η λέξη δεν υπάρχει στο σύγχρονο λεξικό. Όταν διαβάζετε μια λέξη γρήγορα "splls"μοιάζει περισσότερο με «κολλημένοι μεταξύ τους»· όταν είναι αργός, απλώς μπερδεύεται.

Ψηφιοποίηση σήματος

Ο ήχος, ή οι ακουστικές δονήσεις, είναι ένα ημιτονοειδές. Αυτό φαίνεται, για παράδειγμα, στην οθόνη του προγράμματος επεξεργασίας ήχου. Για να μεταφέρετε με ακρίβεια τον ήχο, θα χρειαστείτε έναν άπειρο αριθμό τιμών - ολόκληρο το ημιτονοειδές κύμα. Αυτό είναι δυνατό με αναλογική σύνδεση. Τραγουδάει - ακούς, η επαφή δεν διακόπτεται όσο διαρκεί το τραγούδι.

Στην ψηφιακή επικοινωνία μέσω ενός καναλιού, μπορούμε να μεταδώσουμε μόνο έναν πεπερασμένο αριθμό τιμών. Αυτό σημαίνει ότι ο ήχος δεν μπορεί να αναπαραχθεί με ακρίβεια; Αποδεικνύεται ότι όχι.

Οι διαφορετικοί ήχοι είναι ένα διαφορετικά διαμορφωμένο ημιτονοειδές κύμα. Μεταδίδουμε μόνο διακριτές τιμές (συχνότητες και πλάτη) και δεν χρειάζεται να μεταδώσουμε το ίδιο το ημιτονοειδές - μπορεί να δημιουργηθεί από τη συσκευή λήψης. Δημιουργεί ένα ημιτονοειδές κύμα και η διαμόρφωση υπερτίθεται σε αυτό, που δημιουργείται από τις τιμές που μεταδίδονται μέσω του καναλιού επικοινωνίας. Υπάρχουν ακριβείς αρχές των οποίων οι διακριτές τιμές πρέπει να μεταδίδονται έτσι ώστε ο ήχος στην είσοδο του καναλιού επικοινωνίας να συμπίπτει με τον ήχο στην έξοδο, όπου αυτές οι τιμές υπερτίθενται σε κάποιο τυπικό ημιτονοειδές (αυτό είναι το θεώρημα του Kotelnikov σχετικά με).

Το θεώρημα του Kotelnikov (στην αγγλική λογοτεχνία - θεώρημα Nyquist-Shannon, θεώρημα δειγματοληψίας)- μια θεμελιώδη δήλωση στον τομέα της επεξεργασίας ψηφιακών σημάτων, η οποία συσχετίζει τα συνεχή και διακριτά σήματα και δηλώνει ότι «οποιαδήποτε συνάρτηση F (t), που αποτελείται από συχνότητες από 0 έως f1, μπορεί να μεταδίδεται συνεχώς με οποιαδήποτε ακρίβεια χρησιμοποιώντας αριθμούς που ακολουθούν ο ένας τον άλλον μέχρι το 1 /(2*f1) δευτερόλεπτα.

Κωδικοποίηση ανθεκτική στο θόρυβο. Κωδικοί Hamming

Εάν μεταδώσετε το κωδικοποιημένο κείμενο του Ivan Turgenev μέσω ενός αναξιόπιστου καναλιού, αν και με έναν ορισμένο αριθμό σφαλμάτων, θα λάβετε ένα εντελώς ουσιαστικό κείμενο. Αλλά αν χρειαστεί να μεταδώσουμε τα πάντα με ακρίβεια bit, το πρόβλημα θα είναι άλυτο: δεν ξέρουμε ποια bit είναι λάθος, επειδή το σφάλμα είναι τυχαίο. Ακόμη και ένα άθροισμα ελέγχου δεν βοηθά πάντα.

Αυτός είναι ο λόγος για τον οποίο σήμερα, όταν μεταδίδουν δεδομένα μέσω δικτύων, προσπαθούν όχι τόσο για τη βέλτιστη κωδικοποίηση, στην οποία η μέγιστη ποσότητα πληροφοριών μπορεί να προωθηθεί στο κανάλι, αλλά μάλλον για μια τέτοια κωδικοποίηση (προφανώς περιττή) στην οποία μπορούν να αποκατασταθούν σφάλματα - με τον ίδιο τρόπο, περίπου, όπως αποκαταστήσαμε λέξεις όταν διαβάζαμε απόσπασμα του Ιβάν Τουργκένιεφ.

Υπάρχουν ειδικοί κωδικοί ανθεκτικοί στο θόρυβο που σας επιτρέπουν να επαναφέρετε πληροφορίες μετά από αποτυχία. Ένα από αυτά είναι ο κώδικας Hamming. Ας υποθέσουμε ότι ολόκληρη η γλώσσα μας αποτελείται από τρεις λέξεις: 111000, 001110, 100011. Τόσο η πηγή του μηνύματος όσο και ο παραλήπτης γνωρίζουν αυτές τις λέξεις. Και γνωρίζουμε ότι συμβαίνουν σφάλματα σε ένα κανάλι επικοινωνίας, αλλά κατά τη μετάδοση μιας λέξης, δεν παραμορφώνεται περισσότερο από ένα bit πληροφοριών.

Ας υποθέσουμε ότι μεταδώσαμε πρώτα τη λέξη 111000. Ως αποτέλεσμα το πολύ ενός σφάλματος (έχουμε επισημάνει τα σφάλματα), μπορεί να μετατραπεί σε μία από τις λέξεις:

1) 111000, 0 11000, 10 1000, 110 000, 1111 00, 11101 0, 111001 .

Όταν μεταβιβάζετε τη λέξη 001110, μπορείτε να λάβετε οποιαδήποτε από τις λέξεις:

2) 001110, 1 01110, 01 1110, 000 110, 0010 10, 00110 0, 001111 .

Τέλος, για το 100011 μπορεί να καταλήξουμε σε:

3) 100011, 0 00011, 11 0011, 101 011, 1001 11, 10000 1, 100010 .

Σημειώστε ότι και οι τρεις λίστες είναι χωριστές ανά ζεύγη. Με άλλα λόγια, εάν κάποια λέξη από τη λίστα 1 εμφανιστεί στο άλλο άκρο του καναλιού επικοινωνίας, ο παραλήπτης γνωρίζει με βεβαιότητα ότι η λέξη 111000 μεταδόθηκε σε αυτόν και εάν εμφανιστεί κάποια λέξη από τη λίστα 2 - λέξη 001110 και από τη λίστα 3 - λέξη 100011. Σε αυτή την περίπτωση λένε ότι ο κώδικάς μας διόρθωσε ένα σφάλμα.

Η διόρθωση έγινε λόγω δύο παραγόντων. Πρώτον, ο παραλήπτης γνωρίζει ολόκληρο το «λεξιλόγιο», δηλαδή ο χώρος συμβάντων του παραλήπτη του μηνύματος συμπίπτει με τον χώρο αυτού που μετέδωσε το μήνυμα. Όταν ο κώδικας μεταδόθηκε με ένα μόνο σφάλμα, βγήκε μια λέξη που δεν υπήρχε στο λεξικό.

Δεύτερον, οι λέξεις του λεξικού επιλέχθηκαν με ειδικό τρόπο.Ακόμα κι αν παρουσιαζόταν σφάλμα, ο παραλήπτης δεν μπορούσε να μπερδέψει μια λέξη με μια άλλη. Για παράδειγμα, εάν το λεξικό αποτελείται από τις λέξεις "κόρη", "κουκκίδα", "χτύπημα" και κατά τη μετάδοση το αποτέλεσμα ήταν "vochka", τότε ο παραλήπτης, γνωρίζοντας ότι δεν υπάρχει τέτοια λέξη, δεν θα μπορούσε να διορθώστε το λάθος - οποιαδήποτε από τις τρεις λέξεις μπορεί να αποδειχθεί σωστή. Αν το λεξικό περιλαμβάνει «dot», «daw», «branch» και γνωρίζουμε ότι δεν επιτρέπονται περισσότερα από ένα λάθη, τότε το «vochka» είναι σίγουρα «dot» και όχι «daw». Στους κωδικούς διόρθωσης σφαλμάτων, οι λέξεις επιλέγονται ακριβώς έτσι ώστε να είναι «αναγνωρίσιμες» ακόμη και μετά από ένα σφάλμα. Η μόνη διαφορά είναι ότι ο κωδικός "αλφάβητο" έχει μόνο δύο γράμματα - μηδέν και ένα.

Ο πλεονασμός μιας τέτοιας κωδικοποίησης είναι πολύ μεγάλος και ο αριθμός των λέξεων που μπορούμε να μεταφέρουμε με αυτόν τον τρόπο είναι σχετικά μικρός. Σε τελική ανάλυση, πρέπει να εξαιρέσουμε από το λεξικό οποιαδήποτε λέξη που, αν γίνει λάθος, θα μπορούσε να συμπίπτει με ολόκληρη τη λίστα που αντιστοιχεί στις λέξεις που μεταδίδονται (για παράδειγμα, οι λέξεις "κόρη" και "κουκκίδα" δεν μπορούν να βρίσκονται στο λεξικό). Αλλά η ακριβής μετάδοση μηνυμάτων είναι τόσο σημαντική που καταβάλλεται μεγάλη προσπάθεια για την έρευνα σε κωδικούς ανθεκτικούς σε σφάλματα.

Αίσθηση

Οι έννοιες της εντροπίας (ή της αβεβαιότητας και της μη προβλεψιμότητας) ενός μηνύματος και του πλεονασμού (ή του προσδιορισμού και της προβλεψιμότητας) αντιστοιχούν πολύ φυσικά στις διαισθήσεις μας σχετικά με την ποσότητα των πληροφοριών. Όσο πιο απρόβλεπτο είναι το μήνυμα (τόσο μεγαλύτερη είναι η εντροπία του, γιατί η πιθανότητα είναι μικρότερη), τόσο περισσότερες πληροφορίες μεταφέρει. Μια αίσθηση (για παράδειγμα, μια συνάντηση με έναν κροκόδειλο στο Tverskaya) είναι ένα σπάνιο γεγονός, η προβλεψιμότητά του είναι πολύ χαμηλή και επομένως το κόστος πληροφοριών είναι υψηλό. Οι πληροφορίες ονομάζονται συχνά ειδήσεις - μηνύματα για γεγονότα που μόλις συνέβησαν, για τα οποία δεν γνωρίζουμε ακόμα τίποτα. Αλλά αν μας πουν για το τι συνέβη δεύτερη και τρίτη φορά με περίπου τα ίδια λόγια, ο πλεονασμός του μηνύματος θα είναι μεγάλος, η απρόβλεψή του θα πέσει στο μηδέν και απλά δεν θα ακούμε, ξεμπλοκάροντας τον ομιλητή με τις λέξεις " Ξέρω ξέρω." Γι' αυτό τα μέσα προσπαθούν τόσο πολύ να είναι πρώτα. Είναι αυτή η αντιστοιχία με τη διαισθητική αίσθηση της καινοτομίας, η οποία προκαλεί πραγματικά απροσδόκητες ειδήσεις, που έπαιξε σημαντικό ρόλο στο γεγονός ότι το άρθρο της Shannon, που δεν προοριζόταν καθόλου για τον γενικό αναγνώστη, έγινε αίσθηση, η οποία έγινε αντιληπτή. από τον Τύπο, που έγινε αποδεκτό ως παγκόσμιο κλειδί για τη γνώση της φύσης από επιστήμονες διαφόρων ειδικοτήτων - από γλωσσολόγους και κριτικούς λογοτεχνίας μέχρι βιολόγους.

Αλλά Η έννοια της πληροφορίας του Shannon - αυστηρή μαθηματική θεωρία , και η εφαρμογή του εκτός της θεωρίας της επικοινωνίας είναι πολύ αναξιόπιστη. Αλλά στην ίδια τη θεωρία της επικοινωνίας παίζει κεντρικό ρόλο.

Σημασιολογικές πληροφορίες

Ο Shannon, έχοντας εισαγάγει την έννοια της εντροπίας ως μέτρο πληροφοριών, μπόρεσε να εργαστεί με τις πληροφορίες - πρώτα απ 'όλα, να τις μετρήσει και να αξιολογήσει χαρακτηριστικά όπως η χωρητικότητα καναλιού ή η βέλτιστη κωδικοποίηση. Αλλά η κύρια υπόθεση που επέτρεψε στον Shannon να λειτουργήσει με επιτυχία με πληροφορίες ήταν η υπόθεση ότι η παραγωγή πληροφοριών είναι μια τυχαία διαδικασία που μπορεί να περιγραφεί επιτυχώς με όρους της θεωρίας πιθανοτήτων. Εάν η διαδικασία είναι μη τυχαία, δηλαδή υπακούει σε νόμους (και όχι πάντα σαφείς, όπως συμβαίνει στη φυσική γλώσσα), τότε ο συλλογισμός του Shannon δεν μπορεί να εφαρμοστεί σε αυτήν. Τίποτα που λέει ο Shannon δεν έχει καμία σχέση με το νόημα των πληροφοριών.

Ενώ μιλάμε για σύμβολα (ή γράμματα του αλφαβήτου), μπορούμε εύκολα να σκεφτόμαστε με όρους τυχαίων γεγονότων, αλλά μόλις προχωρήσουμε στις λέξεις μιας γλώσσας, η κατάσταση αλλάζει δραματικά. Η ομιλία είναι μια διαδικασία οργανωμένη με ιδιαίτερο τρόπο και εδώ η δομή του μηνύματος δεν είναι λιγότερο σημαντική από τα σύμβολα με τα οποία μεταδίδεται.

Μέχρι πρόσφατα, φαινόταν ότι δεν μπορούσαμε να κάνουμε τίποτα για να πλησιάσουμε περισσότερο στη μέτρηση της σημασίας ενός κειμένου, αλλά τα τελευταία χρόνιαη κατάσταση άρχισε να αλλάζει. Και αυτό οφείλεται κυρίως στην εφαρμογή τεχνητών νευρωνικών δικτύων στις εργασίες της μηχανικής μετάφρασης, της αυτόματης σύνοψης κειμένων, της εξαγωγής πληροφοριών από κείμενα και της δημιουργίας αναφορών σε φυσική γλώσσα. Όλες αυτές οι εργασίες περιλαμβάνουν μετασχηματισμό, κωδικοποίηση και αποκωδικοποίηση σημαντικών πληροφοριών που περιέχονται στη φυσική γλώσσα. Και σταδιακά σχηματίζεται μια ιδέα σχετικά με τις απώλειες πληροφοριών κατά τη διάρκεια τέτοιων μετασχηματισμών, και επομένως για την έκταση των ουσιαστικών πληροφοριών. Αλλά σήμερα, η σαφήνεια και η ακρίβεια που έχει η θεωρία πληροφοριών του Shannon δεν είναι ακόμη διαθέσιμη σε αυτά τα δύσκολα προβλήματα.