Η επίλυση εξισώσεων στα μαθηματικά κατέχει ιδιαίτερη θέση. Αυτή η διαδικασία προηγείται από πολλές ώρες θεωρίας, κατά τις οποίες ο μαθητής μαθαίνει πώς να λύνει εξισώσεις, να προσδιορίζει τον τύπο τους και να φέρνει την ικανότητα στην πλήρη αυτοματοποίηση. Ωστόσο, η αναζήτηση για ρίζες δεν έχει πάντα νόημα, αφού μπορεί απλώς να μην υπάρχουν. Υπάρχουν ειδικές τεχνικές για την εύρεση ριζών. Σε αυτό το άρθρο θα αναλύσουμε τις κύριες συναρτήσεις, τους τομείς ορισμού τους, καθώς και τις περιπτώσεις που λείπουν οι ρίζες τους.
Ποια εξίσωση δεν έχει ρίζες;
Μια εξίσωση δεν έχει ρίζες εάν δεν υπάρχουν πραγματικά ορίσματα x για τα οποία η εξίσωση είναι πανομοιότυπη αληθής. Για τον λαϊκό αυτή η διατύπωση, όπως οι περισσότεροι μαθηματικά θεωρήματακαι τύπους, φαίνεται πολύ θολή και αφηρημένη, αλλά αυτό είναι στη θεωρία. Στην πράξη, όλα γίνονται εξαιρετικά απλά. Για παράδειγμα: η εξίσωση 0 * x = -53 δεν έχει λύση, αφού δεν υπάρχει αριθμός x του οποίου το γινόμενο με το μηδέν θα έδινε κάτι διαφορετικό από το μηδέν.
Τώρα θα δούμε τα περισσότερα βασικοί τύποιεξισώσεις.
1. Γραμμική εξίσωση
Μια εξίσωση ονομάζεται γραμμική αν η δεξιά και η αριστερή πλευρά της παριστάνονται με τη μορφή γραμμικές συναρτήσεις: ax + b = cx + d ή σε γενικευμένη μορφή kx + b = 0. Όπου a, b, c, d είναι γνωστοί αριθμοί και το x είναι ένα άγνωστο μέγεθος. Ποια εξίσωση δεν έχει ρίζες; Παραδείγματα γραμμικών εξισώσεων παρουσιάζονται στην παρακάτω εικόνα.
Βασικά, οι γραμμικές εξισώσεις λύνονται απλώς μεταφέροντας το αριθμητικό μέρος σε ένα μέρος και τα περιεχόμενα του x σε ένα άλλο. Το αποτέλεσμα είναι μια εξίσωση της μορφής mx = n, όπου m και n είναι αριθμοί και x είναι ένας άγνωστος. Για να βρείτε το x, απλώς διαιρέστε και τις δύο πλευρές με το m. Τότε x = n/m. Οι περισσότερες γραμμικές εξισώσεις έχουν μόνο μία ρίζα, αλλά υπάρχουν περιπτώσεις που υπάρχουν είτε άπειρες ρίζες είτε καθόλου ρίζες. Όταν m = 0 και n = 0, η εξίσωση παίρνει τη μορφή 0 * x = 0. Η λύση μιας τέτοιας εξίσωσης θα είναι απολύτως οποιοσδήποτε αριθμός.
Ωστόσο, ποια εξίσωση δεν έχει ρίζες;
Για m = 0 και n = 0, η εξίσωση δεν έχει ρίζες από το σύνολο πραγματικούς αριθμούς. 0 * x = -1; 0 * x = 200 - αυτές οι εξισώσεις δεν έχουν ρίζες.
2. Τετραγωνική εξίσωση
Μια τετραγωνική εξίσωση είναι μια εξίσωση της μορφής ax 2 + bx + c = 0 για a = 0. Η πιο κοινή λύση είναι μέσω της διάκρισης. Φόρμουλα για την εύρεση του διακριτικού τετραγωνική εξίσωση: D = b 2 - 4 * a * c. Στη συνέχεια υπάρχουν δύο ρίζες x 1,2 = (-b ± √D) / 2 * a.
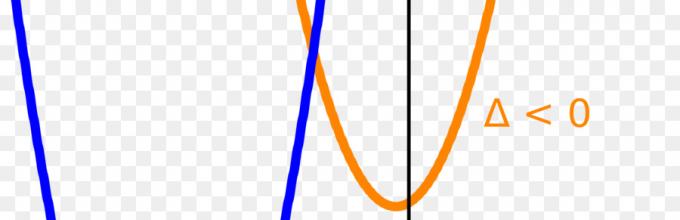
Για D > 0 η εξίσωση έχει δύο ρίζες, για D = 0 έχει μία ρίζα. Αλλά ποια τετραγωνική εξίσωση δεν έχει ρίζες; Ο ευκολότερος τρόπος για να παρατηρήσετε τον αριθμό των ριζών μιας δευτεροβάθμιας εξίσωσης είναι να γράψετε γραφικά τη συνάρτηση, η οποία είναι μια παραβολή. Για a > 0 οι κλάδοι κατευθύνονται προς τα πάνω, για a< 0 ветви опущены вниз. Если дискриминант отрицателен, такое квадратное уравнение не имеет корней на множестве действительных чисел.

Μπορείτε επίσης να προσδιορίσετε οπτικά τον αριθμό των ριζών χωρίς να υπολογίσετε το διαχωριστικό. Για να γίνει αυτό, πρέπει να βρείτε την κορυφή της παραβολής και να προσδιορίσετε προς ποια κατεύθυνση κατευθύνονται οι κλάδοι. Η συντεταγμένη x της κορυφής μπορεί να προσδιοριστεί χρησιμοποιώντας τον τύπο: x 0 = -b / 2a. Σε αυτήν την περίπτωση, η συντεταγμένη y της κορυφής βρίσκεται αντικαθιστώντας απλώς την τιμή x 0 στην αρχική εξίσωση.

Η τετραγωνική εξίσωση x 2 - 8x + 72 = 0 δεν έχει ρίζες, αφού έχει αρνητική διάκριση D = (-8) 2 - 4 * 1 * 72 = -224. Αυτό σημαίνει ότι η παραβολή δεν αγγίζει τον άξονα x και η συνάρτηση δεν παίρνει ποτέ την τιμή 0, επομένως, η εξίσωση δεν έχει πραγματικές ρίζες.
3. Τριγωνομετρικές εξισώσεις
Οι τριγωνομετρικές συναρτήσεις θεωρούνται σε έναν τριγωνομετρικό κύκλο, αλλά μπορούν επίσης να αναπαρασταθούν σε ένα καρτεσιανό σύστημα συντεταγμένων. Σε αυτό το άρθρο θα δούμε δύο βασικά τριγωνομετρικές συναρτήσειςκαι οι εξισώσεις τους: sinx και cosx. Αφού αυτές οι συναρτήσεις σχηματίζονται τριγωνομετρικός κύκλοςμε ακτίνα 1, |sinx| και |cosx| δεν μπορεί να είναι μεγαλύτερη από 1. Άρα, ποια εξίσωση sinx δεν έχει ρίζες; Ας δούμε το γράφημα συναρτήσεις sinx, φαίνεται στην παρακάτω εικόνα.

Βλέπουμε ότι η συνάρτηση είναι συμμετρική και έχει περίοδο επανάληψης 2pi. Με βάση αυτό, μπορούμε να πούμε ότι η μέγιστη τιμή αυτής της συνάρτησης μπορεί να είναι 1 και η ελάχιστη -1. Για παράδειγμα, η έκφραση cosx = 5 δεν θα έχει ρίζες, αφού η απόλυτη τιμή της είναι μεγαλύτερη από μία.
Αυτό είναι το απλούστερο παράδειγμα τριγωνομετρικών εξισώσεων. Στην πραγματικότητα, η επίλυσή τους μπορεί να πάρει πολλές σελίδες, στο τέλος των οποίων συνειδητοποιείτε ότι χρησιμοποιήσατε λάθος τύπο και πρέπει να ξεκινήσετε από την αρχή. Μερικές φορές, ακόμα κι αν βρείτε σωστά τις ρίζες, μπορεί να ξεχάσετε να λάβετε υπόψη τους περιορισμούς στο OD, γι' αυτό εμφανίζεται μια επιπλέον ρίζα ή διάστημα στην απάντηση και ολόκληρη η απάντηση μετατρέπεται σε σφάλμα. Επομένως, ακολουθήστε αυστηρά όλους τους περιορισμούς, επειδή δεν ταιριάζουν όλες οι ρίζες στο πεδίο εφαρμογής της εργασίας.
4. Συστήματα εξισώσεων
Ένα σύστημα εξισώσεων είναι ένα σύνολο εξισώσεων που ενώνονται με σγουρές ή τετράγωνες αγκύλες. Οι σγουρές αγκύλες υποδεικνύουν ότι όλες οι εξισώσεις εκτελούνται μαζί. Δηλαδή, εάν τουλάχιστον μία από τις εξισώσεις δεν έχει ρίζες ή έρχεται σε αντίθεση με μια άλλη, ολόκληρο το σύστημα δεν έχει λύση. Οι αγκύλες υποδεικνύουν τη λέξη "ή". Αυτό σημαίνει ότι αν τουλάχιστον μία από τις εξισώσεις του συστήματος έχει λύση, τότε ολόκληρο το σύστημα έχει λύση.

Η απάντηση του συστήματος c είναι το σύνολο όλων των ριζών των επιμέρους εξισώσεων. Και τα συστήματα με σγουρά τιράντες έχουν μόνο κοινές ρίζες. Τα συστήματα εξισώσεων μπορούν να περιλαμβάνουν εντελώς διαφορετικές συναρτήσεις, επομένως μια τέτοια πολυπλοκότητα δεν μας επιτρέπει να πούμε αμέσως ποια εξίσωση δεν έχει ρίζες.
Βρέθηκε σε προβληματικά βιβλία και σχολικά βιβλία ΔΙΑΦΟΡΕΤΙΚΟΙ ΤΥΠΟΙεξισώσεις: αυτές που έχουν ρίζες και αυτές που δεν έχουν. Πρώτα απ 'όλα, αν δεν μπορείτε να βρείτε τις ρίζες, μην νομίζετε ότι δεν υπάρχουν καθόλου. Ίσως κάνατε ένα λάθος κάπου, τότε απλά πρέπει να ελέγξετε προσεκτικά την απόφασή σας.
Εξετάσαμε τις πιο βασικές εξισώσεις και τους τύπους τους. Τώρα μπορείτε να πείτε ποια εξίσωση δεν έχει ρίζες. Στις περισσότερες περιπτώσεις αυτό δεν είναι δύσκολο να γίνει. Η επιτυχία στην επίλυση εξισώσεων απαιτεί μόνο προσοχή και συγκέντρωση. Εξασκηθείτε περισσότερο, θα σας βοηθήσει να πλοηγηθείτε στο υλικό πολύ καλύτερα και πιο γρήγορα.
Άρα, η εξίσωση δεν έχει ρίζες αν:
- Στη γραμμική εξίσωση mx = n η τιμή είναι m = 0 και n = 0.
- σε μια τετραγωνική εξίσωση, εάν η διάκριση είναι μικρότερη από το μηδέν.
- V τριγωνομετρική εξίσωσητης μορφής cosx = m / sinx = n, αν |m| > 0, |n| > 0;
- σε ένα σύστημα εξισώσεων με σγουρές αγκύλες εάν τουλάχιστον μία εξίσωση δεν έχει ρίζες και με αγκύλες εάν όλες οι εξισώσεις δεν έχουν ρίζες.
Εκμάθηση βίντεο 2: Επίλυση Τετραγωνικών Εξισώσεων
Διάλεξη: Τετραγωνικές εξισώσεις
Η εξίσωση
Η εξίσωση- αυτό είναι ένα είδος ισότητας στις εκφράσεις της οποίας υπάρχει μια μεταβλητή.
Λύστε την εξίσωση- σημαίνει εύρεση ενός αριθμού αντί μιας μεταβλητής που θα τον φέρει σε σωστή ισότητα.
Μια εξίσωση μπορεί να έχει μία λύση, πολλές ή και καμία.
Για να λυθεί οποιαδήποτε εξίσωση, θα πρέπει να απλοποιηθεί όσο το δυνατόν περισσότερο στη μορφή:
Γραμμικός: a*x = b;
Τετράγωνο: a*x 2 + b*x + c = 0.
Δηλαδή, οποιεσδήποτε εξισώσεις πρέπει να μετατραπούν σε τυπική μορφή πριν λυθούν.
Οποιαδήποτε εξίσωση μπορεί να λυθεί με δύο τρόπους: αναλυτικό και γραφικό.
Στο γράφημα, η λύση της εξίσωσης θεωρείται ότι είναι τα σημεία στα οποία το γράφημα τέμνει τον άξονα OX.
Τετραγωνικές εξισώσεις
Μια εξίσωση μπορεί να ονομαστεί τετραγωνική εάν, όταν απλοποιηθεί, έχει τη μορφή:
a*x 2 + b*x + c = 0.
Εν α, β, γείναι συντελεστές της εξίσωσης που διαφέρουν από το μηδέν. ΕΝΑ "Χ"- ρίζα της εξίσωσης. Πιστεύεται ότι μια τετραγωνική εξίσωση έχει δύο ρίζες ή μπορεί να μην έχει καθόλου λύση. Οι ρίζες που προκύπτουν μπορεί να είναι οι ίδιες.
"ΕΝΑ"- ο συντελεστής που βρίσκεται πριν από την τετραγωνική ρίζα.
"σι"- στέκεται μπροστά στο άγνωστο σε πρώτο βαθμό.
"Με" - ελεύθερο μέλοςεξισώσεις
Αν, για παράδειγμα, έχουμε μια εξίσωση της μορφής:
2x 2 -5x+3=0
Σε αυτό, το "2" είναι ο συντελεστής του κύριου όρου της εξίσωσης, το "-5" είναι ο δεύτερος συντελεστής και το "3" είναι ο ελεύθερος όρος.
Επίλυση δευτεροβάθμιας εξίσωσης
Υπάρχει μια τεράστια ποικιλία τρόπων για την επίλυση μιας εξίσωσης δευτεροβάθμιας. Ωστόσο, σε σχολικό μάθημαΣτα μαθηματικά, η λύση μελετάται χρησιμοποιώντας το θεώρημα του Vieta, καθώς και χρησιμοποιώντας τη διάκριση.
Διακριτική λύση:
Κατά την επίλυση με αυτή τη μέθοδοείναι απαραίτητο να υπολογιστεί η διάκριση χρησιμοποιώντας τον τύπο:
![]()
Εάν κατά τους υπολογισμούς σας διαπιστώσετε ότι η διάκριση είναι μικρότερη από το μηδέν, αυτό σημαίνει ότι αυτή η εξίσωση δεν έχει λύσεις.
Αν η διάκριση είναι μηδέν, τότε η εξίσωση έχει δύο πανομοιότυπες λύσεις. Σε αυτήν την περίπτωση, το πολυώνυμο μπορεί να συμπτυχθεί χρησιμοποιώντας τον συντομευμένο τύπο πολλαπλασιασμού στο τετράγωνο του αθροίσματος ή της διαφοράς. Μετά λύστε το σαν γραμμική εξίσωση. Ή χρησιμοποιήστε τον τύπο:
Εάν η διάκριση είναι μεγαλύτερη από το μηδέν, τότε πρέπει να χρησιμοποιήσετε την ακόλουθη μέθοδο:

Το θεώρημα του Βιέτα
Εάν δοθεί η εξίσωση, δηλαδή ο συντελεστής του κύριου όρου είναι ίσος με ένα, τότε μπορείτε να χρησιμοποιήσετε Το θεώρημα του Βιέτα.
Ας υποθέσουμε λοιπόν ότι η εξίσωση είναι:
Οι ρίζες της εξίσωσης βρίσκονται ως εξής:

Ημιτελής τετραγωνική εξίσωση
Υπάρχουν πολλές επιλογές για τη λήψη μιας ημιτελούς τετραγωνικής εξίσωσης, η μορφή της οποίας εξαρτάται από την παρουσία συντελεστών.
1. Αν ο δεύτερος και ο τρίτος συντελεστής είναι μηδέν (b = 0, c = 0), τότε η τετραγωνική εξίσωση θα μοιάζει με:
Αυτή η εξίσωση θα έχει μόνη απόφαση. Η ισότητα θα ισχύει μόνο αν η λύση της εξίσωσης είναι μηδέν.
Ορισμένα προβλήματα στα μαθηματικά απαιτούν την ικανότητα υπολογισμού της τιμής της τετραγωνικής ρίζας. Τέτοια προβλήματα περιλαμβάνουν την επίλυση εξισώσεων δεύτερης τάξης. Σε αυτό το άρθρο θα παρουσιάσουμε αποτελεσματική μέθοδοςυπολογισμούς τετραγωνικές ρίζεςκαι χρησιμοποιήστε το όταν εργάζεστε με τύπους για τις ρίζες μιας τετραγωνικής εξίσωσης.
Τι είναι η τετραγωνική ρίζα;
Στα μαθηματικά, αυτή η έννοια αντιστοιχεί στο σύμβολο √. Τα ιστορικά δεδομένα λένε ότι χρησιμοποιήθηκε για πρώτη φορά γύρω στο πρώτο μισό του 16ου αιώνα στη Γερμανία (το πρώτο γερμανικό έργο για την άλγεβρα του Christoph Rudolf). Οι επιστήμονες πιστεύουν ότι το σύμβολο είναι ένα μετασχηματισμένο λατινικό γράμμα r (radix σημαίνει "ρίζα" στα λατινικά).
Η ρίζα οποιουδήποτε αριθμού είναι ίση με την τιμή της οποίας το τετράγωνο αντιστοιχεί στη ριζική έκφραση. Στη γλώσσα των μαθηματικών, αυτός ο ορισμός θα μοιάζει με αυτό: √x = y, αν y 2 = x.
Η ρίζα ενός θετικού αριθμού (x > 0) είναι επίσης θετικός αριθμός (y > 0), αλλά αν πάρετε τη ρίζα ενός αρνητικού αριθμού (x< 0), то его результатом уже будет μιγαδικός αριθμός, συμπεριλαμβανομένης της φανταστικής ενότητας i.
Ακολουθούν δύο απλά παραδείγματα:
√9 = 3, αφού 3 2 = 9; √(-9) = 3i, αφού i 2 = -1.
Ο επαναληπτικός τύπος του Heron για την εύρεση των τιμών των τετραγωνικών ριζών
Τα παραπάνω παραδείγματα είναι πολύ απλά και ο υπολογισμός των ριζών σε αυτά δεν είναι δύσκολος. Οι δυσκολίες αρχίζουν να εμφανίζονται κατά την εύρεση τιμών ρίζας για οποιαδήποτε τιμή που δεν μπορεί να αναπαρασταθεί ως τετράγωνο φυσικός αριθμός, για παράδειγμα √10, √11, √12, √13, για να μην αναφέρουμε το γεγονός ότι στην πράξη είναι απαραίτητο να βρούμε ρίζες για μη ακέραιους αριθμούς: για παράδειγμα √(12,15), √(8,5) και ούτω καθεξής.

Σε όλες τις παραπάνω περιπτώσεις θα πρέπει να χρησιμοποιείται ειδική μέθοδος υπολογισμού της τετραγωνικής ρίζας. Επί του παρόντος, πολλές τέτοιες μέθοδοι είναι γνωστές: για παράδειγμα, επέκταση της σειράς Taylor, διαίρεση στηλών και μερικές άλλες. Από όλες τις γνωστές μεθόδους, ίσως η απλούστερη και πιο αποτελεσματική είναι η χρήση του επαναληπτικού τύπου του Heron, ο οποίος είναι επίσης γνωστός ως Βαβυλωνιακή μέθοδος προσδιορισμού τετραγωνικών ριζών (υπάρχουν στοιχεία ότι οι αρχαίοι Βαβυλώνιοι τη χρησιμοποιούσαν στους πρακτικούς υπολογισμούς τους).
Ας είναι απαραίτητο να προσδιοριστεί η τιμή του √x. Ο τύπος για την εύρεση της τετραγωνικής ρίζας είναι ο εξής:
a n+1 = 1/2(a n +x/a n), όπου lim n->∞ (a n) => x.
Ας αποκρυπτογραφήσουμε αυτή τη μαθηματική σημειογραφία. Για να υπολογίσετε το √x, θα πρέπει να πάρετε έναν συγκεκριμένο αριθμό a 0 (μπορεί να είναι αυθαίρετος, αλλά για να πάρετε γρήγορα το αποτέλεσμα, θα πρέπει να τον επιλέξετε έτσι ώστε το (a 0) 2 να είναι όσο το δυνατόν πιο κοντά στο x. Στη συνέχεια, αντικαταστήστε τον στο υποδεικνυόμενος τύπος για τον υπολογισμό της τετραγωνικής ρίζας και λάβετε έναν νέο αριθμό a 1, ο οποίος θα είναι ήδη πιο κοντά στην επιθυμητή τιμή. Μετά από αυτό, πρέπει να αντικαταστήσετε ένα 1 στην παράσταση και να πάρετε ένα 2. Αυτή η διαδικασία θα πρέπει να επαναληφθεί μέχρι το απαιτούμενο επιτυγχάνεται η ακρίβεια.
Ένα παράδειγμα χρήσης του επαναληπτικού τύπου του Heron
Ο αλγόριθμος που περιγράφεται παραπάνω για τη λήψη της τετραγωνικής ρίζας ενός δεδομένου αριθμού μπορεί να ακούγεται αρκετά περίπλοκος και μπερδεμένος σε πολλούς, αλλά στην πραγματικότητα όλα αποδεικνύονται πολύ πιο απλά, καθώς αυτός ο τύπος συγκλίνει πολύ γρήγορα (ειδικά αν επιλεγεί ένας επιτυχημένος αριθμός 0) .
Ας δώσουμε ένα απλό παράδειγμα: πρέπει να υπολογίσετε το √11. Ας επιλέξουμε ένα 0 = 3, αφού 3 2 = 9, που είναι πιο κοντά στο 11 παρά στο 4 2 = 16. Αντικαθιστώντας τον τύπο, παίρνουμε:
a 1 = 1/2 (3 + 11/3) = 3,333333;
a 2 = 1/2 (3,33333 + 11/3,33333) = 3,316668;
a 3 = 1/2 (3,316668 + 11/3,316668) = 3,31662.
Δεν έχει νόημα να συνεχίσουμε τους υπολογισμούς, αφού διαπιστώσαμε ότι το 2 και το 3 αρχίζουν να διαφέρουν μόνο στο 5ο δεκαδικό ψηφίο. Έτσι, αρκούσε να εφαρμόσουμε τον τύπο μόνο 2 φορές για να υπολογίσουμε το √11 με ακρίβεια 0,0001.
Σήμερα, οι αριθμομηχανές και οι υπολογιστές χρησιμοποιούνται ευρέως για τον υπολογισμό των ριζών, ωστόσο, είναι χρήσιμο να θυμάστε τον σημειωμένο τύπο για να μπορείτε να υπολογίσετε με μη αυτόματο τρόπο την ακριβή τους τιμή.
Εξισώσεις δεύτερης τάξης
Η κατανόηση του τι είναι τετραγωνική ρίζα και η ικανότητα υπολογισμού της χρησιμοποιείται για την επίλυση τετραγωνικών εξισώσεων. Αυτές οι εξισώσεις ονομάζονται ισότητες με έναν άγνωστο, η γενική μορφή του οποίου φαίνεται στο παρακάτω σχήμα.

Εδώ τα c, b και a αντιπροσωπεύουν ορισμένους αριθμούς και το a δεν πρέπει να είναι ίσο με μηδέν και οι τιμές των c και b μπορεί να είναι εντελώς αυθαίρετες, συμπεριλαμβανομένου του μηδενός.
Οποιεσδήποτε τιμές του x ικανοποιούν την ισότητα που υποδεικνύεται στο σχήμα ονομάζονται ρίζες του (αυτή η έννοια δεν πρέπει να συγχέεται με την τετραγωνική ρίζα √). Εφόσον η εξίσωση που εξετάζουμε είναι 2ης τάξης (x 2), τότε δεν μπορούν να υπάρχουν περισσότερες από δύο ρίζες για αυτήν. Ας δούμε περαιτέρω στο άρθρο πώς να βρείτε αυτές τις ρίζες.
Εύρεση των ριζών μιας τετραγωνικής εξίσωσης (τύπος)
Αυτή η μέθοδος επίλυσης του τύπου των ισοτήτων που εξετάζονται ονομάζεται επίσης καθολική μέθοδος ή μέθοδος διάκρισης. Μπορεί να χρησιμοποιηθεί για οποιεσδήποτε δευτεροβάθμιες εξισώσεις. Ο τύπος για τη διάκριση και τις ρίζες της τετραγωνικής εξίσωσης έχει ως εξής:

Δείχνει ότι οι ρίζες εξαρτώνται από την τιμή καθενός από τους τρεις συντελεστές της εξίσωσης. Επιπλέον, ο υπολογισμός του x 1 διαφέρει από τον υπολογισμό του x 2 μόνο από το πρόσημο μπροστά από την τετραγωνική ρίζα. Η ριζική έκφραση, η οποία είναι ίση με b 2 - 4ac, δεν είναι τίποτα άλλο από τη διάκριση της εν λόγω ισότητας. Η διάκριση στον τύπο για τις ρίζες μιας τετραγωνικής εξίσωσης παίζει σημαντικό ρόλο επειδή καθορίζει τον αριθμό και το είδος των λύσεων. Έτσι, αν είναι ίση με μηδέν, τότε θα υπάρχει μόνο μία λύση, εάν είναι θετική, τότε η εξίσωση έχει δύο πραγματικές ρίζες και, τέλος, μια αρνητική διάκριση οδηγεί σε δύο μιγαδικές ρίζες x 1 και x 2.
Το θεώρημα του Vieta ή κάποιες ιδιότητες των ριζών εξισώσεων δεύτερης τάξης
Στα τέλη του 16ου αιώνα, ένας από τους ιδρυτές της σύγχρονης άλγεβρας, ένας Γάλλος, που μελετούσε τις εξισώσεις δεύτερης τάξης, μπόρεσε να αποκτήσει τις ιδιότητες των ριζών της. Μαθηματικά μπορούν να γραφτούν ως εξής:
x 1 + x 2 = -b / a και x 1 * x 2 = c / a.
Και οι δύο ισότητες μπορούν να ληφθούν εύκολα από οποιονδήποτε· για να γίνει αυτό, χρειάζεται απλώς να εκτελέσετε τις κατάλληλες μαθηματικές πράξεις με τις ρίζες που λαμβάνονται μέσω του τύπου με το διαχωριστικό.

Ο συνδυασμός αυτών των δύο εκφράσεων μπορεί δικαίως να ονομαστεί ο δεύτερος τύπος για τις ρίζες μιας τετραγωνικής εξίσωσης, ο οποίος καθιστά δυνατή την εικασία των λύσεών της χωρίς τη χρήση διαχωριστικού. Εδώ πρέπει να σημειωθεί ότι παρόλο που και οι δύο εκφράσεις είναι πάντα έγκυρες, είναι βολικό να τις χρησιμοποιήσουμε για να λύσουμε μια εξίσωση μόνο εάν μπορεί να παραγοντοποιηθεί.
Το έργο της εμπέδωσης της αποκτηθείσας γνώσης
Ας αποφασίσουμε μαθηματικό πρόβλημα, στο οποίο θα δείξουμε όλες τις τεχνικές που συζητούνται στο άρθρο. Οι συνθήκες του προβλήματος είναι οι εξής: πρέπει να βρείτε δύο αριθμούς για τους οποίους το γινόμενο είναι -13 και το άθροισμα είναι 4.

Αυτή η συνθήκη μας θυμίζει αμέσως το θεώρημα του Vieta· χρησιμοποιώντας τους τύπους για το άθροισμα των τετραγωνικών ριζών και το γινόμενο τους, γράφουμε:
x 1 + x 2 = -b / a = 4;
x 1 * x 2 = c / a = -13.
Αν υποθέσουμε ότι a = 1, τότε b = -4 και c = -13. Αυτοί οι συντελεστές μας επιτρέπουν να δημιουργήσουμε μια εξίσωση δεύτερης τάξης:
x 2 - 4x - 13 = 0.
Ας χρησιμοποιήσουμε τον τύπο με το διακριτικό και ας πάρουμε τις ακόλουθες ρίζες:
x 1,2 = (4 ± √D)/2, D = 16 - 4 * 1 * (-13) = 68.
Δηλαδή, το πρόβλημα περιορίστηκε στην εύρεση του αριθμού √68. Σημειώστε ότι 68 = 4 * 17, τότε, χρησιμοποιώντας την ιδιότητα τετραγωνικής ρίζας, παίρνουμε: √68 = 2√17.
Τώρα ας χρησιμοποιήσουμε τον θεωρούμενο τύπο τετραγωνικής ρίζας: a 0 = 4, τότε:
a 1 = 1/2 (4 + 17/4) = 4,125;
a 2 = 1/2 (4,125 + 17/4,125) = 4,1231.
Δεν χρειάζεται να υπολογίσετε το 3 αφού οι τιμές που βρέθηκαν διαφέρουν μόνο κατά 0,02. Έτσι, √68 = 8,246. Αντικαθιστώντας το στον τύπο για x 1,2, παίρνουμε:
x 1 = (4 + 8,246)/2 = 6,123 και x 2 = (4 - 8,246)/2 = -2,123.
Όπως βλέπουμε, το άθροισμα των αριθμών που βρέθηκαν είναι πραγματικά ίσο με 4, αλλά αν βρούμε το γινόμενο τους, τότε θα είναι ίσο με -12,999, που ικανοποιεί τις συνθήκες του προβλήματος με ακρίβεια 0,001.
Υπενθυμίζουμε ότι μια πλήρης τετραγωνική εξίσωση είναι μια εξίσωση της μορφής:
Η επίλυση πλήρων τετραγωνικών εξισώσεων είναι λίγο πιο δύσκολη (λίγο) από αυτές.
Θυμάμαι, Οποιαδήποτε δευτεροβάθμια εξίσωση μπορεί να λυθεί χρησιμοποιώντας ένα διαχωριστικό!
Έστω και ημιτελής.
Οι άλλες μέθοδοι θα σας βοηθήσουν να το κάνετε γρηγορότερα, αλλά εάν έχετε προβλήματα με τις δευτεροβάθμιες εξισώσεις, πρώτα κατακτήστε τη λύση χρησιμοποιώντας τη διάκριση.
1. Επίλυση δευτεροβάθμιων εξισώσεων με χρήση διαχωριστή.
Η επίλυση τετραγωνικών εξισώσεων χρησιμοποιώντας αυτή τη μέθοδο είναι πολύ απλή· το κύριο πράγμα είναι να θυμάστε την ακολουθία των ενεργειών και μερικούς τύπους.
Αν, τότε η εξίσωση έχει 2 ρίζες. Πρέπει να δώσετε ιδιαίτερη προσοχή στο βήμα 2.
Η διάκριση D μας λέει τον αριθμό των ριζών της εξίσωσης.
- Εάν, τότε ο τύπος στο βήμα θα μειωθεί σε. Έτσι, η εξίσωση θα έχει μόνο ρίζα.
- Εάν, τότε δεν θα μπορέσουμε να εξαγάγουμε τη ρίζα του διακριτικού στο βήμα. Αυτό δείχνει ότι η εξίσωση δεν έχει ρίζες.
Ας στραφούμε στο γεωμετρική αίσθησητετραγωνική εξίσωση.
Η γραφική παράσταση της συνάρτησης είναι παραβολή:
Ας επιστρέψουμε στις εξισώσεις μας και ας δούμε μερικά παραδείγματα.
Παράδειγμα 9
Λύστε την εξίσωση
Βήμα 1παραλείπουμε.
Βήμα 2.
Βρίσκουμε τη διάκριση:
Αυτό σημαίνει ότι η εξίσωση έχει δύο ρίζες.
Βήμα 3.
Απάντηση:
Παράδειγμα 10
Λύστε την εξίσωση
Η εξίσωση παρουσιάζεται σε τυπική μορφή, άρα Βήμα 1παραλείπουμε.
Βήμα 2.
Βρίσκουμε τη διάκριση:
Αυτό σημαίνει ότι η εξίσωση έχει μία ρίζα.
Απάντηση:
Παράδειγμα 11
Λύστε την εξίσωση
Η εξίσωση παρουσιάζεται σε τυπική μορφή, άρα Βήμα 1παραλείπουμε.
Βήμα 2.
Βρίσκουμε τη διάκριση:
Αυτό σημαίνει ότι δεν θα μπορέσουμε να εξαγάγουμε τη ρίζα της διάκρισης. Δεν υπάρχουν ρίζες της εξίσωσης.
Τώρα ξέρουμε πώς να γράφουμε σωστά τέτοιες απαντήσεις.
Απάντηση:χωρίς ρίζες
2. Επίλυση τετραγωνικών εξισώσεων χρησιμοποιώντας το θεώρημα του Vieta
Αν θυμάστε, υπάρχει ένας τύπος εξίσωσης που ονομάζεται μειωμένος (όταν ο συντελεστής a είναι ίσος με):
Τέτοιες εξισώσεις είναι πολύ εύκολο να λυθούν χρησιμοποιώντας το θεώρημα του Vieta:
Άθροισμα ριζών δεδομένοςη τετραγωνική εξίσωση είναι ίση και το γινόμενο των ριζών είναι ίσο.
Απλά πρέπει να επιλέξετε ένα ζεύγος αριθμών των οποίων το γινόμενο είναι ίσο με τον ελεύθερο όρο της εξίσωσης και το άθροισμα είναι ίσο με τον δεύτερο συντελεστή, που λαμβάνεται με το αντίθετο πρόσημο.
Παράδειγμα 12
Λύστε την εξίσωση
Αυτή η εξίσωση μπορεί να λυθεί χρησιμοποιώντας το θεώρημα του Vieta επειδή .
Το άθροισμα των ριζών της εξίσωσης είναι ίσο, δηλ. παίρνουμε την πρώτη εξίσωση:
Και το προϊόν ισούται με:
Ας συνθέσουμε και λύσουμε το σύστημα:
- Και. Το ποσό είναι ίσο με
- Και. Το ποσό είναι ίσο με
- Και. Το ποσό είναι ίσο.
και είναι η λύση στο σύστημα:
Απάντηση: ; .
Παράδειγμα 13
Λύστε την εξίσωση
Απάντηση:
Παράδειγμα 14
Λύστε την εξίσωση
Δίνεται η εξίσωση που σημαίνει:
Απάντηση:
ΤΕΤΑΡΧΟΜΕΝΕΣ ΕΞΙΣΩΣΕΙΣ. ΜΕΣΟ ΕΠΙΠΕΔΟ
Τι είναι μια τετραγωνική εξίσωση;
Με άλλα λόγια, μια τετραγωνική εξίσωση είναι μια εξίσωση της μορφής, όπου - ο άγνωστος, - ορισμένοι αριθμοί, και.
Ο αριθμός ονομάζεται υψηλότερος ή πρώτος συντελεστήςτετραγωνική εξίσωση, - δεύτερος συντελεστής, ΕΝΑ - ελεύθερο μέλος.
Γιατί αν η εξίσωση γίνει αμέσως γραμμική, γιατί θα εξαφανιστεί.
Σε αυτή την περίπτωση, και μπορεί να είναι ίσο με μηδέν. Σε αυτή την καρέκλα καλείται εξίσωση ατελής.
Αν όλοι οι όροι είναι στη θέση τους, δηλαδή, η εξίσωση είναι πλήρης.
Μέθοδοι επίλυσης ημιτελών τετραγωνικών εξισώσεων
Αρχικά, ας δούμε τις μεθόδους για την επίλυση ημιτελών τετραγωνικών εξισώσεων - είναι απλούστερες.
Μπορούμε να διακρίνουμε τους παρακάτω τύπους εξισώσεων:
Ι., στην εξίσωση αυτή ο συντελεστής και ο ελεύθερος όρος είναι ίσοι.
II. , στην εξίσωση αυτή ο συντελεστής είναι ίσος.
III. , σε αυτή την εξίσωση ο ελεύθερος όρος είναι ίσος με.
Τώρα ας δούμε τη λύση για κάθε έναν από αυτούς τους υποτύπους.
Προφανώς, αυτή η εξίσωση έχει πάντα μόνο μία ρίζα:
Ένας τετράγωνος αριθμός δεν μπορεί να είναι αρνητικός, γιατί όταν πολλαπλασιάσετε δύο αρνητικούς ή δύο θετικούς αριθμούς, το αποτέλεσμα θα είναι πάντα ένας θετικός αριθμός. Να γιατί:
αν, τότε η εξίσωση δεν έχει λύσεις.
αν έχουμε δύο ρίζες
Δεν χρειάζεται να απομνημονεύσετε αυτούς τους τύπους. Το κύριο πράγμα που πρέπει να θυμάστε είναι ότι δεν μπορεί να είναι λιγότερο.
Παραδείγματα επίλυσης τετραγωνικών εξισώσεων
Παράδειγμα 15
Απάντηση:
Μην ξεχνάτε ποτέ τις ρίζες με αρνητικό πρόσημο!
Παράδειγμα 16
Το τετράγωνο ενός αριθμού δεν μπορεί να είναι αρνητικό, πράγμα που σημαίνει ότι η εξίσωση
χωρίς ρίζες.
Για να σημειώσουμε εν συντομία ότι ένα πρόβλημα δεν έχει λύσεις, χρησιμοποιούμε το εικονίδιο κενού συνόλου.
Απάντηση:
Παράδειγμα 17
Άρα, αυτή η εξίσωση έχει δύο ρίζες: και.
Απάντηση:
Ας βγάλουμε τον κοινό παράγοντα εκτός παρενθέσεων:
Το γινόμενο είναι ίσο με μηδέν εάν τουλάχιστον ένας από τους παράγοντες είναι ίσος με μηδέν. Αυτό σημαίνει ότι η εξίσωση έχει λύση όταν:
Άρα, αυτή η τετραγωνική εξίσωση έχει δύο ρίζες: και.
Παράδειγμα:
Λύστε την εξίσωση.
Λύση:
Ας συνυπολογίσουμε την αριστερή πλευρά της εξίσωσης και ας βρούμε τις ρίζες:
Απάντηση:
Μέθοδοι επίλυσης πλήρων τετραγωνικών εξισώσεων
1. Διακριτικός
Η επίλυση τετραγωνικών εξισώσεων με αυτόν τον τρόπο είναι εύκολη, το κύριο πράγμα είναι να θυμάστε την ακολουθία των ενεργειών και μερικούς τύπους. Θυμηθείτε, οποιαδήποτε δευτεροβάθμια εξίσωση μπορεί να λυθεί χρησιμοποιώντας ένα διαχωριστικό! Έστω και ημιτελής.
Προσέξατε τη ρίζα από το διακριτικό στον τύπο για τις ρίζες;
Αλλά η διάκριση μπορεί να είναι αρνητική.
Τι να κάνω?
Πρέπει να δώσουμε ιδιαίτερη προσοχή στο βήμα 2. Ο διαχωριστής μας λέει τον αριθμό των ριζών της εξίσωσης.
- Αν, τότε η εξίσωση έχει ρίζες:
- Αν, τότε η εξίσωση έχει τις ίδιες ρίζες, και μάλιστα, μία ρίζα:
Τέτοιες ρίζες ονομάζονται διπλές ρίζες.
- Αν, τότε δεν εξάγεται η ρίζα της διάκρισης. Αυτό δείχνει ότι η εξίσωση δεν έχει ρίζες.
Γιατί είναι δυνατόν διαφορετικές ποσότητεςρίζες?
Ας στραφούμε στη γεωμετρική σημασία της τετραγωνικής εξίσωσης. Η γραφική παράσταση της συνάρτησης είναι παραβολή:

Σε μια ειδική περίπτωση, που είναι μια τετραγωνική εξίσωση, .
Αυτό σημαίνει ότι οι ρίζες μιας τετραγωνικής εξίσωσης είναι τα σημεία τομής με τον άξονα της τετμημένης (άξονα).
Μια παραβολή μπορεί να μην τέμνει καθόλου τον άξονα ή μπορεί να τον τέμνει σε ένα (όταν η κορυφή της παραβολής βρίσκεται στον άξονα) ή δύο σημεία.
Επιπλέον, ο συντελεστής είναι υπεύθυνος για την κατεύθυνση των κλάδων της παραβολής. Αν, τότε οι κλάδοι της παραβολής κατευθύνονται προς τα πάνω και αν, τότε προς τα κάτω.
4 παραδείγματα επίλυσης τετραγωνικών εξισώσεων
Παράδειγμα 18
Απάντηση:
Παράδειγμα 19
Απάντηση: .
Παράδειγμα 20
Απάντηση:
Παράδειγμα 21
Αυτό σημαίνει ότι δεν υπάρχουν λύσεις.
Απάντηση: .
2. Θεώρημα Vieta
Η χρήση του θεωρήματος του Vieta είναι πολύ εύκολη.
Το μόνο που χρειάζεσαι είναι μαζεύωένα τέτοιο ζεύγος αριθμών, το γινόμενο του οποίου είναι ίσο με τον ελεύθερο όρο της εξίσωσης και το άθροισμα είναι ίσο με τον δεύτερο συντελεστή, που λαμβάνεται με το αντίθετο πρόσημο.
Είναι σημαντικό να θυμόμαστε ότι το θεώρημα του Vieta μπορεί να εφαρμοστεί μόνο σε μειωμένες τετραγωνικές εξισώσεις ().
Ας δούμε μερικά παραδείγματα:
Παράδειγμα 22
Λύστε την εξίσωση.
Λύση:
Αυτή η εξίσωση μπορεί να λυθεί χρησιμοποιώντας το θεώρημα του Vieta επειδή . Άλλοι συντελεστές: ; .
Το άθροισμα των ριζών της εξίσωσης είναι:
Και το προϊόν ισούται με:
Ας επιλέξουμε ζεύγη αριθμών των οποίων το γινόμενο είναι ίσο και ας ελέγξουμε αν το άθροισμά τους είναι ίσο:
- Και. Το ποσό είναι ίσο με
- Και. Το ποσό είναι ίσο με
- Και. Το ποσό είναι ίσο.
και είναι η λύση στο σύστημα:
Έτσι, και είναι οι ρίζες της εξίσωσής μας.
Απάντηση: ; .
Παράδειγμα 23
Λύση:
Ας επιλέξουμε ζεύγη αριθμών που δίνουν το γινόμενο και, στη συνέχεια, ελέγξτε αν το άθροισμά τους είναι ίσο:
και: δίνουν συνολικά.
και: δίνουν συνολικά. Για να αποκτήσετε, αρκεί απλώς να αλλάξετε τα σημάδια των υποτιθέμενων ριζών: και, τελικά, το προϊόν.
Απάντηση:
Παράδειγμα 24
Λύση:
Ο ελεύθερος όρος της εξίσωσης είναι αρνητικός και επομένως το γινόμενο των ριζών είναι ένας αρνητικός αριθμός. Αυτό είναι δυνατό μόνο εάν η μία από τις ρίζες είναι αρνητική και η άλλη θετική. Επομένως το άθροισμα των ριζών είναι ίσο με διαφορές των ενοτήτων τους.
Ας επιλέξουμε ζεύγη αριθμών που δίνουν στο γινόμενο και των οποίων η διαφορά είναι ίση με:
και: η διαφορά τους είναι ίση - δεν ταιριάζει.
και: - ακατάλληλο.
και: - ακατάλληλο.
και: - κατάλληλο. Το μόνο που μένει είναι να θυμόμαστε ότι μια από τις ρίζες είναι αρνητική. Εφόσον το άθροισμά τους πρέπει να είναι ίσο, η ρίζα με το μικρότερο συντελεστή πρέπει να είναι αρνητική: . Ελέγχουμε:
Απάντηση:
Παράδειγμα 25
Λύστε την εξίσωση.
Λύση:
Δίνεται η εξίσωση που σημαίνει:
Ο ελεύθερος όρος είναι αρνητικός και επομένως το γινόμενο των ριζών είναι αρνητικό. Και αυτό είναι δυνατό μόνο όταν η μία ρίζα της εξίσωσης είναι αρνητική και η άλλη θετική.
Ας επιλέξουμε ζεύγη αριθμών των οποίων το γινόμενο είναι ίσο και, στη συνέχεια, προσδιορίζουμε ποιες ρίζες πρέπει να έχουν αρνητικό πρόσημο:
Προφανώς, μόνο οι ρίζες και είναι κατάλληλες για την πρώτη συνθήκη:
Απάντηση:
Παράδειγμα 26
Λύστε την εξίσωση.
Λύση:
Δίνεται η εξίσωση που σημαίνει:
Το άθροισμα των ριζών είναι αρνητικό, που σημαίνει ότι τουλάχιστον μία από τις ρίζες είναι αρνητική. Αλλά επειδή το προϊόν τους είναι θετικό, σημαίνει ότι και οι δύο ρίζες έχουν πρόσημο μείον.
Ας επιλέξουμε ζεύγη αριθμών των οποίων το γινόμενο είναι ίσο με:
Προφανώς, οι ρίζες είναι οι αριθμοί και.
Απάντηση:
Συμφωνώ, είναι πολύ βολικό να βρίσκεις ρίζες προφορικά, αντί να μετράς αυτό το δυσάρεστο διαχωριστικό.
Προσπαθήστε να χρησιμοποιείτε το θεώρημα του Vieta όσο πιο συχνά γίνεται!
Αλλά το θεώρημα του Vieta είναι απαραίτητο για να διευκολυνθεί και να επιταχυνθεί η εύρεση των ριζών.
Για να επωφεληθείτε από τη χρήση του, πρέπει να φέρετε τις ενέργειες σε αυτοματοποίηση. Και για αυτό, λύστε άλλα πέντε παραδείγματα.
Αλλά μην εξαπατήσετε: δεν μπορείτε να χρησιμοποιήσετε διακριτικό! Μόνο το θεώρημα του Βιέτα!
5 παραδείγματα του θεωρήματος του Vieta για ανεξάρτητη εργασία
Παράδειγμα 27
Εργασία 1. ((x)^(2))-8x+12=0
Σύμφωνα με το θεώρημα του Vieta:
Ως συνήθως, ξεκινάμε την επιλογή με το κομμάτι:
Ακατάλληλο γιατί το ποσό?
: το ποσό είναι ακριβώς αυτό που χρειάζεστε.
Απάντηση: ; .
Παράδειγμα 28
Εργασία 2.
Και πάλι το αγαπημένο μας θεώρημα Vieta: το άθροισμα πρέπει να είναι ίσο και το γινόμενο πρέπει να είναι ίσο.
Επειδή όμως δεν πρέπει να είναι, αλλά, αλλάζουμε τα σημάδια των ριζών: και (συνολικά).
Απάντηση: ; .
Παράδειγμα 29
Εργασία 3.
Χμ... Πού είναι αυτό;
Πρέπει να μετακινήσετε όλους τους όρους σε ένα μέρος:
Το άθροισμα των ριζών είναι ίσο με το γινόμενο.
Εντάξει, σταμάτα! Η εξίσωση δεν δίνεται.
Αλλά το θεώρημα του Vieta είναι εφαρμόσιμο μόνο στις δεδομένες εξισώσεις.
Άρα πρώτα πρέπει να δώσετε μια εξίσωση.
Εάν δεν μπορείτε να ηγηθείτε, εγκαταλείψτε αυτήν την ιδέα και λύστε τη με άλλο τρόπο (για παράδειγμα, μέσω ενός διακριτικού).
Επιτρέψτε μου να σας υπενθυμίσω ότι για να δώσετε μια τετραγωνική εξίσωση σημαίνει να κάνετε τον συντελεστή που οδηγεί ίσος:
Τότε το άθροισμα των ριζών ισούται με και το γινόμενο.
Εδώ είναι τόσο εύκολο όσο το ξεφλούδισμα των αχλαδιών: τελικά, είναι πρώτος αριθμός (συγγνώμη για την ταυτολογία).
Απάντηση: ; .
Παράδειγμα 30
Εργασία 4.
Το δωρεάν μέλος είναι αρνητικό.
Τι το ιδιαίτερο έχει αυτό;
Και το γεγονός είναι ότι οι ρίζες θα έχουν διαφορετικά σημάδια.
Και τώρα, κατά την επιλογή, δεν ελέγχουμε το άθροισμα των ριζών, αλλά τη διαφορά στις ενότητες τους: αυτή η διαφορά είναι ίση, αλλά προϊόν.
Έτσι, οι ρίζες είναι ίσες με και, αλλά μία από αυτές είναι μείον.
Το θεώρημα του Βιέτα μας λέει ότι το άθροισμα των ριζών είναι ίσο με τον δεύτερο συντελεστή με το αντίθετο πρόσημο, δηλαδή.
Αυτό σημαίνει ότι η μικρότερη ρίζα θα έχει ένα μείον: και, δεδομένου ότι.
Απάντηση: ; .
Παράδειγμα 31
Εργασία 5.
Τι πρέπει να κάνετε πρώτα;
Σωστά, δώστε την εξίσωση:
Και πάλι: επιλέγουμε τους συντελεστές του αριθμού και η διαφορά τους πρέπει να είναι ίση με:
Οι ρίζες είναι ίσες με και, αλλά μία από αυτές είναι μείον. Οι οποίες? Το άθροισμά τους πρέπει να είναι ίσο, πράγμα που σημαίνει ότι το μείον θα έχει μεγαλύτερη ρίζα.
Απάντηση: ; .
Συνοψίζω
- Το θεώρημα του Vieta χρησιμοποιείται μόνο στις δευτεροβάθμιες εξισώσεις που δίνονται.
- Χρησιμοποιώντας το θεώρημα του Vieta, μπορείτε να βρείτε τις ρίζες με επιλογή, προφορικά.
- Εάν δεν δοθεί η εξίσωση ή δεν βρεθεί κατάλληλο ζεύγος παραγόντων του ελεύθερου όρου, τότε δεν υπάρχουν ολόκληρες ρίζες και πρέπει να το λύσετε με άλλο τρόπο (για παράδειγμα, μέσω ενός διαχωριστή).
3. Μέθοδος επιλογής πλήρους τετραγώνου
Εάν όλοι οι όροι που περιέχουν το άγνωστο αντιπροσωπεύονται με τη μορφή όρων από συντομευμένους τύπους πολλαπλασιασμού - το τετράγωνο του αθροίσματος ή της διαφοράς - τότε μετά την αντικατάσταση των μεταβλητών, η εξίσωση μπορεί να παρουσιαστεί με τη μορφή μιας ημιτελούς τετραγωνικής εξίσωσης του τύπου.
Για παράδειγμα:
Παράδειγμα 32
Λύστε την εξίσωση: .
Λύση:
Απάντηση:
Παράδειγμα 33
Λύστε την εξίσωση: .
Λύση:
Απάντηση:
Σε γενικές γραμμές, ο μετασχηματισμός θα μοιάζει με αυτό:
Αυτό υπονοεί: .
Δεν σου θυμίζει τίποτα;
Αυτό είναι κάτι που εισάγει διακρίσεις! Έτσι ακριβώς πήραμε τον τύπο διάκρισης.
ΤΕΤΑΡΧΟΜΕΝΕΣ ΕΞΙΣΩΣΕΙΣ. ΣΥΝΤΟΜΗ ΣΧΕΤΙΚΑ ΜΕ ΤΑ ΚΥΡΙΑ ΠΡΑΓΜΑΤΑ
Τετραγωνική εξίσωση- αυτή είναι μια εξίσωση της μορφής, όπου - ο άγνωστος, - οι συντελεστές της τετραγωνικής εξίσωσης, - ο ελεύθερος όρος.
Πλήρης τετραγωνική εξίσωση- μια εξίσωση στην οποία οι συντελεστές δεν είναι ίσοι με μηδέν.
Μειωμένη τετραγωνική εξίσωση- μια εξίσωση στην οποία ο συντελεστής, δηλαδή: .
Ημιτελής τετραγωνική εξίσωση- μια εξίσωση στην οποία ο συντελεστής και ή ο ελεύθερος όρος c είναι ίσοι με μηδέν:
- αν ο συντελεστής, η εξίσωση μοιάζει με:
- αν υπάρχει ελεύθερος όρος, η εξίσωση έχει τη μορφή:
- αν και, η εξίσωση μοιάζει με: .
1. Αλγόριθμος επίλυσης ημιτελών τετραγωνικών εξισώσεων
1.1. Μια ημιτελής τετραγωνική εξίσωση της μορφής, όπου, :
1) Ας εκφράσουμε το άγνωστο:
2) Ελέγξτε το πρόσημο της έκφρασης:
- αν, τότε η εξίσωση δεν έχει λύσεις,
- αν, τότε η εξίσωση έχει δύο ρίζες.
1.2. Μια ημιτελής τετραγωνική εξίσωση της μορφής, όπου, :
1) Ας βγάλουμε τον κοινό παράγοντα εκτός παρενθέσεων: ,
2) Το γινόμενο είναι ίσο με μηδέν εάν τουλάχιστον ένας από τους παράγοντες είναι ίσος με μηδέν. Επομένως, η εξίσωση έχει δύο ρίζες:
1.3. Μια ημιτελής τετραγωνική εξίσωση της μορφής, όπου:
Αυτή η εξίσωση έχει πάντα μία μόνο ρίζα: .
2. Αλγόριθμος επίλυσης πλήρων τετραγωνικών εξισώσεων της μορφής όπου
2.1. Λύση με χρήση διακριτικού
1) Ας φέρουμε την εξίσωση σε τυπική μορφή: ,
2) Ας υπολογίσουμε τη διάκριση χρησιμοποιώντας τον τύπο: , που δείχνει τον αριθμό των ριζών της εξίσωσης:
3) Βρείτε τις ρίζες της εξίσωσης:
- αν, τότε η εξίσωση έχει ρίζες, οι οποίες βρίσκονται από τον τύπο:
- αν, τότε η εξίσωση έχει μια ρίζα, η οποία βρίσκεται από τον τύπο:
- αν, τότε η εξίσωση δεν έχει ρίζες.
2.2. Λύση χρησιμοποιώντας το θεώρημα του Vieta
Το άθροισμα των ριζών της ανηγμένης δευτεροβάθμιας εξίσωσης (εξίσωση της μορφής όπου) είναι ίσο, και το γινόμενο των ριζών είναι ίσο, δηλ. , ΕΝΑ.
2.3. Λύση με τη μέθοδο επιλογής πλήρους τετραγώνου
Τετραγωνική εξίσωσηή μια εξίσωση δεύτερου βαθμού με έναν άγνωστο είναι μια εξίσωση που, μετά από μετασχηματισμούς, μπορεί να αναχθεί στην ακόλουθη μορφή:
τσεκούρι 2 + bx + ντο = 0 - τετραγωνική εξίσωση
Οπου Χ- αυτό είναι το άγνωστο, αλλά ένα, σιΚαι ντο- συντελεστές της εξίσωσης. Σε τετραγωνικές εξισώσεις έναονομάζεται ο πρώτος συντελεστής ( ένα ≠ 0), σιονομάζεται δεύτερος συντελεστής, και ντοονομάζεται γνωστό ή ελεύθερο μέλος.
Η εξίσωση:
τσεκούρι 2 + bx + ντο = 0
που ονομάζεται πλήρηςτετραγωνική εξίσωση. Αν ένας από τους συντελεστές σιή ντοισούται με μηδέν, ή και οι δύο αυτοί συντελεστές είναι ίσοι με μηδέν, τότε η εξίσωση παρουσιάζεται με τη μορφή ατελούς τετραγωνικής εξίσωσης.
Μειωμένη τετραγωνική εξίσωση
Η πλήρης τετραγωνική εξίσωση μπορεί να αναχθεί σε μια πιο βολική μορφή διαιρώντας όλους τους όρους της με ένα, δηλαδή για τον πρώτο συντελεστή:
Η εξίσωση Χ 2 + px + q= 0 ονομάζεται ανηγμένη τετραγωνική εξίσωση. Επομένως, οποιαδήποτε τετραγωνική εξίσωση στην οποία ο πρώτος συντελεστής είναι ίσος με 1 μπορεί να ονομαστεί μειωμένη.
Για παράδειγμα, η εξίσωση:
Χ 2 + 10Χ - 5 = 0
μειώνεται και η εξίσωση:
3Χ 2 + 9Χ - 12 = 0
μπορεί να αντικατασταθεί από την παραπάνω εξίσωση, διαιρώντας όλους τους όρους της με -3:
Χ 2 - 3Χ + 4 = 0
Επίλυση Τετραγωνικών Εξισώσεων
Για να λύσετε μια δευτεροβάθμια εξίσωση, πρέπει να τη μειώσετε σε μία από τις ακόλουθες μορφές:
τσεκούρι 2 + bx + ντο = 0
τσεκούρι 2 + 2kx + ντο = 0
Χ 2 + px + q = 0
Για κάθε τύπο εξίσωσης υπάρχει ο δικός του τύπος για την εύρεση ριζών:
Προσέξτε την εξίσωση:
τσεκούρι 2 + 2kx + ντο = 0
αυτή είναι η μετασχηματισμένη εξίσωση τσεκούρι 2 + bx + ντο= 0, στην οποία ο συντελεστής σι- ακόμη, που σας επιτρέπει να το αντικαταστήσετε με τον τύπο 2 κ. Επομένως, ο τύπος για την εύρεση των ριζών για αυτήν την εξίσωση μπορεί να απλοποιηθεί αντικαθιστώντας το 2 σε αυτήν καντί σι:

Παράδειγμα 1.Λύστε την εξίσωση:
3Χ 2 + 7Χ + 2 = 0
Δεδομένου ότι ο δεύτερος συντελεστής στην εξίσωση δεν είναι ζυγός αριθμός και ο πρώτος συντελεστής δεν είναι ίσος με ένα, θα αναζητήσουμε ρίζες χρησιμοποιώντας τον πρώτο τύπο, που ονομάζεται γενικός τύπος για την εύρεση των ριζών μιας τετραγωνικής εξίσωσης. Αρχικά
ένα = 3, σι = 7, ντο = 2
Τώρα, για να βρούμε τις ρίζες της εξίσωσης, απλώς αντικαθιστούμε τις τιμές των συντελεστών στον τύπο:

| Χ 1 = | -2 | = - | 1 | , Χ 2 = | -12 | = -2 |
| 6 | 3 | 6 |
| Απάντηση: - | 1 | , -2. |
| 3 |
Παράδειγμα 2:
Χ 2 - 4Χ - 60 = 0
Ας προσδιορίσουμε ποιοι είναι οι συντελεστές:
ένα = 1, σι = -4, ντο = -60
Αφού στην εξίσωση ο δεύτερος συντελεστής είναι Ζυγός αριθμός, τότε θα χρησιμοποιήσουμε τον τύπο για τετραγωνικές εξισώσεις με άρτιο δεύτερο συντελεστή:
Χ 1 = 2 + 8 = 10, Χ 2 = 2 - 8 = -6
Απάντηση: 10, -6.
Παράδειγμα 3.
y 2 + 11y = y - 25
Ας μειώσουμε την εξίσωση σε γενική εμφάνιση:
y 2 + 11y = y - 25
y 2 + 11y - y + 25 = 0
y 2 + 10y + 25 = 0
Ας προσδιορίσουμε ποιοι είναι οι συντελεστές:
ένα = 1, Π = 10, q = 25
Δεδομένου ότι ο πρώτος συντελεστής είναι ίσος με 1, θα αναζητήσουμε ρίζες χρησιμοποιώντας τον τύπο για τις παραπάνω εξισώσεις με έναν άρτιο δεύτερο συντελεστή:
Απάντηση: -5.
Παράδειγμα 4.
Χ 2 - 7Χ + 6 = 0
Ας προσδιορίσουμε ποιοι είναι οι συντελεστές:
ένα = 1, Π = -7, q = 6
Δεδομένου ότι ο πρώτος συντελεστής είναι ίσος με 1, θα αναζητήσουμε ρίζες χρησιμοποιώντας τον τύπο για τις παραπάνω εξισώσεις με περιττό δεύτερο συντελεστή:
Χ 1 = (7 + 5) : 2 = 6, Χ 2 = (7 - 5) : 2 = 1