Τι σημαίνει διαίρεση με υπόλοιπο; Γενική κατανόηση της διαίρεσης φυσικών αριθμών με υπόλοιπο. Γραπτή διαίρεση με δύο ψηφία

Πριν περιγράψουμε λεπτομερώς όλα τα βήματα του αλγορίθμου για τη διαίρεση φυσικών αριθμών με ένα υπόλοιπο, θα απαντήσουμε σε τρεις ερωτήσεις: τι γνωρίζουμε αρχικά, τι πρέπει να βρούμε και με βάση ποιες σκέψεις θα το κάνουμε αυτό; Αρχικά, γνωρίζουμε το μέρισμα α και το διαιρέτη β. Πρέπει να βρούμε το μερικό πηλίκο c και το υπόλοιπο d. Η ισότητα a=b·c+d ορίζει τη σχέση μεταξύ μερίσματος, διαιρέτη, μερικού πηλίκου και υπολοίπου. Από τη γραπτή ισότητα προκύπτει ότι αν παρουσιαστεί το μέρισμα a ως άθροισμα b·c+d, στο οποίο το d είναι μικρότερο από το b (αφού το υπόλοιπο είναι πάντα μικρότερο από το διαιρέτη), τότε θα δούμε και το ημιτελές πηλίκο c. και το υπόλοιπο δ.

Το μόνο που μένει είναι να καταλάβουμε πώς να αντιπροσωπεύσουμε το μέρισμα a ως άθροισμα b·c+d. Ο αλγόριθμος για να γίνει αυτό είναι πολύ παρόμοιος με τον αλγόριθμο για τη διαίρεση φυσικών αριθμών χωρίς υπόλοιπο. Θα περιγράψουμε όλα τα βήματα, και ταυτόχρονα θα λύσουμε το παράδειγμα για μεγαλύτερη σαφήνεια. Διαιρέστε το 899 με το 47.

Τα πρώτα πέντε σημεία του αλγορίθμου θα σας επιτρέψουν να αναπαραστήσετε το μέρισμα ως το άθροισμα πολλών όρων. Πρέπει να σημειωθεί ότι οι ενέργειες από αυτά τα σημεία επαναλαμβάνονται κυκλικά ξανά και ξανά μέχρι να βρεθούν όλοι οι όροι που αθροίζονται στο μέρισμα. Στο τελευταίο έκτο σημείο, το άθροισμα που προκύπτει μετατρέπεται στη μορφή b·c+d (αν το άθροισμα που προκύπτει δεν έχει πλέον αυτή τη μορφή), από όπου το απαιτούμενο ημιτελές πηλίκο και το υπόλοιπο γίνονται ορατά.

Λοιπόν, ας αρχίσουμε να αντιπροσωπεύουμε το μέρισμα 899 ως το άθροισμα πολλών όρων.

Αρχικά, υπολογίζουμε πόσο περισσότερο είναι ο αριθμός των ψηφίων στο μέρισμα από τον αριθμό των ψηφίων του διαιρέτη και θυμόμαστε αυτόν τον αριθμό.

Στο παράδειγμά μας, ο συμβολισμός μερίσματος έχει 3 ψηφία (899 – τριψήφιο αριθμό), και στη σημειογραφία του διαιρέτη υπάρχουν δύο σημάδια (το 47 είναι διψήφιος αριθμός), επομένως, στη σημειογραφία του μερίσματος υπάρχει ένα ακόμη σύμβολο και θυμόμαστε τον αριθμό 1.

Τώρα στην καταχώρηση διαιρέτη στα δεξιά προσθέτουμε τους αριθμούς 0 στο ποσό που προσδιορίζεται από τον αριθμό που λήφθηκε στην προηγούμενη παράγραφο. Επιπλέον, εάν ο γραμμένος αριθμός είναι μεγαλύτερος από το μέρισμα, τότε πρέπει να αφαιρέσετε το 1 από τον αριθμό που θυμάστε στην προηγούμενη παράγραφο.

Ας επιστρέψουμε στο παράδειγμά μας. Στον συμβολισμό του διαιρέτη 47, προσθέτουμε ένα ψηφίο 0 στα δεξιά και παίρνουμε τον αριθμό 470. Από το 470<899 , то запомненное в предыдущем пункте число НЕ нужно уменьшать на 1 . Таким образом, у нас в памяти остается число 1 .

Μετά από αυτό, στον αριθμό 1 στα δεξιά εκχωρούμε τους αριθμούς 0 σε ποσότητα που καθορίζεται από τον αριθμό που απομνημονεύτηκε στην προηγούμενη παράγραφο. Σε αυτή την περίπτωση, παίρνουμε μια μονάδα ψηφίου, με την οποία θα εργαστούμε περαιτέρω.

Στο παράδειγμά μας, εκχωρούμε 1 ψηφίο 0 στον αριθμό 1 και παίρνουμε τον αριθμό 10, δηλαδή θα δουλέψουμε με το μέρος των δεκάδων.

Τώρα πολλαπλασιάζουμε διαδοχικά τον διαιρέτη με 1, 2, 3, ... μονάδες του ψηφίου εργασίας μέχρι να πάρουμε έναν αριθμό μεγαλύτερο ή ίσο με το μέρισμα.

Ανακαλύψαμε ότι στο παράδειγμά μας το ψηφίο εργασίας είναι το ψηφίο των δεκάδων. Επομένως, πολλαπλασιάζουμε πρώτα τον διαιρέτη με μια μονάδα στη θέση των δεκάδων, δηλαδή πολλαπλασιάζουμε το 47 επί 10, παίρνουμε 47 10 = 470. Ο αριθμός 470 που προκύπτει είναι μικρότερος από το μέρισμα 899, οπότε προχωράμε στον πολλαπλασιασμό του διαιρέτη με δύο μονάδες στη θέση των δεκάδων, δηλαδή πολλαπλασιάζουμε το 47 επί 20. Έχουμε 47·20=940. Πήραμε έναν αριθμό που είναι μεγαλύτερος από 899.

Ο αριθμός που προκύπτει στο προτελευταίο βήμα κατά τον διαδοχικό πολλαπλασιασμό είναι ο πρώτος από τους απαιτούμενους όρους.

Στο παράδειγμα που αναλύεται, ο απαιτούμενος όρος είναι ο αριθμός 470 (ο αριθμός αυτός είναι ίσος με το γινόμενο 47·100, θα χρησιμοποιήσουμε αυτήν την ισότητα αργότερα).

Μετά από αυτό, βρίσκουμε τη διαφορά μεταξύ του μερίσματος και του πρώτου όρου που βρέθηκε. Εάν ο αριθμός που προκύπτει είναι μεγαλύτερος από τον διαιρέτη, τότε προχωράμε στην εύρεση του δεύτερου όρου. Για να γίνει αυτό, επαναλαμβάνουμε όλα τα περιγραφόμενα βήματα του αλγορίθμου, αλλά τώρα παίρνουμε τον αριθμό που λαμβάνεται εδώ ως μέρισμα. Εάν σε αυτό το σημείο λάβουμε ξανά αριθμό μεγαλύτερο από τον διαιρέτη, τότε προχωράμε στην εύρεση του τρίτου όρου, επαναλαμβάνοντας για άλλη μια φορά τα βήματα του αλγορίθμου, παίρνοντας ως μέρισμα τον αριθμό που προκύπτει. Και έτσι προχωράμε παρακάτω, βρίσκοντας τον τέταρτο, τον πέμπτο και τους επόμενους όρους έως ότου ο αριθμός που προκύπτει σε αυτό το σημείο είναι μικρότερος από τον διαιρέτη. Μόλις συμβεί αυτό, παίρνουμε τον αριθμό που λάβαμε εδώ ως τον τελευταίο όρο που αναζητούμε (κοιτάζοντας μπροστά, ας πούμε ότι είναι ίσος με το υπόλοιπο) και προχωράμε στο τελικό στάδιο.

Ας επιστρέψουμε στο παράδειγμά μας. Σε αυτό το βήμα έχουμε 899−470=429. Από 429>47, παίρνουμε αυτόν τον αριθμό ως μέρισμα και επαναλαμβάνουμε όλα τα στάδια του αλγορίθμου μαζί του.

Ο αριθμός 429 έχει ένα περισσότερο ψηφίο από τον αριθμό 47, οπότε θυμηθείτε τον αριθμό 1.

Τώρα στον συμβολισμό του μερίσματος στα δεξιά προσθέτουμε ένα ψηφίο 0, παίρνουμε τον αριθμό 470, ο οποίος περισσότερος αριθμός 429. Επομένως, από τον αριθμό 1 που θυμόμαστε στην προηγούμενη παράγραφο, αφαιρούμε το 1, παίρνουμε τον αριθμό 0, τον οποίο θυμόμαστε.

Δεδομένου ότι στην προηγούμενη παράγραφο θυμηθήκαμε τον αριθμό 0, τότε στον αριθμό 1 δεν χρειάζεται να αντιστοιχίσουμε ένα μονοψήφιο 0 στα δεξιά. Σε αυτήν την περίπτωση, έχουμε τον αριθμό 1, δηλαδή το ψηφίο εργασίας είναι το ψηφίο των μονάδων.

Τώρα πολλαπλασιάζουμε διαδοχικά τον διαιρέτη 47 με 1, 2, 3, ... Δεν θα σταθούμε λεπτομερώς σε αυτό. Ας πούμε ότι 47·9=423<429 , а 47·10=470>429. Ο δεύτερος όρος που αναζητούμε είναι ο αριθμός 423 (που ισούται με 47 9, τον οποίο θα χρησιμοποιήσουμε περαιτέρω).

Η διαφορά μεταξύ 429 και 423 είναι 6. Αυτός ο αριθμός είναι μικρότερος από τον διαιρέτη 47, επομένως είναι ο τρίτος (και τελευταίος) όρος που αναζητούμε. Τώρα μπορούμε να περάσουμε στο τελικό στάδιο.

Λοιπόν, φτάσαμε στο τελικό στάδιο. Όλες οι προηγούμενες ενέργειες είχαν ως στόχο την παρουσίαση του μερίσματος ως άθροισμα πολλών όρων. Τώρα το άθροισμα που προκύπτει μένει να μετατραπεί στη μορφή b·c+d. Η κατανεμητική ιδιότητα του πολλαπλασιασμού σε σχέση με την πρόσθεση θα μας βοηθήσει να αντιμετωπίσουμε αυτό το έργο. Μετά από αυτό, το απαιτούμενο ημιτελές πηλίκο και το υπόλοιπο θα γίνουν ορατά.

Στο παράδειγμά μας, το μέρισμα 899 είναι ίσο με το άθροισμα τριών όρων 470, 423 και 6. Το άθροισμα 470+423+6 μπορεί να ξαναγραφτεί ως 47·10+47·9+6 (θυμηθείτε, δώσαμε προσοχή στις ισότητες 470=47·10 και 423=47·9). Τώρα εφαρμόζουμε την ιδιότητα του πολλαπλασιασμού ενός φυσικού αριθμού με ένα άθροισμα και παίρνουμε 47·10+47·9+6= 47·(10+9)+6= 47·19+6. Έτσι, το μέρισμα μετατρέπεται στη μορφή που χρειαζόμαστε 899=47·19+6, από την οποία μπορούν εύκολα να βρεθούν το ημιτελές πηλίκο 19 και το υπόλοιπο 6.

Άρα, 899:47=19 (υπόλοιπο 6).

Φυσικά, όταν λύνετε παραδείγματα, δεν θα περιγράψετε με τόση λεπτομέρεια τη διαδικασία της διαίρεσης με υπόλοιπο.

Το άρθρο εξετάζει την έννοια της διαίρεσης ακεραίων με ένα υπόλοιπο. Ας αποδείξουμε το θεώρημα για τη διαιρετότητα των ακεραίων με υπόλοιπο και ας δούμε τις συνδέσεις μεταξύ μερισμάτων και διαιρετών, ημιτελών πηλίκων και υπολοίπων. Ας δούμε τους κανόνες κατά τη διαίρεση ακεραίων με υπολείμματα, εξετάζοντάς τους λεπτομερώς χρησιμοποιώντας παραδείγματα. Στο τέλος της λύσης θα κάνουμε έλεγχο.

Γενική κατανόηση της διαίρεσης ακεραίων με υπολείμματα

Η διαίρεση ακεραίων με υπόλοιπο θεωρείται ως γενικευμένη διαίρεση με υπόλοιπο φυσικών αριθμών. Αυτό ισχύει γιατί οι φυσικοί αριθμοί είναι συστατικόολόκληρος.

Η διαίρεση με υπόλοιπο αυθαίρετου αριθμού λέει ότι ο ακέραιος αριθμός a διαιρείται με έναν αριθμό b διαφορετικό από το μηδέν. Εάν b = 0, τότε μην διαιρέσετε με υπόλοιπο.

Ακριβώς όπως η διαίρεση των φυσικών αριθμών με ένα υπόλοιπο, οι ακέραιοι a και b διαιρούνται, με το b όχι μηδέν, με τα c και d. Στην περίπτωση αυτή, τα a και b ονομάζονται μέρισμα και διαιρέτης, και d είναι το υπόλοιπο της διαίρεσης, c είναι ακέραιος ή ατελής πηλίκο.

Αν υποθέσουμε ότι το υπόλοιπο είναι ένας μη αρνητικός ακέραιος, τότε η τιμή του δεν είναι μεγαλύτερη από το μέτρο του αριθμού b. Ας το γράψουμε ως εξής: 0 ≤ d ≤ b. Αυτή η αλυσίδα ανισώσεων χρησιμοποιείται κατά τη σύγκριση 3 ή περισσότερων αριθμών.

Εάν το c είναι ένα ημιτελές πηλίκο, τότε το d είναι το υπόλοιπο της διαίρεσης του ακέραιου αριθμού a με το b, το οποίο μπορεί να δηλωθεί εν συντομία: a: b = c (υπόλοιπο d).

Το υπόλοιπο κατά τη διαίρεση των αριθμών a με το b μπορεί να είναι μηδέν, τότε λένε ότι το a διαιρείται με το b πλήρως, δηλαδή χωρίς υπόλοιπο. Η διαίρεση χωρίς υπόλοιπο θεωρείται ειδική περίπτωση διαίρεσης.

Αν διαιρέσουμε το μηδέν με κάποιο αριθμό, το αποτέλεσμα είναι μηδέν. Το υπόλοιπο της διαίρεσης θα είναι επίσης μηδέν. Αυτό μπορεί να εντοπιστεί από τη θεωρία της διαίρεσης του μηδενός με έναν ακέραιο.

Τώρα ας δούμε την έννοια της διαίρεσης ακεραίων με ένα υπόλοιπο.

Είναι γνωστό ότι οι θετικοί ακέραιοι είναι φυσικοί αριθμοί, τότε όταν διαιρούμε με ένα υπόλοιπο, θα έχουμε το ίδιο νόημα όπως όταν διαιρούμε φυσικούς αριθμούς με ένα υπόλοιπο.

Η διαίρεση ενός αρνητικού ακέραιου α με έναν θετικό ακέραιο β έχει νόημα. Ας δούμε ένα παράδειγμα. Φανταστείτε μια κατάσταση όπου έχουμε ένα χρέος αντικειμένων στο ποσό του α που πρέπει να εξοφληθεί από β άτομο. Για να επιτευχθεί αυτό, πρέπει όλοι να συνεισφέρουν ισότιμα. Για να προσδιορίσετε το ύψος του χρέους για το καθένα, πρέπει να δώσετε προσοχή στην αξία των ιδιωτικών s. Το υπόλοιπο d δείχνει ότι ο αριθμός των αντικειμένων μετά την εξόφληση των χρεών είναι γνωστός.

Ας δούμε το παράδειγμα των μήλων. Αν 2 άτομα χρωστάνε 7 μήλα. Αν υπολογίσουμε ότι ο καθένας πρέπει να επιστρέψει 4 μήλα, μετά τον πλήρη υπολογισμό θα του απομείνει 1 μήλο. Ας το γράψουμε ως ισότητα: (− 7) : 2 = − 4 (από τ. 1) .

Η διαίρεση οποιουδήποτε αριθμού α με έναν ακέραιο δεν έχει νόημα, αλλά είναι δυνατή ως επιλογή.

Θεώρημα για τη διαιρετότητα των ακεραίων με υπόλοιπο

Έχουμε εντοπίσει ότι το a είναι το μέρισμα, μετά το b είναι ο διαιρέτης, το c είναι το μερικό πηλίκο και το d είναι το υπόλοιπο. Συνδέονται μεταξύ τους. Θα δείξουμε αυτή τη σύνδεση χρησιμοποιώντας την ισότητα a = b · c + d. Η μεταξύ τους σύνδεση χαρακτηρίζεται από το θεώρημα της διαιρετότητας με το υπόλοιπο.

Θεώρημα

Οποιοσδήποτε ακέραιος μπορεί να αναπαρασταθεί μόνο μέσω ενός ακέραιου και μη μηδενικού αριθμού b με αυτόν τον τρόπο: a = b · q + r, όπου q και r είναι κάποιοι ακέραιοι αριθμοί. Εδώ έχουμε 0 ≤ r ≤ b.

Ας αποδείξουμε τη δυνατότητα ύπαρξης του a = b · q + r.

Απόδειξη

Εάν υπάρχουν δύο αριθμοί a και b, και ο a διαιρείται με το b χωρίς υπόλοιπο, τότε από τον ορισμό προκύπτει ότι υπάρχει ένας αριθμός q και η ισότητα a = b · q θα είναι αληθής. Τότε η ισότητα μπορεί να θεωρηθεί αληθής: a = b · q + r για r = 0.

Τότε είναι απαραίτητο να πάρουμε το q τέτοιο που δίνεται από την ανίσωση b · q< a < b · (q + 1) было верным. Необходимо вычесть b · q из всех частей выражения. Тогда придем к неравенству такого вида: 0 < a − b · q < b .

Έχουμε ότι η τιμή της παράστασης a − b · q είναι μεγαλύτερη από το μηδέν και όχι μεγαλύτερη από την τιμή του αριθμού b, προκύπτει ότι r = a − b · q. Διαπιστώνουμε ότι ο αριθμός a μπορεί να αναπαρασταθεί με τη μορφή a = b · q + r.

Τώρα πρέπει να εξετάσουμε τη δυνατότητα να αναπαραστήσουμε το a = b q + r για αρνητικές τιμέςσι.

Ο συντελεστής του αριθμού αποδεικνύεται θετικός, τότε παίρνουμε a = b · q 1 + r, όπου η τιμή q 1 είναι κάποιος ακέραιος αριθμός, r είναι ένας ακέραιος που πληροί την συνθήκη 0 ≤ r< b . Принимаем q = − q 1 , получим, что a = b · q + r для отрицательных b .

Απόδειξη μοναδικότητας

Ας υποθέσουμε ότι a = b q + r, q και r είναι ακέραιοι με τη συνθήκη 0 ≤ r αληθής< b , имеется еще одна форма записи в виде a = b · q 1 + r 1 , где q 1Και r 1είναι κάποιοι αριθμοί όπου q 1 ≠ q, 0 ≤ r 1< b .

Όταν αφαιρεθεί η ανισότητα από την αριστερή και τη δεξιά πλευρά, τότε παίρνουμε 0 = b · (q − q 1) + r − r 1, που ισοδυναμεί με r - r 1 = b · q 1 - q. Εφόσον χρησιμοποιείται η ενότητα, λαμβάνουμε την ισότητα r - r 1 = b · q 1 - q.

Η δεδομένη συνθήκη λέει ότι 0 ≤ r< b и 0 ≤ r 1 < b запишется в виде r - r 1 < b . Имеем, что qΚαι q 1- ολόκληρο, και q ≠ q 1, τότε q 1 - q ≥ 1. Από εδώ έχουμε ότι b · q 1 - q ≥ b. Οι προκύπτουσες ανισότητες r - r 1< b и b · q 1 - q ≥ b указывают на то, что такое равенство в виде r - r 1 = b · q 1 - q невозможно в данном случае.

Συνεπάγεται ότι ο αριθμός a δεν μπορεί να αναπαρασταθεί με κανέναν άλλο τρόπο παρά μόνο με την εγγραφή a = b · q + r.

Σχέση μερίσματος, διαιρέτη, μερικού πηλίκου και υπολοίπου

Χρησιμοποιώντας την ισότητα a = b · c + d, μπορείτε να βρείτε το άγνωστο μέρισμα a όταν είναι γνωστός ο διαιρέτης b με το ατελές πηλίκο c και το υπόλοιπο d.

Παράδειγμα 1

Προσδιορίστε το μέρισμα εάν, μετά τη διαίρεση, πάρουμε - 21, το μερικό πηλίκο είναι 5 και το υπόλοιπο είναι 12.

Λύση

Είναι απαραίτητο να υπολογιστεί το μέρισμα a με γνωστό διαιρέτη b = − 21, ατελές πηλίκο c = 5 και υπόλοιπο d = 12. Πρέπει να στραφούμε στην ισότητα a = b · c + d, από εδώ παίρνουμε a = (− 21) · 5 + 12. Αν ακολουθήσουμε τη σειρά των ενεργειών, πολλαπλασιάζουμε - 21 με 5, μετά από το οποίο παίρνουμε (− 21) · 5 + 12 = − 105 + 12 = − 93.

Απάντηση: - 93 .

Η σύνδεση μεταξύ του διαιρέτη και του μερικού πηλίκου και του υπολοίπου μπορεί να εκφραστεί χρησιμοποιώντας τις ισότητες: b = (a − d) : c , c = (a − d) : b και d = a − b · c . Με τη βοήθειά τους μπορούμε να υπολογίσουμε τον διαιρέτη, το μερικό πηλίκο και το υπόλοιπο. Αυτό καταλήγει στο να βρίσκουμε συνεχώς το υπόλοιπο όταν διαιρούμε έναν ακέραιο αριθμό α με το b με γνωστό μέρισμα, διαιρέτη και μερικό πηλίκο. Εφαρμόζεται ο τύπος d = a − b · c. Ας εξετάσουμε τη λύση λεπτομερώς.

Παράδειγμα 2

Βρείτε το υπόλοιπο όταν διαιρέσετε τον ακέραιο αριθμό - 19 με τον ακέραιο 3 με ένα γνωστό ημιτελές πηλίκο ίσο με - 7.

Λύση

Για να υπολογίσουμε το υπόλοιπο της διαίρεσης, εφαρμόζουμε έναν τύπο της μορφής d = a − b · c. Ανά συνθήκη, όλα τα δεδομένα είναι διαθέσιμα: a = − 19, b = 3, c = − 7. Από εδώ παίρνουμε d = a − b · c = − 19 − 3 · (− 7) = − 19 − (− 21) = − 19 + 21 = 2 (διαφορά − 19 − (− 21) . Αυτό το παράδειγμαυπολογίζεται χρησιμοποιώντας τον κανόνα της αφαίρεσης ενός αρνητικού ακέραιου αριθμού.

Απάντηση: 2 .

Όλοι οι θετικοί ακέραιοι είναι φυσικοί αριθμοί. Από αυτό προκύπτει ότι η διαίρεση εκτελείται σύμφωνα με όλους τους κανόνες διαίρεσης με υπόλοιπο φυσικών αριθμών. Η ταχύτητα διαίρεσης με τους υπόλοιπους φυσικούς αριθμούς είναι σημαντική, αφού σε αυτήν βασίζονται όχι μόνο η διαίρεση θετικών αριθμών, αλλά και οι κανόνες για τη διαίρεση αυθαίρετων ακεραίων.

Η πιο βολική μέθοδος διαίρεσης είναι μια στήλη, καθώς είναι ευκολότερο και πιο γρήγορο να ληφθεί ένα ημιτελές ή απλά ένα πηλίκο με ένα υπόλοιπο. Ας δούμε τη λύση με περισσότερες λεπτομέρειες.

Παράδειγμα 3

Διαιρέστε το 14671 με το 54.

Λύση

Αυτή η διαίρεση πρέπει να γίνει σε μια στήλη:

Δηλαδή, το μερικό πηλίκο είναι ίσο με 271 και το υπόλοιπο είναι 37.

Απάντηση: 14.671: 54 = 271. (υπόλοιπο 37)

Ο κανόνας για τη διαίρεση με υπόλοιπο θετικού ακέραιου με αρνητικό ακέραιο, παραδείγματα

Για να γίνει διαίρεση με ένα υπόλοιπο θετικού αριθμού με αρνητικό ακέραιο, είναι απαραίτητο να διατυπωθεί ένας κανόνας.

Ορισμός 1

Το ημιτελές πηλίκο της διαίρεσης του θετικού ακέραιου a με τον αρνητικό ακέραιο b δίνει έναν αριθμό που είναι αντίθετος με το ημιτελές πηλίκο της διαίρεσης των συντελεστών των αριθμών a με το b. Τότε το υπόλοιπο είναι ίσο με το υπόλοιπο όταν το α διαιρείται με το β.

Επομένως έχουμε ότι το ατελές πηλίκο της διαίρεσης ενός θετικού ακέραιου με έναν αρνητικό ακέραιο θεωρείται μη θετικός ακέραιος.

Παίρνουμε τον αλγόριθμο:

• διαιρούμε το μέτρο του μερίσματος με το μέτρο του διαιρέτη, τότε παίρνουμε ένα ημιτελές πηλίκο και
• υπόλοιπο;
• Ας γράψουμε τον αντίθετο αριθμό από αυτό που πήραμε.

Ας δούμε το παράδειγμα του αλγορίθμου για τη διαίρεση ενός θετικού ακέραιου με έναν αρνητικό ακέραιο.

Παράδειγμα 4

Διαιρέστε με το υπόλοιπο 17 με - 5.

Λύση

Ας εφαρμόσουμε τον αλγόριθμο για τη διαίρεση με υπόλοιπο ενός θετικού ακέραιου με έναν αρνητικό ακέραιο. Είναι απαραίτητο να διαιρέσετε 17 με - 5 modulo. Από εδώ παίρνουμε ότι το μερικό πηλίκο είναι ίσο με 3 και το υπόλοιπο είναι ίσο με 2.

Παίρνουμε ότι ο απαιτούμενος αριθμός από τη διαίρεση του 17 με - 5 = - 3 με υπόλοιπο ίσο με 2.

Απάντηση: 17: (− 5) = − 3 (απομένουν 2).

Παράδειγμα 5

Πρέπει να διαιρέσετε το 45 με το - 15.

Λύση

Είναι απαραίτητο να διαιρέσετε τους αριθμούς modulo. Διαιρέστε τον αριθμό 45 με το 15, παίρνουμε το πηλίκο του 3 χωρίς υπόλοιπο. Αυτό σημαίνει ότι ο αριθμός 45 διαιρείται με το 15 χωρίς υπόλοιπο. Η απάντηση είναι - 3, αφού η διαίρεση πραγματοποιήθηκε modulo.

45: (- 15) = 45: - 15 = - 45: 15 = - 3

Απάντηση: 45: (− 15) = − 3 .

Η διατύπωση του κανόνα για διαίρεση με υπόλοιπο έχει ως εξής.

Ορισμός 2

Για να λάβετε ένα ημιτελές πηλίκο c κατά τη διαίρεση ενός αρνητικού ακέραιου αριθμού a με ένα θετικό b, πρέπει να εφαρμόσετε το αντίθετο του δεδομένου αριθμού και να αφαιρέσετε 1 από αυτό, τότε το υπόλοιπο d θα υπολογιστεί με τον τύπο: d = a − προ ΧΡΙΣΤΟΥ.

Με βάση τον κανόνα, μπορούμε να συμπεράνουμε ότι κατά τη διαίρεση παίρνουμε έναν μη αρνητικό ακέραιο. Για να διασφαλίσετε την ακρίβεια της λύσης, χρησιμοποιήστε τον αλγόριθμο για τη διαίρεση του a με το b με ένα υπόλοιπο:

• βρείτε τις ενότητες του μερίσματος και του διαιρέτη.
• διαίρεση modulo?
• γράψε το αντίθετο δεδομένου αριθμούκαι αφαιρέστε 1 ;
• χρησιμοποιήστε τον τύπο για το υπόλοιπο d = a − b · c.

Ας δούμε ένα παράδειγμα λύσης όπου χρησιμοποιείται αυτός ο αλγόριθμος.

Παράδειγμα 6

Βρείτε το μερικό πηλίκο και το υπόλοιπο της διαίρεσης - 17 επί 5.

Λύση

Διαιρούμε τους δοσμένους αριθμούς modulo. Διαπιστώνουμε ότι κατά τη διαίρεση, το πηλίκο είναι 3 και το υπόλοιπο είναι 2. Αφού πήραμε 3, το αντίθετο είναι 3. Πρέπει να αφαιρέσετε 1.

− 3 − 1 = − 4 .

Η επιθυμητή τιμή είναι ίση με - 4.

Για να υπολογίσετε το υπόλοιπο, χρειάζεστε a = − 17, b = 5, c = − 4, μετά d = a − b c = − 17 − 5 (− 4) = − 17 − (− 20) = − 17 + 20 = 3 .

Αυτό σημαίνει ότι το ημιτελές πηλίκο διαίρεσης είναι ο αριθμός - 4 με υπόλοιπο ίσο με 3.

Απάντηση:(− 17) : 5 = − 4 (απομένουν 3).

Παράδειγμα 7

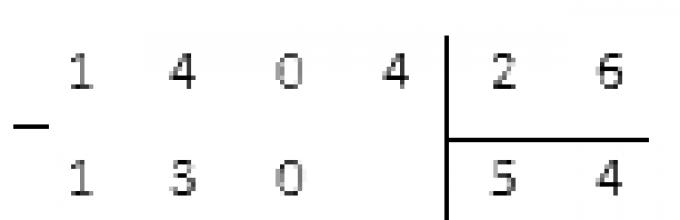
Διαιρέστε τον αρνητικό ακέραιο αριθμό - 1404 με το θετικό 26.

Λύση

Είναι απαραίτητο να γίνει διαίρεση ανά στήλη και ενότητα.

Πήραμε τη διαίρεση των ενοτήτων των αριθμών χωρίς υπόλοιπο. Αυτό σημαίνει ότι η διαίρεση εκτελείται χωρίς υπόλοιπο και το επιθυμητό πηλίκο = - 54.

Απάντηση: (− 1 404) : 26 = − 54 .

Κανόνας διαίρεσης με υπόλοιπο για αρνητικούς ακέραιους, παραδείγματα

Είναι απαραίτητο να διατυπωθεί ένας κανόνας για διαίρεση με υπόλοιπο ακέραιων αριθμών αρνητικούς αριθμούς.

Ορισμός 3

Για να λάβετε ένα ημιτελές πηλίκο c από τη διαίρεση ενός αρνητικού ακέραιου αριθμού a με έναν αρνητικό ακέραιο b, είναι απαραίτητο να εκτελέσετε υπολογισμούς modulo, στη συνέχεια να προσθέσετε 1, τότε μπορούμε να εκτελέσουμε υπολογισμούς χρησιμοποιώντας τον τύπο d = a − b · c.

Από αυτό προκύπτει ότι το ατελές πηλίκο της διαίρεσης αρνητικών ακεραίων θα είναι θετικός αριθμός.

Ας διατυπώσουμε αυτόν τον κανόνα με τη μορφή αλγορίθμου:

• βρείτε τις ενότητες του μερίσματος και του διαιρέτη.
• διαιρέστε το μέτρο του μερίσματος με το μέτρο του διαιρέτη για να λάβετε ένα ημιτελές πηλίκο με
• υπόλοιπο;
• προσθέτοντας 1 στο ημιτελές πηλίκο.
• υπολογισμός του υπολοίπου με βάση τον τύπο d = a − b · c.

Ας δούμε αυτόν τον αλγόριθμο χρησιμοποιώντας ένα παράδειγμα.

Παράδειγμα 8

Βρείτε το μερικό πηλίκο και το υπόλοιπο κατά τη διαίρεση - 17 με - 5.

Λύση

Για την ορθότητα της λύσης εφαρμόζουμε τον αλγόριθμο για διαίρεση με υπόλοιπο. Αρχικά, διαιρέστε τους αριθμούς modulo. Από αυτό παίρνουμε ότι το μερικό πηλίκο = 3 και το υπόλοιπο είναι 2. Σύμφωνα με τον κανόνα, πρέπει να προσθέσετε το ημιτελές πηλίκο και 1. Παίρνουμε ότι 3 + 1 = 4. Από εδώ παίρνουμε ότι το μερικό πηλίκο της διαίρεσης των δεδομένων αριθμών είναι ίσο με 4.

Για να υπολογίσουμε το υπόλοιπο θα χρησιμοποιήσουμε τον τύπο. Με συνθήκη έχουμε ότι a = − 17, b = − 5, c = 4, τότε, χρησιμοποιώντας τον τύπο, παίρνουμε d = a − b c = − 17 − (− 5) 4 = − 17 − (− 20) = − 17 + 20 = 3 . Η απαιτούμενη απάντηση, δηλαδή το υπόλοιπο, είναι ίση με 3 και το μερικό πηλίκο είναι ίσο με 4.

Απάντηση:(− 17) : (− 5) = 4 (απομένουν 3).

Έλεγχος του αποτελέσματος της διαίρεσης ακεραίων με υπόλοιπο

Αφού διαιρέσετε τους αριθμούς με ένα υπόλοιπο, πρέπει να κάνετε έλεγχο. Αυτός ο έλεγχος περιλαμβάνει 2 στάδια. Αρχικά, το υπόλοιπο d ελέγχεται για μη αρνητικό χαρακτήρα, η συνθήκη 0 ≤ d ικανοποιείται< b . При их выполнении разрешено выполнять 2 этап. Если 1 этап не выполнился, значит вычисления произведены с ошибками. Второй этап состоит из того, что равенство a = b · c + d должно быть верным. Иначе в вычисления имеется ошибка.

Ας δούμε παραδείγματα.

Παράδειγμα 9

Η διαίρεση γίνεται - 521 με - 12. Το πηλίκο είναι 44, το υπόλοιπο είναι 7. Εκτελέστε έλεγχο.

Λύση

Εφόσον το υπόλοιπο είναι θετικός αριθμός, η τιμή του είναι μικρότερη από το μέτρο του διαιρέτη. Ο διαιρέτης είναι - 12, που σημαίνει ότι το μέτρο του είναι 12. Μπορείτε να προχωρήσετε στο επόμενο σημείο ελέγχου.

Με συνθήκη, έχουμε ότι a = − 521, b = − 12, c = 44, d = 7. Από εδώ υπολογίζουμε b · c + d, όπου b · c + d = − 12 · 44 + 7 = − 528 + 7 = − 521. Από αυτό προκύπτει ότι η ισότητα είναι αληθής. Η επαλήθευση πέρασε.

Παράδειγμα 10

Εκτελέστε έλεγχο διαίρεσης (− 17): 5 = − 3 (υπόλοιπο − 2). Αληθεύει η ισότητα;

Λύση

Το θέμα του πρώτου σταδίου είναι ότι είναι απαραίτητο να ελέγξουμε τη διαίρεση των ακεραίων με ένα υπόλοιπο. Από αυτό είναι σαφές ότι η ενέργεια εκτελέστηκε λανθασμένα, αφού δίνεται ένα υπόλοιπο ίσο με - 2. Το υπόλοιπο δεν είναι αρνητικός αριθμός.

Έχουμε ότι πληρούται η δεύτερη προϋπόθεση, αλλά όχι επαρκής για αυτήν την περίπτωση.

Απάντηση:Οχι.

Παράδειγμα 11

Ο αριθμός - 19 διαιρέθηκε με - 3. Το μερικό πηλίκο είναι 7 και το υπόλοιπο είναι 1. Ελέγξτε εάν αυτός ο υπολογισμός έγινε σωστά.

Λύση

Δίνεται υπόλοιπο ίσο με 1. Είναι θετικός. Η τιμή είναι μικρότερη από τη μονάδα διαιρέτη, πράγμα που σημαίνει ότι ολοκληρώνεται το πρώτο στάδιο. Ας περάσουμε στο δεύτερο στάδιο.

Ας υπολογίσουμε την τιμή της παράστασης b · c + d. Με συνθήκη, έχουμε b = − 3, c = 7, d = 1, που σημαίνει, αντικαθιστώντας τις αριθμητικές τιμές, παίρνουμε b · c + d = − 3 · 7 + 1 = − 21 + 1 = − 20. Συνεπάγεται ότι a = b · c + d η ισότητα δεν ισχύει, αφού η συνθήκη δίνει a = - 19.

Από αυτό προκύπτει ότι η διαίρεση έγινε με λάθος.

Απάντηση:Οχι.

Εάν παρατηρήσετε κάποιο σφάλμα στο κείμενο, επισημάνετε το και πατήστε Ctrl+Enter

Διαβάστε το θέμα του μαθήματος: «Διαίρεση με υπόλοιπο». Τι γνωρίζετε ήδη για αυτό το θέμα;

Μπορείτε να μοιράσετε 8 δαμάσκηνα εξίσου σε δύο πιάτα (Εικ. 1);

Ρύζι. 1. Εικονογράφηση για παράδειγμα

Μπορείτε να βάλετε 4 δαμάσκηνα σε κάθε πιάτο (Εικ. 2).

Ρύζι. 2. Εικονογράφηση για παράδειγμα

Η ενέργεια που πραγματοποιήσαμε μπορεί να γραφτεί έτσι.

8: 2 = 4

Πιστεύετε ότι είναι δυνατόν να μοιράσουμε 8 δαμάσκηνα εξίσου σε 3 πιάτα (Εικ. 3);

Ρύζι. 3. Εικονογράφηση για παράδειγμα

Ας ενεργήσουμε έτσι. Αρχικά, βάλτε ένα δαμάσκηνο σε κάθε πιάτο και μετά ένα δεύτερο δαμάσκηνο. Θα μας μείνουν 2 δαμάσκηνα, αλλά 3 πιάτα. Αυτό σημαίνει ότι δεν μπορούμε να τα κατανείμουμε ομοιόμορφα περαιτέρω. Βάλαμε 2 δαμάσκηνα σε κάθε πιάτο, και μας έμειναν 2 δαμάσκηνα (Εικ. 4).

Ρύζι. 4. Εικονογράφηση για παράδειγμα

Ας συνεχίσουμε να παρατηρούμε.

Διαβάστε τους αριθμούς. Ανάμεσα στους αριθμούς που δίνονται να βρείτε αυτούς που διαιρούνται με το 3.

11, 12, 13, 14, 15, 16, 17, 18, 19

Δοκίμασε τον εαυτό σου.

Οι υπόλοιποι αριθμοί (11, 13, 14, 16, 17, 19) δεν διαιρούνται με το 3 ή λένε "κοινόχρηστο με το υπόλοιπο."

Ας βρούμε την τιμή του πηλίκου.

Ας μάθουμε πόσες φορές το 3 περιέχεται στον αριθμό 17 (Εικ. 5).

Ρύζι. 5. Εικονογράφηση για παράδειγμα

Βλέπουμε ότι χωράνε 3 οβάλ 5 φορές και μένουν 2 οβάλ.

Η ολοκληρωμένη ενέργεια μπορεί να γραφτεί έτσι.

17: 3 = 5 (απομένουν 2)

Μπορείτε επίσης να το γράψετε σε στήλη (Εικ. 6)

Ρύζι. 6. Εικονογράφηση για παράδειγμα

Δείτε τις φωτογραφίες. Εξηγήστε τις λεζάντες σε αυτά τα σχήματα (Εικ. 7).

Ρύζι. 7. Εικονογράφηση για παράδειγμα

Ας δούμε την πρώτη εικόνα (Εικ. 8).

Ρύζι. 8. Εικονογράφηση για παράδειγμα

Βλέπουμε ότι 15 οβάλ χωρίστηκαν σε 2. 2 επαναλήφθηκαν 7 φορές, με το υπόλοιπο να είναι 1 οβάλ.

Ας δούμε τη δεύτερη εικόνα (Εικ. 9).

Ρύζι. 9. Εικονογράφηση για παράδειγμα

Σε αυτό το σχήμα, 15 τετράγωνα χωρίστηκαν σε 4. 4 επαναλήφθηκαν 3 φορές, με το υπόλοιπο να είναι 3 τετράγωνα.

Ας δούμε την τρίτη εικόνα (Εικ. 10).

Ρύζι. 10. Εικονογράφηση για παράδειγμα

Μπορούμε να πούμε ότι 15 οβάλ χωρίστηκαν σε 3. 3 επαναλήφθηκαν 5 φορές ισόποσα. Σε τέτοιες περιπτώσεις το υπόλοιπο λέγεται ότι είναι 0.

Ας κάνουμε τη διαίρεση.

Χωρίζουμε επτά τετράγωνα σε τρία. Παίρνουμε δύο ομάδες και μένει ένα τετράγωνο. Ας γράψουμε τη λύση (Εικ. 11).

Ρύζι. 11. Εικονογράφηση για παράδειγμα

Ας κάνουμε τη διαίρεση.

Ας μάθουμε πόσες φορές περιέχονται τέσσερα στον αριθμό 10. Βλέπουμε ότι ο αριθμός 10 περιέχει τέσσερις φορές 2 φορές και μένουν 2 τετράγωνα. Ας γράψουμε τη λύση (Εικ. 12).

Ρύζι. 12. Εικονογράφηση για παράδειγμα

Ας κάνουμε τη διαίρεση.

Ας μάθουμε πόσες φορές δύο περιέχονται στον αριθμό 11. Βλέπουμε ότι στον αριθμό 11 δύο περιέχονται 5 φορές και μένει 1 τετράγωνο. Ας γράψουμε τη λύση (Εικ. 13).

Ρύζι. 13. Εικονογράφηση για παράδειγμα

Ας βγάλουμε ένα συμπέρασμα. Διαίρεση με υπόλοιπο σημαίνει να μάθουμε πόσες φορές ο διαιρέτης περιέχεται στο μέρισμα και πόσες μονάδες απομένουν.

Η διαίρεση με υπόλοιπο μπορεί επίσης να πραγματοποιηθεί στην αριθμητική γραμμή.

Στην αριθμητική γραμμή σημειώνουμε τμήματα από 3 διαιρέσεις και βλέπουμε ότι υπάρχουν τρεις διαιρέσεις τρεις φορές και παραμένει μία διαίρεση (Εικ. 14).

Ρύζι. 14. Εικονογράφηση για παράδειγμα

Ας γράψουμε τη λύση.

10: 3 = 3 (απομένει 1)

Ας κάνουμε τη διαίρεση.

Στην αριθμητική γραμμή σημειώνουμε τμήματα από 3 διαιρέσεις και βλέπουμε ότι υπάρχουν τρεις διαιρέσεις τρεις φορές και μένουν δύο διαιρέσεις (Εικ. 15).

Ρύζι. 15. Εικονογράφηση για παράδειγμα

Ας γράψουμε τη λύση.

11: 3 = 3 (απομένουν 2)

Ας κάνουμε τη διαίρεση.

Στην αριθμητική γραμμή σημειώνουμε τμήματα από 3 διαιρέσεις και βλέπουμε ότι πήραμε ακριβώς 4 φορές, δεν υπάρχει υπόλοιπο (Εικ. 16).

Ρύζι. 16. Εικονογράφηση για παράδειγμα

Ας γράψουμε τη λύση.

12: 3 = 4

Σήμερα στο μάθημα εξοικειωθήκαμε με τη διαίρεση με ένα υπόλοιπο, μάθαμε πώς να εκτελούμε την ονομαστική ενέργεια χρησιμοποιώντας ένα σχέδιο και μια αριθμητική γραμμή και εξασκηθήκαμε στην επίλυση παραδειγμάτων για το θέμα του μαθήματος.

Βιβλιογραφία

1. ΜΙ. Moreau, M.A. Μπάντοβα και άλλοι.Μαθηματικά: Σχολικό βιβλίο. Γ΄ τάξη: σε 2 μέρη, μέρος 1. - Μ.: «Διαφωτισμός», 2012.
2. ΜΙ. Moreau, M.A. Μπάντοβα και άλλοι.Μαθηματικά: Σχολικό βιβλίο. Γ΄ τάξη: σε 2 μέρη, μέρος 2. - Μ.: «Διαφωτισμός», 2012.
3. ΜΙ. Moro. Μαθήματα μαθηματικών: Κατευθυντήριες γραμμέςγια τον δάσκαλο. 3η τάξη. - Μ.: Εκπαίδευση, 2012.
4. Κανονιστικό έγγραφο. Παρακολούθηση και αξιολόγηση των μαθησιακών αποτελεσμάτων. - Μ.: «Διαφωτισμός», 2011.
5. "Σχολείο της Ρωσίας": Προγράμματα για δημοτικό σχολείο. - Μ.: «Διαφωτισμός», 2011.
6. ΣΙ. Βόλκοβα. Μαθηματικά: Δοκιμαστική εργασία. 3η τάξη. - Μ.: Εκπαίδευση, 2012.
7. V.N. Rudnitskaya. Δοκιμές. - Μ.: «Εξεταστική», 2012.

1. Nsportal.ru ().
2. Prosv.ru ().
3. Do.gendocs.ru ().

Εργασία για το σπίτι

1. Γράψτε τους αριθμούς που διαιρούνται με το 2 χωρίς υπόλοιπο.

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19

2. Εκτελέστε διαίρεση με ένα υπόλοιπο χρησιμοποιώντας μια εικόνα.

3. Εκτελέστε διαίρεση με ένα υπόλοιπο χρησιμοποιώντας την αριθμητική γραμμή.

4. Δημιουργήστε μια εργασία για τους φίλους σας για το θέμα του μαθήματος.

Ο ευκολότερος τρόπος για να διαιρέσετε πολυψήφιους αριθμούς είναι με μια στήλη. Ονομάζεται επίσης διαίρεση στηλών γωνιακό τμήμα.

Πριν αρχίσουμε να κάνουμε διαίρεση με στήλη, θα εξετάσουμε λεπτομερώς την ίδια τη μορφή εγγραφής της διαίρεσης με στήλη. Πρώτα, σημειώστε το μέρισμα και βάλτε μια κάθετη γραμμή στα δεξιά του:

Πίσω από την κάθετη γραμμή, απέναντι από το μέρισμα, γράψτε τον διαιρέτη και σχεδιάστε μια οριζόντια γραμμή κάτω από αυτόν:

Κάτω από την οριζόντια γραμμή, το πηλίκο που προκύπτει θα γραφεί βήμα προς βήμα:

Οι ενδιάμεσοι υπολογισμοί θα εγγραφούν κάτω από το μέρισμα:

Η πλήρης μορφή γραφής διαίρεση ανά στήλη έχει ως εξής:

Πώς να διαιρέσετε ανά στήλη

Ας υποθέσουμε ότι πρέπει να διαιρέσουμε το 780 με το 12, να γράψουμε την ενέργεια σε μια στήλη και να προχωρήσουμε στη διαίρεση:

Η διαίρεση της στήλης πραγματοποιείται σε στάδια. Το πρώτο πράγμα που πρέπει να κάνουμε είναι να καθορίσουμε το ημιτελές μέρισμα. Εξετάζουμε το πρώτο ψηφίο του μερίσματος:

αυτός ο αριθμός είναι 7, αφού είναι μικρότερος από τον διαιρέτη, δεν μπορούμε να ξεκινήσουμε τη διαίρεση από αυτόν, πράγμα που σημαίνει ότι πρέπει να πάρουμε ένα άλλο ψηφίο από το μέρισμα, ο αριθμός 78 είναι μεγαλύτερος από τον διαιρέτη, οπότε ξεκινάμε τη διαίρεση από αυτόν:

Στην περίπτωσή μας ο αριθμός 78 θα είναι ελλιπής διαιρετέος, λέγεται ελλιπής γιατί είναι μόνο ένα μέρος του διαιρετέου.

Έχοντας καθορίσει το ημιτελές μέρισμα, μπορούμε να μάθουμε πόσα ψηφία θα είναι στο πηλίκο, για αυτό πρέπει να υπολογίσουμε πόσα ψηφία έχουν απομείνει στο μέρισμα μετά το ημιτελές μέρισμα, στην περίπτωσή μας υπάρχει μόνο ένα ψηφίο - 0, αυτό σημαίνει ότι το πηλίκο θα αποτελείται από 2 ψηφία.

Έχοντας ανακαλύψει τον αριθμό των ψηφίων που πρέπει να είναι στο πηλίκο, μπορείτε να βάλετε τελείες στη θέση του. Εάν, κατά την ολοκλήρωση της διαίρεσης, ο αριθμός των ψηφίων αποδειχθεί μεγαλύτερος ή μικρότερος από τα υποδεικνυόμενα σημεία, τότε έγινε κάπου ένα σφάλμα:

Ας αρχίσουμε να χωρίζουμε. Πρέπει να προσδιορίσουμε πόσες φορές το 12 περιέχεται στον αριθμό 78. Για να γίνει αυτό, πολλαπλασιάζουμε διαδοχικά τον διαιρέτη με τους φυσικούς αριθμούς 1, 2, 3, ... μέχρι να πάρουμε έναν αριθμό όσο το δυνατόν πιο κοντά στο ημιτελές μέρισμα ή ίσο με αυτό, χωρίς όμως να το υπερβαίνει. Έτσι, παίρνουμε τον αριθμό 6, τον γράφουμε κάτω από τον διαιρέτη και από το 78 (σύμφωνα με τους κανόνες της αφαίρεσης στηλών) αφαιρούμε το 72 (12 · 6 = 72). Αφού αφαιρέσουμε το 72 από το 78, το υπόλοιπο είναι 6:

Σημειώστε ότι το υπόλοιπο της διαίρεσης μας δείχνει εάν επιλέξαμε σωστά τον αριθμό. Αν το υπόλοιπο είναι ίσο ή μεγαλύτερο από τον διαιρέτη, τότε δεν επιλέξαμε σωστά τον αριθμό και πρέπει να πάρουμε μεγαλύτερο αριθμό.

Στο υπόλοιπο που προκύπτει - 6, προσθέστε το επόμενο ψηφίο του μερίσματος - 0. Ως αποτέλεσμα, παίρνουμε ένα ημιτελές μέρισμα - 60. Προσδιορίστε πόσες φορές το 12 περιέχεται στον αριθμό 60. Παίρνουμε τον αριθμό 5, τον γράφουμε στο το πηλίκο μετά τον αριθμό 6 και αφαιρέστε το 60 από το 60 ( 12 5 = 60). Το υπόλοιπο είναι μηδέν:

Δεδομένου ότι δεν έχουν απομείνει άλλα ψηφία στο μέρισμα, σημαίνει ότι το 780 διαιρείται με το 12 πλήρως. Ως αποτέλεσμα της εκτέλεσης μακράς διαίρεσης, βρήκαμε το πηλίκο - γράφεται κάτω από τον διαιρέτη:

Ας εξετάσουμε ένα παράδειγμα όταν το πηλίκο αποδεικνύεται μηδενικό. Ας υποθέσουμε ότι πρέπει να διαιρέσουμε το 9027 με το 9.

Καθορίζουμε το ημιτελές μέρισμα - αυτός είναι ο αριθμός 9. Γράφουμε το 1 στο πηλίκο και αφαιρούμε το 9 από το 9. Το υπόλοιπο είναι μηδέν. Συνήθως, αν στους ενδιάμεσους υπολογισμούς το υπόλοιπο είναι μηδέν, δεν καταγράφεται:

Αφαιρούμε το επόμενο ψηφίο του μερίσματος - 0. Θυμόμαστε ότι όταν διαιρούμε το μηδέν με οποιονδήποτε αριθμό θα υπάρχει μηδέν. Γράφουμε μηδέν στο πηλίκο (0: 9 = 0) και αφαιρούμε το 0 από το 0 στους ενδιάμεσους υπολογισμούς. Συνήθως, για να μην μπερδεύονται οι ενδιάμεσοι υπολογισμοί, οι υπολογισμοί με μηδέν δεν γράφονται:

Καταργούμε το επόμενο ψηφίο του μερίσματος - 2. Σε ενδιάμεσους υπολογισμούς αποδείχθηκε ότι το ημιτελές μέρισμα (2) είναι μικρότερο από το διαιρέτη (9). Σε αυτήν την περίπτωση, γράψτε μηδέν στο πηλίκο και αφαιρέστε το επόμενο ψηφίο του μερίσματος:

Καθορίζουμε πόσες φορές το 9 περιέχεται στον αριθμό 27. Παίρνουμε τον αριθμό 3, τον γράφουμε ως πηλίκο και αφαιρούμε το 27 από το 27. Το υπόλοιπο είναι μηδέν:

Δεδομένου ότι δεν έχουν απομείνει άλλα ψηφία στο μέρισμα, σημαίνει ότι ο αριθμός 9027 διαιρείται πλήρως με το 9:

Ας εξετάσουμε ένα παράδειγμα όταν το μέρισμα τελειώνει σε μηδενικά. Ας υποθέσουμε ότι πρέπει να διαιρέσουμε το 3000 με το 6.

Καθορίζουμε το ημιτελές μέρισμα - αυτός είναι ο αριθμός 30. Γράφουμε 5 στο πηλίκο και αφαιρούμε το 30 από το 30. Το υπόλοιπο είναι μηδέν. Όπως ήδη αναφέρθηκε, δεν είναι απαραίτητο να γράψετε μηδέν στο υπόλοιπο σε ενδιάμεσους υπολογισμούς:

Αφαιρούμε το επόμενο ψηφίο του μερίσματος - 0. Εφόσον η διαίρεση του μηδενός με οποιονδήποτε αριθμό θα έχει ως αποτέλεσμα μηδέν, γράφουμε μηδέν στο πηλίκο και αφαιρούμε το 0 από το 0 στους ενδιάμεσους υπολογισμούς:

Αφαιρούμε το επόμενο ψηφίο του μερίσματος - 0. Γράφουμε άλλο ένα μηδέν στο πηλίκο και αφαιρούμε το 0 από το 0 στους ενδιάμεσους υπολογισμούς. Επειδή στους ενδιάμεσους υπολογισμούς ο υπολογισμός με μηδέν συνήθως δεν καταγράφεται, η εγγραφή μπορεί να συντομευτεί, αφήνοντας μόνο το υπόλοιπο - 0. Το μηδέν στο υπόλοιπο στο τέλος του υπολογισμού συνήθως γράφεται για να δείξει ότι η διαίρεση έχει ολοκληρωθεί:

Εφόσον δεν υπάρχουν άλλα ψηφία στο μέρισμα, σημαίνει ότι το 3000 διαιρείται με το 6 πλήρως:

Διαίρεση στήλης με υπόλοιπο

Ας υποθέσουμε ότι πρέπει να διαιρέσουμε το 1340 με το 23.

Καθορίζουμε το ημιτελές μέρισμα - αυτός είναι ο αριθμός 134. Γράφουμε το 5 στο πηλίκο και αφαιρούμε το 115 από το 134. Το υπόλοιπο είναι 19:

Αφαιρούμε το επόμενο ψηφίο του μερίσματος - 0. Καθορίζουμε πόσες φορές το 23 περιέχεται στον αριθμό 190. Παίρνουμε τον αριθμό 8, τον γράφουμε στο πηλίκο και αφαιρούμε το 184 από το 190. Παίρνουμε το υπόλοιπο 6:

Δεδομένου ότι δεν έχουν απομείνει άλλα ψηφία στο μέρισμα, η διαίρεση έχει τελειώσει. Το αποτέλεσμα είναι ένα ατελές πηλίκο 58 και ένα υπόλοιπο 6:

1340: 23 = 58 (υπόλοιπο 6)

Απομένει να εξετάσουμε ένα παράδειγμα διαίρεσης με υπόλοιπο, όταν το μέρισμα είναι μικρότερο από το διαιρέτη. Ας πρέπει να διαιρέσουμε το 3 με το 10. Βλέπουμε ότι το 10 δεν περιέχεται ποτέ στον αριθμό 3, οπότε γράφουμε το 0 ως πηλίκο και αφαιρούμε το 0 από το 3 (10 · 0 = 0). Σχεδιάστε μια οριζόντια γραμμή και σημειώστε το υπόλοιπο - 3:

3: 10 = 0 (υπόλοιπο 3)

Αριθμομηχανή μεγάλης διαίρεσης

Αυτή η αριθμομηχανή θα σας βοηθήσει να εκτελέσετε μεγάλη διαίρεση. Απλώς εισάγετε το μέρισμα και τον διαιρέτη και κάντε κλικ στο κουμπί Υπολογισμός.

Τι κάνει η Γ' τάξη στα μαθηματικά; Διαίρεση με υπόλοιπο, παραδείγματα και προβλήματα - αυτό μελετάται στα μαθήματα. Η διαίρεση με ένα υπόλοιπο και ο αλγόριθμος για τέτοιους υπολογισμούς θα συζητηθούν στο άρθρο.

Ιδιαιτερότητες

Ας δούμε τα θέματα που περιλαμβάνονται στο πρόγραμμα που σπουδάζει η Γ' τάξη. Η διαίρεση με υπόλοιπο περιλαμβάνεται σε ειδική ενότητα των μαθηματικών. Περί τίνος πρόκειται? Εάν το μέρισμα δεν διαιρείται ομοιόμορφα με τον διαιρέτη, τότε παραμένει ένα υπόλοιπο. Για παράδειγμα, διαιρούμε το 21 με το 6. Βγαίνει 3, αλλά το υπόλοιπο παραμένει 3.

Στις περιπτώσεις που κατά τη διαίρεση φυσικών αριθμών το υπόλοιπο είναι μηδέν, λέγεται ότι έχει γίνει πλήρης διαίρεση. Για παράδειγμα, αν το 25 διαιρεθεί με το 5, το αποτέλεσμα είναι 5. Το υπόλοιπο είναι μηδέν.

Επίλυση Παραδειγμάτων

Για να γίνει διαίρεση με υπόλοιπο, χρησιμοποιείται μια συγκεκριμένη σημείωση.

Ας δώσουμε παραδείγματα στα μαθηματικά (Γ' δημοτικού). Η διαίρεση με υπόλοιπο δεν χρειάζεται να γράφεται σε στήλη. Αρκεί να γράψετε στη γραμμή: 13:4=3 (υπόλοιπο 1) ή 17:5=3 (υπόλοιπο 2).

Ας δούμε τα πάντα με περισσότερες λεπτομέρειες. Για παράδειγμα, η διαίρεση του 17 με το τρία δίνει τον ακέραιο αριθμό πέντε και αφήνει επίσης ένα υπόλοιπο δύο. Ποια είναι η διαδικασία για την επίλυση αυτού του παραδείγματος για διαίρεση με υπόλοιπο; Πρώτα πρέπει να βρείτε τον μέγιστο αριθμό μέχρι το 17, ο οποίος μπορεί να διαιρεθεί χωρίς υπόλοιπο με το τρία. Το μεγαλύτερο θα ήταν 15.

Στη συνέχεια, διαιρέστε το 15 με τον αριθμό τρία, το αποτέλεσμα της ενέργειας θα είναι ο αριθμός πέντε. Τώρα αφαιρούμε τον αριθμό που βρήκαμε από το μέρισμα, δηλαδή από το 17 αφαιρούμε το 15, παίρνουμε δύο. Μια υποχρεωτική ενέργεια είναι η συμφωνία του διαιρέτη και του υπολοίπου. Μετά την επαλήθευση, πρέπει να καταγραφεί η απάντηση της ολοκληρωμένης ενέργειας. 17:3=15 (υπόλοιπο 2).

Εάν το υπόλοιπο είναι μεγαλύτερο από τον διαιρέτη, η ενέργεια εκτελέστηκε λανθασμένα. Αυτός είναι ο αλγόριθμος που χρησιμοποιείται για την εκτέλεση διαίρεσης κατηγορίας 3 με υπόλοιπο. Τα παραδείγματα αναλύονται αρχικά από τον δάσκαλο στον πίνακα και στη συνέχεια τα παιδιά καλούνται να ελέγξουν τις γνώσεις τους κάνοντας ανεξάρτητη εργασία.

Παράδειγμα με πολλαπλασιασμό

Ένα από τα πιο δύσκολα θέματα που αντιμετωπίζει η τρίτη τάξη είναι η διαίρεση με υπόλοιπο. Τα παραδείγματα μπορεί να είναι πολύπλοκα, ειδικά όταν απαιτούνται πρόσθετοι υπολογισμοί, που καταγράφονται σε μια στήλη.

Ας υποθέσουμε ότι πρέπει να διαιρέσετε τον αριθμό 190 με το 27 για να λάβετε το ελάχιστο υπόλοιπο. Ας προσπαθήσουμε να λύσουμε το πρόβλημα χρησιμοποιώντας τον πολλαπλασιασμό.

Ας επιλέξουμε έναν αριθμό που, όταν πολλαπλασιαστεί, θα δίνει έναν αριθμό όσο το δυνατόν πιο κοντά στον αριθμό 190. Αν πολλαπλασιάσουμε το 27 με 6, θα έχουμε τον αριθμό 162. Αφαιρούμε τον αριθμό 162 από το 190, το υπόλοιπο θα είναι 28. Γυρίζει να είναι μεγαλύτερος από τον αρχικό διαιρέτη. Επομένως, ο αριθμός έξι δεν είναι κατάλληλος ως πολλαπλασιαστής για το παράδειγμά μας. Ας συνεχίσουμε να λύνουμε το παράδειγμα, παίρνοντας τον αριθμό 7 για πολλαπλασιασμό.

Πολλαπλασιάζοντας το 27 επί 7, παίρνουμε το γινόμενο 189. Στη συνέχεια, θα ελέγξουμε την ορθότητα της λύσης, για να το κάνουμε αυτό, αφαιρούμε το αποτέλεσμα που προκύπτει από το 190, δηλαδή αφαιρούμε τον αριθμό 189. Το υπόλοιπο θα είναι 1, που είναι ξεκάθαρα λιγότερο από 27. Έτσι λύνονται σύνθετες εκφράσειςστο σχολείο (Γ' τάξη, τμήμα με υπόλοιπο). Τα παραδείγματα περιλαμβάνουν πάντα την καταγραφή μιας απάντησης. Ολόκληρη η μαθηματική έκφραση μπορεί να γραφτεί ως εξής: 190:27 = 7 (υπόλοιπο 1). Παρόμοιοι υπολογισμοί μπορούν να γίνουν σε μια στήλη.

Αυτός είναι ακριβώς ο τρόπος με τον οποίο ο βαθμός 3 κάνει τη διαίρεση με ένα υπόλοιπο. Τα παραδείγματα που δίνονται παραπάνω θα σας βοηθήσουν να κατανοήσετε τον αλγόριθμο για την επίλυση τέτοιων προβλημάτων.

συμπέρασμα

Προκειμένου για μαθητές δημοτικές τάξειςΕάν έχουν αναπτυχθεί σωστές υπολογιστικές δεξιότητες, ο δάσκαλος, κατά τη διάρκεια των μαθηματικών μαθηματικών, πρέπει να δώσει προσοχή στην εξήγηση του αλγόριθμου των ενεργειών του παιδιού όταν λύνει προβλήματα που περιλαμβάνουν διαίρεση με ένα υπόλοιπο.

Σύμφωνα με το νέο ομοσπονδιακό κράτος εκπαιδευτικά πρότυπαδίνεται ιδιαίτερη προσοχή στην ατομική προσέγγιση της μάθησης. Ο δάσκαλος πρέπει να επιλέγει εργασίες για κάθε παιδί λαμβάνοντας υπόψη τις ατομικές του ικανότητες. Σε κάθε στάδιο διδασκαλίας των κανόνων διαίρεσης με υπόλοιπο, ο δάσκαλος πρέπει να πραγματοποιεί ενδιάμεσο έλεγχο. Του επιτρέπει να εντοπίσει τα κύρια προβλήματα που προκύπτουν με την αφομοίωση της ύλης για κάθε μαθητή, να διορθώσει έγκαιρα τις γνώσεις και τις δεξιότητες, να εξαλείψει τα αναδυόμενα προβλήματα και να επιτύχει το επιθυμητό αποτέλεσμα.