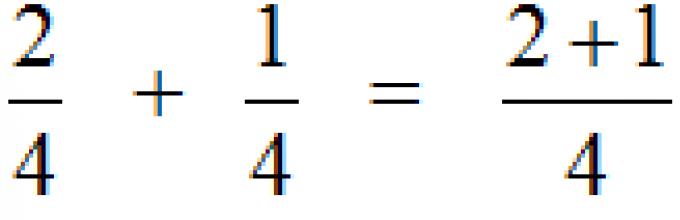Προσθήκη κλάσεων με τους ίδιους παρονομαστές
Η προσθήκη κλάσεων είναι δύο τύποι:
- Προσθήκη κλάσεων με τους ίδιους παρονομαστές
- Προσθήκη κλάσεων S. Διαφορετικός παρονομαστής
Πρώτα μελετάμε την προσθήκη κλάσεων με τους ίδιους παρονομαστές. Όλα είναι απλά εδώ. Για να διπλώσετε τα κλάσματα με τους ίδιους παρονομαστές, πρέπει να διπλώσετε τους αριθμούς τους και ο παρονομαστής παραμένει αμετάβλητος. Για παράδειγμα, διπλώστε τα κλάσματα και. Διπλώμενοι τους αριθμούς και ο παρονομαστής παραμένει αμετάβλητος:

Αυτό το παράδειγμα μπορεί εύκολα να γίνει κατανοητό εάν θυμάστε για την πίτσα, η οποία χωρίζεται σε τέσσερα μέρη. Εάν προσθέσετε πίτσα στην πίτσα, τότε η πίτσα θα είναι:

Παράδειγμα 2. Διπλώστε τα κλάσματα και.

Σε απάντηση, αποδείχθηκε το λάθος κλάσμα. Εάν έρθει το τέλος της εργασίας, τότε από τα λανθασμένα κλάσματα είναι συνηθισμένο να ξεφορτωθείτε. Για να απαλλαγείτε από το λάθος κλάσμα, πρέπει να επισημάνετε ολόκληρο το μέρος σε αυτό. Στην περίπτωσή μας, όλο το μέρος ξεχωρίζει εύκολα - δύο χωρισμένα σε δύο ισούται με ένα:

Αυτό το παράδειγμα μπορεί εύκολα να γίνει κατανοητό εάν θυμηθείτε για την πίτσα, η οποία χωρίζεται σε δύο μέρη. Εάν η πίτσα προστίθεται στην πίτσα, τότε μια ολόκληρη πίτσα θα είναι:

Παράδειγμα 3.. Διπλώστε τα κλάσματα και.
Και πάλι, διπλώνετε τους αριθμούς και ο παρονομαστής παραμένει αμετάβλητος:
![]()
Αυτό το παράδειγμα μπορεί εύκολα να γίνει κατανοητό εάν θυμάστε για την πίτσα, η οποία χωρίζεται σε τρία μέρη. Εάν η πίτσα προστίθεται στην πίτσα, τότε η πίτσα θα είναι:

Παράδειγμα 4. Βρείτε μια τιμή έκφρασης 
Αυτό το παράδειγμα επιλύεται ήδη από τις προηγούμενες. Οι αριθμοί πρέπει να διπλωθούν και ο παρονομαστής παραμένει αμετάβλητος:
Ας προσπαθήσουμε να απεικονίσουμε τη λύση μας χρησιμοποιώντας την εικόνα. Εάν προσθέσετε πίτσα στην πίτσα και προσθέστε πίτσα, τότε θα αποδειχθεί 1 ολόκληρη και πίτσα.

Όπως μπορείτε να δείτε στην προσθήκη κλάσεων με τους ίδιους αρμονικούς, δεν υπάρχει τίποτα περίπλοκο. Αρκεί να κατανοήσουμε τους ακόλουθους κανόνες:
- Να διπλώσουν τα κλάσματα με τον ίδιο παρονομαστή, πρέπει να προσθέσετε τους αριθμούς τους και ο παρονομαστής παραμένει αμετάβλητος.
Προσθήκη κλασμάτων με διαφορετικούς παρονομαστές
Τώρα μάθετε πώς να βάλετε ένα κλάσμα με διαφορετικούς παρονομαστές. Όταν τα κλάσματα είναι διπλωμένα, οι παρονομαστές αυτών των πελμάτων πρέπει να είναι οι ίδιοι. Αλλά δεν είναι πάντα τα ίδια.
Για παράδειγμα, τα κλάσματα μπορούν να διπλωθούν, καθώς έχουν τους ίδιους παρονομαστές.
Αλλά τα fraci και αμέσως το προσθέτουν αδύνατο, επειδή αυτοί οι πείροι έχουν διαφορετικούς παρονομαστές. Σε τέτοιες περιπτώσεις, οι Fraci πρέπει να οδηγήσουν στον ίδιο (γενικό) παρονομαστή.
Υπάρχουν διάφοροι τρόποι για να φέρετε τα κλάσματα στον ίδιο παρονομαστή. Σήμερα θα εξετάσουμε μόνο ένα από αυτά, καθώς οι υπόλοιπες μέθοδοι μπορεί να φαίνονται πολύπλοκες για αρχάριους.
Η ουσία αυτής της μεθόδου είναι ότι αναζητείται για πρώτη φορά στους παρονομαστές (NOC) και των δύο κλασμάτων. Στη συνέχεια, το NOC χωρίζεται σε παρονομαστή του πρώτου κλάσματος και λαμβάνει τον πρώτο πρόσθετο παράγοντα. Είναι παρόμοιο με το δεύτερο κλάσμα - το NOC χωρίζεται σε παρονομαστή του δεύτερου κλάσματος και λαμβάνει έναν δεύτερο πρόσθετο παράγοντα.
Στη συνέχεια, οι αριθμοί και οι παγωνιές κλάσεων πολλαπλασιάζονται με τους πρόσθετους παράγοντες τους. Ως αποτέλεσμα αυτών των ενεργειών, τα κλάσματα των οποίων ήταν διαφορετικοί παρονομαστές, μετατρέπονται σε ένα κλάσμα που έχουν τους ίδιους παρονομαστές. Και πώς να διπλώσει τέτοια κλάσματα που ήδη γνωρίζουμε.
Παράδειγμα 1.. Μετακίνηση του Fraci I.
Πρώτα απ 'όλα, βρίσκουμε τους μικρότερους συνολικούς πολλαπλούς παρονομαστές και των δύο κλασμάτων. Ο παρονομαστής του πρώτου κλάσματος είναι ο αριθμός 3, και ο παρονομαστής του δεύτερου κλάσματος - ένας αριθμός 2. Το μικρότερο σύνολο των αριθμών αυτών των αριθμών είναι 6
NOK (2 και 3) \u003d 6
Τώρα επιστρέφουμε σε κλάσματα και. Στην αρχή χωρίζουμε το NOC στον παρονομαστή του πρώτου κλάσματος και παίρνετε τον πρώτο πρόσθετο παράγοντα. Το NOC είναι ο αριθμός 6, και ο παρονομαστής του πρώτου κλάσματος είναι ο αριθμός 3. Delim 6 έως 3, παίρνουμε 2.
Ο προκύπτων αριθμός 2 είναι ο πρώτος πρόσθετος παράγοντας. Γράψτε το στο πρώτο κλάσμα. Για να το κάνετε αυτό, κάνουμε μια μικρή λοξή γραμμή πάνω από το κλάσμα και να γράψουμε ένα πρόσθετο παράγοντα που βρέθηκε πάνω από αυτό:
Ομοίως, κάνουμε με το δεύτερο κλάσμα. Διαιρούμε το NOC στον παρονομαστή του δεύτερου κλάσματος και έχουμε τον δεύτερο προαιρετικό παράγοντα. Το NOC είναι ο αριθμός 6, και ο παρονομαστής δεύτερου κλάσματος είναι ένας αριθμός 2. Delim 6 έως 2, λαμβάνουμε 3.
Ο προκύπτων αριθμός 3 είναι ο δεύτερος προαιρετικός παράγοντας. Γράψτε το στο δεύτερο κλάσμα. Και πάλι, κάνουμε μια μικρή λοξή γραμμή πάνω από το δεύτερο κλάσμα και γράφουμε ένα προαιρετικό παράγοντα που βρέθηκε πάνω από αυτό:
Τώρα όλα είναι έτοιμα για εθισμό. Παραμένει η πολλαπλασιάστε τους αριθμούς και τους παρονομαστές κλάσεων σχετικά με τους πρόσθετους παράγοντες τους:

Κοιτάξτε προσεκτικά τι ήρθαμε. Ήρθαμε στο γεγονός ότι τα κλάσματα των οποίων είχαν διαφορετικούς παρονομαστές, μετατράπηκαν σε ένα κλάσμα στο οποίο οι ίδιοι παρονομαστές. Και πώς να διπλώσει τέτοια κλάσματα που ήδη γνωρίζουμε. Ας κάνουμε αυτό το παράδειγμα στο τέλος:

Έτσι, το παράδειγμα ολοκληρώνεται. Για να το προσθέσετε αποδεικνύεται.
Ας προσπαθήσουμε να απεικονίσουμε τη λύση μας χρησιμοποιώντας την εικόνα. Εάν προσθέσετε πίτσα στην πίτσα, τότε μια ολόκληρη πίτσα θα πάρει και μια άλλη έκτη πίτσα:

Η φέρουσα κλάσματα στον ίδιο (κοινόχρηστο) παρονομαστή μπορεί επίσης να απεικονιστεί χρησιμοποιώντας μια εικόνα. Αναφερόμενοι κλάσμα και σε έναν κοινό παρονομαστή, έχουμε ένα κλάσμα και. Αυτά τα δύο κλάσματα θα απεικονίζονται με τα ίδια κομμάτια πίτσας. Η διαφορά θα είναι μόνο ότι αυτή τη φορά θα χωριστούν σε πανομοιότυπες μετοχές (εμφανίζονται στον ίδιο παρονομαστή).

Το πρώτο σχέδιο απεικονίζει ένα κλάσμα (τέσσερα τεμάχια έξι) και το δεύτερο σχέδιο απεικονίζει ένα κλάσμα (τρία κομμάτια έξι). Πτυσσόμενα αυτά τα κομμάτια παίρνουμε (επτά κομμάτια έξι). Αυτό το κλάσμα είναι εσφαλμένο, οπότε διατέθηκαν ολόκληρο το μέρος σε αυτό. Ως αποτέλεσμα, έλαβαν (μια ολόκληρη πίτσα και μια άλλη έκτη πίτσα).
Σημειώστε ότι ζωγράφα αυτό το παράδειγμα πολύ λεπτομερώς. ΣΕ Εκπαιδευτικά ιδρύματα Δεν έγινε δεκτή να γράψει τόσο εξερράγη. Πρέπει να είστε σε θέση να βρείτε γρήγορα το NIC και των δύο παρονομαστών και πρόσθετων ελαττωμάτων σε αυτά, καθώς και γρήγορα πολλαπλασιάστε τα πρόσθετα σφάλματα που βρέθηκαν με τους δικούς τους αριθμούς και παρονομαστές. Όντας στο σχολείο, αυτό το παράδειγμα θα πρέπει να γράψει ως εξής:

Αλλά υπάρχει Ι. πίσω πλευρά Μετάλλια. Εάν στα πρώτα στάδια της μελέτης των μαθηματικών να μην κάνουν λεπτομερή αρχεία, τότε αρχίζουν να εμφανίζονται ερωτήσεις "Και πού προέρχεται;", "Γιατί ο Fraraty γυρίζει ξαφνικά σε ένα άλλο κλάσμα; «.
Για να διευκολύνετε την προσθήκη κλασμάτων με διαφορετικούς παρονομαστές, μπορείτε να χρησιμοποιήσετε τις παρακάτω οδηγίες βήμα προς βήμα:
- Βρίσκοντας τα κλάσματα Rannels NOK.
- Διαχωρίστε το NOC στον παρονομαστή κάθε κλάσματος και λάβετε έναν επιπλέον παράγοντα για κάθε κλάσμα.
- Πολλαπλασιάστε τους αριθμούς και τους παρονομαστές κλάσεων σχετικά με τους πρόσθετους παράγοντες τους.
- Διπλώστε τα κλάσματα που έχουν τους ίδιους παρονομαστές.
- Εάν η απάντηση αποδείχθηκε ακατάλληλο κλάσμα, τότε διακρίνεται από ένα ολόκληρο κομμάτι.
Παράδειγμα 2. Βρείτε μια τιμή έκφρασης  .
.
Χρησιμοποιούμε τις οδηγίες που δίνονται παραπάνω.
Βήμα 1. Βρείτε κλάσματα Rannels NOK
Βρίσκουμε το NOC των παρονομαστών και των δύο κλασμάτων. Οι Dannels των κλάσεων είναι αριθμοί 2, 3 και 4

Βήμα 2. Για να διαιρέσετε το NOC στον παρονομαστή κάθε κλάσματος και να πάρετε έναν επιπλέον παράγοντα για κάθε κλάσμα
Delim nok στον παρονομαστή του πρώτου κλάσματος. Το Nok είναι ένας αριθμός 12, και ο παρονομαστής του πρώτου κλάσματος είναι ο αριθμός 2. DELIM 12 έως 2, λαμβάνουμε 6. Έλαβε τον πρώτο πρόσθετο συντελεστή 6. Το γράφουμε πάνω από το πρώτο κλάσμα:
Τώρα διαιρέστε το NOK στον υπογράψει του δεύτερου κλάσματος. Το Nok είναι ένας αριθμός 12, και ο δεύτερος παρονομαστής κλάσματος είναι ο αριθμός 3. Delive 12 έως 3, λαμβάνουμε 4. έλαβε το δεύτερο προαιρετικό εργοστάσιο 4. Γράψτε το πάνω από το δεύτερο κλάσμα:
Τώρα χωρίζουμε το NOC στον παρονομαστή του τρίτου κλάσματος. Το NOK είναι ένας αριθμός 12 και ο παρονομαστής του τρίτου κλάσματος είναι ο αριθμός 4. DELIM 12 έως 4, λαμβάνουμε 3. Λάβατε τον τρίτο πρόσθετο συντελεστή 3. Καταγράψτε το πάνω από το τρίτο κλάσμα:
Βήμα 3. Πολλαπλασιάστε τους αριθμούς και τους παρονομαστές κλάσεων σχετικά με τους πρόσθετους παράγοντες τους
Πολλαπλασιάζουμε τους αριθμούς και τους παρονομαστές στους πρόσθετους παράγοντες τους:
Βήμα 4. Διπλώστε τα κλάσματα στα οποία οι ίδιοι αρμονικοί
Ήρθαμε στο γεγονός ότι τα κλάσματα των οποίων είχαν διαφορετικούς παρονομαστές, μετατράπηκαν σε ένα κλάσμα, οι οποίοι έχουν τους ίδιους (γενικούς) παρονομαστές. Παραμένει να διπλώσετε αυτά τα κλάσματα. Διπλώμενα:

Η προσθήκη δεν ταιριάζει σε μια γραμμή, έτσι μετακινήσαμε την υπόλοιπη έκφραση στην επόμενη γραμμή. Επιτρέπεται στα μαθηματικά. Όταν η έκφραση δεν ταιριάζει για μία γραμμή, μεταφέρεται στην επόμενη γραμμή και είναι απαραίτητο να τεθεί το σημάδι της ισότητας (\u003d) στο τέλος της πρώτης γραμμής και στην αρχή της νέας γραμμής. Το ίσο σημάδι στη δεύτερη γραμμή υποδηλώνει ότι πρόκειται για συνέχεια της έκφρασης που ήταν στην πρώτη γραμμή.
Βήμα 5. Εάν ο λάθος πυροβολισμός αποδείχθηκε στην απάντηση, στη συνέχεια, καταθέστε ολόκληρο το μέρος σε αυτό
Η απάντησή μας αποδείχθηκε ότι είναι λάθος. Πρέπει να τονίσουμε ολόκληρο το μέρος. Επισημάνετε:

Έλαβε την απάντηση
Αφαιρέστε τα κλάσματα με τους ίδιους παρονομαστές
Αφαίρεση κλάσεων συμβαίνει δύο τύπους:
- Αφαιρέστε τα κλάσματα με τους ίδιους παρονομαστές
- Αφαίρεση κλάσεων με διαφορετικούς παρονομαστές
Πρώτα μελετάμε την αφαίρεση των κλασμάτων με τους ίδιους παρονομαστές. Όλα είναι απλά εδώ. Για να αφαιρέσετε από ένα κλάσμα άλλο, πρέπει να βρείτε τον δεύτερο αριθμητή κλάσματος από τον αριθμό του πρώτου κλάσματος και ο παρονομαστής παραμένει για το ίδιο.
Για παράδειγμα, βρείτε την τιμή της έκφρασης. Για την επίλυση αυτού του παραδείγματος, είναι απαραίτητο να αφαιρεθεί ο δεύτερος αριθμητής κλάσματος από τον αριθμό του πρώτου κλάσματος και ο παρονομαστής παραμένει αμετάβλητος. Και το κάνετε:

Αυτό το παράδειγμα μπορεί εύκολα να γίνει κατανοητό εάν θυμάστε για την πίτσα, η οποία χωρίζεται σε τέσσερα μέρη. Εάν κόψετε πίτσα από πίτσα, τότε η πίτσα θα είναι:

Παράδειγμα 2. Βρείτε την τιμή της έκφρασης.
Και πάλι, από τον αριθμό του πρώτου κλάσματος, αφαιρέμεμε τον δεύτερο αριθμητή κλάσματος και ο παρονομαστής παραμένει αμετάβλητος:

Αυτό το παράδειγμα μπορεί εύκολα να γίνει κατανοητό εάν θυμάστε για την πίτσα, η οποία χωρίζεται σε τρία μέρη. Εάν κόψετε πίτσα από πίτσα, τότε η πίτσα θα είναι:

Παράδειγμα 3. Βρείτε μια τιμή έκφρασης 
Αυτό το παράδειγμα επιλύεται ήδη από τις προηγούμενες. Από τον αριθμητή του πρώτου κλάσματος πρέπει να αφαιρέσετε τις ρυθμίσεις των άλλων κλάσεων:

Όπως μπορείτε να δείτε στην αφαίρεση των κλασμάτων με τους ίδιους παρονομαστές δεν υπάρχει τίποτα περίπλοκο. Αρκεί να κατανοήσουμε τους ακόλουθους κανόνες:
- Για να αφαιρέσετε από το ένα κλάσμα άλλο, πρέπει να αφαιρέσετε τον αριθμό του δεύτερου κλάσματος από τον αριθμό του πρώτου κλάσματος και ο παρονομαστής παραμένει αμετάβλητος.
- Εάν η απάντηση αποδείχθηκε ακατάλληλο κλάσμα, τότε πρέπει να επισημάνετε ολόκληρο το μέρος.
Αφαίρεση κλάσεων με διαφορετικούς παρονομαστές
Για παράδειγμα, το κλάσμα μπορεί να αφαιρεθεί, καθώς αυτά τα κλάσματα έχουν τους ίδιους παρονομαστές. Αλλά το κλάσμα δεν μπορεί να αφαιρεθεί, αφού αυτοί οι πελμάτων έχουν διαφορετικούς παρονομαστές. Σε τέτοιες περιπτώσεις, οι Fraci πρέπει να οδηγήσουν στον ίδιο (γενικό) παρονομαστή.
Ο γενικός παρονομαστής βρίσκει την ίδια αρχή που χρησιμοποιήσαμε κατά την προσθήκη κλασμάτων με διαφορετικούς παρονομαστές. Πρώτα απ 'όλα, βρίσκουν το NOC των παρονομαστών και των δύο κλασμάτων. Στη συνέχεια, το NOC χωρίζεται σε παρονομαστή του πρώτου κλάσματος και λαμβάνει τον πρώτο πρόσθετο παράγοντα, το οποίο καταγράφεται πάνω από το πρώτο κλάσμα. Παρομοίως, οι NOC χωρίζονται σε παρονομαστή του δεύτερου κλάσματος και λαμβάνουν έναν δεύτερο επιπλέον παράγοντα, το οποίο καταγράφεται πάνω από το δεύτερο κλάσμα.
Στη συνέχεια, ο Fraraty πολλαπλασιάζεται με τους πρόσθετους παράγοντες τους. Ως αποτέλεσμα αυτών των εργασιών, τα κλάσματα των οποίων είχαν διαφορετικούς παρονομαστές, μετατρέπονται σε ένα κλάσμα που έχουν τους ίδιους παρονομαστές. Και πώς να αφαιρέσουμε αυτά τα κλάσματα που ήδη γνωρίζουμε.
Παράδειγμα 1. Βρείτε την αξία της έκφρασης:
Αυτοί οι πείροι έχουν διαφορετικούς παρονομαστές, οπότε πρέπει να τα φέρετε στον ίδιο (γενικό) παρονομαστή.
Πρώτα βρίσκουμε το NOC των παρονομαστών και των δύο κλασμάτων. Ο παρονομαστής του πρώτου κλάσματος είναι ο αριθμός 3, και ο παρονομαστής του δεύτερου κλάσματος είναι ο αριθμός 4. Το μικρότερο σύνολο των αριθμών αυτών των αριθμών είναι 12
Nok (3 και 4) \u003d 12
Τώρα επιστρέφουμε σε κλάσματα και
Βρείτε έναν πρόσθετο παράγοντα για το πρώτο κλάσμα. Για να το κάνετε αυτό, διαιρούμε το NOC στον παρονομαστή του πρώτου κλάσματος. Το Nok είναι ένας αριθμός 12, και ο παρονομαστής του πρώτου κλάσματος - ο αριθμός 3. Delim 12 έως 3, λαμβάνουμε 4. Γράψτε το τέταρτο πάνω από το πρώτο κλάσμα:
Ομοίως, κάνουμε με το δεύτερο κλάσμα. Διαιρούμε το NOC στον παρονομαστή του δεύτερου κλάσματος. Το NOC είναι ο αριθμός 12, και ο παρονομαστής του δεύτερου κλάσματος είναι ο αριθμός 4. Delim 12 έως 4, λαμβάνουμε 3. Γράψτε τα τρία κορυφαία πάνω από το δεύτερο κλάσμα:
Τώρα όλα είναι έτοιμα για αφαίρεση. Παραμένει η πολλαπλασιασμός του κλάσματος στους πρόσθετους παράγοντες του:

Ήρθαμε στο γεγονός ότι τα κλάσματα των οποίων είχαν διαφορετικούς παρονομαστές, μετατράπηκαν σε ένα κλάσμα στο οποίο οι ίδιοι παρονομαστές. Και πώς να αφαιρέσουμε αυτά τα κλάσματα που ήδη γνωρίζουμε. Ας κάνουμε αυτό το παράδειγμα στο τέλος:

Έλαβε την απάντηση
Ας προσπαθήσουμε να απεικονίσουμε τη λύση μας χρησιμοποιώντας την εικόνα. Εάν κόψετε πίτσα από πίτσα, τότε θα υπάρξει πίτσα

Αυτή είναι μια λεπτομερής έκδοση της λύσης. Ενώ στο σχολείο, θα έπρεπε να λύσουμε αυτό το παράδειγμα μικρότερο. Θα μοιάζει με μια τέτοια λύση ως εξής:

Φέρνοντας τα κλάσματα και σε κοινόχρηστο παρονομαστή μπορούν επίσης να απεικονιστούν χρησιμοποιώντας μια εικόνα. Με αποτέλεσμα αυτά τα κλάσματα στον γενικό παρονομαστή, έχουμε ένα κλάσμα και. Αυτά τα κλάσματα θα απεικονίζονται με τα ίδια κομμάτια πίτσας, αλλά αυτή τη φορά θα χωριστούν σε πανομοιότυπες μετοχές (εμφανίζονται στον ίδιο παρονομαστή):

Το πρώτο σχέδιο απεικονίζει ένα κλάσμα (οκτώ κομμάτια δώδεκα) και το δεύτερο σχέδιο - κλάσμα (τρία κομμάτια δώδεκα). Κόβω από οκτώ κομμάτια τρία κομμάτια που έχουμε πέντε κομμάτια δώδεκα. Κλάσμα και περιγράφει αυτά τα πέντε κομμάτια.
Παράδειγμα 2. Βρείτε μια τιμή έκφρασης 
Αυτά τα κλάσματα έχουν διαφορετικούς παρονομαστές, έτσι πρέπει πρώτα να τα φέρετε στον ίδιο (γενικό) παρονομαστή.
Βρίσκουμε το NOC των παρονομαστών αυτών των πελατών.
Rannels κλάσματα Αυτοί είναι οι αριθμοί 10, 3 και 5. Το μικρότερο σύνολο των αριθμών αυτών των αριθμών είναι 30
NOK (10, 3, 5) \u003d 30
Τώρα βρίσκουμε πρόσθετους πολλαπλασιαστές για κάθε κλάσμα. Για να γίνει αυτό, διαιρούμε το NOC στον παρονομαστή κάθε κλάσματος.
Βρείτε έναν επιπλέον παράγοντα για το πρώτο κλάσμα. Ο Nok είναι ο αριθμός 30 και ο παρονομαστής του πρώτου κλάσματος είναι ο αριθμός 10. Διαχωρίζουμε 30 έως 10, παίρνουμε τον πρώτο πρόσθετο παράγοντα 3. Καταγράψτε το πάνω από το πρώτο κλάσμα:
Τώρα βρίσκουμε έναν επιπλέον παράγοντα για το δεύτερο κλάσμα. Διαιρούμε το NOC στον υπογράψει του δεύτερου κλάσματος. Το NOC είναι ένας αριθμός 30, και το κανάλι του δεύτερου κλάσματος είναι ο αριθμός 3. DELIM 30 έως 3, λαμβάνουμε τον δεύτερο προαιρετικό συντελεστή 10. Το γράφουμε πάνω από το δεύτερο κλάσμα:
Τώρα βρίσκουμε έναν επιπλέον παράγοντα για το τρίτο κλάσμα. Διαιρούμε το NOC στον παρονομαστή του τρίτου κλάσματος. Το NOC είναι ο αριθμός 30 και ο παρονομαστής του τρίτου κλάσματος είναι ο αριθμός 5. Delim 30 έως 5, έχουμε τον τρίτο πρόσθετο συντελεστή 6. Το γράφουμε πάνω από το τρίτο κλάσμα:
Τώρα όλα είναι έτοιμα για αφαίρεση. Παραμένει η πολλαπλασιασμός του κλάσματος στους πρόσθετους παράγοντες του:
Ήρθαμε στο γεγονός ότι το καταδικασμένο από το οποίο είχε διαφορετικούς παρονομαστές, μετατράπηκε σε ένα κλάσμα στο οποίο οι ίδιοι (γενικοί) παρογγιστές. Και πώς να αφαιρέσουμε αυτά τα κλάσματα που ήδη γνωρίζουμε. Ας κάνουμε αυτό το παράδειγμα.
Η συνέχιση του παραδείγματος δεν ταιριάζει σε μια γραμμή, έτσι μεταφέρουμε τη συνέχιση στην επόμενη γραμμή. Μην ξεχνάτε το σημάδι της ισότητας (\u003d) στη νέα γραμμή:

Η απάντηση αποδείχθηκε το σωστό κλάσμα και φαίνεται ότι όλα μας ταιριάζουν, αλλά είναι πολύ δυσκίνητη και άσχημη. Θα ήταν απαραίτητο να διευκολυνθεί. Και τι μπορεί να γίνει; Μπορείτε να κόψετε αυτό το κλάσμα.
Για να μειώσετε το κλάσμα, πρέπει να διαιρέσετε τον αριθμητικό και τους αριθμούς του (NOD) στους αριθμούς 20 και 30.
Έτσι, βρίσκουμε τους κόμβους των αριθμών 20 και 30:

Τώρα επιστρέφουμε στο παράδειγμά μας και χωρίζουμε τον αριθμητή και τον παρονομαστή του κλάσματος στον κόμβο που βρέθηκε, δηλαδή στις 10

Έλαβε την απάντηση
Πολλαπλασιασμός των κλασμάτων με αριθμό
Για να πολλαπλασιάσετε το κλάσμα από τον αριθμό, χρειάζεστε έναν αριθμητή αυτού του κλάσματος για να πολλαπλασιάσει σε αυτόν τον αριθμό και ο παρονομαστής παραμένει αμετάβλητος.
Παράδειγμα 1.. Πολλαπλασιάστε το κλάσμα στον αριθμό 1.
Πολλαπλασιάστε τον αριθμό θραυστήρα 1
![]()
Η εγγραφή μπορεί να γίνει κατανοητή πώς να πάρει μισή ώρα. Για παράδειγμα, εάν η πίτσα παίρνει 1 φορά, τότε θα υπάρξει πίτσα

Από τους νόμους πολλαπλασιασμού, γνωρίζουμε ότι αν ο πολλαπλασιαστής και ο πολλαπλασιαστής αλλάζει σε μέρη, η εργασία δεν θα αλλάξει. Εάν η έκφραση, καταγράψτε, τότε η εργασία θα εξακολουθεί να είναι ίση. Και πάλι, ο κανόνας πολλαπλασιασμού του ακέραιου και του κλάσματος ενεργοποιείται:
![]()
Αυτή η καταχώρηση μπορεί να γίνει κατανοητή ως σύλληψη του μισού από το ένα. Για παράδειγμα, αν υπάρχει 1 ολόκληρη πίτσα και θα πάμε μισά από αυτό, τότε θα έχουμε πίτσα:

Παράδειγμα 2.. Βρείτε μια τιμή έκφρασης
Πολλαπλασιάστε τον αριθμητή θραυστήρα στις 4
![]()
Σε απάντηση, αποδείχθηκε το λάθος κλάσμα. Επισημάνετε ολόκληρο το μέρος σε αυτό:
![]()
Η έκφραση μπορεί να γίνει κατανοητή ως σύλληψη δύο τεταρτημορίων 4 φορές. Για παράδειγμα, αν η πίτσα διαρκέσει 4 φορές, τότε θα πάρετε δύο ολόκληρες πίτσα

Και αν αλλάξετε τον πολλαπλασιαστή στον πολλαπλασιαστή, θα έχουμε έκφραση. Θα είναι επίσης ίσο με 2. Αυτή η έκφραση μπορεί να γίνει κατανοητή ως η σύλληψη δύο πίτσας από τέσσερις ολόκληρες πίτσες:

Ο αριθμός που πολλαπλασιάζεται με το κλάσμα και ο παρονομαστής του κλάσματος επιτρέπεται εάν έχουν ένα κοινό διαχωριστικό, μια μεγαλύτερη μονάδα.
Για παράδειγμα, η έκφραση μπορεί να υπολογιστεί με δύο τρόπους.
Πρώτη μέθοδος. Πολλαπλασιάστε τον αριθμό 4 στον αριθμητή Flush και το Denomote Denomoter να αφήσει αμετάβλητο:
![]()
Δεύτερος τρόπος. Το πολλαπλασιαστικό τέταρτο και το τέταρτο, το οποίο είναι στον δηλωτή, μπορεί να μειωθεί. Μπορείτε να κόψετε αυτά τα τέσσερα, καθώς ο μεγαλύτερος κοινός διαιρέτης για δύο τέταρτα είναι η τέταρτη πλάκα:

Αποδείχθηκε το ίδιο αποτέλεσμα 3. Μετά την κοπή του τέταρτου, σχηματίζονται νέοι αριθμοί στη θέση τους: δύο μονάδες. Αλλά πολλαπλασιάζοντας τη μονάδα με τα τρία πρώτα και στη συνέχεια το τμήμα ανά μονάδα δεν αλλάζει τίποτα. Ως εκ τούτου, η λύση μπορεί να είναι γραμμένη βραχύτερη:
Η μείωση μπορεί να εκτελεστεί ακόμη και όταν αποφασίσαμε να χρησιμοποιήσουμε την πρώτη μέθοδο, αλλά στο στάδιο του πολλαπλασιασμού του αριθμού 4 και του αριθμητή 3, αποφασίσαμε να επωφεληθούμε από τη μείωση:

Αλλά για παράδειγμα, η έκφραση μπορεί να υπολογιστεί μόνο με τον πρώτο τρόπο - πολλαπλασιάστε 7 στο Denomoter του κλάσματος και ο παρονομαστής δεν αλλάζει:
![]()
Αυτό οφείλεται στο γεγονός ότι ο αριθμός 7 και ο παρονομαστής του κλάσματος δεν διαθέτουν κοινό διαχωριστικό, το μεγαλύτερο μέρος της μονάδας και δεν μειώνονται αναλόγως.
Μερικοί φοιτητές κατά λάθος μειώνουν τον πολλαπλασιασμό του αριθμού και τον αριθμητή του Flush. Είναι αδύνατο να το κάνετε αυτό. Για παράδειγμα, η επόμενη καταχώρηση δεν είναι σωστή:
Η μείωση του κλάσματος υποδηλώνει ότι και τον αριθμητή και παρονομαστή θα χωριστεί στον ίδιο αριθμό. Σε μια κατάσταση με την έκφραση, το τμήμα πραγματοποιήθηκε μόνο στον αριθμητή, καθώς σημειώνεται ότι είναι σαν να γράφετε. Βλέπουμε ότι το τμήμα γίνεται μόνο στον αριθμητή και στον παρονομαστή δεν συμβαίνει.
Πολλαπλασιασμός των κλάσεων
Για να πολλαπλασιάσετε τα κλάσματα, πρέπει να πολλαπλασιάσετε τους αριθμούς και τους παρονομαστές τους. Εάν η απάντηση είναι λάθος, η σύνθλιψη είναι δυνατή, πρέπει να επισημάνετε ολόκληρο το μέρος σε αυτό.
Παράδειγμα 1. Βρείτε την τιμή της έκφρασης.
![]()
Έλαβε μια απάντηση. Συνιστάται η μείωση αυτού του κλάσματος. Το κλάσμα μπορεί να μειωθεί κατά 2. Στη συνέχεια, η τελική λύση θα λάβει την ακόλουθη φόρμα:

Η έκφραση μπορεί να γίνει κατανοητή ως τη λήψη πίτσας από το ήμισυ της πίτσας. Ας υποθέσουμε ότι έχουμε μισή πίτσα:
Πώς να πάρετε τα δύο τρίτα από αυτό το μισό; Πρώτα πρέπει να χωρίσετε αυτό το μισό σε τρία ίσα μέρη:

Και να πάρετε δύο κομμάτια από αυτά τα τρία κομμάτια:

Θα έχουμε πίτσα. Θυμηθείτε πώς μοιάζει η πίτσα, χωρισμένη σε τρία μέρη:

Ένα κομμάτι από αυτή την πίτσα και τα δύο κομμάτια που εμάς θα έχουν τις ίδιες διαστάσεις:

Με άλλα λόγια, μιλάμε για την ίδια πίτσα. Επομένως, η τιμή της έκφρασης είναι ίση

Παράδειγμα 2.. Βρείτε μια τιμή έκφρασης
Πολλαπλασιάστε τον αριθμητή του πρώτου κλάσματος στον δεύτερο αριθμητή κλάσματος και ο παρονομαστής του πρώτου κλάσματος στον παρονομαστή του δεύτερου κλάσματος:

Σε απάντηση, αποδείχθηκε το λάθος κλάσμα. Επισημάνετε ολόκληρο το μέρος σε αυτό:
![]()
Παράδειγμα 3. Βρείτε μια τιμή έκφρασης
Πολλαπλασιάστε τον αριθμητή του πρώτου κλάσματος στον δεύτερο αριθμητή κλάσματος και ο παρονομαστής του πρώτου κλάσματος στον παρονομαστή του δεύτερου κλάσματος:
![]()
Η απάντηση αποδείχθηκε το σωστό κλάσμα, αλλά θα είναι καλό αν το κόψετε. Για να μειωθεί αυτό το κλάσμα, χρειάζεστε έναν αριθμητή και παρονομαστή αυτού του κλάσματος για να διαιρέσετε στον μεγαλύτερο κοινό διαχωριστή (κόμβος) αριθμών 105 και 450.
Έτσι, βρείτε τους κόμβους των αριθμών 105 και 450:

Τώρα διαιρέστε τον αριθμητή και ο παρονομαστής της απάντησής μας στον κόμβο, το οποίο βρήκαμε τώρα, δηλαδή στα 15
Την αναπαράσταση ενός ακέραιου ακέραιου με τη μορφή κλάσματος
Οποιοσδήποτε ακέραιος μπορεί να αντιπροσωπεύεται ως κλάσμα. Για παράδειγμα, ο αριθμός 5 μπορεί να εκπροσωπείται ως. Από αυτό το ALARD δεν αλλάζει την αξία του, καθώς η έκφραση σημαίνει "ο αριθμός πέντε για να διαιρέσει από ένα", και αυτό είναι γνωστό στο Top Five:
Αντίστροφα αριθμούς
Τώρα θα εξοικειωθούμε με πολύ Ένα ενδιαφέρον θέμα Στα μαθηματικά. Ονομάζεται "αντίστροφοι αριθμοί".
Ορισμός. Επιστρέψτε στον αριθμόΕΝΑ. Ονομάζεται ο αριθμός που κατά την πολλαπλασιασμόΕΝΑ. Δίνει μια μονάδα.
Ας υποκαταστήσουμε αυτόν τον ορισμό αντί για μια μεταβλητή ΕΝΑ. Αριθμός 5 και προσπαθήστε να διαβάσετε τον ορισμό:
Επιστρέψτε στον αριθμό 5 Ονομάζεται ο αριθμός που κατά την πολλαπλασιασμό 5 Δίνει μια μονάδα.
Είναι δυνατόν να βρεθεί ένας τέτοιος αριθμός που όταν πολλαπλασιάζεται από 5 δίνει ένα; Αποδεικνύεται. Φανταστείτε ένα πέντε με τη μορφή ενός κλάσματος:
Στη συνέχεια, πολλαπλασιάστε αυτό το κλάσμα στον εαυτό μου, αλλάξτε μόνο τον αριθμητή και τον παρονομαστή. Με άλλα λόγια, θα πολλαπλασιάσω ένα κλάσμα στον εαυτό μου, μόνο γύρισε:
Τι συμβαίνει ως αποτέλεσμα αυτού; Αν συνεχίσουμε να λύουμε αυτό το παράδειγμα, θα πάμε μια μονάδα:
![]()
Έτσι, το αντίστροφο στον αριθμό 5 είναι ο αριθμός, αφού όταν πολλαπλασιάζεται 5, λαμβάνεται μια μονάδα.
Ο αντίστροφος αριθμός μπορεί επίσης να βρεθεί για οποιονδήποτε άλλο ακέραιο αριθμό.
Μπορείτε επίσης να βρείτε τη νοημοσύνη για οποιοδήποτε άλλο κλάσμα. Για να το κάνετε αυτό, αρκεί να το γυρίσετε.
Κλάσμα διαίρεσης
Ας υποθέσουμε ότι έχουμε μισή πίτσα:
Το χωρίζουμε εξίσου για δύο. Πόσα πίτσα θα φτάσουν σε όλους;

Μπορεί να φανεί ότι μετά τον διαχωρισμό του μισού της πίτσας, αποδείχθηκαν δύο ίσα κομμάτια, καθένα από τα οποία είναι πίτσα. Έτσι όλοι θα πάρουν την πίτσα.
Τώρα, όταν μάθαμε να διπλώστε και να πολλαπλασιάσουμε ξεχωριστά κλάσματα, μπορείτε να εξετάσετε πιο σύνθετα σχέδια. Για παράδειγμα, τι γίνεται αν η εργασία είναι επίσης εθισμένος και αφαιρώντας και πολλαπλασιάζοντας τα κλάσματα;
Πρώτα απ 'όλα, είναι απαραίτητο να μεταφράσετε όλα τα κλάσματα στο λάθος. Στη συνέχεια, πραγματοποιούμε συνεχώς τις απαιτούμενες ενέργειες - με τον ίδιο τρόπο όπως και για τους συμβατικούς αριθμούς. Και συγκεκριμένα:
- Πρώτον, τίθεται σε ένα πτυχίο - να απαλλαγούμε από όλες τις εκφράσεις που περιέχουν δείκτες.
- Τότε - διαίρεση και πολλαπλασιασμός.
- Το τελευταίο βήμα γίνεται προσθήκη και αφαίρεση.
Φυσικά, εάν υπάρχουν αγκύλες στην έκφραση, η διαδικασία αλλάζει - όλα όσα βρίσκονται μέσα στα στηρίγματα πρέπει να θεωρηθούν πρώτα. Και θυμηθείτε τα λάθος κλάσματα: είναι απαραίτητο να διαθέσετε ολόκληρο το μέρος όταν έχουν ήδη εκπληρωθεί όλες οι άλλες ενέργειες.
Μεταφράζουμε όλα τα κλάσματα από την πρώτη έκφραση στο λάθος και στη συνέχεια εκτελούν ενέργειες:

Τώρα βρείτε την τιμή της δεύτερης έκφρασης. Δεν υπάρχουν κλάσματα με ένα ολόκληρο κομμάτι, αλλά υπάρχουν παρένθεση, οπότε εκτελούμε την πρώτη προσθήκη, και μόνο τότε - διαίρεση. Σημειώστε ότι 14 \u003d 7 · 2. Επειτα:
Τέλος, θεωρούμε το τρίτο παράδειγμα. Υπάρχουν αγκύλες και ένα πτυχίο - καλύτερα θεωρούνται ξεχωριστά. Δεδομένου ότι 9 \u003d 3 · 3, έχουμε:
Δώστε προσοχή στο τελευταίο παράδειγμα. Για την κατασκευή ενός κλάσματος στο βαθμό, είναι απαραίτητο να διαχωριστεί ο αριθμητής ξεχωριστά σε αυτόν τον βαθμό και ξεχωριστά ο παρονομαστής.
Μπορείτε να λύσετε διαφορετικά. Εάν ανακαλέσετε το βαθμό βαθμό, η εργασία θα μειωθεί στον συνήθη πολλαπλασιασμό των κλάσεων:
Πολυώροφαρα κλάσματα
Μέχρι στιγμής, θεωρήσαμε μόνο τα "καθαρά" κλάσματα όταν ο αριθμητής και ο παρονομαστής είναι συνηθισμένοι αριθμοί. Αυτό αντιστοιχεί πλήρως στον προσδιορισμό του αριθμητικού κλάσματος που δίνεται στο πρώτο μάθημα.
Αλλά τι γίνεται αν σε έναν αριθμητή ή παρονομαστή για να τοποθετήσετε ένα πιο περίπλοκο αντικείμενο; Για παράδειγμα, ένα άλλο αριθμητικό κλάσμα; Τέτοιες δομές προκύπτουν αρκετά συχνά, ειδικά όταν εργάζονται με μεγάλες εκφράσεις. Εδώ είναι μερικά παραδείγματα:
Ο κανόνας της εργασίας με πολυώροφα κλάσματα είναι μόνο ένα πράγμα: είναι απαραίτητο να τα ξεφορτωθούμε αμέσως. Αφαιρέστε τα "επιπλέον" δάπεδα είναι αρκετά απλή αν θυμηθείτε ότι το κλασματικό χαρακτηριστικό σημαίνει μια τυπική λειτουργία διαίρεσης. Ως εκ τούτου, οποιοδήποτε κλάσμα μπορεί να ξαναγραφεί ως εξής:
Χρησιμοποιώντας αυτό το γεγονός και παρατηρούμε τη διαδικασία, θα μειώσουμε εύκολα οποιοδήποτε πολυώροφο κλάσμα στο φυσιολογικό. Ρίξτε μια ματιά στα παραδείγματα:
Μια εργασία. Μεταφράστε πολυώροφα κλάσματα στο φυσιολογικό:
Σε κάθε περίπτωση, ξαναγράψτε το κλάσμα χύδην, αντικαθιστώντας τη λειτουργία διαχωρισμού του τμήματος. Θυμάσουμε επίσης ότι ο ακέραιος αριθμός αντιπροσωπεύει με τη μορφή κλάσματος με παρονομαστή 1. Εκείνους. 12 \u003d 12/1; 3 \u003d 3/1. Παίρνουμε:

ΣΕ Το τελευταίο παράδειγμα Πριν μειωθεί ο τελικός πολλαπλασιασμός του κλάσματος.
Την εξειδίκευση της εργασίας με πολυώροφα κλάσματα
Σε πολυώροφα κλάσματα υπάρχει μια λεπτότητα που πρέπει πάντα να θυμάστε, διαφορετικά μπορείτε να πάρετε μια λανθασμένη απάντηση, ακόμα και αν όλοι οι υπολογισμοί ήταν σωστές. Ρίξε μια ματιά:
- Ο αριθμοί είναι ένας ξεχωριστός αριθμός 7, και στον παρονομαστή - το shot 12/5.
- Στον αριθμητή υπάρχει ένα κλάσμα 7/12, και στον παρονομαστή - ένας ξεχωριστός αριθμός 5.
Έτσι, για ένα αρχείο, δύο εντελώς διαφορετικές ερμηνείες που ελήφθησαν. Εάν υπολογιστεί, οι απαντήσεις θα είναι επίσης διαφορετικές:
Για να καταγράψετε πάντοτε να διαβάσετε σίγουρα, χρησιμοποιήστε έναν απλό κανόνα: η κοινή γραμμή του κύριου κλάσματος πρέπει να είναι μεγαλύτερη από το χαρακτηριστικό του χαρακτηριστικού. Κατά προτίμηση - αρκετές φορές.
Εάν ακολουθήσετε αυτόν τον κανόνα, τα παραπάνω χέρια πρέπει να καταγράφονται έτσι:
Ναι, ίσως είναι άσχημο και παίρνει πάρα πολύ χώρο. Αλλά θα εξετάσετε σωστά. Τέλος, ένα ζευγάρι παραδείγματα όπου τα πολυώροφα κλάσματα εμφανίζονται πραγματικά:
Μια εργασία. Βρείτε τις τιμές των εκφράσεων:
Έτσι, δουλεύουμε με το πρώτο παράδειγμα. Μεταφράζουμε όλα τα κλάσματα στο λάθος, και στη συνέχεια εκτελούμε τις λειτουργίες προσθήκης και διαίρεσης:

Ομοίως, προχωρήστε με το δεύτερο παράδειγμα. Μεταφράζουμε όλα τα κλάσματα στο λάθος και εκτελέσουμε τις απαιτούμενες λειτουργίες. Για να μην κουράσω τον αναγνώστη, θα δώσω κάποιους προφανείς υπολογισμούς. Εχουμε:

Λόγω του γεγονότος ότι στον αριθμητή και τον παρονομαστή των κύριων κλασμάτων υπάρχουν ποσά, ο κανόνας καταγραφής πολυώροφων πελμάτων σεβαστεί αυτόματα. Επιπλέον, στο τελευταίο παράδειγμα, αφήσαμε σκόπιμα τον αριθμό 46/1 με τη μορφή κλάσματος για την εκπλήρωση της διαίρεσης.
Σημειώνω επίσης ότι και στα δύο παραδείγματα, ένα κλασματικό χαρακτηριστικό αντικαθιστά στην πραγματικότητα αγκύλες: το πρώτο πράγμα που βρήκαμε το ποσό, και μόνο τότε είναι ιδιωτικές.
Κάποιος θα πει ότι η μετάβαση σε λάθος κλάσματα στο δεύτερο παράδειγμα ήταν σαφώς υπερβολική. Ισως είναι. Αλλά με αυτό ασφαλίζουμε τους εαυτούς μας από λάθη, επειδή η επόμενη φορά που ένα παράδειγμα μπορεί να είναι πολύ πιο περίπλοκο. Επιλέξτε τον εαυτό σας, το πιο σημαντικό: ταχύτητα ή αξιοπιστία.
Πολλαπλασιασμός και διαίρεση κλάσεων.
Προσοχή!
Αυτό το θέμα έχει επιπλέον
Υλικά σε ένα ειδικό τμήμα 555.
Για όσους είναι έντονα "όχι πολύ ..."
Και για όσους είναι "πολύ ...")
Αυτή η λειτουργία είναι πολύ πιο ακριβότερη προσθήκη-αφαίρεση! Επειδή είναι ευκολότερο. Σας υπενθυμίζω: να πολλαπλασιάσετε το κλάσμα στο κλάσμα, πρέπει να πολλαπλασιάσετε τους αριθμητικούς αριθμούς (θα είναι το προκύπτον) και οι παρονομαστές (αυτό θα είναι ο παρονομαστής). Δίνω:
Για παράδειγμα:

Όλα είναι εξαιρετικά απλά. Και παρακαλώ μην ψάξετε για έναν κοινό παρονομαστή! Δεν τον χρειάζονται εδώ ...
Για να διαιρέσετε το κλάσμα για το κλάσμα, πρέπει να γυρίσετε δεύτερος(Αυτό είναι σημαντικό!) Το κλάσμα και πολλαπλασιάστε τους, δηλ.:

Για παράδειγμα:

Εάν πιάστηκε πολλαπλασιασμός ή διαίρεση με ακέραιους ακέραιους και κλάσματα - τίποτα τρομερό. Όπως και με την προσθήκη, κάνουμε ένα κλάσμα με μια μονάδα στον παρονομαστή - και προς τα εμπρός! Για παράδειγμα:

Στα γυμνάσια, είναι συχνά απαραίτητο να αντιμετωπιστούν τριώροφες (ή ακόμα και τεσσάρων ορόφων!) Drok. Για παράδειγμα:
Πώς να φέρετε αυτό το κλάσμα σε ένα αξιοπρεπές μυαλό; Ναι, πολύ απλό! Χρήση διαίρεσης σε δύο σημεία:

Αλλά μην ξεχάσετε τη σειρά της διαίρεσης! Σε αντίθεση με τον πολλαπλασιασμό, είναι πολύ σημαντικό εδώ! Φυσικά, 4: 2, ή 2: 4 Δεν μπερδεύουμε. Αλλά στο τριώροφο κλάσμα είναι εύκολο να κάνετε ένα λάθος. Σημείωση, για παράδειγμα:
Στην πρώτη περίπτωση (έκφραση στα αριστερά):

Στο δεύτερο (έκφραση στα δεξιά):

Νιώθεις τη διαφορά; 4 και 1/9!
Και ποια είναι η τάξη της διαίρεσης; Ή αγκύλες ή (όπως εδώ) το μήκος των οριζόντιων γραμμών. Αναπτύξτε το μετρητή οφθαλμού. Και αν δεν υπάρχουν παρένθεση, ούτε παύλα, όπως:
Στη συνέχεια, διαιρέστε - πολλαπλασιασμός Σε λίγα, αριστερά προς τα δεξιά!
Και μια πολύ απλή και σημαντική τεχνική. Σε ενέργειες με πτυχία, πώς μπορώ να έρθω βολικά! Διαιρούμε τη μονάδα σε οποιοδήποτε κλάσμα, για παράδειγμα, έως τις 13/15:

Το κλάσμα γύρισε! Και συμβαίνει πάντα. Όταν διαιρεί 1 σε οποιοδήποτε κλάσμα, ως αποτέλεσμα, παίρνουμε το ίδιο κλάσμα μόνο ανεστραμμένο.
Αυτές είναι όλες οι ενέργειες με κλάσματα. Το πράγμα είναι αρκετά απλό, αλλά τα λάθη δίνουν κάτι περισσότερο από αρκετό. Σημείωση Πρακτικές συμβουλέςΚαι τα (σφάλματα τους) θα είναι λιγότερο!
Πρακτικές συμβουλές:
1. Το πιο σημαντικό πράγμα που εργάζεστε με κλασματικές εκφράσεις είναι η ακρίβεια και η προσοχή! Δεν είναι Γενικές λέξεις, όχι καλές ευχές! Αυτή είναι μια σκληρή ανάγκη! Όλοι οι υπολογισμοί σχετικά με τις εξετάσεις κάνουν ως πλήρη εργασία, εστιάζοντας και σαφώς. Είναι καλύτερο να γράψετε δύο επιπλέον γραμμές στο σχέδιο, παρά να συσσωρεύσετε κατά τον υπολογισμό του νου.
2. Στα παραδείγματα με Διαφορετικά είδη Κλάσματα - Πηγαίνετε σε συνηθισμένα κλάσματα.
3. Όλα τα κλάσματα κόβονται μέχρι να σταματήσει.
4. Οι πολυώροφες κλασματικές εκφράσεις μειώνεται σε συνηθισμένη, χρησιμοποιώντας τη διαίρεση σε δύο σημεία (ακολουθήστε τη σειρά της διαίρεσης!).
5. Μονάδα κλάσματος Διαχωρίστε κατά νου, απλά γυρίζοντας το κλάσμα.
Εδώ είναι τα καθήκοντα που πρέπει να σπάσετε. Οι απαντήσεις δίνονται μετά από όλα τα καθήκοντα. Χρησιμοποιήστε τα υλικά αυτού του θέματος και πρακτικών συμβουλών. Μετρήστε πόσα παραδείγματα θα μπορούσατε να λύσετε σωστά. Η πρώτη φορά! Χωρίς αριθμομηχανή! Και να κάνει πιστά συμπεράσματα ...
Θυμηθείτε - η σωστή απάντηση, Οι προκύπτουν από τη δεύτερη (ακόμα περισσότερο - το τρίτο) φορές - δεν θεωρούνται! Αυτή είναι μια σκληρή ζωή.
Ετσι, Αποφασίζουμε στη λειτουργία εξέτασης ! Αυτό είναι ήδη προετοιμασμένο για την εξέταση, παρεμπιπτόντως. Λυφίζουμε το παράδειγμα, ελέγξτε, λύστε τα παρακάτω. Αποφάσισαν τα πάντα - έλεγαν και πάλι από το πρώτο που διαρκούν. Μόνο αργότερα Εξετάζουμε τις απαντήσεις.
Υπολογίζω:


Κόψατε;
Ψάχνουμε για απαντήσεις που συμπίπτουν με τη δική σας. Τους κατέγραψα συγκεκριμένα σε αταξία, μακριά από τον πειρασμό, έτσι να μιλήσουμε ... έτσι ώστε να απαντηθούν, το σημείο με το κόμμα καταγράφεται.
0; 17/22; 3/4; 2/5; 1; 25.
Και τώρα κάνουμε συμπεράσματα. Αν συμβεί όλα - χαίρομαι για σένα! Στοιχειώδεις υπολογισμοί με κλάσματα - όχι το πρόβλημά σας! Μπορείτε να κάνετε πιο σοβαρά πράγματα. Αν όχι...
Έτσι έχετε ένα από τα δύο προβλήματα. Ή ταυτόχρονα.) Έλλειψη γνώσης και (ή) απροσεξία. Αλλά αυτό επιλυθεί Προβλήματα.
Αν σας αρέσει αυτό το site ...
Με την ευκαιρία, έχω άλλα δύο ενδιαφέρουσες τοποθεσίες για εσάς.)
Μπορεί να έχει πρόσβαση στην επίλυση παραδειγμάτων και να μάθετε το επίπεδο σας. Δοκιμές με άμεση έλεγχο. Μάθετε - με ενδιαφέρον!)
Μπορείτε να εξοικειωθείτε με χαρακτηριστικά και παράγωγα.
Το άρθρο αυτό θεωρεί τις ενέργειες σε κλάσματα. Οι κανόνες προσθήκης, αφαίρεσης, πολλαπλασιασμού, διαίρεσης ή ανέγερσης των κλασμάτων του κλάσματος Α Β σχηματίζονται και δικαιολογούνται και δικαιολογούνται, όπου τα Α και Β μπορεί να είναι αριθμοί, αριθμητικές εκφράσεις ή εκφράσεις με μεταβλητές. Συμπερασματικά, θα ληφθούν υπόψη παραδείγματα λύσεων με λεπτομερή περιγραφή.
Yandex.rtb r-a-339285-1
Κανόνες για την εκτέλεση ενεργειών με αριθμητικά κλάσματα της γενικής φόρμας
Τα αριθμητικά κλάσματα της γενικής προβολής έχουν έναν αριθμητή και έναν παρονομαστή στο οποίο υπάρχουν φυσικοί αριθμοί ή αριθμητικές εκφράσεις. Εάν θεωρούμε τέτοια κλάσματα, όπως 3 5, 2, 84, 1 + 2,34 · (5-2), 3 4 + 7 8 2, 3-0, 8, 1 2,2, π 1 - 2 3 + Π, 2 0, 5 LN 3, μπορεί να φανεί ότι ο αριθμητής και ο παρονομαστής δεν μπορούν να έχουν μόνο αριθμούς, αλλά και εκφράσεις διαφόρων σχεδίων.
Ορισμός 1.
Υπάρχουν κανόνες για τους οποίους η δράση βρίσκεται σε εξέλιξη με τα συνηθισμένα κλάσματα. Είναι κατάλληλο για τα κλάσματα της γενικής φόρμας:
- Κατά την αφαίρεση των κλασμάτων με τους ίδιους παρονομαστές, αναδιπλώνεται μόνο οι αριθμοί και ο παρονομαστής παραμένει ο ίδιος, δηλαδή: ένα d ± C d \u003d A ± C D, οι τιμές των Α, C και D ≠ 0 είναι ορισμένοι αριθμοί ή αριθμητικές εκφράσεις.
- Κατά την προσθήκη ή αφαιρώντας τα κλάσματα με διαφορετικούς παρονομαστές, είναι απαραίτητο να φέρει σε ένα κοινό, μετά το οποίο προστίθεται ή αφαιρεί τα κλάσματα που λαμβάνονται με τους ίδιους δείκτες. Αλφαβητικά μοιάζει με β ± C d \u003d a · p ± c · r s, όπου οι τιμές Α, B ≠ 0, C, D ≠ 0, P ≠ 0, R ≠ 0, S ≠ 0 είναι Ισχύς αριθμοί, και το b · p \u003d d · r \u003d s. Όταν p \u003d d και r \u003d b, κατόπιν a b ± c d \u003d a · d ± c · d b · d.
- Με τον πολλαπλασιασμό των κλάσεων, μια ενέργεια εκτελείται με αριθμούς, μετά από τους οποίους με τους παρονομαστές, στη συνέχεια λαμβάνουμε ένα b · c d \u003d a · c b · d, όπου a, b ≠ 0, c, d ≠ 0 λειτουργεί ως έγκυρος αριθμοί.
- Κατά τη διαίρεση του κλάσματος στο κλάσμα, το πρώτο πολλαπλασιάζεται με το δεύτερο αντίστροφο, δηλαδή, παράγουμε αντικατάσταση με θέσεις αριθμητικού και παρονομαστή: Α Β: CD \u003d A B · DC.
Αιτιολόγηση των κανόνων
Ορισμός 2.Υπάρχουν οι ακόλουθες μαθηματικές στιγμές που βασίζονται κατά τον υπολογισμό:
- Το κλασματικό χαρακτηριστικό σημαίνει ένα σημάδι της διαίρεσης.
- Το τμήμα θεωρείται πολλαπλασιασμό στην επιστροφή της αξίας.
- εφαρμόζοντας τις ιδιότητες των ενεργειών με έγκυρους αριθμούς.
- Εφαρμογή της κύριας περιουσίας των κλάσεων και αριθμητικών ανισοτήτων.
Με τη βοήθειά τους, μπορείτε να μετατρέψετε τη φόρμα:
ένα d ± C d \u003d A · D - 1 ± C · D - 1 \u003d A ± C · D - 1 \u003d A ± C D; ένα b ± c d \u003d a · p b · p ± c · r d · r \u003d a · p s ± c · e s \u003d a · p ± c · r s; Ab · CD \u003d a · db · d · b · cb · d \u003d a · d · a · d-1 · b · c · b · d - 1 \u003d \u003d a · d · b · c · b · d - 1 · B · d - 1 \u003d a · d · b · cb · d · b · d - 1 \u003d \u003d (α · C) · (b · d) - 1 \u003d a · cb · d
Παραδείγματα
Στην προηγούμενη παράγραφο, αναφέρθηκε για τη δράση με κλάσματα. Ακολουθεί αυτό το κλάσμα χρειάζεται να απλοποιήσει. Αναλυτικά, αυτό το θέμα εξετάστηκε στο σημείο μετατροπής κλάσματος.
Αρχικά, εξετάστε ένα παράδειγμα προσθήκης και αφαιρέστε τα κλάσματα με τον ίδιο παρονομαστή.
Παράδειγμα 1.
Τα κλάσματα 8 2, 7 και 1 2, 7 δίδονται, τότε ο αριθμητής πρέπει να διπλωθεί σύμφωνα με τον κανόνα και να ξαναγράψει τον παρονομαστή.
Απόφαση
Στη συνέχεια, έχουμε ένα κλάσμα της φόρμας 8 + 1 2, 7. Μετά την ολοκλήρωση της προσθήκης, λαμβάνουμε ένα κλάσμα της μορφής 8 + 1 2, 7 \u003d 92, 7 \u003d 90 27 \u003d 313. Έτσι, 8 2, 7 + 1 2, 7 \u003d 8 + 1 2, 7 \u003d 92, 7 \u003d 90 27 \u003d 3 1 3.
Απάντηση: 8 2 , 7 + 1 2 , 7 = 3 1 3
Υπάρχει ένας άλλος τρόπος επίλυσης. Αρχικά, η μετάβαση στο είδος του συνηθισμένου κλάσματος, μετά την οποία απλοποιήσαμε. Μοιάζει με αυτό:
8 2 , 7 + 1 2 , 7 = 80 27 + 10 27 = 90 27 = 3 1 3
Παράδειγμα 2.
Θα αφαιρέσουμε από 1 - 2 3 · Log 2 3 · Κλάσματα αρχείου 2 5 + 1 του τύπου 2 3 3 · Log 2 3 · Log 2 5 + 1.
Δεδομένου ότι δίδονται ίσοι απόρριψη, αυτό σημαίνει ότι εκτελούμε τον υπολογισμό του κλάσματος με τον ίδιο παρονομαστή. Το παίρνουμε
1 - 2 3 · Log 2 3 · log 2 5 + 1 - 2 3 3 · log 2 3 · log 2 5 + 1 \u003d 1 - 2 - 2 3 3 · log 2 3 · log 2 5 + 1
Υπάρχουν παραδείγματα υπολογισμού κλασμάτων με διαφορετικούς παρονομαστές. Ένα σημαντικό σημείο είναι να φέρει σε έναν κοινό παρονομαστή. Χωρίς αυτό, δεν θα μπορέσουμε να εκτελέσουμε περαιτέρω βήματα με κλάσματα.
Η διαδικασία δεσμεύεται εξ αποστάσεως να φέρει σε έναν κοινό παρονομαστή. Δηλαδή, η αναζήτηση του μικρότερου γενικού διαχωριστή γίνεται στον παρονομαστή, μετά την οποία προστίθενται οι παράγοντες που λείπουν για κλάσματα.
Εάν τα πτυσσόμενα κλάσματα δεν έχουν κοινό πολλαπλασιαστές, τότε μπορούν να είναι το έργο τους.
Παράδειγμα 3.
Εξετάστε το παράδειγμα της προσθήκης κλάσεων 2 3 5 + 1 και 1 2.
Απόφαση
Στην περίπτωση αυτή, ο γενικός παρονομαστής εκτελεί το έργο του παρονομαστή. Στη συνέχεια, λαμβάνουμε ότι 2,3 5 + 1. Στη συνέχεια, κατά τη ρύθμιση πρόσθετων παραγόντων, έχουμε ότι το πρώτο κλάσμα είναι ίσο με 2, και το δεύτερο 3 5 + 1. Μετά το πολλαπλασιασμό του κλάσματος δίνεται στη μορφή 4 2,3 5 + 1. Η συνολική μονάδα δίσκου 1 2 θα έχει μία μορφή 3 5 + 1 2,3 5 + 1. Οι προκύπτουσες κλασματικές εκφράσεις διπλώστε και πάρουν αυτό
2 3 5 + 1 + 1 2 \u003d 2,2 2,3 5 + 1 2,3 5 + 1 \u003d 4 2,3 5 + 1 + 3 5 + 1 2,3 5 + 1 \u003d 4 + 3 5 + 1 2 · 3 5 + 1 \u003d 5 + 3 5 2 · 3 5 + 1
Απάντηση: 2 3 5 + 1 + 1 2 \u003d 5 + 3 5 2 · 3 5 + 1
Όταν ασχολούμαστε με τα κλάσματα της γενικής μορφής, τότε ο μικρότερος γενικός παρονομαστής συνήθως δεν έχει σημασία. Ως παρονομαστής, είναι ασύμφορη να πάρει το προϊόν των αριθμών. Για να ξεκινήσετε, ελέγξτε αν υπάρχει ένας αριθμός που είναι μικρότερος από την αξία από την εργασία τους.
Παράδειγμα 4.
Εξετάστε σύμφωνα με το παράδειγμα 1 6 · 2 1 5 και 1 4,23 5, όταν το προϊόν τους θα είναι ίσο με 6,21 5,4,235 \u003d 24,24 5. Στη συνέχεια, λαμβάνουμε 12,23 5 ως γενικός παρονομαστής.
Εξετάστε παραδείγματα πολλαπλασιασμών κλάσεων της γενικής μορφής.
Παράδειγμα 5.
Για να γίνει αυτό, είναι απαραίτητο να παράγεται πολλαπλασιασμός 2 + 1 6 και 2 · 5 3 · 2 + 1.
Απόφαση
Ο ακόλουθος κανόνας, πρέπει να ξαναγράψετε και να γράψετε ένα προϊόν αριθμών με τη μορφή παρονομαστή. Λαμβάνουμε ότι 2 + 1 6,2,5 3,2 + 1 2 + 1,2,56,3,3,2 + 1. Όταν το κλάσμα πολλαπλασιάζεται, μπορεί να μειωθεί για να το απλοποιήσει. Στη συνέχεια 5 · 3 3 2 + 1: 10 9 3 \u003d 5,33 2 + 1,93 10.
Χρησιμοποιώντας τον κανόνα μετάβασης από τη διαίρεση του πολλαπλασιασμού στο πίσω πλάνο, παίρνουμε ένα κλάσμα αντίστροφο αυτό. Για να το κάνετε αυτό, ο αριθμητής και ο παρονομαστής αλλάζουν σε μέρη. Σκεφτείτε το παράδειγμα:
5 · 3 3 2 + 1: 10 9 3 \u003d 5 · 3 3 2 + 1 · 9 3 10
Μετά από αυτό, πολλαπλασιασμός και απλοποιήστε το προκύπτον κλάσμα. Εάν είναι απαραίτητο, τότε απαλλαγείτε από τον παράλογο στον παρονομαστή. Το παίρνουμε
5 · 3 3 2 + 1: 10 9 3 \u003d 5 · 3 3 · 9 3 10 · 2 + 1 \u003d 5 · 2 10 · 2 + 1 \u003d 32 · 2 + 1 \u003d \u003d 3 · 2-12 · 2 + 1 · 2 - 1 \u003d 3 · 2 - 1 2 · 2 2 - 1 2 \u003d 3 · 2 - 1 2
Απάντηση: 5 · 3 3 2 + 1: 10 9 3 \u003d 3 · 2 - 1 2
Αυτό το στοιχείο είναι εφαρμόσιμο όταν ο αριθμός ή η αριθμητική έκφραση μπορεί να αντιπροσωπεύεται ως κλάσμα που έχει παρονομαστή ίσο με 1, τότε η ενέργεια με ένα τέτοιο κλάσμα θεωρείται ξεχωριστό στοιχείο. Για παράδειγμα, η έκφραση 1 6 · 7 4-1 · 3 Μπορεί να φανεί ότι η ρίζα του 3 μπορεί να αντικατασταθεί από άλλη έκφραση 3 1. Στη συνέχεια, αυτή η καταχώρηση θα μοιάζει με πολλαπλασιασμό δύο κλάσματα της μορφής 1 6 · 7 4-1 · 3 \u003d 1 6 · 7 4-1 · 3 1.
Εκτέλεση δράσης με κλάσματα που περιέχουν μεταβλητές
Οι κανόνες που συζητήθηκαν στο πρώτο άρθρο ισχύουν για δράση με κλάσματα που περιέχουν μεταβλητές. Εξετάστε τον κανόνα έκπτωσης όταν οι παρονομητές είναι οι ίδιοι.
Είναι απαραίτητο να αποδειχθεί ότι το Α, C και D (D δεν είναι ίσο με το μηδέν) μπορεί να είναι οποιεσδήποτε εκφράσεις και η ισότητα Α ± CD \u003d A ± CD ισούται με την περιοχή επιτρεπτών τιμών.
Είναι απαραίτητο να πάρετε ένα σύνολο μεταβλητών περίεργο. Τότε a, c, d θα πρέπει να λάβει τις κατάλληλες τιμές ενός 0, C 0 και D 0. Η υποκατάσταση της μορφής Α ± C1 έχει ως αποτέλεσμα τη διαφορά της μορφής Α 0 D 0 ± C 0 D 0, όπου σύμφωνα με τον κανόνα της προσθήκης, λαμβάνουμε τον τύπο της φόρμας Α 0 ± C 0 D 0. Εάν υποκαθιστούμε την έκφραση A ± C D, τότε λαμβάνουμε το ίδιο κλάσμα της μορφής Α 0 ± C 0 D 0. Από εδώ συμπεραίνουμε ότι η επιλεγμένη τιμή που ικανοποιεί την OTZ, A ± C d και D ± C D θεωρείται ότι είναι ίση.
Με οποιαδήποτε αξία μεταβλητών, η έκφραση αυτή θα είναι ίση, δηλαδή, ονομάζονται ταυτόσημα ίση. Έτσι, αυτή η έκφραση θεωρείται αποδεδειγμένη ισότητα της μορφής Α ± CD \u003d A ± CL.
Παραδείγματα προσθήκης και αφαίρεσης κλάσεων με μεταβλητές
Όταν υπάρχουν οι ίδιοι παρονομαστείτε, πρέπει μόνο να διπλώσετε ή να αφαιρέσετε τους αριθμούς. Ένα τέτοιο κλάσμα μπορεί να απλοποιηθεί. Μερικές φορές πρέπει να εργαστείτε με κλάσματα που είναι πανικά ίσα, αλλά με την πρώτη ματιά, είναι ανεπαίσθητο, καθώς είναι απαραίτητο να εκτελέσετε ορισμένους μετασχηματισμούς. Για παράδειγμα, το x 2 3 · x 1 3 + 1 και x 1 3 + 1 2 ή 1 2 · Sin 2 α και αμαρτία a · cos a. Πιο συχνά απλοποιώντας την έκφραση προέλευσης για να δείτε τους ίδιους παρονομαστές.
ΠΑΡΑΔΕΙΓΜΑ 6.
Υπολογίστε: 1) x 2 + 1 x + x - 2 - 5 - xx + x - 2, 2) LG 2 x + 4 Χ · (LGX + 2) + 4 · LGXX · (LGX + 2), X - 1 x - 1 + xx + 1.
Απόφαση
- Για να υπολογίσετε, είναι απαραίτητο να αφαιρέσετε τα κλάσματα που έχουν τους ίδιους παρονομαστές. Στη συνέχεια, λαμβάνουμε ότι το x 2 + 1 x + x - 2 - 5- x x + x - 2 \u003d x 2 + 1 - 5 - x x + x - 2. Μετά από αυτό, μπορείτε να εκτελέσετε την αποκάλυψη παρενθέσεων με την άρση παρόμοιων όρων. Λαμβάνουμε ότι το x 2 + 1 - 5 - x + x-2 \u003d x 2 + 1 - 5 + x x + x - 2 \u003d x 2 + x - 4 x + x - 2
- Δεδομένου ότι οι παρονομαστές είναι οι ίδιοι, παραμένει μόνο να διπλώσει τους αριθμούς, αφήνοντας τον παρονομαστή: LG 2 x + 4 Χ · (LGX + 2) + 4 · LGXX · (LGX + 2) \u003d LG 2 x + 4 + 4 Χ · (LGX + 2)
Η προσθήκη ολοκληρώθηκε. Μπορεί να φανεί ότι είναι δυνατόν να μειωθεί το κλάσμα. Ο αριθμητής του μπορεί να τυλιχτεί από το άθροισμα του αθροίσματος του ποσού, τότε λαμβάνουμε (l g x + 2) 2 Από τους τύπους συντομευμένου πολλαπλασιασμού. Τότε το παίρνουμε αυτό
L g 2 x + 4 + 2 · l g x x · (L g x + 2) \u003d (L g x + 2) 2x · (L g x + 2) \u003d l g x + 2 x - Τα καθορισμένα κλάσματα της μορφής Χ - 1 Χ - 1 + Χ Χ + 1 με διαφορετικούς παρονομαστές. Μετά τη μετατροπή, μπορείτε να πάτε στην προσθήκη.
Εξετάστε μια αμφίδρομη λύση.
Η πρώτη μέθοδος είναι ότι ο παρονομαστής του πρώτου κλάσματος υποβάλλεται σε αποσύνθεση πολλαπλασιαστών με τη βοήθεια τετραγώνων και με την επακόλουθη μείωση της. Παίρνουμε ένα κλάσμα του είδους
x - 1 x - 1 \u003d x - 1 (x-1) · x + 1 \u003d 1 x + 1
Έτσι x - 1 x - 1 + x x + 1 \u003d 1 χ + 1 + x x + 1 \u003d 1 + x x + 1.
Σε αυτή την περίπτωση, είναι απαραίτητο να απαλλαγούμε από τον παράλογο στον παρονομαστή.
1 + x x + 1 \u003d 1 + x · x - 1 x + 1 · x - 1 \u003d x - 1 + x · x - x x - x - 1
Η δεύτερη μέθοδος συνίσταται στην πολλαπλασιασμό του αριθμητή και του παρονομαστή του δεύτερου κλάσματος στην έκφραση X - 1. Έτσι, απαλλαγούμε από τον παράλογο και πηγαίνουμε στην προσθήκη κλάσεων παρουσία του ίδιου παρονομαστή. Επειτα
x - 1 x - 1 + xx + 1 \u003d x - 1 x - 1 + x-x - 1 x + 1 · x - 1 \u003d x - 1 x - 1 + x-x - xx - 1 \u003d x - 1 + x-x - xx - 1
Απάντηση: 1) x 2 + 1 x + x - 2 - 5 - xx + x-2 \u003d x 2 + x - 4 x + x - 2, 2) LG2X + 4 Χ · (LGX + 2) + 4 · LGXX · (LGX + 2) \u003d LGX + 2 Χ, 3) Χ - 1 Χ - 1 + XX + 1 \u003d Χ - 1 + Χ · Χ - ΧΧ - 1.
Στο τελευταίο παράδειγμα, πήραν αναπόφευκτα σε έναν κοινό παρονομαστή. Για να το κάνετε αυτό, απλοποιήστε το κλάσμα. Για να προσθέσετε ή να υποτεθείτε, είναι πάντα απαραίτητο να αναζητήσετε έναν κοινό παρονομαστή, το οποίο μοιάζει με ένα προϊόν παρονομαστών με την προσθήκη πρόσθετων ελαττωμάτων στους αριθμούς.
Παράδειγμα 7.
Υπολογίστε τις τιμές των κλάσεων: 1) x 3 + 1 x 7 + 2 · 2, 2) x + 1 Χ · LN 2 (x + 1) · (2 \u200b\u200bx - 4) - SIN XX 5 · LN (x + 1) · (2 \u200b\u200bx - 4), 3) 1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x
Απόφαση
- Κανένας πολύπλοκος υπολογισμός δεν απαιτεί παρονομαστή, οπότε πρέπει να επιλέξετε το προϊόν της μορφής 3 · Χ 7 + 2 · 2, έπειτα στο πρώτο κλάσμα Χ 7 + 2,2 επιλέγονται ως πρόσθετο παράγοντα και 3 έως δευτερόλεπτα . Όταν πολλαπλασιάζουμε, λαμβάνουμε το κλάσμα της Μορφής Χ 3 + 1 Χ 7 + 2 · 2 \u003d Χ 7 + 2 · 2 3 · Χ 7 + 2 · 2 + 3 · 1 3 · Χ 7 + 2 · 2 \u003d Χ 7 + 2 · 2 + 3 3 · Χ 7 + 2 · 2 \u003d Χ · Χ 7 + 2 · 2 · Χ + 3 3 · Χ 7 + 2 · 2
- Μπορεί να φανεί ότι οι παρονομαστές παρουσιάζονται με τη μορφή εργασίας, πράγμα που σημαίνει περιττό σε πρόσθετες μετασχηματισμούς. Ένας κοινός παρονομαστής θα θεωρηθεί προϊόν της Μορφής Χ 5 · LN 2 Χ + 1 · 2 Χ - 4. Ως εκ τούτου x 4.
Είναι ένας επιπλέον παράγοντας για το πρώτο κλάσμα και LN (x + 1)
στο δεύτερο. Μετά από αυτό παράγουμε αφαίρεση και πάρτε αυτό:
x + 1 Χ · LN 2 (x + 1) · 2 x - 4 - SIN XX 5 · LN (x + 1) · 2 χ- 4 \u003d x + 1 · χ 4 Χ 5 · LN2 (x + 1) · 2 x - 4 - SIN X · LN X + 1 Χ 5 · LN 2 (x + 1) · (2 \u200b\u200bχ- 4) \u003d x + 1 · x 4 - SIN X · LN (X + 1) Χ 5 · LN 2 (Χ + 1) · (2 \u200b\u200bχ- 4) \u003d Χ · Χ 4 + Χ4 - SIN Χ · LN (χ + 1) Χ 5 · LN2 (Χ + 1) · (2 X - 4) - Αυτό το παράδειγμα έχει νόημα όταν εργάζεστε με παρονομαστές. Είναι απαραίτητο να εφαρμοστεί οι τύποι διαφοράς μεγέθους και το τετράγωνο του ποσού, καθώς είναι αυτοί που θα δώσουν την ευκαιρία να πάνε στην έκφραση της μορφής 1 cos x - x · cos x + x + 1 (cos x + x (cos x + x ) 2. Μπορεί να φανεί ότι ο Fraraty δίνεται σε έναν κοινό παρονομαστή. Λαμβάνουμε ότι το cos x - x · cos x + x 2.
Μετά από την οποία το έχουμε αυτό
1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x \u003d \u003d 1 cos x-x · cos x + x + 1 cos x + x 2 \u003d \u003d cos x + x cos x - x · cos x + x 2 + cos x - x cos x - x · cos x + x 2 \u003d \u003d cos x + x + cos x - x cos x - x · cos x + x 2 \u003d 2 · cos x cos x - x · Cos x + x 2
Απάντηση:
1) x 3 + 1 Χ 7 + 2 · 2 \u003d Χ · Χ 7 + 2 · 2 · Χ + 3 3 · χ 7 + 2 · 2, 2) χ + 1 Χ · LN2 (Χ + 1) · 2 X - 4 - SIN XX 5 · LN (x + 1) · 2 χ- 4 \u003d \u003d x · x 4 + x 4 - SIN X · LN (Χ + 1) Χ 5 · LN2 (Χ + 1) · 2 x-4), 3) 1 cos 2 x - x + 1 cos 2 x + 2 · cos x · x + x \u003d 2 · cos x cos x - x · cos x + x 2.
Παραδείγματα πολλαπλασιασμού των κλάσεων με μεταβλητές
Όταν πολλαπλασιάζοντας τα κλάσματα, ο αριθμητής πολλαπλασιάζεται με τον αριθμητή και τον παρονομαστή στον παρονομαστή. Στη συνέχεια, μπορείτε να εφαρμόσετε τη συντομογραφία.
Παράδειγμα 8.
Κάντε τον πολλαπλασιασμό των κλάσεων x + 2 · x x x 2 · LN χ 2 · LN χ + 1 και 3 · Χ 2 1 3 · X + 1 - 2 SIN 2 · X - X.
Απόφαση
Ο πολλαπλασιασμός πρέπει να εκτελείται. Το παίρνουμε
x + 2 · xx 2 · ln x 2 · ln x + 1 · 3 · x 2 1 3 · x + 1 - 2 αμαρτία (2 · x-x) \u003d x - 2, x · 3- x 2 1 3 · X + 1 - 2 x 2 · ln x 2 · ln x + 1 · sin (2 · x - x)
Ο αριθμός 3 μεταφέρεται στην πρώτη θέση για την ευκολία καταμέτρησης και μπορείτε να μειώσετε το κλάσμα στο x 2, τότε λαμβάνουμε την έκφραση
3 · x - 2 · x · x 1 3 · x + 1 - 2 ln x 2 · ln x + 1 · SIN (2 · x - x)
Απάντηση: x + 2 · xx 2 · ln x 2 · ln x + 1 · 3 · x 2 1 3 · x + 1 - 2 αμαρτία (2 · x-x) \u003d 3, x - 2, x · x 1 3 · x + 1 - 2 ln x 2 · ln x + 1 · SIN (2 · X-x).
Διαίρεση
Η διαίρεση σε κλάσματα είναι παρόμοια με τον πολλαπλασιασμό, καθώς το πρώτο κλάσμα πολλαπλασιάζεται με το δεύτερο αντίστροφο. Εάν λάβουμε για παράδειγμα το κλάσμα X + 2 · XX 2 · LN Χ 2 · LN Χ + 1 και διαιρούμενο με 3 · Χ 2 1 3 · X + 1 - 2 SIN 2 · X - X, τότε αυτό μπορεί να γραφτεί έτσι ώστε
x + 2 · xx 2 · ln x 2 · ln x + 1: 3 · x 2 1 3 · x + 1 - 2 αμαρτία (2 · x-x), μετά την οποία αντικαθίσταται από το προϊόν της μορφής x + 2 · xx 2 · ln x 2 · ln x + 1 · 3 · x 2 1 3 · x + 1 - 2 αμαρτία (2 · x - x)
Σε βαθμό
Ας στραφούμε στην εξέταση της δράσης με τα κλάσματα του γενικού τύπου με την άσκηση στο βαθμό. Εάν υπάρχει πτυχίο με φυσική φιγούρα, τότε η ενέργεια θεωρείται ότι πολλαπλασιάζοντας τα ίδια κλάσματα. Αλλά συνιστάται η χρήση μιας κοινής προσέγγισης που βασίζεται στις ιδιότητες των βαθμών. Οποιεσδήποτε εκφράσεις Α και Γ, όπου είναι ταυτόσημα ίση με το μηδέν και οποιοδήποτε έγκυρο R στο OTZ για να εκφράσει τη φόρμα A CR είναι έγκυρη ισότητα A CR \u003d A R C R. Το αποτέλεσμα είναι το κλάσμα, ανεγέρθηκε σε ένα βαθμό. Για παράδειγμα, εξετάστε:
x 0, 7 - π · LN 3 Χ - 2 - 5 x + 1 2, 5 \u003d x 0, 7- π · LN 3 Χ - 2 - 5 2, 5 χ + 1 2, 5
Διαδικασία εκτέλεσης δράσης με κλάσματα
Οι δράσεις για τα κλάσματα εκτελούνται σύμφωνα με ορισμένους κανόνες. Στην πράξη, παρατηρούμε ότι η έκφραση μπορεί να περιέχει αρκετά κλάσματα ή κλασματικές εκφράσεις. Στη συνέχεια, είναι απαραίτητο να εκτελέσετε όλες τις ενέργειες με αυστηρή σειρά: να σηκώσετε το πτυχίο, να πολλαπλασιάσετε, να διαιρέσετε και στη συνέχεια να διπλώσετε και να αφαιρέσετε. Εάν υπάρχουν αγκύλες, η πρώτη ενέργεια εκτελείται σε αυτά.
Παράδειγμα 9.
Υπολογίστε 1 - X COS X - 1 C O S x · 1 + 1 x.
Απόφαση
Δεδομένου ότι έχουμε τον ίδιο παρονομαστή, στη συνέχεια 1 - X COS X και 1 C O S x, αλλά είναι αδύνατο να παραχθεί αφαίρεση σύμφωνα με τον κανόνα, οι πρώτες δράσεις εκτελούνται σε παρένθεση, μετά από τους οποίους ο πολλαπλασιασμός και στη συνέχεια προσθήκη. Στη συνέχεια, κατά τον υπολογισμό του παίρνουμε αυτό
1 + 1 Χ \u003d 1 1 + 1 Χ \u003d x x + 1 x \u003d x + 1 x
Όταν υποκαθιστούν την έκφραση στο πρωτότυπο, λαμβάνουμε ότι το 1 είναι x cos x - 1 cos x · x + 1 x. Όταν πολλαπλασιάζονται τους πείρους, έχουμε: 1 cos x · x + 1 x \u003d x + 1 cos x · x. Με την παραγωγή όλων των υποκαταστάσεων, λαμβάνουμε 1 - x cos x - x + 1 cos x · x. Τώρα είναι απαραίτητο να συνεργαστείτε με κλάσματα που έχουν διαφορετικούς παρονομαστές. Παίρνουμε:
x · 1 - x cos x · x - x + 1 cos x · x \u003d x · 1 - x - 1 + x cos x \u003d x \u003d x - x - x - 1 cos x · x \u003d - x + 1 cos x · Χ.
Απάντηση: 1 - x cos x - 1 c o x · 1 + 1 x \u003d - x + 1 cos x · x.
Εάν παρατηρήσετε ένα λάθος στο κείμενο, επιλέξτε το και πατήστε Ctrl + Enter
1º. Ακέραιοι αριθμοί- Αυτοί είναι αριθμοί που χρησιμοποιούνται με το σκορ. Το σύνολο όλων των φυσικών αριθμών Denotesn, I.E.N \u003d (1, 2, 3, ...).
ΚλάσμαΈνας αριθμός που αποτελείται από διάφορα κομμάτια μονάδας καλείται. Συνηθισμένο κλάσμαΟνομάζεται ο αριθμός των ειδών όπου ο φυσικός αριθμός Ν.δείχνει πόσα ίσα μέρη χωρίζονται από μια μονάδα και έναν φυσικό αριθμό Μ.Δείχνει πόσα τέτοια ίσα μέρη λαμβάνονται. Αριθμοί Μ.και Ν.Που ονομάζεται ανάλογα Αριθμητήςκαι παρονομαστήςκλάσμα.
Εάν ο αριθμητής είναι μικρότερος από τον παρονομαστή, τότε το συνηθισμένο κλάσμα καλείται σωστά? Εάν ο αριθμητής είναι ίσος με τον παρονομαστή ή περισσότερο από αυτό, τότε το κλάσμα καλείται λανθασμένος. Ο αριθμός που αποτελείται από το σύνολο και τα κλασματικά μέρη καλείται Μικτός αριθμός.
Για παράδειγμα,  - σωστά συνηθισμένα κλάσματα,
- σωστά συνηθισμένα κλάσματα,  - Εσφαλμένα τα συνηθισμένα κλάσματα, 1- μεικτό αριθμό.
- Εσφαλμένα τα συνηθισμένα κλάσματα, 1- μεικτό αριθμό.
2º Κατά την εκτέλεση δράσης σε τα συνηθισμένα κλάσματα, πρέπει να θυμόμαστε τους ακόλουθους κανόνες:
1) Η κύρια ιδιοκτησία των Fraci. Εάν ο αριθμητής και ο παρονομαστής του κλάσματος πολλαπλασιάζονται ή χωρίζονται σε έναν και τον ίδιο φυσικό αριθμό, τότε αποδεικνύεται το κλάσμα ίσο με αυτό.
Για παράδειγμα, α)  ? σι)
? σι)  .
.
Η διαίρεση του αριθμητή και του παρονομαστή του κλάσματος στον κοινό τους διαιρέτη, εκτός από ένα, καλείται Μείωση των fraci.
2) Για να γίνει ένας μικτός αριθμός που να υπάρχει υπό τη μορφή ενός λανθασμένου κλάσματος, πρέπει να το πολλαπλασιάσετε ως συνάρτηση του κλασματικού μέρους και να προσθέσετε τον αριθμό κλασματικού μέρους στο προκύπτον προϊόν, γράψτε το προκύπτον άθροισμα του κλάσματος και του Ο παρονομαστής παραμένει για το ίδιο.
Ομοίως, οποιοσδήποτε φυσικός αριθμός μπορεί να γραφτεί ως εσφαλμένο κλάσμα με οποιονδήποτε παρονομαστή.
Για παράδειγμα, α)  , όπως και
, όπως και  ? σι)
? σι)  και τα λοιπά.
και τα λοιπά.
3) έτσι ώστε το λάθος πυροβολισμό να γράφεται με τη μορφή Μικτός αριθμός (δηλ. Από το λανθασμένο κλάσμα για να διαθέσει ένα ολόκληρο μέρος), ένας αριθμητής θα πρέπει να χωρίζεται σε παρονομαστή, ιδιωτικό από το τμήμα να πάρει ως ένα ολόκληρο μέρος, το υπόλειμμα είναι ως αριθμητής, ο παρονομαστής παραμένει για το ίδιο.
Για παράδειγμα, α)  Από το 200: 7 \u003d 28 (OST 4); σι)
Από το 200: 7 \u003d 28 (OST 4); σι)  Από 20: 5 \u003d 4 (OST. 0).
Από 20: 5 \u003d 4 (OST. 0).
4) Για να φέρει το κλάσμα στον μικρότερο κοινό παρονομαστή, είναι απαραίτητο να βρεθεί ο μικρότερος κοινός πολλαπλός (noc) παρονομαστής αυτών των κλάδων (θα είναι ο μικρότερος κοινός παρονομαστής), διαιρέστε τον μικρότερο κοινό παρονομαστή στους παρονομαστές των κλάδων (δηλαδή, βρείτε επιπλέον σφάλματα για κλάσματα), πολλαπλασιάστε τον αριθμητή και παρονομαστή κάθε κλάσματος κατά τον πρόσθετο παράγοντα.
Για παράδειγμα, δίνουμε τα κλάσματα  Στον μικρότερο γενικό παρονομαστή:
Στον μικρότερο γενικό παρονομαστή:
 ,
, ,
, ;
;
630: 18 = 35, 630: 10 = 63, 630: 21 = 30.
Σημαίνει  ;
; ;
; .
.
5) Κανόνες για την αριθμητική δράση πάνω από τα συνηθισμένα κλάσματα:
α) Η προσθήκη και αφαίρεση των κλασμάτων με τους ίδιους παρονομαστές πραγματοποιείται σύμφωνα με τον κανόνα:
 .
.
β) Προσθήκη και αφαίρεση κλάσεων με διαφορετικούς παρονομαστές πραγματοποιείται σύμφωνα με τον κανόνα), προ-οδηγώντας τα κλάσματα στον μικρότερο γενικό παρονομαστή.
γ) Κατά την προσθήκη και αφαίρεση των μικτών αριθμών, μπορείτε να τα ενεργοποιήσετε Εσφαλμένα κλάσματακαι στη συνέχεια να εκτελέσει τους κανόνες των κανόνων) IB),
δ) Όταν ο πολλαπλασιασμός των χλοοκοπτικών χρησιμοποιεί τον κανόνα:
 .
.
ε) Για να διαιρέσετε ένα κλάσμα σε άλλο, είναι απαραίτητο να πολλαπλασιάσετε τον αριθμό, τον αντίστροφο διαχωριστικό:
 .
.
στ) Όταν πολλαπλασιάζοντας και διαιρώντας μικτούς αριθμούς, προ-μεταφέρονται σε εσφαλμένα κλάσματα και στη συνέχεια απολαμβάνουν τους κανόνες) δηλαδή).
3º. Κατά την επίλυση παραδείγματα σε όλα τα βήματα με τα κλάσματα, θα πρέπει να θυμόμαστε ότι οι πρώτες ενέργειες εκτελούνται σε παρένθεση. Τόσο σε παρένθεση όσο και έξω από αυτά εκτελούν πρώτα πολλαπλασιασμό και διαίρεση και στη συνέχεια προσθήκη και αφαίρεση.
Εξετάστε την εκτέλεση των παραπάνω κανόνων σχετικά με το παράδειγμα.
Παράδειγμα 1. Υπολογίστε:  .
.
1)  ;
;
2)  ;
;
5)  . Απάντηση: 3.
. Απάντηση: 3.