Οι αρμονικές δονήσεις περιγράφονται από την εξίσωση. Ταλαντώσεις. Αρμονικές δονήσεις. Εξίσωση αρμονικών δονήσεων. Τι ονομάζεται διπολικός βραχίονας;

Εξίσωση αρμονικής δόνησης

Η εξίσωση της αρμονικής ταλάντωσης καθορίζει την εξάρτηση των συντεταγμένων του σώματος από το χρόνο

Το γράφημα συνημιτόνου στην αρχική στιγμή έχει μέγιστη τιμή και το γράφημα ημιτόνου έχει μηδενική τιμή την αρχική στιγμή. Αν αρχίσουμε να εξετάζουμε την ταλάντωση από τη θέση ισορροπίας, τότε η ταλάντωση θα επαναλάβει ένα ημιτονοειδές. Αν αρχίσουμε να θεωρούμε την ταλάντωση από τη θέση της μέγιστης απόκλισης, τότε η ταλάντωση θα περιγραφεί με συνημίτονο. Ή μια τέτοια ταλάντωση μπορεί να περιγραφεί από τον ημιτονοειδές τύπο με μια αρχική φάση.

Αλλαγή ταχύτητας και επιτάχυνσης κατά την αρμονική ταλάντωση

Όχι μόνο η συντεταγμένη του σώματος αλλάζει με την πάροδο του χρόνου σύμφωνα με το νόμο του ημιτονοειδούς ή συνημιτόνου. Αλλά μεγέθη όπως η δύναμη, η ταχύτητα και η επιτάχυνση αλλάζουν επίσης παρόμοια. Η δύναμη και η επιτάχυνση είναι μέγιστες όταν το ταλαντούμενο σώμα βρίσκεται στις ακραίες θέσεις όπου η μετατόπιση είναι μέγιστη και μηδενίζονται όταν το σώμα διέρχεται από τη θέση ισορροπίας. Η ταχύτητα, αντίθετα, σε ακραίες θέσεις είναι μηδέν, και όταν το σώμα διέρχεται από τη θέση ισορροπίας, φτάνει στη μέγιστη τιμή του.

Αν η ταλάντωση περιγράφεται από το νόμο του συνημιτόνου

Αν η ταλάντωση περιγράφεται σύμφωνα με τον ημιτονοειδή νόμο

Μέγιστες τιμές ταχύτητας και επιτάχυνσης

Έχοντας αναλύσει τις εξισώσεις της εξάρτησης v(t) και a(t), μπορούμε να μαντέψουμε ότι οι μέγιστες τιμές της ταχύτητας και της επιτάχυνσης λαμβάνονται στην περίπτωση που τριγωνομετρικός παράγονταςίσο με 1 ή -1. Καθορίζεται από τον τύπο

§ 6. ΜΗΧΑΝΙΚΕΣ ΔΟΝΗΣΕΙΣΒασικοί τύποι

Αρμονική Εξίσωση

Οπου Χ -μετατόπιση του σημείου ταλάντωσης από τη θέση ισορροπίας. t- χρόνος; ΕΝΑ,ω, φ - πλάτος, γωνιακή συχνότητα, αρχική φάση ταλαντώσεων, αντίστοιχα. - φάση ταλαντώσεων αυτή τη στιγμή t.

Γωνιακή συχνότητα

όπου ν και Τ είναι η συχνότητα και η περίοδος των ταλαντώσεων.

Η ταχύτητα ενός σημείου που εκτελεί αρμονικές ταλαντώσεις είναι

Επιτάχυνση κατά την αρμονική ταλάντωση

Εύρος ΕΝΑη προκύπτουσα ταλάντωση που προκύπτει με την προσθήκη δύο ταλαντώσεων με τις ίδιες συχνότητες, που συμβαίνουν κατά μήκος μιας ευθείας γραμμής, προσδιορίζεται από τον τύπο

Οπου ένα 1 Και ΕΝΑ 2 - πλάτη των στοιχείων δόνησης. Τα φ 1 και φ 2 είναι οι αρχικές τους φάσεις.

Η αρχική φάση φ της προκύπτουσας ταλάντωσης μπορεί να βρεθεί από τον τύπο

Η συχνότητα των παλμών που προκύπτουν όταν προσθέτουμε δύο ταλαντώσεις που συμβαίνουν κατά μήκος μιας ευθείας γραμμής με διαφορετικές αλλά παρόμοιες συχνότητες ν 1 και ν 2,

Εξίσωση της τροχιάς ενός σημείου που συμμετέχει σε δύο αμοιβαία κάθετες ταλαντώσεις με πλάτη A 1 και A 2 και αρχικές φάσεις φ 1 και φ 2,

Εάν οι αρχικές φάσεις φ 1 και φ 2 των συνιστωσών ταλάντωσης είναι ίδιες, τότε η εξίσωση τροχιάς παίρνει τη μορφή

δηλαδή το σημείο κινείται σε ευθεία γραμμή.

Στην περίπτωση που η διαφορά φάσης είναι , η εξίσωση παίρνει τη μορφή

δηλαδή το σημείο κινείται κατά μήκος μιας έλλειψης.

Διαφορική εξίσωση αρμονικών ταλαντώσεων υλικού σημείου

, ή , όπου m είναι η μάζα του σημείου. κ- συντελεστής οιονεί ελαστικής δύναμης ( κ=Τω 2).

Η συνολική ενέργεια ενός υλικού σημείου που εκτελεί αρμονικές ταλαντώσεις είναι

Η περίοδος ταλάντωσης ενός σώματος που αιωρείται σε ένα ελατήριο (εκκρεμές ελατηρίου)

Οπου Μ- μάζα σώματος; κ- ακαμψία ελατηρίου. Ο τύπος ισχύει για ελαστικούς κραδασμούς εντός των ορίων στα οποία ικανοποιείται ο νόμος του Hooke (με μικρή μάζα του ελατηρίου σε σύγκριση με τη μάζα του σώματος).

Περίοδος ταλάντωσης μαθηματικού εκκρεμούς

Οπου μεγάλο- μήκος του εκκρεμούς. σολ- ένταση βαρύτητος. Περίοδος ταλάντωσης φυσικού εκκρεμούς

Οπου J- ροπή αδράνειας του ταλαντούμενου σώματος ως προς τον άξονα

δισταγμός; ΕΝΑ- απόσταση του κέντρου μάζας του εκκρεμούς από τον άξονα ταλάντωσης.

Μειωμένο μήκος ενός φυσικού εκκρεμούς.

Οι τύποι που δίνονται είναι ακριβείς για την περίπτωση απειροελάχιστων πλατών. Για πεπερασμένα πλάτη, αυτοί οι τύποι δίνουν μόνο κατά προσέγγιση αποτελέσματα. Με πλάτη όχι μεγαλύτερα από, το σφάλμα στην τιμή της περιόδου δεν υπερβαίνει το 1%.

Η περίοδος των στρεπτικών δονήσεων ενός σώματος που αιωρείται σε ένα ελαστικό νήμα είναι

Οπου J- ροπή αδράνειας του σώματος σε σχέση με τον άξονα που συμπίπτει με το ελαστικό νήμα. κ- ελαστική ακαμψία νήματος, ίσο με την αναλογίαη ελαστική ροπή που εμφανίζεται όταν το νήμα συστρέφεται, στη γωνία με την οποία συστρέφεται το νήμα.

Διαφορική εξίσωση απόσβεσης ταλαντώσεων , ή ,

Οπου r- συντελεστής αντίστασης. δ - συντελεστής απόσβεσης: ω 0 - φυσική γωνιακή συχνότητα ταλαντώσεων *

Εξίσωση απόσβεσης ταλάντωσης

Οπου Στο)- πλάτος των αποσβεσμένων ταλαντώσεων αυτή τη στιγμή t;ω είναι η γωνιακή τους συχνότητα.

Γωνιακή συχνότητα απόσβεσης ταλαντώσεων

О Εξάρτηση του πλάτους των αποσβεσμένων ταλαντώσεων από το χρόνο

Εγώ

Οπου ΕΝΑ 0 - πλάτος ταλαντώσεων τη στιγμή t=0.

Μείωση λογαριθμικής ταλάντωσης

Οπου Στο)Και A(t+T)- πλάτη δύο διαδοχικών ταλαντώσεων που χωρίζονται χρονικά από μια περίοδο.

Διαφορική εξίσωση εξαναγκασμένων ταλαντώσεων

όπου υπάρχει μια εξωτερική περιοδική δύναμη που δρα σε ένα ταλαντούμενο υλικό σημείο και προκαλεί εξαναγκασμένες ταλαντώσεις. φά 0 - τιμή πλάτους του?

Πλάτος εξαναγκασμένων ταλαντώσεων

Συχνότητα συντονισμού και πλάτος συντονισμού Και

Παραδείγματα επίλυσης προβλημάτων

Παράδειγμα 1.Το σημείο ταλαντώνεται σύμφωνα με το νόμο x(t)=, Οπου Α=2βλ. Προσδιορίστε την αρχική φάση φ αν

Χ(0)=cm και Χ , (0)<0. Построить векторную диаграмму для мо-­ мента t=0.

Λύση. Ας χρησιμοποιήσουμε την εξίσωση της κίνησης και ας εκφράσουμε τη μετατόπιση τη στιγμή t=0 έως την αρχική φάση:

Από εδώ βρίσκουμε την αρχική φάση:

* Στους τύπους αρμονικών δονήσεων που δόθηκε προηγουμένως, η ίδια ποσότητα ορίστηκε απλώς ω (χωρίς το δείκτη 0).

Ας αντικαταστήσουμε τις δεδομένες τιμές σε αυτήν την έκφραση Χ(0) και ΕΝΑ:φ= = . Η τιμή του ορίσματος ικανοποιείται από δύο τιμές γωνίας:

Για να αποφασίσουμε ποια από αυτές τις τιμές της γωνίας φ ικανοποιεί επίσης την συνθήκη, βρίσκουμε πρώτα:

Αντικατάσταση της τιμής σε αυτήν την έκφραση t=0 και εναλλάξ οι τιμές των αρχικών φάσεων και, βρίσκουμε

Τ όπως πάντα ΕΝΑ>0 και ω>0, τότε μόνο η πρώτη τιμή της αρχικής φάσης ικανοποιεί τη συνθήκη. Έτσι, η επιθυμητή αρχική φάση

Χρησιμοποιώντας την ευρεθείσα τιμή του φ, κατασκευάζουμε ένα διανυσματικό διάγραμμα (Εικ. 6.1). Παράδειγμα 2.Υλικό σημείο με μάζα Τ=5 g εκτελεί αρμονικές ταλαντώσεις με συχνότητα ν =0,5 Hz. Πλάτος ταλάντωσης ΕΝΑ=3 εκ. Να προσδιορίσετε: 1) ταχύτητα υ σημεία τη στιγμή που η μετατόπιση x== 1,5 cm; 2) η μέγιστη δύναμη F max που ασκείται στο σημείο. 3) Εικ. 6,1 συνολική ενέργεια μισημείο ταλάντωσης.

και λαμβάνουμε τον τύπο ταχύτητας παίρνοντας την πρώτη χρονική παράγωγο της μετατόπισης:

Για να εκφραστεί η ταχύτητα μέσω μετατόπισης, είναι απαραίτητο να εξαιρεθεί ο χρόνος από τους τύπους (1) και (2). Για να γίνει αυτό, τετραγωνίζουμε και τις δύο εξισώσεις και διαιρούμε την πρώτη με ΕΝΑ 2 , το δεύτερο στο A 2 ω 2 και προσθέστε:

, ή

Έχοντας λύσει την τελευταία εξίσωση για υ , θα βρούμε

Έχοντας εκτελέσει υπολογισμούς χρησιμοποιώντας αυτόν τον τύπο, παίρνουμε

Το σύμβολο συν αντιστοιχεί στην περίπτωση που η κατεύθυνση της ταχύτητας συμπίπτει με τη θετική κατεύθυνση του άξονα Χ,σύμβολο μείον - όταν η κατεύθυνση της ταχύτητας συμπίπτει με την αρνητική κατεύθυνση του άξονα Χ.

Η μετατόπιση κατά την αρμονική ταλάντωση, εκτός από την εξίσωση (1), μπορεί επίσης να προσδιοριστεί από την εξίσωση

Επαναλαμβάνοντας την ίδια λύση με αυτήν την εξίσωση, παίρνουμε την ίδια απάντηση.

2. Βρίσκουμε τη δύναμη που ενεργεί σε ένα σημείο χρησιμοποιώντας τον δεύτερο νόμο του Νεύτωνα:

Οπου ΕΝΑ -επιτάχυνση του σημείου, που λαμβάνουμε λαμβάνοντας τη χρονική παράγωγο της ταχύτητας:

Αντικαθιστώντας την έκφραση της επιτάχυνσης στον τύπο (3), λαμβάνουμε

Εξ ου και η μέγιστη τιμή της δύναμης

Αντικαθιστώντας τις τιμές των π, ν σε αυτήν την εξίσωση, ΤΚαι ΕΝΑ,θα βρούμε

3. Η συνολική ενέργεια ενός ταλαντευόμενου σημείου είναι το άθροισμα της κινητικής και της δυνητικής ενέργειας που υπολογίζεται για οποιαδήποτε χρονική στιγμή.

Ο ευκολότερος τρόπος υπολογισμού της συνολικής ενέργειας είναι τη στιγμή που η κινητική ενέργεια φτάνει στη μέγιστη τιμή της. Αυτή τη στιγμή η δυναμική ενέργεια είναι μηδέν. Επομένως η συνολική ενέργεια μιΤο σημείο ταλάντωσης είναι ίσο με τη μέγιστη κινητική ενέργεια

Καθορίζουμε τη μέγιστη ταχύτητα από τον τύπο (2), βάζοντας: . Αντικαθιστώντας την έκφραση της ταχύτητας στον τύπο (4), βρίσκουμε

Αντικαθιστώντας τις τιμές των ποσοτήτων σε αυτόν τον τύπο και κάνοντας υπολογισμούς, παίρνουμε

ή μJ.

Παράδειγμα 3.Στα άκρα μιας λεπτής ράβδου μήκους μεγάλο= 1 m και μάζα Μ 3 =400 g ενισχυμένες μικρές μπάλες με μάζες Μ 1 =200 γρ Και Μ 2 = 300 γρ. Η ράβδος ταλαντώνεται γύρω από οριζόντιο άξονα, κάθετο

διπλά στη ράβδο και περνώντας από τη μέση της (σημείο Ο στην Εικ. 6.2). Ορίστε την περίοδο Τταλαντώσεις που γίνονται από τη ράβδο.

Λύση. Η περίοδος ταλάντωσης ενός φυσικού εκκρεμούς, όπως μια ράβδος με μπάλες, καθορίζεται από τη σχέση

Οπου J- T -η μάζα του? μεγάλο ΜΕ - την απόσταση από το κέντρο μάζας του εκκρεμούς έως τον άξονα.

Η ροπή αδράνειας αυτού του εκκρεμούς είναι ίση με το άθροισμα των ροπών αδράνειας των σφαιρών J 1 και J 2 και ράβδος J 3:

Παίρνοντας τις μπάλες για υλικά σημεία, ας εκφράσουμε τις στιγμές αδράνειας τους:

Δεδομένου ότι ο άξονας διέρχεται από το μέσο της ράβδου, η ροπή αδράνειας του σε σχέση με αυτόν τον άξονα J 3 = =. Αντικατάσταση των παραστάσεων που προκύπτουν J 1 , J 2 Και J 3 στον τύπο (2), βρίσκουμε τη συνολική ροπή αδράνειας του φυσικού εκκρεμούς:

Έχοντας πραγματοποιήσει υπολογισμούς χρησιμοποιώντας αυτόν τον τύπο, βρίσκουμε

Ρύζι. 6.2 Η μάζα του εκκρεμούς αποτελείται από τις μάζες των σφαιρών και τη μάζα της ράβδου:

Απόσταση μεγάλο ΜΕ Θα βρούμε το κέντρο μάζας του εκκρεμούς από τον άξονα ταλάντωσης με βάση τις ακόλουθες σκέψεις. Αν ο άξονας Χκατευθύνετε κατά μήκος της ράβδου και ευθυγραμμίστε την αρχή των συντεταγμένων με το σημείο ΣΧΕΤΙΚΑ ΜΕ,τότε η απαιτούμενη απόσταση μεγάλοίση με τη συντεταγμένη του κέντρου μάζας του εκκρεμούς, δηλ.

Αντικατάσταση των τιμών των ποσοτήτων Μ 1 , Μ 2 , Μ, μεγάλοκαι αφού κάνουμε υπολογισμούς, βρίσκουμε

Έχοντας κάνει υπολογισμούς χρησιμοποιώντας τον τύπο (1), λαμβάνουμε την περίοδο ταλάντωσης ενός φυσικού εκκρεμούς:

Παράδειγμα 4.Ένα φυσικό εκκρεμές είναι μια ράβδος μήκους μεγάλο= 1 m και μάζα 3 Τ 1 Μεστερεωμένο σε ένα από τα άκρα του με ένα τσέρκι διαμέτρου και μάζας Τ 1 . Οριζόντιος άξονας Οζ

το εκκρεμές διέρχεται από το μέσο της κάθετης σε αυτό ράβδου (Εικ. 6.3). Ορίστε την περίοδο Τταλαντώσεις ενός τέτοιου εκκρεμούς.

Λύση. Η περίοδος ταλάντωσης ενός φυσικού εκκρεμούς καθορίζεται από τον τύπο

(1)

Οπου J- ροπή αδράνειας του εκκρεμούς σε σχέση με τον άξονα ταλάντωσης. T -η μάζα του? μεγάλοντο - την απόσταση από το κέντρο μάζας του εκκρεμούς έως τον άξονα ταλάντωσης.

Η ροπή αδράνειας του εκκρεμούς είναι ίση με το άθροισμα των ροπών αδράνειας της ράβδου J 1 και τσέρκι J 2:

(2).

Η ροπή αδράνειας της ράβδου σε σχέση με τον άξονα που είναι κάθετος στη ράβδο και διέρχεται από το κέντρο μάζας της καθορίζεται από τον τύπο . Σε αυτήν την περίπτωση t= 3Τ 1 και

Βρίσκουμε τη ροπή αδράνειας του στεφάνου χρησιμοποιώντας το θεώρημα του Steiner ,Οπου J- ροπή αδράνειας ως προς έναν αυθαίρετο άξονα. J 0 - ροπή αδράνειας ως προς έναν άξονα που διέρχεται από το κέντρο μάζας παράλληλο προς έναν δεδομένο άξονα. ΕΝΑ -την απόσταση μεταξύ των υποδεικνυόμενων αξόνων. Εφαρμόζοντας αυτόν τον τύπο στο τσέρκι, παίρνουμε

Αντικατάσταση εκφράσεων J 1 και J 2 στον τύπο (2), βρίσκουμε τη ροπή αδράνειας του εκκρεμούς σε σχέση με τον άξονα περιστροφής:

Απόσταση μεγάλο ΜΕ από τον άξονα του εκκρεμούς έως το κέντρο μάζας του ισούται με

Αντικατάσταση των εκφράσεων στον τύπο (1) J, μεγάλο s και τη μάζα του εκκρεμούς, βρίσκουμε την περίοδο των ταλαντώσεων του:

Αφού υπολογίσουμε χρησιμοποιώντας αυτόν τον τύπο παίρνουμε Τ=2,17 s.

Παράδειγμα 5.Προστίθενται δύο ταλαντώσεις της ίδιας κατεύθυνσης, που εκφράζονται με τις εξισώσεις. Χ 2 = =, όπου ΕΝΑ 1 = 1 εκ, ΕΝΑ 2 =2 cm, s, s, ω = =. 1. Προσδιορίστε τις αρχικές φάσεις φ 1 και φ 2 των συνιστωσών του ταλαντωτή

Μπανίγια. 2. Βρείτε το πλάτος ΕΝΑκαι η αρχική φάση φ της ταλάντωσης που προκύπτει. Γράψτε την εξίσωση για τη δόνηση που προκύπτει.

Λύση. 1. Η εξίσωση της αρμονικής δόνησης έχει τη μορφή

Ας μετατρέψουμε τις εξισώσεις που καθορίζονται στη δήλωση προβλήματος στην ίδια μορφή:

Από τη σύγκριση των παραστάσεων (2) με την ισότητα (1), βρίσκουμε τις αρχικές φάσεις της πρώτης και της δεύτερης ταλάντωσης:

Χαρούμενος και χαρούμενος.

2. Για τον προσδιορισμό του πλάτους ΕΝΑτης προκύπτουσας ταλάντωσης, είναι βολικό να χρησιμοποιήσετε το διανυσματικό διάγραμμα που παρουσιάζεται στο ρύζι. 6.4. Σύμφωνα με το θεώρημα του συνημιτόνου, παίρνουμε

πού είναι η διαφορά φάσης των συνιστωσών ταλάντωσης.Αφού , τότε αντικαθιστώντας τις τιμές φ 2 και φ 1 που βρέθηκαν παίρνουμε rad.

Ας αντικαταστήσουμε τις τιμές ΕΝΑ 1 , ΕΝΑ 2 και στον τύπο (3) και εκτελέστε τους υπολογισμούς:

ΕΝΑ= 2,65 εκ.

Ας προσδιορίσουμε την εφαπτομένη της αρχικής φάσης φ της ταλάντωσης που προκύπτει απευθείας από το Σχ. 6.4: , από πού προέρχεται η αρχική φάση;

Ταλαντώσειςονομάζονται κινήσεις ή διαδικασίες που χαρακτηρίζονται από μια ορισμένη επαναληψιμότητα στο χρόνο. Οι διεργασίες ταλάντωσης είναι ευρέως διαδεδομένες στη φύση και την τεχνολογία, για παράδειγμα, η ταλάντευση ενός εκκρεμούς ρολογιού, εναλλασσόμενη ηλεκτρική ενέργειακλπ. Όταν το εκκρεμές ταλαντώνεται, η συντεταγμένη του κέντρου μάζας του αλλάζει, στην περίπτωση εναλλασσόμενο ρεύμαη τάση και το ρεύμα στο κύκλωμα κυμαίνονται. Φυσική φύσηοι κραδασμοί μπορεί να είναι διαφορετικοί, επομένως υπάρχουν μηχανικοί, ηλεκτρομαγνητικοί κ.λπ.. Ωστόσο, διαφορετικοί ταλαντωτικές διεργασίεςπεριγράφονται με τα ίδια χαρακτηριστικά και τις ίδιες εξισώσεις. Εξ ου και η σκοπιμότητα κοινή προσέγγισηστη μελέτη των δονήσεων διαφορετικής φυσικής φύσης.

Οι ταλαντώσεις λέγονται Ελεύθερος, εάν διαπράττονται μόνο υπό την επιρροή εσωτερικές δυνάμειςενεργώντας μεταξύ των στοιχείων του συστήματος μετά την απομάκρυνση του συστήματος από τη θέση ισορροπίας εξωτερικές δυνάμειςκαι αφέθηκε στην τύχη της. Δωρεάν δονήσεις πάντα απόσβεση ταλαντώσεων , γιατί στα πραγματικά συστήματα οι απώλειες ενέργειας είναι αναπόφευκτες. Στην εξιδανικευμένη περίπτωση ενός συστήματος χωρίς απώλεια ενέργειας, οι ελεύθερες ταλαντώσεις (που συνεχίζονται όσο επιθυμείτε) ονομάζονται τα δικά.

Ο απλούστερος τύπος ελεύθερων ταλαντώσεων χωρίς απόσβεση είναι αρμονικές δονήσεις -ταλαντώσεις στις οποίες η ταλαντευόμενη ποσότητα αλλάζει με την πάροδο του χρόνου σύμφωνα με το νόμο του ημιτονοειδούς (συνημίτονο). Οι δονήσεις που βρίσκονται στη φύση και την τεχνολογία έχουν συχνά χαρακτήρα κοντά στον αρμονικό.

Οι αρμονικές ταλαντώσεις περιγράφονται από μια εξίσωση που ονομάζεται εξίσωση αρμονικής ταλάντωσης:

Οπου ΕΝΑ- πλάτος ταλαντώσεων, μέγιστη τιμή της ταλαντούμενης ποσότητας Χ; - κυκλική (κυκλική) συχνότητα φυσικών ταλαντώσεων. - αρχική φάση ταλάντωσης τη στιγμή του χρόνου t= 0; - φάση ταλάντωσης τη στιγμή του χρόνου t.Η φάση ταλάντωσης καθορίζει την τιμή της ταλαντούμενης ποσότητας σε αυτή τη στιγμήχρόνος. Δεδομένου ότι το συνημίτονο ποικίλλει από +1 έως -1, τότε Χμπορεί να πάρει τιμές από + ΕΝΑπριν - ΕΝΑ.

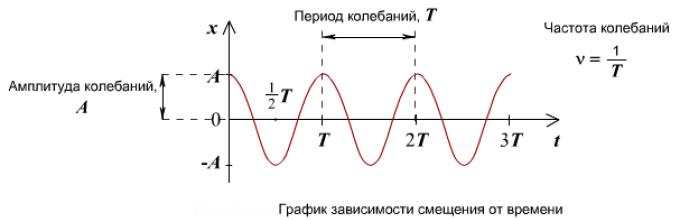
χρόνος Τκατά την οποία το σύστημα ολοκληρώνει μία πλήρη ταλάντωση ονομάζεται περίοδος ταλάντωσης. Στη διάρκεια Τη φάση της ταλάντωσης αυξάνεται κατά 2 π , δηλ.

Οπου . (14.2)

Το αντίστροφο της περιόδου ταλάντωσης

Δηλαδή, ο αριθμός των πλήρων ταλαντώσεων που εκτελούνται ανά μονάδα χρόνου ονομάζεται συχνότητα ταλάντωσης. Συγκρίνοντας (14.2) και (14.3) παίρνουμε

Η μονάδα συχνότητας είναι τα Hertz (Hz): 1 Hz είναι η συχνότητα στην οποία εμφανίζεται μια πλήρης ταλάντωση σε 1 s.

Τα συστήματα στα οποία μπορούν να συμβούν ελεύθερες δονήσεις ονομάζονται ταλαντωτές . Ποιες ιδιότητες πρέπει να έχει ένα σύστημα για να υπάρχουν ελεύθερες δονήσεις σε αυτό; Μηχανικό σύστημαπρέπει να έχουν σταθερή θέση ισορροπίας, κατά την έξοδο που εμφανίζεται επαναφορά της δύναμης που κατευθύνεται προς τη θέση ισορροπίας. Αυτή η θέση είναι γνωστό ότι αντιστοιχεί σε ένα ελάχιστο δυναμική ενέργειασυστήματα. Ας εξετάσουμε πολλά ταλαντευτικά συστήματα που ικανοποιούν τις αναφερόμενες ιδιότητες.

Οι αλλαγές σε οποιαδήποτε ποσότητα περιγράφονται χρησιμοποιώντας τους νόμους του ημιτόνου ή του συνημιτόνου, τότε τέτοιες ταλαντώσεις ονομάζονται αρμονικές. Ας εξετάσουμε ένα κύκλωμα που αποτελείται από έναν πυκνωτή (ο οποίος φορτίστηκε πριν συμπεριληφθεί στο κύκλωμα) και έναν επαγωγέα (Εικ. 1).

Εικόνα 1.

Η εξίσωση αρμονικών κραδασμών μπορεί να γραφτεί ως εξής:

$q=q_0cos((\omega )_0t+(\alpha )_0)$ (1)

όπου $t$ είναι ο χρόνος. $q$ χρέωση, $q_0$-- μέγιστη απόκλιση της χρέωσης από τη μέση (μηδενική) τιμή της κατά τις αλλαγές. $(\omega )_0t+(\alpha )_0$- φάση ταλάντωσης; $(\alpha )_0$- αρχική φάση; $(\omega )_0$ - κυκλική συχνότητα. Κατά τη διάρκεια της περιόδου, η φάση αλλάζει κατά $2\pi $.

Εξίσωση της μορφής:

εξίσωση αρμονικών ταλαντώσεων σε διαφορική μορφή για κύκλωμα ταλάντωσης που δεν θα περιέχει ενεργή αντίσταση.

Οποιοσδήποτε τύπος περιοδικών ταλαντώσεων μπορεί να αναπαρασταθεί με ακρίβεια ως άθροισμα αρμονικών ταλαντώσεων, οι λεγόμενες αρμονικές σειρές.

Για την περίοδο ταλάντωσης ενός κυκλώματος που αποτελείται από ένα πηνίο και έναν πυκνωτή, λαμβάνουμε τον τύπο του Thomson:

Αν διαφοροποιήσουμε την έκφραση (1) σε σχέση με το χρόνο, μπορούμε να λάβουμε τον τύπο για τη συνάρτηση $I(t)$:

Η τάση κατά μήκος του πυκνωτή μπορεί να βρεθεί ως:

Από τους τύπους (5) και (6) προκύπτει ότι η ένταση του ρεύματος είναι μεγαλύτερη από την τάση στον πυκνωτή κατά $\frac(\pi )(2).$

Οι αρμονικές ταλαντώσεις μπορούν να αναπαρασταθούν τόσο με τη μορφή εξισώσεων, συναρτήσεων όσο και με διανυσματικά διαγράμματα.

Η εξίσωση (1) αντιπροσωπεύει ελεύθερες ταλαντώσεις χωρίς απόσβεση.

Εξίσωση απόσβεσης ταλάντωσης

Η αλλαγή στη φόρτιση ($q$) στις πλάκες πυκνωτών στο κύκλωμα, λαμβάνοντας υπόψη την αντίσταση (Εικ. 2), θα περιγραφεί με μια διαφορική εξίσωση της μορφής:

Σχήμα 2.

Εάν η αντίσταση που είναι μέρος του κυκλώματος $R\

όπου $\omega =\sqrt(\frac(1)(LC)-\frac(R^2)(4L^2))$ είναι η συχνότητα κυκλικής ταλάντωσης. $\beta =\frac(R)(2L)-$συντελεστής απόσβεσης. Το πλάτος των αποσβεσμένων ταλαντώσεων εκφράζεται ως:

Εάν σε $t=0$ η φόρτιση του πυκνωτή είναι ίση με $q=q_0$ και δεν υπάρχει ρεύμα στο κύκλωμα, τότε για $A_0$ μπορούμε να γράψουμε:

Η φάση των ταλαντώσεων στην αρχική χρονική στιγμή ($(\alpha )_0$) είναι ίση με:

Όταν $R >2\sqrt(\frac(L)(C))$ η αλλαγή στο φορτίο δεν είναι ταλάντωση, η εκφόρτιση του πυκνωτή ονομάζεται απεριοδική.

Παράδειγμα 1

Ασκηση:Η μέγιστη τιμή χρέωσης είναι $q_0=10\ C$. Μεταβάλλεται αρμονικά με περίοδο $T= 5 s$. Προσδιορίστε το μέγιστο δυνατό ρεύμα.

Λύση:

Ως βάση για την επίλυση του προβλήματος χρησιμοποιούμε:

Για να βρεθεί η τρέχουσα ισχύς, η έκφραση (1.1) πρέπει να διαφοροποιηθεί ως προς το χρόνο:

όπου η μέγιστη (τιμή πλάτους) της ισχύος ρεύματος είναι η έκφραση:

Από τις συνθήκες του προβλήματος γνωρίζουμε την τιμή πλάτους της χρέωσης ($q_0=10\ C$). Θα πρέπει να βρείτε τη φυσική συχνότητα των ταλαντώσεων. Ας το εκφράσουμε ως εξής:

\[(\omega )_0=\frac(2\pi )(T)\αριστερά(1.4\δεξιά).\]

Σε αυτήν την περίπτωση, η επιθυμητή τιμή θα βρεθεί χρησιμοποιώντας τις εξισώσεις (1.3) και (1.2) ως εξής:

Δεδομένου ότι όλες οι ποσότητες στις προβληματικές συνθήκες παρουσιάζονται στο σύστημα SI, θα πραγματοποιήσουμε τους υπολογισμούς:

Απάντηση:$I_0=12,56\ A.$

Παράδειγμα 2

Ασκηση:Ποια είναι η περίοδος ταλάντωσης σε ένα κύκλωμα που περιέχει επαγωγέα $L=1$H και έναν πυκνωτή, εάν η ισχύς του ρεύματος στο κύκλωμα αλλάζει σύμφωνα με το νόμο: $I\left(t\right)=-0.1sin20\ pi t\ \left(A \right);$ Ποια είναι η χωρητικότητα του πυκνωτή;

Λύση:

Από την εξίσωση των διακυμάνσεων του ρεύματος, που δίνεται στις συνθήκες του προβλήματος:

βλέπουμε ότι $(\omega )_0=20\pi $, επομένως, μπορούμε να υπολογίσουμε την περίοδο ταλάντωσης χρησιμοποιώντας τον τύπο:

\ \

Σύμφωνα με τον τύπο του Thomson για ένα κύκλωμα που περιέχει επαγωγέα και πυκνωτή, έχουμε:

Ας υπολογίσουμε την χωρητικότητα:

Απάντηση:$T=0,1$ c, $C=2,5\cdot (10)^(-4)F.$

Εξετάσαμε αρκετά σωματικά πλήρως διάφορα συστήματα, και φρόντισε να μειωθούν οι εξισώσεις κίνησης στην ίδια μορφή

Οι διαφορές μεταξύ των φυσικών συστημάτων εμφανίζονται μόνο σε διαφορετικούς ορισμούς της ποσότητας και με διαφορετικές φυσικές έννοιες της μεταβλητής Χ: αυτό μπορεί να είναι συντεταγμένη, γωνία, φορτίο, ρεύμα κ.λπ. Σημειώστε ότι στην περίπτωση αυτή, όπως προκύπτει από την ίδια τη δομή της εξίσωσης (1.18), η ποσότητα έχει πάντα τη διάσταση του αντίστροφου χρόνου.

Η εξίσωση (1.18) περιγράφει το λεγόμενο αρμονικές δονήσεις.

Η εξίσωση αρμονικής δόνησης (1.18) είναι γραμμική διαφορική εξίσωσηδεύτερης τάξης (καθώς περιέχει τη δεύτερη παράγωγο της μεταβλητής Χ). Η γραμμικότητα της εξίσωσης σημαίνει ότι

αν κάποια λειτουργία x(t)είναι μια λύση αυτής της εξίσωσης, τότε η συνάρτηση Cx(t)θα είναι και η λύση του ( ντο– αυθαίρετη σταθερά).

εάν λειτουργεί x 1(t)Και x 2(t)είναι λύσεις αυτής της εξίσωσης, τότε το άθροισμά τους x 1 (t) + x 2 (t)θα είναι επίσης λύση στην ίδια εξίσωση.

Έχει επίσης αποδειχθεί μαθηματικό θεώρημα, σύμφωνα με την οποία μια εξίσωση δεύτερης τάξης έχει δύο ανεξάρτητες λύσεις. Όλες οι άλλες λύσεις, σύμφωνα με τις ιδιότητες της γραμμικότητας, μπορούν να ληφθούν ως γραμμικοί συνδυασμοί τους. Είναι εύκολο να επαληθευτεί με άμεση διαφοροποίηση ότι οι ανεξάρτητες συναρτήσεις και ικανοποιούν την εξίσωση (1.18). Αυτό σημαίνει ότι η γενική λύση αυτής της εξίσωσης έχει τη μορφή:

Οπου Γ 1,Γ 2- αυθαίρετες σταθερές. Αυτή η λύση μπορεί να παρουσιαστεί με άλλη μορφή. Ας εισάγουμε την τιμή

και προσδιορίστε τη γωνία από τις σχέσεις:

Τότε η γενική λύση (1.19) γράφεται ως

Σύμφωνα με τύπους τριγωνομετρίας, η έκφραση σε αγκύλες είναι ίση με

Επιτέλους φτάνουμε στο γενική λύση της εξίσωσης αρμονικών κραδασμώνόπως και:

Μη αρνητική τιμή ΕΝΑπου ονομάζεται πλάτος δόνησης, - αρχική φάση ταλάντωσης. Ολόκληρο το συνημίτονο όρισμα - ο συνδυασμός - ονομάζεται φάση ταλάντωσης.

Οι εκφράσεις (1.19) και (1.23) είναι εντελώς ισοδύναμες, επομένως μπορούμε να χρησιμοποιήσουμε οποιαδήποτε από αυτές, με βάση τις εκτιμήσεις της απλότητας. Και οι δύο λύσεις είναι περιοδικές συναρτήσειςχρόνος. Πράγματι, το ημίτονο και το συνημίτονο είναι περιοδικά με τελεία . Επομένως, διάφορες καταστάσεις ενός συστήματος που εκτελεί αρμονικές ταλαντώσεις επαναλαμβάνονται μετά από ένα χρονικό διάστημα t*, κατά την οποία η φάση ταλάντωσης λαμβάνει μια αύξηση που είναι πολλαπλάσιο του :

Από αυτό προκύπτει ότι

Το λιγότερο από αυτές τις φορές

που ονομάζεται περίοδος ταλάντωσης (Εικ. 1.8), και - του κυκλική (κυκλική) συχνότητα.

Ρύζι. 1.8.

Χρησιμοποιούν επίσης συχνότητα διακυμάνσεις

Αντίστοιχα, η κυκλική συχνότητα είναι ίση με τον αριθμό των ταλαντώσεων ανά δευτερόλεπτα

Έτσι, εάν το σύστημα κατά το χρόνο tχαρακτηρίζεται από την τιμή της μεταβλητής x(t),τότε η μεταβλητή θα έχει την ίδια τιμή μετά από ένα χρονικό διάστημα (Εικ. 1.9), δηλαδή

Το ίδιο νόημα φυσικά θα επαναληφθεί με την πάροδο του χρόνου 2Τ, ΖΤκαι τα λοιπά.

Ρύζι. 1.9. Περίοδος ταλάντωσης

Η γενική λύση περιλαμβάνει δύο αυθαίρετες σταθερές ( Γ 1, Γ 2ή ΕΝΑ, ένα), οι τιμές των οποίων πρέπει να καθορίζονται από δύο αρχικές συνθήκες. Συνήθως (αν και όχι απαραίτητα) ο ρόλος τους παίζεται από τις αρχικές τιμές της μεταβλητής x(0)και το παράγωγό του.

Ας δώσουμε ένα παράδειγμα. Έστω η λύση (1.19) της εξίσωσης των αρμονικών ταλαντώσεων περιγράφει την κίνηση ενός εκκρεμούς ελατηρίου. Οι τιμές των αυθαίρετων σταθερών εξαρτώνται από τον τρόπο με τον οποίο βγάλαμε το εκκρεμές από την ισορροπία. Για παράδειγμα, τραβήξαμε το ελατήριο σε απόσταση και άφησε την μπάλα χωρίς αρχική ταχύτητα. Σε αυτήν την περίπτωση

Αντικατάσταση t = 0στο (1.19), βρίσκουμε την τιμή της σταθεράς Γ 2

Η λύση λοιπόν μοιάζει με:

Βρίσκουμε την ταχύτητα του φορτίου με διαφοροποίηση ως προς το χρόνο

Αντικατάσταση εδώ t = 0, βρείτε τη σταθερά Γ 1:

Τελικά

Συγκρίνοντας με το (1.23), διαπιστώνουμε ότι είναι το πλάτος των ταλαντώσεων, και η αρχική του φάση είναι μηδέν: .

Ας αποκαταστήσουμε τώρα το εκκρεμές με άλλο τρόπο. Ας χτυπήσουμε το φορτίο ώστε να αποκτήσει αρχική ταχύτητα, αλλά πρακτικά να μην κινείται κατά την κρούση. Τότε έχουμε άλλες αρχικές προϋποθέσεις:

η λύση μας μοιάζει

Η ταχύτητα του φορτίου θα αλλάξει σύμφωνα με το νόμο:

Ας αντικαταστήσουμε εδώ: