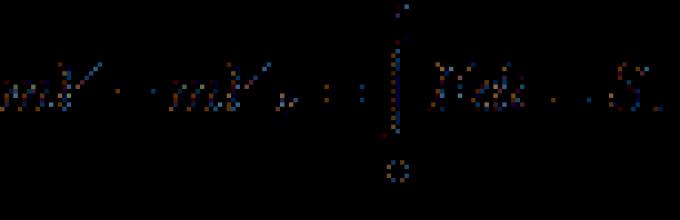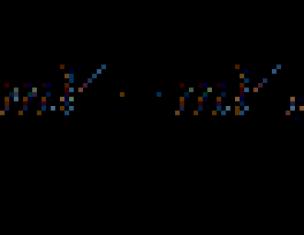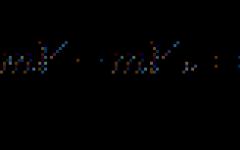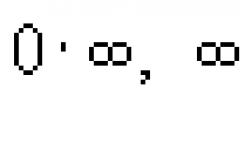Θεώρημα για τη μεταβολή της ορμής ενός σημείου. Μεταβολή της ορμής ενός μηχανικού συστήματος Νόμος της μεταβολής της ορμής ενός σημείου

(Θραύσματα μαθηματικής συμφωνίας)

Η σύνδεση της ώθησης δύναμης με τη βασική εξίσωση της Νευτώνειας δυναμικής εκφράζεται με το θεώρημα της μεταβολής της ορμής ενός υλικού σημείου.

Θεώρημα.Η μεταβολή της ποσότητας κίνησης ενός υλικού σημείου για μια ορισμένη χρονική περίοδο είναι ίση με την ώθηση της δύναμης () που επενεργεί στο υλικό σημείο για την ίδια χρονική περίοδο.Η μαθηματική απόδειξη αυτού του θεωρήματος μπορεί να ονομαστεί τμήμα μιας μαθηματικής συμφωνίας. Εδώ είναι.

Η διαφορική ορμή ενός υλικού σημείου είναι ίση με τη στοιχειώδη ώθηση της δύναμης που ασκεί το υλικό σημείο. Ολοκληρώνοντας την έκφραση (128) για το διαφορικό ορμής ενός υλικού σημείου, έχουμε

(129)

Το θεώρημα αποδεικνύεται και οι μαθηματικοί θεωρούν την αποστολή τους ολοκληρωμένη και οι μηχανικοί, των οποίων η μοίρα είναι να πιστεύουν ιερά τους μαθηματικούς, έχουν ερωτήσεις όταν χρησιμοποιούν την αποδεδειγμένη εξίσωση (129). Αλλά μπλοκάρονται σταθερά από τη σειρά και την ομορφιά των μαθηματικών πράξεων (128 και 129), που συναρπάζουν και μας ενθαρρύνουν να τις ονομάσουμε κομμάτι μιας μαθηματικής συμφωνίας. Πόσες γενιές μηχανικών συμφώνησαν με τους μαθηματικούς και έτρεμαν στο μυστήριο των μαθηματικών τους συμβόλων! Αλλά τότε υπήρχε ένας μηχανικός που διαφώνησε με τους μαθηματικούς και τους έκανε ερωτήσεις.

Αγαπητοί μαθηματικοί!Γιατί κανένα από τα σχολικά σας βιβλία για τη θεωρητική μηχανική δεν συζητά τη διαδικασία εφαρμογής του συμφωνικού αποτελέσματός σας (129) στην πράξη, για παράδειγμα, όταν περιγράφετε τη διαδικασία επιτάχυνσης ενός αυτοκινήτου; Η αριστερή πλευρά της εξίσωσης (129) είναι εξαιρετικά σαφής. Το αυτοκίνητο ξεκινά την επιτάχυνση από μια ταχύτητα και την τελειώνει, για παράδειγμα, με ταχύτητα . Είναι πολύ φυσικό να γίνεται η εξίσωση (129).

Και τίθεται αμέσως το πρώτο ερώτημα: πώς μπορούμε να προσδιορίσουμε τη δύναμη από την εξίσωση (130), υπό την επίδραση της οποίας το αυτοκίνητο επιταχύνεται σε ταχύτητα 10 m/s; Δεν υπάρχει απάντηση σε αυτό το ερώτημα σε κανένα από τα αναρίθμητα εγχειρίδια θεωρητικής μηχανικής. Ας πάμε παρακάτω. Μετά την επιτάχυνση, το αυτοκίνητο αρχίζει να κινείται ομοιόμορφα με την επιτευχθείσα ταχύτητα των 10 m/s. Ποια είναι η δύναμη που οδηγεί το αυτοκίνητο; Δεν έχω άλλη επιλογή από το να κοκκινίσω μαζί με τους μαθηματικούς. Ο πρώτος νόμος της Νευτώνειας δυναμικής δηλώνει ότι όταν ένα αυτοκίνητο κινείται ομοιόμορφα, δεν ασκούνται δυνάμεις πάνω του και το αυτοκίνητο, μεταφορικά μιλώντας, φτερνίζεται με αυτόν τον νόμο, καταναλώνει βενζίνη και λειτουργεί, κινώντας, για παράδειγμα, μια απόσταση 100 km. Και πού είναι η δύναμη που έχει κάνει τη δουλειά για να μετακινήσει το αυτοκίνητο 100 km; Η συμφωνική μαθηματική εξίσωση (130) είναι σιωπηλή, αλλά η ζωή συνεχίζεται και απαιτεί απάντηση. Αρχίζουμε να το ψάχνουμε.

Εφόσον το αυτοκίνητο κινείται σε ευθεία γραμμή και ομοιόμορφα, η δύναμη που το κινεί είναι σταθερή σε μέγεθος και κατεύθυνση, και η εξίσωση (130) γίνεται

(131)

Άρα, η εξίσωση (131) σε αυτή την περίπτωση περιγράφει την επιταχυνόμενη κίνηση του σώματος. Με τι ισούται η δύναμη; Πώς να εκφράσετε την αλλαγή του στο χρόνο; Οι μαθηματικοί προτιμούν να παρακάμψουν αυτή την ερώτηση και να την αφήσουν στους μηχανικούς, πιστεύοντας ότι πρέπει να αναζητήσουν την απάντηση σε αυτήν την ερώτηση. Οι μηχανικοί έχουν μια δυνατότητα - να λάβουν υπόψη ότι εάν, μετά την ολοκλήρωση της επιταχυνόμενης κίνησης του σώματος, αρχίζει μια φάση ομοιόμορφης κίνησης, η οποία συνοδεύεται από μια σταθερή δύναμη, αντιπροσωπεύουν την εξίσωση (131) για τη στιγμή της μετάβασης από επιταχυνθεί σε ομοιόμορφη κίνηση σε αυτή τη μορφή

(132)

Το βέλος σε αυτή την εξίσωση δεν σημαίνει το αποτέλεσμα της ολοκλήρωσης αυτής της εξίσωσης, αλλά τη διαδικασία μετάβασης από την ολοκληρωμένη μορφή της σε μια απλοποιημένη μορφή. Η δύναμη σε αυτή την εξίσωση είναι ισοδύναμη με τη μέση δύναμη που άλλαξε την ορμή του σώματος από το μηδέν στην τελική τιμή. Λοιπόν, αγαπητοί μαθηματικοί και θεωρητικοί φυσικοί, η απουσία της μεθόδου σας για τον προσδιορισμό του μεγέθους της ορμής σας μας αναγκάζει να απλοποιήσουμε τη διαδικασία για τον προσδιορισμό της δύναμης και η έλλειψη μεθόδου για τον προσδιορισμό της διάρκειας αυτής της δύναμης γενικά μας βάζει σε απελπισία κατάσταση και αναγκαζόμαστε να χρησιμοποιήσουμε την έκφραση για να αναλύσουμε τη διαδικασία αλλαγής της ορμής του σώματος . Ως αποτέλεσμα, όσο περισσότερο ενεργεί η δύναμη, τόσο μεγαλύτερη είναι η ορμή της. Αυτό έρχεται σε σαφή αντίφαση με τις μακροχρόνιες ιδέες ότι η ώθηση της δύναμης είναι μεγαλύτερη, όσο μικρότερος είναι ο χρόνος δράσης της.

Ας δώσουμε προσοχή στο γεγονός ότι η αλλαγή της ορμής ενός υλικού σημείου (ώθηση δύναμης) κατά την επιταχυνόμενη κίνησή του συμβαίνει υπό τη δράση της νευτώνειας δύναμης και των δυνάμεων αντίστασης στην κίνηση, με τη μορφή δυνάμεων που σχηματίζονται από μηχανικές αντιστάσεις. και τη δύναμη της αδράνειας. Αλλά η Νευτώνεια δυναμική στη συντριπτική πλειοψηφία των προβλημάτων αγνοεί τη δύναμη της αδράνειας και η Μηχανοδυναμική υποστηρίζει ότι η αλλαγή στην ορμή ενός σώματος κατά την επιταχυνόμενη κίνησή του συμβαίνει λόγω της υπέρβασης της νευτώνειας δύναμης έναντι των δυνάμεων αντίστασης στην κίνηση, συμπεριλαμβανομένων των δύναμη αδράνειας.

Όταν ένα σώμα κινείται σε αργή κίνηση, για παράδειγμα, ένα αυτοκίνητο με σβηστό κιβώτιο ταχυτήτων, δεν υπάρχει νευτώνεια δύναμη και η αλλαγή στην ορμή του αυτοκινήτου οφείλεται στην υπέρβαση των δυνάμεων αντίστασης στην κίνηση πάνω από τη δύναμη της αδράνειας που κινεί το αυτοκίνητο κατά την αργή του κίνηση.

Πώς να επιστρέψετε τώρα τα αποτελέσματα των σημειωμένων «συμφωνικών» μαθηματικών πράξεων (128) στο κανάλι των σχέσεων αιτίου-αποτελέσματος; Υπάρχει μόνο μία διέξοδος - να βρεθεί ένας νέος ορισμός για τις έννοιες της «ώθησης της δύναμης» και της «δύναμης κρούσης». Για να γίνει αυτό, διαιρούμε και τις δύο πλευρές της εξίσωσης (132) με το χρόνο t. Ως αποτέλεσμα, θα έχουμε

. (133)

Ας δώσουμε προσοχή στο γεγονός ότι η έκφραση mV / t είναι ο ρυθμός μεταβολής της ορμής (mV / t) ενός υλικού σημείου ή σώματος. Αν λάβουμε υπόψη ότι το V / t είναι επιτάχυνση, τότε το mV / t είναι μια δύναμη που αλλάζει την ορμή του σώματος. Η ίδια διάσταση αριστερά και δεξιά του πρόσημου ίσου μας δίνει το δικαίωμα να ονομάσουμε τη δύναμη F δύναμη κρούσης και να την ορίσουμε με το σύμβολο, και την ώθηση S - την ώθηση κρούσης και να την ονομάσουμε με το σύμβολο. Από αυτό προκύπτει ένας νέος ορισμός της δύναμης κρούσης. Η δύναμη κρούσης, που ενεργεί σε ένα υλικό σημείο ή σώμα, είναι ίση με τον λόγο της μεταβολής της ορμής του υλικού σημείου ή σώματος προς το χρόνο αυτής της αλλαγής.

Ας δώσουμε ιδιαίτερη προσοχή στο γεγονός ότι μόνο η νευτώνεια δύναμη εμπλέκεται στον σχηματισμό της κρουστικής ώθησης (134), η οποία άλλαξε την ταχύτητα του αυτοκινήτου από μηδέν στη μέγιστη τιμή - άρα η εξίσωση (134) ανήκει εξ ολοκλήρου στην Νευτώνεια δυναμική. Δεδομένου ότι είναι πολύ πιο εύκολο να καθοριστεί η τιμή της ταχύτητας πειραματικά από τις επιταχύνσεις, ο τύπος (134) είναι πολύ βολικός για υπολογισμούς.

Η εξίσωση (134) συνεπάγεται ένα τόσο ασυνήθιστο αποτέλεσμα.

Ας δώσουμε προσοχή στο γεγονός ότι, σύμφωνα με τους νέους νόμους της μηχανοδυναμικής, η γεννήτρια της ώθησης της δύναμης κατά την επιταχυνόμενη κίνηση ενός υλικού σημείου ή σώματος είναι η Νευτώνεια δύναμη. Δημιουργεί μια επιτάχυνση της κίνησης ενός σημείου ή σώματος, στο οποίο δημιουργείται αυτόματα μια δύναμη αδράνειας, που κατευθύνεται αντίθετα από τη νευτώνεια δύναμη, και η κρούση Νευτώνεια δύναμη πρέπει να υπερνικήσει τη δράση της δύναμης αδράνειας, επομένως η δύναμη αδράνειας πρέπει να αναπαρασταθεί σε την ισορροπία δυνάμεων στην αριστερή πλευρά της εξίσωσης (134). Εφόσον η δύναμη της αδράνειας είναι ίση με τη μάζα ενός σημείου ή σώματος, πολλαπλασιαζόμενη με την επιβράδυνση που σχηματίζει, τότε η εξίσωση (134) γίνεται

(136)

Αγαπητοί μαθηματικοί!Μπορείτε να δείτε ποια μορφή έχει το μαθηματικό μοντέλο, περιγράφοντας την ώθηση κρούσης, η οποία επιταχύνει την κίνηση του σώματος χτυπήματος από τη μηδενική ταχύτητα στο μέγιστο V (11). Ας ελέγξουμε τώρα τη δουλειά του στον προσδιορισμό της ώθησης κρούσης , η οποία είναι ίση με τη δύναμη κρούσης που πυροδότησε τη 2η μονάδα ισχύος UGS (Εικ. 120), και θα σας αφήσουμε την άχρηστη εξίσωσή σας (132). Για να μην περιπλέκουμε την παρουσίαση, θα αφήσουμε τον τύπο (134) μόνο του προς το παρόν και θα χρησιμοποιήσουμε τους τύπους που δίνουν τις μέσες τιμές των δυνάμεων. Βλέπεις σε ποια θέση βάζεις έναν μηχανικό να επιδιώκει να λύσει ένα συγκεκριμένο πρόβλημα.

Ας ξεκινήσουμε με τη Νευτώνεια δυναμική. Οι ειδικοί διαπίστωσαν ότι η 2η μονάδα ισχύος ανέβηκε σε ύψος 14 μέτρων. Εφόσον ανέβαινε στο πεδίο της βαρύτητας, τότε σε ύψος h=14m αποδείχθηκε ότι η δυναμική του ενέργεια ήταν ίση με

και η μέση κινητική ενέργεια ήταν

Ρύζι. 120. Φωτογραφία του μηχανοστασίου πριν την καταστροφή

Από την ισότητα της κινητικής (138) και της δυναμικής (137) ενέργειας, ακολουθεί η μέση ταχύτητα ανύψωσης της μονάδας ισχύος (Εικ. 121, 122)

Ρύζι. 121. Φωτόνιο του μηχανοστασίου μετά την καταστροφή

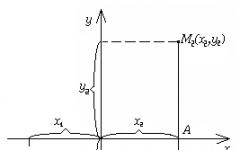
Σύμφωνα με τους νέους νόμους της μηχανοδυναμικής, η άνοδος της μονάδας ισχύος αποτελούνταν από δύο φάσεις (Εικ. 123): την πρώτη φάση ΟΑ - επιταχυνόμενη άνοδος και τη δεύτερη φάση ΑΒ - αργή άνοδο, , .

Ο χρόνος και η απόσταση της δράσης τους είναι περίπου ίση με (). Στη συνέχεια, η κινηματική εξίσωση της φάσης επιταχυνόμενης ανύψωσης της μονάδας ισχύος θα γραφεί ως

. (140)

Ρύζι. 122. Άποψη του φρεατίου της μονάδας ισχύος και της ίδιας της μονάδας ισχύος μετά την καταστροφή

Ο νόμος της αλλαγής της ταχύτητας ανύψωσης της μονάδας ισχύος στην πρώτη φάση έχει τη μορφή

. (141)

Ρύζι. 123. Το μοτίβο αλλαγής της ταχύτητας V της πτήσης της μονάδας ισχύος

Αντικαθιστώντας το χρόνο από την εξίσωση (140) στην εξίσωση (141), έχουμε

. (142)

Ο χρόνος ανύψωσης μπλοκ στην πρώτη φάση προσδιορίζεται από τον τύπο (140)

. (143)

Τότε ο συνολικός χρόνος ανύψωσης της μονάδας ισχύος σε ύψος 14m θα είναι ίσος με . Η μάζα της μονάδας ισχύος και του καλύμματος είναι 2580 τόνοι. Σύμφωνα με τη δυναμική του Νεύτωνα, η δύναμη που ανύψωσε τη μονάδα ισχύος είναι ίση με

Αγαπητοί μαθηματικοί!Ακολουθούμε τα συμφωνικά μαθηματικά σας αποτελέσματα και γράφουμε τον τύπο σας (129), ο οποίος προκύπτει από τη δυναμική του Νεύτωνα, για να προσδιορίσουμε την ώθηση κρούσης που πυροδότησε τη 2η μονάδα ισχύος

και κάντε μια στοιχειώδη ερώτηση: πώς να προσδιορίσετε τη διάρκεια του παλμού κρούσης που πυροδότησε τη 2η μονάδα ισχύος;;;;;;;;;;;;;;;

Αγαπητός!!!Θυμηθείτε πόση κιμωλία έγραψαν οι γενιές των συναδέλφων σας στους εκπαιδευτικούς πίνακες, διδάσκοντας στους μαθητές πώς να προσδιορίζουν την ώθηση πρόσκρουσης και κανείς δεν εξήγησε πώς να καθορίσει τη διάρκεια της ώθησης κρούσης σε κάθε συγκεκριμένη περίπτωση. Θα πείτε ότι η διάρκεια της κρούσης είναι ίση με το χρονικό διάστημα για την αλλαγή της ταχύτητας της μονάδας ισχύος από το μηδέν στη, θα υποθέσουμε, τη μέγιστη τιμή των 16,75 m/s (139). Είναι στον τύπο (143) και ισούται με 0,84 s. Συμφωνούμε μαζί σας προς το παρόν και καθορίζουμε τη μέση τιμή του κρουστικού παλμού

Αμέσως προκύπτει το ερώτημα: γιατί το μέγεθος της κρουστικής ώθησης (146) είναι μικρότερο από τη νευτώνεια δύναμη των 50600 τόνων; Η απάντηση, εσείς, αγαπητοί μαθηματικοί, όχι. Ας πάμε παρακάτω.

Σύμφωνα με τη δυναμική του Νεύτωνα, η κύρια δύναμη που αντιστάθηκε στην ανύψωση της μονάδας ισχύος είναι η βαρύτητα. Δεδομένου ότι αυτή η δύναμη στρέφεται ενάντια στην κίνηση της μονάδας ισχύος, δημιουργεί μια επιβράδυνση, η οποία είναι ίση με την επιτάχυνση ελεύθερης πτώσης. Τότε η βαρυτική δύναμη που ασκεί η μονάδα ισχύος που πετά προς τα πάνω είναι ίση με

Η δυναμική του Νεύτωνα δεν λαμβάνει υπόψη άλλες δυνάμεις που εμπόδισαν τη δράση της νευτώνειας δύναμης των 50600 τόνων (144), και η μηχανοδυναμική ισχυρίζεται ότι η δύναμη αδράνειας είναι ίση με

Αμέσως προκύπτει το ερώτημα: πώς να βρείτε το μέγεθος της επιβράδυνσης της κίνησης της μονάδας ισχύος; Η δυναμική του Νεύτωνα είναι σιωπηλή και η μηχανοδυναμική απαντά: τη στιγμή της δράσης της νευτώνειας δύναμης που σήκωσε τη μονάδα ισχύος, αντιστάθηκε: βαρύτητα και αδράνεια, επομένως η εξίσωση των δυνάμεων που ενεργούν στη μονάδα ισχύος εκείνη τη στιγμή γράφεται ως εξής.

Το μέγεθος της κίνησης είναι ένα μέτρο της μηχανικής κίνησης εάν η μηχανική κίνηση γίνει μηχανική. Για παράδειγμα, η μηχανική κίνηση μιας μπάλας του μπιλιάρδου (Εικ. 22) πριν από την κρούση περνά στη μηχανική κίνηση των μπαλών μετά την κρούση. Για ένα σημείο, η ορμή είναι ίση με το γινόμενο.

Το μέτρο της δράσης της δύναμης σε αυτή την περίπτωση είναι η ορμή της δύναμης

. (9.1)

Η ορμή καθορίζει τη δράση της δύναμης για ένα χρονικό διάστημα . Για ένα υλικό σημείο, το θεώρημα αλλαγής ορμής μπορεί να χρησιμοποιηθεί σε διαφορική μορφή
(9.2) ή ολοκληρωτική (πεπερασμένη) μορφή
. (9.3)

Η μεταβολή της ορμής ενός υλικού σημείου σε μια ορισμένη χρονική περίοδο είναι ίση με την ορμή όλων των δυνάμεων που ασκούνται στο σημείο τον ίδιο χρόνο.

Εικόνα 22

Κατά την επίλυση προβλημάτων, το θεώρημα (9.3) χρησιμοποιείται συχνότερα σε προβολές στους άξονες συντεταγμένων
;

; (9.4)

.

Χρησιμοποιώντας το θεώρημα για την αλλαγή της ορμής ενός σημείου, είναι δυνατό να λυθούν προβλήματα στα οποία ένα σημείο ή ένα σώμα που κινείται μεταφορικά υπόκειται σε σταθερές ή μεταβλητές δυνάμεις που εξαρτώνται από το χρόνο και τον αριθμό των δεδομένων και αναζητούμενων τιμών περιλαμβάνει το χρόνο κίνησης και την ταχύτητα στην αρχή και στο τέλος της κίνησης. Τα προβλήματα που χρησιμοποιούν το θεώρημα λύνονται με την ακόλουθη σειρά:

1. επιλέξτε ένα σύστημα συντεταγμένων.

2. απεικονίζουν όλες τις δεδομένες (ενεργές) δυνάμεις και αντιδράσεις που δρουν σε ένα σημείο.

3. Καταγράψτε το θεώρημα για τη μεταβολή της ορμής ενός σημείου σε προβολές στους επιλεγμένους άξονες συντεταγμένων.

4. προσδιορίστε τις επιθυμητές τιμές.

ΠΑΡΑΔΕΙΓΜΑ 12.

Ένα σφυρί βάρους G=2t πέφτει από ύψος h=1m σε ένα τεμάχιο εργασίας σε χρόνο t=0,01s και σφραγίζει το τμήμα (Εικ. 23). Προσδιορίστε τη μέση δύναμη της σφύρας στο τεμάχιο εργασίας.

ΛΥΣΗ.

1. Η βαρύτητα του σφυριού επενεργεί στο τεμάχιο εργασίας και υποστήριξη αντίδρασης . Η τιμή της αντίδρασης υποστήριξης αλλάζει με το χρόνο, επομένως λάβετε υπόψη τη μέση τιμή της
.

2. κατευθύνετε τον άξονα συντεταγμένων y κατακόρυφα προς τα κάτω και εφαρμόστε το θεώρημα για τη μεταβολή της ορμής ενός σημείου προβολής σε αυτόν τον άξονα:
, (1) όπου - ταχύτητα του σφυριού στο τέλος του χτυπήματος.

- την αρχική ταχύτητα του σφυριού τη στιγμή της επαφής με το τεμάχιο εργασίας.

3. Για να προσδιορίσετε την ταχύτητα συνθέτουμε τη διαφορική εξίσωση κίνησης του σφυριού σε προβολή στον άξονα y:

. (2)

Διαχωρίστε τις μεταβλητές, ενσωματώστε την εξίσωση (2) δύο φορές:
;

;

. Οι σταθερές ολοκλήρωσης С 1 , С 2 μπορούν να βρεθούν από τις αρχικές συνθήκες. Σε t=0 V y =0, τότε C1 =0; y \u003d 0, μετά C 2 \u003d 0. Επομένως, το σφυρί κινείται σύμφωνα με το νόμο
, (3) και η ταχύτητα του σφυριού αλλάζει σύμφωνα με το νόμο
. (4) Θα εκφράσουμε το χρόνο κίνησης του σφυριού από το (3) και θα αντικαταστήσουμε στο (4)
;
. (5)

4. Βρίσκουμε την προβολή της ορμής των εξωτερικών δυνάμεων στον άξονα y με τον τύπο:
. (6) Αντικατάσταση (5) και (6) σε (1):
, από όπου βρίσκουμε την αντίδραση της στήριξης και, κατά συνέπεια, την επιθυμητή πίεση του σφυριού στο τεμάχιο εργασίας
Τ.

Εικόνα 24

ΠΡΟΣ ΤΟ

όπου M είναι η μάζα του συστήματος, V c είναι η ταχύτητα του κέντρου μάζας. Το θεώρημα για τη μεταβολή της ορμής ενός μηχανικού συστήματος μπορεί να γραφτεί σε διαφορική και πεπερασμένη (ολοκληρωτική) μορφή:
;

. (9.7)

Η ποσότητα κίνησης ενός μηχανικού συστήματος μπορεί να οριστεί ως το άθροισμα των ποσών κίνησης των σημείων του συστήματος
. (9.5) Το μέγεθος της κίνησης ενός συστήματος ή ενός άκαμπτου σώματος μπορεί να προσδιοριστεί γνωρίζοντας τη μάζα του συστήματος και την ταχύτητα του κέντρου μάζας
, (9.6)

Η μεταβολή της ποσότητας κίνησης ενός μηχανικού συστήματος σε μια ορισμένη χρονική περίοδο είναι ίση με το άθροισμα των παλμών των εξωτερικών δυνάμεων που δρουν για τον ίδιο χρόνο. Μερικές φορές είναι πιο βολικό να χρησιμοποιήσετε το θεώρημα για την αλλαγή της ορμής στην προβολή στους άξονες συντεταγμένων
; (9.8)
. (9.9)

Ο νόμος της διατήρησης της ορμής ορίζει ότι ελλείψει εξωτερικών δυνάμεων, η ορμή ενός μηχανικού συστήματος παραμένει σταθερή. Η δράση των εσωτερικών δυνάμεων δεν μπορεί να αλλάξει την ορμή του συστήματος. Η εξίσωση (9.6) δείχνει ότι για
,
.

Αν
, τότε
ή
.

ρε

έλικα ή έλικα, τζετ πρόωση. Τα καλαμάρια κινούνται σπασμωδικά, πετώντας νερό από τον μυϊκό σάκο σύμφωνα με την αρχή ενός κανονιού νερού (Εικ. 25). Το απωθημένο νερό έχει μια γνωστή ποσότητα κίνησης προς τα πίσω. Το καλαμάρι κερδίζει την αντίστοιχη ταχύτητα κίνηση προς τα εμπρός λόγω αντιδραστικής ώθησης , γιατί πριν ξεπηδήσει το καλαμάρι, η δύναμη εξισορροπείται από τη βαρύτητα .

η λειτουργία του νόμου της διατήρησης της ορμής ενός μηχανικού συστήματος μπορεί να απεικονιστεί με το παράδειγμα του φαινομένου της ανάκρουσης ή της ανατροπής κατά τη βολή, την εργασία

Η εφαρμογή του θεωρήματος μεταβολής της ορμής καθιστά δυνατό τον αποκλεισμό όλων των εσωτερικών δυνάμεων από την εξέταση.

ΠΑΡΑΔΕΙΓΜΑ 13.

Σε μια σιδηροδρομική πλατφόρμα, ελεύθερο στις ράγες, τοποθετείται ένα βαρούλκο Α με τύμπανο ακτίνας r (Εικ. 26). Το βαρούλκο έχει σχεδιαστεί για να κινείται στην πλατφόρμα του φορτίου Β με μάζα m 1 . Βάρος πλατφόρμας με βαρούλκο m 2 . Το τύμπανο του βαρούλκου περιστρέφεται σύμφωνα με το νόμο
. Την αρχική στιγμή, το σύστημα ήταν κινητό. Παραμελώντας την τριβή, βρείτε τον νόμο της αλλαγής στην ταχύτητα της πλατφόρμας μετά την ενεργοποίηση του βαρούλκου.

R ΑΠΟΦΑΣΗ.

1. Θεωρήστε την πλατφόρμα, το βαρούλκο και το φορτίο ως ένα ενιαίο μηχανικό σύστημα, το οποίο επηρεάζεται από εξωτερικές δυνάμεις: η δύναμη της βαρύτητας του φορτίου και πλατφόρμες και αντιδράσεις και
.

2. Αφού όλες οι εξωτερικές δυνάμεις είναι κάθετες στον άξονα x, δηλ.
, εφαρμόζουμε το νόμο της διατήρησης της ορμής ενός μηχανικού συστήματος σε προβολή στον άξονα x:
. Κατά την αρχική χρονική στιγμή, το σύστημα ήταν ακίνητο, επομένως,

Ας εκφράσουμε το μέγεθος της κίνησης του συστήματος σε μια αυθαίρετη χρονική στιγμή. Η πλατφόρμα προχωρά με ταχύτητα , το φορτίο εκτελεί μια σύνθετη κίνηση, που αποτελείται από μια σχετική κίνηση κατά μήκος της πλατφόρμας με ταχύτητα και φορητή κίνηση μαζί με την πλατφόρμα με ταχύτητα ., που
. Η πλατφόρμα θα κινείται προς την αντίθετη κατεύθυνση από τη σχετική κίνηση του φορτίου.

ΠΑΡΑΔΕΙΓΜΑ 14.

Μ

ΛΥΣΗ.

1. Εφαρμόστε το θεώρημα για τη μεταβολή της ορμής ενός μηχανικού συστήματος σε προβολή στον άξονα x. Αφού όλες οι εξωτερικές δυνάμεις που δρουν στο σύστημα είναι κάθετες, τότε
, τότε
, που
. (1)

2. Εκφράζουμε την προβολή της ποσότητας κίνησης στον άξονα x για το εξεταζόμενο μηχανικό σύστημα
,

Το μηχανικό σύστημα αποτελείται από μια ορθογώνια κατακόρυφη πλάκα 1 με μάζα m 1 =18kg, που κινείται κατά μήκος οριζόντιων οδηγών και ένα φορτίο D με μάζα m 2 =6kg. Τη χρονική στιγμή t 0 =0, όταν η πλάκα κινούνταν με ταχύτητα u 0 =2 m/s, το φορτίο άρχισε να κινείται κατά μήκος του αγωγού σύμφωνα με την εξίσωση S=AD=0,4sin( t 2) (S-in μέτρα, t-in δευτερόλεπτα), (Εικ. 26). Να προσδιορίσετε την ταχύτητα της πλάκας τη χρονική στιγμή t 1 =1s, χρησιμοποιώντας το θεώρημα για τη μεταβολή της ορμής του μηχανικού συστήματος.

που ,
-- το μέγεθος της κίνησης της πλάκας και του φορτίου, αντίστοιχα.

;
, που --απόλυτη ταχύτητα του φορτίουD. Από την ισότητα (1) προκύπτει ότι K 1x + K 2x \u003d C 1 ή m 1 u x + m 2 V Dx \u003d C 1. (2) Για να προσδιορίσουμε το V Dx, θεωρούμε την κίνηση του φορτίου D ως σύνθετη, θεωρώντας την κίνησή του σε σχέση με την πλάκα ως σχετική και την κίνηση της ίδιας της πλάκας ως φορητή, τότε
, (3)
ή στην προβολή στον άξονα x: . (4) Αντικατάσταση (4) σε (2):
. (5) Η σταθερά ολοκλήρωσης C 1 προσδιορίζεται από τις αρχικές συνθήκες: σε t=0 u=u 0 ; (m 1 +m 2)u 0 \u003d C 1. (6) Αντικαθιστώντας την τιμή της σταθεράς C 1 στην εξίσωση (5), παίρνουμε

Κυρία.

Για ένα υλικό σημείο, ο βασικός νόμος της δυναμικής μπορεί να αναπαρασταθεί ως

Πολλαπλασιάζοντας και τα δύο μέρη αυτής της σχέσης στα αριστερά διανυσματικά με το διάνυσμα ακτίνας (Εικ. 3.9), παίρνουμε

(3.32)

Στη δεξιά πλευρά αυτού του τύπου, έχουμε τη ροπή δύναμης σε σχέση με το σημείο Ο. Ας μετατρέψουμε την αριστερή πλευρά εφαρμόζοντας τον τύπο για την παράγωγο του διανυσματικού γινομένου

Αλλά ως διασταυρούμενο γινόμενο παράλληλων διανυσμάτων. Μετά από αυτό παίρνουμε

(3.33)

Η πρώτη χρονική παράγωγος της ροπής ορμής ενός σημείου σε σχέση με οποιοδήποτε κέντρο είναι ίση με τη ροπή δύναμης σε σχέση με το ίδιο κέντρο.

Ένα παράδειγμα υπολογισμού της γωνιακής ορμής ενός συστήματος. Υπολογίστε τη γωνιακή ορμή σε σχέση με το σημείο Ο ενός συστήματος που αποτελείται από κυλινδρικό άξονα με μάζα M = 20 kg και ακτίνα R = 0,5 m και φθίνουσα φόρτιση με μάζα m = 60 kg (Εικόνα 3.12). Ο άξονας περιστρέφεται γύρω από τον άξονα Oz με γωνιακή ταχύτητα ω = 10 s -1 .

Εικόνα 3.12

; ;

Για δεδομένα εισόδου, η γωνιακή ορμή του συστήματος

Θεώρημα για τη μεταβολή της κινητικής ροπής του συστήματος.Εφαρμόζουμε τις προκύπτουσες εξωτερικές και εσωτερικές δυνάμεις σε κάθε σημείο του συστήματος. Για κάθε σημείο του συστήματος, μπορείτε να εφαρμόσετε το θεώρημα για τη μεταβολή της γωνιακής ορμής, για παράδειγμα, στη μορφή (3.33)

Αθροίζοντας όλα τα σημεία του συστήματος και λαμβάνοντας υπόψη ότι το άθροισμα των παραγώγων είναι ίσο με την παράγωγο του αθροίσματος, παίρνουμε

Εξ ορισμού της κινητικής ροπής του συστήματος και της ιδιότητας των εξωτερικών και εσωτερικών δυνάμεων

Επομένως, η αναλογία που προκύπτει μπορεί να αναπαρασταθεί ως

Η πρώτη χρονική παράγωγος της κινητικής ροπής του συστήματος ως προς οποιοδήποτε σημείο είναι ίση με την κύρια ροπή των εξωτερικών δυνάμεων που δρουν στο σύστημα ως προς το ίδιο σημείο.

3.3.5. Δυνατότητα εργασίας

1) Το στοιχειώδες έργο της δύναμης είναι ίσο με το κλιμακωτό γινόμενο της δύναμης και τη διαφορική ακτίνα του διανύσματος του σημείου εφαρμογής της δύναμης (Εικ. 3.13)

Εικόνα 3.13

Η έκφραση (3.36) μπορεί επίσης να γραφτεί με τις ακόλουθες ισοδύναμες μορφές

όπου είναι η προβολή της δύναμης στην κατεύθυνση της ταχύτητας του σημείου εφαρμογής της δύναμης.

2) Το έργο της δύναμης στην τελική μετατόπιση

Ολοκληρώνοντας το στοιχειώδες έργο της δύναμης, λαμβάνουμε τις ακόλουθες εκφράσεις για το έργο της δύναμης στην τελική μετατόπιση από το σημείο Α στο σημείο Β

3) Έργο σταθερής δύναμης

Αν η δύναμη είναι σταθερή, τότε από το (3.38) ακολουθεί

Το έργο μιας σταθερής δύναμης δεν εξαρτάται από το σχήμα της τροχιάς, αλλά εξαρτάται μόνο από το διάνυσμα μετατόπισης του σημείου εφαρμογής της δύναμης.

4) Εργασία δύναμης βάρους

Για τη δύναμη βάρους (Εικ. 3.14) και από (3.39) παίρνουμε

Εικόνα 3.14

Αν η κίνηση είναι από το σημείο Β στο σημείο Α, τότε

Γενικά

Το σύμβολο "+" αντιστοιχεί στην κίνηση του σημείου εφαρμογής της δύναμης "κάτω", το σύμβολο "-" - προς τα πάνω.

4) Το έργο της δύναμης της ελαστικότητας

Αφήστε τον άξονα του ελατηρίου να κατευθύνεται κατά μήκος του άξονα x (Εικ. 3.15) και το άκρο του ελατηρίου μετακινηθεί από το σημείο 1 στο σημείο 2, στη συνέχεια από το (3.38) λαμβάνουμε

Αν η σταθερά του ελατηρίου είναι Με, τότε

ΕΝΑ (3.41)

Εάν το άκρο του ελατηρίου μετακινηθεί από το σημείο 0 στο σημείο 1, τότε σε αυτήν την παράσταση αντικαθιστούμε το , , τότε το έργο της ελαστικής δύναμης θα πάρει τη μορφή

(3.42)

πού είναι η προέκταση του ελατηρίου.

Εικόνα 3.15

5) Το έργο της δύναμης που ασκείται σε ένα περιστρεφόμενο σώμα. Το έργο της στιγμής.

Στο σχ. Το 3.16 δείχνει ένα περιστρεφόμενο σώμα στο οποίο ασκείται αυθαίρετη δύναμη. Κατά την περιστροφή, το σημείο εφαρμογής αυτής της δύναμης κινείται κυκλικά.

Αφήστε το υλικό σημείο να κινηθεί υπό τη δράση της δύναμης φά. Απαιτείται ο προσδιορισμός της κίνησης αυτού του σημείου ως προς το κινούμενο σύστημα Oxyz(βλ. τη σύνθετη κίνηση ενός υλικού σημείου), που κινείται με γνωστό τρόπο σε σχέση με ένα σταθερό σύστημα Ο 1 Χ 1 y 1 z 1 .

Η βασική εξίσωση της δυναμικής σε ένα ακίνητο σύστημα

Γράφουμε την απόλυτη επιτάχυνση ενός σημείου σύμφωνα με το θεώρημα Coriolis

που ένα κοιλιακούς– απόλυτη επιτάχυνση

ένα σχετ– σχετική επιτάχυνση.

ένα λωρίδα– φορητή επιτάχυνση.

ένα πυρήναςείναι η επιτάχυνση Coriolis.

Ας ξαναγράψουμε το (25) λαμβάνοντας υπόψη το (26)

Ας εισάγουμε τη σημειογραφία
- φορητή δύναμη αδράνειας,
είναι η δύναμη Coriolis της αδράνειας. Τότε η εξίσωση (27) παίρνει τη μορφή

Η βασική εξίσωση της δυναμικής για τη μελέτη της σχετικής κίνησης (28) είναι γραμμένη με τον ίδιο τρόπο όπως και για την απόλυτη κίνηση, μόνο οι μεταφορικές δυνάμεις αδράνειας και οι δυνάμεις Coriolis πρέπει να προστεθούν στις δυνάμεις που δρουν στο σημείο.

Γενικά θεωρήματα δυναμικής υλικού σημείου

Κατά την επίλυση πολλών προβλημάτων, μπορείτε να χρησιμοποιήσετε προκατασκευασμένα κενά που λαμβάνονται με βάση τον δεύτερο νόμο του Νεύτωνα. Τέτοιες μέθοδοι επίλυσης προβλημάτων συνδυάζονται σε αυτήν την ενότητα.

Θεώρημα για τη μεταβολή της ορμής ενός υλικού σημείου

Ας παρουσιάσουμε τα ακόλουθα δυναμικά χαρακτηριστικά:

1. Ποσότητα κίνησης υλικού σημείουείναι ένα διανυσματικό μέγεθος ίσο με το γινόμενο της μάζας ενός σημείου και του διανύσματος της ταχύτητάς του

. (29)

2. Παρόρμηση δύναμης

Στοιχειακή ώθηση δύναμης- διανυσματική ποσότητα ίση με το γινόμενο του διανύσματος δύναμης κατά ένα στοιχειώδες χρονικό διάστημα

(30).

Τότε πλήρης παρόρμηση

. (31)

Στο φά=const που παίρνουμε μικρό=πόδια.

Η συνολική ώθηση σε μια πεπερασμένη χρονική περίοδο μπορεί να υπολογιστεί μόνο σε δύο περιπτώσεις, όταν η δύναμη που ασκεί στο σημείο είναι σταθερή ή εξαρτάται από το χρόνο. Σε άλλες περιπτώσεις, είναι απαραίτητο να εκφραστεί η δύναμη σε συνάρτηση με το χρόνο.

Η ισότητα των διαστάσεων της ορμής (29) και της ορμής (30) καθιστά δυνατή τη δημιουργία μιας ποσοτικής σχέσης μεταξύ τους.

Θεωρήστε την κίνηση ενός υλικού σημείου Μ υπό την δράση μιας αυθαίρετης δύναμης φάσε μια αυθαίρετη διαδρομή.

Ο UD:
. (32)

Διαχωρίζουμε τις μεταβλητές στο (32) και ολοκληρώνουμε

. (33)

Ως αποτέλεσμα, λαμβάνοντας υπόψη το (31), λαμβάνουμε

. (34)

Η εξίσωση (34) εκφράζει το ακόλουθο θεώρημα.

Θεώρημα: Η μεταβολή της ορμής ενός υλικού σημείου σε μια ορισμένη χρονική περίοδο είναι ίση με την ώθηση της δύναμης που ασκεί το σημείο στο ίδιο χρονικό διάστημα.

Κατά την επίλυση προβλημάτων, η εξίσωση (34) πρέπει να προβάλλεται στους άξονες συντεταγμένων

Αυτό το θεώρημα είναι βολικό να χρησιμοποιηθεί όταν τα δεδομένα και τα άγνωστα μεγέθη περιλαμβάνουν τη μάζα ενός σημείου, την αρχική και τελική του ταχύτητα, τις δυνάμεις και τον χρόνο κίνησης.

Θεώρημα για τη μεταβολή της γωνιακής ορμής ενός υλικού σημείου

Μ
στιγμή της ορμής ενός υλικού σημείουσε σχέση με το κέντρο ισούται με το γινόμενο του συντελεστή ορμής του σημείου και του βραχίονα, δηλ. μικρότερη απόσταση (κάθετη) από το κέντρο σε μια γραμμή που συμπίπτει με το διάνυσμα της ταχύτητας

, (36)

. (37)

Η σχέση μεταξύ της ροπής της δύναμης (αιτία) και της ροπής της ορμής (αποτέλεσμα) καθορίζεται από το ακόλουθο θεώρημα.

Έστω σημείο M δεδομένης μάζας Μκινείται υπό την επίδραση της δύναμης φά.

,
,

, (38)

. (39)

Ας υπολογίσουμε την παράγωγο του (39)

. (40)

Συνδυάζοντας το (40) και το (38), παίρνουμε τελικά

. (41)

Η εξίσωση (41) εκφράζει το ακόλουθο θεώρημα.

Θεώρημα: Η χρονική παράγωγος του διανύσματος γωνιακής ορμής ενός υλικού σημείου σε σχέση με κάποιο κέντρο είναι ίση με τη ροπή της δύναμης που ασκεί το σημείο σε σχέση με το ίδιο κέντρο.

Κατά την επίλυση προβλημάτων, η εξίσωση (41) πρέπει να προβάλλεται στους άξονες συντεταγμένων

Στις εξισώσεις (42), οι ροπές ορμής και δύναμης υπολογίζονται σε σχέση με τους άξονες συντεταγμένων.

Από το (41) προκύπτει νόμος διατήρησης της γωνιακής ορμής (νόμος Κέπλερ).

Αν η ροπή της δύναμης που ασκείται σε ένα υλικό σημείο σε σχέση με οποιοδήποτε κέντρο είναι ίση με μηδέν, τότε η γωνιακή ορμή του σημείου σε σχέση με αυτό το κέντρο διατηρεί το μέγεθος και την κατεύθυνσή της.

Αν
, τότε
.

Το θεώρημα και ο νόμος διατήρησης χρησιμοποιούνται σε προβλήματα καμπυλόγραμμης κίνησης, ειδικά υπό τη δράση κεντρικών δυνάμεων.

Το μέγεθος της κίνησης του συστήματος, ως διανυσματική ποσότητα, προσδιορίζεται από τους τύπους (4.12) και (4.13).

Θεώρημα. Η χρονική παράγωγος της ορμής του συστήματος είναι ίση με το γεωμετρικό άθροισμα όλων των εξωτερικών δυνάμεων που ασκούνται σε αυτό.

Στις προβολές των καρτεσιανών αξόνων, λαμβάνουμε βαθμωτές εξισώσεις.

Μπορείτε να γράψετε ένα διάνυσμα

(4.28)

και βαθμωτές εξισώσεις

Τα οποία εκφράζουν το θεώρημα για τη μεταβολή της ορμής του συστήματος σε ολοκληρωμένη μορφή: η μεταβολή της ορμής του συστήματος σε μια ορισμένη χρονική περίοδο είναι ίση με το άθροισμα των παλμών για την ίδια χρονική περίοδο. Κατά την επίλυση προβλημάτων, χρησιμοποιούνται συχνότερα οι εξισώσεις (4.27).

Νόμος διατήρησης της ορμής

Θεώρημα για τη μεταβολή της κινητικής ροπής

Το θεώρημα για τη μεταβολή της γωνιακής ορμής ενός σημείου ως προς το κέντρο: η χρονική παράγωγος της γωνιακής ορμής ενός σημείου σε σχέση με ένα σταθερό κέντρο είναι ίση με τη διανυσματική ροπή που ενεργεί στο σημείο δύναμης σε σχέση με το ίδιο κέντρο.

Ή (4.30)

Συγκρίνοντας τα (4.23) και (4.30), βλέπουμε ότι οι ροπές των διανυσμάτων και συνδέονται με την ίδια εξάρτηση με τα ίδια τα διανύσματα και συνδέονται (Εικ. 4.1). Αν προβάλλουμε την ισότητα στον άξονα που διέρχεται από το κέντρο Ο, παίρνουμε

(4.31)

Αυτή η ισότητα εκφράζει το θεώρημα της ροπής ορμής ενός σημείου γύρω από έναν άξονα.

Ρύζι. 4.1.

Το θεώρημα για τη μεταβολή της κύριας ροπής ορμής ή της κινητικής ροπής ενός μηχανικού συστήματος ως προς το κέντρο: η χρονική παράγωγος της κινητικής ροπής του συστήματος ως προς κάποιο σταθερό κέντρο είναι ίση με το άθροισμα των ροπών του όλες οι εξωτερικές δυνάμεις ως προς το ίδιο κέντρο.

(4.32)

Αν προβάλλουμε την παράσταση (4.32) στον άξονα που διέρχεται από το κέντρο Ο, τότε προκύπτει μια ισότητα που χαρακτηρίζει το θεώρημα της μεταβολής της γωνιακής ορμής σε σχέση με τον άξονα.

(4.33)

Αντικαθιστώντας το (4.10) με ισότητα (4.33), μπορεί κανείς να γράψει τη διαφορική εξίσωση ενός περιστρεφόμενου άκαμπτου σώματος (τροχοί, άξονες, άξονες, ρότορες κ.λπ.) σε τρεις μορφές.

(4.34)

(4.35)

(4.36)

Έτσι, είναι σκόπιμο να χρησιμοποιηθεί το θεώρημα για τη μεταβολή της κινητικής ροπής για τη μελέτη της κίνησης ενός άκαμπτου σώματος, που είναι πολύ συνηθισμένο στην τεχνολογία, την περιστροφή του γύρω από έναν σταθερό άξονα.

Ο νόμος διατήρησης της γωνιακής ορμής του συστήματος

1. Αφήστε την έκφραση (4.32) .

Τότε από την εξίσωση (4.32) προκύπτει ότι , δηλ. εάν το άθροισμα των ροπών όλων των εξωτερικών δυνάμεων που εφαρμόζονται στο σύστημα σε σχέση με ένα δεδομένο κέντρο είναι μηδέν, τότε η κινητική ροπή του συστήματος σε σχέση με αυτό το κέντρο θα είναι αριθμητικά και η φορά θα είναι σταθερή.

2. Αν , τότε . Έτσι, εάν το άθροισμα των ροπών των εξωτερικών δυνάμεων που δρουν στο σύστημα ως προς κάποιον άξονα είναι ίσο με μηδέν, τότε η κινητική ροπή του συστήματος ως προς αυτόν τον άξονα θα είναι σταθερή τιμή.

Αυτά τα αποτελέσματα εκφράζουν το νόμο της διατήρησης της γωνιακής ορμής.

Στην περίπτωση ενός περιστρεφόμενου άκαμπτου σώματος, από την ισότητα (4.34) προκύπτει ότι αν , τότε . Από εδώ καταλήγουμε στα εξής συμπεράσματα:

Εάν το σύστημα είναι αμετάβλητο (απόλυτα άκαμπτο σώμα), τότε, κατά συνέπεια, και και το άκαμπτο σώμα περιστρέφεται γύρω από έναν σταθερό άξονα με σταθερή γωνιακή ταχύτητα.

Εάν το σύστημα είναι μεταβλητό, τότε . Με αύξηση (τότε τα επιμέρους στοιχεία του συστήματος απομακρύνονται από τον άξονα περιστροφής), η γωνιακή ταχύτητα μειώνεται, επειδή , και αυξάνεται με τη μείωση, επομένως, στην περίπτωση ενός μεταβλητού συστήματος, με τη βοήθεια εσωτερικών δυνάμεων, είναι δυνατή η αλλαγή της γωνιακής ταχύτητας.

Η δεύτερη εργασία D2 της εργασίας ελέγχου είναι αφιερωμένη στο θεώρημα σχετικά με τη μεταβολή της γωνιακής ορμής του συστήματος σε σχέση με τον άξονα.

Εργασία Δ2

Μια ομοιογενής οριζόντια πλατφόρμα (στρογγυλή με ακτίνα R ή ορθογώνια με πλευρές R και 2R, όπου R = 1,2 m) με μάζα kg περιστρέφεται με γωνιακή ταχύτητα γύρω από τον κατακόρυφο άξονα z, ο οποίος απέχει από το κέντρο της μάζας C της πλατφόρμας στο μια απόσταση OC = b (Εικ. D2.0 – D2.9, πίνακας D2); οι διαστάσεις για όλες τις ορθογώνιες πλατφόρμες φαίνονται στο σχ. D2.0a (κάτοψη).

Τη χρονική στιγμή, ένα φορτίο D με μάζα kg αρχίζει να κινείται κατά μήκος του αγωγού της πλατφόρμας (υπό τη δράση εσωτερικών δυνάμεων) σύμφωνα με το νόμο , όπου το s εκφράζεται σε μέτρα, το t είναι σε δευτερόλεπτα. Ταυτόχρονα, ένα ζεύγος δυνάμεων με ροπή M (δίνεται σε νεοτονόμετρα) αρχίζει να ενεργεί στις πλατφόρμες· στο M< 0 его направление противоположно показанному на рисунках).

Προσδιορίστε, αγνοώντας τη μάζα του άξονα, την εξάρτηση δηλ. γωνιακή ταχύτητα πλατφόρμας ως συνάρτηση του χρόνου.

Σε όλα τα σχήματα, το φορτίο D εμφανίζεται σε μια θέση όπου s > 0 (όταν s< 0, груз находится по другую сторону от точки А). Изображая чертеж решаемой задачи, провести ось z на заданном расстоянии OC = b от центра C.

Κατευθύνσεις.Εργασία Δ2 - σχετικά με την εφαρμογή του θεωρήματος για τη μεταβολή της γωνιακής ορμής του συστήματος. Κατά την εφαρμογή του θεωρήματος σε ένα σύστημα που αποτελείται από μια πλατφόρμα και ένα φορτίο, η γωνιακή ορμή του συστήματος γύρω από τον άξονα z ορίζεται ως το άθροισμα των ροπών της πλατφόρμας και του φορτίου. Σε αυτή την περίπτωση, θα πρέπει να ληφθεί υπόψη ότι η απόλυτη ταχύτητα του φορτίου είναι το άθροισμα των σχετικών και φορητών στροφών, δηλ. . Επομένως, το μέγεθος της κίνησης αυτού του φορτίου . Τότε μπορούμε να χρησιμοποιήσουμε το θεώρημα Varignon (στατική), σύμφωνα με το οποίο ; οι ροπές αυτές υπολογίζονται με τον ίδιο τρόπο όπως οι ροπές των δυνάμεων. Η πορεία της λύσης εξηγείται αναλυτικότερα στο παράδειγμα Δ2.

Κατά την επίλυση του προβλήματος, είναι χρήσιμο να απεικονίσετε στο βοηθητικό σχέδιο μια όψη της πλατφόρμας από πάνω (από το άκρο z), όπως γίνεται στο Σχ. D2.0,a - D2.9,a.

Η ροπή αδράνειας μιας πλάκας με μάζα m ως προς τον άξονα Cz, κάθετη στην πλάκα και διέρχεται από το κέντρο μάζας της, ισούται με: για μια ορθογώνια πλάκα με πλευρές και

;

Για ένα στρογγυλό ένθετο ακτίνας R

Αριθμός κατάστασης	σι	s = F(t)	Μ
	R R/2 R R/2 R R/2 R R/2 R R/2	-0,4 0,6 0,8 10t 0,4 -0,5t -0,6t 0,8t 0,4 0,5	4t -6 -8t -9 6 -10 12

	Ρύζι. D2.0		Ρύζι. D2.0a

	Ρύζι. Δ2.1		Ρύζι. D2.1a

	Ρύζι. Δ2.2		Ρύζι. D2.2a

	Ρύζι. Δ2.3		Ρύζι. D2.3a

	Ρύζι. Δ2.4
		Ρύζι. D2.4a

		Ρύζι. D2.5a
	Ρύζι. D2.5

	Ρύζι. Δ2.6		Ρύζι. D2.6a

	Ρύζι. D2.7		Ρύζι. D2.7a

	Ρύζι. D2.8		Ρύζι. D2.8a

	Ρύζι. D2.9		Ρύζι. D2.9a

	Ρύζι. Δ 2

Παράδειγμα Δ2. Μια ομοιογενής οριζόντια πλατφόρμα (ορθογώνια με πλευρές 2l και l), με μάζα, στερεώνεται άκαμπτα σε έναν κατακόρυφο άξονα και περιστρέφεται μαζί του γύρω από έναν άξονα zμε γωνιακή ταχύτητα (Εικ. E2a ). Τη χρονική στιγμή, μια ροπή M αρχίζει να ενεργεί στον άξονα, κατευθυνόμενη αντίθετα ; ταυτόχρονα φορτίο ρεμάζα που βρίσκεται στην υδρορροή ΑΒστο σημείο ΜΕ,αρχίζει να κινείται κατά μήκος του αγωγού (υπό τη δράση εσωτερικών δυνάμεων) σύμφωνα με το νόμο s = CD = F(t).

Δίνονται: m 1 \u003d 16 kg, t 2= 10 κιλά, μεγάλο\u003d 0,5 m, \u003d 2, s \u003d 0,4t 2 (s - σε μέτρα, t - σε δευτερόλεπτα), Μ= kt,που κ=6 Nm/s. Προσδιορίστε: - τον νόμο μεταβολής της γωνιακής ταχύτητας της πλατφόρμας.

Λύση.Εξετάστε ένα μηχανικό σύστημα που αποτελείται από μια πλατφόρμα και ένα φορτίο ΡΕ.Για να προσδιορίσουμε το w, εφαρμόζουμε το θεώρημα για τη μεταβολή της γωνιακής ορμής του συστήματος ως προς τον άξονα z:

(1)

Ας απεικονίσουμε τις εξωτερικές δυνάμεις που δρουν στο σύστημα: οι δυνάμεις βαρύτητας της αντίδρασης και η ροπή M. Δεδομένου ότι οι δυνάμεις και είναι παράλληλες με τον άξονα z, και οι αντιδράσεις τέμνουν αυτόν τον άξονα, οι ροπές τους σε σχέση με τον άξονα z είναι ίσες στο μηδέν. Στη συνέχεια, λαμβάνοντας υπόψη τη θετική κατεύθυνση για τη στιγμή (δηλαδή, αριστερόστροφα), παίρνουμε και η εξίσωση (1) θα πάρει αυτή τη μορφή.