Όριο με το l'Hopital. Κανόνες του Lopital. Παραδείγματα λύσεων. Κανόνας του L'Hopital: Ιστορία και ορισμός

Ο κανόνας του L'Hopital

Ο κανόνας του L'Hopitalείναι μια μέθοδος υπολογισμού ορίων που έχουν αβεβαιότητα τύπου ή . Αφήνω έναείναι κάποιος πεπερασμένος πραγματικός αριθμός ή ισούται με άπειρο. Ο κανόνας του L'Hospital μπορεί επίσης να εφαρμοστεί σε αβεβαιότητες του τύπου . Οι δύο πρώτες αβεβαιότητες μπορούν να αναχθούν σε τύπους ή με αλγεβρικούς μετασχηματισμούς. Και οι αβεβαιότητες μειώνονται σε τύπο χρησιμοποιώντας τη σχέση Ο κανόνας του L'Hopital ισχύει επίσης για μονόπλευρα όρια.

Παράδειγμα 1

Υπολογίστε το όριο. Λύση. Διαφοροποιώντας τον αριθμητή και τον παρονομαστή, βρίσκουμε την τιμή του ορίου:

Παράδειγμα 2

Υπολογίστε το όριο. Λύση. Εφόσον η άμεση αντικατάσταση οδηγεί σε απροσδιοριστία τύπου, εφαρμόζουμε τον κανόνα του L'Hospital.

Παράδειγμα 3

Υπολογισμός ορίου . Λύση. Εδώ έχουμε να κάνουμε με ασάφεια τύπου. Μετά από απλούς μετασχηματισμούς, παίρνουμε

Παράδειγμα 4

Βρείτε το όριο. Λύση. Χρησιμοποιώντας τον κανόνα του L'Hopital, μπορεί κανείς να γράψει

Παράδειγμα 5

Βρείτε το όριο. Λύση. Εδώ συναντάμε ασάφεια τύπου. Ας υποδηλώσουμε . Αφού πάρουμε τον λογάριθμο, παίρνουμε Αντίστοιχα,

Παράδειγμα 6

15. Κανόνες του L'Hospital*

Ελβετός μαθηματικός Johann I Bernoulli(1667-1748) αφού αποφοίτησε επιτυχώς από το Πανεπιστήμιο της Βασιλείας, ταξιδεύοντας σε όλη την Ευρώπη, το 1690 έφτασε στο Παρίσι. Στο λογοτεχνικό σαλόνι του φιλοσόφου Nicolas Malebranche (1638-1715), ο Johann συναντά τον Γάλλο μαθηματικό, Marquis Guillaume Francois Antoine de Lopital (1661-1704). Κατά τη διάρκεια μιας ζωντανής συνομιλίας, ο Lopital εξεπλάγη πόσο εύκολα, «σαν να έπαιζε», ο νεαρός Μπερνούλι έλυνε δύσκολα προβλήματα σύμφωνα με τον νέο λογισμό. Ως εκ τούτου, η L'Hopital του ζήτησε να διαβάσει μερικές διαλέξεις. Στον Λ' Χόπιταλ άρεσαν οι προφορικές συνομιλίες και για μια αξιοπρεπή αμοιβή άρχισε να λαμβάνει υλικό γραπτώς. Σημειώστε ότι τον γνωστό πλέον «κανόνα του L' Hopital» για την αποκάλυψη αβεβαιοτήτων του πέρασε και ο Γιόχαν. Ήδη από το 1696, εμφανίστηκε η περίφημη πραγματεία του L'Hopital «Εισαγωγή στην ανάλυση των απειροελάχιστων για την κατανόηση των καμπυλών γραμμών». Το δεύτερο μέρος του μαθήματος που δίδαξε ο Johann I Bernoulli δημοσιεύτηκε μόλις το 1742 και ονομαζόταν «Μαθηματικές διαλέξεις για τη μέθοδο των ολοκληρωμάτων και άλλα. γράφτηκε για τον διάσημο Μαρκήσιο του Νοσοκομείου. έτη 1691-1692». Το 1921 ανακαλύφθηκαν χειρόγραφα αντίγραφα των διαλέξεων του Johann I Bernoulli, τα πρωτότυπα των οποίων μεταφέρθηκαν στο L'Hopital το 1691-1692. Από αυτούς, οι επιστήμονες ανακάλυψαν απροσδόκητα ότι ο Λόπταλ στην «Ανάλυσή» του σχεδόν δεν παρέκκλινε από τις διαλέξεις του νεαρού δασκάλου του.

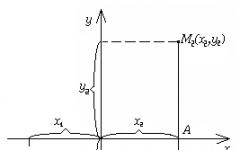
Θεώρημα (Cauchy).Αφήστε τις συναρτήσεις και να είναι συνεχείς και διαφοροποιήσιμες στις και . Τότε :

Απόδειξη.Εξετάστε τη συνάρτηση

Ας επιλέξουμε έτσι ώστε να πληρούνται όλες οι προϋποθέσεις του θεωρήματος του Rolle, δηλ. .

Σύμφωνα με το θεώρημα του Rolle, υπάρχει:

Πρώτος κανόνας του L'Hospital

Ορισμός.Αφήστε τις συναρτήσεις , να είναι συνεχείς σε , να είναι διαφοροποιήσιμες σε , και . Αφήστε . Τότε η σχέση στο λέγεται ότι είναι αβεβαιότητα της μορφής .

Θεώρημα.

Ας εφαρμόσουμε το θεώρημα του Cauchy στο διάστημα , όπου . Υπάρχει :

και ως εκ τούτου,

Αυτό σημαίνει ότι .

Στην περίπτωση που είναι άπειρο, η ανισότητα (1) αντικαθίσταται από

ανάλογα με το σημάδι. Η υπόλοιπη απόδειξη δεν αλλάζει.

Ο δεύτερος κανόνας του L'Hospital

Ορισμός.Αφήστε τις συναρτήσεις , να είναι συνεχείς και διαφοροποιήσιμες σε , και . Αφήστε . Τότε η σχέση στο λέγεται ότι είναι αβεβαιότητα της μορφής .

Θεώρημα.Εάν, υπό αυτές τις προϋποθέσεις, υπάρχει

Απόδειξη.Αφήστε φυσικά. Επιλέγοντας : το διάστημα ικανοποιεί την ανισότητα

Ορίστε μια συνάρτηση από τη συνθήκη

στο . Ας εφαρμόσουμε το θεώρημα Cauchy στο τμήμα. Ας καταλάβουμε ότι υπάρχει:

Για όσους

Αφού είναι αυθαίρετα μικρό, λοιπόν

Στην περίπτωση που , η ανισότητα (2) αντικαθίσταται από

και η ανισότητα (4) στην ανισότητα

που λαμβάνει χώρα σε αρκετά κοντά σε ένα λόγω (3).

Η περίπτωση εξετάζεται ανάλογα.

Λύση διαδικτυακά όρια λειτουργιών. Βρείτε την οριακή τιμή μιας συνάρτησης ή συναρτητικής ακολουθίας σε ένα σημείο, υπολογίστε περιορίζονταςτιμή συνάρτησης στο άπειρο. καθορίστε τη σύγκλιση μιας σειράς αριθμών και πολλά περισσότερα μπορούν να γίνουν χάρη στην ηλεκτρονική μας υπηρεσία -. Σας επιτρέπουμε να βρίσκετε τα όρια λειτουργιών στο διαδίκτυο γρήγορα και με ακρίβεια. Εσείς ο ίδιος εισάγετε τη μεταβλητή συνάρτησης και το όριο στο οποίο αυτή επιδιώκει, η υπηρεσία μας κάνει όλους τους υπολογισμούς για εσάς, δίνοντας μια ακριβή και απλή απάντηση. Και για εύρεση του ορίου στο Διαδίκτυομπορείτε να εισάγετε τόσο αριθμητικές σειρές όσο και αναλυτικές συναρτήσεις που περιέχουν σταθερές σε μια κυριολεκτική έκφραση. Σε αυτήν την περίπτωση, το όριο συνάρτησης που βρέθηκε θα περιέχει αυτές τις σταθερές ως σταθερά ορίσματα στην έκφραση. Η υπηρεσία μας επιλύει κάθε περίπλοκο πρόβλημα εύρεσης όρια στο διαδίκτυο, αρκεί να καθορίσετε τη συνάρτηση και το σημείο στο οποίο είναι απαραίτητο να υπολογιστεί όριο λειτουργίας. Χρήση υπολογιστή όρια στο διαδίκτυο, μπορείτε να χρησιμοποιήσετε διάφορες μεθόδους και κανόνες για την επίλυσή τους, ενώ συγκρίνετε το αποτέλεσμα με λύση περιορισμού στο διαδίκτυοστο www.site, που θα οδηγήσει στην επιτυχή ολοκλήρωση της εργασίας - θα αποφύγετε τα δικά σας λάθη και τυπογραφικά λάθη. Ή μπορείτε να μας εμπιστευτείτε πλήρως και να χρησιμοποιήσετε το αποτέλεσμά μας στην εργασία σας, χωρίς να ξοδέψετε επιπλέον κόπο και χρόνο σε ανεξάρτητους υπολογισμούς του ορίου συνάρτησης. Επιτρέπουμε την εισαγωγή οριακών τιμών όπως το άπειρο. Πρέπει να εισαγάγετε έναν κοινό όρο της αριθμητικής ακολουθίας και www.siteθα υπολογίσει την τιμή όριο στο διαδίκτυοστο συν ή πλην άπειρο.

Μία από τις βασικές έννοιες της μαθηματικής ανάλυσης είναι όριο λειτουργίαςκαι όριο ακολουθίαςσε ένα σημείο και στο άπειρο, είναι σημαντικό να μπορείς να λύνεις σωστά όρια. Με την υπηρεσία μας δεν θα είναι δύσκολο. Γίνεται μια απόφαση όρια στο διαδίκτυομέσα σε δευτερόλεπτα, η απάντηση είναι ακριβής και πλήρης. Η μελέτη του λογισμού ξεκινά με πέρασμα στο όριο, όριαχρησιμοποιούνται σχεδόν σε όλες τις ενότητες των ανώτερων μαθηματικών, επομένως είναι χρήσιμο να έχετε διαθέσιμο διακομιστή περιορίστε τις διαδικτυακές λύσεις, που είναι matematikam.ru.

Φανταστείτε ένα κοπάδι από σπουργίτια με διογκωμένα μάτια. Όχι, δεν είναι βροντή, ούτε τυφώνας, ούτε καν ένα αγοράκι με μια σφεντόνα στα χέρια. Απλώς μια τεράστια, τεράστια οβίδα πετάει στο χοντρό των νεοσσών. Ακριβώς τοπικούς κανόνεςασχοληθείτε με τα όρια στα οποία υπάρχει αβεβαιότητα ή .

Οι κανόνες του L'Hopital είναι μια πολύ ισχυρή μέθοδος που σας επιτρέπει να εξαλείψετε γρήγορα και αποτελεσματικά αυτές τις αβεβαιότητες, δεν είναι τυχαίο ότι σε συλλογές προβλημάτων, σε δοκιμές, δοκιμές, βρίσκεται συχνά μια σταθερή σφραγίδα: "υπολογίστε το όριο, χωρίς να χρησιμοποιήσει τον κανόνα του L'Hopital". Η απαίτηση με έντονους χαρακτήρες μπορεί να αποδοθεί με καθαρή συνείδηση ​​σε οποιοδήποτε όριο μαθημάτων Όρια. Παραδείγματα λύσεων, Αξιοσημείωτα όρια. Μέθοδοι επίλυσης ορίων, Αξιοσημείωτες Ισοδυναμίες, όπου εμφανίζεται η αβεβαιότητα "μηδέν στο μηδέν" ή "άπειρο στο άπειρο". Ακόμα κι αν η εργασία διατυπωθεί εν συντομία - "υπολογίστε τα όρια", τότε εννοείται σιωπηρά ότι θα χρησιμοποιήσετε ό,τι θέλετε, αλλά όχι τους κανόνες του L'Hospital.

Υπάρχουν δύο κανόνες συνολικά και μοιάζουν πολύ μεταξύ τους, τόσο στην ουσία όσο και στον τρόπο εφαρμογής τους. Εκτός από τα άμεσα παραδείγματα για το θέμα, θα μελετήσουμε επίσης πρόσθετο υλικό που θα είναι χρήσιμο στην πορεία περαιτέρω μελέτης της μαθηματικής ανάλυσης.

Θα κάνω μια κράτηση αμέσως ότι οι κανόνες θα δοθούν σε μια συνοπτική "πρακτική" μορφή και εάν πρέπει να περάσετε τη θεωρία, σας συνιστώ να απευθυνθείτε στο σχολικό βιβλίο για πιο αυστηρούς υπολογισμούς.

Πρώτος κανόνας του L'Hospital

Εξετάστε τις συναρτήσεις που απείρως μικρόσε κάποιο σημείο. Εάν υπάρχει ένα όριο στη σχέση τους, τότε για να εξαλείψουμε την αβεβαιότητα, μπορούμε να πάρουμε δύο παράγωγα- από τον αριθμητή και από τον παρονομαστή. Εν: , αυτό είναι .

Σημείωση : το όριο πρέπει επίσης να υπάρχει, διαφορετικά δεν ισχύει ο κανόνας.

Τι προκύπτει από τα παραπάνω;

Πρώτα, πρέπει να μπορείτε να βρείτε παράγωγα συναρτήσεωνΚαι όσο καλύτερα, τόσο καλύτερα =)

Δεύτερον, οι παράγωγοι λαμβάνονται ΧΩΡΙΣΤΑ από τον αριθμητή και ΞΕΧΩΡΙΣΤΑ από τον παρονομαστή. Παρακαλώ μην μπερδεύεστε με τον κανόνα της διαφοροποίησης του πηλίκου !!!

Και, τρίτον, το "x" μπορεί να τείνει οπουδήποτε, συμπεριλαμβανομένου του άπειρου - αν υπήρχε μόνο αβεβαιότητα.

Ας επιστρέψουμε στο Παράδειγμα 5 του πρώτου άρθρου σχετικά με τα όρια, το οποίο έδωσε το ακόλουθο αποτέλεσμα:

Για την αβεβαιότητα 0:0, εφαρμόζουμε τον πρώτο κανόνα του L'Hospital:

Όπως μπορείτε να δείτε, η διαφοροποίηση αριθμητή και παρονομαστή μας οδήγησε στην απάντηση με μισή στροφή: βρήκαμε δύο απλές παραγώγους, αντικαταστήσαμε το "δύο" σε αυτές, και αποδείχθηκε ότι η αβεβαιότητα εξαφανίστηκε χωρίς ίχνος!

Δεν είναι ασυνήθιστο οι κανόνες της L'Hopital να εφαρμόζονται διαδοχικά δύο ή περισσότερες φορές (αυτό ισχύει και για τον δεύτερο κανόνα). Ας το βγάλουμε για ένα ρετρό βραδινό Παράδειγμα 2 μαθήματα για υπέροχα όρια:

Δυο κουλούρια κρυώνουν ξανά στην κουκέτα. Ας εφαρμόσουμε τον κανόνα του L'Hospital:

Σημειώστε ότι στο πρώτο βήμα λαμβάνεται ο παρονομαστής παράγωγο μιγαδικής συνάρτησης. Μετά από αυτό, πραγματοποιούμε μια σειρά από ενδιάμεσες απλοποιήσεις, ειδικότερα, απαλλαγούμε από το συνημίτονο, υποδεικνύοντας ότι τείνει προς την ενότητα. Η αβεβαιότητα δεν έχει εξαλειφθεί, επομένως εφαρμόζουμε ξανά τον κανόνα L'Hopital (δεύτερη γραμμή).

Δεν επέλεξα συγκεκριμένα το πιο εύκολο παράδειγμα για να κάνετε έναν μικρό αυτοέλεγχο. Αν δεν είναι απολύτως σαφές πώς βρέθηκαν παράγωγα, θα πρέπει να ενισχύσετε την τεχνική διαφοροποίησής σας, εάν δεν καταλαβαίνετε το κόλπο συνημιτονίου, παρακαλώ επιστρέψτε στο υπέροχα όρια. Δεν βλέπω πολύ νόημα στα σχόλια βήμα-βήμα, αφού έχω ήδη μιλήσει για παράγωγα και όρια με αρκετή λεπτομέρεια. Η καινοτομία του άρθρου έγκειται στους ίδιους τους κανόνες και σε ορισμένες τεχνικές λύσεις.

Όπως έχει ήδη σημειωθεί, στις περισσότερες περιπτώσεις οι κανόνες του L'Hopital δεν χρειάζεται να χρησιμοποιούνται, αλλά συχνά συνιστάται η χρήση τους για έναν πρόχειρο έλεγχο της λύσης. Συχνά, αλλά όχι πάντα. Έτσι, για παράδειγμα, είναι πολύ πιο κερδοφόρο να ελέγξετε το παράδειγμα που μόλις σκεφτήκατε να χρησιμοποιήσετε υπέροχες ισοδυναμίες.

Ο δεύτερος κανόνας του L'Hospital

Ο Brother-2 τσακώνεται με δύο οκτώ που κοιμούνται. Ομοίως:

Αν υπάρχει όριο σχέσης απείρως μεγάλοστο σημείο συνάρτησης: , τότε για να εξαλείψουμε την αβεβαιότητα, μπορούμε να πάρουμε δύο παράγωγα– ΧΩΡΙΣΤΕ από τον αριθμητή και ΧΩΡΙΣΤΕ από τον παρονομαστή. Εν: , αυτό είναι κατά τη διαφοροποίηση του αριθμητή και του παρονομαστή, η τιμή του ορίου δεν αλλάζει.

Σημείωση : όριο πρέπει να υπάρχει

Και πάλι, σε διάφορα πρακτικά παραδείγματα η τιμή μπορεί να είναι διαφορετική, συμπεριλαμβανομένων των άπειρων. Είναι σημαντικό να υπάρχει αβεβαιότητα.

Ας ελέγξουμε το Παράδειγμα #3 του πρώτου μαθήματος: . Χρησιμοποιούμε τον δεύτερο κανόνα του L'Hospital:

Επειδή μιλάμε για γίγαντες, ας αναλύσουμε δύο κανονικά όρια:

Παράδειγμα 1

Υπολογισμός ορίου

Δεν είναι εύκολο να λάβουμε μια απάντηση με «συνηθισμένες» μεθόδους, επομένως, για να αποκαλύψουμε την αβεβαιότητα «άπειρο στο άπειρο», χρησιμοποιούμε τον κανόνα L'Hopital:

Με αυτόν τον τρόπο, μια γραμμική συνάρτηση μεγαλύτερης τάξης ανάπτυξης από έναν λογάριθμο με βάση μεγαλύτερη από ένα( και τα λοιπά.). Φυσικά, το «x» σε υψηλότερες δυνάμεις θα «τραβάει» και τέτοιους λογάριθμους. Πράγματι, η συνάρτηση μεγαλώνει αρκετά αργά και είναι πρόγραμμαείναι πιο ήπιο σε σχέση με το ίδιο «χ».

Παράδειγμα 2

Υπολογισμός ορίου

Άλλο ένα ξεθωριασμένο πλαίσιο. Για να εξαλείψουμε την αβεβαιότητα, χρησιμοποιούμε τον κανόνα L'Hopital, επιπλέον, δύο φορές στη σειρά:

Εκθετική συνάρτηση, με βάση μεγαλύτερη από μία( και τα λοιπά.) υψηλότερη τάξη ανάπτυξης από μια συνάρτηση ισχύος με θετικό βαθμό.

Παρόμοια όρια συναντώνται κατά τη διάρκεια πλήρης μελέτη λειτουργίας, δηλαδή, κατά την εύρεση ασύμπτωτο γραφημάτων. Φαίνονται επίσης σε ορισμένες εργασίες στο θεωρία πιθανοτήτων. Σας συμβουλεύω να σημειώσετε τα δύο παραδείγματα που εξετάστηκαν, αυτή είναι μια από τις λίγες περιπτώσεις που δεν υπάρχει τίποτα καλύτερο από το να διαφοροποιήσετε τον αριθμητή και τον παρονομαστή.

Περαιτέρω στο κείμενο, δεν θα κάνω διάκριση μεταξύ του πρώτου και του δεύτερου κανόνα του L'Hopital, αυτό έγινε μόνο για τον σκοπό της δομής του άρθρου. Γενικά, από την άποψή μου, είναι κάπως επιβλαβές να υπεραριθμούνται μαθηματικά αξιώματα, θεωρήματα, κανόνες, ιδιότητες, καθώς φράσεις όπως "σύμφωνα με το συμπέρασμα 3 σύμφωνα με το θεώρημα 19 ..." είναι ενημερωτικές μόνο στο πλαίσιο ενός ή άλλο σχολικό βιβλίο. Σε μια άλλη πηγή πληροφοριών, το ίδιο θα ήταν το "συμπέρασμα 2 και το θεώρημα 3". Τέτοιες δηλώσεις είναι επίσημες και βολικές μόνο για τους ίδιους τους συγγραφείς. Στην ιδανική περίπτωση, είναι καλύτερο να αναφερθούμε στην ουσία ενός μαθηματικού γεγονότος. Η εξαίρεση είναι ιστορικά καθιερωμένοι όροι, για παράδειγμα, πρώτο υπέροχο όριοή δεύτερο υπέροχο όριο.

Συνεχίζουμε να αναπτύσσουμε το θέμα, το οποίο μας έριξε το μέλος της Ακαδημίας Επιστημών του Παρισιού, Marquis Guillaume Francois de Lopital. Το άρθρο αποκτά έναν έντονο πρακτικό χρωματισμό και σε μια αρκετά κοινή εργασία απαιτείται:

Για να ζεσταθούμε, ας ασχοληθούμε με μερικά μικρά σπουργίτια:

Παράδειγμα 3

Το όριο μπορεί να απλοποιηθεί προκαταρκτικά με την απαλλαγή από το συνημίτονο, αλλά θα δείξουμε σεβασμό για την συνθήκη και θα διαφοροποιήσουμε αμέσως τον αριθμητή και τον παρονομαστή:

Στην ίδια τη διαδικασία εύρεσης παραγώγων, δεν υπάρχει τίποτα μη τυπικό, για παράδειγμα, χρησιμοποιείται ο συνήθης παρονομαστής κανόνας διαφοροποίησηςέργα .

Το εξεταζόμενο παράδειγμα καταστρέφεται και διαμέσου υπέροχα όρια, μια παρόμοια περίπτωση συζητείται στο τέλος του άρθρου Σύνθετα όρια.

Παράδειγμα 4

Υπολογίστε το όριο σύμφωνα με τον κανόνα του L'Hopital

Αυτό είναι ένα παράδειγμα "φτιάξ' το μόνος σου". Καλό αστείο =)

Μια τυπική κατάσταση είναι όταν, μετά τη διαφοροποίηση, λαμβάνονται τριώροφα ή τετραώροφα κλάσματα:

Παράδειγμα 5

Υπολογίστε το όριο χρησιμοποιώντας τον κανόνα του L'Hospital

Παρακαλώ για αίτηση αξιοσημείωτη ισοδυναμία, αλλά η διαδρομή είναι σκληρά κωδικοποιημένη από την συνθήκη:

Μετά τη διαφοροποίηση, συνιστώ ανεπιφύλακτα να απαλλαγείτε από το κλάσμα πολυώροφων και να πραγματοποιήσετε τις μέγιστες απλοποιήσεις. Φυσικά, οι πιο προχωρημένοι μαθητές μπορούν να παραλείψουν το τελευταίο βήμα και να σημειώσουν αμέσως: , αλλά σε κάποια όρια ακόμη και οι αριστούχοι μαθητές θα μπερδευτούν.

Παράδειγμα 6

Υπολογίστε το όριο χρησιμοποιώντας τον κανόνα του L'Hospital

Παράδειγμα 7

Υπολογίστε το όριο χρησιμοποιώντας τον κανόνα του L'Hospital

Αυτά είναι παραδείγματα αυτοβοήθειας. Στο Παράδειγμα 7, δεν μπορείτε να απλοποιήσετε τίποτα, αποδεικνύεται πολύ απλό μετά τη διαφοροποίηση του κλάσματος. Αλλά στο Παράδειγμα 8, μετά την εφαρμογή του κανόνα L'Hopital, είναι πολύ επιθυμητό να απαλλαγούμε από την τριώροφη δομή, καθώς οι υπολογισμοί δεν θα είναι οι πιο βολικοί. Πλήρης λύση και απάντηση στο τέλος του μαθήματος. Εάν έχετε οποιοδήποτε πρόβλημα - τριγωνομετρικός πίνακαςνα βοηθήσω.

Και, οι απλουστεύσεις είναι απολύτως απαραίτητες όταν, μετά τη διαφοροποίηση, η αβεβαιότητα δεν εξαλείφεται.

Παράδειγμα 8

Υπολογίστε το όριο χρησιμοποιώντας τον κανόνα του L'Hospital

Πηγαίνω:

Είναι ενδιαφέρον ότι η αρχική αβεβαιότητα μετά την πρώτη διαφοροποίηση μετατράπηκε σε αβεβαιότητα και ο κανόνας του L'Hôpital εφαρμόζεται αδιατάρακτα περαιτέρω. Παρατηρήστε επίσης πώς μετά από κάθε «προσέγγιση» εξαλείφεται το κλάσμα των τεσσάρων ορόφων, και οι σταθερές αφαιρούνται από το οριακό πρόσημο. Σε πιο απλά παραδείγματα, είναι πιο βολικό να μην βγάζουμε σταθερές, αλλά όταν το όριο είναι σύνθετο, απλοποιούμε τα πάντα-όλα-τα πάντα. Η ύπουλα του λυμένου παραδείγματος έγκειται και στο ότι όταν , αλλά, επομένως, στην πορεία της εξάλειψης των ιγμορείων, δεν είναι περίεργο να μπερδεύεστε στα ζώδια. Στην προτελευταία σειρά, τα ιγμόρεια δεν θα μπορούσαν να έχουν σκοτωθεί, αλλά το παράδειγμα είναι μάλλον βαρύ, συγχωρέσιμο.

Τις προάλλες συνάντησα μια ενδιαφέρουσα εργασία:

Παράδειγμα 9

Για να είμαι ειλικρινής, αμφέβαλα λίγο με τι θα ισοδυναμούσε αυτό το όριο. Όπως αποδείχθηκε παραπάνω, το "x" είναι υψηλότερη τάξη ανάπτυξης από τον λογάριθμο, αλλά θα "βαρύνει" τον κυβικό λογάριθμο; Προσπαθήστε να μάθετε μόνοι σας ποιος θα κερδίσει.

Ναι, οι κανόνες του L'Hopital δεν είναι μόνο να πυροβολείτε σπουργίτια από κανόνι, αλλά και επίπονη δουλειά ....

Προκειμένου να εφαρμοστούν οι κανόνες του L'Hôpital σε bagels ή κουρασμένα οχτάρια, μειώνονται οι αβεβαιότητες της φόρμας.

Η αντιμετώπιση της αβεβαιότητας συζητείται λεπτομερώς στα Παραδείγματα #9-13 του μαθήματος. Μέθοδοι επίλυσης ορίων. Ας πάρουμε ένα άλλο για χάρη του:

Παράδειγμα 10

Υπολογίστε το όριο μιας συνάρτησης χρησιμοποιώντας τον κανόνα του L'Hopital

Στο πρώτο βήμα, φέρνουμε την έκφραση σε έναν κοινό παρονομαστή, μετατρέποντας έτσι την αβεβαιότητα σε αβεβαιότητα. Και μετά χρεώνουμε τον κανόνα L'Hopital:

Εδώ, παρεμπιπτόντως, συμβαίνει όταν είναι άσκοπο να αγγίξουμε την τετραώροφη έκφραση.

Η αβεβαιότητα επίσης δεν αντιστέκεται στο να μετατραπεί σε ή:

Παράδειγμα 11

Υπολογίστε το όριο μιας συνάρτησης χρησιμοποιώντας τον κανόνα του L'Hopital

Το όριο εδώ είναι μονόπλευρο και τέτοια όρια έχουν ήδη συζητηθεί στο εγχειρίδιο Γραφήματα και ιδιότητες συναρτήσεων. Όπως θυμάστε, το γράφημα του «κλασικού» λογάριθμου δεν υπάρχει στα αριστερά του άξονα, επομένως μπορούμε να προσεγγίσουμε το μηδέν μόνο από τα δεξιά.

Οι κανόνες της L'Hôpital για μονόπλευρα όρια λειτουργούν, αλλά η αβεβαιότητα πρέπει πρώτα να αντιμετωπιστεί. Στο πρώτο βήμα, κάνουμε το κλάσμα τριώροφο, παίρνοντας την αβεβαιότητα και, στη συνέχεια, η λύση ακολουθεί το σχήμα του προτύπου:

Αφού διαφοροποιήσουμε τον αριθμητή και τον παρονομαστή, απαλλαγούμε από το τετραώροφο κλάσμα για να κάνουμε απλοποιήσεις. Ως αποτέλεσμα, προέκυψε η αβεβαιότητα. Επαναλαμβάνουμε το κόλπο: κάνουμε πάλι το κλάσμα τριώροφο και εφαρμόζουμε ξανά τον κανόνα L'Hopital στην αβεβαιότητα που προκύπτει:

Ετοιμος.

Θα μπορούσε κανείς να προσπαθήσει να μειώσει το αρχικό όριο σε δύο ντόνατς:

Αλλά, πρώτον, η παράγωγος στον παρονομαστή είναι πιο δύσκολη και, δεύτερον, δεν θα βγει τίποτα καλό από αυτό.

Με αυτόν τον τρόπο, πριν λύσετε παρόμοια παραδείγματα, πρέπει να αναλύσετε(προφορικά ή σε προσχέδιο) ΣΕ ΤΙ είναι πιο κερδοφόρο να μειωθεί η αβεβαιότητα - στο «μηδέν στο μηδέν» ή στο «άπειρο στο άπειρο».

Με τη σειρά τους, οι σύντροφοι που πίνουν και οι πιο εξωτικοί σύντροφοι σύρονται στο φως. Η μέθοδος μετασχηματισμού είναι απλή και τυπική.

• Κανόνας της L'Hopital και αποκάλυψη αβεβαιοτήτων
• Αποκάλυψη αβεβαιοτήτων των τύπων "μηδέν διαιρούμενο με μηδέν" και "άπειρο διαιρούμενο με άπειρο"
• Αποκάλυψη αβεβαιοτήτων της μορφής "μηδέν πολλαπλασιασμένο επί άπειρο"
• Αποκάλυψη αβεβαιοτήτων των τύπων «μηδέν στη δύναμη του μηδέν», «άπειρο στη δύναμη του μηδέν» και «ένα στη δύναμη του απείρου»
• Αποκάλυψη αβεβαιοτήτων της μορφής "άπειρο μείον άπειρο"

Κανόνας της L'Hopital και αποκάλυψη αβεβαιοτήτων

Η γνωστοποίηση αβεβαιοτήτων της μορφής 0/0 ή ∞/∞ και ορισμένων άλλων αβεβαιοτήτων απλοποιείται σημαντικά χρησιμοποιώντας τον κανόνα L'Hopital.

ουσία τοπικούς κανόνες είναι ότι στην περίπτωση που ο υπολογισμός του ορίου αναλογιών δύο συναρτήσεων δίνει αβεβαιότητες της μορφής 0/0 ή ∞/∞, το όριο του λόγου δύο συναρτήσεων μπορεί να αντικατασταθεί από το όριο του λόγου των παραγώγων τους και , έτσι, μπορεί να επιτευχθεί ένα συγκεκριμένο αποτέλεσμα.

Γενικά, οι κανόνες του L'Hopital σημαίνουν πολλά θεωρήματα που μπορούν να μεταφερθούν στην ακόλουθη διατύπωση.

Ο κανόνας του L'Hopital. Εάν λειτουργεί φά(Χ) και σολ(Χ) είναι διαφοροποιήσιμα σε κάποια γειτονιά του σημείου , με πιθανή εξαίρεση το ίδιο το σημείο, και σε αυτήν τη γειτονιά

(1)

Με άλλα λόγια, για αβεβαιότητες της μορφής 0/0 ή ∞/∞, το όριο του λόγου δύο συναρτήσεων ισούται με το όριο του λόγου των παραγώγων τους, αν υπάρχει η τελευταία (πεπερασμένη ή άπειρη).

Στην ισότητα (1), η τιμή , στην οποία τείνει η μεταβλητή, μπορεί να είναι είτε πεπερασμένος αριθμός, είτε άπειρο, είτε μείον άπειρο.

Οι αβεβαιότητες άλλων τύπων μπορούν επίσης να μειωθούν σε αβεβαιότητες των τύπων 0/0 και ∞/∞.

Αποκάλυψη αβεβαιοτήτων των τύπων "μηδέν διαιρούμενο με μηδέν" και "άπειρο διαιρούμενο με άπειρο"

Παράδειγμα 1Υπολογίζω

ΧΤο =2 οδηγεί σε απροσδιοριστία της μορφής 0/0. Επομένως, εφαρμόζουμε τον κανόνα του L'Hopital:

Παράδειγμα 2Υπολογίζω

Λύση. Αντικατάσταση σε μια δεδομένη συνάρτηση τιμής Χ

Παράδειγμα 3Υπολογίζω

Λύση. Αντικατάσταση σε μια δεδομένη συνάρτηση τιμής ΧΤο =0 οδηγεί σε απροσδιοριστία της μορφής 0/0. Επομένως, εφαρμόζουμε τον κανόνα του L'Hopital:

Παράδειγμα 4Υπολογίζω

Λύση. Η αντικατάσταση της τιμής του x ίση με συν άπειρο σε μια δεδομένη συνάρτηση οδηγεί σε απροσδιοριστία της μορφής ∞/∞. Επομένως, εφαρμόζουμε τον κανόνα του L'Hopital:

Σχόλιο. Εάν το όριο του λόγου των παραγώγων είναι μια αβεβαιότητα της μορφής 0/0 ή ∞/∞, τότε ο κανόνας L'Hopital μπορεί να εφαρμοστεί ξανά, δηλ. πηγαίνετε στο όριο του λόγου των δεύτερων παραγώγων κ.λπ.

Παράδειγμα 5Υπολογίζω

Λύση. Βρίσκουμε

Εδώ ο κανόνας του L'Hospital εφαρμόζεται δύο φορές, αφού τόσο το όριο του λόγου των συναρτήσεων όσο και το όριο του λόγου των παραγώγων δίνουν μια αβεβαιότητα της μορφής ∞/∞.

Παράδειγμα 6Υπολογίζω

Έχουμε ήδη αρχίσει να ασχολούμαστε με τα όρια και τη λύση τους. Ας συνεχίσουμε στο hot pursuit και ας ασχοληθούμε με τη λύση των ορίων σύμφωνα με τον κανόνα του L'Hopital. Αυτός ο απλός κανόνας μπορεί να σας βοηθήσει να ξεφύγετε από τις ύπουλες και δύσκολες παγίδες που λατρεύουν να χρησιμοποιούν οι δάσκαλοι σε παραδείγματα σε τεστ ανώτερων μαθηματικών και μαθηματικής ανάλυσης. Η λύση με τον κανόνα του L'Hopital είναι απλή και γρήγορη. Το κύριο πράγμα είναι να μπορείς να διαφοροποιήσεις.

Κανόνας του L'Hopital: Ιστορία και ορισμός

Στην πραγματικότητα, αυτός δεν είναι ακριβώς ο κανόνας της L'Hopital, αλλά ο κανόνας L' Hospital-Bernoulli. Διατυπώθηκε από έναν Ελβετό μαθηματικό Γιόχαν Μπερνούλι, και οι Γάλλοι Guillaume Lopitalπρωτοδημοσιεύτηκε στο σχολικό του βιβλίο απειροελάχιστα στο ένδοξο 1696 έτος. Μπορείτε να φανταστείτε πώς έπρεπε οι άνθρωποι να λύσουν τα όρια με την αποκάλυψη αβεβαιοτήτων πριν συμβεί αυτό; Δεν είμαστε.

Πριν προχωρήσετε στην ανάλυση του κανόνα L'Hopital, σας συνιστούμε να διαβάσετε το εισαγωγικό άρθρο σχετικά με τις μεθόδους και τις μεθόδους επίλυσής τους. Συχνά στις εργασίες υπάρχει μια διατύπωση: βρείτε το όριο χωρίς να χρησιμοποιήσετε τον κανόνα L'Hopital. Μπορείτε επίσης να διαβάσετε για τις τεχνικές που θα σας βοηθήσουν σε αυτό στο άρθρο μας.

Εάν έχετε να κάνετε με τα όρια ενός κλάσματος δύο συναρτήσεων, να είστε προετοιμασμένοι: σύντομα θα συναντήσετε μια αβεβαιότητα της μορφής 0/0 ή άπειρο/άπειρο. Τι σημαίνει? Στον αριθμητή και στον παρονομαστή, οι εκφράσεις τείνουν στο μηδέν ή στο άπειρο. Τι να κάνουμε με ένα τέτοιο όριο, με την πρώτη ματιά, είναι εντελώς ακατανόητο. Ωστόσο, αν εφαρμόσεις τον κανόνα της L'Hopital και σκεφτείς λίγο, όλα μπαίνουν στη θέση τους.

Ας διατυπώσουμε όμως τον κανόνα L'Hospital-Bernoulli. Για να είμαστε απόλυτα ακριβείς, εκφράζεται με ένα θεώρημα. Κανόνας του L'Hopital, ορισμός:

Αν δύο συναρτήσεις είναι διαφοροποιήσιμες σε μια γειτονιά ενός σημείου x=a εξαφανίζονται σε αυτό το σημείο, και υπάρχει ένα όριο στην αναλογία των παραγώγων αυτών των συναρτήσεων, τότε για Χ φιλοδοξώντας να ένα υπάρχει ένα όριο στον λόγο των ίδιων των συναρτήσεων, το οποίο είναι ίσο με το όριο του λόγου των παραγώγων.

Ας γράψουμε τον τύπο και όλα θα γίνουν αμέσως πιο εύκολα. Κανόνας του L'Hopital, τύπος:

Εφόσον μας ενδιαφέρει η πρακτική πλευρά του ζητήματος, δεν θα παρουσιάσουμε εδώ την απόδειξη αυτού του θεωρήματος. Είτε θα πρέπει να δεχτείτε τη λέξη μας, είτε να το βρείτε σε οποιοδήποτε εγχειρίδιο λογισμού και να βεβαιωθείτε ότι το θεώρημα είναι σωστό.

Παρεμπιπτόντως! Για τους αναγνώστες μας υπάρχει τώρα έκπτωση 10%.

Αποκάλυψη αβεβαιοτήτων σύμφωνα με τον κανόνα της L'Hopital

Ποιες αβεβαιότητες μπορεί να βοηθήσει να αποκαλυφθούν ο κανόνας του L'Hospital; Νωρίτερα μιλήσαμε κυρίως για αβεβαιότητα 0/0 . Ωστόσο, αυτό απέχει πολύ από τη μόνη αβεβαιότητα που μπορεί να συναντήσει κανείς. Ακολουθούν άλλοι τύποι αβεβαιοτήτων:

Ας εξετάσουμε τους μετασχηματισμούς που μπορούν να χρησιμοποιηθούν για να φέρουν αυτές τις αβεβαιότητες στη μορφή 0/0 ή άπειρο/άπειρο. Μετά τον μετασχηματισμό, θα μπορείτε να εφαρμόσετε τον κανόνα L'Hospital-Bernoulli και να κάνετε κλικ σε παραδείγματα όπως καρύδια.

Αβεβαιότητα ειδών άπειρο/άπειρο ανάγεται σε απροσδιοριστία της μορφής 0/0 απλός μετασχηματισμός:

Ας υπάρχει ένα γινόμενο δύο συναρτήσεων, εκ των οποίων η μία τείνει στο μηδέν και η δεύτερη στο άπειρο. Εφαρμόζουμε τον μετασχηματισμό και το γινόμενο μηδέν και απείρου μετατρέπεται σε απροσδιοριστία 0/0 :

Για να βρείτε όρια με αβεβαιότητες τύπου άπειρο μείον άπειρο χρησιμοποιούμε τον ακόλουθο μετασχηματισμό που οδηγεί σε αβεβαιότητα 0/0 :

Για να χρησιμοποιήσετε τον κανόνα του L'Hopital, πρέπει να είστε σε θέση να λαμβάνετε παράγωγα. Ακολουθεί ένας πίνακας παραγώγων στοιχειωδών συναρτήσεων που μπορείτε να χρησιμοποιήσετε κατά την επίλυση παραδειγμάτων, καθώς και κανόνες για τον υπολογισμό των παραγώγων μιγαδικών συναρτήσεων:

Τώρα ας περάσουμε στα παραδείγματα.

Παράδειγμα 1

Βρείτε το όριο σύμφωνα με τον κανόνα του L'Hospital:

Παράδειγμα 2

Υπολογίστε χρησιμοποιώντας τον κανόνα του L'Hopital:

Σημαντικό σημείο! Αν το όριο της δεύτερης και των επόμενων παραγώγων συναρτήσεων υπάρχει για Χ φιλοδοξώντας να ένα , τότε ο κανόνας του L'Hopital μπορεί να εφαρμοστεί πολλές φορές.

Ας βρούμε το όριο ( n - φυσικός αριθμός). Για να το κάνετε αυτό, εφαρμόστε τον κανόνα του L'Hospital n μια φορά:

Σας ευχόμαστε καλή επιτυχία στην κατάκτηση της μαθηματικής ανάλυσης. Και αν χρειάζεται να βρείτε το όριο χρησιμοποιώντας τον κανόνα L'Hospital, να γράψετε ένα δοκίμιο για τον κανόνα L'Hospital, να υπολογίσετε τις ρίζες μιας διαφορικής εξίσωσης ή ακόμα και να υπολογίσετε τον τανυστή αδράνειας ενός σώματος, επικοινωνήστε με τους συγγραφείς μας. Θα χαρούν να σας βοηθήσουν να καταλάβετε τις περιπλοκές της λύσης.
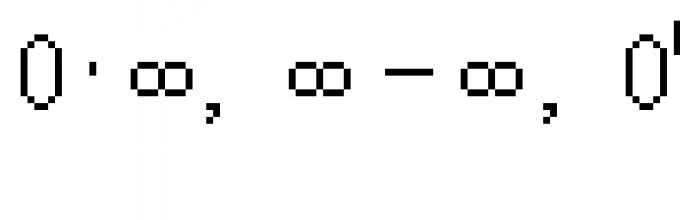